Abstract
This paper presents a review plus new data that describes the role hierarchical nanostructural properties play in developing an understanding of the effect of scale on the material properties (chemical, elastic and electrical) of calcified tissues as well as the interfaces that form between such tissues and biomaterials. Both nanostructural and microstructural properties will be considered starting with the size and shape of the apatitic mineralites in both young and mature bovine bone. Microstructural properties for human dentin and cortical and trabecular bone will be considered. These separate sets of data will be combined mathematically to advance the effects of scale on the modeling of these tissues and the tissue/biomaterial interfaces as hierarchical material/structural composites. Interfacial structure and properties to be considered in greatest detail will be that of the dentin/adhesive (d/a) interface, which presents a clear example of examining all three material properties, (chemical, elastic and electrical). In this case, finite element modeling (FEA) was based on the actual measured values of the structure and elastic properties of the materials comprising the d/a interface; this combination provides insight into factors and mechanisms that contribute to premature failure of dental composite fillings. At present, there are more elastic property data obtained by microstructural measurements, especially high frequency ultrasonic wave propagation (UWP) and scanning acoustic microscopy (SAM) techniques. However, atomic force microscopy (AFM) and nanoindentation (NI) of cortical and trabecular bone and the dentin–enamel junction (DEJ) among others have become available allowing correlation of the nanostructural level measurements with those made on the microstructural level.
Keywords: Nanostructure, Microstructure, Bone, Dentin, Hierarchies, Interfaces
1. Introduction
Skeletal tissues and their interactions with materials provide a research microcosm for nanostructured materials. Clearly, both bone, Fig. 1, and teeth, Fig. 2, are hierarchical structures whose material properties change with changes in scale. Both tissues are organized as hierarchical composites. Thus, they must be studied at each scale level, i.e., at the nano-, micro- and macro-structural levels in order to understand their intrinsic behavior as well as to determine the appropriate design considerations for composite material replacements that are generated using either synthetic processing or tissue engineering.
Fig. 1.
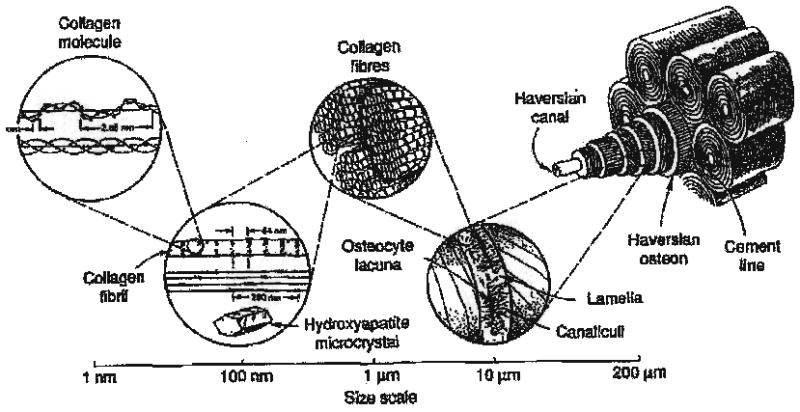
Hierarchical structure of human bone (R. Lakes, Viscoelastio Solids, 1998, with permission of CRC Press, Boca Raton, FL [160]).
Fig. 2.
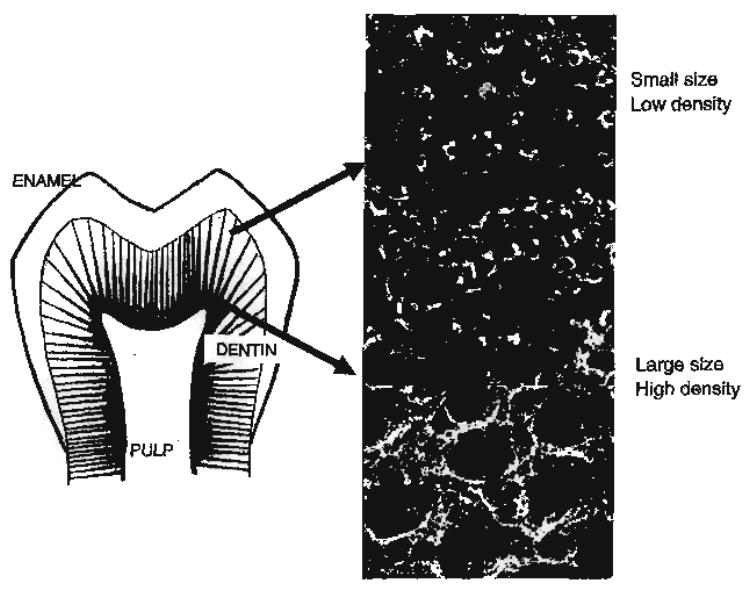
Hierarchical structure of human tooth, inserts representing tubule characteristics as a function of position in reference to dentin-enamel junction (DEJ). In close proximity to the DEJ, low density distribution of tubules and small size. Tubules of large size and high density are noted in close proximity to the pulp and high-resolution image of intertubular dentin from this region treated with EDTA to reveal collagen network.
Scale considerations play a significant role in understanding and modeling the behavior of these calcified tissues. On the nanoscale, they are essentially material composites based on the interdigitation of the collagen, the most prevalent biopolymer in the body, and an apatitic mineralite component, the inorganic substance [1–5]. These tissues then organize into microstructural composites to support loads, one of their primary functions [3–5]. The macroscopic anisotropic properties of femoral cortical bone prescribes what both the haversian microstructure and the appropriate nanostructural organization of collagen and apatite [2–5] should be in order to provide for the appropriate macroscopic function and behavior. The molecular structures of the collagen and apatite (nanostructural level) must organize firstly. Subsequently, these combine to form the haversian system microscopic morphology into the appropriate fiber-like composite material behavior [3–5] necessary to provide the bone and dentin microstructures with the required appropriate strength and stiffness [2–5].
We describe the various experimental and computational techniques that have been incorporated to investigate these hierarchical structure/property relationships, followed by details of the structure/property measurements, their analyses and the mathematical modeling based on the acquired experimental data. This leads to a better understanding of the structure, property and function (SPF) of the tissue at each scale level
2. Experimental/computational techniques
2.1. Atomic force microscopy (AFM) and nanoindentation
High-resolution scanning techniques for determining the physical properties of materials at the micro- to nanolevels are available. These techniques include scanning tunneling microscopy, atomic force microscopy (AFM), scanning near-field optical microscopy and various microwave near-field microscopy methods. Rapid improvements in the range of capabilities of AFM now provide the opportunity to study the nanomechanics of materials as well as the morphology/topology. AFM and associated nanoindentation provides the means to study structure and/or morphology as well as properties on both natural tissues and synthetic materials at resolutions down to the order of a nanometer.
Nanoindentation provides load–displacement measurements at the nanostructural level and thus is an important addition to mechanical experimental methods. NI can be used to calculate elastic modulus, hardness and even time dependent deformation properties such as creep and strain rate dependence [6–9]. An introduction and extensive description of the used of the NI technique may be found in Ref. [8] and related papers [6,7,9]. The following is a short introductory description of how such an NI instrument would be used. A high precision x–y–z table, used for mounting the specimen, is positioned under computer control, with a microscope providing an initial view of the indenter location. Loads of the order of 75 nm and displacements of 0.04 nm resolution can be applied while the sample position is monitored; x–y spatial resolution of the order of hundreds of nanometers is maintained [8]. The procedural steps are as follows: firstly, the optical microscope locates the area of interest; then a defined force load or deformation limit is set; indentation is applied and held until equilibration is achieved; next, there is the unloading cycle at the same rate to ~90% of maximum that is held for a longer time so that thermal drift can be taken into consideration; and finally, it is fully unloaded. The indenter shape is typically a three-sided pyramid. In the case of viscoelastic materials, such as found in skeletal tissues, a multiple-loading cycle is used to obtain the load-displacement data. Only the data from the upper half of the final unloading run are used to determine properties such as the specimen’s hardness and elastic modulus at the indentation point. Calibration is necessary for such materials so an isotropic elastic material such as fused silica is used to calibrate the indenter shape function [8].
2.2. Scanning acoustic microscopy (SAM)
SAM is based on the use of focused acoustic waves to study the intrinsic material properties of a material. What is essentially measured is the acoustic impedance of the material being studied. Acoustic impedance (AI), Z, is defined as the product of the local density, ρ, at the point on the material and the longitudinal acoustic velocity, v, i.e., Z = ρ × v. It is measured in Rayls, e.g., water at 0 °C has a value Z = 1.40 Mrayl, while at body temperature, 37 °C, Z = 1.51 Mrayl, due to the variation in water’s acoustic properties with temperature.
SAM operation is as follows (Fig. 3). A radio frequency (RF) signal is used to excite a piezoelectric transducer mounted on the end of a synthetic sapphire single crystal buffer rod with a hemispherical-shaped cut at the other end. The RF signal is converted by the piezoelectric transducer into an acoustic wave converged by the lens and focused onto the sample through a coupling liquid. At the liquid/specimen interface, a portion of the acoustic signal is reflected back to the lens, to the piezoelectric transducer so that the acoustic signal is transformed back into a voltage, V, proportional to the acoustic signal. It is the reflection coefficient, r, measured in Mrayl, where r =(Z2−Z1)/(Z2+Z1) that determines the voltage and thus the gray level; r is thus a dimensionless number, less than 1. An acoustic image of the desired area is obtained by rastering the lens over the sample surface pixel by pixel. The depth of penetration of the SAM wave into the surface of the specimen depends upon the wavelength of the sound being used. Both bone and dentin the materials of concern herein have AIs in a range of Z=~7.5 Mrayl, thus resulting in a reflection coefficient r = 0.67 in water at 37 °C. The shade of gray at each pixel on the monitor screen is a reflection of the r value at that pixel, so that a dark gray level corresponds to a lower value of AI at the point being measured, while a bright gray level corresponds to a higher AI value.
Fig. 3.
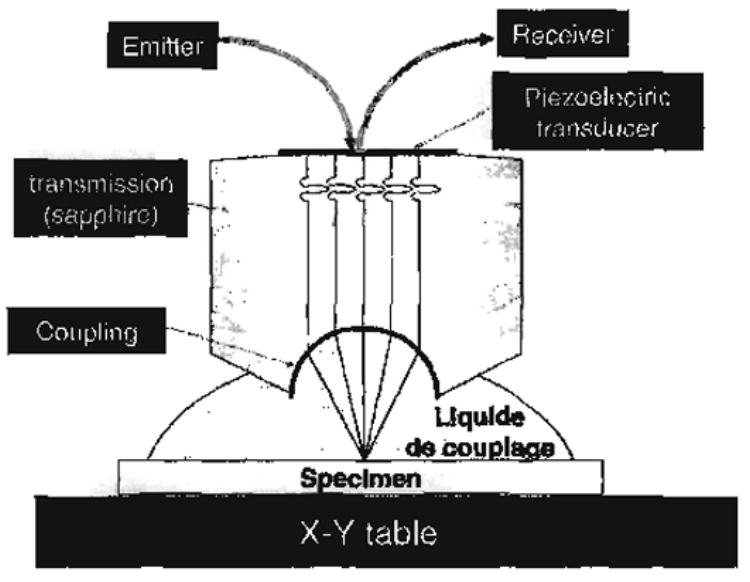
Diagram of the lens and specimen configuration for scanning acoustic microscopy (SAM).
While the SAM provides a high-resolution acoustic image of the sample, it does not provide quantitative values directly of the acoustic property it is measuring, i.e., the reflection coefficient r and thus of the AI value Z. One way to obtain quantitative values of Z and thus eventually of Young’s modulus, E, is to use a calibration method. Acoustic velocities and densities are measured for a set of known materials, e.g., polyethylene, PMMA, Durango apatite, aluminum, titanium and stainless steel. Young’s modulus, E, is then calculated either as E = ρv2 or as E = 9KG/(3K+ G) based on measurements of the densities and both the shear and dilatational longitudinal wave speeds for a similar set of known materials. These same materials are also imaged on the SAM in order to obtain their r values. The voltages corresponding to these r values are plotted on a graph of r vs. V. This leads eventually to a Z vs. E graph for the known sample materials. Young’s moduli for the materials under study are obtained by an interpolation sequence using the Z vs. E graphs of the known materials. A dark gray level in the acoustic image represents a lower value of AI (and thus of Young’s modulus, E) at the point being measured; correspondingly, a bright gray level in the image represents a higher AI value (and thus a higher value of E).
Samples analyzed using SAM must be maintained in a fluid environment, i,e., the fluid couples the acoustic wave between the lens and the material being studied. This requirement makes this technique particularly well suited for studying biologic specimens, such as bone, collagen and cartilage. These tissues can be severely damaged or altered by the desiccating procedures that are frequently used with macromechanical testing. SAM may be used to obtain the micromechanical elastic properties of both fresh and embedded specimens.
2.3. Micro-Raman spectroscopy
Raman spectroscopy permits structural analysis of samples by identifying specific light-induced molecular vibrations. Characteristic functional groups give rise to vibrational bands near the same frequency irrespective of the molecule in which they are found. Different molecules have different vibrational states and can therefore be distinguished with this technique. Information about the composition, secondary structure and interaction of molecules, including the chemical micro-environment of molecular subgroups, can be determined through careful analysis of the positions, intensities and widths of the bands in the Raman spectra of biological tissues such as collagen. Unlike infrared spectroscopy, water does not present a strong Raman signal within the biological “fingerprint” region. Thus, specific functional groups of molecules can be identified in wet biological specimens with minor spectral interference from water.
By combining spectroscopy with microscopy, Raman microspectroscopy can be used to detect and quantify the molecular chemistry of microscopic samples; molecular information can be obtained at a spatial resolution comparable to optical microscopy. In this technique, the spatial resolution is defined by the laser profile used to excite a particular part of the specimen. Functional groups are identified by their specific wavenumber position in the Raman spectrum, and the relative amounts of these groups are determined by the magnitude of intensity at each wavenumber. Samples can be analyzed directly, in air or water, at room temperature and pressure, wet or dry, without destroying the sample. The capability of performing spatially resolved chemical analyses of microscopic regions of samples in situ has been applied to both material science and the biological sciences. Raman microspectroscopy is an exceptional tool for investigating the chemistry of material/tissue interfaces, because it does not rely on homogenization, extraction or dilution, but rather each structure is analyzed in situ.
2.4. FTIR chemical imaging
When a molecule is exposed to an incident beam of light, energy can be absorbed by the molecule. The energy absorption can enable a transition among electronic, vibrational or rotational energy levels. Thus, the basis for an infrared spectrum is the absorption of infrared light and the interaction of that absorption with the vibrational modes of a molecule. Infrared absorptions require that the molecular vibrations produce a change in the permanent dipole moment of the molecule. Raman spectroscopy similarly involves transitions among the vibrational energy levels of a molecule, but the energy exchange occurs in a completely different manner. Raman spectra result from vibrational motions that cause a change in a source-induced molecular dipole moment
FTIR spectroscopic images are formed on the basis of the inherent contrast offered by the unique chemical bonds of the various components that make up the sample. Unique frequencies in the FTIR spectrum may be plotted as a function of spatial position and spectral intensity to provide a chemical image of each component. As an example, FTIR microspectroscopy can be used to determine the relative composition, degree of cure and homogeneity across the length and breadth of a material/tissue interface. FTIR images can be acquired in minutes, but the spatial resolution is generally limited to about 10 μm.
2.5. Scanning evanescent microwave probe (SEMP)
The scanning evanescent microwave probe (SEMP) is a form of local probes that use evanescent electromagnetic fields to non-destructively study electromagnetic properties of materials at 1–20 GHz. These probes are used to perform microwave microscopy and imaging with spatial resolution approximating atomic force microscopy. Such an unprecedented high spatial resolution with electromagnetic fields having relatively large wavelengths (λfree space ≈ 1.5–30 cm) has been made possible by small spatial decay constants of evanescent fields generated at the terminal end of a microwave resonator near a wire tip. Upon interaction with a sample placed near this tip, the reflection coefficient of the resonator shifts to lower frequencies enabling the characterization of the microwave properties of the sample which are affected by various factors including density, moisture, polymerization, carrier mobility and concentration, impurities, oxidation state and temperature. The SEMP non-intrusive technique is capable of imaging non-uniformities in organic and inorganic conductors, semiconductors and insulators. Thus, by using the SEMP, a variety of organic and inorganic materials including metals, semiconductors, insulators, composites, ferromagnetic materials, tooth enamel, bone, dentin, adhesives, composites, botanical and agricultural samples have been imaged. The principles of operation of the SEMP, parameters affecting its spatial and permittivity/permeability/conductivity resolutions, and examples of its applications are introduced in this chapter.
Evanescent fields were first used by Bethe in calculating the coupling coefficient of microwave waveguides connected to each other through a hole much smaller than the microwave wavelength [10]. Baez is credited as the first individual to image objects using sonic evanescent waves [11] followed by Soohoo who performed similar experiments using microwaves [12]. Ash is credited with generating evanescent microwave fields in a very elaborate test rig to demonstrate that these fields can be used to resolve metallic features on the order of λ/100 [13]. Others have studied evanescent fields in the context of imaging as well [14,15]. Several research groups, including our own, have used microwave resonators in the characterization of semiconductors with λ/100 [16–23]. The evanescent microwave probe (EMP) used in our work is a planar structure [19] that readily lends itself to implementation on a silicon cantilever beam. We started working on evanescent microwave probes for imaging applications in the late 1980s, and our initial resolution using a microstripline resonator was around 80 μm at 1 GHz [19]. The EMPs applications in a variety of areas were also explored by us [24–41]. Recently, we achieved nearly atomic resolution by coupling the microwave probe to the atomic force microscope (AFM) and scanning tunneling microscope (STM) [26,36]. We have shown that a variety of materials ranging from conductors to insulators can be imaged using the EMP [19,24–41].
Our work in microwave super-resolution imaging of biological and botanical specimens, e.g., woods and fruits, has shown that interesting microwave resistivity maps can be obtained and used to study aging and other processes in these materials. For example, EMP can be used to monitor electrical activities in bone samples [24,25,34]. Resorption and remodeling of bone have been attributed to osteocytic cells sensing changes in streaming potentials generated during deformation of the tissue. Thus, measurements of the electromagnetic properties of such tissues could prove crucial in the development of models to explain bone remodeling. EMP is sensitive to moisture and ionic mineral content such as variations in tooth enamel. EMP is capable of detecting the onset of caries—believed to be accompanied by minute surface blemishes with increased moisture and varying degrees of mineralization. Having a microwave power of less than nano-Watts, this unique probe promises to significantly reduce the time-to-detection of cavity formation, enabling timely prevention [24].
The EMP has the following important characteristics: (i) The EMP uses coherent microwave sources that are readily and inexpensively available over a wide range of frequencies covering 100 MHz up to 100 GHz. (ii) The EMP does not require conducting or optically transmitting/reflecting samples. (iii) The spatial resolution of the EMP can be varied over a wide range, even at a fixed frequency, by using different probe configurations. (iv) The EMP can image sub-surface defects and non-uniformities within the microwave skin depth inside the sample. (v) The EMP does not require any coupling medium and it can be used in air, vacuum or in a suitable liquid. (vi) Operating at very high frequencies and using the homodyne detection technique, the EMP can achieve very high scan rates (up to a few centimeters per second) over hot and cold samples. (vii) Many different parallel EMPs can be used simultaneously to scan over large areas.
2.6. Finite element modeling
A numerical simulation method can very often benefit the imaging technique by acting as a tool for data interpretation and for iterative refinement of the imaging procedure. The finite element (FE) method is an established numerical simulation technique that may be used to compute the distributions of field quantities within the domain that is to be imaged. Since no single imaging modality provides a complete picture of the physico-chemico-mechanical properties, in the FE computations, properties measured with diverse imaging techniques of different modalities and spatial resolution are utilized. The computation results are expected to provide insight to the likely response of the different phases composing the domain to the applied field. These results may then be utilized to verify the data interpretation of a particular imaging modality and to refine the imaging procedure. For instance, the FE method may be used to obtain distributions of stress and strain fields in a given region that is to be imaged by directly utilizing the measured data from the high-resolution analytical techniques such as SAM and micro-Raman spectroscopy [42]. The resulting stress distributions provide insight to likely failure location and mechanisms, and may indicate the need to further refine the mechanical property and chemical measurements in regions of stress concentrations and its proximity.
As a computational technique, the FE method provides certain advantages: (1) it is a completely non-destructive technique; (2) several models may be executed on computers at the same time; (3) parameters that cannot be easily modified in the laboratory setting may be easily varied in the FE model; and (4) the model may be exercised for a variety of conditions. The disadvantage of the FE method stems from the less-than-perfect empirical information available to make the models realistic. However, by combining the imaging technique and the FE method, successive refinement of both the imaging procedure and the FE model may be achieved resulting in superior imaging data interpretation and accurate prediction of the system behavior under applied stimulus.
2.7. Ultrasonic wave propagation (UWP)
UPW, at lower frequencies than those used with SAM, also has been used to obtain elastic properties of calcified tissues. Both shear (transverse) and longitudinal sound waves are used with this technique. For longitudinal wave propagation, the relationship between the acoustic wavelength, λ, and sample cross-section dimension, d, affects the calculation of Young’s modulus when determining the elastic properties of the material being measured: For λ>d, an extensional longitudinal wave, VL, is generated in the material (also known as a BAR wave) yielding the Young’s modulus, E, for an isotropic material as, , where ρ is the material density. This UWP experiment for elastic materials corresponds to an uniaxial mechanical testing experiment in obtaining the same value of E; for viscoelastic materials, the value of E will be different because of dispersion. For λ<d, a dilatational longitudinal wave is generated in the material (denoted in this paper as a BULK wave). Both the shear (transverse), Vt, and dilatational, V1, velocities must be measured in isotropic materials in order to calculate values of both the shear modulus, , and the bulk modulus, , as Young’s modulus for a BAR wave, E = 9KG/(3K+G). For elastic materials, this UWP experiment corresponds to the mechanical testing experiment where the load is applied along one axis while the transverse sides are constrained; again, as described above, the modulus measured will have a different value for a viscoelastic material.
Both the longitudinal (dilatational) and transverse ultrasound measurements should be made in a number of structural directions corresponding to the observed symmetry in an anisotropic material [3]. In the case of transverse isotropic symmetry–where there is a unique axis transverse to a plane of symmetry [3]-there are five independent elastic constants (Cij), whereas for orthotropic symmetry–where there are three independent orthogonal axes-nine independent Cij [3] are required. Table 1 contains both the five transverse isotropic Cij for human haversian bone and nine orthotropic Cij for bovine plexiform bone. In both cases, the bone axis direction is denoted by 3; in the plane orthogonal to the 3 direction, the radial direction is denoted by 1 and the transverse direction by 2. Thus, the respective C33 elastic constants are 40.8 GPa for the bovine sample and 30.0 GPa for the human sample. Similarly, the C11 values are 30.8 and 21.1 and the C22 values are 25.7 and 20.1 for the plexiform bovine and human haversian bone samples, respectively. It is the significant difference between the C11 and C22 for the plexiform bovine bone that confirms the assignment of orthotropic symmetry for that type of bone; it reflects its plywood-like structural organization. For human haversian bone, it is the lack of significance between the C11 and C22 stiffness coefficients that supports the assignment of transverse isotropic symmetry; this also holds true for bovine haversian bone as well [43]. Values of the scalar shear and compression anisotropy factors have been adapted for both transverse isotropy [44] and orthotropic symmetry [45].
Table 1.
Average dimensions of young and mature bone mineralites
| Length (nm) | Width (nm) | Thickness (nm) | Description | |
|---|---|---|---|---|
| Mature bovine | 15 | 11 | 0.6 | Thin, plate-like |
| Young postnatal bovine | 9 | 6 | 2 | Thick, plate-like |
3. Overview of structural characteristics of selected calcified tissues
3.1. Bone
The principal components of bone are an organic phase, the biopolymer collagen, and an inorganic phase, apatite mineralites. Many of the physiological functions and mechanical characteristics of bone are dependent on the size of the apatitic mineralites and their 3-D spatial relationships to the collagen molecules in the organic matrix. Results from electron microscopy and low-angle X-ray and neutron diffraction provide clear evidence that the apatitic mineralites of bone are deposited almost exclusively within the collagen fibrils [46–50]. In this case, the structure–function relationships depend on the amount and distribution of the solid mineral phase, which in turn effects the molecular conformation of the collagen molecules and the supramolecular structure of the fibrils.
The apatite mineralites are of very small size; their shape plays a key role both biologically and in providing the biomechanical properties in support of the function attributes of various bones. Atomic force microscopy (AFM) has been used to measure the three-dimensional shape and size of mature bovine bone mineralites as well as young postnatal bovine bone [2,51,52]. In the mature bone, approximately 98% of the mineralites are less than 2 nm thick displaying a plate-like habit (Table 1). The distributions of both thickness and width of the mineralites in mature bovine bone show single peaks. In mature bone, the distribution of lengths of the mineralites may be multimodal with distinct peaks separated by ~6 nm. Using AFM, the mean mineralite size in young postnatal bovine bone is 9 nm × 6 nm × 2 nm, significantly shorter and thicker than the mineralites of mature bovine bone. Thus, the AFM results indicate that the average bovine bone mineralite becomes greater in length and width as the animal matures; these results are consistent with TEM data on isolated mineralites [53].
3.2. Dentin
Dentin is the hydrated composite structure that constitutes the body of each tooth, providing both a protective covering for the pulp and serving as a support for the overlying enamel. Because of its exceptionally high mineral content, enamel is a very brittle tissue. Enamel is so brittle that without the support of the more resilient dentin structure it would fracture when exposed to the forces of mastication. Dentin supports as well as compensates for the brittle nature of the enamel. In contrast to enamel, dentin is a vital tissue containing the cell processes of odontoblasts and neurons. Since the odontoblasts can be stimulated to deposit more dentin, this tissue is capable of limited repair. The structure–property relationships of dentin vary with location, physiological, aging and disease processes.
Dentin is composed of approximately 50% inorganic material, 30% organic material and 20% fluid by volume. Dentin mineral is a carbonate rich, calcium deficient apatite [1,54]. The organic component is predominantly type I collagen with minor contribution from other proteins that can be categorized as phosphoproteins, glycoproteins and γ-carboxyglutamate-containing proteins [55]. The composition of dentinal fluid is reportedly similar to plasma but to date, it has been poorly characterized [54].
Results from small angle X-ray scattering suggest that the mineral crystallites are more plate-like in the dentin nearest the dentin–enamel junction and needle-like in the more recently formed dentin near the pulp [56]. Even though there is a significant change in shape of the crystallite with position, the thickness remains approximately 5 nm irregardless of the position [56]. Previous authors have reported the size of the sound dentin crystal as 3 nm in width, 20 nm in thickness and 20 nm in length (in review by Daculsi et al. [57]); these values differ from those found for the isolated bone mineralites. Because of the recent findings on the shape and size of isolated bone mineralites from both young (post-natal) and mature bovine bone indicating only plate-like structures of smaller size than found in the X-ray diffraction studies [2,51,52], this strongly suggests that similar AFM studies must be done on the intertubular and peritubular dentin mineralites. There may be real differences between cortical bone mineralites and dentin mineralites due to differences in the intertubular and peritubular collagen matrix morphology.
A unique feature of the dentin structure is the tubules that traverse the structure from the pulp cavity to the region just below the dentin–enamel junction (DEJ) or the dentin–cementum junction (CEJ). The tubules, which could be modeled as narrow tunnels a few microns or less in diameter, represent the tracks taken by the odontoblastic cells from the pulp chamber to the respective junctions. Dentinal tubule diameter measures approximately 2.5 μm near the pulp and 0.9 μm near the DEJ [58]. Tubule density and orientation vary from location to location, density is lowest at the DEJ and highest at the predentin surface at the junction to the pulp chamber. For example, in young premolar and molar teeth, their numbers range from 50,000 to 75,000 mm−2 at the pulpal surface to approximately half as many per square millimeter in the proximity of the DEJ [58]. The content of the tubules includes fluid and odontoblast processes for all or part of their course. In contrast to root dentin, the tubules in coronal dentin are surrounded by a collar of highly mineralized peritubular dentin [59].
The composition of the peritubular dentin is carbonate apatite with very small amounts of organic matrix whereas intertubular dentin, i.e., the dentin separating the tubules, is type I collagen matrix reinforced with apatite. Thus, the composition of intertubular dentin is primarily mineralized collagen fibrils; the fibrils are described as a composite of a collagen framework and thin plate-shaped carbonate apatite crystals whose c-axes are aligned with the collagen fibril axis [60]. In healthy dentin, the majority of the mineralized collagen fibrils are perpendicular to the tubules [56].
The difference in composition between the peritubular and intertubular dentin is reflected in the hardness values, i.e., 2.3 and 0.5 GPa, respectively [61]. Using atomic force microscopy (AFM), these hardness values were determined for indentations made parallel with the tubule axis. Based on measurement with AFM, the modulus of elasticity for peritubular and intertubular dentin is 28.6 and 20 GPa, respectively [62].
Using scanning acoustic microscopy (SAM), Katz et al. [63] reported a modulus of elasticity for bulk dentin of 28 GPa. The modulus of elasticity of partially demineralized dentin as determined by scanning acoustic microscopy was 13 GPa and increased linearly to the in situ bulk property [63]. The modulus at the dentin/adhesive interface also reflects the diffusion of the acid through the dentin substrate; thus, there is a gradual decrease from the mineralized dentin to partial demineralization and complete demineralization; this points out the capabilities of measuring the continuum of elastic properties at the material/tissue interface using the functional imaging power provided by SAM. The modulus for demineralized dentin collagen was found to be 1.76 GPa based on extrapolation on the calibration curves described earlier in this chapter [64,65].
3.3. Dentin smear layer
Tooth surfaces that have been prepared with cutting or abrading instruments are characteristically covered with a 0.5–2 μm thick smear layer. The diamond bur-created smear layer shows a substantial loss of any fibrous-like structure; the top of this loosely organized smear layer has been dislodged from the subjacent dentin (Fig. 4B). In comparison, the smear layer formed with the carbide bur appears fibrous (Fig. 4A). The generation of frictional heat and plastic/elastic deformation during cutting and abrading are all factors in the formation of the smear layer. Smear layers formed on dentin cover the normal structural components, i.e., the intertubular dentin and penetrate several micrometers into the tubules to form smear plugs. Using scanning electron microscopy (SEM), Eick [66] directly observed, at high magnification, tooth surfaces after cutting, and claimed that the dentin smear layer could be described as a disturbed film of organic and hydroxyapatite particles, generally less man 2 μm thick. Although it has been generally accepted that the composition of the dentin smear layer is a mixture of partly denatured collagen and mineral [66–68], definitive compositional, structural and chemical reactivity data have been published recently [69,70].
Fig. 4.

(A) Transmission electron micrograph of carbide bur smear layer. (B) Transmission electron micrograph of diamond bur smear layer (Spencer et al. with permission of IADR/AADR, Alexandria, VA [70]).
Acids with a high reactivity rate with the mineral component of dentin have been considered a good reagent for removing the smear layer. These evaluations were based largely on scanning electron micrographs of acid-etched dentin, which portrayed a smooth dentin surface, free of solid deposits and open tubules. With few exceptions, these studies largely disregarded the collagen remnants of the smear or overlooked the inability of acid to act as a solvent for collagen [68,71]. This oversight may be attributed in part to the microscopic nature of the smear layer and lack of resolution of many of the techniques used to study dentin demineralization [68]. The conclusions that acid removes the smear layer are based primarily on morphologic evidence of open dentin tubules, but these observations largely reflect the effect of a–e on smear plugs overlying the tubules. To date, there has limited morphologic and/or chemical investigation of the smear that covers the intertubular dentin.
Micro-Raman spectroscopy is well suited to the chemical characterization of smear-covered intertubular dentin surfaces and the effect of acid etchants on these surfaces. A distinct advantage of the micro-Raman spectroscopic technique described here is the ability to record spectral data from samples that are wet throughout the analysis. Collecting spectral data from the demineralized dentin under wet conditions reduces the potential for collagen collapse as a result of desiccation. Environmental SEM has been used to image wet demineralized dentin specimens, but image resolution was unsatisfactory [72]. Raman spectroscopy is sensitive to the backbone conformation or secondary structure of proteins. Thus, it can provide critical data on triple helix to random coil transitions that may occur in dentin collagen as a result of heat, acid or other degrading reagents. In the Raman spectra of collagen, bands associated with amide I and III are particularly sensitive to conformational changes in the triple helix [73].
Amide I and III regions were broadened and the ratio of the relative intensities is considerably different in the spectra of the acid-treated smear layers as compared to the demineralized dentin (Fig. 5). The most striking difference is seen in the amide III region. There is substantial broadening and loss of intensity of the features associated with amide III in the spectra of both carbide and diamond bur-created smear layers following a 15 s etch with phosphoric acid. Broadening and the accompanying change in the ratio of the relative intensities of the amide I and III suggests that the collagen within the acid-treated smear layers is disorganized and denatured [161]. The relative intensity of the P–O group in the spectra of the acid-treated smear layers suggests that the mineral is not accessible to the acid. These results further suggest that, upon acid exposure, the disorganized collagen within the smear layer forms a gelatinous matrix around the mineral; the mineral is trapped within this denatured gel and thus shielded from the acid. The spectral results suggest that as a result of the heat and potentially, mechanical stress produced during preparation of the dentin the collagen within the smear layer is disorganized. This disorganized collagen is denatured by 15 s exposure to the 35% phosphoric acid gel used in this study.
Fig. 5.
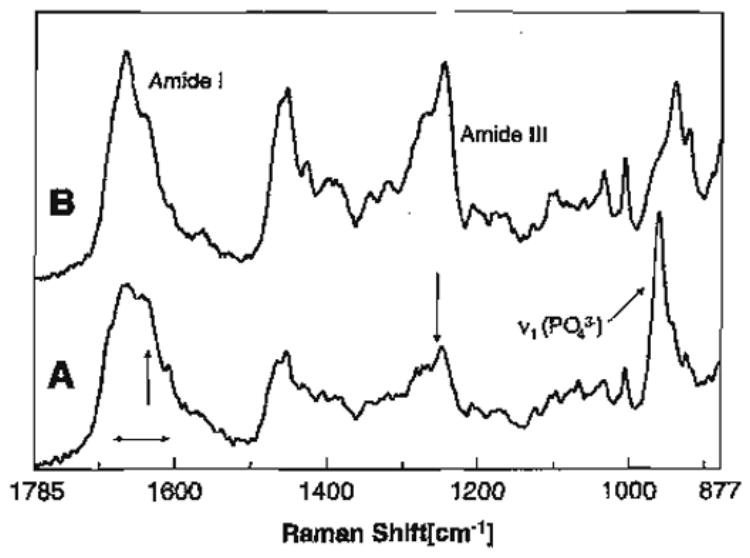
Raman spectrum of acid-etched carbide bur-created smear layer (A); Raman spectrum of completely demineralized dentin (B).
There are interesting differences in the spectra of the acid-treated carbide and diamond bur smear layers (Fig. 6A,B). The spectral feature associated with mineral trapped in a gelatinous matrix, i.e., the P–O group at 960 cm−1, is evident to a depth of ~4 μm in the a–e diamond bur-created smear layer (Fig. 6B). The relative concentration of phosphate in the gelatinous matrix is about 10–20% of the concentration of phosphate in mineralized dentin (Fig. 7). In comparison, the phosphate group associated with mineral trapped in the gelatinous matrix is only apparent in the first spectrum of the a–e carbide bur-created smear layer. In the spectral map of the a–e diamond bur-created smear layer, the features associated with the amide III show a substantial loss of intensity and the C–C stretch associated with the organic component is not apparent until several microns. These results suggest that the diamond bur smear layer is thicker and more condensed than the smear layer created with the carbide bur. Using high-resolution TEM with phosphotungstic acid staining, the smear layers created by 600 grit SiC reported to create smear layers similar to medium to coarse diamond burs [74] were shown to be 3.3 to 4.6 μm thick.
Fig. 6.
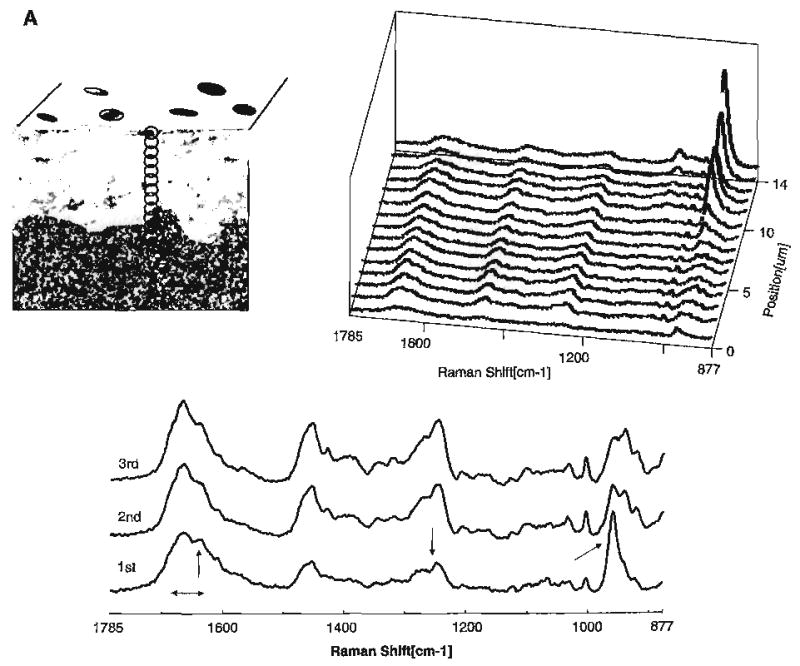
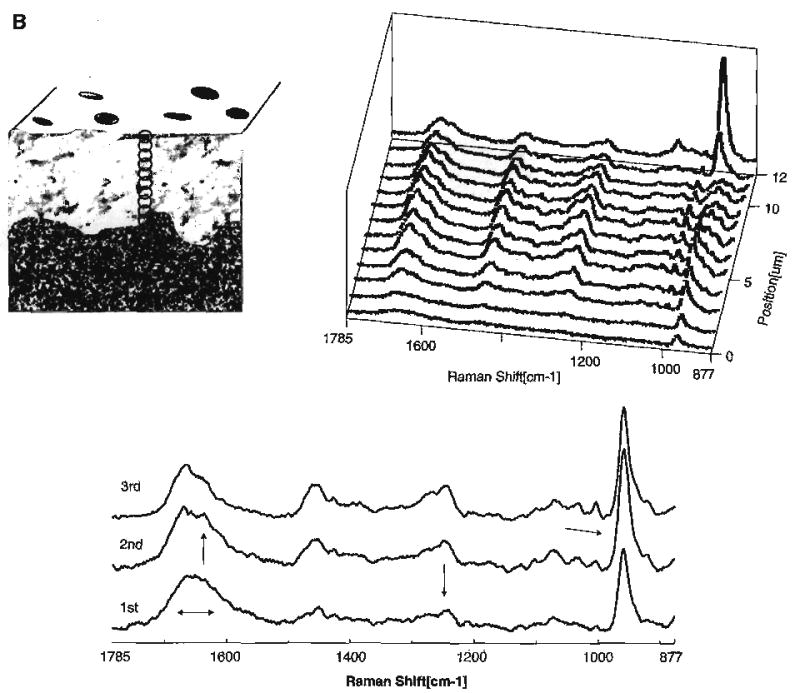
(A) Raman map of dentin specimen fractured to provide cross-sectional view of the acid etched carbide bur-created smear layer/demineralized dentin/undisturbed dentin. Spectra acquired at 1-μm intervals beginning at the acid etched carbide bur-created smear layer, extending into the demineralized dentin and, finally, into the undisturbed dentin. (B) Raman map of the molecular structure of the acid etched diamond bur-created smear layer and subjacent demineralized/undisturbed dentin. Spectra acquired at 1-μm intervals beginning at the acid etched diamond bur-created smear layer and continuing into the undisturbed dentin (Spencer et al. [70] with permission of IADR/AADR).
Fig. 7.
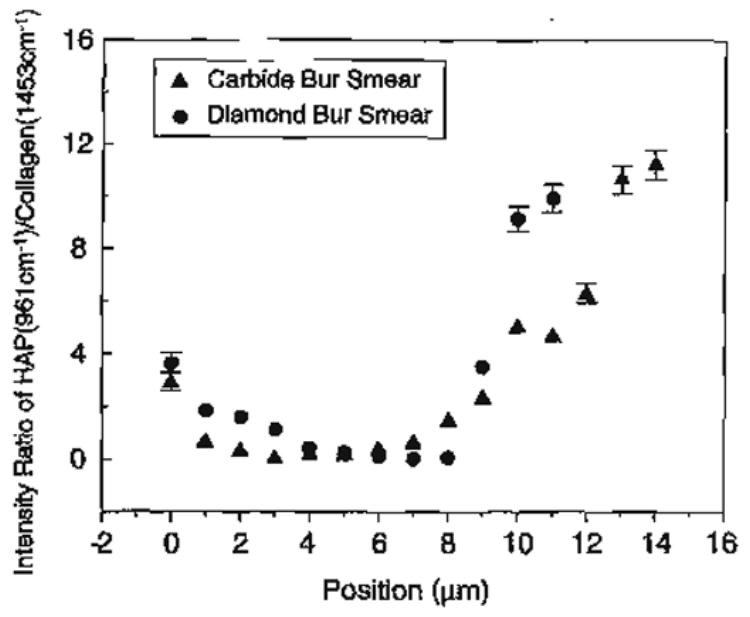
Effect of smear layer type on degree of demineralization produced by 35% H3PO4 etching for 15 s.
The higher mineral content within the a–e diamond bur-created smear layer as compared to the a–e carbide bur smear layer reflects the thicker and more condensed layer created with the diamond (Fig. 6). These characteristics, i.e., a thicker and more compacted smear layer created with the diamond bur, are also reflected in the transition from complete to partial demineralization. This transition is abrupt in the a–e diamond bur smear layer as compared to the smear formed with the carbide bur. The gradual gradient of dentin demineralization recorded with the a–e carbide bur-created smear layer as opposed to the sharp change noted with the diamond bur smear layer suggests that it is easier for the acid to diffuse through the smear layer formed with the carbide.
The TEM images correspondingly reflect a compressed smear layer in the specimens prepared with the diamond bur. The collagen in the diamond bur-created smear layer appears severely disrupted and disorganized. In comparison, the carbide bur-created smear layer does not have the appearance of severely disturbed collagen (Fig. 4).
The work presented in this study is the first molecular structural analysis of a–e smear layers [69, 70]. It is also the first study to quantitate dentin demineralization under conditions that permit hydration of the specimen throughout the analysis [69]. Hydration is critical to these efforts since it is widely accepted that the collagen within the demineralized dentin will collapse if it is allowed to dry [54]; such collapse would lead to inaccurate characterization of the extent or degree of dentin demineralization. The spectral results indicate that collagen within the smear layer is disorganized but not denatured. This disorganized collagen is denatured by the 15 s acid treatment used in this study. The results provide clear evidence that the collagen of the smear layer is not removed by acid-etching and residual mineral is trapped in the denatured, gelatinized collagen. Ultimately, this gelatinous layer could inhibit the formation of an impervious seal at the dentin/adhesive interface; it could act as a weak link in the coupling of adhesive to dentin.
3.4. Dentin–enamel junction
The dentin–enamel junction (DEJ), the natural connector between the hard, brittle enamel and subjacent softer, tougher dentin, plays a critical role in maintaining the biomechanical integrity of the tooth. In a healthy mouth, the DEJ serves as a natural barrier to cyclic fatigue crack growth. The DEJ structure is generally described as a series of 25–100 μm diameter scallops with their convexities directed toward the dentin [75,76]. There appear to be microscallops housed within each scallop and a finer nanolevel structure within each microscallop [77]. The DEJ is also characterized by parallel 80–120 nm diameter collagen fibrils that directly insert into the enamel mineral and also merge with the interwoven fibrillar network of the dentin collagen matrix [77]. This scalloped structure with the associated collagen fibrils crossing between enamel and dentin may lead to enhanced mechanical bonding between the two calcified tissues.
Besides the unique structure, the DEJ is also characterized by a region of distinct or functionally graded properties between the enamel and the dentin [78,79]. Thus, the DEJ is considered an interphase rather than an interface; an interface refers to the presence of a sharp two-dimensional boundary between two phases, i.e., polymer and glass [80]. The mechanical property gradient has been reported as a smooth gradient across the DEJ, with hardness and elastic modulus values highest in the enamel, intermediate across the DEJ and lowest in the bulk dentin [81,82]. In contrast, other investigators have reported that hardness and the associated elastic modulus are lowest at the DEJ [79,83,84]. The DEJ configuration is known to be an effective obstacle for enamel-initiated crack propagation [85–87]. Even with high stress concentrations at the DEJ, failure at this natural junction between the dentin and enamel is not typical. SAM and SEMP have also been used to obtain qualitative images of the DEJ (Katz and Tabib-Azar, private communication).
4. Property measurement of selected calcified tissues
4.1. Mechanical analysis with ultrasonic wave propagation techniques
One of the early mechanical testing studies of human dentin [88] is still used as a reference base for comparison with modem studies [89]. In order to take advantage of the ability to work with the small specimens available for both dentin and enamel, other researchers began to utilize bulk acoustic (also called ultrasonic) wave propagation techniques to measure these properties. Lees and Rollins [90] and Gilmore et al. [91] used both longitudinal and shear wave propagation to obtain values of Young’s, Shear and bulk moduli for both dentin and enamel. The latter data were also used by Spears [89] in his 3-D finite element analysis (FEA) of prismatic enamel. An early review of some of the mechanical and physical properties of teeth through 1979 [92] summarizes the state-of-the-art prior to the development of modern micro- and nanotechniques of measuring tissue properties. Bulk acoustic wave propagation techniques were used to measure the properties of dental materials in a number of studies by Katz and his colleagues and students: dentin and enamel [91], amalgams [93–95], cements [96], composites [97–99], alloys [100] and anticipating tissue engineering based on apatites, a series of studies of various synthetic and biological apatites [101–103]. The availability of such detailed data on properties has also allowed the development of various models to explain and/or predict the properties both of natural [104] and synthetic biomaterials [105–107]. These bulk acoustic measurements provide useful information about the macromechanical properties of materials, biological, natural or synthetic. Indeed, variations of the acoustic techniques described above have been used to study abnormalities or defects in skeletal tissues in vitro [108] and in vivo [109].
4.2. Micromechanical analysis with scanning acoustic microscopy (SAM)
In the 1970s, the development of a new technique, scanning acoustic microscopy (SAM), enabled the analysis of the biomechanical properties of materials at much higher resolution than was achieved by the bulk ultrasonic technique [110–112], SAM made it possible to measure the elastic properties of biological tissues and tissue/material interfaces at the microstructural level, providing the transition from macro- to micromechanical analysis of biological systems. A significant advantage of SAM is the ability to investigate the properties of internal and subsurface structures in addition to the surface properties of most materials, including those that are optically opaque. An additional advantage of this technique when applied to the study of biological materials is that a liquid couplant (usually water) must be used to transmit the acoustic waves from the acoustic lens to the specimen being studied The specimen is kept wet during all measurements, contrary to both TEM and SEM which require the specimens to be placed within a vacuum chamber during observations. Thus, fresh tissue specimens can be used as well as embedded specimens. In addition, the use of high quality, high frequency focusing acoustic lenses permits examination of the elastic properties of biological materials on a scale comparable to optical histologic studies.
A large variety of mostly opaque polymeric materials and composites have been investigated nondestructively using both the pulse and burst operating modes in SAM [113]. These modes complement each other in the characterization and analysis of different features within the material. The pulse mode, which operates in the low-frequency range (10–200 MHz), permits in-depth imaging of internal defects and discontinuities. This mode has been used to show delaminations in composites [114] or internal damage, inclusions or voids in materials [112]. The burst mode is used to analyze the surface and subsurface microstructural features of materials. For example, the dispersivity of filler particles in polymeric matrices has been studied using SAM in burst mode [113]. Images of strain fields around the particles in a PVC matrix have been generated using SAM in burst mode [113].
In the early 1980s, the bone research group at Rensselaer Polytechnic Institute (RPI) began to use a transmission SAM to study skeletal tissue micromechanics [108,115,116]. The limitations of the transmission technique led to the design and development in Paris, France of a reflection SAM system working in the pulse mode in the 20 to 50 MHz frequency range [117]. It was used to study the effects of hip implants on the surrounding bone, especially the properties of the remodeled bone that surrounded the implant [118].
SAM in the burst mode has been used to study the in vitro micromechanical elastic properties of human compact cortical femoral bone [119] and trabecular bone [120]. In this study, the authors were able to image the properties of the individual osteonic lamellae at high enough resolution so that three new micromechanical observations were made: (1) the outermost lamellae always appear to be more compliant; (2) the outermost lamellae of adjacent abutting osteons appear to have the same acoustic impedance (and thus Young’s modulus), even though structurally distinct; and (3) adjacent lamellae within an osteon alternate in their acoustic impedance (and thus Young’s modulus). Due to the large scattering and absorption of acoustic waves at high frequencies, the burst mode cannot provide images very deep below the surface. However, defects close to the surface can be imaged through the interference pattern occurring between the burst signal reflected from either the surface or the subsurface defect. This technique is of special interest when investigating the adhesion between a thin coating and a substrate.
The Kraemer KSI 2000 high frequency SAM at the Martin-Luther-University Halle-Wittenberg Medical School in Halle-Saale, Germany, has been used to study the changes in calcified tissues with age. Specimen from the proximal femora of pairs of both females and males, ages in the 20 s, 60 s and 70 s, were cut, under flowing water, at 15° intervals from along the bone axis to the transverse direction to study the bone anisotropy as well Frequencies used in this study ranged from 400 MHz (nominal lateral resolution 2.5 μm) to 800 MHz (nominal lateral resolution 1.25 μm). Preliminary results of these studies were presented at the Augustusburg Conference of Advanced Science on “Mechanical Properties of Cells and Tissues: Contributions of Scanning Acoustic Microscopy and Atomic Force Microscopy” October 11–13, 1999 on Augustusburg, Saxony, Germany.
5. Synthetic material/calcified tissue interfaces
Scanning acoustic microscopy has also been applied to study interfaces of dental as well as medical interest. To fully appreciate the application of this technology to investigations of this nature, it is necessary to begin by reviewing the characteristics of material/tissue interfaces of particular interest in dentistry. The interfacial structure and properties of the dentin/adhesive (d/a) interface will be presented in greatest detail.
5.1. The d/a interface
With the public’s concern about mercury release from dental amalgam and the environmental issues associated with discharge of mercury into the waste water, it is expected that dentists will frequently turn to other synthetic replacement materials such as composite resin to repair both anterior and posterior teeth. A key factor in the long-term clinical success of these repairs is successful attachment or bonding of the composite material to the tooth surface. Breakdown of the composite/tooth bond leads to the formation of gaps at the material/tooth interface; the gaps act as a conduit for penetration of bacterial enzymes, bacteria, fluids and ions. This exchange of fluids and bacteria at the interface is commonly referred to as microleakage and is recognized as a major factor contributing to hypersensitivity [121] as well as secondary caries [122].
The bond at the tooth surface/composite material interface actually involves two distinctly different substrates, i.e., dentin and enamel. The composition of the enamel is approximately 98% mineral and 2% protein while the dentin is 50% mineral, 30% protein and 20% water by volume [123]. Acid-etching provides effective mechanical bonding between the composite restoration and treated enamel, but there is substantial evidence that the bond at the dentin surface experiences premature degradation [121,122,124]. Breakdown of the bond at the tooth surface/composite material interface has thus been linked directly to the failure of our current materials to consistently seal and adhere to the dentin [125].
Current theories on dentin bonding suggest that two fundamental processes are involved in bonding an adhesive to dentin. First, the mineral phase must be extracted from the dentin substrate without altering the collagen matrix and second, the voids left by the mineral must be filled with adhesive resin that undergoes complete in situ polymerization, i.e., the formation of a resin-reinforced or hybrid layer [126]. The ideal hybrid layer would be characterized as a three-dimensional polymer/collagen network that provides both a continuous and stable link between the bulk adhesive and dentin substrate. There is substantial evidence to suggest that this ideal objective is not achieved. Instead of serving as a stable connection between the bulk adhesive and subjacent intact dentin the hybrid layer has been called the weakest link in the dentin/adhesive bond [127].
Dentin can be regarded as a biological composite of a collagen matrix which is highly filled with nanometer-sized apatite crystals. After extracting the mineral from the collagen fibrils, the voids can be filled with a resin, thus forming a new composite made up of resin matrix filled with a fibrous collagen. This new structure is a hybrid of resin and collagen [128]. This optimum hybrid structure was achieved when adhesive resin infiltrated dehydrated, demineralized dentin prepared under controlled conditions, but not at the d/a interface formed using the wet bonding technique [129]. Using the histomorphologic technique described here and reported previously [130,131], any collagen that is not encased in adhesive resin is available for reaction with the Goldner’s trichrome stain. The distinct red zone at the d/a interface indicated that the adhesive did not penetrate the full depth of the demineralized layer, i.e., it did not encapsulate the collagen fibrils throughout the width of the demineralized dentin [129]. This novel staining technique, which identifies exposed collagenous protein at the light microscopic level, provides a unique, clear representation of the extent and degree to which the adhesive resins envelope the collagen fibrils of the demineralized dentin matrix.
Corresponding Raman spectra recorded from the intertubular area of the d/a interface and the sections from the optimum hybrid structure confirmed the above observation [129]. The spectrum of d/a interface has lower adhesive contribution as compared to the spectrum of the optimum hybrid structure, indicating limited diffusion of resin monomers into the wet d/a interface. The Raman spectral bands collected as a function of position across the d/a interface also showed a gradual decrease in adhesive concentration. Gradual decreases in intensity of Raman bands associated with adhesive have been reported previously [132,133], but in these studies, the authors measured the amount of resin penetration based on the absolute intensity of adhesive bands [133], totally ignoring the collagen matrix, the key component of acid-etched dentin. The absolute intensity of backscattering Raman band is dramatically effected by many factors, such as the smoothness of the sample surface, the position of focusing, the depth of detection, fluorescence of biological components and the stability of the instrument and laser power, etc. [134,135]. Since it is very difficult to maintain all of the above conditions the same across the breadth of the sample, the band intensity may vary from one measurement to the next even at the same spot on the sample. In order to account for the effect of instrumental fluctuation and errors, the Raman band associated with the collagen matrix was used as internal standard throughout our studies [129,131,136]. The quantitative band intensity ratios of adhesive and collagen across the d/a interface indicate that at the first micrometer of the d/a interface, only ~68% of the concentration of BisGMA in the original adhesive penetrated the demineralized dentin. In comparison, the resin components (including HEMA) diffused more readily into the demineralized dentin zone than the BisGMA component [129].
With wet bonding techniques, the tubular channels and intertubular area between the demineralized dentin collagen fibrils are filled with water, conditioner and/or oral fluids. For example, hydrated demineralized dentin is 30% collagen and 70% water by volume [54,71]. The only mechanism available for adhesive resin infiltration is diffusion of the resin into whatever fluid is in the spaces of the substrate and along the collagen fibers. Ideally, the solvent/HEMA combination conditions the collagen to remain expanded during adhesive infiltration. However, HEMA can dramatically reduce the evaporation of water, i.e., the addition of HEMA reduces the mole fraction of water and therefore reduces the partial pressure of water according to Dalton’s law of partial pressures. As the partial pressure of water drops it becomes more and more difficult to remove residual water from the demineralized dentin. Hydrophobic monomers, such as BisGMA, would resist diffusing into the sites where there is residual water. As reported in a recent study, SB adhesive may separate into hydrophobic BisGMA-rich and hydrophilic HEMA-rich phases as it interacts with the wet demineralized dentin matrix [137].
Phase separation of the adhesive that infiltrates the demineralized dentin matrix would compromise the structural integrity of the resultant hybrid layer. In contrast to an impervious three-dimensional collagen/polymer network, adhesive phase separation would lead to a very porous hybrid layer characterized by hydrophobic BisGMA-rich particles distributed in a hydrophilic HEMA-rich matrix [137]. Because of its low cross-link density HEMA is unstable in aqueous environments and thus, this phase will degrade when exposed to oral fluids [138]. In addition, unprotected demineralized collagen fibrils are more susceptible to hydrolysis than are mineralized collagen fibrils. This may explain the decreased bond strength in aqueous environments over the long term.
Molecular microanalysis in conjunction with a novel histomorphologic technique provides a clear, quantitative method for determining the quality of the hybrid layer. The results suggest that under wet bonding the d/a interface is not an impervious collagen/polymer network but a porous web; the composition of this web is predominately collagen and HEMA with less contribution from the BisGMA component. The results of this study suggest that the critical dimethacrylate component (BisGMA), which contributes the most to the cross-linked polymeric adhesive, infiltrates a fraction of the total wet demineralized, intertubular dentin layer.
If composite resins are to be considered a viable alternative to dental amalgam, the durability of the interfacial bond must be addressed. Under in vivo conditions, this bond can be the first defense against substances that may penetrate and ultimately undermine the restoration. The durability of the dentin/adhesive bond is directly related to the quality of the hybrid layer that connects the bulk adhesive to the subjacent, intact dentin. Determining the quality of this layer has been a formidable problem and to date, the majority of our techniques have provided only an indirect assessment of quality. For example, testing methods that measure fracture resistance of bulk dentin/adhesive specimens before and after water immersion are not sensitive enough to identify interfacial defects where degradation begins. High-resolution analytical techniques that allow direct nondestructive, in situ detection of molecular structure and micromechanics and provide us with the capability of measuring these properties at a spatial resolution approximately equivalent to a hybrid layer (~2–10 μm) are needed [63–65,139].
5.2. Properties of the components at the d/a interface
Using scanning acoustic microscopy, the modulus of elasticity for demineralized dentin collagen was 1.76 GPa [64]. The modulus of elasticity for the demineralized dentin collagen specimen that has been infused with adhesive (optimum hybrid) was 1.84 GPa and the modulus of elasticity of the infiltrated adhesive was 3.5 GPa. These specimens were different so that there is no guarantee that the collagen thicknesses and orientations were comparable. Small differences in those factors could be responsible for the 4.3% difference between the two collagen values. Since the acoustic beam width, although quite small, is finite an additional possibility is that the thin film of adhesive, of higher modulus, surrounding the collagen has affected the measurement. As these values are obtained directly from the fibrils themselves, they are compatible with the value of 3 GPa for the Young’s modulus of tendon collagen molecules, obtained by X-ray diffraction measurements of the changes in their D period, when strained in tension [140]. The extremely low values of demineralized dentin collagen matrices measured by mechanical testing [141,142] are on porous meshes and do not reflect the properties of either the molecules or the fibrils directly. It is well known that the modulus of such soft materials lessens considerably with an increase in porosity.
The lower modulus of the adhesive infiltrate as compared to the value recorded for the adhesive sample separately (5 GPa) may be related to several [63,64]. As a result of residual solvent and/or water, the degree of monomer/polymer conversion in the adhesive infiltrate may have been less than the sample composed solely of adhesive. The lower modulus of elasticity of the infiltrate may reflect less polymerization and/or cross-linking of the material that infiltrated the wet demineralized dentin matrix as compared to the separate adhesive sample. The value for the adhesive infiltrate was, however, within the range reported by previous investigators. For example, using tensile stress-strain tests Sano et al. [143] obtained moduli of elasticity for resin-infiltrated demineralized dentin ranging between 2 and 3.6 GPa. With a modified AFM nanoindenter, previous investigators reported the modulus of elasticity of Single Bond-infiltrated dentin between 1.3 and 5.1 GPa, depending upon the degree of hydration of the substrate [144].
Characterization of the d/a interface specimens using scanning evanescent microwave probe (EMP) technology clearly showed region of high electrical activity and permittivity in certain areas of the sample. We are currently investigating the origin of this non-uniformity. EMP, owing to the penetration of its sensing signal inside the sample, is capable of detecting the properties of dentin–adhesive interface. When used along with SAM and Raman microspectroscopy, important and critical information regarding bonding strength and uniformity is obtained [139].
In a recent meta-analysis of bond strength results published between 1992 and 1996, the authors concluded that although conventional tests are simple and fast, they have many drawbacks [145]. The bond strength tests measure d/a reactions primarily at the point of fracture. They do not provide mechanical data at a resolution that would permit the identification of interfacial defects where failure likely initiates. Using conventional testing techniques, an investigator cannot identify the initial flaw nor can the investigator directly correlate this flaw with the structure and chemistry of the substrate or the bonded assembly. As described in our recent publications [63,65] by combining the unique capabilities of μRS, SAM and optical microscopy we can perform chemical, mechanical and morphologic characterization over the same small region of the d/a interface. These complementary technologies provide direct nondestructive hi situ detection of the interfacial molecular structure, micromechanics and morphologic features of the bonded assembly. This is exemplified by the corresponding patterns recorded in the optical image and the SAM image of the demineralized dentin collagen infiltrated with adhesive. The data collected from these synergistic techniques provide added insight into the potential problems at the weak d/a interface; problems that may be avoided by altering the materials and/or the method of application.
5.3. Finite element modeling of the d/a interface
The structure of the dentin–adhesive interface as well as the modulus of elasticity of the dental composite, the hybrid layer, the demineralized dentin collagen and the adhesive profoundly affects the load transfer at the d/a interface. The in situ microstructural and micromechanical property measurements obtained from micro-Raman spectroscopy, scanning acoustic microscopy and optical microscopy were used in finite element analyses to predict stress concentration and distributions at the interface under tensile loading [42].
The finite element results indicate that the stresses concentrate in the peritubular dentin in proximity of the hybrid/exposed collagen layer. As the thickness of the hybrid/exposed collagen layer increases the area of stress concentration zones increases. The stress concentrations in peritubular dentin are exacerbated for cases with lower elastic moduli or nonlinear gradation of elastic moduli in the hybrid/exposed collagen layers. Based on the results of the Raman microspectroscopic and scanning acoustic microscopic investigations, the exposed collagen layer is a result of incomplete adhesive infiltration and/or adhesive phase [63,65,129,131,136,137]. The larger stress concentration zones for interfaces with thicker hybrid/exposed collagen layer indicates an increased likelihood of failure initiating in the peritubular region close to the hybrid layer. The stress concentration is found to be higher for wider intertubular dentin and narrower peritubular dentin, illustrating the effect that modulus of elasticity and microstructure has upon stress distribution and concentration at the d/a interface [42].
The conventional opinion that the low elastic modulus as a result of phase separation in the adhesive could offer a mechanical advantage to the system is not true. In other words, based on our previous investigations, a commercial adhesive with a relatively high concentration of hydrophobic components undergoes phase separation in the presence of water with the demineralized dentin matrix [137]. In a bonded joint such as occurs under ideal conditions at the d/a interface, the globules of resin (as a result of adhesive phase separation) distributed within the demineralized dentin matrix would potentially reflect defects within the joint that would inhibit an even transfer of stresses across the d/a interface. Although this may be true, one might expect that the stresses would dissipate quickly in the low modulus region. The results from the finite element analyses indicate this is not true because the low modulus regions lead to stress concentration in relatively high elastic modulus regions [42].
Although the applied stress is considerably smaller than dentin strength, the stress concentration caused by interface geometry and interface-component elastic moduli will likely lead to an overall d/a interface strength that is considerably less than the individual strengths of the interface components. For the simple mode and loading case considered in the preliminary calculations, complex multi-axial stresses exist at the microscopic-level; consequently, a mixed mode fracture mechanism is more likely [42]. By devising full-depth high modulus hybrid layer we may considerably reduce the stress concentration zone and the magnitude of stress concentration in the peritubular dentin next to the hybrid/exposed collagen layer.
5.4. Properties of the bone/implant interface
One advantage of using SAM in studying the effect of implants on the surrounding tissues is that it is a nondestructive technique allowing use of the same samples for other studies. Thus, the initial major use of the low frequency pulse-mode SAM designed and built at the Laboratoire de Recherches Orthopediques in Paris [117] was in a study of the effects of a hip implant on the surrounding femoral compact cortical bone [118]. In this study, the SAM images of the inhomogeneities in both the implanted and contralateral femora were compared at the same levels both above and below the tip of the implant. These results were correlated with both histology and traditional bulk ultrasonic wave propagation measurements of Young’s moduli. While the samples from above the tip in the implanted femur showed considerable bone loss in certain regions due to stress shielding effects, as expected, the samples from the same levels in the contralateral femur exhibited normal bone quality. However, there was no significant difference in bone quality between the samples cut from below the implant tip in both femora [118].
A high frequency study using the Olympus UH3 SAM (Olympus Co., Tokyo, Japan) at Case Western Reserve University (CWRU) was performed using a 400 MHz burst-mode lens on histologically prepared samples of porous Ti plugs with and without hydroxyapatite coatings that had been inserted in rabbits at CWRU [146–148]. The SAM study showed that there were significant differences in formation and remodeling from woven to haversian bone as a function of both time of implantation and the presence or absence of hydroxyapatite coating in the pores [149].
The real power of using SAM to study the micromechanical elastic properties that are found in tissue-implant interactions, especially at their interfaces, comes into play when it is correlated with the properties measured by other micro- and/or nanoscanning modalities, such, as micro-Raman and FTIR for chemical properties and scanning evanescent microwaves for electrical properties. This came to fruition when these scanning modalities were combined in the ongoing studies of the multispectral properties of the dentin/adhesive (d/a) as described in this section.
6. Discussion
6.1. Multiscale model combining molecular/continuum mechanics
Numerical simulation methods may be utilized as tools for data interpretation and for iterative refinement of the imaging/experimental procedure to understand system behavior at various length scales. The finite element (FE) method in combination with appropriate scale bridging constitutive relationships offers a powerful numerical simulation technique that may be used to compute the distributions of field quantities within the domain whose behavior needs to be investigated. Since no single imaging modality or experimental technique provides a complete picture of the physico-chemico-mechanical properties, properties measured with diverse imaging techniques of different modalities and spatial resolution are utilized in the FE computations. The computation results are expected to provide insight to the likely response of the different phases composing the domain to the applied field. These results may then be utilized to verify the data interpretation of a particular imaging modality or experimental technique and to refine the imaging or experimental procedure. Since FE method is a continuum mechanics approach, FE models that implement scale bridging stress–strain relationships, which bridge the discrete molecular scale to the continuum material (element) scale, are likely to capture the nanoscale phenomena.
Stress–strain relationships for materials have been traditionally established through direct phenomenological modeling based upon experimental observations. However, it is widely accepted that the material stress–strain behavior critically depends upon the underlying mechanisms that occur at scales smaller than the material sample scale. Modeling methodologies that account for the underlying mechanisms governing the material behavior and explicitly model material microstructure are expected to provide better insight to the material stress–strain behavior and bridge the scale between continuum and discrete representations. For instance, micromechanical models considering particle interactions have been successfully used for describing stress–strain behavior of granular materials [150,151], while lattice models of concrete microstructure have been found useful for describing concrete fracture behavior [152].
Along this approach, we consider the material-scale to be composed of nanoscale grains (representing molecular bonds) whose centroids represent material points. Similar granular or discrete microstructure models have been considered in the past for developing constitutive relations, such as the virtual internal bond model developed by Gao and Klein [153], the higher order constitutive relationships developed by Chang et al. [154], the ‘doublet’ mechanics models [155] and the micromechanics models [151,156–158]. In analogy with atomistic-scale interactions, these nanoscale grains are viewed as interacting with each other through pseudo-bonds. A schematic depiction of such a model is given in Fig. 8. Under an applied load on a sample of such a material, the conceptual grams may translate or rotate. Considering each grain to have six degrees of freedom, i.e., three translational and three rotational degrees of freedom, the relative displacement δi between two nearest neighbor grams n and p (see Fig. 8) is given by
Fig. 8.
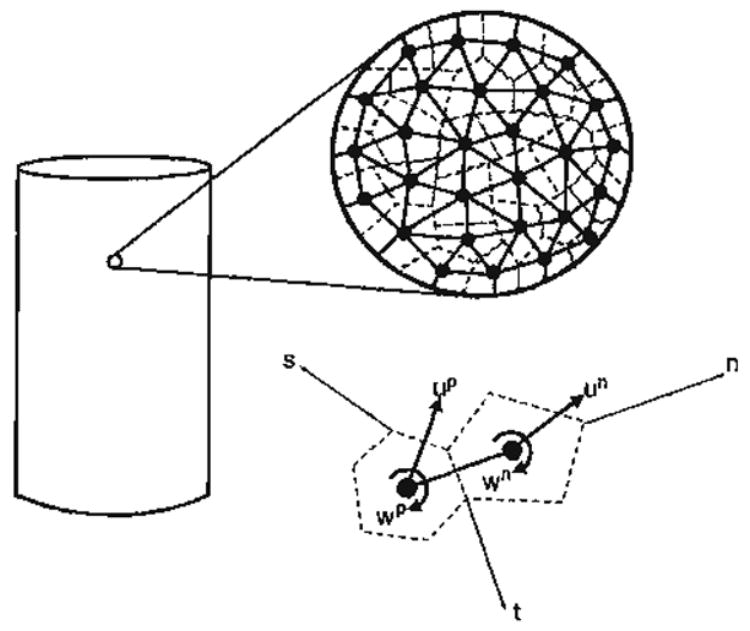
From a microscopic viewpoint, the material contains a large number of molecular bonds whose average behavior in a given direction may be represented by nanoscale grains interacting through pseudo-bonds in that direction.
| (1) |
where ui=particle displacement, ωj=particle rotation, rk = vector joining the particle centroid to the contact point, superscripts refer to the particles and eijk = permutation symbol.
The relative displacement δi between two grains may be decomposed into two components, one along the pseudo-bond connecting the conceptual grains denoted by δn and the other tangential to the pseudo-bond denoted by δw. Thus, upon an increment of deformation, the center-to-center distance between two granular material points, L, becomes, Lo + δn, where Lo is the initial center-to-center distance, and the tangential distortion between the two granular material points, w, becomes δw. From an energy approach, the interactions between materials points through bonds may be formulated in terms of potential function, Φ(L, w), which, for simplicity, may be written as a summation of a central potential, φ(L), dependent upon the center-to-center distance of two nearest neighbor grains, L, and a non-central potential, ϕ(w), dependent upon the tangential distortion from the initial equilibrium position for the two nearest neighbor grains, w.
The potential functions envisaged in the proposed methods are inspired by the atomic-interaction potentials and represent the average behavior of a large number of molecular bonds in a given direction. Thus, under compression as the center-to-center distance is decreased, we expect the pseudo-bond potential function to account for the effects of molecular bond compression, buckling or bending. Similar molecular bond-scale mechanisms need to be accounted for when the grains are deformed in the direction tangential to the pseudo-bond. For example, in contrast with tension, under compression, greater energy may be required to initiate deformation in the direction tangential to the pseudo-bond. Such phenomena may be caused by the differences in interactions at the interfaces under tensile or compressive conditions. Hence, under compression, a deeper potential-well is expected for the non-central potential, φ(w). The pseudo-bond potential functions have to be formulated accordingly. These potential functions may be utilized to establish expressions for average force–displacement relationships of a pseudo-bond. Schematic examples of bond force-displacement relationships are shown in Fig. 9, which gives the plot of the force functions in normal as well as tangential direction of a bond. As seen from Fig. 9, the force functions have a reasonable ability to model the phenomenological behavior of a pseudo-bond. For instance, under purely central compression along a bond, the sub-granular scale yielding or damage will result in the gradual flattening of the force function as the center-to-center distance decreases. Similarly, under compression accompanied with tangential relative displacement, the sub-granular scale mechanisms may result in a tangential force function that reaches a peak and, subsequently, softens upon further deformations.
Fig. 9.
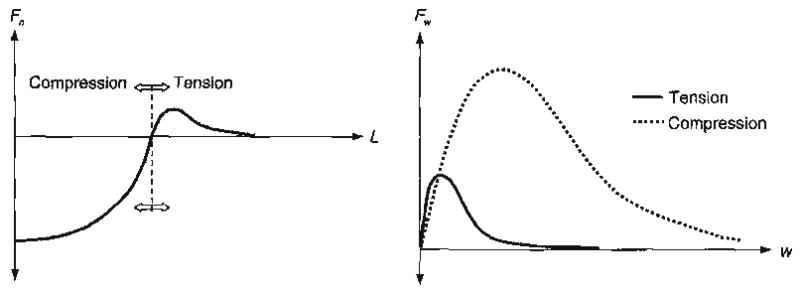
Likely forms of pseudo-bond force–displacement relationship in normal, Fn, and tangential, Fw, directions under compression and tension.
Based upon these force functions, the increment of pseudo-bond force Δfi may be related to the increment of relative displacement Δδj through the stiffness Kij as
| (2) |
The stiffness Kij may be written in terms of the stiffness in the normal direction Kn and that in the tangential direction Kw as
| (3) |
Considering the kinematic assumption that the relative displacement Δδj is linearly related to the overall strain, the pseudo-bond force-displacement relationships may be combined with its orientation to derive the incremental stress and stiffness tensors in the following form:
| (4) |
| (5) |
where the integration is performed over all the bonds in a given volume, Np is the bond density per unit volume and ξ(Ω) is the directional density function of pseudo-bonds, such that the product Npξ(Ω)dΩ denotes the bond density in the direction represented by the interval between solid angles Ω and Ω + dΩ. Alternatively, utilizing a static assumption that relates the pseudo-bond force Δfi to the stress tensor, the pseudo-bond force–displacement relationships may be combined with its orientation to derive the incremental strain and compliance tensors in the following form:
| (6) |
| (7) |
where Akp is obtained as the inverse of “fabric” tensor Fpk given by:
| (8) |
Since, in general, the force and stiffness functions depend upon orientations, closed form integration of Eqs. (4), (5), (6) and (7) may only be obtained under certain simple loading conditions or under infinitesimally small strains in which case the stiffness, Kn and Kw, reduce to constant values. For instance, based upon the kinematic approach, the initial isotropic material properties under infinitesimally small strains maybe obtained as follows from Eq. (5):
| (9) |
| (10) |
Similarly, based upon the static approach, the initial isotropic material properties under infinitesimally small strains may be obtained as follows from Eq. (7):
| (11) |
| (12) |
The stress–strain relationship derived following the methodology described above may be implemented in FE model to understand the relationship between the overall applied stimulus and measured behavior at the sample scale through imaging or experimental techniques. For instance, the FE method may be used to obtain distributions of stress and strain fields in a given region that is to be imaged by directly utilizing the measured data from the high-resolution analytical techniques such as SAM and micro-Raman spectroscopy [159]. The resulting stress distributions provide insight to likely failure location and mechanisms, and may indicate the need to further refine the mechanical property and chemical measurements in regions of stress concentrations and its proximity.
As a computational technique, the multiscale modeling method provides certain advantages, in that the parameters that cannot be easily modified in the laboratory may be easily varied in the FE model, and the model may be exercised for a variety of conditions. The disadvantage of the multiscale method stems from the less-than-perfect empirical information available to make the models realistic. However, by combining the imaging/experimental technique and the multiscale modeling method, successive refinement of both the imaging or experimental procedure and the multiscale modeling model may be achieved resulting in superior imaging data interpretation, and an accurate prediction and understanding of the system behavior under applied stimulus at various hierarchical scales.
Acknowledgments
A contribution of the University of Missouri-Kansas City Center for Research on Interfacial Structure and Properties (UMKC-CRISP). This investigation was supported in part by USPHS Research Grant R01 DE12487 (PS), R01 DE14392 (PS) and K25 DE015281 (YW) from the National Institute of Dental and Craniofacial Research and USPHS Major Instrumentation Grant RR16710, National Institutes of Health, Bethesda, MD 20892.
References
- 1.LeGeros RZ. In: Monographs in Oral Science. Meyers HM, editor. Karger: Basel; 1991. p. 121. [PubMed] [Google Scholar]
- 2.Eppell SJ, Tong WL, Katz JL, Spearing WL, Glimcher MJ. Journal of Orthopaedic Research. 2001;19:1027. doi: 10.1016/S0736-0266(01)00034-1. [DOI] [PubMed] [Google Scholar]
- 3.Cowin S. Bone Mechanics. CRC Press; Boca Raton: 2001. [Google Scholar]
- 4.Katz JL. Advances in Bioengineering. ASME; New York, NY: 1976. [Google Scholar]
- 5.Katz JL. Nature. 1980;283:106. doi: 10.1038/283106a0. [DOI] [PubMed] [Google Scholar]
- 6.Rho JY, Pharr GM. Journal of Materials Science Materials in Medicine. 1999;10:1. doi: 10.1023/a:1008901109705. [DOI] [PubMed] [Google Scholar]
- 7.Rho JY, Roy ME, Tsui TY, Harr GMP. Journal of Biomedical Materials Research. 1999;45:48. doi: 10.1002/(sici)1097-4636(199904)45:1<48::aid-jbm7>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- 8.Rho JY, Tsui TY, Harr GMP. Biomaterials. 1997;18:1325. doi: 10.1016/s0142-9612(97)00073-2. [DOI] [PubMed] [Google Scholar]
- 9.Rho JY, Zioupos P, Currey JD, Pharr GM. Bone. 1999;25:295. doi: 10.1016/s8756-3282(99)00163-5. [DOI] [PubMed] [Google Scholar]
- 10.Bethe HA. Physical Review. 1944;66:163. [Google Scholar]
- 11.Baez V. Journal of the Optical Society of America. 1956;46:901. doi: 10.1364/josa.46.0901_1. [DOI] [PubMed] [Google Scholar]
- 12.Soohoo RF. Journal of Applied Physics. 1962;33(Suppl):1276. [Google Scholar]
- 13.Ash EA, NIcholls G. Nature. 1972;237:510. doi: 10.1038/237510a0. [DOI] [PubMed] [Google Scholar]
- 14.Pohl DW, Denk W, Lanz M. Applied Physics Letters. 1984;44:651. [Google Scholar]
- 15.Lukosz W. Workshop on Unconventional Imagery. 1984:73–74. [Google Scholar]
- 16.Weiss JA, Hawks DA. IEEE MTT-S Digest. 1987:457. [Google Scholar]
- 17.Gutmann RJ, Borrego JM, Chakrabarti P, Wang MS. IEEE MTT-S Digest. 1987:281. [Google Scholar]
- 18.Fee M, Chu S, Hansch TW. Optics Communications. 1989;69:219. [Google Scholar]
- 19.Tabib-Azar M, Shoemaker N, Harris S. Measurement Science and Technology. 1993;4:583. [Google Scholar]
- 20.Stranick SJ, Weiss PS. Journal of Physical Chemistry. 1994;98:1762. [Google Scholar]
- 21.Gao X, Duewer F, Lu Y, Xiancy XD. Applied Physics Letters. 1997;71:1872. [Google Scholar]
- 22.Golosovksy M, Lann A, Davidov D. Ultramicroscopy. 1998;71:133. [Google Scholar]
- 23.Thanawalla S, Dutta SK, Vlahacos CP, Steinhauser DE, Feenstra BJ, Anlage SM, Wlllstood FC. Applied Physics Letters. 1998;73:2491. [Google Scholar]
- 24.Tabib-Azar M, Katz JL, LeClair S. IEEE Transactions on Instrumentation and Measurement. 1999;48:1111. [Google Scholar]
- 25.Tabib-Azar M, Bumrerraj S, Katz JL, You SH. Biomedical Microdevices. 1999;2:73. [Google Scholar]
- 26.Tabib-Azar M, Su DP, Pohar A, Leclair SR, Ponchak G. Review of Scientific Instruments. 1999;70:1725. [Google Scholar]
- 27.Tabib-Azar M, Pathak PS, Ponchak G, Leclair SR. Review of Scientific Instruments. 1999;70:2783. [Google Scholar]
- 28.Tabib-Azar M, Akinwande D, Ponchak G, Leclair SR. Review of Scientific Instruments. 1999;70:3083. [Google Scholar]
- 29.Tabib-Azar M, Akinwande D, Ponchak G, Leclair SR. Review of Scientific Instruments. 1999;70:3381. [Google Scholar]
- 30.Tabib-Azar M, Ciocan R, Ponchak G, Leclair SR. Review of Scientific Instruments. 1999;70:3387. [Google Scholar]
- 31.Tabib-Azar M, Sutapun B. Review of Scientific Instruments. 1999;70:3707. [Google Scholar]
- 32.Tabib-Azar M, Ciocan R, Leclair SR. Microscale Thermophysical Engineering. 1999;3:321. [Google Scholar]
- 33.Tabib-Azar M, Garcia-Valenzuela A, Ponchak G. Evanescent microwave microscopy for high resolution characterization of materials. Kluwer Academic Publishing; Boston: 2000. [Google Scholar]
- 34.Tabib-Azar M, Akinwande D. Review of Scientific Instruments. 2000;71:1725. [Google Scholar]
- 35.Tabib-Azar M, Leclair SR. Sensors and Actuators. B, Chemical. 2000;67:112. [Google Scholar]
- 36.Tabib-Azar M, Muller R, Leclair SR. Engineering Applications of Artificial Intelligence. 2000;13:549. [Google Scholar]
- 37.Tabib-Azar M, Wang R. Review of Progress in Quantitative Nondestructive Evaluation. 2000;20A:446. [Google Scholar]
- 38.Tabib-Azar M. Review of Progress in Quantitative Nondestructive Evaluation. 2000;20A:400. [Google Scholar]
- 39.Tabib-Azar M. Canadian Society for Nondestructive Testing. 2000 [Google Scholar]
- 40.Tabib-Azar M. Material Evaluations. 2001:70. [Google Scholar]
- 41.Katz JL, Yoon HS, Tabib-Azar M, Mozayeni-Azar M, Bumrerraj S. In: Early Detection of Caries II. Stookey GK, editor. Indiana University Press; Blomington, IN: 2000. pp. 443–449. [Google Scholar]
- 42.Misra A, Spencer P, Wang Y, Katz JL. Journal of Dental Research. 2003;82:1643. doi: 10.1177/154405910308200213. [DOI] [PubMed] [Google Scholar]
- 43.Katz JL, Lipson S, Yoon HS, Maharidge R, Meunier A, Christel P. Calcified Tissue International. 1984;36:S31. doi: 10.1007/BF02406131. [DOI] [PubMed] [Google Scholar]
- 44.Katz JL, Meunier A. Journal of Biomechanics. 1987;20:1063. doi: 10.1016/0021-9290(87)90024-8. [DOI] [PubMed] [Google Scholar]
- 45.Katz JL, Meunier A. Journal of Materials Science Materials in Medicine. 1990;1:1. [Google Scholar]
- 46.Berthet-Colominas C, Miller A, White SW. Journal of Molecular Biology. 1979;134:431. doi: 10.1016/0022-2836(79)90362-0. [DOI] [PubMed] [Google Scholar]
- 47.Ascenzi A, Baschieri P, Benvenuti A. Journal of Biomechanics. 1994;27:875. doi: 10.1016/0021-9290(94)90260-7. [DOI] [PubMed] [Google Scholar]
- 48.Arsenault AL. Calcified Tissue International. 1988;43:202. doi: 10.1007/BF02555136. [DOI] [PubMed] [Google Scholar]
- 49.Arsenault AL. Bone and Mineral. 1989;6:165. doi: 10.1016/0169-6009(89)90048-2. [DOI] [PubMed] [Google Scholar]
- 50.Akiva U, Wang HD, Weiner S. Journal of Materials Science. 1998;33:1497. [Google Scholar]
- 51.Tong W, Eppell SJ. Journal of Biomedical Materials Research. 2002;61:346. doi: 10.1002/jbm.10165. [DOI] [PubMed] [Google Scholar]
- 52.Tong W, Glimcher MJ, Katz JL, Kuhn L, Eppell SJ. Calcified Tissue International. 2003;72:592. doi: 10.1007/s00223-002-1077-7. [DOI] [PubMed] [Google Scholar]
- 53.Blair JM, Sorensen LB, Arnsdorf MF, Lal R. Seminars in Arthritis and Rheumatism. 1995;24:359. doi: 10.1016/s0049-0172(95)80005-0. [DOI] [PubMed] [Google Scholar]
- 54.Marshall GW, Marshall SJ, Kinney JH, Balooch M. Journal of Dentistry. 1997;25:441. doi: 10.1016/s0300-5712(96)00065-6. [DOI] [PubMed] [Google Scholar]
- 55.Butler WT. Operative Dentistry. 1992;(Suppl 5):18. [PubMed] [Google Scholar]
- 56.Kinney J, Pople HJA, Marshall GW, Marshall SJ. Calcified Tissue International. 2001;69:31. doi: 10.1007/s00223-001-0006-5. [DOI] [PubMed] [Google Scholar]
- 57.Daculsi G, Bouler JM, LeGerost RZ. International Review of Cytology. 1997;172:129. doi: 10.1016/s0074-7696(08)62360-8. [DOI] [PubMed] [Google Scholar]
- 58.Ten Gate AR. Mosby; St Louis: 1994. p. 174. [Google Scholar]
- 59.Wang R, Weiner S. Connective Tissue Research. 1998;39:269. doi: 10.3109/03008209809021502. [DOI] [PubMed] [Google Scholar]
- 60.Weiner S, Veis A, Beniash E, Arad T, Dillon JW, Sabsay B, Siddiqui F. Journal of Structural Biology. 1999;126:27. doi: 10.1006/jsbi.1999.4096. [DOI] [PubMed] [Google Scholar]
- 61.Kinney JH, Balooch M, Marshall SJ, Marshall GW, Weihs TP. Journal of Biomechanical Engineering. 1996;118:9. doi: 10.1115/1.2795939. [DOI] [PubMed] [Google Scholar]
- 62.Kinney JH, Balooch M, Marshall GW, Marshall SJ. Archives of Oral Biology. 1999;44:813. doi: 10.1016/s0003-9969(99)00080-1. [DOI] [PubMed] [Google Scholar]
- 63.Katz JL, Bumrerraj S, Dreyfuss J, Wang Y, Spencer P. Part B Applied Biomaterials. Journal of Biomedical Materials Research. 2001;58:366. doi: 10.1002/jbm.1030. [DOI] [PubMed] [Google Scholar]
- 64.Katz JL, Spencer P, Nomura T, Wagh A, Wang Y. Journal of Biomedical Materials Research. 2003;66A:120. doi: 10.1002/jbm.a.10551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Katz JL, Spencer P, Wang Y, Wagh A, Nomura T, Bumrerraj S. In: Tissue Engineering and Biodegradable Equivalents: Scientific and Clinical Applications. Lewandrowski K, Wise D, Trantolo D, Gresser J, Yaszemski M, Altobelli D, editors. Marcel Decker; 2002. pp. 775–793. [Google Scholar]
- 66.Eick JD. Proceedings of the Finnish Dental Society. 1992;88(Suppl 1):225. [PubMed] [Google Scholar]
- 67.Eick JD, Wilko RA, Anderson CH, Sorenson S. Journal of Dental Research. 1970;49:1359. doi: 10.1177/00220345700490063601. [DOI] [PubMed] [Google Scholar]
- 68.Pashley DH. Proceedings of the Furnish Dental Society. 1992;88(Suppl 1):215. [PubMed] [Google Scholar]
- 69.Wang Y, Spencer P. Journal of Biomedical Materials Research. 2002;60:300. doi: 10.1002/jbm.10108. [DOI] [PubMed] [Google Scholar]
- 70.Spencer P, Wang Y, Walker MP, Swafford JR. Journal of Dental Research. 2001;80:1802. doi: 10.1177/00220345010800090601. [DOI] [PubMed] [Google Scholar]
- 71.Pashley DH, Ciucchi B, Sano H, Homer JA. Quintessence International. 1993;24:618. [PubMed] [Google Scholar]
- 72.Gwinnett AJ. Dental Materials. 1994;10:150. doi: 10.1016/0109-5641(94)90024-8. [DOI] [PubMed] [Google Scholar]
- 73.Frushour BG, Koenig JL. Biopolymers. 1975;14:379. doi: 10.1002/bip.1975.360140211. [DOI] [PubMed] [Google Scholar]
- 74.Wahle JJ, Wendt SL. Journal of Prosthetic Dentistry. 1993;69:160. doi: 10.1016/0022-3913(93)90135-b. [DOI] [PubMed] [Google Scholar]
- 75.Avery JK, Steele PF, editors. Oral Development and History. New York: 2002. p. 74. [Google Scholar]
- 76.Ten Gate AR. Oral Histology. Mosby; St Louis: 1994. [Google Scholar]
- 77.Lin C, Douglas WH, Erlandsen SL. Journal of Histochemistry and Cytochemistry. 1993;41:381. doi: 10.1177/41.3.8429200. [DOI] [PubMed] [Google Scholar]
- 78.White SN, Paine ML, Luo W, Sarikaya M, Fong H, Yu Z, Li ZC, Snead ML. Journal of the American Ceramic Society. 2000;83:238. [Google Scholar]
- 79.Tesch W, Eidelman N, Roschger P, Goldenberg F, Klaushofer K, Fratzl P. Calcified Tissue International. 2001;69:147. doi: 10.1007/s00223-001-2012-z. [DOI] [PubMed] [Google Scholar]
- 80.Hodzic A, Stachurski ZH, Kim JK. Polymer. 2000;41:6895. [Google Scholar]
- 81.Marshall GW, Jr, Balooch M, Gallagher RR, Gansky SA, Marshall SJ. Journal of Biomedical Materials Research. 2001;54:87. doi: 10.1002/1097-4636(200101)54:1<87::aid-jbm10>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 82.Urabe I, Nakajima S, Sano H, Tagami J. American Journal of Dentistry. 2000;13:129. [PubMed] [Google Scholar]
- 83.Meredith N, Sherriff M, Setchell DJ, Swanson SA. Archives of Oral Biology. 1996;41:539. doi: 10.1016/0003-9969(96)00020-9. [DOI] [PubMed] [Google Scholar]
- 84.Maev RG, Denisova LA, Maeva EY, Denissov AA. Ultrasound in Medicine & Biology. 2002;28:131. doi: 10.1016/s0301-5629(01)00480-x. [DOI] [PubMed] [Google Scholar]
- 85.Rasmussen ST. Journal of Dental Research. 1984;63:1279. doi: 10.1177/00220345840630110501. [DOI] [PubMed] [Google Scholar]
- 86.Xu HH, Smith DT, Jahanmir S, Romberg E, Kelly JR, Thompson VP, Rekow ED. Journal of Dental Research. 1998;77:472. doi: 10.1177/00220345980770030601. [DOI] [PubMed] [Google Scholar]
- 87.Lin CP, Douglas WH. Journal of Dental Research. 1994;73:1072. doi: 10.1177/00220345940730050901. [DOI] [PubMed] [Google Scholar]
- 88.Craig RG, Peyton FA. Journal of Dental Research. 1958;37:710. doi: 10.1177/00220345580370041801. [DOI] [PubMed] [Google Scholar]
- 89.Spears IR. Journal of Dental Research. 1997;76:1690. doi: 10.1177/00220345970760101101. [DOI] [PubMed] [Google Scholar]
- 90.Lees S, Rollins FRJ. Journal of Biomechanics. 1972;5:557. doi: 10.1016/0021-9290(72)90027-9. [DOI] [PubMed] [Google Scholar]
- 91.Gilmore RS, Pollack RP, Katz JL. Archives of Oral Biology. 1970;15:787. doi: 10.1016/0003-9969(70)90042-7. [DOI] [PubMed] [Google Scholar]
- 92.Walters NE. In: The Mechanical Properties of Biological Materials. Vincent JFV, Currey JD, editors. Cambridge University Press; Cambridge: 1980. p. 99. [Google Scholar]
- 93.Grenoble DE, Katz JL. Journal of Biomedical Materials Research. 1971;5:503. doi: 10.1002/jbm.820050506. [DOI] [PubMed] [Google Scholar]
- 94.Grenoble DE, Katz JL. Journal of Biomedical Research. 1971;5:489. doi: 10.1002/jbm.820050505. [DOI] [PubMed] [Google Scholar]
- 95.Grenoble DE, Katz JL. Journal of Dental Research. 1971;50:109. doi: 10.1177/00220345710500010301. [DOI] [PubMed] [Google Scholar]
- 96.Hall DR, Nakayama WT, Grenoble DE, Katz JL. Journal of Dental Research. 1973;52:393. doi: 10.1177/00220345740530050901. [DOI] [PubMed] [Google Scholar]
- 97.Singh S, Katz JL. Journal of Materials Science Letters. 1989;8:165. [Google Scholar]
- 98.Singh S, Katz JL, Antonucci J, Penn RW, Tesk JA. Journal of Non-Crystalline Solids. 1988;102:112. [Google Scholar]
- 99.Singh S, Katz JL, Antonucci J, Penn RW, Tesk JA. Materials Research Society Symposium Proceedings: Biomedical Materials and Devices. Pittsburgh: 1989. pp. 599–604. [Google Scholar]
- 100.Singh S, Katz JL. MRS Proceedings. 1988:599–604. [Google Scholar]
- 101.Gilmore RS, Katz JL. Journal of Materials Science. 1982;17:1131. [Google Scholar]
- 102.Katz JL. Bulletin de la Société Chimique de France. 1985;4:514. [PubMed] [Google Scholar]
- 103.Katz JL, Akers AS, Germiller JA, Obremski S, Singh S. Bioceramics (Proceedings of 1st International Bioceramics Symposium) Tokyo: 1989. pp. 86–91. [Google Scholar]
- 104.Lakes RS, Katz JL. Journal of Biomechanics. 1974;7:259. doi: 10.1016/0021-9290(74)90017-7. [DOI] [PubMed] [Google Scholar]
- 105.Katz JL, Ukraincik K. Journal of Biomechanics. 1971;4:221. doi: 10.1016/0021-9290(71)90007-8. [DOI] [PubMed] [Google Scholar]
- 106.Katz JL. Journal of Materials Science Letters 0261-8028/88. 1988 [Google Scholar]
- 107.Katz JL. Journal of Materials Science Letters. 1988;7:133. [Google Scholar]
- 108.Yoon HS, Katz JL. 1984 Ultrasonic Symp Proc. New York City: 1985. pp. 786–789. [Google Scholar]
- 109.Katz JL, Kwon SJ. Advances in Dental Research. 1987;1:39. doi: 10.1177/08959374870010011001. [DOI] [PubMed] [Google Scholar]
- 110.Lemons RA, Quate CF. Applied Physics Letters. 1974;24:163. [Google Scholar]
- 111.Lemons RA, Quate CF. Physical Acoustics. 1979;14:1. [Google Scholar]
- 112.Briggs GAD. Acoustic Microscopy. Clarendon Press; Oxford: 1992. [Google Scholar]
- 113.Lisy F, Hiltner A, Baer E, Katz JL, Meunier A. Journal of Applied Polymer Science. 1994;52:329. [Google Scholar]
- 114.Wilson RG, Weiglein Journal of Applied Physics. 1984;55:3261. [Google Scholar]
- 115.Biro L, Das P, Meunier A, Katz JL. Ultrasonics Intemational’83 Proceedings. 1983:79–84. [Google Scholar]
- 116.Das P, Biro L, Meunier A, Yoon HS, Katz JL. 1982 Ultrasonics Symposium Proceedings. 1983:718–723. [Google Scholar]
- 117.Meunier A, Katz JL, Christel P, Sedel L. Journal of Orthopaedic Research. 1988;6:770. doi: 10.1002/jor.1100060521. [DOI] [PubMed] [Google Scholar]
- 118.Zimmerman MC, Meunier A, Katz JL, Christel P. Transactions on Biomedical Engineering. 1990;37:433. doi: 10.1109/10.55634. [DOI] [PubMed] [Google Scholar]
- 119.Katz JL, Meunier A. Journal of Biomechanical Engineering. 1993;115:543. doi: 10.1115/1.2895537. [DOI] [PubMed] [Google Scholar]
- 120.Bumrerraj S, Katz JL. Annals of Biomedical Engineering. 2001;29:1. doi: 10.1114/1.1424908. [DOI] [PubMed] [Google Scholar]
- 121.Chan MF, Glynn Jones JC. Journal of Dental Research. 1992;20:287. [Google Scholar]
- 122.Dunne SM, Gainsford ID, Wilson NHF. International Dental Journal. 1997;47:123. doi: 10.1002/j.1875-595x.1997.tb00777.x. [DOI] [PubMed] [Google Scholar]
- 123.Marshall GW, Balloch M, Tench RJ, Kinney JH, Marshall SJ. Dental Materials. 1993;9:265. doi: 10.1016/0109-5641(93)90072-x. [DOI] [PubMed] [Google Scholar]
- 124.Nordbo H, Leirskar J, von der Fehr FR. Quintessence International. 1998;29:5. [PubMed] [Google Scholar]
- 125.Meiers JC, Kresin J. Operative Dentistry. 1996;21:153. [PubMed] [Google Scholar]
- 126.Nakabayashi N, Saimi Y. Journal of Dental Research. 1996;75:1706. doi: 10.1177/00220345960750091401. [DOI] [PubMed] [Google Scholar]
- 127.Sano H, Yoshikawa T, Pereira PNR, Kanemura N, Morigami M, Tagami J, Pashley DH. Journal of Dental Research. 1999;78:906. doi: 10.1177/00220345990780041101. [DOI] [PubMed] [Google Scholar]
- 128.Nakabayashi N. Proceedings of the Finnish Dental Society. 1992;88(Suppl 1):321. [PubMed] [Google Scholar]
- 129.Wang Y, Spencer P. Journal of Dental Research. 2003;82:141. doi: 10.1177/154405910308200213. [DOI] [PubMed] [Google Scholar]
- 130.Spencer P, Swafford JR. Quintessence International. 1999;30:501. [PubMed] [Google Scholar]
- 131.Spencer P, Wang Y, Walker MP, Wieliczka DM, Swafford JR. Journal of Dental Research. 2000;79:1458. doi: 10.1177/00220345000790070501. [DOI] [PubMed] [Google Scholar]
- 132.Van Meerbeek B, Celis MHJP, Roos JR, Braem M, Lambrechts P, Vanherle G. Journal of Dental Research. 1993;72:1423. doi: 10.1177/00220345930720101201. [DOI] [PubMed] [Google Scholar]
- 133.Hashimoto M, Ohno H, Kaga M, Sano H, Endo K, Oguchi H. Journal of Dental Research. 2002;81:74. doi: 10.1177/002203450208100116. [DOI] [PubMed] [Google Scholar]
- 134.Chase DB. In: Analytical Raman Spectroscopy. Grasselli JG, Bulkin BJ, editors. John Wiley & Sons, Inc; 1991. pp. 21–43. [Google Scholar]
- 135.Walton AD, Deveney MJ, Koenig JL. Calcified Tissue Research. 1970;6:162. doi: 10.1007/BF02196195. [DOI] [PubMed] [Google Scholar]
- 136.Wang Y, Spencer P. Journal of Biomedical Materials Research. 2002;59:46. doi: 10.1002/jbm.1215. [DOI] [PubMed] [Google Scholar]
- 137.Spencer P, Wang Y. Journal of Biomedical Materials Research. 2002;62:447. doi: 10.1002/jbm.10364. [DOI] [PubMed] [Google Scholar]
- 138.Yourtee DM, Smith RE, Russo KA, Burmaster S, Cannon JM, Eick JD, Kostoryz EL. Journal of Biomedical Materials Research. 2001;57:523. doi: 10.1002/1097-4636(20011215)57:4<522::aid-jbm1198>3.0.co;2-9. [DOI] [PubMed] [Google Scholar]
- 139.Spencer P, Katz JL, Tabib-Azar M, Wang Y, Wagh A, Nomura T. In: Tissue Engineering and Novel Delivery Systems. Lewandrowski KU, Wise DL, Trantolo DJ, Haserci V, Yaszemski M, Altobeli DE, editors. Marcel Decker; New York: 2004. p. 599. [Google Scholar]
- 140.Sasakik N, Odajima S. Journal of Biomechanics. 1996;29:655. doi: 10.1016/0021-9290(95)00110-7. [DOI] [PubMed] [Google Scholar]
- 141.Balooch M, Wu-Magidi IC, Balaz A, Lundkvist AS, Marshall SJ, Marshall GW, Siekhaus WJ, Kinney JH. Journal of Biomedical Materials Research. 1998;40 doi: 10.1002/(sici)1097-4636(19980615)40:4<539::aid-jbm4>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 142.Zhang Y, Agee K, Nor J, Carvalho R, Sachar B, Russell C, Pashley D. Dental Materials. 1998;14:222. doi: 10.1016/s0109-5641(98)00035-9. [DOI] [PubMed] [Google Scholar]
- 143.Sano H, Takatsu T, Ciucchi B, Russell CM, Pashley DH. Journal of Dental Research. 1995;74:1093. doi: 10.1177/00220345950740041001. [DOI] [PubMed] [Google Scholar]
- 144.Schulze KA, Marshall OSSAGW, Gansky SA, Marshall SJ. Journal of Dental Research. 2002;81:139. [Google Scholar]
- 145.Leloup G, D’Hoore W, Bouter D, Degrange M, Vreven J. Journal of Dental Research. 2001;80:1605. doi: 10.1177/00220345010800070301. [DOI] [PubMed] [Google Scholar]
- 146.Dean JC, Tisdel CL, Goldberg VM, Parr J, Davy D, Stevenson S. Journal of Arthroplasty. 1995;10:830. doi: 10.1016/s0883-5403(05)80083-x. [DOI] [PubMed] [Google Scholar]
- 147.Goldberg VM, Stevenson S, Feighan J, Davy D. Clinical Orthopaedics and Related Research. 1995;319:122. [PubMed] [Google Scholar]
- 148.Feighan J, Goldberg VM, Davy D, parr JA, Stevenson S. Journal of Bone and Joint Surgery. 1995;77:1380. doi: 10.2106/00004623-199509000-00015. [DOI] [PubMed] [Google Scholar]
- 149.Bumrerraj S. Department of Biomedical Engineering. Case Western Reserve University; Cleveland, OH: 1999. [Google Scholar]
- 150.Chang CS, Misra A. Journal of Engineering Mechanics. 1990;116:1077. [Google Scholar]
- 151.Misra A, Chang CS. International Journal of Solids and Structures. 1993;30:2547. [Google Scholar]
- 152.Van Mier JGM. Fracture Processes of Concrete. CRC Press; Boca Raton, FL: 1997. [Google Scholar]
- 153.Gao H, Klein P. Journal of the Mechanics and Physics of Solids. 1998;46:187. [Google Scholar]
- 154.Chang CS, Askes H, Sluys LJ. Engineering Fracture Mechanics. 2002;69:1907. [Google Scholar]
- 155.Ferrari M, Granik VT, Imam A, Nadeau JC. Advances in Doublet Mechanics. Springer Verlag; Berlin: 1997. [Google Scholar]
- 156.Misra A. Journal of Geophysical Research-Solid Earth Sciences. 1999;104:23,175. [Google Scholar]
- 157.Misra A. In: Numerical Models in Geomechanics. Pietruszczak S, Pande G, Balkema AA, editors. Rotterd, Netherlands: 2004. p. 5. [Google Scholar]
- 158.Thiagarajan G, Misra A. International Journal of Solids and Structures. 2004;41:2919. [Google Scholar]
- 159.Misra A, Spencer P, Marangos O, Wang Y, Katz JL. Journal of Biomedical Materials Research. 2004;70B:56. doi: 10.1002/jbm.b.30012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160.Lakes RS. Viscoelastic Solids. CRC Press; Boca Raton: 1998. [Google Scholar]
- 161.Renugopalakrishnan V, Carrpira LA, Collette TW, Dobbs JC, Chandraksasan G, Lord RC. Z Naturforsch. 1998;53C:383. doi: 10.1515/znc-1998-5-613. [DOI] [PubMed] [Google Scholar]


