Identifying foldable regions in protein sequence from the hydrophobic signal

Abstract

Structural genomics initiatives aim to elucidate representative 3D structures for the majority of protein families over the next decade, but many obstacles must be overcome. The correct design of constructs is extremely important since many proteins will be too large or contain unstructured regions and will not be amenable to crystallization. It is therefore essential to identify regions in protein sequences that are likely to be suitable for structural study. Scooby-Domain is a fast and simple method to identify globular domains in protein sequences. Domains are compact units of protein structure and their correct delineation will aid structural elucidation through a divide-and-conquer approach. Scooby-Domain predictions are based on the observed lengths and hydrophobicities of domains from proteins with known tertiary structure. The prediction method employs an A*-search to identify sequence regions that form a globular structure and those that are unstructured. On a test set of 173 proteins with consensus CATH and SCOP domain definitions, Scooby-Domain has a sensitivity of 50% and an accuracy of 29%, which is better than current state-of-the-art methods. The method does not rely on homology searches and, therefore, can identify previously unknown domains.

INTRODUCTION

Completion of 200 genome-sequencing projects has led to an astronomical growth in sequence data, leaving the massive task of structural and functional annotation to be addressed. The vast and growing gap between protein sequence and structural data has motivated structural genomics initiatives, which aim to elucidate representative 3D structures for the majority of protein families. A major bottleneck in structural studies is the correct design of constructs: many proteins are either too large or contain unstructured regions, and are thus unsuitable for structural solution (1). It is therefore essential to identify regions in protein sequences likely to be amenable to structural elucidation (2).

The component of globularity in proteins is the domain: a compact, semi-independent, structural unit (3). Wetlaufer (4) first proposed the concept: defining domains as stable units of protein structure that can fold autonomously. Nature often brings several domains together to form multidomain and multifunctional proteins with the possibility of a vast number of combinations. Because domains mostly fold independently, large proteins that may not be amenable to structural solution may yield to a divide-and-conquer approach.

Methods for domain prediction can be divided into three groups: homology searches, analysis of sequence features and de novo structure prediction. Domain assignment methods that are based on homology searches include Domaination (5) and PASS (6). Other such methods include those used to generate domain databases such as Pfam (7–10). Both Domaination and PASS identify domains using the positions of the N- and C-termini of aligned homologous sequences. While effective at identifying distant family members, homology-based methods will not identify the exact structural limits of a domain, which is essential for structural elucidation (11) and will fail to identify domains that have not been rearranged during evolution (5).

Many methods have been developed to delineate domains using sequence features. The amino acids that make up inter-domain linking peptides are distinct from those in domain or loop regions (12). This signal has been utilized by several groups. Armadillo (13) and Domcut (14) predict linkers using a table of likelihood scores for each amino acid to be within a linker region. Bae et al. (15) uses a hidden Markov model and linker index with combined Gibbs sampling and Markov Chain Monte Carlo to estimate the parameters and posterior probabilities. Miyazaki et al. (16), Dong et al. (17) and Sikder and Zomaya (18) utilize position-specific scoring matrices (PSSM) generated from PSI-BLAST to predict domain boundaries. Miyazaki et al. (16) employs a neural network to identify signals between linkers and domains while Dong et al. (17) applies a linker propensity index and Sikder and Zomaya (18) utilizes a support vector machine and linker predictions made by Domcut.

Other methods apply predicted secondary structure and multiple sequence alignment to predict domain location (19–22). DomSSEA (20) applies a simple threading protocol while CHOPnet (19) utilizes a neural network using amino acid flexibility, secondary structure, solvent accessibility and amino acid composition.

Many of these sequence-feature-based methods are no better than a simple guess based on the predicted number of domains, as applied in Domain Guess by Size (DGS) (23). Furthermore, few methods tackle the prediction of discontinuous domains. Discontinuous domain prediction is an important problem because 45% of multidomain proteins have one or more domains wound from non-contiguous sequence in the polypeptide chain (24).

Finally, SnapDragon (25) and Ginzu-RosettaDOM (26) are programs that utilize de novo protein structure prediction to delineate domains. Although these methods showed some success, exact domain boundary placement is often limited to proteins with two or three domains and the time required for prediction is too long for genome-scale assignment.

The Scooby-Domain (SequenCe hydrOphOBicitY predicts DOMAINs) web application was recently introduced to visually identify foldable regions in a protein sequence (27). Here we present benchmark performance of a new algorithm to automatically predict domain boundaries. Scooby-Domain uses the distribution of observed lengths and hydrophobicities in domains with known 3D structure to predict novel domains and their boundaries in a protein sequence. It utilizes a multilevel smoothing window to determine the percentage of hydrophobic amino acids within a putative domain-sized region in a sequence. Using the observed distribution of domain lengths and percentage hydrophobicities, the probability that the region can fold into a domain or be unfolded is then calculated. A novel algorithm is then applied to calculate the most likely domain architecture of the protein.

Scooby-Domain was benchmarked on proteins with known 3D structure and defined domain architecture. Precise domain definition, even with a known structure, is a difficult problem and several databases with alternative definitions exist. To fairly test our methodology we have used two databases, CATH (28) and SCOP (29), as well as a consensus definition. The benchmark sets contain proteins with a range of domain number and domain–domain connectivity and is a challenging test for domain prediction algorithms.

MATERIALS AND METHODS

Domain size and percentage hydrophobicity

The distribution of domain size and hydrophobicity was calculated using the S35 domain representatives from the CATH domain database version 3.0.0 (28). No domain in this set has >35% sequence identity with any other domain. Only the first three classes of the CATH classification were used since class-four proteins have few secondary structures and are unlikely to be comprised of globular domains. Full-sequence data was taken from the corresponding CATH COMBS file. Unlike the ATOM sequences, which may have missing residues, the COMBS sequences attempt to provide the full sequence, by filling in any missing residues in the PDB atom fields with those in the PDB SEQRES fields. The length of the domain sequences was restricted to between 34 and 251 residues. Domains outside this range are unlikely to have a single hydrophobic core (30). For each domain, percentage hydrophobicity was calculated using a simple binary hydrophobicity scale, where 11 amino acid types are considered as hydrophobic: Ala, Cys, Phe, Gly, Ile, Leu, Met, Pro, Val, Trp and Tyr (31). Other scales were trialled but were found to produce poorer results in benchmarking.

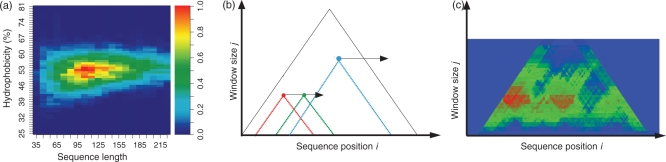
A 3D histogram of the distribution of domain sequence lengths versus their corresponding hydrophobicities was created using a square averaging window. The window sums the number of domain sequences that it encapsulates within the distribution. The resulting value is then placed at the central position of the window. The window moves along the distribution one unit at a time, covering the entire dataset. The square window has a size of 19 residues by 1 unit percentage hydrophobicity, which means that it captures all domain sequences within a length of 19 residues and with an average hydrophobicity resolution of 1%. Each position in the final 3D histogram was then scaled to a value between 0 and 1, where 1 is the highest point in the distribution corresponding to the most frequent observation (Figure 1a). These values were used as a reference to judge whether a sequence fragment can form a domain based on its length and average hydrophobicity.

Figure 1.

(a) Domain probability matrix. CATH domains as a function of their sequence length and percentage hydrophobicity. The red areas represent regions that have a high frequency of domain occurrence, while the blue areas represent regions that have a low frequency of domain occurrence. (b) Multilevel smoothing window. Smoothing windows of increasing length are used to calculate the average hydrophobicity along the sequence. The horizontal axis corresponds to the sequence position, i, and the vertical axis represents the window length, j. Hydrophobicity values are plotted at the position representing the sequence position of the centre point of the smoothing window and the window length (i, j). (c) Domain prediction. For each position in the multilevel smoothing (b) the length of the smoothing window and calculated average hydrophobicity is converted to a probability that it will fold into a domain, based on the lengths and hydrophobicities observed in the distribution of CATH domains (a).

Generating the domain probability matrix

Scooby-Domain uses a multilevel smoothing window to predict the location of domains in a novel sequence (Figure 1b). The window size, representing the length of a putative domain, is incremented starting from the smallest domain size observed in the database to the largest domain size. The window size must be an odd number and the size is incremented by two each time. Each smoothing window calculates the fraction of hydrophobic residues it encapsulates along a sequence, and places the value at its central position. This leads to a 2D matrix, where the value at cell (i, j) is the average hydrophobicity encapsulated by a window of size j that is centred at residue position i. The matrix has a triangular shape with the apex corresponding to a window size equal to the length of the sequence.

Matrix values are converted to probability scores by referring to the observed distribution of domain sizes and hydrophobicities described earlier, i.e. given an average hydrophobicity and window length, the probability that it can fold into a domain is found directly from the observed data. Visualization of Scooby-Domain plots can be used to effectively identify regions that are likely to fold into domains, as well as unstructured regions (27).

Automatic domain boundary assignment

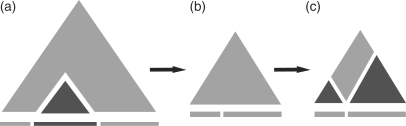
Scooby-Domain employs an A*-search algorithm to search through a large number of alternative domain annotations. The top ten highest probabilities in the Scooby-Domain plot are identified, each one becoming the first predicted domain in a set of alternative predictions (Figure 2). To encourage alternative predictions that are distinct, a new start site must not be within a diamond-shaped region, of width 17 residues, surrounding an old start site.

Figure 2.

Protocol for domain assignment. (a) The highest scoring window (first predicted domain) is identified in the probability matrix and the sequence region it encapsulates (dark grey triangle) is removed from the sequence. (b) The resulting sequence fragments are rejoined and the probability matrix recalculated. (c) The smoothing windows that encapsulate the last 15 residues of the N-terminal fragment and the first 15 residues of the C-terminal fragment have their probabilities set to zero (white bands). If the next highest scoring region is found in the light grey region, then the excised domain will be discontinuous, otherwise it will be continuous.

The corresponding sequence stretch for the first predicted domain is removed from the sequence (Figure 2a). Therefore, the first predicted domain will always have a continuous sequence and further domain predictions can encompass discontinuous domains. If the excised domain occupies an interior position in the sequence, the resulting N- and C-terminal fragments are rejoined and a new probability matrix is recalculated (Figure 2b).

Upon rejoining the sequence fragments, once a domain has been removed, it is important that the probabilities on either side of a join are down-weighted to avoid small fragments being involved in subsequent domain delineations. To enforce this, a minimum discontinuous segment size of 15 residues is applied (Figure 2c).

The search process is repeated until there are <34 residues remaining—the size of the smallest domain; or until there are no probabilities greater than 0.33—an arbitrary cutoff to prevent non-domain-like regions from being predicted as a domain.

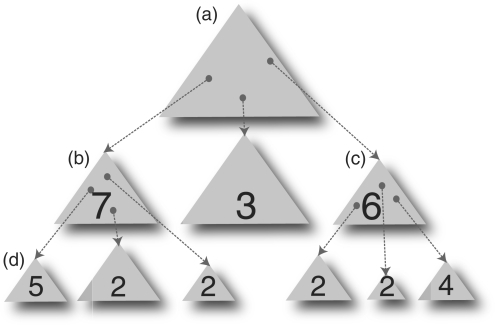
The A*-search algorithm considers combinations of different domain sizes, using a heuristic function to guide the search (Figure 3). Instead of just considering the domain prediction with the highest score for each step of the algorithm, A*-search memorizes a list of up to ten possible domain predictions, and each of these are represented as a node in the tree-like search space. Each possible domain solution will be a path or branch in the search tree. The heuristic score of new predictions is compared with the heuristic scores from domains predicted in the previous step. Consideration of these alternative paths to other possible solutions would avoid the search being trapped in a local maximum. Since A*-search is a generic algorithm, its description can be found in other texts that cover artificial intelligence, for example, the original paper by Hart et al. (32). The implementation details specific to domain prediction are discussed below.

Figure 3.

Different stages in the A*-search algorithm. (a) The top-most triangle represents the Scooby-Domain domain-probability matrix for a protein sequence. The search for protein domains in a query sequence is like travelling through a maze. The centre of the maze being the best domain prediction. In this figure, each triangle is like a different path through the maze, and each level below the first triangle represents one more domain region being predicted. Each ‘hotspot’ in the triangular matrix, is used to locate the exact region of the sequence with highest probability of a globular domain being formed. Three highest scoring hotspots in the first matrix are identified and highlighted with a dot in the figure, with scores of 7, 3 and 6, respectively. This leads to the addition of three new paths, with each one being the recalculated matrix for the remaining sequence, after the first domain region was predicted and removed from the original sequence. (b) Each triangle also represents a node in the search tree, where each node could branch to a different path that may lead to the solution. The highest scoring triangle (7) is searched for new hotspots, which have scores of 5, 2 and 2. (c) Regardless of level, the node with the next highest score would be searched upon, until no further domain regions can be predicted. In this example, it is the node with a score of 6. This allows the algorithm to consider different parallel paths through the ‘maze’, covering a larger area, and avoiding the search being confined to a ‘dead end’ path. (d) The next node to search following the highest scoring predictions has a score of 5.

The heuristic score, h, is defined by the following equation:

1

where ∑P is the sum of probabilities for each domain predicted so far; b represents the number of boundaries assigned; L is the length of the original sequence and l is the remaining length of the sequence in which no domain has yet been predicted.

To prevent large numbers of connections between domains, a penalty is applied when a discontinuous domain segment is assigned: b + 1 equals the number of protein domains if all domains are continuous, otherwise this value will be larger and effectively lowers the score.

Other heuristic measures were trialled, but the one described here had the best benchmark results. The heuristic increases the likelihood of a boundary being close to the middle of the sequence, but this had no detrimental effect on discontinuous domain predictions, where boundaries are often not in the middle of the sequence.

In an optimal A*-search, an admissible heuristic function would be used, which means the estimated cost to reach the optimal solution would always need to be larger than the actual cost of finding the optimal solution, otherwise the optimal solution is not guaranteed. Since the equation used is not proven to be admissible, there is no guarantee that an optimal solution will always be reached (33).

Integration of multiple sequence alignment

The performance of Scooby-Domain was assessed with the inclusion of homology information. Homologues of the query sequence were detected using PSI-BLAST (34) searches of the SWISS-PROT database (35) and multiple sequence alignments (MSA) were generated using PRALINE (36). Only those sequences with <90% sequence identity and >70% coverage of the query sequence were kept for alignment to the query sequence. All sequences in the alignment were trimmed such that they matched the start and end points of the query sequence.

A domain-probability matrix was constructed for each sequence in the MSA and the scoring matrices from each of the multiply-aligned sequences were summed and cumulated into a master array for tallying scores. Each value in the master matrix is divided by the number of sequences in the MSA. The positions in the master matrix that correspond to gaps in the query sequence are removed, resulting in a matrix with the same width as the length of the query sequence. This final matrix is used for automatic domain-boundary assignment as discussed earlier.

Integration of linker propensities

Two linker prediction scoring systems, Domcut (14) and PDLI (17) were used independently to complement Scooby-Domain's; prediction. A negative number represents a higher propensity for a linker in both of these scoring schemes. Therefore, the scores were multiplied by −1 to reverse the polarity of the scoring. Scaling was performed on these scoring schemes such that the range of the scores is within 0.0 and 0.5. The Scooby-Domain multi-dimensional smoothing window adds the linker prediction scores at its N- and C- termini to the domain probability matrix (the combined linker prediction will have a maximum score of 1.0). To avoid increasing the chance of assigning a domain in a large unstructured region, the scores were added to the triangular matrix only if the domain probability value exceeds a threshold probability score. A threshold of 0.25 was found to be best after assessing a number of test cases.

To test the added value of the combined approach, the Domcut and PDLI methods were re-implemented and their domain-prediction performances were compared with Scooby-Domain: as a stand-alone predictor; or with complementary predictions made by Domcut or PDLI. When Scooby-Domain was combined with Domcut, the raw Domcut score, rather than the normalized score was used for Scooby-Domain predictions. For the Scooby-Domain, Domcut and MSA combination, Domcut predictions were obtained for the query sequence only, and not for each sequence in the MSA. This is because when Domcut is applied to all sequences in the MSA prediction, results for Domcut are close to random. When PDLI and MSAs are combined with Scooby-Domain, PDLI uses all sequences in the MSA to make a prediction.

Benchmarking

Predictions were assessed using a set of proteins with known structural domain assignments. A non-redundant list of protein sequences, with known 3D structures, was obtained from the VAST non-redundant PDB chain set (www.ncbi.nlm.nih.gov/Structure/VAST/nrpdb.html). This was matched with the corresponding entries in CATH (28) and SCOP (29), to create two test sets: a non-redundant CATH test set and a non-redundant SCOP test set. Where a domain boundary consists of several residues, the central position between the start and end of the boundary is used. Full-length sequences were taken from the PDB SEQRES fields of the ASTRAL database (37). Our test sets are much more rigorous than those used by other methods, as they contain sequences with three or more domains and sequences with discontinuous domains. These sequences were often under-represented or omitted by other groups, for example Liu et al. (19) and Dong et al. (17).

Both the CATH and SCOP databases define a domain as a particular core structure of secondary structure elements. Both of these databases allow some degree of elaboration upon domain definition, however, CATH's; definition is more flexible and delineates smaller domains in comparison to SCOP (38). Direct comparisons of the two databases showed that they agree on the majority of domain annotations (39, 40). As an additional test, the intersection of CATH and SCOP was also used as an optimal test set, using a consensus approach (CATH ∩ SCOP). For this set, only proteins that had boundary assignments corresponding to within 10 residues between the two definitions were used.

Scooby-Domain performance was compared to PDLI, Domcut and an equal-cut method. Equal-cut is a naive method, similar to DGS (23), that is used as an experimental control. First, a rough estimate of the number of domains in a sequence is calculated by dividing the sequence length by the average domain size of 100 residues, and rounding to the closest integer. The sequence was then chopped as evenly as possible based on the number of domains. It was impossible to fairly assess other methods on our test sets. For example, DomSSEA (20) uses a threading procedure that would identify the original query and others apply domain-profile searches in an initial attempt to find known domains.

Predictions were assessed using various error-window sizes around the known domain boundary. A correct boundary prediction is one that falls within the error window. Two measures of performance for the predictions were utilized. The first measure is sensitivity, which is the percentage of boundaries, out of all the boundaries collected from all proteins, that were correctly predicted:

2

where TP is the number of true positive boundary predictions and FN the number of false negatives. The second measure of performance is positive predictive value (PPV), which is the percentage of all boundary predictions that are correct:

3

where FP is the number of false positive boundary predictions. PPV is called accuracy for the purpose of this study.

RESULTS

Comparison of different test sets

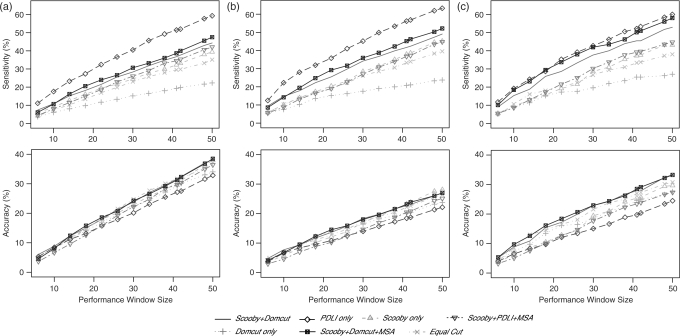
Three test sets were used in this study: CATH, SCOP and CATH ∩ SCOP. The number of sequences in each test set is shown in Table 1. Accuracies for all methods tested were around 10% higher in the CATH test set compared to the SCOP set (Figure 4 and Table 2). This could be attributed to the higher proportion of linkers in the CATH set, which makes it easier to predict boundaries by chance. The equal cut method achieved its highest accuracy on this set.

Table 1.

Number of proteins in each dataset

	CATH	SCOP	CATH ∩ SCOP
All	611	496	173
Continuous	336	418	150
Discontinuous	275	78	23
Total number of unique sequences			789

Figure 4.

Sensitivity and accuracy versus different performance window size around the domain boundary. Window size is the total number of residues making up the window. Sensitivity (top) and accuracy (bottom) are shown for the CATH dataset (a), SCOP dataset (b), and the CATH ∩ SCOP dataset (c). Continuous line, Scooby+Domcut; Diamond with dashed line, PDLI only; triangle with dashed line, Scooby only; inverted triangle with dashed line, Scoopy+PDLI+MSA; plus sign with dotted line, Domcut only; crossed square with continuous line, Scooby+Domcut+MSA; Cross mark with dashed dotted line, Equal cut.

Table 2.

Sensitivity and accuracy at performance window size ± 20 residues

	CATH		SCOP		CATH ∩ SCOP
Methods	Sensitivity	Accuracy	Sensitivity	Accuracy	Sensitivity	Accuracy
Scooby+Domcut+MSA	38.7	31.3	45.2	23.2	50.2	28.5
Scooby+Domcut	36.8	31.6	41.7	22.7	45.5	27.9
Scooby only	32.3	30.4	37.9	23.3	37.3	25.5
Domcut only	19.3	29.3	20.8	20.1	25.5	24.6
Equal cut	29.5	31.7	33.2	22.2	33.3	27.0
PDLI only	51.5	27.3	56.7	18.4	52.2	19.7
Scooby+PDLI+MSA	34.5	29.7	36.7	20.5	39.2	23.5

CATH assigns more domains and linkers in a protein than SCOP, and has an average 2.52 linkers per protein (1376 linkers in 611 proteins) while SCOP has an average 1.50 linkers per protein (746 linkers in 496 proteins). However, Scooby-Domain achieved similar prediction accuracies in both CATH and CATH ∩ SCOP sets. CATH ∩ SCOP has the smallest average number of linkers per protein, 1.47 (255 linkers in 173 proteins), suggesting that Scooby-Domain prediction accuracies are not artificially improved by a larger number of linkers in CATH.

CATH assigns domains purely on the basis of structure, whereas SCOP domains are assigned on the basis of inherited functional units. Therefore, SCOP domains can often be made up of two or more CATH domains. The Scooby-Domain algorithm tries to predict domains based on sequence characteristics related to structural principles and should therefore perform better on the CATH set compared to the SCOP set, which it does. Interestingly, Scooby-Domain had the best overall performance on the consensus CATH ∩ SCOP set, suggesting that Scooby-Domain can successfully identify domains that qualify as being both structural and functional.

Enhanced sensitivity with linker predictions

Predictions made by utilizing domain-boundary predictions produced from other sources are compared in Figure 4 and Table 2. A window size of ±20 residues (41 residues) is used for the results presented below. Alone, Scooby-Domain scored a sensitivity of 37.3% on the CATH ∩ SCOP test set. Domcut is the least sensitive method amongst those tested, but addition of the Domcut predictions into Scooby-Domain surprisingly increases Scooby-Domain's; overall score. The sensitivity for Domcut alone is 25.5%, less than the equal-cut method (33.3%). The combination of Scooby-Domain and Domcut achieved a sensitivity of 45.5% and an accuracy of 27.9%. The combined Scooby-Domain and Domcut method was determined to be the best of the three in terms of sensitivity and accuracy.

Homology information enhances prediction

We further determined whether improvements in performance could be obtained if combined Scooby-Domain and Domcut methodology was used in combination with homology information. Domcut benchmark results were close to random when Domcut was applied to all sequences in the MSAs. Therefore, when combined with Scooby-Domain, Domcut was applied to the query sequence only, while Scooby-Domain was applied to all sequences in the MSA. Sensitivity was improved from 45.5% to 50.2% and accuracy was improved from 27.9% to 28.5%.

PDLI, which makes linker predictions based on MSA, has the best sensitivity (52.2%) but the worst accuracy (19.7%). Because PDLI overpredicts linkers, it finds more linkers in the CATH set (Figure 4), but consistently has the lowest accuracy compared to other methods assessed. The combination of the PDLI method with Scooby-Domain significantly reduces the sensitivity and accuracy.

Scooby-Domain (Scooby+Domcut+MSA) has the highest sensitivity, 50.2%, in the CATH ∩ SCOP set in comparison to the other two datasets, with an accuracy of 28.5%. For the CATH dataset, it achieved a sensitivity of 38.7% and the highest accuracy, 31.3%, of the three datasets. For the SCOP dataset, Scooby-Domain achieved a sensitivity of 45.1%, but a lower accuracy of 23.1%.

Results for different domain numbers and types

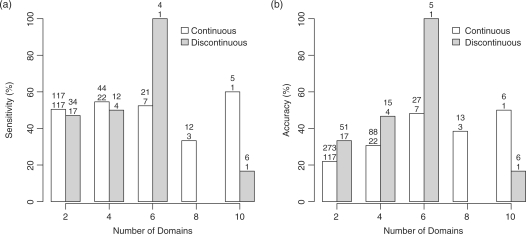
The sensitivity and accuracy of prediction for multidomain proteins as a function of domain number is shown in Figure 5. Proteins are divided into two groups: continuous and discontinuous. In the latter group, at least one domain is wound from non-contiguous portions of the polypeptide chain.

Figure 5.

Sensitivity (a) and accuracy (b) of Scooby-Domcut (Scooby+Domcut+MSA), at window size of ± 20, for proteins with more than one domain. The white bars represent proteins with continuous domains only. The grey bars represent proteins containing discontinuous domains. There are two numbers above each bar. The top number has a different meaning for each graph: in the sensitivity graph (a) it represents the number of real linkers for each domain; and in the accuracy graph (b) it represents the number of linkers predicted for the binned proteins. For both graphs, the bottom number is the number of proteins with the corresponding number of domains.

The method is equally sensitive at delineating proteins with either continuous or discontinuous domains. Sensitivity is 50.4% and 47.1% for two-domain proteins with continuous and discontinuous domains respectively and 54.6% and 50.0% for three domains.

The method more accurately delineates proteins with discontinuous domains. The accuracy for two-domain proteins is 22.0% and 33.3%, for proteins with continuous and discontinuous domains respectively; and for three domain proteins, 30.7% and 46.7% (Figure 5b). The majority of domain prediction methods have not been developed to identify discontinuous domains and ignore such proteins in their benchmarking tests.

Sensitivity and accuracy for proteins with four or more domains is not statistically significant due to the lack of proteins in the test data. However, it is interesting to note that 100% sensitivity and accuracy is scored for a protein which includes one discontinuous domain (PDB 1dq3A). The results show that Scooby-Domain delineates proteins with discontinuous domains with a sensitivity and accuracy as good as for proteins with continuous domains. This is important to the structural genomics initiative because the presence of discontinuous domains in the protein sequence would not confound prediction results, thus the predictions are more reliable, and will aid the discovery of previously unknown protein domains.

Examples of predictions for proteins with both continuous and discontinuous domains are shown in Figure 6 and 7. The corresponding protein structures are shown and coloured by the predicted domain region. Each is bounded by the predicted middle position of a probable linker region. In Figure 6a, two distinctive hotspots representing the two larger domains of 1LK5 chain A (Figure 6b) are discernible. Scooby-Domain had difficulty predicting the exact domain boundary (junction of red and green region) at the end of a β-strand. Figure 7a shows an example of a successful discontinuous domain prediction by Scooby-Domain. The two segments of the discontinuous domain are coloured in red and pink, respectively. Similar to the previous example, Scooby-Domain did not precisely match the inter-domain region, however, the boundary is within the ±20 residue window. Figure 7b demonstrates how Scooby-Domain accurately delineated the monoclonal antibody heavy chain for Mus musculus (PDB 1IGT, chain B).

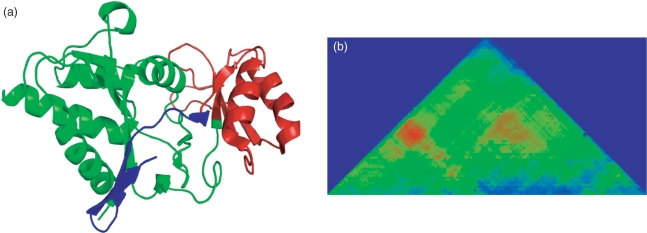
Figure 6.

The Scooby–Domain (Scooby+Domcut+MSA) prediction for the hyperthermostable D–ribose–5–phosphate isomerase from Pyrococcus horikoshii (PDB 1LK5, chain A). (a) The structure of 1LK5, coloured according to the linker prediction by Scooby–Domain. A discontinuous domain is predicted at residues 1–136 (green) and 207–229 (blue). A second domain is predicted at residues 137–206 (red). The CATH domain annotation consists of two domains, a discontinuous domain made of two segments 1–128 and 208–229; and the continuous domain 129–207. (b) The Scooby–Domain probability plot for 1LK5.

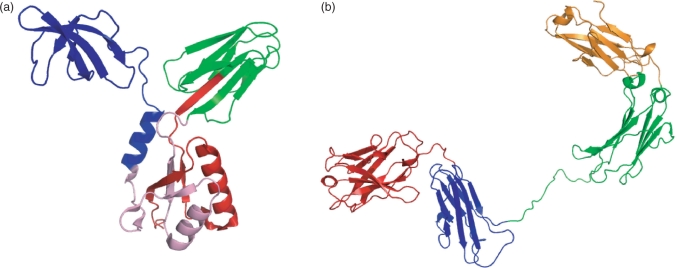
Figure 7.

The Scooby–Domain (Scooby+Domcut+MSA) predictions mapped to structures. (a) Transcription factor NusG from Aquifex aeolicus (PDB 1M1G, chain C), coloured according to the linker prediction by Scooby–Domain. A discontinuous domain is predicted at residues 1–55 (red) and 131–174 (pink), two continuous domains are predicted at residues 56–130 (green) and 175–249 (blue). The CATH domain annotation consists of three domains; a discontinuous domain (1–49,131–190) and two continuous domains (50–131 and 191–249). (b) IgG2 monoclonal antibody heavy chain from Mus musculus (PDB 1IGT, chain B), coloured according to the linker prediction by Scooby–Domain. Four continuous domains are predicted at residues 1–117 (red), 118–228 (blue), 229–360 (green) and 361–474 (orange). The corresponding CATH domain annotation consists of four continuous domains at residues 1–114, 115–236, 250–360 and 361–474.

In summary, Scooby-Domain can successfully identify discontinuous regions and can easily delineate distinct domains separated by long linker regions. Precise domain boundary placement is a very difficult problem, even when a structure is known. For example, the CATH domain database uses a consensus of computational methods, combined with a manual assessment when automatic methods do not agree (24). Scooby-Domain, therefore, performs very well at identifying domains and their boundaries using only sequence information.

DISCUSSION

Domain prediction based on hydrophobicity

The globular structure of a protein cannot be achieved by any combination of amino acids, as certain principles of structure must be obeyed. Previous studies have shown that there is a required ratio of hydrophobic to hydrophilic residues. Molecules with too many hydrophobic residues aggregate in solution, and largely hydrophilic proteins fail to form a stable hydrophobic core (41,42).

Scooby-Domain is a domain prediction method based on the observed properties of proteins with known 3D structure. Smaller domains are found to have a higher proportion of hydrophilic residues, while larger domains that maintain a single hydrophobic core are constrained by their length, with an average size of 100 residues (Figure 1). Scooby-Domain takes advantage of the above criteria to identify local deviations in hydrophobicity to predict the protein domain architecture.

Given the simplicity of our method, Scooby-Domain is surprisingly powerful. It is likely that its performance can be further improved by incorporating other information, for example, secondary structure prediction (20). Furthermore, using information from methods that predict transmembrane regions is likely to improve Scooby-Domain's; ability to delineate solvent-exposed domains in membrane proteins.

Comparison with other methods

At a window size of ±20 residues, Scooby-Domain has a sensitivity of 50.2% and an accuracy of 28.5% (CATH ∩ SCOP set). Performance is similar to CHOPnet (19), which has a sensitivity of 46–51%. The accuracy of CHOPnet was not computed.

Armadillo has a sensitivity of 27 ± 3% and an accuracy of 35 ± 4% (13) and the PDLI method (17) has a sensitivity of 71% and specificity of 34%. However, Armadillo and PDLI assess a linker as a region consisting of multiple residues, rather than as a single residue position as applied here, which implicitly makes the window size larger and the predictions easier. On our dataset, PDLI has a sensitivity of 52.2% and accuracy of 19.7%. Domcut (14) is reported by Dong et al. (17) to have low sensitivity (23%) and specificity (9%) in comparison to other methods, which is consistent with our observation.

DomainDiscovery (18), which also applies linker predictions from Domcut, has a sensitivity (termed recall in their paper) and accuracy (termed precision in their paper) of ∼31% and 9%, respectively at a window size of ±15 residues. At this window size, Scooby-Domain with Domcut and MSA has a sensitivity of 42.0% and accuracy of 22.9%.

DomSSEA (20) used the CATH database for their test set, therefore, its performance will be compared with Scooby-Domain tested with our CATH test set. For multi-domain proteins, DomSSEA has a sensitivity of 24.7% and Scooby-Domain has a sensitivity of 38.7%. For proteins with two continuous domains, DomSSEA has a sensitivity of 49% compared with Scooby-Domain's; 50.4%. For proteins with two domains and at least one discontinuous domain, Scooby-Domain has a higher sensitivity (35.4%) than DomSSEA (33.1%), but a lower accuracy (36.0%) than DomSSEA (49.7%). It can be observed from these rough comparisons that the performance of Scooby-Domain is comparable, and often better, than other sequence-feature-based methods.

Domaination (5) is an example of a method that uses homology searches to predict domains. We applied Domaination to our test set and added the predictions to Scooby-Domain. The combined method has a similar sensitivity (50.6%) and accuracy (29.3%) to Scooby+Domcut+MSA, and has a higher sensitivity but lower accuracy than Domaination alone. However, Domaination is significantly more computationally expensive, therefore, its use is restricted to small datasets. In addition, homology methods cannot identify seldom encountered domains. Combining Domaination and Scooby-Domain would likely improve Domaination's; homology detection.

The ab initio methods SnapDRAGON (25) and RosettaDOM (26) currently have the best sensitivities and accuracies for boundary prediction. Both these methods employ protein-fold prediction to identify domain boundaries. For a window size of ±10 residues, RosettaDOM has lower sensitivity (28.6%) than SnapDRAGON (42.3%). However, RosettaDOM is more accurate (54.6%) than SnapDRAGON (39.8%). Both of these methods are more sensitive and accurate than Scooby-Domain for this window size, but much more computationally expensive.

It is important to note that different protein test sets and assessment criteria were used in the above comparisons. Therefore, these comparisons only provide a ballpark figure of how each of these methods perform in relation to each other. For example, the test set used for this study contains multi-domain sequences and sequences with one or more discontinuous domains, whereas only sequences with two continuous domains were used by Dong et al. (17).

To further assess our methods against others we have applied the Scooby-Domain algorithm to benchmark 2 from Holland et al. (43), which was used in their assessment of methods that assign domains using 3D structure. The dataset is built using a similar methodology as applied in our consensus set, i.e. looking for a consensus between CATH and SCOP definitions. However, while we ensure that boundaries between domains are at equivalent positions in CATH and SCOP, the consensus in benchmark 2 is based on the number of domains assigned and unlike our set, benchmark 2 contains single domain proteins.

Scooby-Domain, using Domcut and MSA, scored a sensitivity of 41.6% and accuracy of 29.0% on the benchmark 2 set, and correctly predicted single domain proteins in 59.3% of cases. Predictions for all proteins can be found in Supplementary Table 1. Scooby-Domain predicted the exact domain number for nearly half of the proteins (71/156), but often overpredicted domain number (65/156). Interestingly, many structure based methods also tend to overpredict domain number on this set (43).

The multidomain proteins in benchmark 2 are particularly hard to predict, as nearly half are made up of discontinuous domains, but Scooby-Domain performs well on the discontinuous subset with a sensitivity of 39.4% and accuracy of 34.8%.

We also tested Scooby-Domain on a set of proteins used by Sikder and Zomaya (18) in their analysis of seven other state-of-the-art methods. This set is based on 50 randomly selected proteins from the benchmark 2 dataset. It is unclear whether these other methods were fairly tested as most use AI algorithms that learn from proteins with known 3D structure, and performances could be artificially enhanced by making predictions on the proteins used to train them. Furthermore, the webservers for some of these methods will perform an initial homology search to first identify any known structures with domain definitions, again leading to an unfair assessment. Nevertheless, predictions by Scooby-Domain with Domcut and MSA (Supplementary Table 2) are comparable to the other seven methods and scores the highest domain placement accuracy, 4.04.

Application of A*-search in structure prediction

Reinert et al. (44) previously used A*-search to efficiently perform near optimal MSA, but to our knowledge, Scooby-Domain is the first method that uses an A*-search in protein structure prediction. A*-search is a very flexible method, and it may be easily adapted and improved to include more sophistication in its predictions. For example, a more biologically accurate heuristic function could be developed by incorporating more feature-based parameters, such as the flexibility of the peptide backbone and the presence of possible disulphide bonds.

Another future area of research and development is to adapt the A*-search algorithm to predict protein-folding pathways. An obvious but interesting property of A*-search is that it explores the hypothetical folding space in a tree-like search pattern. Because Scooby-Domain predictions rely on the hydrophobicity of the protein sequence, it is possible, therefore, to simulate hydrophobic collapse and protein-folding pathways by backtracking through the search tree. Finally, the A*-search algorithm, or similar heuristics, could in theory be incorporated into a protein tertiary structure-prediction algorithm to simulate and predict folding pathways.

CONCLUSION

Percentage hydrophobicity and domain size are good variables for domain prediction and have been successfully applied to predict domain boundaries in the Scooby-Domain algorithm. Precise boundary positioning is still a difficult problem. Domains that are connected by small linkers may not be identifiable by Scooby-Domain, because window averaging may lose any signal at the linker. Scooby-Domain is therefore more useful when identifying modules separated by clear linker regions in large proteins. However, Scooby-Domain does produce encouraging results. Predictions made from the Scooby-Domcut combination are better than other previously described sequence-feature-based methods. Unlike other methods, it achieves similar prediction sensitivity and accuracy regardless of whether the domain is discontinuous or continuous.

Scooby-Domain stands out from other prediction methods because it is able to predict discontinuous domains and successful predictions are not limited by the length of the query sequence, which can be too complex or time-consuming for other methods to calculate.

The inclusion of difficult targets for benchmarking domain prediction, such as discontinuous domains, is essential to drive future developments in this area. Our test sets are available as Supplementary Data.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online.