Skip to main content
PMC home page
Nucleic Acids Research logoLink to Nucleic Acids Research
. 2007 Dec 17;36(3):897–904. doi: 10.1093/nar/gkm1110

What drives the binding of minor groove-directed ligands to DNA hairpins?

Jurij Lah 1,*, Igor Drobnak 1, Marko Dolinar 1, Gorazd Vesnaver 1
PMCID: PMC2241884  PMID: 18086706

Abstract

Understanding the molecular basis of ligand–DNA-binding events, and its application to the rational design of novel drugs, requires knowledge of the structural features and forces that drive the corresponding recognition processes. Existing structural evidence on DNA complexation with classical minor groove-directed ligands and the corresponding studies of binding energetics have suggested that this type of binding can be described as a rigid-body association. In contrast, we show here that the binding-coupled conformational changes may be crucial for the interpretation of DNA (hairpin) association with a classical minor groove binder (netropsin). We found that, although the hairpin form is the only accessible state of ligand-free DNA, its association with the ligand may lead to its transition into a duplex conformation. It appears that formation of the fully ligated duplex from the ligand-free hairpin, occurring via two pathways, is enthalpically driven and accompanied by a significant contribution of the hydrophobic effect. Our thermodynamic and structure-based analysis, together with corresponding theoretical studies, shows that none of the predicted binding steps can be considered as a rigid-body association. In this light we anticipate our thermodynamic approach to be the basis of more sophisticated nucleic acid recognition mechanisms, which take into account the dynamic nature of both the nucleic acid and the ligand molecule.

INTRODUCTION

One of the key questions in the molecular recognition of DNA is: what drives small organic molecules to bind into the minor groove of DNA with a particular affinity and specificity? The answer to this question is of both practical (rational design of novel drugs) and fundamental (understanding of ligand–DNA interactions) interest (1–3). Organic molecules that bind into the DNA minor groove have a wide range of biological activities; they are important in biotechnology as fluorescent DNA strains, and they are potential agents for modulation of gene expression (4–8). Moreover, binding studies of such compounds have provided fundamental information about DNA recognition properties and they continue to act as important models in the study of DNA complexes (2,3,9–16). It is now well established that molecular understanding of DNA minor groove recognition by small organic ligands requires the detailed thermodynamic information that cannot be obtained by structural or computational studies alone (2,3,9–11,17).

Existing structural evidence suggests that there is little, if any, change in the conformation of DNA or the minor groove binder on association. Therefore, the minor groove binding has been considered to be a rigid-body association accompanied by zero conformational free energy change (2,3,9–11). On the other hand, it is always possible that, in solution at different ligand/DNA ratios, various conformations of DNA exist that differ from those observed in 3D structures of ligand-free and fully ligated DNA. Our results provide firm experimental evidence that conformational changes of DNA can be induced by binding of classical minor groove agents. Therefore, to understand DNA recognition at the molecular level we need to answer the question: what are the forces that drive the binding-coupled conformational changes?

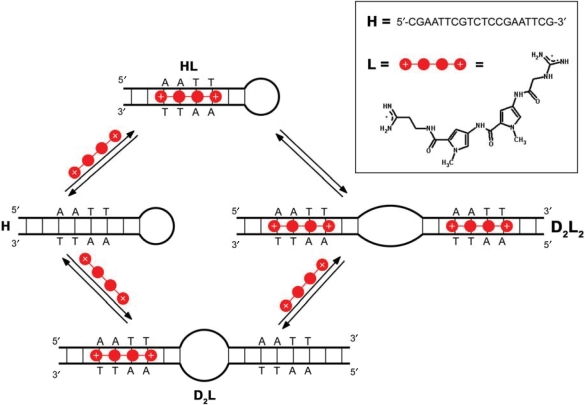
To investigate the linkage between the thermodynamics of ligand binding and DNA structural alterations, we studied binding of the dicationic minor groove binder netropsin (L) to a DNA oligonucleotide that folds into hairpin (H) and contains a specific netropsin-binding site AATT (Figure 1) by using isothermal titration calorimetry (ITC), circular dichroism spectroscopy (CD) and native gel electrophoresis (PAGE).

Figure 1.

Figure 1.

Open in a new tab

Mechanism of binding of the minor groove-directed ligand to the DNA oligonucleotide. The proposed mechanism that is well supported by experimental data (Figure 4) shows that the binding-coupled conformational changes are crucial for interpretation of DNA (hairpin=H) association with a classical minor groove binder (netropsin=L). D2L and D2L2 represent the duplex conformations complexed by one or two molecules of L, respectively.

MATERIALS AND METHODS

DNA and ligand preparation

Purified (HPLC) samples of oligonucleotide (H) 5′-CGAATTCGTCTCCGAATTCG-3′ containing a netropsin (L; see Figure 1) binding site sequence were obtained from Midland (USA) and Invitrogen (Germany) while netropsin (L) was obtained from Sigma Aldrich (USA). The concentration of H in the measuring solution was verified by UV spectroscopy with a molecular extinction coefficient determined using a nearest neighbour calculation for single-strand DNA at 25°C (18) and the absorbance at 260 nm of thermally denatured oligonucleotide extrapolated back to 25°C (εH,260=161 000 M−1· cm−1). The concentration of L was verified by absorbance at 296 nm and 25°C using the published extinction coefficient (εL,296=21 500 M−1· cm−1) (19). H and L solutions were prepared in phosphate buffer (10 mM Na-phosphate, 200 mM NaCl, 1 mM EDTA, pH = 7.0) that enables relatively good comparison with previous reports on spectral and thermodynamic characteristics of netropsin–DNA association (2,3,11,19,20). Prior to each calorimetric and spectroscopic measurement, H and L solutions were degassed for ∼20 min.

Isothermal titration calorimetry (ITC)

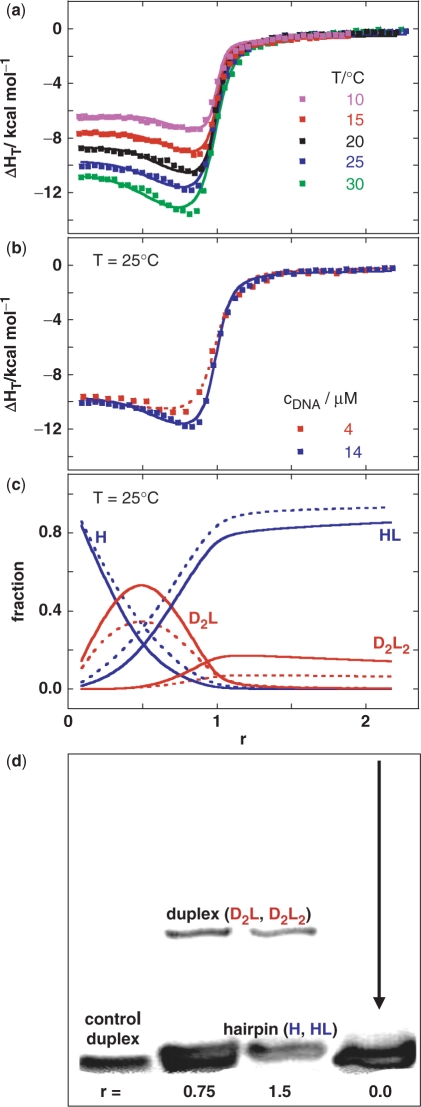
ITC experiments were performed between 10 and 30°C by titrating a solution of L (cL ∼ 200 μM) into a solution of H (cDNA ∼ 15 μM, V = 1.386 ml) using a VP-ITC isothermal titration calorimeter from Microcal Inc. (Northampton, MA, USA). The area under the peak following each injection of L solution was obtained by integration of the raw signal, corrected for the corresponding heat of dilution and expressed per mole of added L per injection, to give the enthalpy of interaction (ΔHT). The experimental ΔHT (Figure 4a and b) data were modelled as described below.

Figure 4.

Figure 4.

Open in a new tab

Model analysis of anomalous heats of ligand–DNA association is supported by the gel electrophoresis experiment. (a) Enthalpies of netropsin association with the model DNA measured by ITC at various netropsin/DNA (single strand) molar ratios (r) and temperatures (cDNA ∼15 μM) and the corresponding best global fit (lines) of the model [Figure 1, Equation (1)]. The best-fit parameters are presented in Supplementary Table 1. (b) ITC curves (symbols) measured at 25°C at cDNA = 4 μM and 14 μM. Dotted line (4 μM) and full line (14 μM) are model functions calculated from the best-fit parameters presented in Supplementary Table 1. (c) Distribution functions of species H, HL, D2L and D2L2 (Figure 1) at cDNA = 4 μM (dotted line) and 14 μM (full line) obtained from the best-fit model thermodynamic parameters (Supplementary Table 1). The fraction of HL is corrected for the small contribution of HL2 species (non-specific binding) and actually represents the sum of the HL and HL2 fractions. The non-specific (low affinity) binding step HL + L ↔ HL2 was added to the model in order to achieve its better agreement with the ITC curves at r > 1. Thermodynamic parameters accompanying the other binding events (Figure 1) are not significantly correlated to parameters required for description of the HL + L ↔ HL2 step (see Supplementary Data). (d) PAGE mobility pattern of model DNA (T = 18°C) mixed with netropsin at different netropsin/DNA molar ratios (r). Control DNA = self-complementary duplex formed from two 5′-CGGAATTCCG-3′ strands should show approximately the same mobility as the hairpin form H (Figure 1).

Differential scanning calorimetry (DSC)

DSC measurements were performed with a Nano-II DSC scanning calorimeter (CSC, UT, USA). Thermal unfolding of H (cDNA ∼130 μM, V = 0.299 ml) was monitored between 5 and 95°C in terms of the solute partial molar heat capacity CP (raw signal corrected for the buffer contribution and normalized per mol of H) versus T thermograms (Figure 2a). The differences between CP and the corresponding partial molar heat capacity of the folded DNA state (ΔCP) were analysed in a model-independent way (integration of the ΔCP versus T curve to obtain the calorimetric enthalpy of unfolding, ΔHU,cal) as well as in a model-dependent way (fitting of the reversible monomolecular two-state model (H ↔ U) to obtain the transition temperature, Tm, standard enthalpy of unfolding, ΔHU° and standard heat capacity of unfolding, ΔCP,U°) (21,22).

Figure 2.

Figure 2.

Open in a new tab

Thermodynamics of unfolding of the model oligonucleotide. (a) DSC thermograms (CP as a function of T). (b) UV melting curves (molar extinction coefficient at 260 nm as a function of T). (c) CD melting curves (molar ellipticity at 250 nm as a function of T). Insets: The corresponding excess heat capacity (ΔCP; every tenth experimental point) (panel a) and the fraction of the unfolded oligonucleotide (panels b and c) temperature profiles obtained from the presented raw data. Lines represent the best fit of the reversible two-state model (H ↔ U). The resulting thermodynamic parameters are presented for DSC, UV and CD, respectively: Tm (°C) = 71.19(±0.01), 72.48(±0.05), 70.25(±0.16); 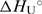Inline graphic at Tm (kcal·mol−1) = 61.67(±0.04), 64.39(±0.70), 65.91(±2.68); 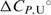Inline graphic (kcal mol−1·K−1) = 0.193(±0.004). 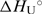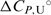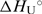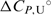Inline graphic and Inline graphic are in agreement with the recently reported values of Inline graphic and Inline graphic for unfolding of the (5′-CGAATTCG-3′)2 duplex (37). The shapes of the model UV and CD melting curves do not depend significantly on parameter 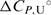Inline graphic so reliable 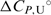Inline graphic values cannot be obtained by the model analysis of the presented UV and CD data. The errors are s.d. (square roots of diagonal elements of variance–covariance matrix). The parameter errors due to the variation of possible folded and unfolded state baseline positions may be up to ten times higher than the presented s.d. The model-independent (integration of DSC thermogram) ΔHU, cal = 61.5(±1.0) kcal·mol−1. Thermodynamic profile of unfolding at 25°C obtained from the model analysis of DSC data (values in kcal·mol−1): 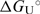Inline graphic = 7.6 (±0.1), 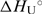Inline graphic = 52.8 (±1.0), 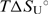Inline graphic = 45.2 (±1.0).

UV-absorption spectroscopy (UV)

All absorbance measurements were performed in a Cary Bio 100 UV spectrophotometer (Varian, Australia) equipped with a thermoelectrically controlled cell holder. UV melting curves of H at 260 nm (Figure 2b) measured in a 1 cm cuvette (cDNA ∼5 μM) and in 0.25 mm cuvette (cDNA ∼130 μM) were analysed in terms of the two-state model of unfolding (21,22).

Circular dichroism spectroscopy (CD)

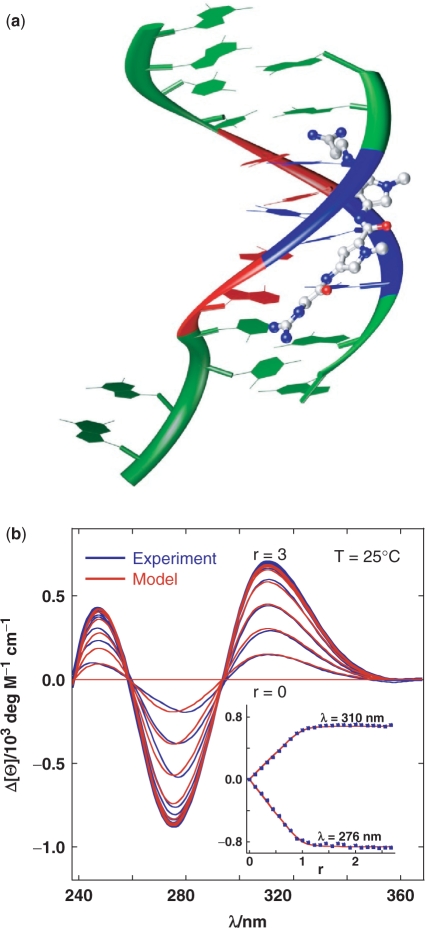
CD spectra were measured with an AVIV Model 62A DS spectropolarimeter (Aviv Associates, Lakewood, NJ, USA) equipped with a thermoelectrically controlled cell holder. Thermal unfolding of H was followed by recording CD spectra in a 1 cm cuvette (cDNA ∼5 μM) and in 0.25 mm cuvette (cDNA ∼130 μM) at different temperatures with the temperature step of 3°C. The corresponding CD melting curves obtained at 250 nm were analysed in terms of the two-state model of unfolding [Figure 2c; (21,22)]. CD titrations were conducted at 25°C by incrementally injecting aliquots of L solution into a 2.2 ml (1 cm cuvette) of ∼10 μM H solution. Since L is not optically active, the presented difference molar ellipticities Δ[θ] (Figure 3b) were obtained from the measured CD spectra by subtracting the corresponding ligand-free H spectra and normalizing to 1 M H concentration and 1 cm optical pathlength. The difference CD spectra were successfully described by the H + L ↔ HL binding model for which Δ[θ] at any wavelength is expressed in terms of the model function: Δ[θ] = Δ[θ]HLαHL, where Δ[θ]HL=[θ]HL − [θ]H and αHL is the fraction of bound H. In the model function Δ[θ]HL is obtained from the difference spectra observed at saturation (average spectrum at saturation multiplied by a parameter A) while αHL depends on the known total concentrations of H and L and the apparent binding constant (K). Thus the shape and the intensity of the model binding induced spectra can be described by only two adjustable parameters A and K. To obtain their values we developed an algorithm for global fitting of the model spectra to the experimental spectra based on the non-linear Levenberg–Marquardt χ2 regression procedure (23).

Figure 3.

Figure 3.

Open in a new tab

Structural information and circular dichroism experiments suggest a bimolecular ligand–DNA association. (a) Crystal structure of the netropsin–DNA complex [NDB entry=BD0078 (38); netropsin: nitrogen=blue, oxygen=red, carbon=grey; DNA=(5′-GGCCAATTGG-3′)2: guanine and cytosine=green, adenine=red, thymine=blue] on the basis of which our structure-based thermodynamic calculations for a rigid-body ligand–DNA association were performed (Figure 5; see Supplementary Data). (b) CD difference spectra of netropsin association with the model DNA (Figure 1) measured at various netropsin/DNA (single strand) molar ratios (r) at 25°C. For clarity reasons only every second spectrum is presented. The simple DNA + L ↔ DNAL binding model shows very good agreement with experimental data and results in the apparent binding constant of 9.3 (±0.7)·106 M−1. Inset: the corresponding binding isotherms constructed at two wavelengths.

Native polyacrylamide gel electrophoresis (PAGE)

Samples of DNA oligonucleotides were mixed with an appropriate amount of ligand to achieve an oligonucleotide concentration of 100 μM and the desired ligand/DNA molar ratio (r). Ten microlitre of this sample mixture was added to 2 μl of loading buffer, then loaded onto a 22% (w/v) polyacrylamide gel (acrylamide: bisacrylamide ratio 37:1) and subjected to a constant voltage of 110 V for 2–3 h. The running buffer was 0.5×TBE buffer, containing 45 mM Tris, 45 mM boric acid and 1 mM EDTA at pH ∼ 8.5. To prevent thermally induced conformational changes to oligonucleotides, the electrophoresis cell was placed in a water bath maintained at a constant temperature of 18°C. After the electrophoresis, the gels were stained using ethidium bromide for ∼10 min and the fluorescent stains visualized and photographed under UV light using the DNr MiniBis Pro camera (DNr, Israel).

RESULTS AND DISCUSSION

DSC thermograms, CD and UV melting curves show only one major (helix-to-coil) transition (Tm ∼71°C) that is independent of oligonucleotide concentration, scanning rate and the method applied (Figure 2). The two-state model (H ↔ U) shows very good agreement with DSC, UV and CD melting curves [Figure 2 (insets)] and the resulting model-dependent ΔHU° values agree well with the model-independent ΔHU, cal and with the corresponding nearest neighbour estimate of 63.1 kcal·mol−1 (24). It follows that the observed melting process can be considered as a reversible monomolecular two-state transition. This fact and the observed shape of the pre-transitional DSC, UV and CD signals suggests that at lower temperatures (in the given concentration range) hairpin form is the sole DNA form in solution. The existence of hairpin as the only DNA form in the solution is in accordance with the ITC DNA dilution experiments showing a complete absence of heat effects that are characteristic for dissociation events like duplex-to-single strands transition (Supplementary Figure 1) and was confirmed by the PAGE experiment (Figure 4d).

The binding induced circular dichroism (CD) spectra (Figure 3b) show typical characteristics (shape, isoelliptic points, intensities) of 1:1 L binding to B-type double-helical DNA, and can be described by a single site binding model. Isothermal titration calorimetry (ITC) measurements also indicate a high affinity L-DNA association with 1:1 stoichiometry (Figure 4a and b). However, in contrast to CD titrations they show that the observed binding is obviously not a simple bimolecular H + L ↔ HL process. In the course of our experimental work, Freyer et al. (25–27) reported that the binding of some minor groove agents to several hairpin-forming DNA sequences is accompanied by ‘anomalous’ ITC curves that can be described in terms of a ‘two-fractional-sites’ model. The model assumes the existence of pairs of DNA structures, ligand structures or ligand–DNA structures that are separated by a large energy barrier so that paired structures are not in equilibrium, at least at temperatures and on the timescale of the ITC experiments. Since this mathematically correct model has not been supported by any experimental evidence apart from its good agreement with the ITC curves, we started looking for a physically more appropriate binding model which would be able to account for the ITC data, and which would be indubitably supported by another experimental method.

It is well known that segments of DNA in vivo or model oligonucleotides in solution can adopt various conformations involving loops, junctions, mismatches, etc. (28–33). Thus, the unusual shape of the ITC curves may be ascribed to binding-coupled conformational changes in the DNA. It is possible to show that the observed shape of the ITC curves cannot be caused by reversible monomolecular changes (hairpin–hairpin, hairpin-unfolded, duplex–duplex, etc.), but only by alterations that are accompanied by a change of an oligomeric DNA state such as a hairpin-to-duplex transition. According to the melting (Figure 2), ITC (Supplementary Figure 1) and PAGE (Figure 4d) experiments, the starting (ligand-free) DNA conformation in all ITC experiments is the hairpin form. It follows that the formation of any duplex or higher oligomeric conformation that might accompany the titration could be induced only by binding of the minor groove-directed ligand. The model of the binding mechanism presented in Figure 1 is based on this conclusion. It assumes that, at a given temperature (T) and any ligand/DNA molar ratio (r), the equilibrium in the solution involves the following species: L, H, HL, D2L and D2L2 (defined in Figure 1). Thus the enthalpy change at a given temperature (ΔHT) induced by the binding of L and expressed per mol of added ligand is (11,34):

graphic file with name gkm1110m1.jpg 1

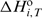where Inline graphic is the standard enthalpy of formation of the complex i from H and L, and 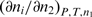Inline graphic represents the corresponding partial derivative in which ni is the amount of the complex i and n2 is the total amount of added ligand. We developed an algorithm for global fitting of the model function [Equation (1)] to the experimental ITC curves based on the iterative non-linear Levenberg–Marquardt χ2 regression procedure (23). 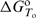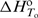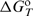Each binding step (Figure 1) is described in terms of changes of standard thermodynamic (adjustable) parameters: Gibbs free energy (Inline graphic) and enthalpy (Inline graphic) at the reference temperature To = 25°C and heat capacity (Inline graphic; assumed to be temperature independent) that define Inline graphic at any T by the Gibbs–Helmholtz relation, [∂(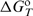Inline graphic/T)/∂T]P=−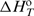Inline graphic/T2, and Kirchhoff's law, [∂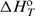Inline graphic/∂T]P=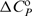Inline graphic. 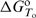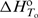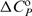Thus, with the adjustable parameters Inline graphic, Inline graphic and Inline graphic known for each step in the binding mechanism (Figure 1), the equilibrium populations of species in solution (Figure 4c) and the model function [Equation (1)] are completely defined. The model shows good agreement with the ITC data (Figure 4a and b), and the resulting speciation diagram (Figure 4c) is supported by the corresponding PAGE experiment (Figure 4d) which shows that the mobility of a significant fraction of the DNA complexed with the bound ligand is about half that of the ligand-free DNA hairpin (r = 0). This observation strongly suggests the presence of a higher oligomeric DNA conformation (bulged duplex) resulting from binding of the minor groove-directed ligand, as predicted by the model. The model can also give a reasonable description of the ITC curves measured at different concentrations (Figure 4b) and suggests that the bulged duplex states are less populated at lower DNA concentration (Figure 4c). We found that the model assuming just one pathway of formation of fully ligated higher oligomeric conformation (duplex, triplex) from H and L (via HL complex) fails to describe the ITC curves. Moreover, ITC experiments performed within the time interval of ∼1 h and one day resulted in the same calorimetric isotherms (data not shown) indicating that the observed unusual signals (Figure 4a and b) are not due to kinetically limited processes. In addition, it should be mentioned that PAGE does not support all the details in the predicted binding mechanism. Namely, a close inspection of PAGE experiment (Figure 4d) suggests that the ligand-free DNA lane may consists of two close-running bands, rather than one. According to melting experiments (Figure 2), the more mobile band at 18°C does not result from the unfolded structure, but more likely reflects another hairpin conformation. Its contribution to the overall binding energetics, however, cannot be obtained independently from the model analysis of the ITC data (total correlation of additional adjustable parameters with the existing fitting parameters). In the light of our PAGE experiment, the proposed binding mechanism is somewhat speculative since one could expect that pairs of hairpin (H, HL) and bulged duplex (D2L, D2L2) species have slightly different mobilities in the non-denaturing gel. Nevertheless, the binding mechanism is entirely consistent with the observed ITC data and, moreover, our key suggestion that a classical minor groove binder may induce conformational alterations on DNA (hairpin-to-duplex transition) is fully supported by the PAGE experiment.

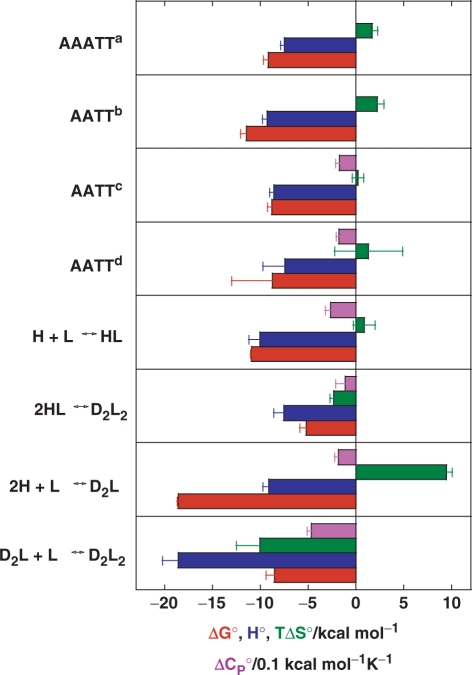
A thermodynamic description of the binding mechanism (Figure 5) shows that formation of the fully ligated duplex (D2L2) from the ligand-free hairpin (H), which is possible via two pathways, 2H+2L → 2HL → D2L2 and 2H+L → D2L+L → D2L2, is an enthalpy-driven process. The accompanying significant negative heat capacity changes suggest that the hydrophobic effect plays an important role in determining this binding event. More specifically, H+L ↔ HL association can be considered as an ordinary enthalpy-driven binding of netropsin to the AATT site, commonly reported in the literature (3,19,20), in which the favourable entropy contributions of the hydrophobic and polyelectrolyte effects are compensated by the loss of translational, rotational and configurational freedom of H and L. Moreover, the binding constant determined by ITC for the H+L ↔ HL step (1.0 (±0.1)·108 M−1) is an order of magnitude higher than the corresponding apparent overall constant estimated from the CD titration (9.3·(±0.7)106 M−1) clearly showing that the single site binding model is inappropriate, for thermodynamic description of the observed binding process. 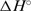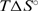For the 2HL → D2L2 step, Inline graphic and Inline graphic are both less than zero, suggesting that formation of the fully ligated bulged duplex is governed by additional short-range interactions (stacking, H-bond) that take place within the internal loop of the duplex. 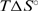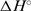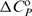Comparing the 2H+L → D2L and H+L ↔ HL steps, the observed Inline graphic value is much more positive and the Inline graphic and Inline graphic values both slightly less negative for the former. 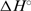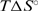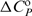Comparing the steps D2L+L → D2L2 and H+L ↔ HL, however, much more negative Inline graphic, Inline graphic and Inline graphic values for the former are indicative for formation of additional short-range interactions mentioned above. In addition, the thermodynamics of netropsin–DNA binding can be reasonably well predicted by structure-based (Figure 3a) thermodynamic calculations that have been successfully used in characterizing protein folding, protein–protein association and micelle formation (34,35). Due to large errors in the thermodynamic quantities predicted by the parameterization, based on the changes in solvent accessible surface areas induced by the rigid-body binding and the additivity of several enthalpy and entropy contributions (Supplementary Data), this approach cannot describe the complicated, sequence-dependent thermodynamics of minor groove binding. However, the comparison with experimental data (Figure 5) suggests that it may successfully set the thermodynamic limits within which the minor groove binding (netropsin to AATT) can be considered as a commonly observed (key-and-lock) association.

Figure 5.

Figure 5.

Open in a new tab

Energetics of netropsin binding to the AATT site contained in various DNA oligonucleotides. Thermodynamic profiles at 25°C accompanying netropsin association with the model oligonucleotide (Figure 1) based on the model analysis of the ITC data (Figure 4) in comparison to the corresponding structure-based (Figure 3a) thermodynamic calculations for a rigid-body netropsin association with the AATT site (d; see Supplementary Data) and the thermodynamic profiles taken from the literature [a = Ref. (19), b=Ref. (20), c=Ref. (3)]. Error bars are estimated s.d. The standard thermodynamic quantities are presented in the following colours: Gibbs free energy (red), enthalpy (blue), entropy contribution (green) and heat capacity (violet).

We have shown for the first time that consideration of the binding-induced DNA conformational changes may be crucial for understanding the classical minor groove binding of small molecules at the molecular level. Since many DNA sequences have a tendency to form different types of conformations, understanding the molecular mechanism of ligand–DNA association requires the combination of thermodynamics with independent information on the binding-induced changes of DNA conformation. Only one step in the binding mechanism presented here, H+L ↔ HL, does not involve a significant alteration in the DNA conformation. However, even in this case it would be wrong to denote the binding as a rigid-body association since, according to recent theoretical studies (36), the accompanying configurational entropy loss of the ligand molecule is not negligible. Therefore, we may conclude that full understanding of the forces that drive the binding of minor groove-directed ligands to DNA is only possible by taking into account the dynamic nature of both DNA and the ligand molecule.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

[Supplementary Data]
nar_gkm1110_index.html (653B, html)

ACKNOWLEDGEMENTS

We thank Prof. R.H. Pain for critical reading of the manuscript. This work was supported by the Ministry of Higher Education, Science and Technology and by the Agency for Research of Republic of Slovenia through the Grants No. P1-0201 and J1-6653. Funding to pay the Open Access publication charges for this article was provided by Agency for Research of Republic of Slovenia.

Conflict of interest statement. None declared.

REFERENCES

  • 1.White S, Szewczyk JW, Turner JM, Baird EE, Dervan PB. Recognition of the four Watson-Crick base pairs in the DNA minor groove by synthetic ligands. Nature. 1998;391:468–471. doi: 10.1038/35106. [DOI] [PubMed] [Google Scholar]
  • 2.Chaires JB. Energetics of drug-DNA interactions. Biopolymers. 1997;44:201–215. doi: 10.1002/(SICI)1097-0282(1997)44:3<201::AID-BIP2>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
  • 3.Haq I. Thermodynamics of drug-DNA interactions. Arch. Biochem. Biophys. 2002;403:1–15. doi: 10.1016/S0003-9861(02)00202-3. [DOI] [PubMed] [Google Scholar]
  • 4.Dervan PB, Poulin-Kerstien AT, Fechter EJ, Edelson BS. Regulation of Gene expression by synthetic DNA-binding ligands. Top. Curr. Chem. 2005;253:1–31. [Google Scholar]
  • 5.Geierstanger BH, Wemmer DE. Complexes of the minor groove of DNA. Annu. Rev. Biophys. Biomol. Struct. 1995;24:463–493. doi: 10.1146/annurev.bb.24.060195.002335. [DOI] [PubMed] [Google Scholar]
  • 6.Reddy BS, Sharma SK, Lown JW. Recent developments in sequence selective minor groove effectors. Curr. Med. Chem. 2001;8:475–508. doi: 10.2174/0929867003373292. [DOI] [PubMed] [Google Scholar]
  • 7.Neidle S. Nucleic Acid Structure and Recognition. Oxford, pp. 89–137: Oxford University Press; 2002. [Google Scholar]
  • 8.Wemmer DE. Designed sequence-specific minor groove ligands. Annu. Rev. Biophys. Biomol. Struct. 2000;29:439–461. doi: 10.1146/annurev.biophys.29.1.439. [DOI] [PubMed] [Google Scholar]
  • 9.Mazur S, Tanious FA, Ding D, Kumar A, Boykin DW, Simpson IJ, Neidle S, Wilson WD. A thermodynamic and structural analysis of DNA minor-groove complex formation. J. Mol. Biol. 2000;300:321–337. doi: 10.1006/jmbi.2000.3869. [DOI] [PubMed] [Google Scholar]
  • 10.Haq I, Ladbury JE, Chowdhry BZ, Jenkins TC, Chaires JB. Specific binding of Hoechst 33258 to the d(CGCAAATTTGCG)2 duplex: calorimetric and spectroscopic studies. J. Mol. Biol. 1997;271:244–257. doi: 10.1006/jmbi.1997.1170. [DOI] [PubMed] [Google Scholar]
  • 11.Lah J, Vesnaver G. Energetic diversity of DNA minor-groove recognition by small molecules displayed through some model ligand-DNA systems. J. Mol. Biol. 2004;342:73–89. doi: 10.1016/j.jmb.2004.07.005. [DOI] [PubMed] [Google Scholar]
  • 12.Lah J, Vesnaver G. Binding of distamycin A and netropsin to the 12mer DNA duplexes containing mixed AT*GC sequences with at most five or three successive AT base pairs. Biochemistry. 2000;39:9317–9326. doi: 10.1021/bi000748u. [DOI] [PubMed] [Google Scholar]
  • 13.Lah J, Carl N, Drobnak I, Šumiga B, Vesnaver G. Competition of some minor groove binders for a single DNA binding site. Acta Chim. Slov. 2006;53:284–291. [Google Scholar]
  • 14.Zimmer C, Wahnert U. Nonintercalating DNA-binding ligands: specificity of the interaction and their tools in biophysical, biochemical and biological investigations of the genetic material. Prog. Biophys. Mol. Biol. 1986;47:31–112. doi: 10.1016/0079-6107(86)90005-2. [DOI] [PubMed] [Google Scholar]
  • 15.Abu-Daya A, Fox KR. Interaction of minor groove binding ligands with long AT tracts. Nucleic Acids Res. 1997;25:4962–4969. doi: 10.1093/nar/25.24.4962. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Bostock-Smith CE, Harris SA, Laughton CA, Searle MS. Induced fit DNA recognition by a minor groove binding analogue of hoechst 33258: fluctuations in DNA A tract structure investigated by NMR and molecular dynamics simulations. Nucleic Acids Res. 2001;29:693–702. doi: 10.1093/nar/29.3.693. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Dolenc J, Oostenbrink C, Koller J, van Gunsteren WF. Molecular dynamics simulations and free energy calculations of netropsin and distamycin binding to an AAAAA DNA binding site. Nucleic Acids Res. 2005;33:725–733. doi: 10.1093/nar/gki195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Cantor CR, Warshaw MM, Shapiro H. Oligonucleotide interactions. 3. Circular dichroism studies of the conformation of deoxyoligonucleotides. Biopolymers. 1970;9:1059–1077. doi: 10.1002/bip.1970.360090909. [DOI] [PubMed] [Google Scholar]
  • 19.Rentzeperis D, Marky LA, Dwyer TJ, Geierstanger BH, Pelton JG, Wemmer DE. Interaction of minor groove ligands to an AAATT/AATTT site: correlation of thermodynamic characterization and solution structure. Biochemistry. 1995;34:2937–2945. doi: 10.1021/bi00009a025. [DOI] [PubMed] [Google Scholar]
  • 20.Marky LA, Breslauer KJ. Origins of netropsin binding affinity and specificity: correlations of thermodynamic and structural data. Proc. Natl Acad. Sci. USA. 1987;84:4359–4363. doi: 10.1073/pnas.84.13.4359. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Lah N, Lah J, Zegers I, Wyns L, Messens J. Specific potassium binding stabilizes pI258 arsenate reductase from Staphylococcus aureus. J. Biol. Chem. 2003;278:24673–24679. doi: 10.1074/jbc.M303194200. [DOI] [PubMed] [Google Scholar]
  • 22.Lah J, Prislan I, Kržan B, Salobir M, Francky A, Vesnaver G. Erythropoietin unfolding: thermodynamics and its correlation with structural features. Biochemistry. 2005;44:13883–13892. doi: 10.1021/bi0512952. [DOI] [PubMed] [Google Scholar]
  • 23.Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical Recipes. Oxford, pp. 650–694: Cambridge University Press; 1992. [Google Scholar]
  • 24.Allawi HT, SantaLucia J., Jr Thermodynamics and NMR of internal G.T mismatches in DNA. Biochemistry. 1997;36:10581–10594. doi: 10.1021/bi962590c. [DOI] [PubMed] [Google Scholar]
  • 25.Freyer MW, Buscaglia R, Nguyen B, Wilson WD, Lewis EA. Binding of netropsin and 4,6-diamidino-2-phenylindole to an A2T2 DNA hairpin: a comparison of biophysical techniques. Anal. Biochem. 2006;355:259–266. doi: 10.1016/j.ab.2006.04.049. [DOI] [PubMed] [Google Scholar]
  • 26.Freyer MW, Buscaglia R, Cashman D, Hyslop S, Wilson WD, Chaires JB, Lewis EA. Binding of netropsin to several DNA constructs: evidence for at least two different 1:1 complexes formed from an -AATT-containing ds-DNA construct and a single minor groove binding ligand. Biophys. Chem. 2007;126:186–196. doi: 10.1016/j.bpc.2006.06.009. [DOI] [PubMed] [Google Scholar]
  • 27.Freyer MW, Buscaglia R, Hollingsworth A, Ramos J, Blynn M, Pratt R, Wilson WD, Lewis EA. Break in the heat capacity change at 303 K for complex binding of netropsin to AATT containing hairpin DNA constructs. Biophys. J. 2007;92:2516–2522. doi: 10.1529/biophysj.106.098723. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Bacolla A, Wells AD. Non-B DNA conformations, genomic rearrangements, and human disease. J. Biol. Chem. 2004;279:47411–47414. doi: 10.1074/jbc.R400028200. [DOI] [PubMed] [Google Scholar]
  • 29.Kaushik M, Kukreti R, Grover D, Brahmachari SK, Kukreti S. Hairpin-duplex equilibrium reflected in the A–>B transition in an undecamer quasi-palindrome present in the locus control region of the human beta-globin gene cluster. Nucleic Acids Res. 2003;31:6904–6915. doi: 10.1093/nar/gkg887. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Kadrmas JL, Ravin AJ, Leontis NB. Relative stabilities of DNA three-way, four-way and five-way junctions (multi-helix junction loops): unpaired nucleotides can be stabilizing or destabilizing. Nucleic Acids Res. 1995;23:2212–2222. doi: 10.1093/nar/23.12.2212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Nakano S, Kirihata T, Fujii S, Sakai H, Kuwahara M, Sawai H, Sugimoto N. Influence of cationic molecules on the hairpin to duplex equilibria of self-complementary DNA and RNA oligonucleotides. Nucleic Acids Res. 2007;35:486–494. doi: 10.1093/nar/gkl1073. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Marky LA, Blumenfeld KS, Kozlowski S, Breslauer KJ. Salt-dependent conformational transitions in the self-complementary deoxydodecanucleotide d(CGCAATTCGCG): evidence for hairpin formation. Biopolymers. 1983;22:1247–1257. doi: 10.1002/bip.360220416. [DOI] [PubMed] [Google Scholar]
  • 33.SantaLucia J, Jr, Hicks D. The thermodynamics of DNA structural motifs. Annu. Rev. Biophys. Biomol. Struct. 2004;33:415–440. doi: 10.1146/annurev.biophys.32.110601.141800. [DOI] [PubMed] [Google Scholar]
  • 34.Lah J, Bešter-Rogač M, Perger T-M, Vesnaver G. Energetics in correlation with structural features: the case of micellization. J. Phys. Chem. B. 2006;110:23279–23291. doi: 10.1021/jp062796f. [DOI] [PubMed] [Google Scholar]
  • 35.Robertson AD, Murphy KP. Protein structure and the energetics of protein stability. Chem. Rev. 1997;97:1251–1267. doi: 10.1021/cr960383c. [DOI] [PubMed] [Google Scholar]
  • 36.Dolenc J, Baron R, Oostenbrink C, Koller J, van Gunsteren WF. Configurational entropy change of netropsin and distamycin upon DNA minor groove binding. Biophys. J. 2006;91:1460–1470. doi: 10.1529/biophysj.105.074617. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Drobnak I, Seručnik M, Lah J, Vesnaver G. Stability of a short DNA duplex as a function of temperature: the effect of ΔCp and added salt concentration. Acta Chim. Slov. 2007;54:445–451. [Google Scholar]
  • 38.Van Hecke K, Nam PC, Nguyen MT, Van Meervelt L. Netropsin interactions in the minor groove of d(GGCCAATTGG) studied by a combination of resolution enhancement and ab initio calculations. FEBS J. 2005;272:3531–3541. doi: 10.1111/j.1742-4658.2005.04773.x. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
nar_gkm1110_index.html (653B, html)
nar_gkm1110_1.pdf (212.1KB, pdf)

Articles from Nucleic Acids Research are provided here courtesy of Oxford University Press

RESOURCES