Re-engineering redox-sensitive green fluorescent protein for improved response rate

Abstract

Redox-sensitive variants of the green fluorescent protein (roGFPs) had previously been developed that allow “real-time” monitoring of the redox status of cellular compartments by fluorescence excitation ratiometry. However, the response time of these probes limits the study of certain rapid oxidative events, such as H₂O₂ bursts in cell signaling. The substitution of up to three positively charged amino acids adjacent to the introduced disulfide in roGFP1 (variants designated roGFP1-R1 through -R14) substantially improved the response rate. The pseudo first-order rate constants for oxidation by H₂O₂ and reduction by DTT and redox midpoint potentials were determined. The rate constants approximately doubled with each additional positively charged substitution, to nearly an order of magnitude total. The midpoint potentials are highly correlated with the rate increases, becoming more oxidizing with increasing numbers of positive substitutions. Crystal structures of two variants with opposite disulfide oxidation states have been determined: a 2.2 Å resolution structure of oxidized “R7” containing two basic substitutions, and a 1.95 Å resolution structure of reduced “R8” with one basic and one acidic substitution. Nonlinear Poisson-Boltzmann (PB) calculations are shown to accurately predict the effects of the substitutions on the rate constants. The effects of the substitutions on dimer formation, relative oxidative midpoint potentials, and oxidation and reduction rates are discussed. roGFPs are demonstrated to constitute an excellent model system for quantitative analysis of factors influencing thiol transfer reactions. roGFP1-R12 is most suitable for use in live cells, due to significantly increased reaction rate and increased pI.

The green fluorescent protein from Aequorea victoria has two widely separated excitation maxima whose ratio depends on the structure of the molecule and hence can depend on external conditions (Ormo et al. 1996; Tsien 1998). The two excitation maxima correspond to the neutral and anionic forms of the chromophore (Chattoraj et al. 1996; Brejc et al. 1997), which have absorbance maxima at ~395 and 475 nm, respectively. This feature, which is unique among fluorescent proteins characterized to date, allows the construction of ratio-metric indicators that can be targeted to subcellular organelles (Nagai et al. 2001; Hanson et al. 2002). Based on this principle, redox-sensitive probes have been developed (Hanson et al. 2004). In these indicators, surface-exposed cysteine pairs were introduced onto neighbouring strands of the β-barrel, in positions that allow disulfide formation (roGFP1–6). Structural studies of roGFP2 in the reduced and oxidized states reveal that formation of the Cys147–Cys204 disulfide causes small structural rearrangements, which evidently perturb the chromophore environment in such a way as to influence the population ratio of neutral to anionic chromophore. This leads to a very desirable ratiometric increase in fluorescence excitation at the 395-nm peak with an accompanying decrease in excitation at 475 nm (Hanson et al. 2004).

roGFPs were expressed in the cytosol and mitochondria of mammalian cells and were shown to be effective indicators of the ambient redox potential, as perturbed by exogenous oxidants and reductants, as well as by physiological redox changes (Dooley et al. 2004; Rossignol et al. 2004). Although the probes appear to be ideally suited for the two different reducing environments investigated, these data suggest that two features will limit the usefulness of existing roGFPs in some applications: (1) the slow response to stepwise changes in redox potential—some tens of minutes—and (2) very reducing midpoint potentials (~ −280 mV).

A potential application for which rapid response time is important is the study of H₂O₂ bursts in cell signaling events. H₂O₂ is a second messenger that is produced in response to various extracellular stimuli, such as cytokines and peptide growth factors, and its intracellular production affects the function of a variety of proteins, including protein kinases, phosphatases, ion channels, and transcription factors (Finkel 1998; Rhee et al. 2000, 2003). However, low levels of H₂O₂ are constantly produced by reactions in aerobic metabolism, and thus, all aerobic cells are equipped with enzymatic defense mechanisms that act to quickly eliminate H₂O₂ (Rhee 1999). In addition, redox buffering systems such as the GSSG/GSH pair are thought to serve as protection against H₂O₂ (Chesney et al. 1996). Bursts of H₂O₂ are thus believed to be quite transient and restricted to microdomains of the cell (Rhee et al. 2000); consequently, study of these events will require probes that respond quite rapidly and specifically.

It is generally accepted that the key reactive species in the active sites of enzymes catalyzing thiol transfer reactions is the cysteine thiolate, which in turn is believed to be stabilized by adjacent positive charges or dipoles within the active site (Lindley 1960; Kim et al. 2000). Thus, one approach to improving the response time of roGFPs is to introduce basic groups near the reactive thiols, thus reducing the cysteine pK_a values. Indeed, several research groups have shown this approach to be successful (Zhang and Dixon 1993; Dyson et al. 1997; Dooley et al. 2004; Glauser et al. 2004). However, the active sites of thiol transfer enzymes often contain anionic groups such as aspartate or glutamate, the function of which is unknown. For example, the active site of the methionine sulfoxide reductase, pilB, contains an additional acidic group adjacent to the conserved basic residue, forming a unique Cys–Arg–Asp catalytic triad (Lowther et al. 2002). Efforts to understand the contributions of such components have been hampered by the lack of a model system that affords a convenient assay for quantitative evaluation of reaction rates or permits comparison between theory and experiment. Such a model system is now provided by redox-sensitive GFPs.

Here, we analyze the results of basic and acidic substitutions near the key cysteine residues of roGFP1. Kinetic and equilibrium measurements reveal significantly higher response rates and less negative midpoint potentials. Crystal structure analyses of two of these mutants, one in the oxidized and one in the reduced state, verify the reversible formation of a disulfide bond and provide atomic coordinates for the introduced groups. The effects of the substitutions were accurately predicted at various ionic strengths by using nonlinear Poisson-Boltzmann theory as implemented in the program DelPhi (Rocchia et al. 2001, 2002).

Results

Spectroscopic properties

Nine variants of roGFP1 were constructed in which one to four surface residues near the engineered disulfide were replaced with a lysine, an arginine, or an aspartate residue (Table 1). In all cases, titration against a 1-mM DTT redox buffer resulted in fluorescence excitation changes similar to what is seen for the parent roGFP1 (Hanson et al. 2004). Excitation peaks at ~395 and 475 nm correspond to the protonated (neutral) and deprotonated (anionic) states of the chromophore, respectively, with most of the intensity at 395 nm. As the protein is reduced, 395-nm peak intensity decreases while that of the 475-nm peak increases. The dynamic range (δ, defined as the maximum observed ratio of excitation peak ratios) varies somewhat between mutants from δ_R11 = 5.4 to δ_R8 = 7.5 compared with δ_roGFP1 = 6.5. The quantum yield of fluorescence (Φ_F) for emission with excitation at 400 nm varies from Φ_F (R8) = 0.42 to Φ_F (R10) = 0.65 with Φ_F (roGFP1) = 0.64. Extinction coefficients for absorbance at 400 nm vary from ɛ_R8 = 12,600 M⁻¹cm⁻¹ to ɛ_R7 = 25,700 M⁻¹cm⁻¹ compared with ɛ_roGFP1 = 20,200 M⁻¹cm⁻¹. See Table 1 for complete spectroscopic results.

Table 1.

Summary of spectroscopic properties for roGFP1-R mutants

Varianta	ID	δb	Φc	ɛd (M−1 cm−1)
S147C/Q204C	roGFP1	6.5	0.64	20,200
S147C/Q204C/F223R	R1	5.6	0.60	24,100
S147C/Q204C/N149K	R3	7.0	0.58	20,100
S147C/Q204C/F223R/S202K	R7	6.2	0.64	25,700
S147C/Q204C/F223R/K41D	R8	7.5	0.42	12,600
S147C/Q204C/N149K/Y151D	R9	7.2	0.64	15,200
S147C/Q204C/F223R/S202K/K41D	R10	6.2	0.65	22,500
S147C/Q204C/N149K/F223R	R11	5.4	0.60	18,700
S147C/Q204C/N149K/F223R/S202K	R12	5.6	0.62	23,100
S147C/Q204C/N149K/F223R/S202K/Y151D	R14	5.6	0.60	20,700

^a Variants also contain the two phenotypically neutral substitutions, C48S and Q80R.

^b The dynamic range value (δ) is the maximum observed δ-fold change in excitation peak ratio.

^c The fluorescence quantum yield for emission with excitation at 400 nm.

^d Extinction coefficients for absorbance at 400 nm.

Characterization of rate constants

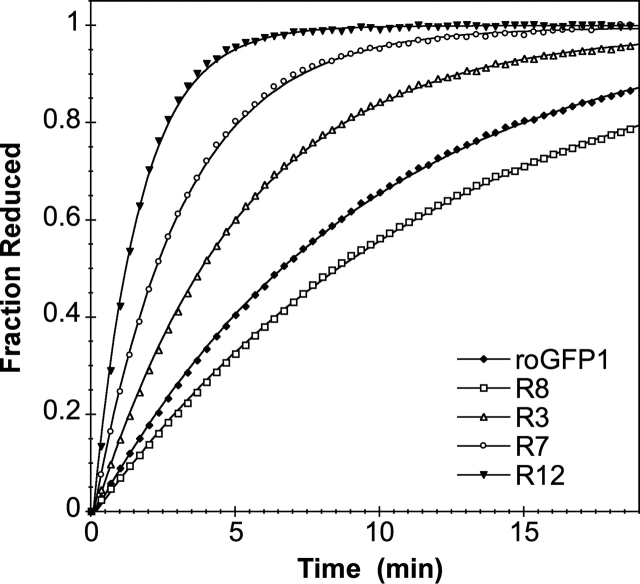
The first-order rate constant for reduction of each of the variants was determined in low-salt buffer (50 mM HEPES) by monitoring the fluorescence excitation over time, after the addition of a large excess (1 mM) of DTT at pH 7. Rate constants for this reaction ranged from k_DTT (R8)= 0.09 min⁻¹ to k_DTT (R12)= 0.66 min⁻¹ with k_DTT (roGFP1) = 0.11 min⁻¹ (Table 2). On average, mutants with one basic substitution near the disulfide have approximately double the rate constant of the parent roGFP1, with each additional basic substitution increasing this rate enhancement approximately twofold (Fig. 1). Introducing an acidic group (aspartate) had different effects depending on context. Rate constants for variants with the acidic substitution K41D were significantly decreased (i.e., cf. R8 and R1, R10 and R7), while rate constants for variants with/without the other acidic substitution, Y151D, were essentially unchanged (i.e., R9 and R3, R12 and R14).

Table 2.

Summary of kinetic parameters for roGFP1-R mutants

Variant	ka (DTT, high salt, min−1)	kb (DTT, low salt, min−1)	kc (H2O2, low salt, min−1)	Eo′ (DTT, V)d
roGFP1	0.13	0.11	0.42	− 0.281e
R1	0.16	0.19	0.89	− 0.269
R3	0.15	0.19	0.75	− 0.282
R7	0.19	0.28	1.41	− 0.268
R8	0.10	0.09	0.24	− 0.284
R9	0.17	0.18	0.59	− 0.278
R10	0.12	0.11	0.67	− 0.284
R11	0.22	0.32	0.55	− 0.275
R12	0.29	0.66	2.05	− 0.265
R14	0.31	0.56	1.22	− 0.263

^a Pseudo first-order reduction rate constants (k) determined at high ionic strength (300 mM NaCl, 50 mM HEPES), using 1 mM DTT.

^b Pseudo first-order reduction rate constants (k) determined at low ionic strength (0 mM NaCl, 50 mM HEPES), using 1 mM DTT.

^c Pseudo first-order oxidation rate constants (k) determined at low ionic strength (0 mM NaCl, 50 mM HEPES), using 1 mM H₂O₂ .

^d Midpoint potentials from titration against DTT (assumed E^o′, −323 mV) at 25° and pH 7. Average estimated error for the measurements is ± 0.0011 V.

^e This measurement was repeated by titration against lipoic acid (assumed E^o′, −290 mV) at 25° and pH 7, and was found to be −285 mV.

Figure 1.

A comparison of the rates of several roGFP1 variants. Shown is the fraction of protein reduced over time, after the addition of an excess of DTT. Pseudo first-order rate constants were determined by fitting the rate curves to a first-order rate equation.

Ionic strength dependence of rate enhancement

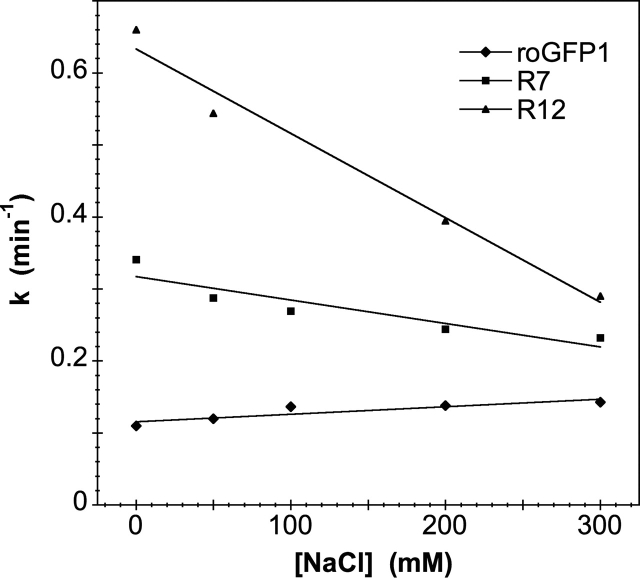
To explore the ionic strength dependency of the DTT reduction reaction, the rate constants were measured at pH 7 by using NaCl concentrations from 0–300 mM. Results are summarized in Table 2. Some representative results are plotted in Figure 2. As expected from Debye screening theory (Tanford and Kirkwood 1957; Ramos and Baldwin 2002), most of the variants had decreasing rates with increasing salt concentrations, with a greater difference between low and high salt concentration rates observed for mutants with more basic substitutions. Interestingly, the rate constants for both the parent roGFP1 and variants containing K41D increased with increasing salt concentrations, consistent with the high net negative charge on roGFP1 at neutral pH (see Discussion).

Figure 2.

First-order rate constants for a few representative mutants plotted against ionic strength. In general, mutants with more basic substitutions exhibit a steeper slope.

Characterization of rate constants for oxidation with H₂O₂

To investigate the effect of the charged substitutions on the oxidation reaction, pseudo first-order rate constants were determined in vitro for each of the mutants using H₂O₂. Table 2 compares these rate constants to those measured using DTT. As found for the reduction reaction, increasing basic charge near the disulfide leads to increasing rates of disulfide formation. A comparison of the rate enhancements for the DTT and the H₂O₂ reactions gives a correlation coefficient of 0.84. The largest discrepancy is for R11, which has k_DTT (R11) that is three times greater than that of roGFP1, while k_H2O2 (R11) is only 1.3 times that of roGFP1 (error for each measurement is < ± 0.03 min⁻¹).

Redox midpoint potentials

The redox midpoint potentials of all the roGFP1 mutants were determined from the equilibrium constant for the reaction of roGFP1 with DTT and ranged from E°^′_R14 = −263 mV to E°^′_R8 = −284 mV (Table 2). Although the variation is not large between mutants, there is a strong correlation between midpoint and the number of basic substitutions, with more positive charges near the disulfide corresponding to more oxidizing midpoints. The correlation coefficient for the comparison of k_DTT with E°^′ is 0.84; for k_H2O2 with E°^′, it is 0.82.

Crystal structure analysis of R7

The R7 mutant (roGFP1+S202K/F223R) crystals have space group P3₂21, with two molecules per asymmetric unit and diffracted to 2.2 Å by using a conventional rotating anode X-ray source. The structure was solved by molecular replacement by using the GFP S65T (Protein Data Bank [PDB] code 1EMA; Ormo et al. 1996) structure as search model. Refinement was performed without imposing noncrystallographic symmetry restraints, and thus, the two molecules in the asymmetric unit provide independent views of the protein in unique crystal-packing environments. Final model statistics are presented in Table 3.

Table 3.

Data collection and refinement statistics for oxidized R7 and reduced R8

Data collection	R7 (oxidized)	R8 (reduced)
Crystal
Total observations	272,860	473,006
Unique reflections	36,457	45,355
Cell dimensions (a, b, c) (Å)	126.3, 126.3, 78.4	79.7, 79.7, 166.9
Resolution (Å)	40.0–2.20	50.0–1.95
Highest resolution shell (Å)	2.28–2.20	2.02–1.95
Completenessa (%)	99.9 (100)	99.5 (99.9)
Multiplicitya	7.48	10.4
Average I/σa	21.6 (2.6)	50.7 (8.8)
Rmergea,b	0.096 (0.634)	0.141 (0.483)
Refinement
Space group	P3221	P3121
No. of moleculesc	2	2
No. of protein atomsc	3546	3456
No. of solvent atomsc	168	211
Resolution range (Å)	24.0–2.20	50.0–1.95
Crystallographic R-factord (reflections)	0.196 (32,733)	0.199 (40,816)
Rfree (reflections)	0.280 (3722)	0.275 (4530)
Rfactor (all data)	0.202	0.204
Average B-factors (Å2)
Protein atoms (main chain)	40.3	36.4
Solvent	45.3	47.3
Root mean square deviations from ideality
Bond lengths (Å)	0.014	0.013
Bond angles (degrees)	2.6	2.6
B-factor correlations (Å2)	4.7	4.1

^a Values in parentheses indicate statistics for the highest resolution shell.

^b R_merge = ∑|I–〈I〉|/∑〈I〉, where I is the observed intensity, and 〈I〉 is the average of intensities obtained from multiple observations of symmetry-related reflections.

^c Per asymmetric unit.

^d R_factor = ∑||F_o|–|F_c||/∑|F_o|, where F_o and F_c are the observed and calculated structure amplitudes, respectively.

The two molecules in the asymmetric unit form a different dimer from that seen for either wild-type GFP (wtGFP) (Yang et al. 1996) or roGFP2 (Hanson et al. 2004). With the A-molecules of R7 and wtGFP aligned, a rotation of −82.8° and translation of 0.3 Å align the B-molecule of R7 on wtGFP. In R7, the normally flexible C terminus is ordered (see below). This feature, in combination with replacement of several of the wild-type residues (S147C, Q204C, S202K, and F223R) that form dimer contacts in crystals of wtGFP, prohibits formation of the same dimer in R7. The disulfides of the two protomers are positioned adjacent to each other, separated by ~4 Å, centered within the dimer interface. The electron density map provides no evidence for intermolecular disulfide formation. Ultracentrifugation experiments indicated that R7 is a monomer in solution at concentrations <1 mM (data not shown); hence, dimer formation is presumed to be an artifact of crystal packing.

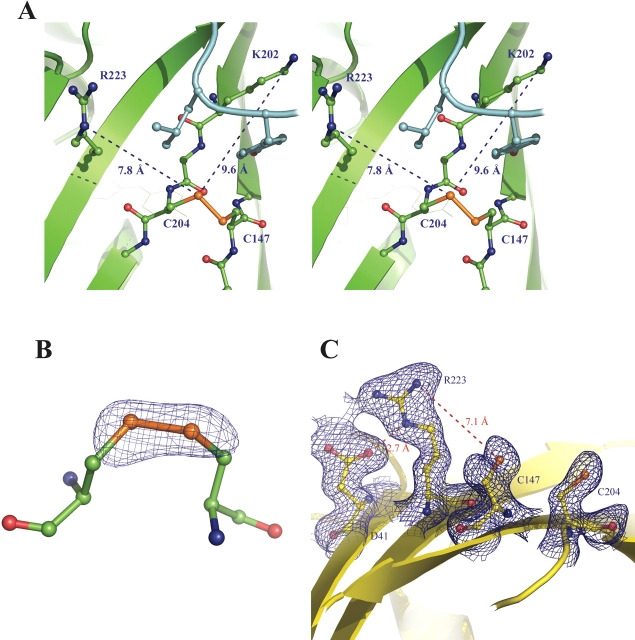
The cysteine residues 147 and 204 form a disulfide with full occupancy in both protomers comprising the asymmetric unit (Fig. 3). This disulfide shares the pg⁻g⁻ (positive χ_ss torsion angle with “gauche-“ χ¹ values ~ − 60°) conformation with the disulfides found in the oxidized structure of roGFP2 (PDB code 1JC1 [Hanson et al. 2004]; roGFP2 is roGFP1 with the additional substitution S65T). The descriptive parameters for the disulfides (with successive values corresponding to the A- and B-protomers), are as follows: χ¹₁₄₇ = (−49.4°, −60.0°); χ¹₂₀₄ = (−61.8°, −48.8°); χ²₁₄₇ = (−112.9°, −101.3°); χ²₂₀₄ = (−67.7°, −90.5°); χ_ss = (101.5°, 107.6°);Cα–Cα distance (4.06 Å, 4.06 Å); Cβ–Cβ distance (4.11 Å, 4.06 Å). These values fall within 1 SD of those observed for the naturally strained disulfides occasionally found between adjacent anti-parallel β-strands (Srinivasan et al. 1990). Table 4 compares the disulfide geometry statistics for R7, for roGFP2, and for the PDB files analyzed by Srinivasan and coworkers (1990). Although χ_ss values are typical, the R7 disulfide Cα–Cα distances are much shorter than the average value of 5.2 Å ± 0.7 Å is for disulfides bridging across β-strands (Srinivasan et al. 1990). Although this is evidence for some strain, the R7 disulfides are less strained than those found in the roGFP2 crystal structure (Hanson et al. 2004).

Figure 3.

The R7 and R8 structures, showing surface cysteine residues. (A) Stereo image of the “active site” of R7. The disulfide and basic substitutions are shown in ball-and-stick format. The ordered C-terminal segment is shown in cyan, and C-terminal residues that are near the disulfide are shown in ball-and-stick format. (B) F_o − F_c omit map of the R7 disulfide, contoured at 3σ. (C) The “active site” of R8, with cysteines and substitutions shown in ball-and-stick format. 2F_o − F_c map, contoured at 1σ, is also shown for these residues. Figure produced with PyMOL version 0.98 (DeLano Scientific).

Table 4.

Comparison of disulfide torsion angles

	χss	χ11	χ12	χ21	χ22	Cα–Cα
Population avg.a	95 ± 11	−66 ± 11	−63 ± 13	−73 ± 17	−68 ± 17	4.54 ± 0.3
roGFP2 avg.b	116d	−66	−63	−100d	−79	4.04d
R7 avg.	105	−55	−55	−107d	−79	4.06d
SRH avg.c	106 ± 5.0	−62 ± 6	−27 ± 54	−97 ± 19	−108 ± 32	4.36 ± 0.4
roGFP2 avg.	116d	−66	−63	−100	−79	4.04
R7 avg.	105	−55d	−55	−107	−79	4.06

^a Average torsion angle values (± 1 SD) for the population in which the roGFP disulfide would fall, from the group of disulfides compared by Srinivasan et al. (1990). The distribution for each torsion angle can be represented by three or four discrete populations separated by at least 20°, Cα–Cα distance distribution is divided into three populations of small (3.8–4.8 Å), medium (4.8–5.8 Å), and large (>5.8 Å).

^b roGFP2 torsion angles from PDB file 1JC1 (Hanson et al. 2004).

^c Average torsion angle values (± 1 SD) for the SRH group of five disulfides defined by Srinivasan et al. (1990) as bridging across anti-parallel β-strands.

^d Values that deviated by >1 SD were excluded from the population average.

The two R7 surface mutations, S202K and F223R, are clearly defined by the electron density map. The side chains of these two residues are oriented away from the disulfide, with the charged groups located ~8 Å from the disulfide sulfur atoms (Fig. 3).

A unique characteristic of the oxidized R7 structure is that the C-terminal residues 230–238 are ordered, forming a short β-strand that lies along the outside surface of the β-barrel and terminating quite near the position of the engineered disulfide. Specific interactions between the C-terminal strand and the β-barrel (including the introduced Lys202) suggest that this is not an artifact of crystal packing. These interactions include hydrogen bonds between the Oɛ₁ of Glu235 and the Nζ of Lys202, between the phenol hydroxide of Tyr237 and both Nδ of Asn149 and the backbone oxygen of His148, as well as nonpolar interaction between Leu236 and the disulfide. This places the last four residues of the C terminus very close to the disulfide environment so that the side chain of Leu236 is oriented between Arg223 and the disulfide, and so that the phenol of Tyr237 is between Lys202 and the disulfide (Fig. 3).

Crystal structure analysis of R8

Two variants (R8 and R10) contain additional basic residues near the disulfide but did not show increased disulfide reduction rates compared with roGFP1, possibly due to the substitution K41D. Crystals of reduced R8 (roGFP1+F-223R/K41D) have space group P3₁21 and diffracted to 1.95 Å on APS beamline 14BM-C. The structure was solved by molecular replacement as described for R7.

The asymmetric unit of the R8 crystals again contains a protein dimer that is different from that of either R7 or wtGFP. The backbone oxygen of Lys209 is positioned between the thiols of Cys147 and Cys204 of the neighboring molecule, with Lys209 O an average of 3.5 Å away from the cysteine sulfur atoms. With the A-molecules of R8 and wtGFP aligned, a rotation of 79.1° and translation of 3.5 Å align the B-molecule of R8 with wtGFP.

As expected, the electron density map of R8 shows no evidence for a disulfide bond between cysteines 147 and 204. The Cα–Cα distance between Cys147 and Cys204 is 4.6 Å, compared with a distance of 4.0 Å in the oxidized R7 structure. An overlay of the R7 and R8 models shows that the R8 Cys204 backbone is clearly shifted away from the Cys147 backbone compared with R7, while the position of Cys147 remains essentially the same, as observed for roGFP2 (Hanson et al. 2004). There is no evidence of further cysteine oxidation by oxygen or cross-links with other molecules to Cys147 or Cys204 in either of the two molecules in the asymmetric unit.

The introduced residues Asp41 and Arg223 form a salt bridge. The distance between the Oδ₁ of Asp41 and the Nɛ of Arg223 is 2.8 Å in both molecules (Fig. 3). This electrostatic interaction evidently nullifies the effect of Arg223, as the R3 mutant—which contains F223R but lacks K41D—shows an almost twofold rate enhancement over roGFP1, whereas R8 has essentially the same activity as roGFP1 (Table 2).

An attempt was made to produce oxidized crystals of R8 by transferring the reduced crystals to a solution without DTT. The crystals survived this process and diffracted well a week after being transferred; however, the electron density map showed no evidence of disulfide formation. A similar result occurred when an attempt was made to produce a reduced form of R7 from the oxidized crystals. In each case, dimer formation within the crystal seems to preclude modification of the cysteine redox status. R8 was also crystallized under different conditions without any reducing agent present. However, these crystals diffracted too poorly for structural studies (data not shown).

Electrostatics calculations

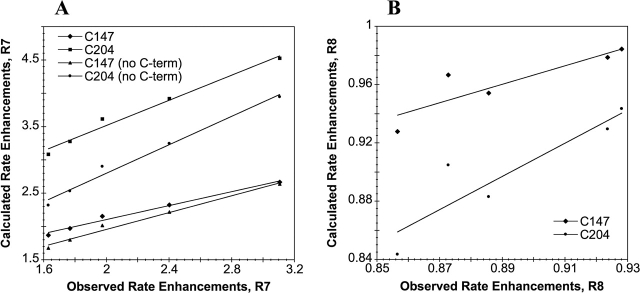
The program DelPhi (Rocchia et al. 2001, 2002) was employed to evaluate the electrostatic contributions of the substitutions in R7 and R8 at the cysteine positions. The expected change in pK_a resulting from the charged substitutions was calculated from the change in site potential at the coordinates of the sulfur atoms in residues 147 and 204 (A-molecules only). In the R7 crystal, the nine C-terminal residues partially occlude cysteines 147 and 204 as well as S202K, so pK_a changes were also calculated for R7 with residues 230–238 deleted. From these calculated ΔpK_as, rate enhancements over parent roGFP1 were calculated (Table 5) and plotted against experimentally observed rates as a function of ionic strengths (Fig. 4), assuming that pH << pK_a and, therefore, that the change in concentration of reactive roGFP (thiolate) is directly proportional to the change in K_a. The plots are linear over the range of ionic strengths tested, indicating a strong correlation between theory and experiment. Experimentally, R8 was observed to have higher k_DTT at higher ionic strengths, and this is correctly predicted by the calculations. In each case Cys204 is predicted to have a larger ΔpK_a than is Cys147 due to the charged substitutions, suggesting that it is the more reactive group. However, this is expected because the sites of basic substitutions are closer to Cys204 than Cys147. Cys204 should therefore possess a lower pK_a and thus act as a more efficient nucleophile.

Table 5.

Calculated vs. experimental rate enhancements for reduction with DTT

	Calculated ΔpKa		Calculated rate
Ionic strength (mM)	C147	C204	C147	C204	Enhancements avg.a	Observedb
A. roGFP1-R8
50	0.033	0.074	0.928	0.844	0.886	0.857
100	0.020	0.054	0.954	0.883	0.919	0.886
150	0.015	0.043	0.967	0.905	0.936	0.873
250	0.009	0.032	0.979	0.929	0.954	0.924
350	0.007	0.025	0.984	0.943	0.964	0.928
CC:c			0.88	0.91	0.90
B. roGFP1-R7
50	–0.426	–0.656	2.666	4.525	3.595	3.107
100	–0.366	–0.593	2.323	3.918	3.120	2.402
150	–0.333	–0.558	2.154	3.613	2.883	1.975
250	–0.295	–0.515	1.971	3.277	2.624	1.768
350	–0.271	–0.489	1.868	3.083	2.475	1.630
CC:c			0.99	0.99	0.99
C. R7 with C-terminal residues removed
50	–0.421	–0.596	2.636	3.947	3.291	3.107
100	–0.346	–0.511	2.217	3.246	2.731	2.402
150	–0.304	–0.463	2.014	2.901	2.458	1.975
250	–0.255	–0.403	1.798	2.531	2.164	1.768
350	–0.224	–0.365	1.677	2.319	1.998	1.630
CC:c			0.99	0.99	0.99

^a From ΔpK_a, calculated using the program DelPhi (see Materials and Methods).

^b From comparison of roGFP1 and full-length roGFP1-R7 or roGFP1-R8 experimental rate constants using DTT (see Materials and Methods).

^c Correlation coefficient of calculated to experimental rate enhancements.

Figure 4.

Calculated rate enhancements (over those of pseudo wild-type roGFP1) vs. those observed experimentally for R7 (A) and R8(B), over a range of ionic strengths. Calculations were performed by using solutions to the PB equation (see Materials and Methods). Calculations were done with and without the eight C-terminal residues for the R7 model.

Calculations performed on the R7 model with C-terminal residues present predict a ΔpK_a of −0.43 (Cys147) to −0.66 (Cys204) (at 50 mM ionic strength), corresponding to a rate enhancement of 3.6 (average) over parent roGFP1. Calculations using the R7 model with C-terminal residues removed predict a ΔpK_a of −0.42 to −0.60, corresponding to a rate enhancement of 3.3 over roGFP1. Although both of these predicted values are close to the observed rate enhancement of 3.1, the same calculations performed on the R7 model with C-terminal residues removed and the Arg223 side chain repositioned so that its guanidinium group is within 4 Å of the Sγ of Cys204 (a movement that is not possible with the C-terminal residues in their crystallographic positions) predict a ΔpK_a of −0.82 to −1.5, which corresponds to a rate enhancement of ~18-fold over roGFP1.

Discussion

Although the general principles that govern the rate of formation of protein disulfide bonds are understood in outline, the relative importance of several factors, such as cysteine pK_a (Kallis and Holmgren 1980; Chivers et al. 1997b; Dyson et al. 1997) and geometric strain (Burns and Whitesides 1990), remains unclear. This is primarily due to the lack of a convenient quantitative assay suitable for rapid kinetic measurements of the rate of bond dissolution or formation. Even less well understood are the factors that govern the thermodynamic stability of protein disulfides, because no model system has been available in which the parameters of interest can be manipulated and the outcome readily evaluated.

In this report, we explored the use of a redox-sensitive GFP (roGFP1) (Hanson et al. 2004) as a tool to study the effect of introducing one or more nearby positive charges on the rate of disulfide formation and breakage. We also introduced a negative charge, a feature of the cysteine-basic residue-acidic residue catalytic triad conserved in many cysteine-based enzymes active sites (Mei and Zalkin 1989; Lowther et al. 2002; Quigley et al. 2003), in order to gain some insight into its possible function. The effect of the external milieu was evaluated by varying the ionic strength. Finally, the overall importance of generalized electrostatic influences was evaluated by comparing predictions based on classical electrostatic theory with the experimental results.

Correlation of rate enhancements with electrostatic effects

Rate-enhanced redox-sensitive GFPs have been successfully developed by the introduction of basic residues near the key cysteines. The substitutions increased both the rate of disulfide reduction by DTT and the rate of oxidation by H₂O₂. Each additional positive charge near the disulfide increased the rate by about a factor of two, with up to a sixfold increase in the first-order rate constant. Except for the electrostatic influence on the reactive cysteines, the mutations had minimal influence on the protein structure, as the overall structure of the protein, the fluorescence quantum yield, and the excitation and emission maxima vary little from that seen for the parent roGFP1. As expected from electrostatic screening arguments and consistent with the basic substitutions providing medium-range electrostatic stabilization of the cysteine thiolates, increasing salt concentrations generally led to attenuated rate enhancements for most of the mutants. Finally, the measured rate enhancements are in excellent agreement with the predictions by nonlinear Poisson-Boltzmann theory, as implemented in DelPhi (Rocchia et al. 2001, 2002).

Similar experiments were recently described by Hansen et al. (2005), who took the same approach toward enhancement of the redox-sensitive construction rxYFP (Ostergaard et al. 2001). Up to three positive charges were substituted near the introduced disulfide (in this case, Cys149–Cys202), and rate enhancements of up to 13-fold were reported for the oxidation of reduced rxYFP by negatively charged GSSG. However, rate enhancements toward uncharged oxidized β-mercaptoethanol were lower (up to a factor of 4.3), suggesting that generalized electrostatic interactions between enhanced rxYFP and GSSG are important. While this group did not directly measure rates for reduction of oxidized rxYFP, the results for the oxidation reaction are in excellent agreement with ours. Thus, the general approach is validated on rather different indicator backgrounds.

roGFP1 mutants with the substitution K41D (R8 and R10) had significantly reduced rate enhancements over roGFP1 compared with the same mutants without K41D. The crystal structure of reduced R8 reveals that a salt bridge is formed between the side chains of K41D and F223R, and this would be expected to minimize the electrostatic effect of Arg223 on the reactive cysteines.

Nevertheless, some results are initially counterintuitive and deserve further discussion. For example, the parent roGFP1, as well as R8 and R10 (which include the acidic substitution K41D), shows increasing rates of oxidation/reduction with increasing salt concentrations (Table 2), suggesting that the K41D substitution reduces the electrostatic effect of the basic substitution(s). This behavior was successfully predicted by DelPhi for the R8 mutant. To rationalize this result, we note that roGFP1 is quite acidic (theoretical pI = 5.8), with an estimated net charge at neutral pH of ~ −9, so cysteine pK_as are expected to be substantially higher than the textbook value of 8.3. Attempts to estimate the apparent pK_a for reduction of oxidized roGFP by kinetic analyses were hampered by pH-dependent spectral changes (data not shown). However, the results suggested that the predominant thiol has a pK_a somewhat higher than 9. Debye screening of the long-range interactions in high ionic strength should thus reduce the effect of the overall protein negative charge on the cysteine pK_as, as observed.

Two mutants, R9 and R14, had a different acidic substitution (Y151D); however, the behavior of these mutants over the range of ionic strengths tested is similar to those lacking Y151D (R3 and R12). This is not surprising for two reasons: First, the net change in charge for Y151D (neutral to negative) would be less than for K41D (positive to negative); second, in the R8 model, residue 41 is closer to Cys204 (9.3 Å, Cα–Cα distance) than is residue 151 (14.4 Å), reducing the influence of the acidic substitution relative to K41D.

Effect on midpoint potentials

Oxidative midpoint potentials were measured for each of the mutants to determine the degree to which the thermodynamic stabilities of the disulfide bonds were affected by the substitutions. Midpoints varied by up to 21 mV, from E°^′ = −284 to −263 mV (R8 and R14, respectively). However, rate constant and midpoint potential correlated well (correlation coefficient = 0.84), with the faster mutants having less negative midpoint potentials. This suggests a strong correlation between thiol pK_a and thermodynamic stability. Nevertheless, the midpoint potentials for the introduced disulfide remain quite negative in comparison with other protein disulfides.

As pointed out earlier, the relative influence of electrostatic influences and geometric strain on the thermodynamic stability of protein disulfides remains unclear. Lower thiol pK_a in a disulfide cysteine leads to a more stable thiolate and, in general, a less stable disulfide (Creighton 1975; Nelson and Creighton 1994). The relationship between midpoint potential and thiol pK_a has been studied in the thioredoxin family (Martin 1995): E°^′ for formation of the disulfide ranges from −122 mV for DsbA to −270 mV for thioredoxin 1 (Aslund and Beckwith 1999); however, the disulfide geometry is very similar for all members (Martin et al. 1993) so geometric influences cannot be accurately assessed. The pK_a of the surface-exposed catalytic cysteine of DsbA is considerably more acidic (3.5) than that of thioredoxin (6.7), which has been attributed to differential electrostatic stabilization of the cysteine thiolate (Gane et al. 1995; Grauschopf et al. 1995).

Nevertheless, electrostatic considerations cannot account entirely for the differences in midpoint potential among thioredoxins, and it has been argued that subtle differences in tertiary structure probably also play an important role (Chivers et al. 1997a; Moutevelis and Warwicker 2004). Burns and Whitesides (1990) studied ring formation in small molecule dithiols and showed that higher geometric strain corresponded to lower disulfide stability. Higher geometric strain also leads to less stable disulfides in proteins (Katz and Kossiakoff 1986; Wells and Powers 1986). Disulfides bridging anti-parallel β-strands are relatively rare in proteins, and the disulfide geometry imposed by this conformation leads to a characteristically strained bond (Hogg 2003).

A comparison of the disulfide geometry of roGFP2 with other examples found in the PDB implies that the roGFP2 disulfide is quite strained. Surprisingly, however, this bond is very stable with E°^′_roGFP2 = −272 mV (Hanson et al. 2004). This value is comparable to that of the catalytic disulfide in the Escherichia coli thiol reductase thioredoxin, despite the latter having a much lower apparent cysteine pK_a. While the geometry of the R7 disulfide appears to be somewhat less strained than that of roGFP2, it is slightly less stable (E°^′_R7 = −268 mV) than that of roGFP2 or roGFP1 (E°^′_roGFP1 = −281 mV). It is remains unclear, therefore, whether geometric strain or electrostatic influences can be invoked to explain the high stability of the roGFP disulfides.

Effect of unexpected localization of C-terminal residues

As described earlier, a unique feature of crystalline R7 is the well-ordered extended strand formed by C-terminal residues 230–238. This segment is disordered in most GFP structures currently on file in the PDB. The extended structure partially occludes the introduced disulfide and conceivably provides a low-dielectric environment, enhancing the influence of nearby positively charged groups. Alternatively, if the C-terminal segment is also ordered in solution, steric effects might lower the reactivity of the disulfides. In the R7 electron density map, the side chains of introduced Lys202 and Arg223 are clearly visible in the vicinity of the disulfide but are not within hydrogen bond distance of either of the cysteines. In the crystal, the ordered C-terminal residues and segments from the adjacent molecule contact the disulfide, possibly forcing residues 202 and 223 away from the cysteines. Electrostatics calculations in the presence and the absence of the eight C-terminal residues yielded similar ΔpK_a results. However, the same calculations using the C-terminal truncated R7 model with the Arg223 side chain modeled in a position closer to Cys204 than is possible with the C-terminal residues in their crystallographic positions predicted a considerably more negative ΔpK_a and, consequently, much higher rate enhancement than was observed experimentally. Although this may suggest a role for the R7 C terminus in the positioning of Arg223 and Lys202, its relevancy in solution remains unclear.

Concluding remarks

Redox-sensitive GFPs with improved response times and less negative midpoint potentials were developed by mimicking features found in the active sites of cysteine-dependent redox-sensitive enzymes. Although rate enhancements are modest, we have demonstrated the usefulness of redox-sensitive GFP as a convenient model system for the quantitative evaluation of the various factors influencing disulfide reactivity and stability. The solvent-exposed location of the reactive cysteines on the convex GFP β-barrel imposes natural limits on the effectiveness of the approach, as physical interactions with introduced charges are at best medium-range. However, the results are in excellent agreement with theory, suggesting that similar efforts, if conducted in a low-dielectric cleft resembling an enzyme active site, could lead to far greater rate enhancements and, hence, more useful redox probes. Finally, the mutant with the most significant rate enhancement for both the oxidation and the reduction reaction was roGFP1-R12. With three additional positive substitutions near the engineered disulfide, this mutant possesses the most nucleophilic cysteine of the mutants tested. In addition, roGFP-R12 has higher estimated pI (~6.2) and, consequently, lower net charge at neutral pH. We therefore recommend roGFP1-R12 for general usage in vivo.

Materials and methods

Three surface-exposed sites near the roGFP disulfide were selected for mutation by visual inspection of the atomic model of roGFP2 (Hanson et al. 2004) and S65T GFP (PDB codes 1JC1 and 1EMA, respectively; Ormo et al. 1996). Model building suggested that a basic substitution at position 149, 202, or 223 might reasonably result in an electrostatic interaction with the disulfide cysteines. In the first round of mutagenesis, three single mutants of roGFP1 (GFP with C48S/S147C/Q204C) were constructed by site-directed mutagenesis of each site to lysine or arginine. Subsequent rounds of mutagenesis added additional charged groups for a total of nine variants with one to four amino acid positions replaced with lysine, arginine, or aspartate (for nomenclature, see Table 1). Aspartate was included to investigate the role of the Cys–Arg–Asp catalytic triad found in some redox-sensitive enzymes.

Gene construction and protein expression/purification

Mutations were introduced using a version of the QuikChange (Stratagene) protocol that allows multiple amino acid substitutions in the same round of mutagenesis using a single primer for each mutation (Sawano and Miyawaki 2000). DNA sequencing of the entire GFP coding region verified each mutation. Mutations were introduced into a His-tagged version of roGFP1 (with Q80R) in the plasmid pRSET_B.

Mutant protein was expressed in E. coli strain JM109(DE3) using the pRSET_B expression system with an N-terminal His₆ tag and grown to an OD₆₀₀ of 0.8 at 37° in a 4-L fermenter. IPTG was added, and cells were allowed to induce overnight at 18°. Cells were pelleted by centrifugation and then resuspended in 50 mM HEPES (pH 7.9), 300 mM NaCl, and 10% glycerol and then were sonicated for 5 min. Cell lysate was centrifuged, and the supernatant was applied to a column of Ni²⁺-nitrilotriacetic acid-agarose resin (Qiagen) for purification. Since GFP is quite resistant to protease degradation, incubation with 2% (w/w) α-chymotrypsin (20 h, room temperature) was used to cleave the Histag and further remove protein impurities. Samples were concentrated by filtration (Amicon Centrion 30; Millipore) and buffer-exchanged with PD-10 Sephadex columns (Amersham Biosciences) 50 mM HEPES (pH 7.9) with 300 mM NaCl.

Spectroscopy

Fluorescence excitation ratios were determined by using an LS55 fluorescence spectrophotometer (PerkinElmer Life-sciences) at 395 and 475 nm, with emission measured at 510 nm. Titration curves were fit by using KaleidaGraph (Synergy Software).

Fluorescence quantum yields were determined for each variant. Samples of protein were prepared so that absorbance at 400 nm was equal to that of a 9-aminoacridine (λ_{max, abs} = 400 nm) standard dissolved in water. Total emission with excitation at 400 nm was measured, and quantum yields were determined from the total emission ratios by using the accepted values for the dye standard (Φ_F = 0.98 for 9-aminoacridine) (Weber and Teale 1957). Emission spectra were corrected for wavelength-dependent photomultiplier sensitivity by using the manufacturer-supplied correction curves and were integrated by using the supplied software (FL Winlab). As a control, the quantum yield (λ_ex = 400 nm) of wtGFP was determined by using the same method and was found to be 0.78. This is in good agreement with values previously reported (Patterson et al. 1997).

Rate determinations

In vitro rates for the reaction of roGFP1 and its variants with DTT and H₂O₂ were determined at low salt concentration by monitoring the fluorescence excitation ratio over time after the addition of a large excess of reagent. All solutions were degassed before use, and buffers were then bubbled with nitrogen to remove any remaining dissolved molecular oxygen. Experiments were carried out at 25° in disposable 2-mL cuvettes with ~0.5 μM protein (0.01 mg/mL). Reaction buffer was 50 mM HEPES (pH 7.0) with 1 mM EDTA. For H₂O₂ experiments, samples were first diluted from a storage concentration of 1.0–0.1 mM to ~10 μM in 20 μL of reaction buffer and then incubated at room temperature for 60 min with 1 mM DTT to ensure reduction of the disulfide. Samples were diluted in disposable cuvettes to 2 mL with 50 mM HEPES (pH 7.0). Fluorescence excitation was measured every 10–20 sec after the addition of 1 mM DTT or H₂O₂. This was repeated at least twice for each mutant. The fraction of reduced roGFP (R) was calculated from the ratio of excitation peaks as previously described (Hanson et al. 2004). The pseudo first-order rate constant for the reaction was determined by using a curve fit to Equation 1.

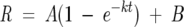(1)

To determine the effect of salt concentration, the rate constants for reduction with DTT were determined in 50 mM HEPES (pH 7.0) with 0, 50, 100, 200, or 300 mM NaCl for each of the variants.

Midpoint determinations

Samples of all variants were prepared at 1 μM in 100 mM HEPES (pH 7.0) with 1 mM total DTT (mixture of oxidized and reduced forms) in 2-mL cuvettes and allowed to incubate for 3–4 h at 25°. To minimize air oxidation, all buffers and solutions were degassed, and all samples were prepared and incubated in an anaerobic glove-box. After incubation, cuvettes were capped and removed from the glove-box for fluorescence excitation measurements. Apparent redox midpoint potentials for all roGFP1 variants were determined as described previously (Hanson et al. 2004). As a check, the midpoint potential of roGFP1 was verified by using lipoic acid (10 mM total). Midpoint potentials at pH 7.0 and 25° were assumed to be E°^′_(Lip) = −0.270 V (Lees and Whitesides 1993) and E°^′ _(DTT) = −0.323 V (Szajewski and Whitesides 1980).

Crystal structure determinations

R7 (roGFP1+S202K/F223R) was concentrated to 40 mg/mL in 50 mM HEPES (pH 7.9) and 300 mM NaCl. Crystals grew in 1–2 d by hanging drop vapor diffusion against 1.1 M Na citrate and 0.1 M imidazole (pH 7.6). With normal oxygenated buffer and no reducing agent, the protein is completely oxidized, so no disulfide catalyst was necessary. Drops contained 2 μL of protein solution and 2 μL of well solution. For low temperature diffraction data collection, crystals were transferred to the same well solution plus 15% glycerol.

R8 (roGFP1+K41D/F223R) was concentrated to 32 mg/mL in 50 mM HEPES (pH 7.9) and 300 mM NaCl. Long, hexagonal rod crystals grew overnight by hanging drop vapor diffusion against 1.9 M ammonium sulfate, 0.1 M sodium phosphate/citrate (pH 4.6), and 5 mM DTT. Drops contained 1 μL of protein solution and 1 μL of well solution. For low temperature diffraction data collection, crystals were transferred to the same well solution plus 20% glycerol.

X-ray diffraction data were collected from a single frozen crystal on an Raxis-IV system for R7 and from a single frozen crystal on APS beamline 14BM-C for R8. Data sets were indexed and reduced by using Denzo and Scalepack, or the HKL2000 suite (Otwinowski and Minor 1997). Molecular replacement solutions were found with EPMR (Kissinger et al. 1999), using the GFP S65T coordinate file (PDB code 1EMA) as the search model, with positions of amino acid substitution changed to alanines. Positional refinement was initiated by using data from 6.0–4.0 Å resolution and then increased in stages to the limit of resolution, using the program TNT (Tronrud et al. 1987). Electron density maps (2F_o − F_c and F_o − F_c) were analyzed and the model rebuilt by using the program O (Jones et al. 1991). B-factor refinement was performed by using the default TNT B-factor correlation library. Solvent molecules were added only if indicated by large positive features in the (F_o − F_c) electron density maps and in reasonable proximity to hydrogen bond partners. In the final rounds of refinement, 100% of diffraction data was used.

Electrostatics calculations

To predict cysteine pK_a differences between roGFP1 and mutants, the nonlinear form of the PB equation was solved by using finite difference methods with version 4 of the program DelPhi (Rocchia et al. 2001, 2002). Differences in the site potential (ΔΔ G) at the reactive cysteines (Cys147 and Cys204) for the mutants with and without charges at the positions of substitution were used to calculate changes in the cysteine pK_a through Equation 2 (Yang et al. 1993).

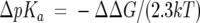(2)

If the reaction mechanism proceeds through the thiolate anion, then a reduction of cysteine pK_a by 1 unit should lead to a 10-fold increase in the concentration of the reactive species and therefore a 10-fold increase in the pseudo first-order rate constant (assuming pH >> pK_a). PDB files of the oxidized R7 and reduced R8 structures without solvent molecules were used (A protomers only). Solvent dielectric was set to 80 and protein interior dielectric to 4.0, while a Stern layer of 2.0 Å was specified. The program iteratively solved the nonlinear PB equation until the maximum change in potential between iterations was <10⁻⁴ kT. ΔΔG was calculated for the cysteines of both R7 and R8 with all substituted residues uncharged, each individually charged and finally with all substitutions charged. This was repeated with ionic strength set to 0, 50, 100, 150, 250, 300, and 350 mM. Since the substitution K41D in R8 replaces a basic residue with an acidic one, potential differences for R8 were determined with either a negative charge at Asp41 or with a positively charged lysine residue modeled at that site. Calculations were also performed on the R7 model with the eight C-terminal residues removed and with the side chain of Arg223 repositioned so that its guanidinium group is within 4 Å of the Sγ of Cys204. This repositioning was done by rotating the side-chain torsion angles, keeping bond distances and angles unchanged while maintaining reasonable contact distances with other side chains.

Data deposition

The atomic coordinates and structure factors have been deposited in the Protein Data Bank, with PDB ID codes 2AH8 (R7) and 2AHA (R8).

Abbreviations

• GFP, green fluorescent protein

• roGFP, redox-sensitive GFP

• rxYFP, redox-sensitive yellow fluorescent protein

• DTT, dithiothreitol

• GSH, glutathione

• GSSG, glutathione disulfide

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.051734306.