The redox couple of the cytochrome c cyanide complex: The contribution of heme iron ligation to the structural stability, chemical reactivity, and physiological behavior of horse cytochrome c

Abstract

Contrary to most heme proteins, ferrous cytochrome c does not bind ligands such as cyanide and CO. In order to quantify this observation, the redox potential of the ferric/ferrous cytochrome c–cyanide redox couple was determined for the first time by cyclic voltammetry. Its E⁰′ was −240 mV versus SHE, equivalent to −23.2 kJ/mol. The entropy of reaction for the reduction of the cyanide complex was also determined. From a thermodynamic cycle that included this new value for the cyt c cyanide complex E⁰′, the binding constant of cyanide to the reduced protein was estimated to be 4.7 × 10⁻³ LM⁻¹ or 13.4 kJ/mol (3.2 kcal/mol), which is 48.1 kJ/mol (11.5 kcal/mol) less favorable than the binding of cyanide to ferricytochrome c. For coordination of cyanide to ferrocytochrome c, the entropy change was earlier experimentally evaluated as 92.4 Jmol⁻¹K⁻¹ (22.1 e.u.) at 25 K, and the enthalpy change for the same net reaction was calculated to be 41.0 kJ/mol (9.8 kcal/mol). By taking these results into account, it was discovered that the major obstacle to cyanide coordination to ferrocytochrome c is enthalpic, due to the greater compactness of the reduced molecule or, alternatively, to a lower rate of conformational fluctuation caused by solvation, electrostatic, and structural factors. The biophysical consequences of the large difference in the stabilities of the closed crevice structures are discussed.

In both the ferric and ferrous states, the heme iron of cytochrome c (cyt c) is hexacoordinated and lies at the center of a “closed heme coordination” structure (George and Lyster 1958; Harbury et al. 1965) represented as

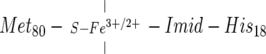where the vertical lines signify the equatorial coordination by the heme pyrrole nitrogens. The iron has two axial ligands, Met₈₀ and His₁₈. The His₁₈ imidazole is on what is commonly called the “right side” of the protein, and the thioether sulfur of Met₈₀ is on the “left side” (Takano and Dickerson 1981).

Understanding the structural basis of the stability and the physiological behavior of this protein requires a thorough knowledge of the thermodynamic and kinetic consequences of this peculiar ligation of the metal. The Met₈₀S–Fe³⁺ bond is weaker than the Fe³⁺–ImidHis₁₈ bond, since the former can be broken by exogenous ligands, such as cyanide, which allows the measurement of its stability (George and Tsou 1952; George et al. 1967). However, an analogous evaluation of the same parameter in the ferrous state cannot be made, because typical ligands such as CO, O₂, and CN⁻ cannot break the Met₈₀S–Fe²⁺ bond. Indeed, since the earliest days of cyt c research it has been known that when the iron is in the reduced state, the protein is remarkably stable (Keilin 1930; Keilin and Hartree 1937), and, contrary to most heme proteins, unable to bind CO below pH 13 (Butt and Keilin 1962). This unusual characteristic of cyt c has, until now, remained only as a qualitative observation, lacking a definite quantitative measure and a consequent evaluation of its importance in the chemical and physiological behavior of the protein.

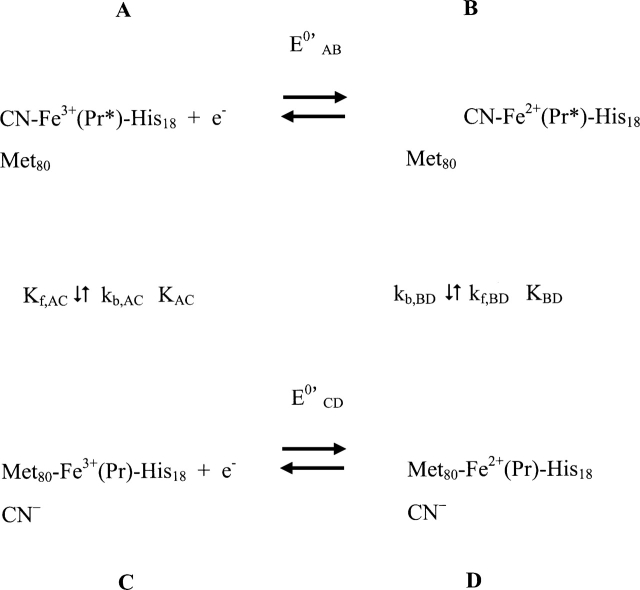
The redox-dependent ligand exchange of cyanide ion with Met₈₀, proposed here to follow the 2 × 2 square mechanism (Evans 1990; Balducci and Costa 1993; Feinberg et al. 1998), is shown in Scheme 1. Since the redox potential of cytochrome c (see reaction C → D) (Scheme 1) and the affinity of its ferric state for cyanide (reaction C → A) (Scheme 1) are known, it is possible, in principle, to provide a detailed thermodynamic characterization of the complete cycle by determining the redox potential of the cyanide complex (A → B) and deducing the stability of the Met₈₀S–Fe²⁺ bond (D → B) using the thermodynamic cycle shown in Scheme 1.

Scheme 1.

The 2 × 2 square mechanism for the redox driven ligand exchange of cytochrome c in the presence of cyanide ion. Pr represents the native protein, and Pr^* symbolizes the protein after undergoing the structural changes concomitant with the displacement of the native ligand Met-80 away from the iron by CN⁻.

In Scheme 1, Pr represents the native protein, and Pr^* symbolizes the protein after undergoing the structural changes concomitant with the displacement of the native ligand (Met₈₀) away from the iron by CN⁻. Once the redox potential of the cytochrome c cyanide complex is known (reaction A → B) (Scheme 1), the only unknown remaining in the thermodynamic cycle is the right-hand, bottom-to-top reaction (D → B, k_f,BD), namely, the binding of cyanide to the ferrocytochrome c iron:

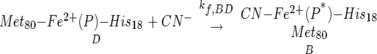It is known, however, that when the ferrocytochrome c cyanide complex is formed at pH 13 by reducing the ferric cyanide complex, and then taken to neutrality, it dissociates readily with a half-life of 170 sec (George and Schejter 1964) back to Met₈₀—Fe²⁺—His₁₈. This has precluded an accurate measurement of the equilibrium reduction potential of this complex by conventional equilibrium titration techniques, such as potentiometry or spectroelectrochemistry.

Cyclic voltammetry (CV) (Bard and Faulkner 2001), in combination with modern computer simulation methods, permits the determination of the redox potential of species with short half-lives, such as the CN—Fe^3+/2+— His₁₈ redox couple. We report in this paper the indirect measurement of the stability of the Met₈₀S–Fe²⁺ bond of cytochrome c using CV. Our results show that the Met₈₀S–Fe²⁺ bond is 48.1 kJ/mol (11.5 kcal/mol) more stable (ΔΔG) in the reduced state than in the oxidized state, thus, providing the first quantitative answer to a fundamental and long-standing problem in the chemistry of this paradigmatic heme protein. On this basis, we are able to explain the large difference in the stabilities of the two oxidation states of the protein against denaturation. We also note how this difference plays a major role in the regulation of the redox potential of cytochrome c and in protecting the reduced iron from being oxidized by oxygen.

Materials and methods

Preparative procedures

Horse heart cytochrome c was prepared as described by Margoliash and Walassek (1967) and Brautigan et al. (1978).

Electrochemical methods

Cyclic voltammetry

While CV is not as sensitive as square-wave voltammetry (SWV), it possesses some important advantages, including (1) the direct observation of the redox couples and the relative contributions of reducing/oxidizing current to each couple and (2) a more direct interpretation of the voltammogram, especially as a function of the scan rate. Cyclic voltammetric data at two or more scan rates are typically simulated within the framework of a specific mechanism (e.g., Scheme 1), and can provide the E⁰′ of the participating redox couples and/or the associated equilibrium and rate constants. In CV, a triangular waveform is applied to the electrode (Bard and Faulkner 2001). The potential is first scanned in one direction and then, at some point, switched and scanned in the reverse direction. For example, for a ferricyt c solution when the potential is scanned in the negative direction, the ferricyt c is reduced to the ferrous form as the potential approaches and goes past its E⁰′; a cathodic peak current is observed; and then, upon scanning the potential in the reverse direction, the reduced form is reoxidized to give the anodic peak current. The complete voltammogram gives a pair of peaks of the same current amplitude but in the opposite direction with the E⁰′ being between the two peak potentials with a peak potential separation of 60 mV/n (n = number of electrons per equivalent used in the redox reaction) when the redox reaction is fast and reversible (Nernstian).

Simulation of cyclic voltammograms

A relatively new and fast method for simulating cyclic voltammograms has been developed (Rudolph 1990, 1995; Rudolph et al. 1994), which, in principle, permits the determination of the E⁰′, equilibrium constants and rates of production of new products and intermediates in the context of a specific mechanism and as a function of scan rate. The simulation program has now been formalized as the computer software, Digisim (Bioanalytical Systems, Inc.), which is used in this work.

Square-wave voltammetry

SWV is a voltammetric method that provides a high signal to noise response (Ramely and Kranse 1969). In SWV a potential is applied over time in the form of a square wave superimposed on a staircase. The applied potential is progressively stepped in fixed increments and pulsed positively and negatively at each step with a specific step potential, the square-wave amplitude. Experimentally, the positive (forward) and negative (reverse) currents are collected separately and then the differences are taken for forward and reverse currents to provide the observed “net” SW voltammogram. In the absence of kinetic complications, the potential at which the voltammetric peak is observed defines the equilibrium reduction potential, E⁰′. In this paper, the variation of E⁰′ with temperature was obtained with SWV and used to determine the entropy of reaction, ΔS⁰′_Rxn, for reduction reaction:

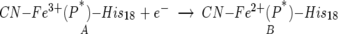ΔS⁰′_Rxn was determined via nonisothermal electrochemical measurements of the equilibrium reduction potential, E⁰′, as a function of temperature. Error analysis for the experiments in Figure 2 and shown in Table 1 were obtained with weighted least-squares method to calculate ΔS and ΔH. It was assumed that the potentials observed were ±1.5 mV. The experimental details for using SWV to determine the ΔS⁰′_Rxn have been reported (Bertrand et al. 1995; Feinberg et al. 1998). In earlier work, SWV and CV were used to understand the redox-driven axial ligand exchange of the Phe82His variant of iso-1-cytochrome c (Feinberg et al. 1998), which followed the 2 × 2 square mechanism similar to that shown in Scheme 1.

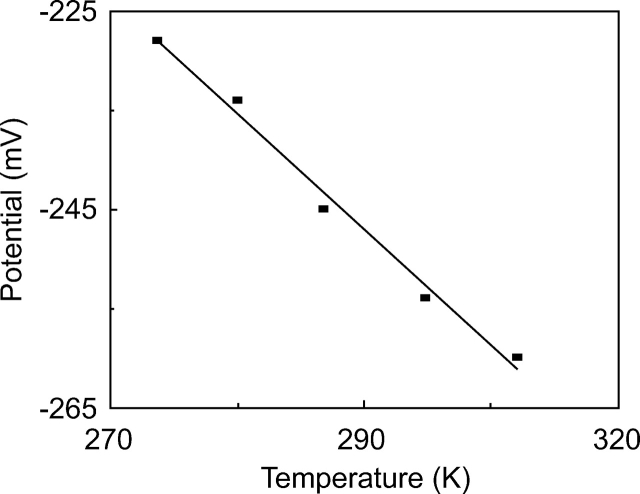
Figure 2.

Temperature dependence of the equilibrium reduction potential (E⁰′) of the cyanide complex of horse cytochrome c.

Table 1.

Thermodynamic parameters for the reduction of horse cytochrome c and its cyanide complex pH 7.0 and 25°C

	E0′ mV	ΔG kJ/mol kcal/mol	ΔH kJ/mol kcal/mol	ΔS J/mol·K e.u.
Cytochrome ca	+260	−25.1	−69.9	−150.6
		−6.0	−16.7	−36.0
Cytochrome c cyanide	−240	+23.2 ± 0.2	−3.8 ± 1	−90.0 ± 4
		+5.5 ± 0.03	−0.9 ± 0.3	−21.5 ± 1

^aGeorge and Lyster 1958; Margalit and Schejter 1973.

Instrumentation

All electrochemical experiments were done with a BAS 100 B/W Electrochemical Analyzer (Bioanalytical Systems). Potentials were reported against either the Standard Hydrogen Electrode (SHE) or the Ag/AgCl/3 M KCl reference electrode. To convert Ag/AgCl potentials to the SHE, 210 mV was added to that potential. A 0.1 M solution of KCN buffered at pH 7.0 with Tris was prepared. Samples (100 μL) of horse cytochrome c were then microdialyzed into this cyanide solution overnight at 4 °C and used immediately thereafter. Triple-distilled water (Purification Systems) with a conductivity of 18 Mohms/cm was used throughout. Final protein concentrations were 0.5–1 mM. All experiments were done at a bis (4-pyridyl) disulfide modified gold electrode. Experimental details, including the modification of the gold electrode with 5 mM bis(4-pyridyl) disulfide (Aldrich Chemical Co.) have been described (Feinberg et al. 1998).

A specially designed anaerobic semimicrocell that permitted samples of ~30-μL volume to be examined was used for the electrochemical experiments (Smith and Feinberg 1990; Smith et al. 1991). Oxygen was removed by passing wet 99.99% pure argon over the sample and through the cell for 20 min prior to the experiment. The reference electrode, which was separated from the sample with a double frit, was the Ag/AgCl/3 M KCl electrode (Bioanalytical Systems). The counter electrode was 18-gauge platinum wire. For the entropy of reaction measurements, E⁰′s were measured at 1.6°, 9.4°, 18.0°, 28.1°, and 37.1°C.

Results

Cyclic voltammetry

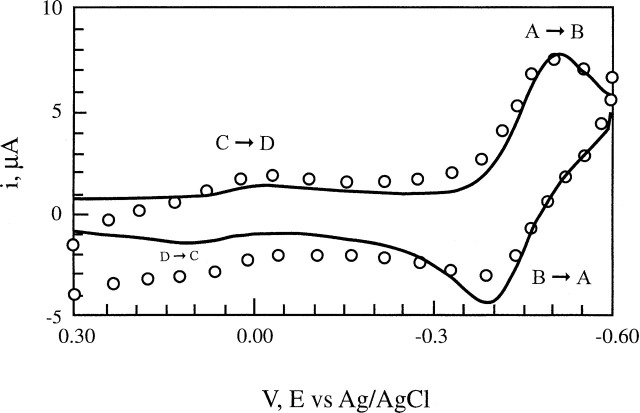
Figure 1 shows the cyclic voltammogram of cytochrome c in 0.1 M KCN (pH 7.0), 25°C, at a 50 mV/sec scan rate, along with the computer simulation of that voltammogram with Digisim using the 2 × 2 square mechanism shown in Scheme 1. In following the course of the voltammogram (see Fig. 1; Scheme 1), when the voltammetric experiment was started at 0.3 V, all the cytochrome near the electrode surface was oxidized. As the applied potential was moved in the negative (reducing) direction, a small cathodic peak (C → D) close to the E⁰′ of native horse cytochrome c was observed. This peak, assigned to the reduction of the ferric cyt c, is quite small and shows that nearly all the cyt c has the Met₈₀ ligand displaced by CN⁻. That is, the cytochrome is mostly in the form CN—Fe³⁺—His₁₈, leaving very little in the Met₈₀—Fe³⁺—His₁₈ form. As the scan was continued in the negative direction, a much larger cathodic (reduction) peak (A → B) was observed at ~−500 mV (vs. Ag/AgCl), which is assigned to the reduction of the ferric cyt c cyanide complex. At −600 mV, the direction of the potential scan was switched and moved in the positive (oxidizing) direction. Soon after the return scan was initiated, a nearly full “reverse current” peak (B → A) was observed for the reoxidation of the ferrous cyt c cyanide complex. This indicated that the cyanide was still the primary sixth axial ligand, even with the iron in the ferrous state. The reason that this large “reverse current” was observed is that on the timescale of the voltammetric experiments, the rate of dissociation of the ferrocyt c cyanide is slow, so that most of the cyt c was still in the CN⁻ coordinated form (B) at the time it was reoxidized (A). As the scan was continued in the oxidizing direction, another small peak was observed near the redox potential of the native cyt c (D → C). Summing up, in the complete voltammogram two relatively undistorted yet interconnected (see Scheme 1) redox couples were observed: one for the native cyt c and one for the cyt c–cyanide complex. Fortunately, two factors combine to allow us to observe the E⁰′ of cyt c–CN complex: one is the large difference between the E⁰′ of the cyt c and cyt c–CN complex redox couples, i.e., 260 mV versus ~−220 mV, respectively, and the other is the slow rate of the ferrous cyt c–cyanide complex dissociation relative to the potential scan rate. Thus, even prior to simulation, which takes into account the kinetic effects, the voltammogram in Figure 1 provides an approximate value for the E⁰′ ≈−220 mV versus SHE for the CN—Fe^3+/2+—His₁₈ couple and E⁰′ = +260 mV for the native cyt c.

Figure 1.

Cyclic voltammogram of 1 mM horse cytochrome c in the presence of 0.1 M KCN at pH 7.0, Tris buffer, 25°C at a scan rate of 50 mV/sec. The circles (○) are the experimental data; the solid line, the computer simulation of the CV with Digisim using the 2 × 2 mechanism shown in Scheme 1.

Simulation of the cyclic voltammograms: Determining the E⁰′ of the cytochrome c cyanide complex via the 2 × 2 square mechanism

Shown in Figure 1 is the voltammogram and its simulation of cyt c in 0.1 M NaCN at a scan rate of 50 mV/sec. The other scan rate used was 100 mV/sec and was also used in the simulation. Simulations made with Digisim using the 2 × 2 square mechanism (Scheme 1) took into account the extent to which kinetics shifted the observed reduction potential. In fact, kinetic effects are real but not extensive at the scan rates used here, and the cyclic voltammogram is dominated by equilibrium processes. In starting the simulation, the approximate K_eq = k_f,AC/k_b,AC ≈ 0.01 used. This approximate K_eq was obtained from the ratio of the cathodic voltammetric currents of peaks C → D and A → B of the voltammogram. The relatively fast heterogenous electron transfer rate constant of k_s = 3 × 10⁻³ cm/sec was employed since it gave the best fit for both scan rates and was used in conjunction with the cross-reaction:

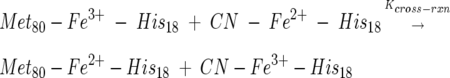where K_cross-rxn was quite large by virtue of the relative E⁰′s of the wild-type cyt c (+260 mV) and its cyanide complex (−240 mV). For the equilibrium,

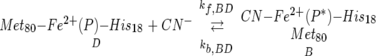the simulated (calculated) value of K_eq = K_BD = k_f,BD/₋k_b,BD was 5.2 × 10 ⁷.

The scan rates employed to obtain an accurate E⁰′ (50 and 100 mV/sec) were relatively fast on the timescale of the dissociation of CN—Fe²⁺—His₁₈, and thus did not place these voltammograms well into the kinetic region, i.e., where significant potential shifts and changes in cathodic and anodic currents would have been observed for both the Met₈₀—Fe^3+/2+ —His₁₈ and CN—Fe^3+/2+ —His₁₈ redox couples. Moreover, by choosing the somewhat faster scan rates (where the voltammograms were in the “equilibrium region”), we have obtained an accurate value for the E⁰′ of the CN—Fe^3+/2+—His₁₈ couple, but obtained less precise information on the kinetic parameters shown in Scheme 1. To explore the kinetics of the redox driven cyanide ligand exchange under these conditions, voltammetric experiments would need to be done at significantly slower scan rates.

Square-wave voltammetry as a function of temperature

Figure 2 shows the variation of the reduction potential of the CN—Fe^3+/2+—His₁₈ couple as a function of temperature, which in turn, provided the entropy of reaction (Feinberg et al. 1998) used to calculate the overall entropy change (Taniguchi et al. 1980) via the expression: ΔS⁰′ = ΔS⁰′_Rxn − 66.5 J/mol · K.

Calculation of the thermodynamics of cyanide binding

From the cycle of Scheme 1, it follows, starting with native cyt c, that

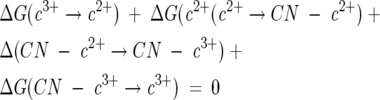(1)

where all the ΔG terms are written in a counterclockwise direction as one moves around Scheme 1. The bottom reaction (C → D) is the reduction of ferricyt c (E⁰′ = +260 mV) to ferrocyt c for which ΔG (c³⁺ → c²⁺) = −25.1 kJ/mol (6.0 kcal/mol) (Margalit and Schejter 1973). The top reaction (B → A), from right to left, is the oxidation of ferrous cyt c cyanide to ferric cyt c cyanide, ΔG (CN—c²⁺ → CN—c³⁺, E⁰′ = −0.240 mV) which corresponds to −23.0 kJ/mol (5.5 kcal/mol). The left top-to-bottom reaction, A → C, ΔG (CN—c³⁺ → c³⁺), is the dissociation of the cyanide from the ferric protein, for which the free energy change is +34.7 kJ/mol (8.3 kcal/mol) (George and Tsou 1952; George et al. 1967). When these values are introduced into Equation 1, the free energy of binding of cyanide to ferrocyt c, (D → B), ΔG (CN⁻ + c²⁺ → CN—c²⁺) at 25°C was calculated to be 13.4 kJ/mol (3.2 kcal/mol). This is equivalent to a binding constant of 4.7 × 10⁻³ LM⁻¹, a distinctly low affinity that explains why the cyanide complex of reduced cyt c cannot be formed directly at neutral pH.

Applying our electrochemical data (see Fig. 2) to the equation d(ΔG)/dT = ΔS, the entropy change attending the reduction of the ferricyt c–cyanide complex was evaluated as −90 J/mol · K (21.5 e.u.) at 25°C. Expanding the free energy terms into their enthalpic and entropic components, an equation similar to Equation 1 can be written for the entropies of the reactions described in Scheme 1. Since the entropies of reduction and cyanide binding of ferricyt c are known to be −150.6 J/mol · K (36 e.u.) (Margalit and Schejter 1973) and 132 J/mol · K (31.5 e.u.) (George and Tsou 1952; George et al. 1967), respectively, the entropy of cyanide binding to ferrocyt c was evaluated as 92.4 J/mol · K (22.1 e.u.).

These results are listed in Tables 1 and 2, together with the corresponding heats of binding of cyanide to ferric and ferrous cyt c. The latter was evaluated, using the Gibbs equation ΔG = ΔH − T · ΔS, as 41.0 kJ/mol (9.8 kcal/mol).

Table 2.

Thermodynamic parameters for the reactions of ferric and ferrous cytochrome c with cyanide, at pH 7.0 and 25°C^a

	ΔG kJ/mol kcal/mol	ΔH kJ/mol kcal/mol	ΔS J/mol·K e.u.	TΔS kJ/mol
Ferric cytochrome c	−34.7	4.6	132.0	39.3
	−8.3	1.1	31.5
Ferrous cytochrome c	13.4	41.0	92.4	27.5
	3.2	9.8	22.1
Note: ΔΔG = 48.1kJ/mol (11.5 kcal/mol); ΔΔH = 36.4 kJ/mol; T (ΔΔS) = 11.8 kJ/mol

^aGeorge and Tsou 1952; George 1967; Margalit and Schejter 1973.

Discussion

The preceding results show that the free energy change (difference) concomitant with the binding of cyanide to the ferrous heme iron of cyt c is 48.1 kJ/mol (11.5 kcal/mol) less favorable than when the iron is in the ferric state (see Table 2). The data in Table 2 show that ~75% of the difference between the stabilities (ΔΔG) of the closed heme coordination structures (George and Lyster 1958; Takano and Dickerson 1981) of the ferric and ferrous states arises from the difference between the enthalpies (ΔΔH) of the reactions of the latter, which amounts to 36.4 kJ/mol (8.7 kcal/mol), i.e., 36.4/48.1 kJ/mol ≈ 0.75. The term “heme coordination stability” is synonymous with the earlier term “heme crevice stability,” i.e., the amount of free energy required to break the methionyl S–Fe bond. The fact that the driving force of cyanide binding to ferric cyt c has a large favorable entropy change, led to earlier speculations that attributed the lack of reactivity of the ferrous form to the absence of an entropic contribution (George and Schejter 1964; Margoliash and Schejter 1966). Indeed, cyanide coordination to ferrous cyt c does make an entropy contribution (T · ΔΔS) to the free energy of the binding reaction, but of only ~40 J/mol · K (9.4 e.u.), which amounts to 11.8 kJ/mol (2.8 kcal/mol) at 25°C (see Table 2), or ~25% of the total free energy.

The large difference in enthalpies can be accounted for by two major factors: electrostatic and structural. First, an important contribution must stem from the fact that cyanide binding to the ferric state implies a cancellation of a charge that is absent in the ferrous state. The second factor should involve the structural differences between the ferric and ferrous proteins (Takano and Dickerson 1981) in the region of the molecule to which the Met₈₀ side chain is necessarily displaced upon breaking its coordination to the iron. Although structural studies indicate that packing of the reduced and the oxidized proteins is essentially the same in both oxidation states (Brayer and Murphy 1996), there is significant evidence that the oxidized and the reduced molecules differ in their hydrodynamic properties. Thus, the intrinsic viscosity of the reduced state is lower than that of the oxidized state (Fisher et al. 1973), and the radius of gyration (Trewhella et al. 1988) and adiabatic compressibility (Eden et al. 1982) are correspondingly smaller. All these differences indicate a dynamically more “open” structure in the oxidized state and a more compact structure in the reduced state. In the now more compact ferrous cyt c, it is more difficult to find space for the displaced Met₈₀ side chain, further impeding CN⁻ binding. This difference must also play a significant role in the regulation of the redox potential of cyt c by virtue of stabilizing the reduced form. Further work will be performed to parse the diverse contributions to this parameter arising from intrinsic ligand-metal affinities, protein conformation differences, and overall electrostatic influences.

Moreover, the preceding results also explain, quantitatively, the extreme resistance of the ferrous cyt c coordination structure being broken (i.e., breaking the axial methionyl S–Fe²⁺ heme coordination bond) by exogenous ligands including oxygen, and thus its resistance to oxidation by oxygen. Another demonstration that reduction increases the affinity of the heme iron for a methionyl sulfur is the fact that substitution of histidine for the Phe₈₂ in iso-1 cyt c results in the displacement of Met₈₀ from the ferric iron by the new residue (Hawkins et al. 1994). However, upon reduction of the metal, the normal Met₈₀–Fe²⁺ bond is restored (Schejter et al. 1996; Feinberg et al. 1998). For comparison, in Met-65,80-dicarboxymethyl cyt c, a chemically modified cyt c in which the alkylated Met₈₀ sulfur is displaced from the iron, the reduced metal binds oxygen rapidly and is oxidized to the ferric state within a few minutes (Schejter and Aviram 1970). This ability of native cyt c to remain reduced in the presence of oxygen, which is essential for its proper function in the respiratory chain, depends directly on the high stability of the native heme crevice.

It is interesting that the high stability of the reduced cyt c closed-crevice structure is reflected almost quantitatively in the increased overall stability of the protein in the reduced state. Specifically, the free energy of chemical denaturation of horse ferrous cytochrome c is 77.0 kJ/mol (18.4 kcal/mol) (Jones et al. 1993), while the corresponding value for ferric cyt c is 33.9 kJ/mol (8.1 kcal/mol) (Knapp and Pace 1974; Schejter et al. 1998). Strikingly, this higher stability of the reduced protein structure of 10.3 kcal/mol (43.1 kJ/mol) is very close to the increase in stability of the native heme crevice upon reduction, i.e., 48.1 kJ/mol (11.5 kcal/mol; ΔΔG from Table 2). This correspondence of free energies may very well be coincidental, since it has been shown with Saccharomyces cerevisiae iso-1-cyt c that the source of the increase in thermal stability of the reduced the protein is nearly entirely entropic (Cohen and Pielak 1995), albeit at pH 4.6. In rationalizing the increased enthalpic stabilization of heme coordination (a local effect) versus the entropically driven increase in overall stability of the reduced protein, it is important to point out that the energetics presented in this paper refer specifically to the enthalpic barrier to breaking the Met₈₀–Fe²⁺ bond by both endogenous ligands and exogenous ligands such as cyanide, imidazole, or oxygen. Since there is evidence that reduction and increased overall stability are concomitant with the protein becoming more compact (see the above discussion), the more compact structure may make ligand exchange energetically more difficult just from simple molecular mechanical considerations. Invoking increased Met₈₀–Fe²⁺ bond strength and thus an increased enthalpic contribution is not a likely option, since, again, in the thermal denaturation study of the overall stability of reduced iso-1 cyt c, Cohen and Pielak (1995) found that the enthalpic change upon reduction was destabilizing.

In summary, the preceding results provide a quantitative measure of the difference in the stabilities of the closed structures of reduced and oxidized cyt c. They also demonstrate that this feature plays an important role in the determination of the redox potential of this heme protein, in its resistance to oxidation by molecular oxygen, and on the stabilization of the native protein structure.

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.051825906.