Abstract
Quantitative studies of membrane protein folding and unfolding can be difficult because of difficulties with efficient refolding as well as a pronounced propensity to aggregate. However, mixed micelles, consisting of the anionic detergent sodium dodecyl sulfate and the nonionic detergent dodecyl malto-side facilitate reversible and quantitative unfolding and refolding. The 4-transmembrane helix protein DsbB from the inner membrane of Escherichia coli unfolds in mixed micelles according to a three-state mechanism involving an unfolding intermediate I. The temperature dependence of the kinetics of this reaction between 15° and 45°C supports that unfolding from I to the denatured state D is accompanied by a significant decrease in heat capacity. For water-soluble proteins, the heat capacity increases upon unfolding, and this is generally interpreted as the increased binding of water to the protein as it unfolds, exposing more surface area. The decrease in DsbB's heat capacity upon unfolding is confirmed by independent thermal scans. The decrease in heat capacity is not an artifact of the use of mixed micelles, since the water soluble protein S6 shows conventional heat-capacity changes in detergent. We speculate that it reflects the binding of SDS to parts of DsbB that are solvent-exposed in the native DM-bound state. This implies that the periplasmic loops of DsbB are relatively unstructured. This anomalous thermodynamic behavior has not been observed for β-barrel membrane proteins, probably because they do not bind SDS so extensively. Thus the thermodynamic behavior of membrane proteins appears to be intimately connected to their detergent-binding properties.
Keywords: membrane protein, folding kinetics, detergents, temperature, heat capacity
The thermodynamics of unfolding of membrane proteins has not been studied to the same extent as that of water-soluble proteins (Haltia and Freire 1995). This is due to a number of reasons, such as the difficulty of obtaining membrane proteins in sufficient amounts for these studies, the complexity of their interactions with surrounding lipids or detergents, the restricted conditions under which they can refold, and their tendency to aggregate upon denaturation. However, thermodynamic studies can provide insights into the nature of the forces stabilizing membrane proteins and the structural changes they undergo at higher temperatures, as well as highlighting specific features of a protein in an amphiphilic environment. Typically, three thermodynamic parameters can be obtained, namely the enthalpy (ΔHD−N), entropy (ΔSD−N), and specific heat capacity (ΔCp) of unfolding. ΔHD−N and ΔSD−N can be difficult to interpret, because they are a sum of many different contributions including both protein-protein, protein-solvent, and solvent-solvent interactions (Creighton 1993; Johnson and Fersht 1995; Otzen and Oliveberg 2004). ΔCp is easier to interpret in structural terms. It is generally viewed as a measure of the amount of hydro-phobic surface area exposed on unfolding (Privalov and Gill 1988; Privalov et al. 1989; Livingstone et al. 1991; Spolar et al. 1992; Otzen 2005), and may be obtained as the slope of ΔHD−N versus the melting temperature Tm. Generally, ΔCp is much lower for membrane proteins than for water-soluble proteins. This is connected to the inability of membrane proteins to unfold completely in a lipid or detergent environment at higher temperatures, simply because water is not available to hydrogen bond to the peptide bond in the membrane to the same extent as for water-soluble proteins (Popot and Engelman 1990). For bacteriorhodopsin, the most intensely studied model membrane protein, differential scanning calorim-etry studies in purple membranes estimate a specific heat capacity of around 0.046 cal/K/g, which is only ∼30% of that of a water-soluble protein such as myoglobin (Brouillette et al. 1987). Bacteriorhodopsin has a very large number of hydrophobic side chains, mostly embedded in the membrane. Clearly, only a small number of them, most likely only those in the loop regions (Haltia and Freire 1995), become exposed on thermal denaturation. This is in agreement with the small ΔHD−N (100 kcal/mol) (Brouillette et al. 1987), which can entirely be accounted for by the unfolding of the 90 water-exposed loop residues (Haltia and Freire 1995).
Recently, the use of mixed micelles consisting of an anionic and a nonionic detergent has emerged as an alternative to lipids to study membrane protein behavior quantitatively. The advantage of this approach is that unfolding is reversible, allowing both the measurement of folding and unfolding, and can be carried out isother-mally. For some detergent pairs, complications can arise because of preferential partitioning of one of the detergent components into micelles (Sehgal et al. 2005). However, the combination of dodecyl maltoside and sodium dodecyl sulfate appears to lead to a linear relationship between the free energy of unfolding and the bulk mole fraction of SDS (Lau and Bowie 1997), and this has been used to measure the stability of mutants of bacteriorhodopsin (Faham et al. 2004; Yohannan et al. 2004) and diacyl glycerate kinase (Nagy and Sanders 2003). We have combined SDS-DM mixed micelles with stopped-flow kinetics to analyze the unfolding and refolding of the inner membrane protein DsbB from Escherichia coli. DsbB's behavior is consistent with a three-state folding model involving the SDS-denatured state, the native state in DM and an unfolding intermediate that accumulates above 0.4–0.5 mole fractions SDS (Otzen 2003). To obtain more insight into this process, we have measured the folding kinetics between 15° and 45°C. Remarkably, unfolding of the intermediate to the denatured state is characterized by a decrease in the heat capacity of unfolding. This unexpected observation is backed up by equilibrium studies. Control studies with the water-soluble protein S6 show that this is not an artifact of the use of mixed micelles but appears to be a genuine property of the interaction between detergents and membrane proteins. We speculate that it may relate to the lack of structure in the large periplasmic loop regions.
Results
DsbB shows unusual heat capacity changes in the SDS-DM mixed micelle system
To obtain thermodynamic parameters that may shed more light on the properties of membrane proteins, we measured the rate constants of folding and unfolding of DsbB over the temperature range 15°–45°C. The lower limit of this range is set by the Krafft point for SDS, below which it precipitates. This value is around 18°C in 0.1 M NaCl (Nakayama and Shinoda 1967; Lange and Schwuger 1968). In practice, our SDS solutions can be cooled to 15°C (but not 10°C) without precipitation, forming a metastable micellar solution. The upper limit is determined by DsbB's denaturation temperature in DM micelles, which is around 45°C (see below).
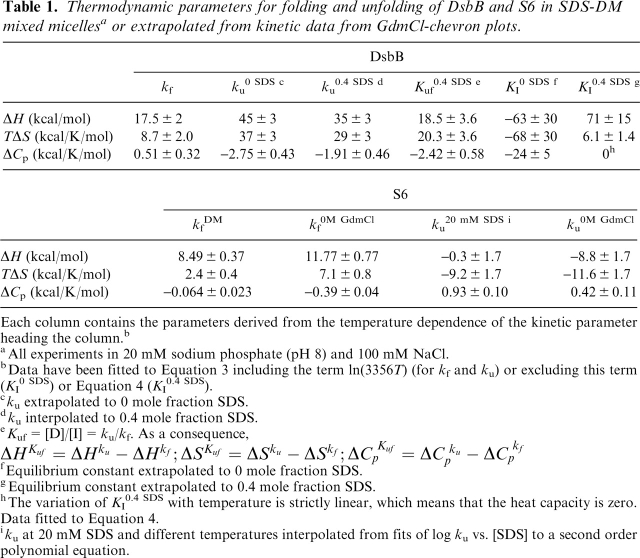
At all temperatures over this range, a logarithmic plot of DsbB's observed rate constant versus the SDS mole fraction shows the characteristic sigmoidal plot that can satisfactorily be fitted to the equation describing a three-state folding system (Fig. 1A). At each temperature, we thus obtain the rate constants of folding and unfolding and the equilibrium constant for formation of the unfolding intermediate I. The temperature variation of these parameters (Fig. 1B-D) in turn provides the enthalpies, entropies, and heat capacities summarized in Table 1. The activation barrier between D and I characterized by kf and ku has comparable contributions from enthalpy and entropy. The magnitude of the entropic barrier is dependent on the pre-exponential factor, for which we use the term 33 56 T (see Materials and Methods). While the magnitude of the pre-exponential factor is debatable, this factor cancels out when we use the relationship Kuf = [D]/[I] = ku/kf to describe the intermediate I relative to D (see Table 1, footnote “e”). The stabilization of I relative to D has exactly equal contributions from enthalpy and entropy, which strengthens our deductions about the activation barrier. Similarly, the step between I and N, characterized by KI, has enthalpic and entropic activation barriers of similar signs.
Figure 1.
(A) Kinetic plots of the refolding and unfolding rate constants of DsbB in mixed SDS/DM micelles measured between 15° and 45°C in steps of 5°C. Data are fitted to Equation 2. (B) Temperature dependence of the refolding rate of DsbB kf extrapolated to 0 mole fraction SDS. Data are fitted to Equation 3 (summarized in Table 1). (C) Temperature dependence of the unfolding rate of DsbB ku extrapolated to 0 mole fraction SDS (•) and at 0.4 mole fraction SDS (○). Data are fitted to Equation 3 (summarized in Table 1). (D) Temperature dependence of the equilibrium constant KI extrapolated to 0 mole fraction SDS (•) and at 0.4 mole fraction SDS (○). Data at 0 mole fraction are fitted to Equation 3 without the term ln(3356T), while data at 0.4 mole fraction are fitted to Equation 4.
Table 1.
Thermodynamic parameters for folding and unfolding of DsbB and S6 in SDS-DM mixed micellesa or extrapolated from kinetic data from GdmCl-chevron plots.
Each column contains the parameters derived from the temperature dependence of the kinetic parameter heading the column.b
aAll experiments in 20 mM sodium phosphate (pH 8) and 100 mM NaCl.
bData have been fitted to Equation 3 including the term ln(3356T) (for kf and ku) or excluding this term  or Equation 4
or Equation 4 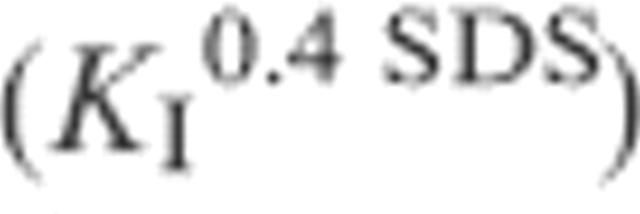 .
.
cku extrapolated to 0 mole fraction SDS.
dku interpolated to 0.4 mole fraction SDS.
eKuf = [D]/[I] ku/kf. As a consequence, 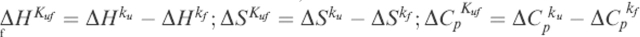
fEquilibrium constant extrapolated to 0 mole fraction SDS.
gEquilibrium constant extrapolated to 0.4 mole fraction SDS.
hThe variation of KI0.4 SDS with temperature is strictly linear, which means that the heat capacity is zero.
Data fitted to Equation 4.
iku at 20 mM SDS and different temperatures interpolated from fits of log ku vs. [SDS] to a second order polynomial equation.
The heat capacities are very unusual, since the activation heat capacity for kf is positive (0.51 kcal/K/mol), while that for ku is negative (−2.75 kcal/K/mol). This is evident from the curvature in Figure 1, BCwhich is positive for kf and negative for ku, respectively. The traditional interpretation of this, based on the analysis of water-soluble proteins, would be that folding of DsbB is accompanied by an increase in solvent-exposed hydrophobic regions, while unfolding is accompanied by a decrease. An even more dramatic conclusion is reached from the heat capacity associated with the N → I transition, which indicates an enormous decrease in heat capacity of −24 ± 5 kcal/K/mol. A typical heat-capacity value (describing the transition from N to D) for a water-soluble protein of DsbB's size would be ∼ + 2 kcal/K/mol (Otzen and Olive-berg 2004). However, the KI-values on which this is based are obtained by extrapolation from a very steep transition zone around 0.3–0.4 mole fraction SDS (cf. Fig. 1A). Furthermore, the slope of this transition (the mI-value) increases dramatically at higher temperatures, rising from a value around 7–11 between 15° and 30°C to a value around 40 at 45°C (data not shown). If we instead use KI-values interpolated to 0.4 mole fraction SDS, there is no curvature (Fig. 1D) and the heat capacity shrinks to zero. In contrast, the negative curvature remains when ku0.4 SDS-values are used (Fig. 1C), indicating that this is a reliable value. No extrapolation problem exists for kf, which is measured at very low SDS mole fractions. Thus, the heat capacity increases by 2.4–3.3 kcal/K/mol (0.12–0.16 cal/K/g) on going from D to I.
The water-soluble protein S6 shows conventional heat-capacity changes in the SDS-DM system
Nevertheless, it is unclear whether these paradoxical heat capacity values are an artifact of working in a micellar system. It is difficult to resolve this completely. However, one approach is to carry out similar studies for a water-soluble protein. We have previously shown that the ribosomal protein S6 can be unfolded in SDS (using 25 mM Tris at pH 8 and 20 mM NaCl) with a linear dependence of log ku on 1/T (Otzen 2002), indicating an apparent heat-capacity change of zero upon unfolding. On the other hand, unfolding rate constants in buffer (50 mM MES at pH 6.3), extrapolated from values obtained in the denaturant GdmCl, shows positive curvature and a heat capacity of +0.42 kcal/K/mol (cf. Fig. 2A) (Otzen and Oliveberg 2004). Thus, it would appear that SDS reduces the apparent heat capacity of the unfolding reaction. Nevertheless, buffers and salts will influence the micellar behavior of detergents (Jönsson et al. 1998). Therefore, in the present study we have analyzed the temperature dependence of the refolding of S6 from the SDS-denatured state into DM, as well as unfolding into SDS in the presence of DM with the same PN buffer used for DsbB.
Figure 2.
(A) Temperature dependence of unfolding of S6 in 0 molar GdmCl (•) (data from Otzen and Oliveberg 2004) and in 20 mM SDS (○) and 100 mM SDS (×). Data fitted to Equation 3 and summarized in Table 1. (Inset) ku as a function of SDS concentration in 20 mM Tris (pH 8) (○) and 100 mM NaCl (data from Otzen 2002) and in PN buffer in the presence of 5 mM DM (•). Data are fitted to a second order polynomial. (B) Temperature dependence of refolding of S6 from SDS into DM (○) and at 0 molar GdmCl (•) (data from Otzen and Oliveberg 2004). Data fitted to Equation 3 and summarized in Table 1. (C) Variation of heat capacity of unfolding of S6 in SDS with SDS concentration in the presence of 5 mM DM. For each SDS concentration and temperature, the unfolding rate constant was interpolated from second order polynomials (see inset in A). (D) Time profile of unfolding of S6 into 20 mM SDS and 5 mM DM at 45°C. The inset highlights the 0.2-sec lag phase. The line represents the best fit of the data after 0.2 sec to a single exponential decay with drift.
We will first comment on the magnitude of the measured rate constants. The temperature dependence of unfolding rate constants in 20 and 100 mM SDS is shown in Figure 2A. Unfolding rate constants in SDS cannot be compared directly with those in GdmCl because of the different mechanisms of unfolding (Otzen and Oliveberg 2002). S6 unfolds in SDS according to one of two modes, depending on the concentration of salt and SDS, though both are suggested to involve a rapid and saturable binding of SDS to S6 prior to unfolding (Otzen 2002). The inset to Figure 2A shows that the presence of DM slows down unfolding significantly compared with unfolding of S6 directly into SDS without DM present. DM may become incorporated into SDS micelles and, by its presence herein, slow down unfolding. This agrees with the observation that at higher concentrations of SDS, where the mole fraction of DM in the mixed micelles drops, the difference between unfolding rate constants narrows, though other phenomena could also lead to this behavior (see below).
S6's refolding from 5 mM SDS into 5–15 mM DM follows a simple exponential decay with a small amount of linear drift, similar to refolding from the GdmCl-denatured state (Otzen et al. 1999). As shown in Figure 2B, refolding rate constants are ∼10 times lower in the DM-SDS system than in the GdmCl system over the whole temperature range. More precisely, the difference is fivefold rather than 10-fold, if we take into account the accumulation of an off-pathway intermediate, which in practice, slows down refolding of the GdmCl-denatured state at very low denaturant concentrations by a factor of 2 (Otzen and Oliveberg 1999, 2001). The fivefold difference is unlikely to be because the SDS-state traps S6 in a low-energy well. If SDS is removed by α-cyclo-dextrin in the dead time of mixing in the stopped-flow apparatus and no other detergents are present, we obtain values of kf, which perfectly match the values expected at 0 M denaturant (Otzen and Oliveberg 2001). Although micellar dynamics are very rapid and occur in the microseconds-low milliseconds time range even at room temperature (Aniansson and Wall 1974), it cannot be ruled out that folding may be partially decelerated by the extraction of SDS micelles from S6 and their incorporation into DM micelles. However, in such a case, one would expect folding to occur more rapidly at higher DM concentrations, which is not the case. An alternative possibility is that SDS and DM form mixed micelles that remain attached to S6, and the very presence of a hydro-phobic environment may impede the folding reaction to some extent. Nevertheless, both refolding and unfolding data suggest that S6 interacts with mixed micelles. This makes it reasonable to compare the thermodynamic behavior of DsbB and S6.
As shown in Figure 2C, the heat capacity for unfolding of S6 in SDS in the presence of 0.1 M NaCl and 5 mM DM decreases from 0.93 ± 0.10 kcal/K/mol in 20 mM SDS to ∼0.6 kcal/K/mol in 60–80 mM SDS. This systematic variation could be caused by a change in the composition of the micelles. Alternatively, it could arise from the progressive accumulation of an unfolding intermediate at higher SDS concentrations, whose heat capacity is closer to that of the transition state of unfolding than the native state. From this perspective, the value at 20 mM SDS (0.93 ± 0.10 kcal/K/mol) is the true activation heat capacity of unfolding, representing the difference between the native and the transition state. This value is more than twice as large as the 0.42 kcal/K/mol obtained from GdmCl-experiments (which does not vary with GdmCl concentration) (Otzen and Oliveberg 2004).
For refolding data, the heat capacity change has changed from ∼ −0.39 kcal/K/mol (kf extrapolated from refolding in GdmCl) (Otzen and Oliveberg 2004) to ∼ −0.06 kcal/K/mol (refolding in DM from SDS) (Fig. 2B). Both of these heat-capacity values are independent of GdmCl and DM concentration.
Thus, we conclude that both SDS and DM make heat-capacity changes associated with folding and unfolding more positive than the values obtained from kinetics in GdmCl. Nevertheless, the heat-capacity changes retain their conventional sign, that is, negative (loss of exposed surface area) upon folding and positive (increase in exposed surface area) upon unfolding, in contrast to the values reported for DsbB. Thus, the change in sign appears to be specific for membrane proteins rather than a general feature of all proteins in a mixed micelle system.
Decrease in heat capacity upon unfolding of DsbB in thermal scans
To verify this unusual observation, we have attempted to obtain complementary measurements of the heat-capacity change. Isothermal equilibrium denaturation in mixed SDS-DM micelles followed by fluorescence at different temperatures is not feasible due to solvent effects from changes in micelle composition (Otzen 2003). Instead, we have used thermal denaturation studies at different mole fractions of SDS, followed by far-UV CD spectroscopy. Unfolding data can be fitted to a simple two-state model with isodichroic points around 202 and 239 nm (Fig. 3A). Unfolding is irreversible and leads to precipitation above the melting temperature, as seen for many other proteins. The CD spectrum of the denatured and precipitated state has a broad minimum around 215 nm, which is consistent with the presence of β-sheet structure, confirmed by Fourier Transform Infrared Spectroscopy (L.W. Nesgaard and D.E. Otzen, unpubl.). The level of b-sheet structure only decreases slightly when DsbB is heat denatured in the presence of up to 0.4 mole fraction SDS, indicating that the denaturation process is not significantly altered by including SDS (data not shown).
Figure 3.
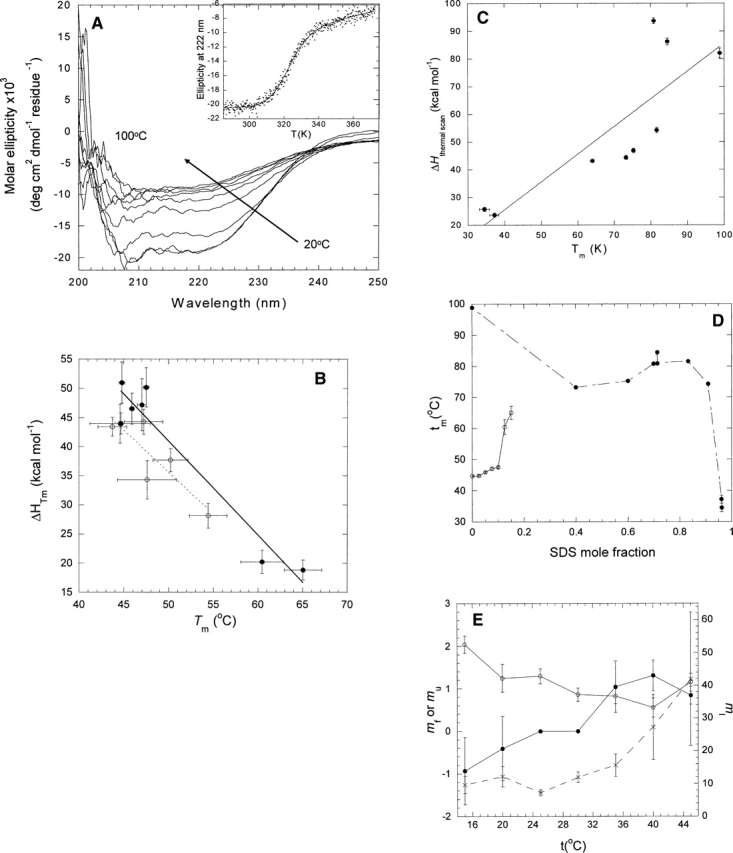
(A) Far UV CD scans of the thermal denaturation of DsbB between 20° and 100°C. (Inset) Change in ellipticity at 222 nm as a function of temperature. Data fitted to Equation 1. (B) ΔHD−N of DsbB as a function of Tm. Data obtained by fitting scans from A to Equation 1 at different mole fractions of SDS and DM (•) or SDS and UM (○). (C) ΔHD−N of S6 as a function of Tm in 20 mM NaOAc (pH 4) at different mole fractions of SDS in SDS-DM mixed micelles. (D) Tm as a function of SDS mole fraction for DsbB (○) and S6 (•). Data points are joined for clarity. (E) Kinetic m-values for DsbB as a function of temperature. (•) mf, (○) mu, (×) mI.
Before we analyze these data, we should address one question: Are the conformational states, and thus the heat-capacity change, measured under equilibrium conditions comparable to those measured by kinetics? In equilibrium kinetics, the micelle composition stays the same throughout the experiment, assuming that the micelle composition is essentially temperature independent. This means that we are measuring the change in heat capacity between the native state and the heat-denatured state. In kinetic experiments, unfolding or refolding occurs by transferring the protein from one micelle composition to another. The two states involved in a given rate constant are the ground state from which the reaction starts (formed in the dead time of the stopped-flow apparatus by the mixing of detergent 2 with the protein in detergent 1) and the transition state. It is a key issue whether the detergent environment surrounding the protein in the ground state has the same composition as that in the transition state or whether this changes over the course of the reaction. Unfortunately, it is not possible to measure this directly. We will, however, for simplicity, assume that mixing is rapid and occurs prior to unfolding. In several cases, we see a short lag phase (with a duration up to 25% of the half-life of the unfolding reaction) preceding the actual decline in fluorescence that accompanies unfolding of S6 in SDS (Fig. 2D). Note that the dead time of mixing in our stopped-flow apparatus is ∼5 msec, while the lag time is ∼200 msec. This suggests that micellar mixing has to reach at least a certain threshold of completion before unfolding can occur. By adding heat capacity changes from folding and unfolding data, we are looking at the change in heat capacity between the two ground states of folding and unfolding. The folding ground state can be assumed to be in 5 mM DM. In contrast, the unfolding ground state is in a variable mole fraction of SDS in combination with 5 mM DM. However, this can be extrapolated to 0 mM SDS based on the assumed linear relationship between the log of rate constants and the SDS mole fraction. Thus, heat capacity changes from thermal scans should, in principle, be comparable to extrapolated values from kinetic studies.
In fact, a plot of the measured enthalpy change of unfolding versus Tm shows a clear negative correlation (Fig. 3B) with a slope around −1.5 kcal/K/mol. Data from unfolding of DsbB in mixed micelles of SDS and undecyl maltoside (UM) are also included, which show the same linear trend and provide complementary data points. This value is close to the total heat capacity obtained from kinetic studies (in which the heat capacity from KI is set to 0). Thus, there is independent support for the unusual heat-capacity changes observed for DsbB. A similar experiment with S6, in which the protein is unfolded at different concentrations of DM and SDS, yields a positive slope (Fig. 3C) with a heat capacity around 1 kcal/K/mol, essentially identical to that obtained from thermal scans in GdmCl (Otzen and Oliveberg 2004). S6 precipitates upon thermal denaturation in the SDS/DM system, unlike the GdmCl system, but this does not appear to affect the outcome of the analysis, and we similarly assume that the precipitation of DsbB will not complicate our analysis. Note that for DsbB, the variation in Tm with SDS mole fraction is unusual, since it increases with increasing SDS concentration, unlike that of S6 (Fig. 3D). It is precisely the combination of increasing Tm and decreasing enthalpy that leads to a negative heat capacity. It may also be seen from the kinetic plots in Figure 1A that the steep transition region has shifted slightly to higher SDS concentrations at higher temperatures, again indicating that higher SDS mole fractions are accompanied by higher thermostability.
Changes in m-values with temperature
The m-values provide insight into the affinity of SDS for different states of the protein. mf and mu indicate the relative increase in binding of SDS upon folding or unfolding, respectively. Conventionally, mf should be negative (SDS released upon folding) and mu positive (SDS bound upon unfolding). However, mf increases steadily from negative to positive with temperature, while mu decreases but remains positive (Fig. 3E). Thus, more and more SDS remains bound or binds to a larger extent during folding, while the increase in bound SDS upon unfolding becomes smaller. This supports the apparent thermostabilization of DsbB by SDS. It is more difficult to interpret the change in the mI-value, which has large errors associated with it. Despite the apparent increase shown in Figure 3E, mI, in fact, remains constant within error between 15° and 45°C.
Discussion
Reliability of heat-capacity values
The main observation we present is that the heat capacity of the membrane protein DsbB follows exactly the opposite behavior of that observed for water-soluble proteins. There is a clear and stepwise increase in heat capacity upon going from the denatured state via the transition state to the intermediate state. Between I and N, it is unclear whether there is any substantial change in heat capacity. Extrapolation to 0 molar SDS, relying on a very steep transition zone, provides an unrealistically high heat-capacity increase for the I → N step, but this is contradicted by interpolated values and equilibrium denaturation experiments. However, the heat capacity values based on kf and ku are based on very short extrapolations of rate constants directly obtained from time-resolved relaxation profiles. Even if the specific three-state unfolding scheme for DsbB proves to be incorrect, the linear relationships between rate constants and SDS mole fraction suggests that kf and ku represent simple molecular events.
The unusual heat-capacity change may reflect unstructured loop regions in the native state
How can we interpret I's increase in heat capacity relative to D? The increase is not a simple artifact of the use of an SDS-DM micelle system. Firstly, SDS and DM have approximately the same heat capacity, as they have the same chain length (Kresheck 1998) and the head group does not make a large contribution to heat capacity (Király and Dekány 2001). Secondly, and more importantly, control experiments with the water-soluble protein S6 do not lead to the same unusual heat-capacity behavior. DM tends to make heat-capacity changes associated with folding of S6 smaller and more positive compared with refolding from the GdmCl-denatured state, while SDS makes unfolding heat-capacity changes larger and more negative. However, the overall change in heat capacity, namely the sum of the activation heat capacities of refolding and unfolding, is identical to that obtained from equilibrium experiments. Thus, the difference in compactness between the denatured and the native states has not changed substantially, but the transition state for folding has been brought closer to the denatured state and farther from the native state. In other words, the energy landscape through which the protein folds has changed sufficiently to alter the structure of the rate-limiting ensemble. The SDS-denatured ground state from which refolding starts has a native-like level of secondary structure (Otzen and Oliveberg 2002), but obviously this does not affect the overall level of compactness, indicating that the denatured state is very extended, with only isolated patches of structure.
The simplest explanation for DsbB's decrease in heat capacity upon unfolding from I to D is that SDS shields DsbB's hydrophobic residues to a greater extent than DM, so that as the protein exchanges DM with SDS it actually becomes somewhat less water-accessible. It is generally believed that SDS solvates protein molecules as “beads on a string” (Ibel et al. 1990), so that the protein exists as a collection of spatially separated regions, each of which is surrounded by an SDS micelle or hemimicelle. SDS is able to bind to essentially all parts of a protein, due to its combination of electrostatic and hydrophobic attractions. This means that it will also be able to bind to parts of DsbB that are not in contact with the membrane in the native state, such as the two large periplasmic loops (residues 32–49 and 90–144) or the water-exposed N-terminal 14 residues and the 14 C-terminal residues. Together, the extramembraneous residues make up ∼57% of the entire protein. In contrast, DM will tend to stabilize the native structure, which is more compact, but not so extensively in contact with detergent. This may imply that the loop regions are highly water-exposed and therefore not particularly structured in the native state. These loops contain two disulfide bonds (Cys 41–44 and Cys 104–130), which undergo redox exchange with the periplasmic protein DsbA (Bardwell et al. 1993). There are no structures available for DsbB, but it is tempting to speculate that a flexible and water-exposed loop region would more easily expose these disulfide bonds to contact with DsbA. In contrast, S6 is a highly compact structure in the native state and is unlikely to be more shielded in the SDS-denatured state. We are currently attempting to establish a system to monitor the association of pep-tides representing the transmembrane helices only in order to eliminate the contribution of the loops to the process.
Thermo dynamic differences between α-helical and β-barrel membrane proteins
It is interesting that the β-barrel membrane protein AIDA shows a conventional increase in heat capacity upon unfolding as judged by thermal scans carried out at different SDS mole fractions (Mogensen et al. 2005). In the absence of thermodynamic data on other membrane proteins in mixed micelle systems, it is premature to speculate extensively on the differences between the two membrane classes of β-barrels and α-helices. However, it is worth pointing out that β-barrel proteins such as AIDA cannot be unfolded in SDS at room temperature but require very elevated temperatures for this to occur. SDS is in other words not an effective denaturant and is not able to bind extensively to the protein, which may prevent it from shielding hydrophobic residues sufficiently from the solvent to reduce the protein's heat capacity below that of the native state.
Materials and methods
DsbB (Otzen 2003) and S6 (Otzen et al. 1999) were expressed and purified as described. Stopped-flow kinetic experiments for DsbB were carried out between 15° and 45°C in PN-buffer (20 μM phosphate buffer at pH 8.0 and 100 mM NaCl). To measure the rate of refolding of S6, 10 mM S6 (denatured in 5 mM SDS) in PN buffer was mixed with DM micelles by diluting the S6 solution 1:10 into PN buffer containing DM to final concentrations of 5, 10, 15, 20, 30, 40, and 50 DM between 15° and 65°C. Data for S6 refolding could be fitted to single exponentials with drift to give the observed refolding constant kf. At each temperature, kf was essentially constant between ∼15 and 50 mM DM. The rate constant at each temperature was calculated as the average of the measured kf-values. Unfolding rate constants were obtained by diluting a solution containing 10 μM S6 and 55 mM DM 1:10 into PN buffer containing SDS to final concentrations of 20, 40, 60, 80, and 100 mM SDS. Data could be fitted to single exponentials with drift.
Far-UV wavelength and thermal scans were recorded on a Jasco J-810 spectropolarimeter (Jasco Spectroscopic Co. Ltd.) with a typical concentration of 15 μM DsbB and a total detergent concentration of 5–7 mM. A 1-mm quartz cuvette was used at a bandwidth of 1 nm, using steps of 0.2 nm at a scan speed of 50 nm/min. The change in ellipticity at 220 nm was monitored for both S6 and DsbB. All DsbB thermal scans were carried out in PN buffer. The high thermal stability of S6 at neutral pH (Otzen and Oliveberg 2004) required us to carry out thermal scans of the protein in 20 mM NaOAc (pH 4) with different concentrations of SDS and DM in order to denature the protein in an experimentally accessible temperature range.
Data analysis
Thermal scan data for both DsbB and S6 fitted to a two-state unfolding model, assuming a linear dependence of the pre- and post-transition baselines on temperature (Sehgal et al. 2005):
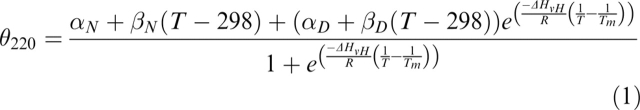 |
where θ220 is the observed ellipticity at a given temperature; αN and αD are the ellipticities of the native and the denatured state, respectively, at 298 K; βN and βD are the slopes of the native and the denatured state baselines, respectively; T is the temperature; Tm is the midpoint denaturation temperature; ΔHvH is the van't Hoff enthalpy change of unfolding; and R is the gas constant.
At a given temperature, the dependence of DsbB's observed rate constant of folding or unfolding on the SDS mole fraction XSDS was analyzed according to the following three-state model (Otzen 2003):
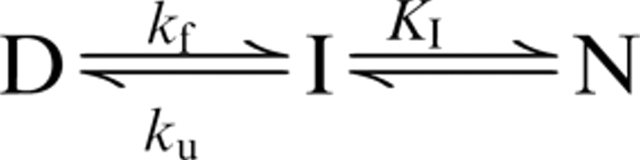 |
where D is the SDS-denatured state, I is an intermediate, N is the native state, kf and ku are the rate constants of folding and unfolding, and KI = [I]/[N]. Specifically, the observed rate constant kobs is fitted to the following equation (Otzen 2003):
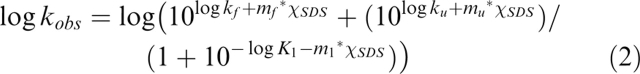 |
The temperature dependence of kinetic rate constants k was analyzed according to the following equation (Otzen 2005):
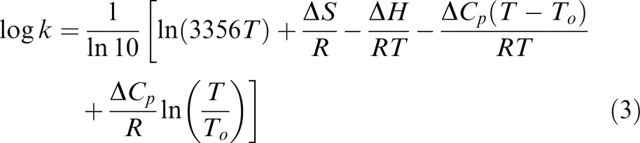 |
The pre-exponential factor (here 3356T) represents the lifetime of the transition state. In simple chemical reactions (Fersht 1999), the prefactor used is conventionally the term for vibrational frequency (kBT/h ≈ 1013 sec−1), where kB is Boltzmann's constant and h is Planck's constant. For our analysis, this term has been replaced with the factor 3356T (which is 106 sec−1 at 298 K), which represents the fastest step in protein folding, namely closing of a loop (Hagen et al. 1996; Parker et al. 1998).
The temperature dependence of the equilibrium constant KI at 0 mole fraction SDS was fitted to Equation 2 with omission of the term ln(3356T) (Otzen 2005). At 0.4 mole fraction SDS, there is no curvature and the equation reduces to:
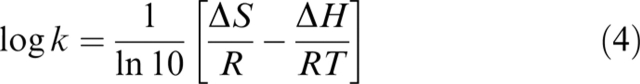 |
Acknowledgments
P.S. was supported by a grant from the Danish Natural Science Research Council. D.E.O. is supported by the Villum Kann Rasmussen Foundation and the Danish Research Foundation. We thank Lise W. Nesgaard for recording FTIR spectra.
Abbreviations
D, denatured stateDM, dodecyl maltosideDsbB, disulfide bond forming protein BI, Intermediatekf, refolding rate constantku, unfolding rate constantKI, equilibrium constant for formation of I from NN, native stateSDS, sodium dodecyl maltosideTm, melting temperatureUM, undecyl maltoside
Footnotes
Reprint requests to: Daniel E. Otzen, Department of Life Sciences, Aalborg University, Sohngaardsholmsvej 49, DK-9000 Aalborg, Denmark; e-mail: dao@bio.aau.dk; fax: +45-98-14-18-08.
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.052031306.
References
- Aniansson E.G. and Wall S.N. 1974. On the kinetics of stepwise micelle association J. Phys. Chem. 78: 1024–1030. [Google Scholar]
- Bardwell J.C.A., Lee J.-O., Jander G., Martin N., Belin D., Beck-with J. 1993. A pathway for disulfide bond formation in vivo Proc. Natl. Acad. Sci. 90: 1038–1042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brouillette C.G., Muccio D.D., Finney T.K. 1987. pH dependence of bacteriorhodopsin thermal unfolding Biochemistry 26: 7431–7438. [DOI] [PubMed] [Google Scholar]
- Creighton T.E. In Proteins. Structures and molecular properties . 1993. 2d ed. W.H. Freeman & Co, New York.
- Faham S., Yang D., Bare E., Yohannan S., Whitelegge J.P., Bowie J.U. 2004. Side-chain contributions to membrane protein structure and stability J. Mol. Biol. 335: 297–305. [DOI] [PubMed] [Google Scholar]
- Fersht A.R. In Structure and mechanism in protein science. A guide to enzyme catalysis and protein folding. . 1999. W.H. Freeman & Co, New York.
- Hagen S.J., Hofrichter J., Szabo A., Eaton W.A. 1996. Diffusion-limited contact formation in unfolded cytochromec: Estimating the maximum rate of protein folding Proc. Natl. Acad. Set 93: 11615–11617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haltia T. and Freire E. 1995. Forces and factors that contribute to the structural stability of membrane proteins Biochim. Biophys. Acta 1228: 1–27. [DOI] [PubMed] [Google Scholar]
- Ibel K., May R.P., Kirschner K., Szadkowski H., Mascher E., Lundahl P. 1990. Protein-decorated micelle structure of sodium-dode-cyl-sulfate-protein complexes as determined by neutron scattering Eur. J. Biochem. 190: 311–318. [DOI] [PubMed] [Google Scholar]
- Johnson C.M. and Fersht A.R. 1995. Protein stability as a function of denaturant concentration: The thermal stability of barnase in the presence of urea Biochemistry 34: 6795–6804. [DOI] [PubMed] [Google Scholar]
- Jönsson B., Lindman B., Holmberg K., Kronberg B. In Surfactants and polymers in aqueous solutions pp. 61–89. 1998. Wiley & Sons, New York.
- Király Z. and Dekány I. 2001. A thermodynamic titration study on the micelle formation of sodium decyl sulfate in water J. Colloid Interface Sci. 242: 214–219. [Google Scholar]
- Kresheck G.C. 1998. Comparison of the calorimetric and van't Hoff enthalpy of micelle formation for a nonionic surfactant in H2O and D2O solutions from 15 to 40°C. J.Phys. Chem. B 102: 6596–6600. [Google Scholar]
- Lange H. and Schwuger M.J. 1968. Mizellbildung und Krafft-Punkte in der homologen Reihe der Natrium-n-alkyl-sulfate einschliesslich der ungeradzahligen Glieder Koll. Z.Z. Polym. 223:–145.
- Lau F.W. and Bowie J.U. 1997. A method for assessing the stability of a membrane protein Biochemistry 36: 5884–5892. [DOI] [PubMed] [Google Scholar]
- Livingstone J.R., Spolar R.S., Record M.T. 1991. Contribution to the thermodynamics of protein folding from the reduction in water-accessible nonpolar surface area Biochemistry 30: 4237–4244. [DOI] [PubMed] [Google Scholar]
- Mogensen J.E., Tapadar D., Schmidt M.A., Otzen D.E. 2005. Barriers to folding of the transmembrane domain of the Escherichia coli autotransporter adhesin involved in diffuse adherence Biochemistry 44: 4533–4545. [DOI] [PubMed] [Google Scholar]
- Nagy J.K. and Sanders C.R. 2003. Destabilizing mutations promote membrane protein misfolding Biochemistry 43: 19–25. [DOI] [PubMed] [Google Scholar]
- Nakayama H. and Shinoda K. 1967. Effect of added salts on the solubilities and Krafft points Bull. Chem. Soc. Jpn. 40:–1797.
- Otzen D.E. 2002. Protein unfolding in detergents: Effect of micelle structure, ionic strength, pH, and temperature Biophys. J. 83: 2219–2230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2003. Folding of DsbB in mixed micelles: A kinetic analysis of the stability of a bacterial membrane protein J. Mol. Biol. 330: 641–649 ——. [DOI] [PubMed] [Google Scholar]
- 2005. Expansion during folding of a collapsed state Biochim. Biophys. Acta 1750: 146–153 ——. [DOI] [PubMed] [Google Scholar]
- Otzen D.E. and Oliveberg M. 1999. Salt-induced detour through compact regions of the protein folding landscape Proc. Natl. Acad. Sci. 96: 11746–11751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2001. A simple way to measure protein refolding rates in water J. Mol. Biol. 313: 479–483 ——. [DOI] [PubMed] [Google Scholar]
- 2002. Burst-phase expansion of native protein prior to global unfolding in SDS J. Mol. Biol. 315: 1231–1240 ——. [DOI] [PubMed] [Google Scholar]
- 2004. Correspondence between anomalous m- and ΔCp-values in protein folding Protein Sci. 13: 3253–3263 ——. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otzen D.E., Kristensen O., Proctor M., Oliveberg O. 1999. Structural changes in the transition state of protein folding: An alternative interpretation of curved chevron plots Biochemistry 38: 6499–6511. [DOI] [PubMed] [Google Scholar]
- Parker M.J., Lorch M., Sessions R.B., Clarke A.R. 1998. Thermodynamic properties of transient intermediates and transition states in the folding of two contrasting protein structures Biochemistry 37: 2538–2545. [DOI] [PubMed] [Google Scholar]
- Popot J.-L. and Engelman D.M. 1990. Membrane protein folding and oligomerization: The two-stage model Biochemistry 29: 4031–4037. [DOI] [PubMed] [Google Scholar]
- Privalov P.L. and Gill S.J. 1988. Stability of protein structure and hydro-phobic interaction Adv. Protein Chem. 39: 191–234. [DOI] [PubMed] [Google Scholar]
- Privalov P.L., Tiktopulo E.I., Venyaminov S.Y., Griko Y.V., Makha-tadze G.I., Khechinashvili N.N. 1989. Heat capacity and conformation of proteins in the denatured state J. Mol. Biol. 205: 737–750. [DOI] [PubMed] [Google Scholar]
- Sehgal P., Mogensen J.E., Otzen D.E. 2005. Using micellar mole fractions to assess membrane protein stability in mixed micelles Biochim. Biophys. Acta 1716: 59–68. [DOI] [PubMed] [Google Scholar]
- Spolar R.S., Livingstone J.R., Record M.T. 1992. Use of liquid hydrocarbon and amide transfer data to estimate contributions to thermodynamic functions of protein folding from the removal of non-polar and polar surface from water Biochemistry 31: 3947–3955. [DOI] [PubMed] [Google Scholar]
- Yohannan S., Yang D., Faham S., Boulting G., Whitelegge J.P., Bowie J.U. 2004. Proline substitutions are not easily accommodated in a membrane protein J. Mol. Biol. 341: 1–6. [DOI] [PubMed] [Google Scholar]