Skip to main content
PMC home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2006 May;15(5):1000–1009. doi: 10.1110/ps.052050306

The contribution of the residues from the main hydrophobic core of ribonuclease A to its pressure-folding transition state

Josep Font 1, Antoni Benito 1, Reinhard Lange 2, Marc Ribó 1, Maria Vilanova 1
PMCID: PMC2242501  PMID: 16597833

Abstract

The role of hydrophobic interactions established by the residues that belong to the main hydrophobic core of ribonuclease A in its pressure-folding transition state was investigated using the Φ-value method. The folding kinetics was studied using pressure-jump techniques both in the pressurization and depressurization directions. The ratio between the folding activation volume and the reaction volume (βp-value), which is an index of the compactness or degree of solvation of the transition state, was calculated. All the positions analyzed presented fractional Φf-values, and the lowest were those corresponding to the most critical positions for the ribonuclease A stability. The structure of the transition state of the hydrophobic core of ribonuclease A, from the point of view of formed interactions, is a relatively, uniformly expanded form of the folded structure with a mean Φf-value of 0.43. This places it halfway between the folded and unfolded states. On the other hand, for the variants, the average of βp-values is 0.4, suggesting a transition state that is 40% native-like. Altogether the results suggest that the pressure-folding transition state of ribonuclease A looks like a collapsed globule with some secondary structure and a weakened hydrophobic core. A good correlation was found between the Φf-values and the Δβp-values. Although the nature of the transition state inferred from pressure-induced folding studies and the results of the protein engineering method have been reported to be consistent for other proteins, to the best of our knowledge this is the first direct comparison using a set of mutants.

Keywords: protein folding, high pressure, pressure-jumps, ribonuclease A, pressure-folding transition state

To understand the folding of a protein, it is important to characterize all the states involved in this process, i.e., the native or folded state, the unfolded state, the intermediate states (if present), and the transition states, structurally and thermodynamically, as well as the kinetic relationship between them. X-ray crystallography and NMR spectroscopy have been used extensively in determining the three-dimensional structure of native proteins. Heteronuclear multidimensional NMR techniques, among other biophysical techniques, have been used to characterize the unfolded states of the proteins (Logan et al. 1993; Wang and Shortle 1995; Freund et al. 1996; Smith et al. 1996; Wong et al. 1996; Zhang and Forman-Kay 1997). From these studies it has become clear that unfolded proteins usually contain regions of residual structure (Shortle 1993). In the case of proteins with folding intermediates, different techniques have been used to characterize them (Baldwin 1993). Intermediates were thought to be essential to the folding process in order to help restrict the conformational space and direct the protein to its folded conformation. However, well-populated intermediates do not always seem to be required for the fast efficient folding of a protein (Jackson and Fersht 1991). In addition, many small proteins have now been shown to fold with simple two-state kinetics (Jackson 1998). The transition states, due to their fleeting nature, are the least well-populated productive “intermediates” on the folding pathway, which precludes their direct experimental investigation. Instead, experimental studies have been limited to indirect approaches in which the properties of the transition state were inferred at first from the kinetic consequences of changes in environmental conditions (Tanford 1968) and later from studies of the kinetic consequences of mutations, i.e., by applying the protein engineering method or Φ-value analysis initially developed by Fersht and coworkers. Since this pioneering work (Matouschek et al. 1989; Fersht et al. 1992) to the present day, the Φ-value analysis has been applied with varying levels of completeness to more than two dozen proteins (Raleigh and Plaxco 2005), and has become one of the experimental methods with most potential for characterizing folding transition states (Fersht 2004).

In most of these studies, the kinetics of folding-unfolding processes has been monitored by stopped-flow techniques using chemical denaturants to induce the transition. In comparison, there are few works describing the transition state of the folding/unfolding processes of a protein induced by a physical agent, such as pressure. However, with the development of the pressure-jump techniques, an increased number of folding kinetic studies have been performed with different proteins. Some of them have used pressure alone (Vidugiris et al. 1995; Desai et al. 1999; Mohana-Borges et al. 1999; Panick et al. 1999; Panick and Winter 2000; Woenckhaus et al. 2001; Tan et al. 2005) or pressure in combination with other denaturing agents (Pappenberger et al. 2000) to study the folding kinetics of a wild-type protein. Very few works deal with using mutants to study the pressure-folding transition state of a protein (Jacob et al. 1999; Perl et al. 2001).

In the present work, we have performed an approach to this research subject that uses pancreatic ribonuclease A (RNase A) as a model protein. The folding kinetics of RNase A variants from the most critical positions for enzyme stability, i.e., Val 47, Val 54, Val57, Ile81, Ile106, Ile107, and Val108, which have been described previously (Coll et al. 1999; Torrent et al. 1999, 2001; Font et al. 2006), have been studied using pressure-jump techniques.

The pressure-jump technique has several advantages over other trigger mechanisms: it does not significantly change the solvent properties, pressure propagates rapidly so that sample homogeneity is not a problem, and pressure-jumps can be performed bidirectionally, i.e., in both the positive and negative pressure directions. In addition, using pressure as a denaturant agent allows the reaction volume to be calculated (equilibrium measurements) as well as the activation volumes for folding and unfolding reactions, which can give information on the solvation of the transition state. These parameters are not available using other denaturing agents.

The results obtained indicate a pressure-folding transition state for the main hydrophobic core of RNase A that is approximately halfway between the native and unfolded states. The Φ-value analysis shows that it is a relatively uniformly expanded form of the folded structure presenting a weakened hydrophobic core.

Results

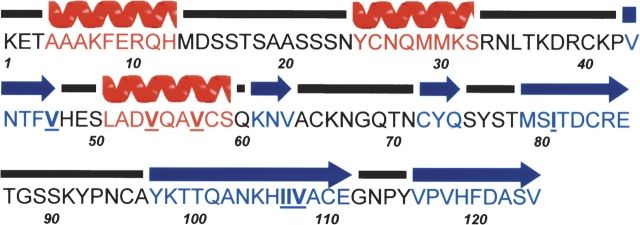
Nondisruptive mutants (Fersht et al. 1992; Fersht and Sato 2004) constructed in positions that belong to the main hydrophobic core of RNase A, whose contribution to protein stability has been previously characterized by pressure and temperature-equilibrium unfolding studies (Coll et al. 1999; Torrent et al. 1999, 2001; Font et al. 2006), were selected to test their contribution to the transition state of the pressure-induced unfolding/refolding processes of RNase A. Xaa to Ala substitutions were chosen to apply the Φ-value analysis. This change is described as the most convenient, since it is unlikely that Ala will form new non-native interactions when substituted into a protein (Zarrine-Afsar and Davidson 2004). According to the RNase A structure solved by X-ray crystallography (Wlodawer et al. 1988) and NMR (Rico et al. 1991), the elements of secondary structure where the mutations were introduced are the β-strands 1, 4, and 5 and the α-helix 3 (Fig. 1). Table 1 shows the mutations produced in RNase A, their location, and accessibility, as well as the contacts of the deleted groups. All the performed mutations form hydrophobic contacts. They affect local interactions and, at the same time, involve long-range interactions. Therefore, they report on both the integrity of a particular region of the protein and on the tertiary structure of the protein. Val54Ala and Val57Ala substitutions may report on helix α3, Ile106Ala, Ile107Ala, and Val108Ala substitutions may report on strand β5, and Ile81Ala change may report on strand β4. Val47, located near the C-terminal edge of strand β1, reports mainly on tertiary contacts.

Figure 1.

Figure 1.

Open in a new tab

Amino acid sequence of RNase A and secondary structure assignment. The secondary structure elements are graphically represented, and were calculated with the program PROCHECK (Laskowski et al. 1993), helix α1 (residues 4–12), helix α2 (residues 25–32), strand β1 (residues 43–47), helix α3 (residues 51–59), and strands β2 (residues 61–63), β3 (residues 72–74), β4 (residues 79–86), β5 (residues 97–111), and β6 (residues 116–124). The mutated residues are underlined in the sequence.

Table 1.

Location, accessibility, and contacts of the modified chemical groups of the different RNase A variants

graphic file with name 1000tbl1.jpg

Open in a new tab

aInteractions in a sphere of 6 Å have been determined using the program CONTACT from the CCP4 package (Potterton et al. 2003).

bCalculated with the XAM program in the wild-type structure (7rsa) (Xia 1992).

Pressure-induced equilibrium unfolding studies

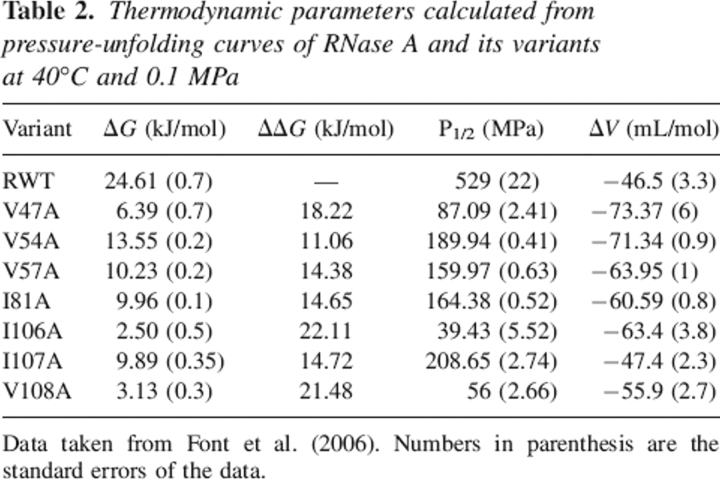
Table 2 summarizes the free energy of unfolding (ΔG) as well as the changes in reaction volume upon unfolding (ΔV) for the wild-type enzyme and the variants that have been kinetically characterized in this work and previously published in Coll et al. (1999), Torrent et al. (1999, 2001), and Font et al. (2006). As expected for core hydrophobic residues, the mutant's stability decreases significantly with respect to the wild-type enzyme, and the positions that are most affected are 47, 106, and 108.

Table 2.

Thermodynamic parameters calculated from pressure-unfolding curves of RNase A and its variants at 40°C and 0.1 MPa

graphic file with name 1000tbl2.jpg

Open in a new tab

Data taken from Font et al. (2006). Numbers in parenthesis are the standard errors of the data.

The observed changes in reaction volumes (ΔV) for all the variants, with the exception of the Ile107Ala variant, are more negative than the value found for wild-type protein. The volume of the native RNase A at 40°C is increased 46.51 ± 3.3 cm3/mol compared with the denatured form. This value and the values found for the variants are similar to the reaction volumes for folding of many other small single domain proteins (Heremans 1982; Royer 2002).

Analysis of two-state behavior

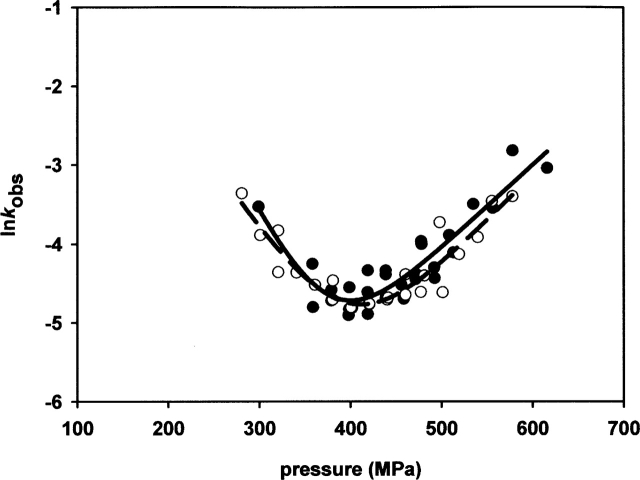
One of the advantages of the pressure-jump techniques is that it is possible to follow the process being studied in the two directions: pressurization and depressurization. Therefore, this allows comparing the changes in the observed rate constants (kobs) versus pressure for the positive (unfolding process) and negative (refolding process) jumps. In a simple two-state process, the observed rate constants should be the same for forward and backward pressure-jumps. If this is not the case, the process under consideration is path-dependent. Figure 2 shows the plot of lnkobs versus pressure for the wild-type protein. Our data show that the observed rate constants do not depend on the direction of the jump, which indicates that the process is consistent with a two-state model. The same was found for each variant analyzed (data not shown).

Figure 2.

Figure 2.

Open in a new tab

Observed rate constants of RNase A after pressure-jumps of 20–50 MPa amplitude in the pressurization (filled circles) and depressurization (open circles) direction at pH 5.0 and 40°C. The solid line (pressurization) and the dashed line (depressurization) are the fit of the data to the following equation: In ln kobs = ln (kf(0.1MPa)e−Δ V≠fp/RT + ku(0.1MPa)e−Δ V≠up/RT) where kobs is the observed rate constant, kf (0.1 MPa) and ku (0.1 MPa) are the microscopic rate folding and unfolding constants, ΔV≠f and ΔV≠u are the activation volumes for folding and unfolding, and p is the final pressure of each jump.

Kinetic analysis

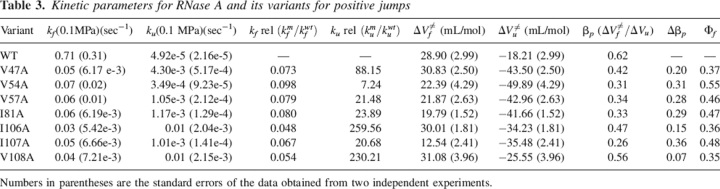
For wild-type RNase A and the variants, linear plots of natural logarithms of kf and ku versus pressure allowed both constants to be calculated at 0.1 MPa. Table 3 summarizes the unfolding and refolding kinetic parameters obtained for RNase A and the variants for positive jumps. Similar results were obtained for negative jumps (data not shown). The values of the mutant unfolding rate constants relative to the parent molecule ku rel (kmu/kwtu) as well as the values of the mutant folding rate constants relative to parent enzyme kf rel (kmf/kwtf) are detailed in Table 3. All the variants appear to fold slower than the wild-type enzyme by about one order of magnitude, while much more diversity is observed in the unfolding rates. The variant Val54Ala has an unfolding rate constant that is only one order of magnitude greater than that of wild-type enzyme. Variants Val57Ala, Ile81Ala, and Ile107Ala have an unfolding rate constant about 1.5 orders of magnitude greater than that of RNase A, and finally, Val47Ala, Ile106Ala, and Val108Ala present an unfolding rate constant between two to three orders of magnitude greater than the one of wild-type enzyme. Overall, the unfolding process is more significantly affected than the folding process for Val47A, Ile106A, and V108A, whereas for the other variants the destabilization can be considered to be a consequence of affecting both processes by a much more similar magnitude.

Table 3.

Kinetic parameters for RNase A and its variants for positive jumps

graphic file with name 1000tbl3.jpg

Open in a new tab

Numbers in parentheses are the standard errors of the data obtained from two independent experiments.

The activation volumes for folding (ΔV≠f) and unfolding (ΔV≠u) reflect the slopes of the plots of lnkf or lnku versus pressure. Figure 3 presents the plots of lnkf and lnku versus pressure for positive jumps. The slopes differ for the different mutants.

Figure 3.

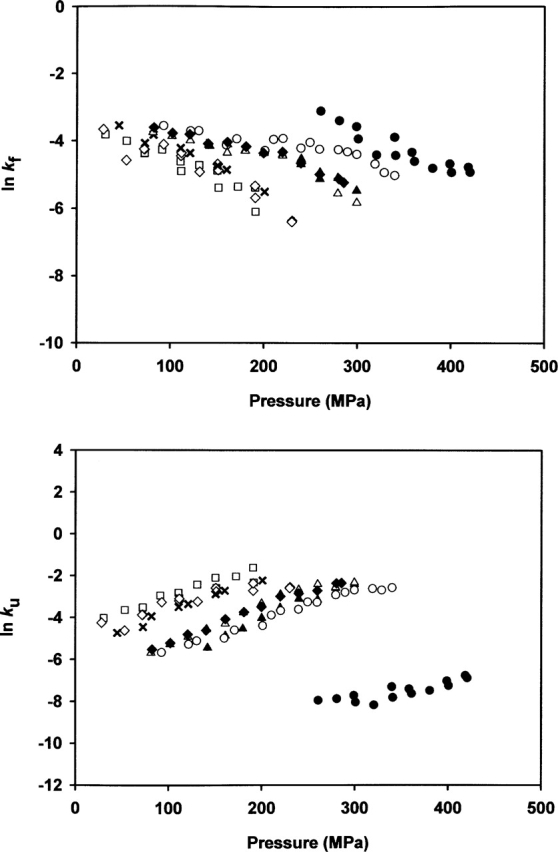
Figure 3.

Open in a new tab

Pressure dependence of the microscopic folding (kf) and unfolding (ku) rate constants for the wild-type enzyme and variants. Microscopic rate constants were determined as indicated in Materials and Methods according to Equations 4 and 5. (•) Wild-type enzyme, (×) Val47Ala, (▴) Val54Ala, (Δ) Val57Ala, (▴) Ile81Ala, (□) Ile106Ala, (○) Ile107Ala, and (♦) Val108Ala.

In chemical denaturant-induced folding studies, the denaturant dependence of the kinetic rate constants can provide information about the solvent accessibility of the transition state. This can be expressed in terms of the Tanford β-value (βT) (Tanford 1970; Fersht 1999), which is a useful index of the compactness of the transition state and provides an approximate measure of the position of the transition state on the reaction coordinate. An analogous parameter, which is called βp (for pressure), can be derived from the volume changes associated with pressure-induced unfolding:

graphic file with name 1000equ1.jpg

where ΔV≠ is the activation volume and ΔV is the volume change measured upon unfolding at equilibrium (Perrett and Zhou 2002). Comparing activation and equilibrium volume changes has likewise been used to measure the extent to which the transition state resembles the native state or to estimate the position of the transition state along the reaction coordinate (Vidugiris et al. 1995; Desai et al. 1999; Pappenberger et al. 2000; Woenckhaus et al. 2001). When βT and βp were compared for the same protein, the values were found to be similar (Desai et al. 1999; Pappenberger et al. 2000).

The equivalence between βT and βp is particularly true if volume changes during the folding of a protein arise mainly from changes in solvent interactions of the polypeptide chain and packing deficiencies in the hydrophobic core (Pappenberger et al. 2000). This is the case for RNase A and the variants studied here (see Discussion). The βp-values are listed in Table 3 for positive jumps. The more destabilized variants present βp-values closer to the value found for the wild-type enzyme (0.62, 0.56, 0.47, and 0.42 for wild type, V108A, I106A, and V47A, respectively) than the other more stable variants, which present lower values ranging from 0.26 to 0.34.

Protein engineering analysis

The Φf-values for the single destabilizing mutations of the hydrophobic core of RNase A are presented in Table 3 for positive jumps. A good agreement is found between the Φf-values obtained from positive and negative jumps. No mutation of the hydrophobic core of RNase A results in a Φf-value of 1 or 0, rather all the Φf-values are fractional, ranging from 0.35 to 0.55. Therefore, none of the RNase A core residues analyzed in the present work present their interactions completely formed or lost in the transition state. By comparing the location and contacts of the different variants (Table 1), it is shown that each altered side chain establishes contacts both with residues belonging to the secondary structure element at which it belongs and with residues from other elements of secondary structure as well. Thus, it is not possible to discern between the contribution of side chains in the formation of a particular element of secondary structure and their implication in long-range interactions. Therefore, the results have to be interpreted globally, considering the participation of the side chains in both types of interactions in the hydrophobic core of RNase A.

The most critical positions for RNase A stability, 108, 106, and 47, are those for which the change for Ala gives the lowest Φf-values, 0.35, 0.36, and 0.37, respectively. The rest of the variants present Φf-values between 0.46 and 0.55. These results indicate that the interactions of the side chains of Val108, Ile106, and Val47 are less formed in the transition state than the interactions of the rest of the variants. On average, the Φf-value for all the core side chains studied here is 0.43. This value is consistent with a transition state in which all the interactions established by the side chains of these core residues in the native state are 43% formed.

Brønsted behavior: Single versus parallel pathways

Intermediate Φ-values are difficult to interpret since they could correspond to partial formation of interactions or to a mixture of fully folded and unfolded states arising from parallel pathways. Fersht et al. (1994) used simple physicochemical reasoning to show that it is possible to distinguish between these two possibilities by performing a Brønsted plot analysis. If there are simple relationships between the rate constants and the changes in interaction energies, and assuming that all mutations are testing the same degree of structure formation, the natural logarithm of the unfolding/folding rate constants should exhibit Brønsted behavior, in which plots of lnku and lnkf versus ΔΔG/RT for a set of mutants are approximately linear.

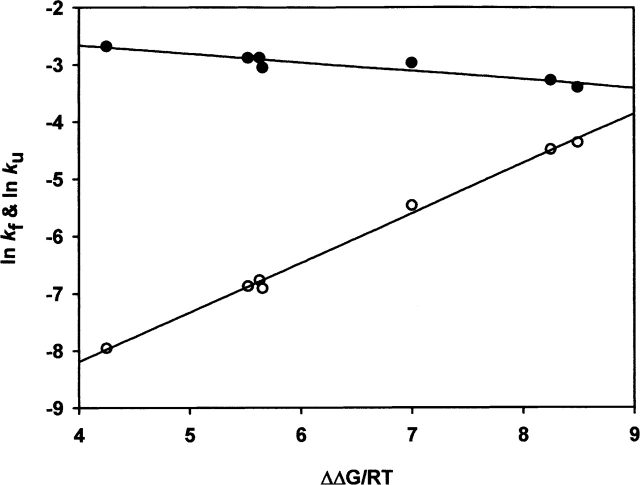
The variation in lnkf and lnku versus the difference in energy between the wild type and the different mutants is plotted in Figure 4. There is a very good linear correlation between these two variables for the unfolding reaction (r = 0.99) and for the folding reaction (r = 0.94), which indicates that there are no discrete populations with different degrees of structure in the transition state.

Figure 4.

Figure 4.

Open in a new tab

Brønsted plots for the unfolding (open circles) and refolding rate constants (filled circles) of the variants listed in Table 1. The solid lines are linear regression fits.

Discussion

Although intermediates for the folding and unfolding process of RNase A have been detected and described (Neira and Rico 1997; Nogués 1997; Kimura et al. 2005) in the present study no stable intermediates have been detected, and thus the only structure to be analyzed was the transition state. The structure of the transition state of the main hydrophobic core of RNase A has been mapped by comparing the kinetics and equilibrium of folding of seven mutants belonging to this core. According to the protein engineering method the Φf-values obtained from pressurization experiments and Φu-values obtained from depressurization experiments accomplishes the relationship Φf = 1 − Φu. The same complementary is observed for the activation volumes for folding and unfolding, obtained from the positive and negative-jumps kinetics. Both analysis shows that the structure of the transition state obtained is kinetically indistinguishable when measured in the direction of unfolding and refolding. Therefore, the results of the Φ-value analysis and those of the βp-value analysis satisfactorily prove the energetic changes as well as the degree of compactness of the transition state and, by inference, the structural properties of this transition state induced by a pressure increase or release. Recently, there has been some discussion in the literature about which is the lowest ΔΔGU-value acceptable for calculating valid Φ-values (Sánchez and Kiefhaber 2003; Fersht and Sato 2004). Sánchez and Kiefhaber propose that Φ-values for ΔΔG < 1.7 kcal/mol are artifactual, while Fersht and Sato suggest that for deletion mutations in suitable proteins the threshold could be as low as 0.6 kcal/mol. All the variants studied in this work present a ΔΔG-value > 1.7 kcal/mol, which reinforces the confidence in the calculated Φ-values.

Our data for wild-type RNase A and mutants fit well to a single-exponential relaxation process both for unfolding and refolding. A kinetic study of RNase A using pressure-jump techniques monitored by FTIR (Panick and Winter 2000) showed that the relaxation profiles for the pressurization and depressurization fit well with a model that assumes two-exponential relaxation processes. The discrepancy might be due to the different experimental conditions used. In our work the pressure-jumps are done at 40°C, while in the work of Panick and Winter (2000) the pressure-jumps are done at 20°C. Moreover, a different pH for the protein solution is used: 2.5 in the FTIR work, while we have used a pH of 5.5.

Characteristics of the transition state of RNase A inferred from βp-values

It has been described that contributions to the reaction volume, ΔV, obtained from equilibrium experiments, may arise from packing deficiencies in the native state (Frye et al. 1996; Frye and Royer 1998; Hummer et al. 1998) and differences in solvent interactions between native and unfolded protein (Heremans 1982; Dill 1990; Hummer et al. 1998). The structure of the native RNase A shows no indication for cavities (Wlodawer et al. 1988); however, the observed volume change corresponds to only about 0.33% of the total protein volume. Thus, even minor packing deficiencies in the native protein might contribute to the reaction volume. Other contributions to ΔV are known to arise from changes in interactions between the solvent and the protein chain. This effect is especially pronounced around charged groups (electrostriction). From our data, we cannot discard this contribution to ΔV; however, RNase A is a basic protein with a pronounced number of basic groups compared to acidic ones. Since no basic groups are buried in the native state, contributions from electrostriction around positive charges are not expected (Wlodawer et al. 1988), and although a small contribution from acidic groups at the experimental pH can account for the changes in ΔV, this contribution is assumed to be minor. Therefore, in our case, and in accordance with what has been described for other proteins the decrease in the volume of the pressure-unfolded state is mainly a consequence of packing deficiencies in the hydrophobic core of the protein as well as changes in solvent interaction of the polypeptide chain (Royer et al. 1993; Frye et al. 1996; Frye and Royer 1998; Pappenberger et al. 2000). For the variants, the greater values of the reaction volumes compared to the wild type may be directly related to packing deficiencies as a consequence of methyl/ene deletions as well as to differences in solvent interactions of the polypeptide chain between the native and denatured state. Since there are no changes in charged groups between the wild type and the variants, electrostriction contribution from these types of residues to reaction volumes of the variants should be the same as in the wild-type enzyme.

Since volume changes that occur during RNase A and variants folding arise mainly from changes in solvent interactions of the polypeptide chain and packing deficiencies in the hydrophobic core, measuring the activation volumes for the refolding reaction relative to the reaction volume gives structural information on the transition state (Pappenberger et al. 2000; Perrett and Zhou 2002).

For wild-type RNase A the activation volumes for the refolding and unfolding reaction of 28.90 and −18.21 cm3/mol show that the volume of the transition state is about 60% native-like, suggesting that it is still partially solvated. For the variants, the results obtained for the βp-values indicate that those that are more destabilized present a transition state, at least from the point of view of solvation, which is closer to the native state of each variant. That is, for V108A, I106A, and V47A the transition states are about 56%, 47%, and 42% native-like, respectively, while for the other variants the transition state is around 26%–34% native-like. In other words, the Ala changes introduced at positions 108, 106, and 47 bring the transition state closer to the native state than the changes introduced at the rest of the positions studied in this work. This means that the transition state is found to move progressively closer to the folded state on destabilization of the protein by mutation according to the Hammond postulate (Hammond 1955), which states that the structure of the transition state of a chemical reaction becomes more product-like when the product is destabilized. For protein folding reactions a pressure-induced structural movement of the transition state might be explained mainly by the weakening of hydrophobic interactions, accompanied by an increase in solvation of the polypeptide chain increasing pressure (Heremans 1982; Mozhaev et al. 1994; Hummer et al. 1998). As a result, a larger number of interactions are required, and consequently, a dehydration of the polypeptide chain to compensate for the loss in conformational entropy during the folding process. This effect leads to a more native-like transition state. The Hammond postulate has also been proposed to explain the movements of the transition state for folding of other proteins like barnase, chymotrypsin inhibitor 2 (CI2), and tendamistat, studied using other denaturing agents (Matouschek et al. 1995; Pappenberger et al. 2000).

Characteristics of the transition state of RNase A inferred from Φ-values

All the mutations in this work are changes of larger hydrophobic side chains to smaller ones, and as a consequence, according to the protein engineering method, their fractional Φf-values are indicative of the extent of structure formation mapped out at the level of individual residues. In fact, the nice linear fitting of the Brønsted plot corroborates this hypothesis (Matouschek et al. 1989, 1990; Fersht et al. 1992).

The residues of the major hydrophobic core of RNase A studied in this work can be split into two categories: those mutations that result in a Φf-value around 0.35 (Val108, Ile106, and Val47) and the rest of the mutants, which present Φf-values around 0.5 (between 0.46 and 0.55). A priori, the opposite would be expected and higher Φf-values would also be expected for all the positions analyzed, since refolding quench flow experiments combined with 2D NMR allowed to identify the protons which are protected early during the refolding reaction of RNase A, among which were Val47, Val54, Ile81, Ile106, and Val 108 (Udgaonkar and Baldwin 1990). In addition, most of the amide protons protected early in the folding reaction are among the ones which exchange by global unfolding events or those for which this process is a major pathway for exchange when the H/D exchange behavior of amide protons has been studied by 2D NMR (Neira et al. 1999). Nevertheless, our results suggest that part of the interactions of the residues 47, 106, and 108 are formed later than the interactions of the rest of the positions analyzed, which in turn, do not present Φf-values > 0.55. Probably, the interactions of the residues analyzed and in particular those of the three residues which have the lowest Φf-values, are more important for stabilizing the folded structure of the RNase A than for directing its folding. This is in accordance with the hypothesis that hydrophobic clusters are more important for stability (Kim et al. 1998). The discrepancy between the results of the protein engineering method applied in this work and those found in the 2D NMR studies might be due to the fact that NMR monitors the behavior of the main chain while the protein engineering method monitors the side chain interactions. It is possible that in the transition state the main hydrophobic core of RNase A presents a structured backbone while the side chains are not in their native conformation.

For other proteins, that are not all α or all β, like CI2 (Itzhaki et al. 1995), the activation domain of human procarboxypeptidase A2 (ADA2h) (Villegas et al. 1998), immunophilin FKBP12 (Fulton et al. 1999), and the CheY chemotactic protein (Lopez-Hernandez and Serrano 1996), low Φf-values have been obtained for the amino acids that belong to the hydrophobic core. It has been proposed that the transition state for these proteins looks like a collapsed globule with some secondary structure and a weakened hydrophobic core.

Consistency of the results obtained from Φf-values and βp-values

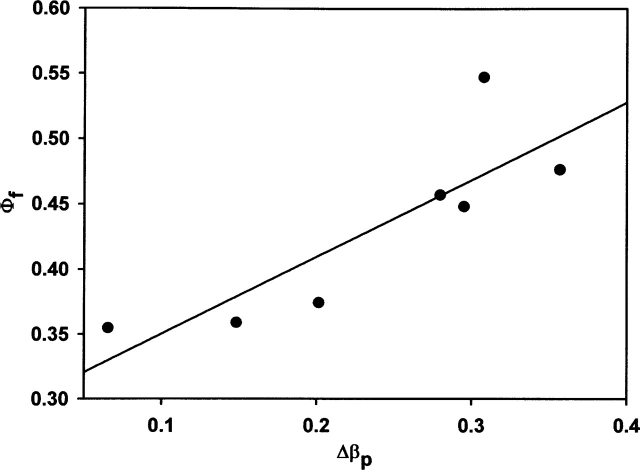
The conclusions about the transition state drawn from the protein engineering method are consistent with the ones obtained from βp-values, which can be specifically obtained from pressure studies. A good correlation (Fig. 5) exists between the Φf-values and the differences between the βp-value of wild-type enzyme and the βp-values of the different variants, Δβp, in Table 3. The side chains for which a minor number of the interactions are present in the transition state relative to the interactions that are present in the native state, also give rise to minor differences between the degree of solvation/compactness of the transition state relative to the native state compared to this parameter (βp) for the wild-type enzyme.

Figure 5.

Figure 5.

Open in a new tab

Correlation between the Φf-values and the Δβp-values(βp = ΔV≠f/ΔV) of each variant. The solid line shows the best fit to a linear equation (r = 0.85).

Although it has been stated that the nature of the transition state inferred from pressure-induced studies is consistent with the results of the protein engineering method (Perrett and Zhou 2002), to the best of our knowledge, this is the first direct comparison using a set of mutants.

Conclusion: The transition state of RNase A for the pressure-folding process

The structure of the transition state of the hydrophobic core of RNase A from the point of view of formed interactions is a relatively uniformly expanded form of the folded structure with a mean Φf-value of 0.43, which places it halfway between the folded and unfolded states. This means that, on average, 43% of the free energy of interaction is lost on reaching the transition state for unfolding from the folded state.

Both the wild-type enzyme and the variants present a negative unfolding activation volume, which places the transition state between the native and unfolded states. On average, the βp-value for the variants is around 0.4, suggesting a transition state that is 40% native-like from the point of view of compactness. Taking into account that it has been described that the pressure-denatured state of RNase A contains some partial secondary structure (Torrent et al. 2001), and that the unfolded-state appears to display some characteristics of a molten globule with native-like secondary structure and a liquid interior (Zhang et al. 1995) it seems reasonable to propose a transition state that has a significant degree of secondary structure formed and a weakened hydrophobic core. This, in turn, may suggest a pressure-folding pathway according to a nucleation-condensation mechanism for the main hydrophobic core of nonreduced RNase A.

Materials and methods

Mutagenesis, protein expression, and purification

RNase A variants were constructed by site-directed mutagenesis using the Quick-Change kit (Stratagene) essentially as recommended by the manufacturer. Protein expression and purification was performed according to the procedures previously described (Torrent et al. 1999; Font et al. 2006).

Pressure-induced equilibrium unfolding

The stabilities of each of the variants in this study were previously characterized by pressure unfolding at 40°C and monitoring the change in absorbance at 287 nm according to Font et al. (2006).

Kinetic experiments: Pressure-jumps

The lyophilized proteins were dissolved to a concentration of 0.5 mg/mL in the same buffer used for the equilibrium experiments (50 mM MES, pH 5.0).

The protein intrinsic fluorescence was measured by exciting the sample at 280 nm (4 nm slit) and recording the emission at 305 nm (16 nm slit) to minimize photobleaching. The dead time of the equipment was shorter than 5 msec.

Fluorescence measurements were carried out using an Aminco Bowman Series 2 fluorescence-spectrophotometer (SLM Aminco). The sample compartment was modified to accommodate a thermostated high-pressure optical cell, allowing measurements up to 700 MPa. The protein solution was placed in a 5-mm diameter quartz cuvette, closed at the top with a flexible membrane and held with a rubber O-ring. Pressure-jumps consisted of sudden changes of pressure (up to 40 MPa) within a pressure range of 0.1–600 MPa, and were made by using a home-made pressure-jump device connected to the high-pressure optical cell placed in the above-mentioned fluorescence spectrophotometer. Pressure-jumps were carried out by opening an electrically driven pneumatic valve localized between the high-pressure optical cell and a ballast tank.

The pressure-jumps were small enough so that the adiabatic heating or cooling of the sample amounted to no more than 0.35°C, which at the sample temperature of 40°C would not perturb the folding equilibrium of the proteins significantly. Therefore, the adiabatic heating did not contribute significantly to the exponential decay induced by the pressure-jump.

Data analysis

Determining kinetic parameters from relaxation profiles

The relaxation profiles of the unfolding/refolding, after each pressure-jump, were fitted to a single exponential decay, according to Equation 1.

graphic file with name 1000equ2.jpg

where I(t) and I0 are the fluorescence intensities at time t and at time zero, A is the phase amplitude, and kobs is the measured rate constant at the final pressure p.

In agreement with a two-state folding/unfolding reaction, the measured apparent rate constant at a given pressure kobs is equal to the sum of the microscopic rate constant for folding kf (p)and unfolding ku(p)

graphic file with name 1000equ3.jpg

Equation 2 was used to calculate the microscopic rate constants introducing a constrained analysis, which takes into account the relationship between the rate constants and the equilibrium constant for each jump (Herberhold et al. 2003). The equilibrium constant at pressure p was calculated using Equation 3

graphic file with name 1000equ4.jpg

where ΔG and ΔV are the free energy and volume change of unfolding obtained from equilibrium experiments, and p is the final pressure of each jump.

Linear plots of lnkf(p)/lnku(p) versus the final pressure of each jump allowed us to calculate ΔV≠fand ΔV≠u the activation volumes for folding and unfolding, respectively, according to equations:

graphic file with name 1000equ5.jpg
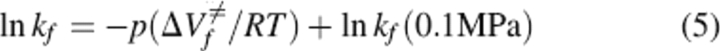graphic file with name 1000equ6.jpg

Protein engineering method: Calculation of the Φ-values

The free energy changes of the transition state upon mutation (ΔΔGf and ΔΔGu) were calculated using the following equations:

graphic file with name 1000equ7.jpg
graphic file with name 1000equ8.jpg

where kmf and kwtf are the rate constant for folding for the mutant and wild type, respectively. The same applies for the unfolding ones. The Φf-values, which report on the degree of formation of the interactions broken upon mutation in the transition state, were calculated using the equation:

graphic file with name 1000equ9.jpg

The protein engineering method has been extensively reviewed, mainly by Fersht and coworkers (Matouschek et al. 1989; Fersht et al. 1992; Serrano et al. 1992; Fersht 1995, 1997, 2004).

Acknowledgments

This work was supported by grants BMC2003-08458-CO2-02 from the Ministerio de Educación y Ciencia (Spain) and SGR01-00196 from DGR, Generalitat de Catalunya. J.F. acknowledges a fellowship from the University of Girona. Support was also received from the “Fundació M. F. de Roviralta” of Barcelona for equipment purchasing grants. This work was also undertaken in the frame of the European COST-D30 action. We thank Claude Balny for helpful discussions and advice on the pressure-jump experiments and Christian Valentin for excellent technical help.

Footnotes

Reprint requests to: Maria Vilanova, Laboratori d'Enginyeria de Proteïnes, Departament de Biologia, Facultat de Ciències, Universitat de Girona, Campus de Montilivi s/n 17071 Girona, Spain; e-mail: maria.vilanova@udg.es; fax: 34-972-418-150.

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.052050306.

References

  1. Baldwin E.P. 1993. Pulsed H/D-exchange studies of folding intermediates Curr. Opin. Struct. Biol. 3: 84–91. [Google Scholar]
  2. Coll M.G., Protasevich I.I., Torrent J., Ribó M., Lobachov V.M., Makarov A.A., Vilanova M. 1999. Valine 108, a chain-folding initiation site-belonging residue, crucial for the ribonuclease A stability Biochem. Biophys. Res. Commun. 265: 356–360. [DOI] [PubMed] [Google Scholar]
  3. Desai G., Panick G., Zein M., Winter R., Royer C.A. 1999. Pressure-jump studies of the folding/unfolding of trp repressor J. Mol. Biol. 288: 461–475. [DOI] [PubMed] [Google Scholar]
  4. Dill K.A. 1990. Dominant forces in protein folding Biochemistry 29: 7133–7155. [DOI] [PubMed] [Google Scholar]
  5. Fersht A.R. 1995. Characterizing transition states in protein folding: An essential step in the puzzle Curr. Opin. Struct. Biol. 5: 79–84. [DOI] [PubMed] [Google Scholar]
  6. Fersht A.R. 1997. Nucleation mechanisms in protein folding Curr. Opin. Struct. Biol. 7: 3–9. [DOI] [PubMed] [Google Scholar]
  7. Fersht A.R. 1999. Kinetics of protein folding In Structure and mechanism in protein science pp. 540–572. W.H. Freeman, New York.
  8. Fersht A.R. 2004. Relationship of Leffler (Bronsted) α values and protein folding Φ values to position of transition-state structures on reaction coordinates Proc. Natl. Acad. Sci. 101: 14338–14342. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Fersht A.R. and Sato S. 2004. Φ-Value analysis and the nature of protein-folding transition states Proc. Natl. Acad. Sci. 101: 7976–7981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Fersht A.R., Matouschek A., Serrano L. 1992. The folding of an enzyme. I. Theory of protein engineering analysis of stability and pathway of protein folding J. Mol. Biol. 224: 771–782. [DOI] [PubMed] [Google Scholar]
  11. Fersht A.R., Itzhaki L.S., elMasry N.F., Matthews J.M., Otzen D.E. 1994. Single versus parallel pathways of protein folding and fractional formation of structure in the transition state Proc. Natl. Acad. Sci. 91: 10426–10429. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Font J., Torrent J., Benito A., Lange R., Ribó M., Vilanova M. 2006. Pressure- and temperature-induced unfolding studies: Thermodynamics of core hydrophobicity and packing of ribonuclease A Biol. Chem. (in press). [DOI] [PubMed]
  13. Freund S.M., Wong K.B., Fersht A.R. 1996. Initiation sites of protein folding by NMR analysis Proc. Natl. Acad. Sci. 93: 10600–10603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Frye K.J. and Royer C.A. 1998. Probing the contribution of internal cavities to the volume change of protein unfolding under pressure Protein Sci. 7: 2217–2222. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Frye K.J., Perman C.S., Royer C.A. 1996. Testing the correlation between ΔA and ΔV of protein unfolding using m value mutants of staphylococcal nuclease Biochemistry 35: 10234–10239. [DOI] [PubMed] [Google Scholar]
  16. Fulton K.F., Main E.R., Daggett V., Jackson S.E. 1999. Mapping the interactions present in the transition state for unfolding/folding of FKBP12 J. Mol. Biol. 291: 445–461. [DOI] [PubMed] [Google Scholar]
  17. Hammond G.S. 1955. A correlation of reaction rates J. Am. Chem. Soc. 77: 334–338. [Google Scholar]
  18. Herberhold H., Marchal S., Lange R., Scheyhing C.H., Vogel R.F., Winter R. 2003. Characterization of the pressure-induced intermediate and unfolded state of red-shifted green fluorescent protein—A static and kinetic FTIR, UV/VIS and fluorescence spectroscopy study J. Mol. Biol. 330: 1153–1164. [DOI] [PubMed] [Google Scholar]
  19. Heremans K. 1982. High pressure effects on proteins and other biomolecules Annu. Rev. Biophys. Bioeng. 11: 1–21. [DOI] [PubMed] [Google Scholar]
  20. Hummer G., Garde S., Garcia A.E., Paulaitis M.E., Pratt L.R. 1998. The pressure dependence of hydrophobic interactions is consistent with the observed pressure denaturation of proteins Proc. Natl. Acad. Sci. 95: 1552–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Itzhaki L.S., Otzen D.E., Fersht A.R. 1995. The structure of the transition state for folding of chymotrypsin inhibitor 2 analysed by protein engineering methods: Evidence for a nucleation-condensation mechanism for protein folding J. Mol. Biol. 254: 260–288. [DOI] [PubMed] [Google Scholar]
  22. Jackson S.E. 1998. How do small single-domain proteins fold? Fold. Des. 3: R81–R91. [DOI] [PubMed] [Google Scholar]
  23. Jackson S.E. and Fersht A.R. 1991. Folding of chymotrypsin inhibitor 2. 1. Evidence for a two-state transition Biochemistry 30: 10428–10435. [DOI] [PubMed] [Google Scholar]
  24. Jacob M., Holtermann G., Perl D., Reinstein J., Schindler T., Geeves M.A., Schmid F.X. 1999. Microsecond folding of the cold shock protein measured by a pressure-jump technique Biochemistry 38: 2882–2891. [DOI] [PubMed] [Google Scholar]
  25. Kim D.E., Gu H., Baker D. 1998. The sequences of small proteins are not extensively optimized for rapid folding by natural selection Proc. Natl. Acad. Sci. 95: 4982–4986. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kimura T., Akiyama S., Uzawa T., Ishimori K., Morishima I., Fujisawa T., Takahashi S. 2005. Specifically collapsed intermediate in the early stage of the folding of ribonuclease a J. Mol. Biol. 350: 349–362. [DOI] [PubMed] [Google Scholar]
  27. Laskowski R.A., MacArthur M.W., Moss D.S., Thornton J.M. 1993. PROCHECK: A program to check the stereochemical quality of protein structures J. Appl. Crystallogr. 26: 283–291. [Google Scholar]
  28. Logan T.M., Olejniczak E.T., Xu R.X., Fesik S.W. 1993. A general method for assigning NMR spectra of denatured proteins using 3D HC(CO)NH-TOCSY triple resonance experiments J. Biomol. NMR 3: 225–231. [DOI] [PubMed] [Google Scholar]
  29. Lopez-Hernandez E. and Serrano L. 1996. Structure of the transition state for folding of the 129 aa protein CheY resembles that of a smaller protein, CI-2 Fold. Des. 1: 43–55. [PubMed] [Google Scholar]
  30. Matouschek A., Kellis Jr. J.T., Serrano L., Fersht A.R. 1989. Mapping the transition state and pathway of protein folding by protein engineering Nature 340: 122–126. [DOI] [PubMed] [Google Scholar]
  31. Matouschek A., Kellis Jr. J.T., Serrano L., Bycroft M., Fersht A.R. 1990. Transient folding intermediates characterized by protein engineering Nature 346: 440–445. [DOI] [PubMed] [Google Scholar]
  32. Matouschek A., Otzen D.E., Itzhaki L.S., Jackson S.E., Fersht A.R. 1995. Movement of the position of the transition state in protein folding Biochemistry 34: 13656–13662. [DOI] [PubMed] [Google Scholar]
  33. Mohana-Borges R., Silva J.L., Ruiz-Sanz J., de Prat-Gay G. 1999. Folding of a pressure-denatured model protein Proc. Natl. Acad. Sci. 96: 7888–7893. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Mozhaev V.V., Bec N., Balny C. 1994. Pressure effects on enzyme reactions in mainly organic media: α-Chymotrypsin in reversed micelles of Aerosol OT in octane Biochem. Mol. Biol. Int. 34: 191–199. [PubMed] [Google Scholar]
  35. Neira J.L. and Rico M. 1997. Folding studies on ribonuclease A, a model protein Fold. Des. 2: R1–R11. [DOI] [PubMed] [Google Scholar]
  36. Neira J.L., Sevilla P., Menendez M., Bruix M., Rico M. 1999. Hydrogen exchange in ribonuclease A and ribonuclease S: Evidence for residual structure in the unfolded state under native conditions J. Mol. Biol. 285: 627–643. [DOI] [PubMed] [Google Scholar]
  37. Nogués M.V. 1997. Pancreatic ribonucleases In Ribonucleases: Structures and function (eds. D'Alessio G. and Riordan J.F.) . pp. 271–304. Academic Press, New York.
  38. Panick G. and Winter R. 2000. Pressure-induced unfolding/refolding of ribonuclease A: Static and kinetic Fourier transform infrared spectroscopy study Biochemistry 39: 1862–1869. [DOI] [PubMed] [Google Scholar]
  39. Panick G., Vidugiris G.J., Malessa R., Rapp G., Winter R., Royer C.A. 1999. Exploring the temperature-pressure phase diagram of staphylococcal nuclease Biochemistry 38: 4157–4164. [DOI] [PubMed] [Google Scholar]
  40. Pappenberger G., Saudan C., Becker M., Merbach A.E., Kiefhaber T. 2000. Denaturant-induced movement of the transition state of protein folding revealed by high-pressure stopped-flow measurements Proc. Natl. Acad. Sci. 97: 17–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Perl D., Holtermann G., Schmid F.X. 2001. Role of the chain termini for the folding transition state of the cold shock protein Biochemistry 40: 15501–15511. [DOI] [PubMed] [Google Scholar]
  42. Perrett S. and Zhou J.M. 2002. Expanding the pressure technique: Insights into protein folding from combined use of pressure and chemical denaturants Biochim. Biophys. Acta 1595: 210–223. [DOI] [PubMed] [Google Scholar]
  43. Potterton E., Briggs P., Turkenburg M., Dodson E. 2003. A graphical user interface to the CCP4 program suite Acta Crystallogr. D Biol. Crystallogr. 59: 1131–1137. [DOI] [PubMed] [Google Scholar]
  44. Raleigh D.P. and Plaxco K.W. 2005. The protein folding transition state: What are Φ-values really telling us? Protein Pept. Lett. 12: 117–122. [DOI] [PubMed] [Google Scholar]
  45. Rico M., Santoro J., Gonzalez C., Bruix M., Neira J.L., Nieto J.L., Herranz J. 1991. 3D structure of bovine pancreatic ribonuclease A in aqueous solution: An approach to tertiary structure determination from a small basis of 1H NMR NOE correlations J. Biomol. NMR 1: 283–298. [DOI] [PubMed] [Google Scholar]
  46. Royer C.A. 2002. Revisiting volume changes in pressure-induced protein unfolding Biochim. Biophys. Acta 1595: 201–209. [DOI] [PubMed] [Google Scholar]
  47. Royer C.A., Hinck A.P., Loh S.N., Prehoda K.E., Peng X., Jonas J., Markley J.L. 1993. Effects of amino acid substitutions on the pressure denaturation of staphylococcal nuclease as monitored by fluorescence and nuclear magnetic resonance spectroscopy Biochemistry 32: 5222–5232. [DOI] [PubMed] [Google Scholar]
  48. Sánchez I.E. and Kiefhaber T. 2003. Origin of unusual φ-values in protein folding: Evidence against specific nucleation sites J. Mol. Biol. 334: 1077–1085. [DOI] [PubMed] [Google Scholar]
  49. Serrano L., Kellis Jr. J.T., Cann P., Matouschek A., Fersht A.R. 1992. The folding of an enzyme. II. Substructure of barnase and the contribution of different interactions to protein stability J. Mol. Biol. 224: 783–804. [DOI] [PubMed] [Google Scholar]
  50. Shortle D. 1993. Denatured states of proteins and their roles in folding and stability Curr. Opin. Struct. Biol. 3: 66–74. [Google Scholar]
  51. Smith L.J., Fiebig K.M., Schwalbe H., Dobson C.M. 1996. The concept of a random coil. Residual structure in peptides and denatured proteins Fold. Des. 1: R95–106. [DOI] [PubMed] [Google Scholar]
  52. Tan C.Y., Xu C.H., Wong J., Shen J.R., Sakuma S., Yamamoto Y., Lange R., Balny C., Ruan K.C. 2005. Pressure equilibrium and jump study on unfolding of 23-kDa protein from spinach photosystem II. Biophys J. 88: 1264–1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Tanford C. 1968. Protein denaturation Adv. Protein Chem. 23: 121–282. [DOI] [PubMed] [Google Scholar]
  54. Tanford C. 1970. Protein denaturation. C. Theoretical models for the mechanism of denaturation Adv. Protein Chem. 24: 1–95. [PubMed] [Google Scholar]
  55. Torrent J., Connelly J.P., Coll M.G., Ribó M., Lange R., Vilanova M. 1999. Pressure versus heat-induced unfolding of ribonuclease A: The case of hydrophobic interactions within a chain-folding initiation site Biochemistry 38: 15952–15961. [DOI] [PubMed] [Google Scholar]
  56. Torrent J., Rubens P., Ribó M., Heremans K., Vilanova M. 2001. Pressure versus temperature unfolding of ribonuclease A: An FTIR spectroscopic characterization of 10 variants at the carboxy-terminal site Protein Sci. 10: 725–734. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Udgaonkar J.B. and Baldwin R.L. 1990. Early folding intermediate of ribonuclease A Proc. Natl. Acad. Sci. 87: 8197–8201. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Vidugiris G.J., Markley J.L., Royer C.A. 1995. Evidence for a molten globule-like transition state in protein folding from determination of activation volumes Biochemistry 34: 4909–4912. [DOI] [PubMed] [Google Scholar]
  59. Villegas V., Martinez J.C., Aviles F.X., Serrano L. 1998. Structure of the transition state in the folding process of human procarboxypeptidase A2 activation domain J. Mol. Biol. 283: 1027–1036. [DOI] [PubMed] [Google Scholar]
  60. Wang Y. and Shortle D. 1995. The equilibrium folding pathway of staphylococcal nuclease: Identification of the most stable chain-chain interactions by NMR and CD spectroscopy Biochemistry 34: 15895–15905. [DOI] [PubMed] [Google Scholar]
  61. Wlodawer A., Svensson L.A., Sjolin L., Gilliland G.L. 1988. Structure of phosphate-free ribonuclease A refined at 1.26 A Biochemistry 27: 2705–2717. [DOI] [PubMed] [Google Scholar]
  62. Woenckhaus J., Kohling R., Thiyagarajan P., Littrell K.C., Seifert S., Royer C.A., Winter R. 2001. Pressure-jump small-angle x-ray scattering detected kinetics of staphylococcal nuclease folding Biophys. J. 80: 1518–1523. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Wong K.B., Freund S.M., Fersht A.R. 1996. Cold denaturation of barstar: 1H, 15N and 13C NMR assignment and characterisation of residual structure J. Mol. Biol. 259: 805–818. [DOI] [PubMed] [Google Scholar]
  64. Xia T.H. “Software determination and visual display of NMR structures of proteins” Ph.D. thesis 1992. ETH Zürich, Switzerland.
  65. Zarrine-Afsar A. and Davidson A.R. 2004. The analysis of protein folding kinetic data produced in protein engineering experiments Methods 34: 41–50. [DOI] [PubMed] [Google Scholar]
  66. Zhang J., Peng X., Jonas A., Jonas J. 1995. NMR study of the cold, heat, and pressure unfolding of ribonuclease A Biochemistry 34: 8631–8641. [DOI] [PubMed] [Google Scholar]
  67. Zhang O. and Forman-Kay J.D. 1997. NMR studies of unfolded states of an SH3 domain in aqueous solution and denaturing conditions Biochemistry 36: 3959–3970. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES