Mechanical and Failure Properties of Extracellular Matrix Sheets as a Function of Structural Protein Composition

Abstract

The goal of this study was to determine how alterations in protein composition of the extracellular matrix (ECM) affect its functional properties. To achieve this, we investigated the changes in the mechanical and failure properties of ECM sheets generated by neonatal rat aortic smooth muscle cells engineered to contain varying amounts of collagen and elastin. Samples underwent static and dynamic mechanical measurements before, during, and after 30 min of elastase digestion followed by a failure test. Microscopic imaging was used to measure thickness at two strain levels to estimate the true stress and moduli in the ECM sheets. We found that adding collagen to the ECM increased the stiffness. However, further increasing collagen content altered matrix organization with a subsequent decrease in the failure strain. We also introduced collagen-related percolation in a nonlinear elastic network model to interpret these results. Additionally, linear elastic moduli correlated with failure stress which may allow the in vivo estimation of the stress tolerance of ECM. We conclude that, in engineered replacement tissues, there is a tradeoff between improved mechanical properties and decreased extensibility, which can impact their effectiveness and how well they match the mechanical properties of native tissue.

Introduction

There is growing interest in the use of tissue engineering (TE) methodologies to develop tissues for transplantation into the human body. Recent data indicate that the functional properties of tissue-engineered constructs are a key component to their successful use (1). The creation of these tissue constructs routinely involves the seeding of cells on or within a scaffold or matrix. The combination of the extracellular scaffold and seeded cells results in a tissue with complex, nonlinear mechanical behavior (2). Both the mechanical and failure properties of the TE scaffold are an integral part of the tissues’ functional properties. Moreover, it is becoming increasingly clear that the TE construct must match the functional properties of the native tissue to be a viable option.

The protein composition as well as the stiffness of the scaffold can also affect various attributes of the resident cells. Cells bind to the extracellular matrix (ECM) via adhesive contacts or receptors and then arrange their cytoskeleton to exert force on the surrounding ECM to support the cell interior (3). The intracellular stress distribution created can influence a number of cell functions. These include cell spreading and motility (4), apoptosis (5), signal transduction (6), and ECM remodeling (7). Differences in the stiffness of the ECM could alter the intracellular stress distribution considerably and therefore affect these critical cell processes.

Over the last decade, ECM from a variety of tissues including bladder (8–10), heart valve (11–13), blood vessel (14–16), small intestinal submucosa (17,18), skin (19), and liver (20) have been investigated as a tissue scaffold to be used in tissue engineering or regenerative medicine. Collagen and elastin are the two important structural proteins of the ECM that afford different mechanical properties to these tissues. Elastin is a highly elastic rubberlike protein that has the ability to stretch to 2–3 times its initial length and snap back with little energy loss, while collagen is nearly 100 times stiffer and nearly inextensible (2,21). Both collagen and elastin are present in various amounts in different tissues and the mechanical properties of these tissues can vary widely depending on the amounts and organization of these two proteins.

Recent studies have demonstrated the importance of cell-matrix interactions and mechanical properties in collagen gel-based tissue constructs. Grinnell and colleagues have shown the importance of matrix tension on fibroblast cytoskeletal formation and quiescence (22,23). Similarly, Elson and colleagues have delineated cell versus matrix mechanics in collagen gel-based tissue constructs (24). However, these groups did not investigate the effects of varying collagen concentration on matrix mechanics. Tranquillo and co-workers have created fibrin gel-based constructs and measured their mechanical properties as well as the amount of new collagen deposited by the cells (25,26). They reported that increased collagen content results in increased mechanical stiffness. However, much of the construct remaining after culture is un-remodeled fibrin and they report little to no elastin production in their constructs. Voytik-Harbin and colleagues investigated microstructure and mechanical properties of varying concentrations of collagen gels (27) as well as the cellular response to changes in mechanical properties (28). However, the data for these studies were collected on reconstituted type I collagen gels, which contain no elastin and morphologically are different from native ECM. In addition, studies on varying concentrations of collagen gels to date have only investigated quasistatic mechanical properties but not dynamic mechanical and failure properties. The dynamic mechanical response is critical to consider when constructs are to replace tissues operating in dynamic conditions such as blood vessels or lung parenchyma.

Elastolytic injury plays a significant role in a number of diseases such as emphysema (29) or vessel wall aneurysm (30). While many groups have compared the mechanical properties of collagen gel-based constructs to native tissue, none have investigated the effects that elastolytic injury has on the mechanical and failure properties of the constructs. Such data could be critical when using TE constructs to replace elastolytically injured tissues.

The goal of this study was to determine the mechanical and failure properties of ECM sheets produced in vitro by cultured cells with varying amounts of both collagen and elastin as a model of the alteration in structural protein content in TE constructs. These properties were also assessed in the presence of elastase digestion as a model of elastolytic injury present in diseases such as emphysema and vessel wall aneurysm. To this end, we cultured neonatal rat aortic smooth muscle cells (NNRASMC) in different media to alter the types and amounts of structural proteins present in the ECM produced by these cells. Our results indicate that, when creating scaffolds for TE constructs, there may be an important balance between the failure strength and the elastic properties of TE constructs with alterations in their composition.

Methods

Tissue and cell culture

Two main types of ECM sheets were analyzed in this study: sheets that contained only elastin and sheets that contained both collagen and elastin. The ECM sheets were derived from NNRASMC cultures, which are highly elastogenic (31). NNRASMCs were isolated from 1–3-day-old Sprague-Dawley rats and grown in primary culture with Dulbecco's modified Eagle's medium containing 3.1 mg/ml sodium bicarbonate, 1% sodium pyruvate, 1% penicillin, and streptomycin (DV3.7), and 20% fetal bovine serum as described previously (31). After subcultivation into first passage in 25 cm² tissue culture flasks (2 × 10⁴ cells/cm²), the cells were maintained for six weeks with 5 ml of DV3.7 containing 10% fetal bovine serum, resulting in cultures that were ∼15–17 cells deep (∼50 μm thick with cells intact). NNRSMC cultures require sodium ascorbate in the media for the cells to produce fibrillar collagen. For those cultures selected to have collagen, sodium ascorbate was added to the media from weeks 3–5 in two different concentrations, 50 μg/ml and 20 μg/ml. In all cultures, the medium was changed twice weekly and the cell cultures were routinely monitored by phase contrast microscopy. After six weeks in culture the cells were killed with 5% sodium azide in Puck's saline (140 mM NaCl, 5.4 mM KCl, 1.1 mM KH₂PO₄, 1.1 mM Na₂HPO₄, and 6.1 mM glucose, pH 7.4) (32), and stored at 4°C. Before use, the cultures were infiltrated with a gelatin solution, which, after the gelatin solidified, allowed the cultures to be stripped from the culture flasks. Previous studies that used this technique have shown that the cultures were removed intact (33).

Structural protein content

To quantify the structural protein content in cultures that had been lifted from the culture flasks, rectangular pieces of gelatin containing the ECM sheet were heated at 50°C to melt the gelatin, washed several times and the cell layer was subjected to hot alkali treatment (0.1 N NaOH at 95°C for 45 min) (34). The hot alkali method is used to remove material from the cell layer that is not mature (cross-linked) elastin. The hot alkali insoluble residue (elastin) was hydrolyzed in 6N HCl for 24 h at 110°C. Amino-acid analysis was performed (model No. 6300 with System Gold software; Beckman, Palo Alto, CA) to confirm the characteristic amino-acid composition of the elastin, consisting of the elastin cross-links desmosine and isodesmosine, and >80% nonpolar amino acids (31). The amount of elastin was calculated as the sum of the amino acids (in nmoles) multiplied by the average amino-acid mass of 85 ng/nmol.

To quantify the total collagen content of the samples the supernatant of the hot alkali treatment underwent amino-acid analysis and the amount of total collagen was quantified from the hydroxyproline content (31). In addition, fibrillar collagen can be isolated by elastase digestion of the sample and quantified by amino-acid analysis of the fibrillar residue which contains pyridinoline cross-links (35). The values for fibrillar collagen determined by these two methods should agree within 10%. Type IV collagen, which is found mostly in basement membrane, minor nonfibrillar collagen types, and most other proteins are solubilized by treatment with elastase and therefore are not counted in the second method.

The absolute concentration of elastin and collagen was quite variable among the three groups since samples in different groups came from different cohorts of cells. As mentioned above, sodium ascorbate was added in two concentrations: 50 μg/ml (27 ± 1 μg/cm² of collagen, 279 ± 3 μg/cm² of elastin) and 20 μg/ ml (12 ± 1 μg/cm² of collagen, 64 ± 8 μg/cm² of elastin). Similarly, the elastin-only group contained 73 ± 13 μg/cm² of elastin and no measurable fibrillar collagen. However, since our results suggested that the moduli and the failure properties of the ECM sheets were most sensitive to the relative protein content as well as their structural organization, we characterized the groups’ compositions with the ratio of total elastin content to total collagen content which was used throughout the study. Thus, adding sodium ascorbate to the cell cultures in concentrations of 50 μg/ml and 20 μg/ml resulted in ECM sheets with elastin/collagen ratios of 10:1 (by weight) and 6:1, respectively.

Microscopic imaging of ECM thickness

Calculation of the stress in the material requires the measurement of the cross-sectional area which is the product of the ECM sheet thickness and the sample width to which the samples were cut. To measure the thickness, we imaged samples that were still contained in the lifting gelatin and also after the gelatin had been melted off, the latter corresponding to a completely relaxed state. From length measurements taken before and after the gelatin was melted off between several markers on the samples, it was determined that when still encased in the gelatin, the samples were held at an overall strain in a given direction of 21.2% ± 2.1%. This strain in the flask was due to a prestress in the ECM that was created by the contractile cells.

The imaging of the thickness was done with a model No. FV-1000 laser scanning confocal microscope (Olympus, Melville, NY). The confocal pinhole and the Z-step size were matched to the microscope objective to optimize optical sectioning and subsequent measurement of material thickness. Since native collagen and elastin autofluoresce, no specific labeling was necessary. The emission spectrum was mapped using a 488-nm argon laser excitation and collecting images generated from emission between 500 and 600 nm. Multiple stacked images differing in Z-position were collected and the thickness of the ECM sheets was determined from the variation in emission intensity by Z-position according to the method described in the Data Analysis. Our data indicated that there was significant intrasample variability of the thickness as compared to the intersample variability of the mean thickness within each group. Therefore, thickness data was taken on only two samples at 0% strain and two samples at 20% for each of the three ECM sheet groups at 10 different locations in each sample.

Experimental setup and data acquisition

The mechanical testing was carried out on an existing uniaxial tissue-stretching system that was previously described (36). Briefly, the system consists of a computer-controlled lever arm with a built in large-scale force transducer (model 300B dual-mode lever system; Aurora Scientific, Ontario, Canada) on one side of a tissue bath and a smaller scale force transducer on the other (model No. 305 force transducer; Aurora Scientific). The large-scale force transducer was needed to record the force data for failure tests of the samples, since the forces during these tests exceeded those that could be measured with the more sensitive force transducer. A LABView (National Instruments, Austin, TX) program was developed to run the system and record displacement and force data. The data were low-pass filtered at a cutoff frequency of 10 Hz (901P Filter Bank; Frequency Devices, Haverhill, MA) before being sampled by the data acquisition card (DAQCard-6062E, National Instruments) and connector block (BNC-2110, National Instruments) at a sampling rate of 30 Hz.

The alignment and accuracy of the system was tested as described previously (36). Specifically, we measured the dynamic mechanical properties of a steel spring, which has a constant storage modulus over the frequency range of the measurements. The measured storage modulus of the spring increased <0.1% across the frequencies of interest and the loss modulus was nearly two orders-of-magnitude smaller than the storage modulus.

Mechanical testing protocol

The ECM sheets were cut into 5 mm wide by 15 mm long strips from the sheet of gelatin that was lifted from the culture flasks. Samples were affixed to small metal plates (5 mm × 5 mm) with cyanoacrylate glue while still encased in the gelatin leaving the working area of 5 mm × 5 mm. These small metal plates were attached to the force transducers and length controller via steel wires. Once the sample was attached to the system, the chamber was filled with 22 ml of phosphate-buffered saline (PBS) and the whole system was placed on top of a hot plate which was subsequently turned on. The sample was heated until the gelatin dissolved. This required that the hotplate reach a maximum temperature of 50°C but only for <1 min. While this temperature is reasonably close to the denaturation temperature of mammalian collagen (60°C), a previous study has shown that heating lung-tissue strips—that contain both collagen and elastin—to 55°C to remove agarose had no effect on the mechanical properties of the samples (37). The PBS containing the solubilized gelatin was then removed and the sample was rinsed 3–4 times with room temperature PBS. The bath was refilled with 22 ml of fresh PBS also at room temperature and the sample was shortened to find its initial length, l₀, defined as the shortest length at which a change in force was first detected with an incrementally small increase in strain.

Initially, three baseline quasistatic stress-strain curves to 25% strain were collected to precondition the sample (strain rate of 0.75%/s). The uniaxial stress, T, was calculated as the recorded force divided by the cross-sectional area and strain, ɛ, as the displacement divided by the sample's initial length. The initial cross-sectional area was calculated as the thickness of the ECM sample taken from confocal microscopy images of the ECM after the gelatin was melted multiplied by the samples initial width, which was measured after the sample was at its initial length. The three stress-strain curves were followed by a dynamic measurement in which pseudorandom length oscillations of peak-to-peak amplitude 10% strain were superimposed on a static operating strain of 20%. To do this, the force was recorded during a broadband displacement signal, which is the sum of six sine waves with frequencies between 0.11 and 3.45 Hz that were chosen according to Suki and Lutchen (38). Force and length data were recorded for the dynamic measurements for a minimum of seven cycles of the waveform. After the dynamic measurement, there was a 5-min equilibration period followed by another baseline stress-strain curve to 25% strain and another dynamic measurement. For control samples, the stress-strain and dynamic mechanics measurements were repeated at 5 min, 10 min, 20 min, and 30 min after the last baseline measurement. For treatment of samples with elastase, porcine pancreatic elastase (PPE) (Sigma, St. Louis, MO) was added to the bath at a final concentration of 0.06 IU/ml and the stress-strain curve and dynamic mechanics measurements were repeated at 2 min, 5 min, 10 min, 20 min, and 30 min after the addition of PPE. All samples were then stretched to failure—defined as complete separation of the samples into two halves—at the end of the 30-min measurement period. This protocol was implemented on seven control samples and seven PPE-digested samples from each of the three groups.

Data analysis

Image analysis of ECM thickness

To determine the thickness we analyzed the z-stack images from the confocal microscope using ImageJ (National Institutes of Health, Bethesda, MD). Briefly, a circular region of interest (ROI) ∼1/50th the size of the entire image was drawn on the first slice in the stack. The average intensity of the ROI as a function of slice number was plotted. The shape of the profile was that of a spread peak. The number of slices between the half-height points of the peak intensity was determined and this was converted to a thickness value in units of microns. The measurement was repeated at 10 randomly selected ROIs for each image of the different ECM compositions and the data were averaged to determine the thickness of the ECM sheets at ∼20% strain (while still encased in the gelatin) and at 0% strain (after the gelatin was melted).

Dynamic mechanics analysis

The dynamic moduli of the engineered tissue sheets were calculated as a function of frequency for the time points described in the protocol above. First, force and length data were converted to stress-strain data (see Mechanical Testing Protocol). Since our oscillatory measurements were made at a static strain of 20% and the strain of the samples in gelatin was found to be ∼20%, we normalized the force data by the thickness measurements taken from the samples in gelatin so that the dynamic mechanics would reflect the true mean stress in the material. We then determined the complex modulus of the tissue, E*, which is defined as the ratio of stress as a function of frequency divided by strain as a function of frequency. The E* spectrum was actually estimated as the ratio of the cross-power spectrum of T with ɛ and the autopower spectrum of ɛ. Using fast Fourier transformations, the cross- and autopower spectra were calculated on blocks of data using 75% overlap and then ensemble-averaged. The data were taken for several cycles of the waveform to obtain a sufficient number of blocks in the spectral estimates. The coherence function was also calculated to assess the quality of the spectra and E* (38). The real part of E*, is the storage modulus (E′), a measure of the ability of the sample to elastically store energy as a function of frequency. The imaginary part of E* is the loss modulus (E″), a measure of the amount of energy loss the sample undergoes in a cycle as a function of frequency.

The E* spectra were then fit with the a viscoelastic model, proposed by Hantos et al. (39) for lung tissue and modified by Brewer et al (40):

$$E^{\ast }=H{\omega }_{\text{n}}^{\beta }+jG{\omega }_{\text{n}}^{\beta }+jR\omega +jI\omega \text{.}$$ (1)

Here, G is the tissue loss modulus coefficient; H is the tissue storage modulus coefficient; R is a Newtonian viscous resistance; I is an inertial term; ω_n is the normalized angular frequency (i.e., ω_n = ω/(1 rad/s), a normalization that results in a stress unit for G and H) (40); and β is the stress relaxation exponent defined by the equation

$$\beta =\frac{2}{\pi }\text{arctan}\frac{G}{H}\text{.}$$ (2)

Since R is generally small and I is mostly determined by the equipment, the model described by Eqs. 1 and 2 is called the constant phase model because the phase angle of E* (βπ/2) is independent of frequency (39). The parameters G and H are used to simplify the comparison of the storage and loss moduli before and after digestion of ECM sheets. The inertance is associated more with the system than the ECM sheets and is not reported.

Stress-strain curve analysis

All force-displacement data were converted to stress-strain data as described above. To quantify the changes in the stress-strain relationship while elastin was being degraded, the ascending limbs, or loading portions, of the stress-strain curves were fit with a two-parameter exponential curve with the form

$$T=\epsilon A{e}^{\text{b}\epsilon }\text{.}$$ (3)

The two parameters A and b in the stress-strain curve model describe the quasistatic properties of the ECM sheets: A represents the amplitude of the curve, and b represents how nonlinear the curve is. Dividing by strain and taking the log of both sides, this equation can be written into a form in which simple linear regression can be used to estimate A and b:

$$\text{ln}\left(\frac{T}{\epsilon }\right)=\text{ln}(A)+b\epsilon \text{.}$$ (4)

Failure curve analysis

Each failure test curve was converted to a stress-strain relation and two key indices from each curve were measured to determine the effect that elastase digestion had on the failure properties of the sheets. These indices were the maximum stress during the failure test and the failure strain, which we defined as strain value where the stress returned to zero (complete separation of the sample).

Statistics

Model parameters and stress-strain curve exponential fit parameters were analyzed by two-way ANOVA for repeated measures (SigmaStat, San Rafael, CA). Differences between sample groups and treatments were considered statistically significant at p < 0.05. Student-Newman-Keuls analysis was used for all pairwise multiple comparisons. Statistical significance was defined as p < 0.05. All data are presented as mean ± standard deviation (SD).

Results

Microscopic measurements of ECM thickness

Fig. 1 A displays a sample slice from the bottom layer of each of the three sample types. Note that qualitatively the 6:1 elastin/collagen ECM (EC6) appears denser than the 10:1 elastin/collagen ECM (EC10), which in turn is denser than the elastin-only ECM (EO). The average thickness values for the ECM sheets at 0% and 20% strain are shown in Fig. 1 B. The EO sheets were the thickest at both strains, followed by the EC10 and the EC6. All three groups showed a decrease in the mean thickness between 0% and 20% strain. In fact, both the EC6 and the EC10, but not the EO, thicknesses decreased statistically significantly with strain (p < 0.001). In addition, at 0% strain, the EC6 group had a statistically significantly decreased thickness value as compared to the EO group (p < 0.03), and at 20% strain, all three groups were statistically significantly different from each other (p < 0.03 for all comparisons), implying that changes in the elastin/collagen ratio also effects the Poisson ratio of the ECM sheets.

Figure 1.

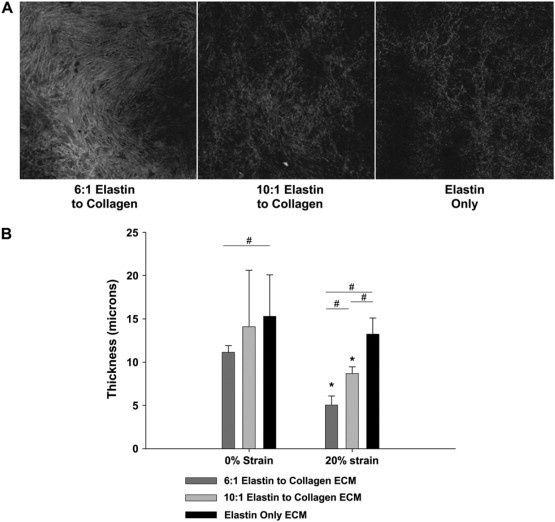
(A) Confocal image examples of autofluorescence taken from the bottom layer of each of the three ECM sheet types while still encased in gelatin. (B) The average thickness data for all three ECM sheet groups at 0% strain (left) and ∼20% strain (right). The asterisk denotes a significant difference compared to 0% strain (p < 0.05). The pound sign denotes a significant difference between groups at a given strain (p < 0.05).

Dynamic mechanical properties

Dynamic mechanical properties are presented in Fig. 2. Since the storage modulus coefficient, H, showed no time dependence in any of the control groups, the H-values were averaged over time. The corresponding mean ± SD values of H were 219.8 ± 152.6 kPa for the EO group, 463.7 ± 121 kPa for the EC10 group, and 1198 ± 482.4 kPa for the EC6 group. Since there was a statistically significant difference among the groups (p < 0.001), the protein composition of the ECM had a considerable impact on the sheets’ dynamic stiffness. Individually, the EC6 group's H was significantly higher than the EC10 and EO groups’ control H at all time points (p < 0.001). In Fig. 2, panels A–C, compare the mean ± SD values of H in the control and elastase-digestion groups as a function of time for the EO, EC10, and EC6 groups, respectively. There was a statistically significant interaction between elastase treatment and time in all three groups (p < 0.001, two-way ANOVA). Elastase digestion significantly decreased the H-values from the 0 min time point in all three groups by 5 min after the addition of elastase (p < 0.001 for all ECM groups). In addition, there was a statistically significant difference between H-values corresponding to the control and the elastase-digested groups at 20 min and 30 min after digestion for the EO and EC6 groups and at 10 min, 20 min, and 30 min after digestion for the EC10 group. Also, the EC6 group had significantly higher H-values during digestion at all time points when compared to the EO group and at all time points up to 20 min after the addition of elastase when compared to the EC10 group. Since the percent decrease in H by 30 min was similar in all groups, the rate of digestion was not influenced by tissue composition.

Figure 2.

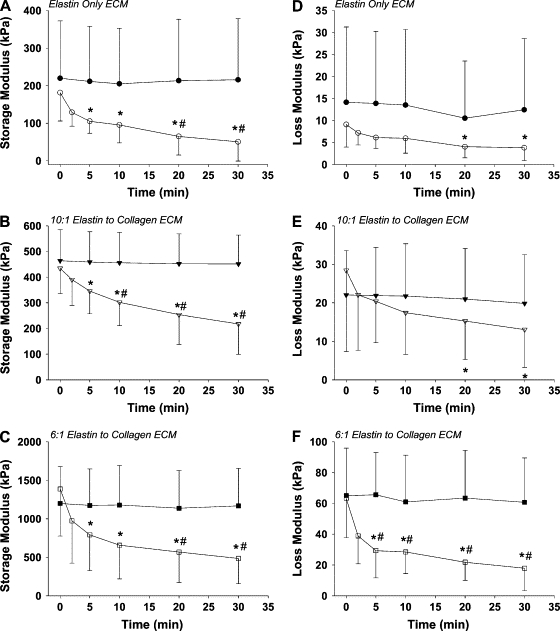
Time course of the mean ± SD of the stiffness parameter, H, and the damping parameter, G, for the control (solid shapes) and elastase-digested (open shapes) samples. Panels A–C display H-values for the EO, EC10, and EC6 groups, respectively. Panels D–F display G-values for the EO, EC10, and EC6 groups, respectively. The asterisk denotes a significant difference within group compared to the value at 0 min (p < 0.05). The pound sign denotes a significant difference between digested and control samples at a given time point (p < 0.05).

The loss modulus coefficient, G, showed a similar pattern as H. In the control, the mean ± SD values of G were 14.2 ± 17.1 kPa for the EO group, 22 ± 11.5 kPa for the EC10 group, and 65.1 ± 30.8 kPa for the EC6 group and showed no time dependence in any of the groups. Similar to H, ECM sheet composition had a significant effect on G (p < 0.001). The EC6 group had a significantly higher control G-value than the EC10 and EO groups control G-values at all time points (p < 0.003). In Fig. 2, panels D–F, compare the control and elastase digestion time plots for the EO, EC10, and EC6 groups, respectively. There was a significant interaction between elastase treatment and time only for the G-values of the EC6 group (p < 0.001, two-way ANOVA). However, all three groups displayed significant decreases in their G-values with elastase treatment from the 0 min value at 20 min and 30 min after treatment (pairwise comparison within each elastase-treated group, p < 0.03 for all cases). In addition, the EC6 group had significantly higher G-values during digestion at all time points up to 20 min after the digestion of elastase when compared to the EO group and at all time points up to 5 min after the addition of elastase when compared to the EC10 group.

Stress-strain data

Stress-strain curve examples are shown in Fig. 3. At any given strain, stress increases gradually with the addition of collagen to the tissues. The loading portions of the curves were analyzed using Eqs. 3 and 4. The average control stress-strain amplitude parameter, A, increased from 18.1 ± 13.8 kPa in the EO group, to 58.2 ± 19.4 kPa in the EC10 group and finally to 73.8 ± 30.3 kPa in the EC6 group showing no time dependence in any of the groups. Again, there was a significant effect of ECM sheet composition on the control A-value (p = 0.001). Specifically, the EC6 group had a larger control A-value than the EC10 and EO groups at all time points (p < 0.02). In Fig. 4, A–C, compare the control and elastase digestion time plots for the EO, EC10, and EC6 groups, respectively. We found a significant interaction between elastase digestion and time for all three groups (p < 0.002, two-way ANOVA for all cases). All three groups showed a statistically significant decrease with elastase digestion from their 0 min value to 5 min after the addition of elastase. In addition, the EC6 and EC10 groups showed a significant difference between the control and elastase digested A-values at all time points from 5 min on (p < 0.02 for all cases).

Figure 3.

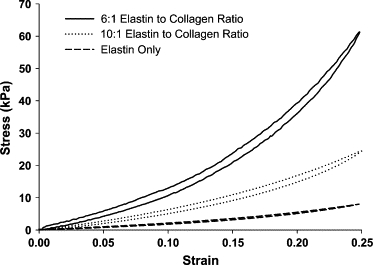
Representative examples of the stress-strain curves for the three sample groups.

Figure 4.

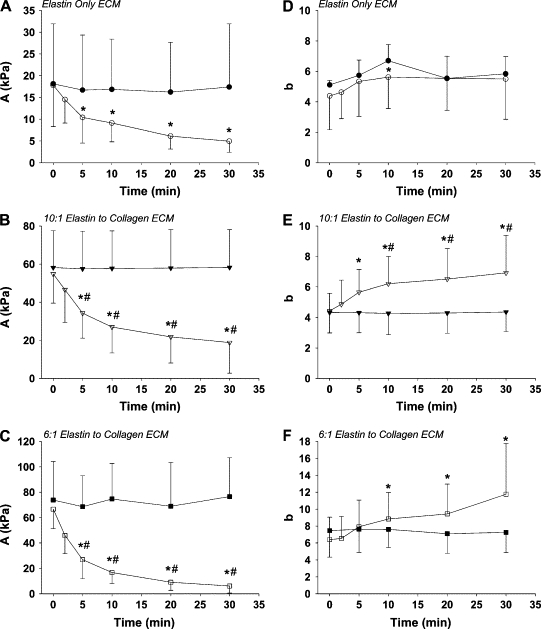
Time course of the mean ± SD of the amplitude parameter A and the nonlinearity parameter b for the control (solid shapes) and elastase-digested (open shapes) samples. Panels A–C display A-values for the EO, EC10, and EC6 groups, respectively. Panels D–F display b-values for the EO, EC10, and EC6 groups, respectively. The asterisk denotes a significant difference within group compared to the value at 0 min (p < 0.05). The pound sign denotes a significant difference between digested and control samples at a given time point (p < 0.05).

The control stress-strain curve nonlinearity parameter, b, was 5.1 ± 0.3 for the EO group, 4.3 ± 1.3 for the EC10 group, and 7.5 ± 3.1 for the EC6 group and showed no time dependence in any of the groups. Overall, there was a significant effect of ECM sheet composition on the control b-value (p < 0.03). Specifically, there was a significant difference between the control b-values for the EC6 group and the EC10 groups at all time points. In Fig. 4, panels D–F, compare the control and elastase digestion time plots for the EO, EC10, and EC6 groups, respectively. There was a significant interaction between elastase digestion and time in both the EC6 and EC10 groups (p = 0.001 and p < 0.001, respectively), but interestingly not in the EO group. Note that the EC6 group had significantly increased b-values with digestion from the 10-min time point on (p < 0.01 for all time points), and the EC10 b-values significantly increased from the 5-min time point on (p < 0.001 for all time points). In addition, the EC10 elastase digested b-values were significantly different from control values from 10 min on (p < 0.02 for all time points). These results imply that while the moduli of the collagen containing sheets decreased, their nonlinearity increased during digestion, an effect not seen in the EO sheets.

Failure data

The mean ± SD values of the maximum stress during failure tests for control samples and samples that were digested with elastase are shown in Fig. 5 A. Overall, there was a significant effect of ECM composition on maximum stress in both the control and elastase-digested data sets (p < 0.001 for both cases). Note that the control maximum stress is significantly higher in the EC6 samples than in both the EC10 samples (p < 0.03) and the EO samples (p < 0.001). In addition, the EC10 control maximum stress is significantly higher than the EO value (p < 0.03). While samples containing collagen had increased maximum stress as expected, all three groups displayed a significant decrease in failure stress with elastase digestion (p < 0.001 in all cases). Even after digestion, both the EC6 and EC10 groups had a significantly higher maximum stress than the EO group (p < 0.001 and p = 0.006, respectively); however, they were not statistically different from each other.

Figure 5.

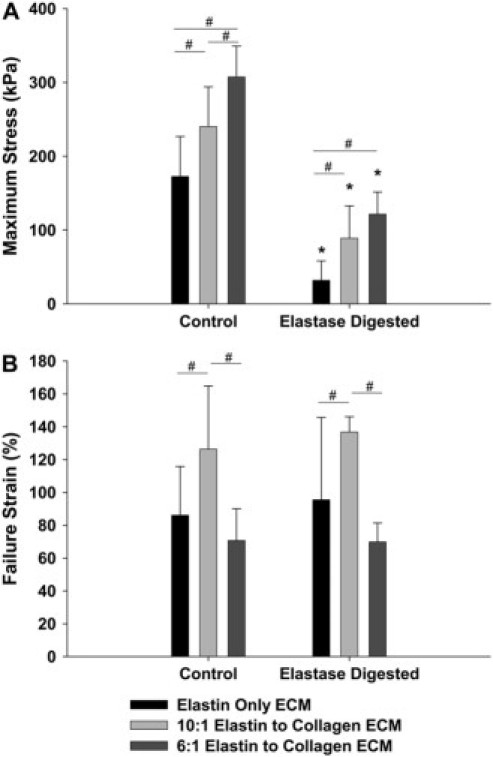
(A) The mean ± SD values of the maximum stress during a failure test for control samples (left) and elastase-digested samples (right) for all three ECM sheet types. (B) The mean ± SD of the failure strain for control samples (left) and elastase-digested samples (right) for all three ECM sheet types. The asterisk denotes a significant difference between elastase-digested and control values within a group (p < 0.05). The pound sign denotes a significant difference between group values at a given treatment (p < 0.05).

Fig. 5 B displays the failure strain data for all three ECM sheet groups for control samples and samples digested with elastase. Overall, there was a significant effect of ECM sheet composition on the failure strain for both control and elastase-digested data (p = 0.009 and p = 0.001, respectively). The control failure strain for the EC10 sample group was significantly higher than that of the EC6 and EO sample groups (p < 0.008 and p < 0.03, respectively). There was no significant difference between the control failure strain for the EC6 and EO groups. There was not a significant difference between control failure strain and elastase-digested failure strain for any of the three groups, but after digestion, the failure strain of the EC10 samples was still significantly larger than both the EC6 and EO samples (p < 0.001 and p < 0.02, respectively). There was no significant difference between the elastase-digested failure strain of the EC6 and EO groups. These results are intriguing since digestion significantly reduced failure stress, but did not affect failure strain independent of ECM composition.

Discussion

The goal of this study was to determine the changes in the mechanical and failure properties of ECM sheets with varying amounts of collagen and elastin as a model of the alteration in structural protein content in these neonatal rat aortic smooth muscle-based TE scaffolds. The major finding of this study is that a gradual increase in relative collagen content progressively increased the quasistatic and dynamic stiffness as well as the failure stress over sheets that contained only elastin. However, the highest relative collagen content also served to significantly decrease the failure strain of the material. Before interpreting these results, we first discuss the technical limitations of the study.

Data collection and imaging limitations

The most important limitation in the data collection of this study is related to the resolution of the large-scale force transducer during failure tests. This transducer has a resolution of 0.03 g-force, which when making measurements on such thin samples after elastase digestion, could have introduced some noise into our failure stress data. Using the average thickness values at 0% strain (Fig. 1) and the median sample width recorded (4 mm) to calculate cross-sectional areas, we estimated that the resolutions of the stress measurement were ∼4.4 kPa, 4.8 kPa, and 6.1 kPa for the EO, EC10 and EC6 groups, respectively. After digestion, the average failure stress values were ∼7, 19, and 20 times larger than these resolutions for the EO, EC10, and EC6 groups, respectively. Even though the thickness decreases with increasing strain, the error in the recorded stress should be random and in a population of samples should average out. Therefore, it is likely that the resolution was not a large factor in the observed variability of the failure stress data (Fig. 5 A) even after digestion.

There were several limitations to the imaging component of this study. First and foremost is that we were only able to image two samples in each of the strain conditions from each group. In addition, these two samples were both taken from the ECM that was in the center of the culture flask to reduce variability in the thickness measurements possibly due to the different density of cells closer to the edges of the flask. Ideally, images would be taken on each individual sample, which could have greatly reduced the variability we saw in the mechanical parameters, and done dynamically to have more precise thickness as a function of strain. We made attempts to measure the thickness of ECM sheets while they were attached to the tissue stretching system. However, with the current design, we were unable to solve the issue of getting the sample close enough to the objective to be accurately imaged without compromising either the hydration of the sample or the ability of the transducers to correctly measure the force. Thus, in this case we did not have true stress estimates as a function of strain; instead we used a single value of the estimated thickness corresponding to 20% strain.

ECM thickness as a function of strain

The results displayed in Fig. 1 B indicate that increases in the amount of collagen relative to the amount of elastin in the ECM sheets decreased their thickness and also resulted in a further decrease in thickness from 0% strain to 20% strain. The thickness of the EO sheets decreased by 14% with the increase in strain, while EC10 and EC6 sheets thickness values decreased by 38% and 55%, respectively. The decrease in thickness with increased collagen content indicates that the Poisson ratio of the sheet significantly depends on the protein composition. This dependence could be related to increased cross-linking of fibers in the samples with more collagen. Larger numbers of cross links between collagen fibers or between collagen and elastin fibers could result in a translation of axial strain into lateral strain, creating greater lateral contraction of the tissue at a given axial strain. Additionally, recently it has been argued that the Poisson ratio of the lung tissue is sensitive to the amount of proteoglycans in the ECM (41). If the increase in relative collagen content also reduced the amount of proteoglycans, the folding of the fibers under uniaxial strain could become easier, resulting in an apparent increase in the Poisson ratio. Nevertheless, an important implication is that this apparent alteration in density with an increase in the relative amount of collagen could have a significant impact on how cells adhere to the TE constructs as well as on the ability of the cells to secrete and organize matrix molecules.

Dynamic mechanical properties

Addition of collagen to the ECM sheets also significantly increased the dynamic mechanical parameters. While the EC10 samples had a greater amount of collagen per unit surface area than the EC6 samples (27 μg/cm² compared to 12 μg/cm²), all the measures of mechanical properties were larger in the EC6 group. This implied that it is not the absolute concentration of collagen that determines the mechanical material properties, but perhaps the relative amount of collagen to elastin and more importantly, their spatial organization (see below). In addition, while the average control values of H for the EC6 samples (1.2 MPa) seem fairly large, they are still smaller than the modulus values of intact collagen fibrils (5 MPa) (42).

The loss modulus parameter, G, also showed a significant increase with increases in the relative amount of collagen. This increase could be explained by the fact that collagen is more hysteretic than elastin (43), and therefore would contribute more to the ECM sheets’ ability to dissipate energy with strain. While the decrease in G with elastase digestion in the EO group was not statistically significant, those in the EC10 and EC6 sheets were. Cribb et al. (44) suggested that proteoglycan bridges between collagen fibrils play a part in transmitting and resisting tensile stresses in tendons, contributing to the strength of the tissue. Based on this hypothesis, the decrease in G in the collagen-containing cultures after treatment could be due to the reduction of friction between adjacent collagen fibers in the sheets caused by the digestion of proteoglycans via elastase (45). Therefore not only would the loss of proteoglycans reduce G, but with the destruction of linkages between collagen fibers, perhaps less collagen would be probed with the dynamic displacement waveform, also resulting in a lower G-value.

Stress-strain amplitude and nonlinearity

The stress-strain amplitude parameter, A, showed a significant increase with the addition of collagen to the ECM sheets (Fig. 4), however, there was no difference between the control A-values of the EC6 and EC10 sheets. The increase with the addition of collagen is expected since A is related to the ECM sheet modulus. The lack of a difference in A between the two collagen-containing groups could in part be due to the large intragroup variability. However, another possibility is that the amplitude of our stress-strain curve (25% strain) was too small to fully probe the quasistatic properties of the collagen. Collagen is thought to become more involved in the stress-strain properties of tissues at higher strains where its higher tensile strength helps prevent tissues from tearing or rupturing (2). If this is the case, then 25% strain may only begin to stretch the collagen fibers that are wavy at 0% strain (see below) and the intragroup variability of the EC6 and EC10 samples could be large enough to prevent statistical significance. After digestion, the largest decrease in A occurred in the EC6 samples (91%), which could again be related to the loss of proteoglycan cross links connecting the collagen network.

The increase in the stress-strain nonlinearity parameter, b, with increases in the relative amount of collagen in the ECM sheets is expected, since collagen has a more nonlinear stress-strain relationship than elastin (42,46) and is thought to become more involved in the stress-strain properties of tissues at higher strains (2). To gain further insight into whether this was the case in the ECM sheets, we prepared electron microscopic images of EC6 sheets at 0% strain (Fig. 6 A) and at 30% strain (Fig. 6 B). Here the elastin is the amorphous white substance (denoted with an e) and the collagen fibers are clearly visible by their hallmark striations (black arrows). At 0% strain, the collagen fibers are curved and somewhat wavy with random orientations. By strains as low as 30%, most collagen fibers are oriented parallel and pulled taut (Fig. 6 B). This implies that they must be taking part in the generation of stress at these strains, and, therefore, would have an impact on the nonlinearity parameter, b. Interestingly, while the b-values for the EO sheets stayed relatively constant with elastase digestion, the values for both the EC10 and EC6 sheets increased significantly with elastase digestion. After digestion, the stress at low strains is reduced from the control sheet due to the destruction and/or weakening of elastin fibers. Since the collagen fibers would remain unaffected by digestion, the collagen starts being stretched at lower strains than before digestion, making the stress-strain curve more nonlinear due either to the collagen's inherent nonlinearity or the early recruitment of collagen in the recoil stress of the sheet. Both of these mechanisms increase the apparent value of b as obtained by fitting the model to the data.

Figure 6.

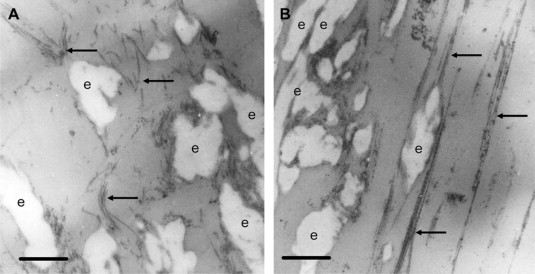
Electron microscopic images of EC6 sheets at 0% (A) and 30% (B) strain. Images were taken at 12,500×. Arrows denote collagen fibers and e denotes elastin. Scale bar represents 0.5 μm.

Spring network model

To better understand the origin of the differences in the stress-strain parameters between the sheet types, we adapted a previously developed hexagonal spring network model (41). Briefly, this model consists of a hexagonal network whose line elements are springs with both a linear and nonlinear component corresponding to elastin and collagen. In addition, at the juncture of any two line elements there is an angular spring mimicking the role of proteoglycans, which prevents the two line elements from folding into each other. The energy, E_s, for any given spring is defined as

$$E_{\text{s}}=\frac{1}{2}{K}_0\Delta l^2+\frac{1}{3}{K}_1\Delta l^3\text{.}$$ (5)

Here, K₀ is the linear spring constant, K₁ is the nonlinear spring constant, and Δl is the displacement of the spring. The energy, E_a, of the angular spring can be expressed as

$$E_{\text{a}}=\frac{1}{2}r\Delta {\theta }^2,$$ (6)

where r is the so-called bond bending constant and Δθ is the change in angle between two neighboring line elements. For any given macroscopic the strain, the network configuration can be found by minimizing the total energy of the system.

To investigate the effects of different densities of collagen fibers in the ECM on the stress-strain curve, we initially set all springs with the following parameters: K₀ = 10, K₁ = 0, and r = 0.1. To model the collagen in the ECM we randomly changed springs so that they were 80 times stiffer and nonlinear (K₀ = 800, K₁ = 200, and r = 0.1). This was done so that the percentage of springs that were designated as collagenlike springs ranged from 0% to 90% and the stress-strain curves of these networks were simulated. In addition, a network was created in which the ratio of normal to stiff springs was 6:1 (similar to the EC6 sheet), but in this case the stiff springs were organized into a long fiber that traversed the length of the network in the direction of stretching. Examples of this organized network and one with 40% of the springs being randomly made stiffer are shown in Fig. 7 at a strain of 40% (left and right, respectively). Note that darker shading represents higher forces and lighter shading represents lower forces carried by the line elements. Also note that in the case of the organized network there is one dark shaded fiber running down the middle that is taking up essentially all of the stress.

Figure 7.

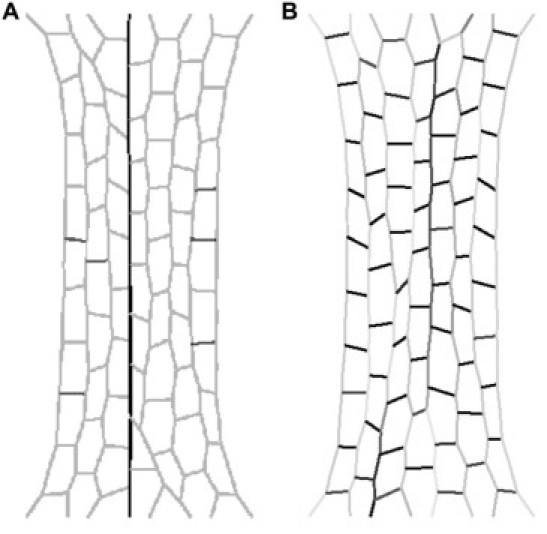
Examples of (A) an organized network with stiffer springs comprising ∼14% of the network but organized into a single fiber, and (B) a network in which stiff springs make up 40% of the network but are randomly distributed. Both networks are strained to 40% strain. Note that darker shading represents higher force and lighter shading represents lower force.

We then simulated the stress-strain curve for all cases and the results are shown in Fig. 8. It is evident from Fig. 8 that at lower percentages of stiff springs (<40%) there is little change in the amplitude (stress magnitude) or nonlinearity (convexity) of the stress-strain curve. Even when the stiff springs make up ∼50% of the network (dark shaded inverted triangles in Fig. 8), we only see a mild increase in the amplitude and nonlinearity. In contrast, there is a massive change in the stress when we organize the stiffer springs into a fiber that traverses the network from one side to the other, similar to the increase in stress with increasing collagen displayed in Fig. 3. These pathways of force transmission are similar to those found by Maksym et al. (47) using a two-dimensional spring network model of lung tissue. This behavior is consistent with percolation theory (48), which can be described as follows. Consider a square lattice, where neighboring sites can be connected by bonds randomly with probability p or not connected with probability 1-p. Occupied and empty bonds may stand for very different physical properties. At low concentration p, the occupied bonds are either isolated or form small clusters of nearest neighbors; however, the set of bonds within a contiguous cluster do not connect the opposite edges of the lattice. At large p-values, on the other hand, many paths between opposite edges exist. At some concentration in between, a critical concentration p_c must exist where for the first time the bonds percolate from one edge to the other. This threshold concentration is called the percolation threshold. The percolation problem has been studied in elastic spring networks before (49), although not with nonlinear springs in the presence of bond-bending. In addition, the concept of percolation of cells entrapped in a biological gel matrix has been used to model alterations in the mechanical properties of artificial tissues with cellular concentration (50,51). However, to our knowledge this is the first use of percolation to describe the formation of collagen within an elastin network and its effects on mechanical stiffness. In our model, the critical concentration at which significant changes first occur in the stress-strain curve appears to be ∼50% of the network containing stiff springs. Only beyond this point do we begin to see the effects of the presence of stiff springs, representing collagen, on the stress-strain curves.

Figure 8.

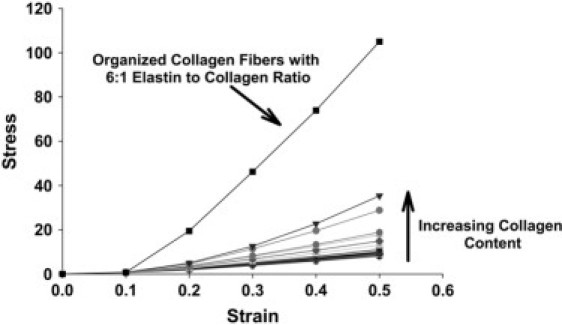
Stress-strain curves from network model simulations of varying amounts of collagen content by randomly dispersing stiffer springs in a homogeneous network. Note that the solid line with square symbols represents a simulation of a network with 6:1 normal to stiff spring ratio in which the stiff springs have been organized into fibers that transverse the network. Stress is given in arbitrary units.

While there was an increase in the amplitude and nonlinearity of the simulated stress-strain curves above the critical concentration, the increase in stress (measured at 20% strain representing the parameter A) was much less than the 3–4-fold increase seen in the experimental data for the parameter A. Thus, in the random percolation model, even having an unrealistic elastin/collagen ratio of 1:1 is unable to mimic the experimental results. In contrast to the random arrangement of stiff springs, when we organize them into a single percolating cluster of collagen fibers (correlated percolation) at concentrations similar to the EC6 samples, we are able to reproduce the observed difference in the stress-strain curve (Fig. 3). One possible explanation for the large differences in A in the ECM sheet data is that the collagen is concentrated in one region of the tissue sheet. In the case of these cultures it is known that they form multiple layers of ECM over the six-week culture period. Since the ascorbate is added for only two weeks it is possible that the collagen is only present in a specific layer or layers of the ECM. In this case, the overall ratio of elastin to collagen of the entire ECM could be 6:1, however, there would exist a layer that contains mostly collagen while others contain mostly elastin. The collagen layer would likely have fibers percolating the sample which would increase its stress-strain properties. Thus, our network modeling suggests that the increase in stiffness seen in the experimental data is more related to the spatial organization of the collagen within the ECM than it is to the absolute concentration of collagen or the ratio of collagen and elastin.

To test this model prediction, we first note that, in Fig. 1 A showing the bottom layer of the EC6 sample, it does appear that the bottom of the ECM network has a higher degree of organization. To further analyze this more quantitatively, we evaluated the variability of the structure from the bottom, middle, and top of the confocal z-stacks of the three ECM sheet types. This was done by computing the coefficient of variation (COV) of the magnitude of the two-dimensional fast Fourier-transform of 64 × 64 pixel sections of the images (full image size was 512 × 512 pixels) averaged over nonoverlapping blocks for four consecutive images in each region. The COV is expected to be larger in images that contain structural organization. We found that both the EC6 and EC10 samples had significantly larger COV than the EO sheets at all regions (p < 0.0006), implying that both of the collagen-containing sample types are more organized than the EO samples. In addition, both the EC6 and EC10 samples showed a significantly larger COV in the bottom layer when compared to the top layer (p < 0.03), implying that the collagen-containing samples had significant variability in organization through their thickness. Finally, the EC6 sample had a significantly larger COV than the EC10 sample in the bottom and middle regions (p < 0.04), indicating that the bottom and middle of the EC6 sample are more organized than the same regions in the EC10 sample. While this analysis supports the model predictions in this layered tissue in suggesting that organization is also an important contributor to the stiffness of our multilayered ECM sheets, further studies separately visualizing elastin and collagen in three-dimensional culture systems or tissues would be needed to quantitatively correlate absolute amounts, protein ratios, and fiber organization to macroscopic stiffness.

Failure properties

It is important to note that similar results regarding increased strength with increased collagen content have been reported previously. However, these data were collected on either reconstituted collagen gels (27) or samples containing mostly fibrin with little to no elastin (25). In addition, neither of these studies investigated the failure strain or the effects of enzymatic digestion on the failure properties. The failure properties of our TE constructs can be explained in view of the percolation network model. The observation that the failure stress increases with increasing relative collagen content of the samples (Fig. 5 A) is consistent with our network simulations in Fig. 8. Furthermore, since elastase does not digest collagen, the contribution of collagen to failure stress after digestion is also consistent with the network simulations. The reduction in maximum stress is due to the elimination of part of the elastinlike springs from the network. An interesting observation is that the EC10 samples had a higher failure strain than EO and EC6 samples (Fig. 5 B).

To understand this, we note that the EO samples had a mean failure strain of ∼85%,which is significantly less than the 200% for purified elastin (1). This suggests that proteoglycans links among elastin fibers significantly contribute to the failure strain but not the failure stress of the EO samples. This is consistent with what has been found in tendon (52). Indeed, removing over 90% of glycosaminoglycans from tendon did not change the modulus of the sample while the mode of failure was due to slippage of collagen and hence failure of proteoglycans links (52). Adding collagen to the EC10 samples increased the failure strain to >120%. Since collagen has a low failure strain as low as 10% (40), this observation then implies that part of the proteoglycan matrix was replaced by collagen and the overall failure strain became more similar to that of purified elastin. However, the collagen network must not form a percolation network in the EC10 samples, otherwise the failure strain would be similar to that of collagen. In the EC6 samples, the collagen network is likely to be nearly or completely percolating (see above). This should drive the failure strain closer to that of the collagen. But as Fig. 6 shows, the collagen is likely wavy even in the percolating layer. Before it starts stretching, the waves must be straightened out, which increases the failure threshold of the EC6 sheets above that of pure collagen. Furthermore, to the extent that elastase has no effect on collagen and a much smaller effect on proteoglycans than elastin (31,53), one would expect that digestion would not change this picture significantly, which is consistent with our data in Fig. 5 B.

To investigate whether there is an overriding relationship between failure properties and the stress-strain curve parameters, we correlated these properties for all three sample groups. Fig. 9 displays the correlation of failure stress and parameter A for control conditions. The overall correlation for all of the data is reasonable with an r² value of 0.40. This correlation is especially interesting when one considers that A is a measure of an entirely different phenomenon than that of mechanical failure and takes place in a distinctly different strain regime. Indeed, A is derived from the stress-strain curves only up to 25% strain while failure occurs between 70% and 120% strain, depending on the group. In addition, when correlating these parameters for each individual group a trend emerges. The strength of the correlation increases with increasing amounts of collagen and is even more correlated (r² = 0.67) in the samples with the highest amount of collagen (6:1 elastin/collagen samples), which are closer to native tissue. Another intriguing result of the correlation analysis is that failure stress and failure strain did not correlate for either all the groups taken as a whole or any of the individual groups (data not shown, r² ranged from 0.02 to 0.2). The fact that these quantities are decoupled further supports the notion that the failure stress is determined by the amount and types of fibers whereas the failure strain is significantly influenced by the proteoglycans. Taken as a whole, measurement of the stress-strain curve of tissues in vivo may allow the estimation of the stress tolerance of the material without having to test the material to failure.

Figure 9.

Correlation between failure stress and the stress-strain amplitude parameter, A, for all three groups at control conditions. Note that A is a reasonable predictor of failure stress as evidenced by the regression coefficient (r² = 0.40).

Implications for TE constructs and biomaterials

The results of this study have three important implications for the engineering of tissue constructs to be used as replacement tissues. First, there appears to be a tradeoff between increasing stiffness by increasing the relative amount of collagen and decreasing failure strain. Second, adding collagen can greatly affect the nonlinearity of the tissues quasistatic stress-strain properties and have an even greater impact on the loss modulus coefficient of the dynamic mechanical properties of the tissue. These first two factors become critically important for tissues which require some degree of both elasticity and yet resistance to rupture at high strains, such as blood vessels and lung. Based on these results the optimal design of the groups tested here would likely be the EC10 group, which displayed increased stiffness and failure stress over the EO group but not the decreased failure strain or increased mechanical nonlinearity that was present in the EC6 group. The third implication is that TE constructs used in tissues in which elastolytic injury can occur may have serious degradation in mechanical function when the collagen network construction is not contiguous, implying that organization of the collagen network is as important as how much collagen is integrated into the network. Along these lines, it might be possible to separately tune the stiffness and the failure strain of a TE construct by the addition of ascorbate in the media to cause the cells to create multiple layers of more organized collagen within the sample at specific times. In conclusion, increasing the stiffness and failure stress of TE constructs and biomaterials with the addition of collagen to better match the properties of native tissue can also lead to increased viscous losses, higher tissue mechanical nonlinearity, and lower failure strains, which can greatly affect the functionality of the construct as a replacement tissue.