Abstract
While defibrillation is the only means for prevention of sudden cardiac death, key aspects of the process, such as the intramural virtual electrodes (VEs), remain controversial. Experimental studies had attempted to assess intramural VEs by using wedge preparations and recording activity from the cut surface; however, applicability of this approach remains unclear. These studies found, surprisingly, that for strong shocks, the entire cut surface was negatively polarized, regardless of boundary conditions. The goal of this study is to examine, by means of bidomain simulations, whether VEs on the cut surface represent a good approximation to VEs in depth of the intact wall. Furthermore, we aim to explore mechanisms that could give rise to negative polarization on the cut surface. A model of wedge preparation was used, in which fiber orientation could be changed, and where the cut surface was subjected to permeable and impermeable boundary conditions. Small-scale mechanisms for polarization were also considered. To determine whether any distortions in the recorded VEs arise from averaging during optical mapping, a model of fluorescent recording was employed. The results indicate that, when an applied field is spatially uniform and impermeable boundary conditions are enforced, regardless of the fiber orientation VEs on the cut surface faithfully represent those intramurally, provided tissue properties are not altered by dissection. Results also demonstrate that VEs are sensitive to the conductive layer thickness above the cut surface. Finally, averaging during fluorescent recordings results in large negative VEs on the cut surface, but these do not arise from small-scale heterogeneities.
Introduction
While defibrillation of the heart by timely application of a strong electric shock is now recognized as the only effective means for prevention of sudden cardiac death, the mechanisms by which shocks terminate life-threatening arrhythmias have challenged researchers for many years. The last decade of investigation has brought a significant increase in our understanding of the basic mechanisms by which a shock defibrillates the heart; however, key aspects regarding the interaction between electric shock and myocardial structure remain controversial. The most sought-after among these insights is the nature of the intramural virtual electrodes (VEs).
While it is well understood that the defibrillation shock creates regions of positive and negative membrane polarization (i.e., VEs) throughout the myocardium, direct experimental recording of these has been achieved only on the surfaces of the preparation. (Note that, in this article, as well as in previously published articles (1–3), we refer to regions of positive and negative membrane polarization as “virtual electrodes,” although virtual electrodes are sometimes used to denote regions of membrane polarization away from the physical electrodes (4). The reason for our choice is that for far-field stimulation/defibrillation, regions of membrane polarization in the vicinity of the electrodes often fuse with those away from them, making it difficult to distinguish between the two.) The optical mapping technique, the only technique that provides direct recording of the changes in membrane potential during the shock, is limited in its ability to record potentials from tissue below the myocardial surface. While reports might disagree on the depth of penetration of the optical signal, it is clear that the spatiotemporal characteristics of shock-induced activity in the depths of the myocardium cannot be currently resolved; efforts to achieve this through the insertion of an optical fiber into the wall (optrode), although promising, remain at a nascent stage (5,6), providing information about the shock-induced change in transmembrane potential at the location of the optrode only.
The importance of elucidating the nature of and the mechanisms by which the intramural VEs are generated is underscored by the fact that it is believed that there is a dramatic difference between the magnitude and pattern of shock-induced VEs in the surface layers and in the depth of the myocardium. As determined by simulation studies (7,8), these differences emanate from the different mechanisms that govern surface polarization and polarization in the tissue bulk. Such VE differences have been shown to result in different postshock electrophysiological behavior on the surfaces and in depth (1,9). Thus, recording intramural VEs remains a key issue in defibrillation research.
In a series of studies, Fast and co-workers (10–13) attempted to record intramural VEs by using isolated coronary-perfused left-ventricular (LV) wall preparations excised from pig hearts. The effect of a uniform-field shock was examined on the transmural (cut) surface of the wedge preparation, using both impermeable and permeable boundary conditions (cut surface in contact with a glass window, and cut surface in contact with perfusing bath and ∼2 mm away from the glass, respectively). The studies found surprising results; namely, that for strong shocks (∼28 V/cm and above), the entire transmural surface was negatively polarized, regardless of shock polarity or boundary conditions. While wedge preparations and recordings from the transmural (cut) surface are routinely used in examining the transmural electrophysiological properties of the ventricular wall (14–16), it remains unclear whether shock-induced VEs on the cut surface faithfully represent VEs in the intact cardiac wall. A simulation study (17) has demonstrated that fibers terminating at an angle to a surface (rather than being parallel or perpendicular to it) result in an additional shock-induced polarization on that surface, thus differences could be expected. However, these could be diminished or even alleviated by the orientation of the applied field with respect to fiber orientation (7). Furthermore, reasons for the negative polarization throughout the cut surface have been speculated about, but never fully investigated.
The goal of this study was to examine, by means of bidomain modeling and computer simulations, whether VEs recorded on the cut surface of a ventricular wedge represent a good approximation to VEs recorded from the depth of the intact wall. Furthermore, we aimed to explore the possible mechanisms that could give rise to negative polarization on the cut surface. To achieve the aims of the study, we used a model wedge preparation, in which the fiber orientation with respect to the direction of the applied electric field could be controlled, and where the transmural cut surface was subjected to both permeable and impermeable boundary conditions. Small-scale structural mechanisms for polarization were also considered. To determine whether any distortions in the recorded VEs arise from the averaging properties of the optical mapping technique, we also used a novel model of optical mapping (18), employed in our previous study of shock-induced VEs (19). This study thus provides a comprehensive analysis of the origin of the intramural VEs and their interpretation in the experimental optical recordings.
Methods
Wedge preparation
Fig. 1, left panel, presents a sketch of the experimental LV wedge preparation as used in the study by Fast and co-workers (10). Preparations were placed into a perfusing chamber. A piston in the chamber pushed the preparation toward a glass plate, through which transmembrane potentials on the cut surface were optically mapped. The LV wedge was paced via an electrode placed at the preparation edge (Fig. 1, STIM). The flattened LV preparation was subjected to rectangular shocks of duration 10 ms applied via two large mesh electrodes located at opposite borders of the tissue-bath chamber (uniform applied field E). To examine the effect of permeable versus impermeable boundary conditions on VEs from the cut surface, the piston released the wedge, moving it ∼2 mm away from the glass plate (10).
Figure 1.
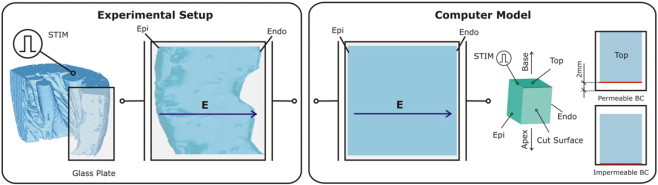
Schematics of the experimental setup in the studies by Fast and co-workers (10–12) and of the computer model. In both model and experiment, the wedge preparation was paced via an electrode located at the preparation edge (STIM). Rectangular shocks were delivered via two large mesh electrodes located at opposite borders of the tissue-bath chamber. The direction of the applied electric field E is indicated by the arrows. The wedge model is of dimensions 1.2 × 1.2 cm of the endo- and epicardial surfaces, and a transmural thickness of 1 cm. The computer model panel also presents a schematic of how permeable and impermeable boundary conditions were implemented on the cut surface of the wedge in accordance with the experimental procedure.
Similar preparation was used in the simulations here (Fig. 1, right panel). A rectangular tissue wedge of dimensions 1.2 × 1.2 cm of the endocardial and epicardial surfaces and a transmural thickness of 1 cm was surrounded by 1-mm-thick perfusing bath layer on all sides. The model, both tissue and bath, was placed between two large plate electrodes that faced endo- and epicardium. Rectangular shocks of varying strength and of duration the same as in the experiments were delivered through these shock electrodes, following pacing at a location equivalent to that in the experiment (Fig. 1).
Boundary conditions on the transmural surface were altered in the simulations by either moving the preparation such that the cut surface became in contact with the isolating boundary of the chamber (impermeable, i.e., no-flux boundary conditions) on the cut surface, or moving it further away from that boundary such that a layer of perfusate of thickness the same as in the experiment, 2 mm, covered the cut surface (Fig. 1, right panel). In addition, in the simulations, the thickness of this volume conductor layer over the cut surface was varied at intermediate steps, 125, 250, 500 μm, and 1 mm, to explore the effect of uncertainty in the thickness of the perfusing-bath layer under the glass plate in the experiment.
As in the experiment (10), shocks in the simulations were delivered during the action potential plateau of the last paced activation (coupling interval of 60 ms after the onset of the last pacing pulse), in order that VEs were not masked by the flow of sodium current. Shocks of various strengths were given; however, the majority of the results presented here are for shocks of 28 V/cm and higher, since, only for these high shock strengths, negative polarization encompassed the entire cut surface of the wedge. The pattern of VE, i.e., the spatial distribution of the change in transmembrane potential Vm, ΔVm, on the transmural surface was determined as the difference between a linear regression fit of the action potential plateau before the shock and the Vm value at the end of the shock at each location on that surface.
In the wedge model, fibers rotated linearly in the transmural direction, from −60° at the endocardium to +60° at the epicardium (20) (angle, α, is measured with respect to the y axis; see Fig. 2), with fibers in the exact middle of the wedge (midmyocardium) orthogonal to the cut surface (Fig. 2). This means that the fibers encountered the cut surface on the endocardial side at an angle of −60°, and at an angle of +60° at the epicardial surface, with the fiber angle monotonously changing between these two values and passing through 0° at the midmyocardial line of the cut surface (dark blue line in Fig. 2). Furthermore, to examine the degree to which fiber orientation along the cut surface influenced ΔVm, two additional wedges were constructed, where fibers were assumed to be parallel or orthogonal to the cut surface at every point on that surface.
Figure 2.
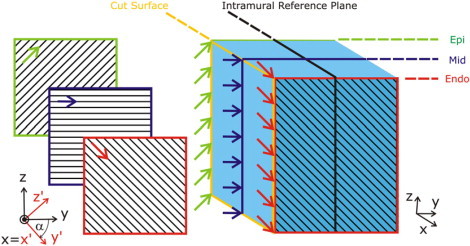
Fiber orientation in the wedge model. Fibers rotate linearly in the transmural direction, from −60° at the endocardium (red lines) to +60° at the epicardium (green lines). The angle of rotation, α, is measured with respect to the y axis. Fibers in the middle of the wedge (midmyocardium, mid, dark blue lines) are orthogonal to the cut surface (yellow outline). Patterns of shock-induced VE are compared on the cut surface and on a intramural reference plane (thick black outline). The local coordinate system (the coordinate system attached to the fibers) is denoted x′,y′,z′ (shown in red and aligned with the fibers on the endocardium), while the global coordinate system is x,y,z (shown in black).
Bidomain representation of the tissue
Transmembrane potentials in the model were calculated based on the spatial distributions of both intracellular and extracellular potentials (bidomain representation of the myocardium). The bidomain equations are the following set of differential equations,
| (1) |
| (2) |
| (3) |
with
| (4) |
| (5) |
| (6) |
where Φi and Φe are intracellular and extracellular/interstitial potentials, respectively, and Vm is transmembrane voltage; Im is transmembrane current density and Ie is current density of the external electrical source (the defibrillation shock); Gi and Ge are conductivity tensors in the intra- and extracellular spaces, respectively; Gb is the isotropic conductivity of the fluid in which the preparation is immersed; Cm is membrane capacitance per unit area and β is surface to volume ratio; and denotes the membrane model state variables, their change being represented by the function g.
Incorporating small-scale resistive heterogeneities in the wedge model
The studies by Fast and co-workers (10–13) suggested that resistive heterogeneities in the myocardium arising from microscopic discontinuities in tissue structure, such as intercellular clefts and collagen septa, could underlie the overwhelming negative polarization observed on the cut surface of the wedge. To test this hypothesis, a subset of simulations was conducted with the eigenvalues of the intracellular conductivity tensor Gi varied stochastically of up to 50% of their nominal values, as described in Plank et al. (21).
Membrane kinetics representation and numerical considerations
Membrane kinetics were represented by the Puglisi-Bers model of the rabbit ventricular action potential (22), augmented for defibrillation (23). The use of this membrane model was particularly important for this study, since the membrane model augmentations ensured that the experimentally observed negative bias, in the asymmetry of transmembrane potential changes (ΔVm) induced by strong shocks on the plateau of the action potential (10,24–28), is reproduced by the membrane model.
The computational domain, including wedge preparation and perfusing bath, was discretized at a spatial resolution of 125 μm. Further detail regarding the numerical and computational aspects of the study is described elsewhere (37).
Simulating optical mapping of the transmural surface
To compare the results of the simulations regarding VEs on the cut surface of the wedge with those obtained via optical mapping by Fast et al. (10), three-dimensional Vm distributions throughout the wedge were used as an input to software developed to synthesize optical maps. As in our previous publication (19), the distribution of photon density after uniform epicardial illumination was calculated throughout the wedge preparation using the steady-state photon diffusion equation. It was then convolved with the local value of Vm to represent fluorescent emission intensity. The photon diffusion equation was again solved to calculate photon density at the emission wavelength. Fick's Law was used to relate the gradient of this photon density at the imaged surface to the photon flux recorded by the detector (Vopt). Optical signals were thus synthesized solely on the transmural (cut) surface. Tissue optical properties at illumination and emission wavelengths were represented by penetration depths of 0.90 mm and 2.10 mm, respectively, as measured in experiments (18). The advantage of this approach to simulating the optical maps is that it takes into account photon scattering in three dimensions, rather than only in the tissue depth, as in earlier attempts to simulate optical mapping (29).
Results
Are VEs on the cut surface the same as in the depth of the intact wall?
Consistent with the goals of this study, in this section we examine whether VEs recorded on the cut surface of a ventricular wedge represent a good approximation to VEs recorded from the depth of the intact wall for the experimental setup used in Fast and co-workers (10–12). Specifically, we compare VEs on the cut surface of the wedge model with the VEs on an intramural reference plane (Fig. 2). In this analysis, we assume that tissue remains viable, and of the same properties all the way to the cut surface.
An answer to the question posed here can be obtained by examining the set of bidomain equations in Methods. During the plateau phase of the action potential, right before the shock is delivered, it is reasonable to ascertain that there are no gradients in Vm, Φi, or Φe and the net transmembrane current density Im is zero throughout the 1.2 × 1.2 × 1 cm wedge. The shock delivery establishes a potential distribution, termed the primary potential distribution (30), . Depending on the type of shock delivery system, either Ie becomes nonzero (current stimulation) or Φe at the location of the shock electrodes is fixed at a particular value via the boundary conditions to the left-hand side of Eq. 3 (voltage stimulation).
Rewriting Eq. 1 and substituting Φe with
| (7) |
reveals that an activating function (30), S, which is a function of Φe, acts to induce changes in Vm. These changes in Vm, in their turn, affect, via the transmembrane current density Im, the extracellular potential distribution through the relationships in Eq. 2, causing an additional (secondary) change in extracellular potential, . Thus, if Eqs. 1 and 2 are solved simultaneously, the resulting extracellular potential is a superposition of these two potential components, i.e., . Sobie et al. (30) demonstrated that during a strong shock can be neglected. Thus, shock-induced changes in Vm are driven by only. Therefore, we examine here whether the effect of the primary potential distribution is the same on the cut surface and on the intramural reference plane.
As shown by Sobie et al., the activating function S can be decomposed into two components,
| (8) |
which reveals that field-induced changes in Vm are driven either by the component S1 (the spatial variation in the intracellular conductivities, ∇ · Gi, weighted by the applied electric field ) or by the component S2 (the spatial variation in the applied electric field , weighted by the intracellular conductivity tensor Gi).
The bidomain conductivity tensors in the global coordinate system x,y,z (Fig. 2), Gi and Ge, are spatially dependent functions since the fibers change direction throughout the wedge (they rotate transmurally). In a coordinate system aligned with the local fiber direction (the primed coordinate system), the conductivity tensors and are of the following (diagonal) form,
| (9) |
assuming that the two conductivity components in direction transverse to the fibers are the same, i.e., gt. The longitudinal conductivity component gl is typically larger than the gt component for both the intra- and extracellular spaces. The position of the conductivity components on the diagonal reflects the choice of the coordinate system in our case, as shown in Fig. 2.
A conductivity tensor in the global coordinate system is typically obtained from the (known) conductivity tensor in the local (primed) coordinate system
| (10) |
employing knowledge regarding the change in fiber orientation throughout the preparation, i.e., knowing the matrix A. Since the fibers in the wedge rotate transmurally from endo- to epicardium (in direction x, see Fig. 2), the transformation matrix A is the following function of the fiber angle α:
| (11) |
Therefore, the conductivity tensor expressed in the global coordinate system becomes
| (12) |
The structure of the matrix G is therefore
| (13) |
where a, b, and c are functions of x defined as
and A, B, and C are notations for the matrix components in Eq. 13.
The two components of the activating function can then be expressed as
| (14) |
| (15) |
Since the defibrillation electrodes here are large plate electrodes, during the shock the applied electric field is spatially homogeneous and all field lines are oriented along the x axis (i.e., is constant). Therefore, the function S2 is zero everywhere and has no contribution to Vm either on the cut surface or on the intramural reference plane. Inspection of Eq. 14 similarly reveals that since the y and z components of ∇Φe are zero because of the nature of the applied field, the only nonzero component of the activating function S1 is . However, since this component is a function of x only, it does not contribute to differences in Vm on the cut and the intramural planes.
Thus, with a uniform applied field, in this model setup, as well as in the experimental setup by Fast and co-workers (10), no differences are expected between VEs on a cut surface, on which impermeable boundary conditions are enforced, and on a intramural reference plane parallel to it, provided that the tissue properties are the same throughout the wedge (not affected by the process of excising the wedge).
We next conducted numerical simulations to confirm the findings of the analysis above. There are several factors that might cause the numerical results to differ from the analytical analysis. These include:
-
1.
Possible nonzero contribution of for this setup, which is different from that evaluated by Sobie et al. (30).
-
2.
Nonuniformity in the applied electric field arising from the presence of both bath and tissue between the electrodes.
-
3.
Finite dimensions of the wedge (in units of space constants, ≈16 longitudinal length constants, λl, and ≈44 transverse length constants, λt).
With three different sets of fiber orientations in the wedge (rotating from endo- to epicardium, or parallel or perpendicular to the cut surface) and impermeable boundary conditions imposed, the VE pattern on the cut surface was similar between the three cases for all shock strengths tested (see Fig. 3) for an example of a 28 V/cm applied field). In all three wedge models, for the direction of the applied field as shown in the figure, ΔVm distribution exhibited predominant positive polarization with negative ΔVm only in immediate proximity of the boundaries. Differences between VEs on the cut surface include the magnitude of the positive ΔVm and penetration of the negative polarization in the tissue.
Figure 3.
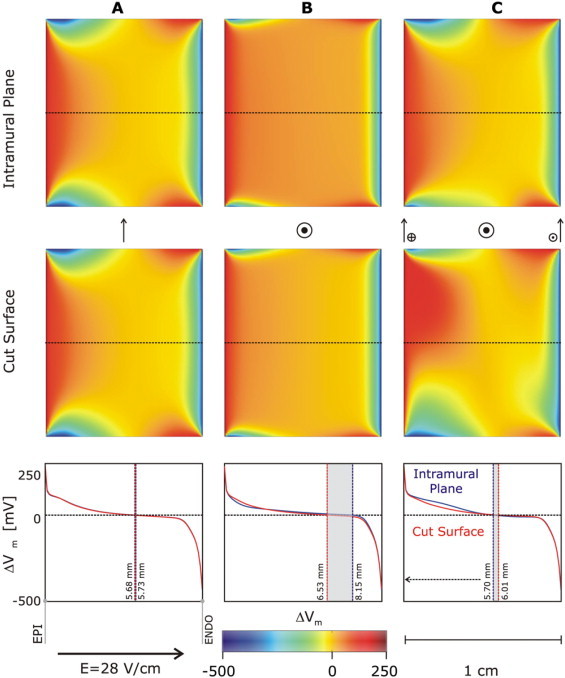
Maps of the shock-induced change in transmembrane potential, ΔVm, at the end of the 10-ms shock on the intramural reference plane (top row) and on the cut surface (middle row) for three wedge preparations with different fiber orientation. (A) Fibers oriented parallel to the cut surface (arrow). (B) Fibers oriented perpendicularly to the cut surface (circle and dot). (C) Fibers rotating transmurally as shown in Fig. 2. In all three cases, impermeable boundary conditions are enforced on the cut surface. Field strength, E, is 28 V/cm. Plots of ΔVm profiles (red and blue lines) along the dotted line (direction epi- to endocardium) in the middle of the ΔVm maps are presented at the bottom. Vertical lines delineate areas of zero ΔVm and their locations with respect to the epicardium.
VE patterns on the cut surface and on a plane parallel to it within the intact myocardium were nearly identical regardless of fiber orientation, with only subtle differences evident in the ΔVm maps. These differences were the largest in the case of rotational (asymmetrical) fiber orientation, where, in contrast to the other two cases, the VE patterns at the bottom and top halves of the cut surface differed (Fig. 3). Plots of ΔVm along the central dotted lines on the cut surface and the intramural reference plane are shown in the bottom graphs; crossover from positive to negative ΔVm occurs in all cases in the range 5.60–6.15 mm from the epicardial surface (see Fig. 3, bottom panel). Clearly, differences between graphs are the largest in Fig. 3 C. Since differences are relatively small, we then conclude, consistent with the analytical analysis above, that in the wedge model, when the applied field is spatially uniform and impermeable boundary conditions are applied to the cut surface (via a glass plate, for instance), then regardless of fiber orientation, VEs obtained from the cut surface fairly faithfully represent those on an intramural plane parallel to it, as long as the electrophysiological properties of the tissue in the wedge remain unaffected by the dissection.
Do permeable boundary conditions alter the similarity between VE patterns on the cut surface and on an intramural reference plane?
With a 2 mm layer of volume conductor added over the cut surface, as shown in Fig. 1, right panel (permeable boundary conditions, same thickness as in the experiment (10)), intramural VEs on the reference plane remained identical to those shown in Fig. 3 (top row), for all fiber orientations and shock strengths tested. Fig. 4 presents a comparison between VEs on the cut surface for the two types of boundary conditions and the same shock strength, 28 V/cm; the wedge has a rotational fiber orientation. Shown are maps of ΔVm, a plot of ΔVm along the centrally located line between endo- and epicardium (as in Fig. 3), and individual traces of shock-induced responses on the plateau of the action potential at numbered locations along this line. Side views of VEs on the endo- and epicardial surfaces of the wedge are also presented. Note that for each boundary condition (either blue or red deflections in traces), the negative deflections were always larger than the positive, as expected from the modifications implemented in the membrane model (23), and consistent with experimental findings (24–28).
Figure 4.
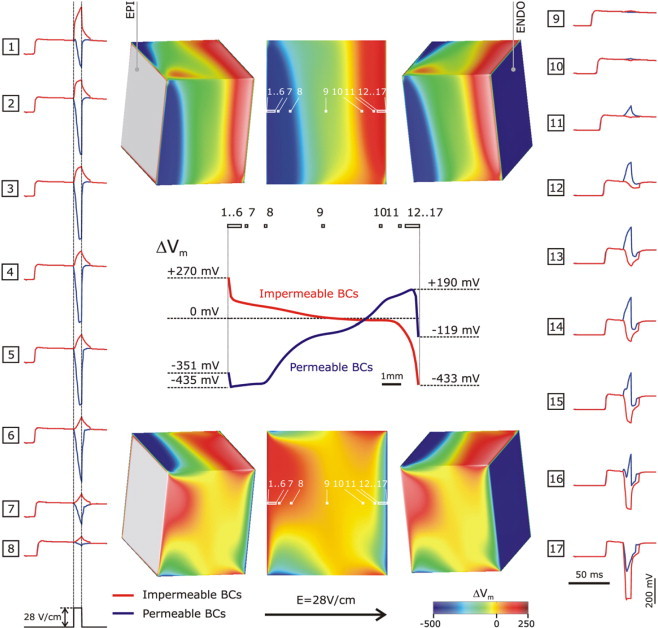
Maps of the shock-induced change in transmembrane potential, ΔVm, at shock-end on the cut surface for impermeable (top row) and permeable (bottom row) boundary conditions. Shock strength is 28 V/cm; fiber orientation is rotational (as in Fig. 2). Side views of ΔVm distributions on the endo- and epicardial surfaces of the wedge are also shown. Middle panel shows a plot of ΔVm profiles along the centrally located horizontal line (endo- to epicardium) in the middle of the ΔVm maps. Individual traces of shock-induced responses on the plateau of the action potential at numbered locations along the same line are shown in vertical columns (locations denoted, in white, on the ΔVm maps). Red lines refer to impermeable boundary conditions, while blue ones refer to permeable.
Major differences in shock-induced Vm distributions on the cut surface were observed upon enforcing permeable boundary conditions (compare top to bottom rows in Fig. 4). Tissue at and in proximity of the endocardium experienced negative polarization that penetrated more than half of the wedge width. Along the midline, the most negative ΔVm, −435 mV was observed at a distance of z = 125 μm away from the epicardial surface, with ΔVm remaining almost at that level for additional ∼1.8 mm, crossing the zero level at 7.21 mm before changing sign (Fig. 4). At the endocardium, ΔVm was also negative (−119 mV), but rapidly switched sign with a maximum positive polarization of 190 mV at a distance of 250 μm from the endocardial surface (see Fig. 4, blue traces 16 and 17). Clearly, exposing the cut surface to a perfusing bath layer changed not only the sign of the polarization in the vicinity of the respective surface (endo- or epicardium), but also imposed a nonmonotonic ΔVm profile in the direction of endo- to epicardium. However, the cut surface did not become of predominantly negative polarization, as observed in the experiments of Fast and co-workers (10–13,27). On the contrary, it retained a region of strong positive ΔVm with a maximum magnitude that was 44% of the maximum negative ΔVm magnitude.
While a 2-mm conductive layer was used to represent impermeable boundary conditions in the experiment, this layer is still fairly thin for all practical purposes. We conducted additional simulations with a much thicker conductive layer and observed minimal changes in VEs (data not shown).
Fig. 5 presents the progressive changes in the VEs at the cut surface of the wedge for intermediate (0–2 mm) thickness of the bath layer, for the same wedge model and field strength as in Fig. 4. As the thickness of the layer is increased, negative polarization begins to occupy larger parts of the surface, penetrating predominantly from the bottom left corner. Positive polarization retracts from the epicardium toward the endocardium. The change in the sign of polarization is particularly evident in the ΔVm plots along the midline through the surface. These results demonstrate that while VEs are sensitive to the thickness of the conductive layer over the cut surface of the wedge, there is no likelihood of observing predominantly negative polarization on that surface for any thickness of that layer.
Figure 5.
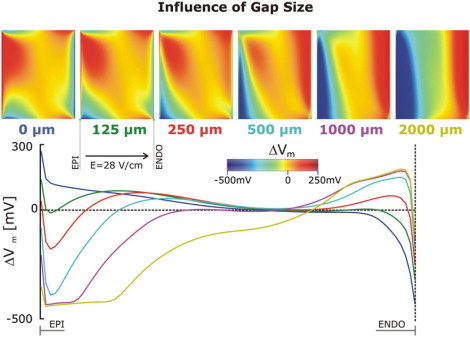
Maps of the shock-induced change in transmembrane potential, ΔVm, at shock-end on the cut surface of the same wedge as in Fig. 4 as the thickness of the bath layer over it is increased from 0 to 2 mm, together with a plot of ΔVm profiles along the centrally located horizontal line (endo- to epicardium) in the middle of the ΔVm maps. The different colors correspond to the thickness of the bath layer as indicated under each ΔVm map.
Additional factors affecting VEs on the cut surface
To assess the effect of small-scale resistive heterogeneities inherent to myocardial structure on VEs on the cut surface, and to determine whether their presence could lead to the formation of a predominantly negative polarization on that surface, stochastic fluctuations in the conductivity values at each element in the computational mesh were incorporated as described in the Methods. The results of the simulations for the same field strength, 28 V/cm, are shown in Fig. 6, top row. VEs for both permeable and impermeable boundary conditions are shown; the VE patterns are characterized with fluctuations in ΔVm superimposed over the large-scale VEs arising from the geometry of the preparation. Comparison with the respective ΔVm maps on the cut surface shown in Fig. 4 reveals that there is no significant change in the overall appearance of the VEs for both sets of boundary conditions. This is confirmed by the middle graph in the top row of Fig. 6, where the potential fluctuations are superimposed over the baseline large-scale ΔVm profile, and is consistent with previous theoretical results (30). These results demonstrate that small-scale resistive heterogeneities in the myocardium could not be responsible per se for the appearance of predominantly negative polarization on the cut surface.
Figure 6.
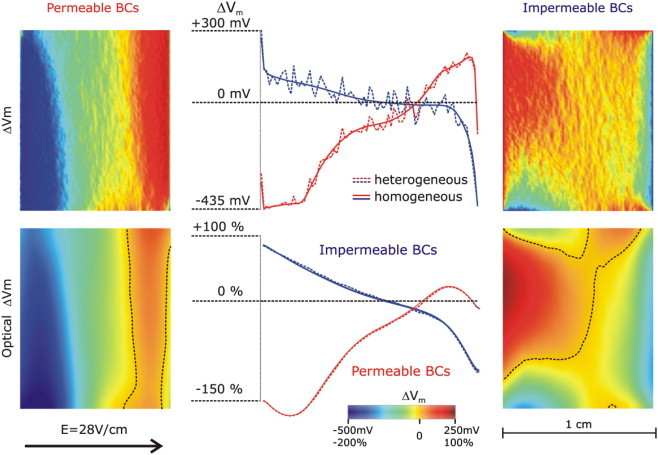
(Top row) Effect of small-scale resistive heterogeneities on the shock-induced ΔVm distribution on the cut surface of the same wedge as in Fig. 4 for permeable and impermeable boundary conditions (right and left panels, respectively). Middle panel shows a plot of ΔVm profiles, with and without small-scale heterogeneities, along the centrally located horizontal line (endo- to epicardium) in the middle of the ΔVm maps. (Bottom row) Optical maps of ΔVm (ΔVopt) on the cut surface for permeable and impermeable boundary conditions (right and left panels, respectively). Dotted lines in the maps are zero iso-fluorescence lines. Middle panel shows a plot of ΔVopt profiles, with and without small-scale heterogeneities, along the centrally located horizontal line (endo- to epicardium) in the middle of the ΔVopt maps. Optical potentials are normalized as percent of normal action potential magnitude. Shock strength is 28 V/cm; fiber orientation is rotational (as in Fig. 2).
In the experiment, shock-induced VEs on the cut surface were recorded via optical mapping. To determine whether distortion in the optical signal resulting from three-dimensional photon scattering in the myocardium could result in a negative bias in the recorded VEs on the cut surface, optical maps were calculated, as described in the Methods, for the two wedge models used in Figs. 4 and 5 (i.e., without and with small-scale heterogeneities, respectively) and the two sets of boundary conditions. Fluorescent maps of ΔVm are presented in Fig. 6, bottom row. As a result of the optical mapping, small-scale fluctuations in ΔVm were averaged out, resulting in identical optical maps of ΔVm for the wedge models with and without heterogeneities (see superimposed ΔVm profiles in the middle of bottom row in Fig. 6). Interestingly, however, the optical maps exhibit a significant shift toward negative potentials; the positive polarization occupies a much smaller area (≈31%) of the cut surface (dotted lines represent zero ΔVm). In the case of permeable boundary conditions, the maximum positive ΔVm (as a fraction of maximum negative ΔVm) is significantly decreased, to 13%. Thus, based on these simulations, we conclude that membrane potential averaging that takes place during fluorescent recordings of Vm is the only factor that could lead to the appearance of large regions of negative polarization on the cut surface, particularly in the case of permeable boundary conditions.
Fig. 7 examines whether increasing shock strength (from 28 to 40 V/cm as an example) can augment the negative bias in optical ΔVm, ΔVopt, on the cut surface. Plots of ΔVopt along the endo-to-epi midline across the cut surface (left) and a map of the 40 V/cm-shock induced ΔVopt with zero crossing lines for both shock strengths superimposed demonstrate that, with the increase in shock strength, the area experiencing positive ΔVopt did not change appreciably, although the magnitude of the negative ΔVopt increased. Thus, we conclude that while three-dimensional photon scattering contributes significantly to the appearance of negative polarization on the cut surface of a wedge (particularly with permeable boundary conditions enforced), it does not result in negative ΔVopt over the entire surface.
Figure 7.
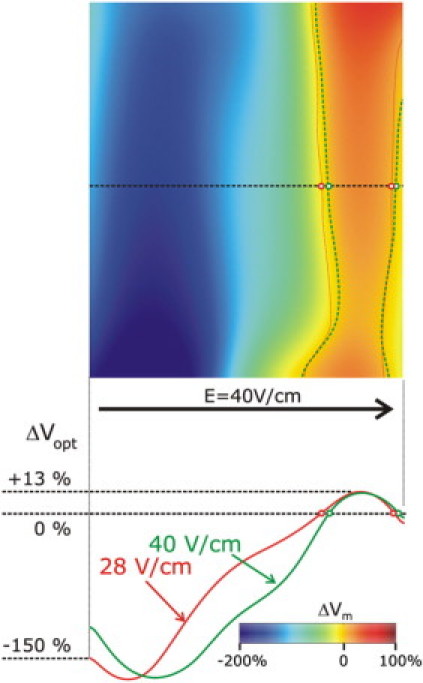
(Top) Map of ΔVopt on the cut surface for a shock of 40 V/cm strength. Green (40 V/cm shock) and red (28 V/cm shock) dotted lines refer to locations where ΔVm changes sign. (Bottom) Effect of the increase in shock strength from 28 V/cm to 40 V/cm on the optical ΔVopt profile along a centrally located horizontal line (endo- to epicardium) on the cut surface of the same wedge as in Fig. 4, with permeable boundary conditions. Optical potentials are normalized as percent of normal action potential magnitude.
Discussion
Intramural versus surface VEs in the isolated wedge preparation
In a series of optical mapping studies, Fast and co-workers (10–13) attempted to assess the distribution and pattern of intramural VEs in the porcine LV wedge preparation induced by uniform-field defibrillation shocks, thus intending to provide insight into a key aspect regarding the interaction between electric shock and myocardial structure. In the studies, the shocks were delivered in the epi-to-endocardial direction during the action potential plateau, and optical mapping was performed from the cut surface of the preparation, through a glass plate serving as an insulator. The underlying assumption in these experiments was that shock-induced VEs on the cut surface are exposed by the dissection and thus faithfully represent VEs in the intact cardiac wall. This assumption possibly stems from the fact that numerous studies have routinely used transmural recording from the cut surface to elucidate electrophysiological mechanisms (14–16). However, the question whether shock-induced VEs on the cut surface faithfully represent VEs in the intact cardiac wall has never been addressed. The answer to this question cannot be directly inferred from the utility of transmural recordings from the cut surface during pacing and arrhythmias since shock-induced responses are different on the surface of a preparation and in its bulk (7,8). While these differences could be diminished by the use of the insulating glass plate, the degree to which this is true remains to be determined. This necessitates direct assessment of the differences between intramural VEs and these recorded from a surface exposed by dissection. Such analysis is provided by this study. Since true assessment of intramural VEs cannot be achieved by the current optical mapping techniques, which record activity predominantly from the surface of the preparation, we conducted computer simulations of the experimental conditions, including simulations of fluorescent recordings.
Both analytical considerations and results from the numerical simulations presented here demonstrate that for (nearly) uniform-field shocks delivered in the epi-to-endocardial direction, the distribution of VEs on the cut surface, on which impermeable boundary conditions are enforced, fairly faithfully represents that on an intramural plane parallel to the cut surface, as long as the electrophysiological properties of the tissue in the wedge are not altered by the dissection. Whether dissection alters tissue properties near the cut surface enough to affect VEs remains unclear. An editorial by Efimov (31) suggests that this might be indeed the case, thus distortion of surface VEs might be expected. In an attempt to address this issue, a follow-up study by Sharifov and Fast (32) repeated the experiments but mapped optically the epicardial rather than the cut surface. We ascertain that in this case the correspondence between VEs on the epicardium and on an intramural plane parallel to it will remain valid, since the latter is largely independent of fiber orientation, as demonstrated by results presented in Fig. 3.
It is important to underscore that the correspondence documented in this study between VEs on a surface and on an intramural reference plane is only valid if the applied electric field is spatially uniform or nearly-uniform, with impermeable boundary conditions enforced on the surface. Any significant deviation from field spatial uniformity, such as introduced by a different configuration of the shock electrodes (other than large parallel plates), would markedly alter the VEs throughout the preparation (33) and render VEs on the surface dissimilar to those intramurally.
Effect of boundary conditions on VEs on the cut surface
The study of Fast et al. (10) also included an examination of the effect of boundary conditions (permeable versus impermeable) on the pattern of VEs on the cut surface. The study concluded that lifting the glass plate ∼2 mm away from the cut surface had virtually no effect on the recorded optical potential distribution. This result is in stark contrast with the findings in this study. Our simulations demonstrate that a 2 mm layer of perfusate over the surface of recording alters significantly the distribution of ΔVm on that surface. Clearly, we conclude that if the glass plate is lifted from the imaged surface, the correspondence of VEs on the surface to those on an intramural reference plane, as established above, is no longer maintained. Our results, as presented in Fig. 5, also demonstrate that a conductive layer of thickness as small as 500 μm is sufficient to introduce major differences in VEs in the cut surface.
Our findings are consistent with those from a body of simulation research (17,34) demonstrating the large impact a conducting medium surrounding the tissue has on shock-induced VEs on the tissue-bath interface. An elegant simulation/experimental study by Entcheva et al. (35) found that pressing a glass plate to the surface of the heart changed the pattern of the VEs after an ICD shock, mainly by increasing spatial nonuniformity in ΔVm. Similar results are presented in Fig. 5 here. The discrepancy between the results by Fast et al. (10), on one side, and by us and others, on the other, indicate that cellular damage caused by dissection might be the root of the matter. Indeed, viable myocardial cells beneath the surface layer are most likely uncoupled from damaged myocardium and thus have different electrophysiological properties than cells in the intact myocardium. As stated by Efimov in the aforementioned editorial (31), damaged layers most likely isolate viable tissue from the effects of the bath, diminishing its effects on surface VEs. In this study, we did not attempt to model the effect of tissue damage on VEs on the cut surface. A careful examination of the literature regarding the effects of tissue damage on electrophysiological and structural properties of the tissue revealed a paucity of data that can be used as an input to the electrophysiological model and the model of the optical maps. Assembling a model of shock-induced responses in damaged tissue and the corresponding optical maps without the necessary input would have been highly speculative and thus unlikely to resolve the issue regarding the discrepancy between our results and those of Fast et al.
Negative polarization at high-strength shocks: artifact or reality?
The optical recordings of the surface shock-induced polarization in the porcine LV wedge found that for strong shocks (∼28 V/cm and above), surprisingly, the entire imaged surface was negatively polarized, regardless of shock polarity or boundary conditions. Throughout the series of studies, Fast and co-workers consistently speculated that the predominantly negative polarization at high shock strengths was due to microscopic discontinuities in tissue structure. Two reasons were given to support this argument. First, as stated in Sharifov and Fast (32), the authors maintained that VEs on the imaged (cut) surface “were not a result of fiber rotation, because it occurs predominantly in the plane parallel to the epicardial surface,” thus these can only be due to microscopic heterogeneities, such as blood vessels, collagen septa, and intercellular clefts. The second reason involved distortions inherent to optical mapping: since there is a negative bias in the transmembrane potential transients induced by high-strength shocks during the action potential plateau (23,26–28) (shocks ∼28 V/cm and above), spatial averaging of fluorescence emanating from microscopic VEs results in predominantly negative ΔVopt over the entire imaged surface.
This simulation study evaluated the proposed mechanisms by dissecting the various contributions. First, our results demonstrate that, in the wedge preparation, despite the fact that fiber rotation occurs predominantly in the plane parallel to the endo- and epicardial surfaces, there is a significant nonzero ΔVm on the transmural surface. Thus, one cannot assume that VEs on the cut surface arise from microscopic heterogeneities only—they are likely also to arise from large-scale effects, such as the geometry of the preparation.
Second, to verify whether negative bias in the cellular transmembrane potential transients induced by high-strength shocks during the action potential plateau (transients as shown in Fig. 4) could indeed result in distortion in ΔVopt maps toward the negative polarization, in this study simulations were conducted with our recent model of three-dimensional optical mapping (19). The results (Fig. 6) confirmed the expectations. The findings of the optical mapping model here are consistent with the results of a recent combined experimental/simulation study of optical fluorescence associated with defibrillation shocks in the intact rabbit heart performed by our group (18).
Adding small-scale heterogeneities to the wedge resulted in small-scale VEs superimposed over the large-scale VEs throughout the wedge, similar to previous results (21,36). However, when optical maps of the response of the wedge with small-scale heterogeneities were calculated, they turned out identical to those from the model without them for all shock strengths. Thus, we conclude that predominantly large-scale VEs give rise to the optical ΔVm patterns. This is not to say that small-scale VEs are not part of the response of the myocardium to the shock; our simulations only demonstrate that they do not contribute to the optical maps recorded at the standard resolution typically used for studying arrhythmias and defibrillation. Our findings are consistent with those of Sharifov et al. (12), who examined the shock-induced response at action potential plateau at two resolutions of the optical mapping system—i.e., low, 1.2 mm/diode (the resolution used in all studies by Fast and co-workers referred to in this study), and high, 0.11 mm/diode. The authors were able to demonstrate presence of small-scale positive and negative VEs at high resolution, and predominantly negative VEs at low resolution for shocks of high strengths.
In these optical mapping simulation results, negative polarization encompassing the entire imaged surface, as found by Fast and co-workers, was never obtained. As demonstrated by Fig. 7, this is independent of shock strength. Even for very high shock strengths, a small area of positive polarization of low magnitude was always present in the optical maps. We speculate that the cell damage caused by dissection might again be the reason for the discrepancy: it can alter not only the electrophysiological properties of these cells, but also cause additional distortions in the optical mapping signal. Indeed, a damaged layer might have different optical parameters than normal myocardium. Since our model of optical mapping uses optical parameters (diffusivity and coefficient of absorption) obtained experimentally for healthy tissue (18), our optical maps cannot reproduce fluorescence recordings from a surface that has cell damage. Our study clearly indicates that negative polarization encompassing the entire imaged surface is, most likely, an artifact of both the optical mapping technique and the tissue damage inflicted by dissection.
Implications of the study
In this article, we do not make a prediction or even suggestion per se regarding what type of VEs, whether small-scale or large-scale, contribute to the success or failure of a defibrillation shock. Predictions and speculations have been made previously (8,10), but in the absence of an adequate experimental technology to record the three-dimensional transmural transmembrane potential distribution in the ventricles, it remains difficult to obtain a concrete evidence regarding behavior hidden in the ventricular wall. Instead, this article focuses on the formation of VEs during the plateau of a paced activation, a protocol used extensively to study the nature of the shock-induced VEs in cardiac tissue (3,10,13), to offer a reconciliation between simulations and experiments and to provide a detailed analysis and interpretation of experimental results on VEs in ventricular wedges. It is our expectation that such analysis and “deconstruction” of the mechanisms underlying an optical recording of VEs would be of paramount importance not only in uncovering the mechanisms of defibrillation but in a whole range of electrophysiological studies.
Acknowledgments
This work was supported by Marie Curie Fellowship grant No. MC-OIF 040190 from the European Commission and the SFB grant No. F3210-N18 from the Austrian Science Fund FWF (to G.P.), and National Institutes of Health awards No. HL063195 and HL082729 (to N.A.T.). The authors acknowledge support provided by the funders of the Integrative Biology project: the Engineering and Physical Sciences Research Council (Ref. No. GR/S72023/01) and IBM.
Footnotes
Editor: David A. Eisner.
References
- 1.Rodriguez B., Eason J., Trayanova N. Differences between left and right ventricular anatomy determine the types of reentrant circuits induced by an external electric shock. A rabbit heart simulation study. Progr. Biophys. Mol. Biol. 2006;90:399–413. doi: 10.1016/j.pbiomolbio.2005.06.008. [DOI] [PubMed] [Google Scholar]
- 2.Trayanova N. Defibrillation of the heart: insights into mechanisms from modeling studies. Exp. Physiol. 2006;91:323–337. doi: 10.1113/expphysiol.2005.030973. [DOI] [PubMed] [Google Scholar]
- 3.Wikswo J.P., Jr., Lin S.F., Abbas R.A. Virtual electrodes in cardiac tissue: a common mechanism for anodal and cathodal stimulation. Biophys. J. 1995;69:2195–2210. doi: 10.1016/S0006-3495(95)80115-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Roth B.J., Krassowska W. The induction of reentry in cardiac tissue. The missing link: how electric fields alter transmembrane potential. Chaos. 1998;8:204–220. doi: 10.1063/1.166298. [DOI] [PubMed] [Google Scholar]
- 5.Byars J.L., Smith W.M., Ideker R.E., Fast V.G. Development of an optrode for intramural multisite optical recordings of Vm in the heart. J. Cardiovasc. Electrophysiol. 2003;14:1196–1202. doi: 10.1046/j.1540-8167.2003.03203.x. [DOI] [PubMed] [Google Scholar]
- 6.Hooks D.A., LeGrice I.J., Harvey J.D., Smaill B.H. Intramural multisite recording of transmembrane potential in the heart. Biophys. J. 2001;81:2671–2680. doi: 10.1016/S0006-3495(01)75910-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Trayanova N.A., Skouibine K., Aguel F. The role of cardiac tissue structure in defibrillation. Chaos. 1998;8:221–233. doi: 10.1063/1.166299. [DOI] [PubMed] [Google Scholar]
- 8.Entcheva E., Trayanova N.A., Claydon F.J. Patterns of and mechanisms for shock-induced polarization in the heart: a bidomain analysis. IEEE Trans. Biomed. Eng. 1999;46:260–270. doi: 10.1109/10.748979. [DOI] [PubMed] [Google Scholar]
- 9.Rodriguez B., Li L., Eason J.C., Efimov I.R., Trayanova N.A. Differences between left and right ventricular chamber geometry affect cardiac vulnerability to electric shocks. Circ. Res. 2005;97:168–175. doi: 10.1161/01.RES.0000174429.00987.17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fast V.G., Sharifov O.F., Cheek E.R., Newton J.C., Ideker R.E. Intramural virtual electrodes during defibrillation shocks in left ventricular wall assessed by optical mapping of membrane potential. Circulation. 2002;106:1007–1014. doi: 10.1161/01.cir.0000027103.54792.9c. [DOI] [PubMed] [Google Scholar]
- 11.Sharifov O.F., Fast V.G. Optical mapping of transmural activation induced by electrical shocks in isolated left ventricular wall wedge preparations. J. Cardiovasc. Electrophysiol. 2003;14:1215–1222. doi: 10.1046/j.1540-8167.2003.03188.x. [DOI] [PubMed] [Google Scholar]
- 12.Sharifov O.F., Ideker R.E., Fast V.G. High-resolution optical mapping of intramural virtual electrodes in porcine left ventricular wall. Cardiovasc. Res. 2004;64:448–456. doi: 10.1016/j.cardiores.2004.07.016. [DOI] [PubMed] [Google Scholar]
- 13.Sharifov O.F., Fast V.G. Intramural virtual electrodes in ventricular wall: effects on epicardial polarizations. Circulation. 2004;109:2349–2356. doi: 10.1161/01.CIR.0000127962.74368.D9. [DOI] [PubMed] [Google Scholar]
- 14.Liu T., Brown B.S., Wu Y., Antzelevitch C., Kowey P.R., Yan G.X. Blinded validation of the isolated arterially perfused rabbit ventricular wedge in preclinical assessment of drug-induced proarrhythmias. Heart Rhythm. 2006;3:948–956. doi: 10.1016/j.hrthm.2006.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Extramiana F., Antzelevitch C. Amplified transmural dispersion of repolarization as the basis for arrhythmogenesis in a canine ventricular-wedge model of short-QT syndrome. Circulation. 2004;110:3661–3666. doi: 10.1161/01.CIR.0000143078.48699.0C. [DOI] [PubMed] [Google Scholar]
- 16.Akar F.G., Nass R.D., Hahn S., Cingolani E., Shah M., Hesketh G.G., DiSilvestre D., Tunin R.S., Kass D.A., Tomaselli G.F. Dynamic changes in conduction velocity and gap junction properties during development of pacing-induced heart failure. Am. J. Physiol. Heart Circ. Physiol. 2007;293:H1223–H1230. doi: 10.1152/ajpheart.00079.2007. [DOI] [PubMed] [Google Scholar]
- 17.Roth B.J., Patel S.G., Murdick R.A. The effect of the cut surface during electrical stimulation of a cardiac wedge preparation. IEEE Trans. Biomed. Eng. 2006;53:1187–1190. doi: 10.1109/TBME.2006.873386. [DOI] [PubMed] [Google Scholar]
- 18.Bishop, M., B. Rodriguez, F. Qu, I. Efimov, D. Gavaghan, and N. Trayanova. 2007. The role of photon scattering in optical signal distortion during arrhythmia and defibrillation. Biophys. J. In press. [DOI] [PMC free article] [PubMed]
- 19.Bishop M.J., Rodriguez B., Eason J., Whiteley J.P., Trayanova N., Gavaghan D.J. Synthesis of voltage-sensitive optical signals: application to panoramic optical mapping. Biophys. J. 2006;90:2938–2945. doi: 10.1529/biophysj.105.076505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Streeter D. Handbook of Physiology: The Cardiovascular System. American Physiological Society; Bethesda, MD: 1979. Gross morphology and fiber geometry of the heart. [Google Scholar]
- 21.Plank G., Leon L., Kimber S., Vigmond E. Defibrillation depends on conductivity fluctuations and the degree of disorganization in reentry patterns. J. Cardiovasc. Electrophysiol. 2005;16:205–216. doi: 10.1046/j.1540-8167.2005.40140.x. [DOI] [PubMed] [Google Scholar]
- 22.Puglisi J., Bers D. LabHEART: an interactive computer model of rabbit ventricular myocyte ion channels and Ca transport. Am. J. Physiol. Cell Physiol. 2001;281:C2049–C2060. doi: 10.1152/ajpcell.2001.281.6.C2049. [DOI] [PubMed] [Google Scholar]
- 23.Ashihara T., Trayanova N.A. Asymmetry in membrane responses to electric shocks: insights from bidomain simulations. Biophys. J. 2004;87:2271–2282. doi: 10.1529/biophysj.104.043091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhou X., Ideker R.E., Blitchington T.F., Smith W.M., Knisley S.B. Optical transmembrane potential measurements during defibrillation-strength shocks in perfused rabbit hearts. Circ. Res. 1995;77:593–602. doi: 10.1161/01.res.77.3.593. [DOI] [PubMed] [Google Scholar]
- 25.Zhou X., Rollins D.L., Smith W.M., Ideker R.E. Responses of the transmembrane potential of myocardial cells during a shock. J. Cardiovasc. Electrophysiol. 1995;6:252–263. doi: 10.1111/j.1540-8167.1995.tb00397.x. [DOI] [PubMed] [Google Scholar]
- 26.Cheek E.R., Ideker R.E., Fast V.G. Nonlinear changes of transmembrane potential during defibrillation shocks: role of Ca2+ current. Circ. Res. 2000;87:453–459. doi: 10.1161/01.res.87.6.453. [DOI] [PubMed] [Google Scholar]
- 27.Fast V.G., Rohr S., Ideker R.E. Nonlinear changes of transmembrane potential caused by defibrillation shocks in strands of cultured myocytes. Am. J. Physiol. Heart Circ. Physiol. 2000;278:H688–H697. doi: 10.1152/ajpheart.2000.278.3.H688. [DOI] [PubMed] [Google Scholar]
- 28.Cheek E.R., Fast V.G. Nonlinear changes of transmembrane potential during electrical shocks: role of membrane electroporation. Circ. Res. 2004;94:208–214. doi: 10.1161/01.RES.0000111526.69133.DE. [DOI] [PubMed] [Google Scholar]
- 29.Bray M.A., Wikswo J.P. Examination of optical depth effects on fluorescence imaging of cardiac propagation. Biophys. J. 2003;85:4134–4145. doi: 10.1016/S0006-3495(03)74825-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sobie E., Susil R., Tung L. A generalized activating function for predicting virtual electrodes in cardiac tissue. Biophys. J. 1997;73:1410–1423. doi: 10.1016/S0006-3495(97)78173-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Efimov I.R., Nikolski V.P. Diastolic shocking experience: do virtual electrodes exist only during systole? J. Cardiovasc. Electrophysiol. 2003;14:1223–1224. doi: 10.1046/j.1540-8167.2003.03442.x. [DOI] [PubMed] [Google Scholar]
- 32.Sharfov O.F., Fast V.G. Role of intramural virtual electrodes in shock-induced activation of left ventricle: optical measurements from the intact epicardial surface. Heart Rhythm. 2006;3:1063–1073. doi: 10.1016/j.hrthm.2006.05.018. [DOI] [PubMed] [Google Scholar]
- 33.Knisley S.B., Trayanova N., Aguel F. Roles of electric field and fiber structure in cardiac electric stimulation. Biophys. J. 1999;77:1404–1417. doi: 10.1016/S0006-3495(99)76989-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Trayanova N.A. Effects of the tissue-bath interface on the induced transmembrane potential: a modeling study in cardiac stimulation. Ann. Biomed. Eng. 1997;25:783–792. doi: 10.1007/BF02684162. [DOI] [PubMed] [Google Scholar]
- 35.Entcheva E., Eason J., Efimov I.R., Cheng Y., Malkin R., Claydon F. Virtual electrode effects in transvenous defibrillation-modulation by structure and interface: evidence from bidomain simulations and optical mapping. J. Cardiovasc. Electrophysiol. 1998;9:949–961. doi: 10.1111/j.1540-8167.1998.tb00135.x. [DOI] [PubMed] [Google Scholar]
- 36.Trayanova N. Discrete versus syncytial tissue behavior in a model of cardiac stimulation. II. Results of simulation. IEEE Trans. Biomed. Eng. 1996;43:1141–1150. doi: 10.1109/10.544338. [DOI] [PubMed] [Google Scholar]
- 37.Plank G., Liebmann M., Weber dos Santos R., Vigmond E., Haase G. Algebraic multigrid preconditioner for the cardiac bidomain model. IEEE Trans. Biomed. Eng. 2007;54:585–596. doi: 10.1109/TBME.2006.889181. [DOI] [PMC free article] [PubMed] [Google Scholar]


