Monovalent Cation Binding by Curved DNA Molecules Containing Variable Numbers of A-Tracts

Abstract

Monovalent cation binding by DNA A-tracts, runs of four or more contiguous adenine or thymine residues, has been determined for two curved ∼200 basepair (bp) restriction fragments, one taken from the M13 origin of replication and the other from the VP1 gene of SV40. These two fragments have previously been shown to contain stable, centrally located bends of 44° and 46°, respectively, located within ∼60 bp “curvature modules” containing four or five irregularly spaced A-tracts. Transient electric birefringence measurements of these two fragments, sequence variants containing reduced numbers of A-tracts in the SV40 curvature module or changes in the residues flanking the A-tracts in the M13 curvature module, have been combined with the free solution electrophoretic mobilities of the same fragments using known equations to estimate the effective charge of each fragment. The effective charge is reduced, on average, by one-third charge for each A-tract in the curvature module, suggesting that each A-tract binds a monovalent cation approximately one-third of the time. Monovalent cation binding to two or more A-tracts is required to observe significant curvature of the DNA helix axis.

Introduction

The binding of monovalent cations in the minor groove of DNA A-tracts, runs of 4–6 contiguous adenine (or thymine) residues, is a topic of continuing interest (1,2). The localization of cations in the A-tract minor groove would lead to asymmetric neutralization of the charged phosphate residues (3–5), giving directionality to the bending fluctuations of the helix backbone (6–10) and providing a molecular explanation for the A-tract-induced curvature of DNA (11). Recent x-ray diffraction and NMR studies have indicated that the A-tract minor groove is occupied ∼10% of the time by Na⁺ ions (12), ∼40% of the time by Rb⁺ ions (12), ∼50% of the time by Cs⁺ ions (13), and ∼10% of the time by Tl⁺ ions (14). Tl⁺ ions also appear to be localized ∼30% of the time in the major groove of G/C-tracts adjacent to A-tracts (14). The bound cations are readily exchangeable with each other and with water molecules in the solvent; water molecules occupy the ion binding sites when cations are not present (15).

X-ray diffraction and NMR measurements are indirect methods of determining cation binding to DNA. A more direct method of measuring cation binding is free solution capillary electrophoresis (CE) (16–18). The mobility of an analyte is determined by the ratio between its effective charge, Q, and its frictional coefficient, f. Therefore, according to the Nernst-Einstein equation

$$\mu =Q/f=Q{D}_{\text{t}}/k_{\text{B}}T=z_{\text{eff}}{e}_{\text{o}}{D}_{\text{t}}/k_{\text{B}}T$$ (1)

where μ is the electrophoretic mobility, D_t is the translational diffusion coefficient, k_B is Boltzmann's constant, T is the absolute temperature, z_eff is the effective number of charged phosphate residues, and e_o is the (unsigned) charge of the electron (19,20). If the translational diffusion coefficient is independent of sequence, as it is for small DNA oligomers (21), the free solution mobility becomes a direct measure of the effective charge (16,18). In our previous study of monovalent cation binding to DNA A-tracts, we showed that 20-basepair (bp) oligomers containing phased A- or T-tracts migrate more slowly than an oligomer of the same size without A-tracts, indicating that A-tracts bind monovalent cations, reducing the effective net charge of the oligomer (16). A subsequent study showed that the free solution mobility of a stably curved, 199-bp restriction fragment taken from the VP1 gene in simian virus 40 (SV40) increased progressively as the number of A-tracts in the “curvature module” in the center of the fragment was decreased (17), again indicating that DNA A-tracts bind monovalent cations.

More quantitative analysis of monovalent cation binding to the A-tracts in the SV40 sequence variants requires knowledge of the translational diffusion coefficients of the various mutants. The translational diffusion coefficients can be calculated from the corresponding rotational diffusion coefficients using known equations (22) if the DNA molecules can be approximated as rigid rods. Previous studies have shown that this approximation is reasonable for DNA molecules in the size range considered here (23–25). From the calculated translational diffusion coefficients and the measured free solution mobilities, the effective charge of various DNA molecules can be estimated from Eq. 1. Comparison of the effective charge of DNA molecules containing the same number of bps but different numbers of A-tracts then provides a quantitative measure of monovalent cation binding to DNA A-tracts.

The curved DNA molecules used in this study were a 199-bp fragment taken from the VP1 gene in SV40 and a 217-bp fragment taken from the M13 origin of replication that was cloned into the plasmid Litmus 28. Transient electric birefringence (TEB) measurements, using the method of overlapping fragments (26), have shown that the SV40 and M13 fragments contain stable, centrally located bends of 44° ± 2° and 46° ± 2°, respectively (26–28). The apparent bend angle in the M13 fragment has been confirmed by atomic force microscopy (29).

The apparent bend centers in the SV40 and M13 fragments are located within 50–60 bp “curvature modules” containing four or five irregularly spaced A- or T-tracts. The sequences of the curvature modules are given in Scheme 1; the locations of the apparent bend centers are indicated by double vertical lines. The curvature modules are necessary and sufficient to cause stable bending of the DNA helix axis; replacing the curvature modules by random inserts of the same size eliminates the curvature (26–28).

Scheme 1.

Sequences of the curvature modules in the VP1 gene of SV40 and the M13 origin of replication

The A-tracts are highlighted in bold; the locations of the apparent bend centers are indicated by double vertical lines.

Sequence variants of the SV40 fragment were constructed in which the A- and T-tracts, singly and together, were mutated to other sequences, generating 30 fragments containing 0–5 permuted A-tracts. Sequence variants of the M13 curvature module had the GT and CA dinucleotides flanking the A₃T₅ and T₇ groups mutated to other residues; in another construct, the A₃T motif near the apparent bend center was replaced by a T₄ group. The sequences of the mutated SV40 and M13 curvature modules are given in Tables S1 and S2 of the Supplementary Material. The M13 mutants were studied to indicate the generality of the results obtained with the SV40 sequence variants and to explore the effect of the flanking nucleotides on monovalent cation binding. Several polyacrylamide gel electrophoresis studies have suggested that the A-tract-induced curvature of DNA is modulated by the flanking nucleotides (30–36).

The results obtained with the parent SV40 and M13 fragments and their sequence variants indicate that the effective charge of curved, A-tract-containing DNAs is reduced, on average, by one-third charge per A-tract. Hence, each A-tract in a curvature module binds a monovalent cation approximately one-third of the time. Monovalent counterion binding by DNA A-tracts does not appear to be influenced by the flanking sequences; rather it is influenced only by the number of A-tracts in the curvature module. Significant curvature of the DNA helix axis requires monovalent cation binding by two or more closely spaced A-tracts.

Materials and methods

DNA samples

Restriction fragments from the M13 origin of replication, which has been cloned into the plasmid Litmus 28 (coordinates 1047–1254), and the VP1 gene in SV40 (coordinates 1826–2017) were prepared by methods described previously (26–28). The A- and T-tracts in the curvature module of the SV40 fragment and the CA and TG dinucleotides flanking the A-tracts in the M13 curvature module were modified by site-directed mutagenesis, as described previously (17). The final purification step in all cases was adsorption of the DNA onto small diethylaminoethyl cellulose (D52, Whatman) columns; the fragments were then eluted into the desired buffer and stored at −20°C. All fragments were sequenced to confirm their identities. The sequences of the SV40 and M13 curvature modules and the various mutants are given in Tables S1 and S2 of the Supplementary Material. The various fragments were also characterized by polyacrylamide gel electrophoresis, using methods described previously (37). The anomalously slow mobilities of the curved fragments were analyzed by calculating μ-decrements, defined as Δμ/μ = [(μ_normal – μ_curved)/μ_normal] × 100. The μ-decrements observed for the parent SV40 and M13 fragments and their curvature module variants are given in Tables S1 and S2.

Buffers

The buffer usually used for the TEB experiments was 1 mM Tris-Cl, pH 8.0, plus 0.1 mM EDTA, called buffer B in previous work (26,27,38). Equivalent results were obtained using 0.2 mM Tris-Cl buffer (buffer C). CE experiments were carried out using Tris-acetate-EDTA (TAE) buffers (13 or 40 mM Tris base titrated to pH 8.0 with glacial acetic acid, plus 2 mM EDTA). Equivalent results were obtained in the two buffers.

Transient electric birefringence measurements

The apparatus and procedures used to carry out the TEB measurements have been described previously (26–28,38,39). Each DNA solution was pulsed 15 times in the single-shot mode under a given set of experimental conditions, and the field-free decay of each birefringence signal was analyzed using a nonlinear least-squares fitting program (CURVEFIT) adapted from the program designed by Bevington (40). The decay curves were fit with a single relaxation time, τ. Attempts to analyze the decay curves with two relaxation times led to significant increases in the uncertainties of the fitted τ-values. The relaxation times observed for the various fragments were constant within ±2%, even when different, independently prepared DNA stock solutions were used. Control experiments showed that the relaxation times were independent of DNA concentration, pulse length, and electric field strength. Therefore, a standard set of operating conditions—DNA concentration = 14 μg/mL (21 μM bp), electric field strength = 5 kV/cm, and pulse length = 8 μs—was used for all measurements. The temperature was 20°C ± 1°C.

The relaxation times of normal fragments containing the same number of bps as the curved fragments were calculated from standard curves of the logarithm of the relaxation times plotted as a function of the logarithm of the number of bps in each fragment (26,27,38). The τ-values of curved and normal fragments containing the same number of bps were used to calculate τ-decrements, defined as Δτ/τ = [(τ_normal – τ_curved)/τ_normal] × 100.

Capillary electrophoresis measurements

Capillary zone electrophoresis measurements were carried out using a P/ACE MDQ Capillary Electrophoresis System (Beckman Coulter, Fullerton, CA) operated in the reverse polarity mode (detector at the anode) with ultraviolet detection at 254 nm, using methods described previously (17,41). The capillaries (Bio-Rad, Hercules, CA) were typically 40 cm in length (29.7 cm to the detector) and were coated internally with polyacrylamide to minimize the electroosmotic flow (EOF) of the solvent. Previous studies have shown that polyacrylamide coatings do not affect the observed mobilities (41). DNA samples containing ∼50 μg/mL were injected by pressure into the capillary; the sample plug occupied ∼1% of the capillary length. The applied electric field strength was 200 V/cm. Control experiments showed that the observed mobilities were independent of DNA concentration, sample plug length, and applied electric field strength. All measurements were made at 20°C ± 1°C.

The migration times of the parent SV40 and M13 fragments and their sequence variants were measured at least two to three times under a given set of conditions. Because the EOF mobility was negligible, the electrophoretic mobilities, μ, could be calculated directly from the migration times, t, according to Eq. 2:

$$\mu =L_{\text{d}}/\text{Et},$$ (2)

where L_d is the length of the capillary to the detector and E is the electric field strength (19,20). Replicate measurements made on the same day were constant within ±0.04%; the average day-to-day variation in the mobilities was ±0.2%.

Theory

The rotational diffusion coefficient of a rigid, rod-like macromolecule is related to its size and shape as shown in Eq. 3:

$$D_{\text{r}}=\frac{3k_{\text{B}}T(\text{ln}p+\delta )}{\pi \eta L^3},$$ (3)

where D_r is the rotational diffusion coefficient, k_B is Boltzmann's constant, T is the absolute temperature, p is the axial ratio (p = L/d, where L is the end-to-end length of the rod and d is the diameter), η is the viscosity of the solvent, and δ is a correction for end effects, which can be expressed as δ = −0.662 + 0.917/p – 0.050/p² (22). The rotational diffusion constant is calculated from the birefringence relaxation time, τ, using the well-known relationship: D_r = 1/6τ (42).

Eq. 3 contains two unknowns, the length and the diameter (or axial ratio) of the macromolecule. For small DNA restriction fragments, d is often taken to be 26 Å, somewhat larger than the crystallographic diameter, to allow for hydration effects and/or moderate coiling of the helix backbone (39,43). Since the diameter (or axial ratio) enters only through a logarithmic term in Eq. 3, reasonable variations in d have little effect on the calculated length.

The translational diffusion coefficient, D_t, of a rigid rod-like molecule is also related to its size and shape, according to Eq. 4:

$$D_{\text{t}}=\frac{k_{\text{B}}T(\text{ln}p+\nu )}{3\pi \eta L},$$ (4)

where v is a correction for end effects, defined as ν = 0.312 + 0.565/p – 0.100/p² (22). Combining Eqs. 3 and 4 relates the translational diffusion constant of a rod to its rotational diffusion coefficient, according to Eq. 5:

$$D_{\text{t}}={\left(\frac{k_{\text{B}}T}{9\pi \eta }\right)}^{2/3}{D}_{\text{r}}^{1/3}\left(\frac{\text{ln}p+\nu }{{(\text{ln}p+\delta )}^{1/3}}\right)\text{.}$$ (5)

Inspection of Eq. 5 shows that the second term in parentheses is essentially constant for sequence isomers containing the same number of bps. Inserting the appropriate value for the 199-bp SV40 sequence isomers, evaluating the various constants in Eqs. 1 and 5, remembering that e_o/k_BT = 39.6 V⁻¹ at 20°C, and converting to birefringence relaxation times instead of rotational diffusion coefficients leads to a simple expression for the effective charge of each of the SV40 sequence variants:

$$z_{\text{eff}}=6.45\times {10}^6\mu {\tau }^{1/3}\text{.}$$ (6)

The constant in Eq. 6 is based on the assumption that the temperature is 20°C, the mobility is expressed as cm²/Vs, and the relaxation time is given in seconds. The constant is also weakly dependent on the DNA axial ratio, as can be seen from Eq. 5. For the 217-bp M13 sequence variants, the appropriate value of the constant is 6.54 × 10⁶.

Eq. 6 also assumes that equations that have been derived for straight rods (22) can be used to describe the relationship between D_t and D_r for moderately curved molecules, such as the SV40 and M13 sequence mutants studied here, keeping the value of p constant for the various sequence mutants. This assumption was evaluated by calculating z_eff for several of the SV40 sequence mutants using the actual values of p calculated from the birefringence relaxation times, instead of using a constant p for all mutants. No significant differences in z_eff were obtained by the two methods of calculation.

The quantity of interest in this study is not z_eff but the decrease in z_eff as a function of the number of A-tracts in the curvature module. Equating the decrease in the effective charge to the increase in the number of bound cations, ΔN, leads to

$$\begin{array}{l}\Delta N=z_{\text{eff}}(\text{normal}\text{fragment}\text{of}\text{the}\text{same}\text{size}\text{as}\text{the}\\ \text{curved}\text{fragment})-z_{\text{eff}}(\text{curved}\text{fragment})\text{.}\end{array}$$ (7)

The normal fragment used as the control for the SV40 mutants was 199K, which has no A-tracts in the curvature module. The normal fragment used for the M13 mutants was a 219 bp fragment taken from plasmid Litmus 28. Although this control fragment has two extra bps, its birefringence relaxation time and free solution mobility are very close to the values expected for a normal fragment containing 217 bp (17,38), as shown below by the last two entries in Table 2.

Table 2.

Birefringence relaxation times and free solution mobilities observed for M13 curvature module mutants

Name	Sequence change in curvature module	τ × 106, s*	μ × 104, cm2/Vs*
217A	Unmodified	4.94	3.1246
217C	CA→TA after A3T	4.82	3.1245
217H	CA→CG before T6	4.84	3.1275
217M	GT→AT after T5	4.74	3.1254
217K	Replace A3T by T4	4.93	3.1368
219	Control	5.68	3.1569
217	Calculated control†	5.43	3.1654

All mutants contained four A-tracts.

^*Standard deviations are given in footnote to Table 1.

^†Calculated from data obtained for normal DNA fragments of various sizes (17,38).

Results and discussion

Characterization of SV40 and M13 curvature module sequence variants

A typical birefringence signal observed for the parent 199-bp SV40 fragment is shown in the inset of Fig. 1. The decay of the birefringence, shown in the main part of the figure, is monoexponential, with a relaxation time of 3.74 ± 0.06 μs. Similar monoexponential decay curves were observed for all mutants of the SV40 and M13 curvature modules and for normal fragments ranging in size from 79 to 250 bps (38). Typical birefringence relaxation times observed for the parent SV40 fragment and its curvature module sequence variants are given in Table 1; the relaxation times of the M13 mutants and controls are given in Table 2. Previous studies have shown that the τ-decrements observed for the curved SV40 and M13 molecules and their sequence variants are essentially independent of the buffer in which the measurements are carried out, indicating that the parent fragments and their sequence variants are stably curved, not anisotropically flexible (26–28).

Figure 1.

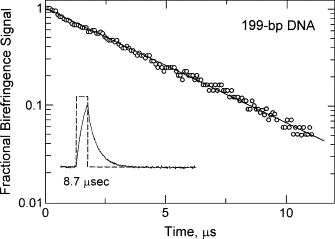
Analysis of the birefringence decay curve observed for the parent 199-bp SV40 fragment in 1 mM Tris-Cl buffer. The logarithm of the fractional birefringence signal remaining after time, t, is plotted as a function of the time after removal of the electric field. The birefringence decay curve is monoexponential, as shown by the straight line through the data points; the relaxation time is 3.74 ± 0.06 μs. The inset shows the applied 8.7 μs square-wave pulse (dashed line) and the corresponding birefringence signal (noisier curved line). Adapted from Lu et al. (26) with permission.

Table 1.

Birefringence relaxation times and free solution mobilities observed for SV40 curvature module variants

Name	Number of A-tracts in curvature module	τ × 106, s*	μ × 104, cm2/Vs†
199	5	3.71	3.1087
198A	4	3.73	3.1120
199B	4	3.87	3.1190
199E	4	3.77	3.1209
199F	4	4.11	3.1125
198C	3	4.02	3.1375
199Q	3	4.08	3.1332
199U	3	4.05	3.1358
199G	3	4.03	3.1308
199P	3	3.99	3.1279
199D	3	4.08	3.1254
199R	3	3.88	3.1225
198B	3	3.87	3.1245
199V	3	3.91	3.1208
199O	2	4.11	3.1443
199H	2	4.00	3.1339
198I	2	4.13	3.1353
198J	2	4.16	3.1520
198H	2	4.15	3.1429
198G	2	3.98	3.1263
199T	2	4.10	3.1432
198D	2	3.99	3.1392
199S	2	4.17	3.1425
199J	1	4.13	3.1369
199N	1	4.18	3.1487
199I	1	4.12	3.1435
199E	1	3.96	3.1209
198F	1	3.99	3.1379
199K	0	4.24	3.1445

^*In buffer B. The average standard deviation of triplicate measurements of each sample was ±0.04.

^†In 40 mM TAE. The average standard deviation of triplicate measurements of each sample was ±0.0008.

Typical electropherograms observed by free solution CE for the 199-bp SV40 fragment and a mutant, 199K, in which all the A-tracts in the curvature module have been mutated to other sequences are illustrated in the inset of Fig. 2. Both peaks are nearly Gaussian in shape, but the parent 199-bp fragment migrates significantly more slowly than oligomer 199K. Similar electropherograms were observed for the other fragments used in this study (not shown).

Figure 2.

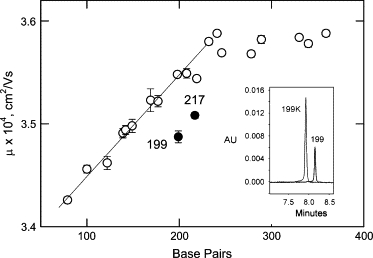
Comparison of the free solution mobility of the parent SV40 (199-bp) and M13 (217-bp) restriction fragments (●) with the mobilities of normal, non-A-tract-containing fragments of various sizes (○), measured in 13 mM TAE buffer. The error bars represent the standard deviation of triplicate measurements; the straight line is drawn to guide the eye. Inset: Typical electropherograms observed for the curved 199-bp SV40 fragment (right peak) and oligomer 199K, which had all five A-tracts in the curvature module mutated to other sequences (left peak). The optical density, in arbitrary units, is plotted as a function of migration time.

The dependence of the free solution mobility of normal, non-A-tract-containing DNA restriction fragments on molecular weight is illustrated in the main part of Fig. 2 (open circles). The mobilities increase approximately linearly with molecular weight until leveling off at a constant plateau value for fragments larger than ∼250 bp. Similar results have been observed for other DNA restriction fragments in the same molecular weight range (17,41). The mobilities of the curved SV40 (199-bp) and M13 (217-bp) fragments are significantly lower than expected on the basis of their molecular weights, as shown by the solid circles in the same figure. The free solution mobilities of the various SV40 and M13 sequence mutants are given in the last columns of Tables 1 and 2.

Preferential counterion binding to DNA A-tracts

The effective charge of the curved 199-bp SV40 fragment and mutants containing reduced numbers of A-tracts in the curvature module was calculated from Eq. 6; the apparent number of cations bound to the A-tracts, ΔN, was then calculated from Eq. 7. The parent SV40 fragment contains five A-tracts in the curvature module. Five sequence variants contained one A-tract, nine mutants contained two A-tracts in various positions, nine mutants contained three permuted A-tracts, five mutants contained four permuted A-tracts, and one mutant, 199K, had all five A-tracts mutated to other sequences. To focus on the generality of the results, and not on cation binding to specific A-tracts, the ΔN values obtained for all mutants containing the same number of A-tracts in the curvature module were averaged. The average ΔN value is plotted in Fig. 3 as a function of the number of A-tracts in the curvature module (open circles).

Figure 3.

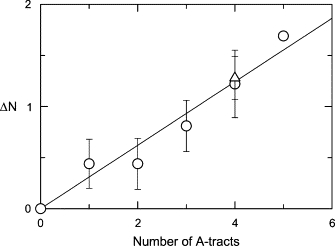
Dependence of the change in the average number of bound cations, ΔN, on the number of A-tracts in the curvature module. (○) SV40 sequence variants; (▵), M13 sequence variants. The error bars correspond to the standard deviation of the ΔN values observed for sequence variants containing the same number of A-tracts. The line was drawn by linear regression (r² = 0.96); the slope of the line is 0.31.

The results in Fig. 3 indicate that the average number of bound cations increases approximately linearly with the number of A-tracts in the curvature module. The slope of the line is 0.31, indicating that a Tris⁺ ion is bound to an A-tract approximately one-third of the time. Stated differently, approximately one-third of the A-tracts in the SV40 curvature module bind a Tris⁺ ion at any given time. Preferential cation binding to the A-tracts appears to be independent of A-tract length and polarity, since there is no correlation between the number of bound cations and the presence or absence of a particular A-tract in the curvature module (data not shown). The average occupancy rate of ∼30% indicates that the preferential binding of Tris⁺ ions to DNA A-tracts is within the range of values observed for the binding of other monovalent cations to the AATT motif in the Dickerson-Drew dodecamer (12–14). The consistency of monovalent cation binding to DNA A-tracts observed by x-ray diffraction, NMR, and birefringence/electrophoresis methods lends confidence to the interpretation of the results obtained by all three methods.

The apparent number of cations bound to sequence variants of the M13 curvature module agrees with that observed for the SV40 mutants, as shown by the open triangle in Fig. 3. Hence, preferential cation binding to DNA A-tracts is not limited to the particular A-tracts in the SV40 curvature module. In addition, the apparent number of cations bound by the A-tracts in the M13 curvature module is approximately independent of the presence or absence of CA or TG dinucleotides adjacent to the A₃T₅ and T₇ groups, indicating that the flanking dinucleotides do not affect monovalent cation binding to DNA A-tracts. Replacing the A₃T sequence near the apparent bend center by a T₄ group also does not affect monovalent cation binding, suggesting that these two sequence motifs bind Tris⁺ ions to a similar extent. A comparison of the binding of monovalent cations to A-tracts of different types will be described in a future communication (Q. Dong, E. Stellwagen, and N. C. Stellwagen, manuscript in preparation).

The results in Fig. 3 do not address the issue of whether monovalent cations are bound in the major or minor groove of DNA A-tracts; they address only the fact that A-tracts bind more monovalent cations than random sequence DNA. Regardless of the binding site, the juxtaposition of several A-tracts within a relatively short sequence span, as observed in the SV40 and M13 curvature modules, would lead to a patch of reduced charge density along the helix backbone. This patch of reduced charge density, with or without electrostatic collapse of the helix backbone toward the minor groove (6,7,10,36,44), could be part of the recognition signal used by transcription factors and other proteins to find their targets on the DNA surface (15,44–46) and/or may contribute to indirect readout (47) when the residues in an A-tract are not directly contacted by the protein side chains.

Monovalent cation binding to the A-tracts in the SV40 and M13 curvature modules is directly correlated with the anomalous electrophoretic mobilities observed in polyacrylamide gels, as shown in Fig. 4 A, where the average number of cations bound to sequence variants containing the same number of A-tracts is plotted as a function of the average gel mobility decrements, Δμ/μ, observed for the same fragments. The linear correlation indicates that a primary determinant of the anomalously slow electrophoretic mobilities observed for A-tract-containing DNAs in polyacrylamide gels is their reduced effective charge density. The differences in the effective charge are amplified by the sieving effects of the polyacrylamide gel matrix, explaining why polyacrylamide gel electrophoresis is such a good reporter of DNA curvature (48).

Figure 4.

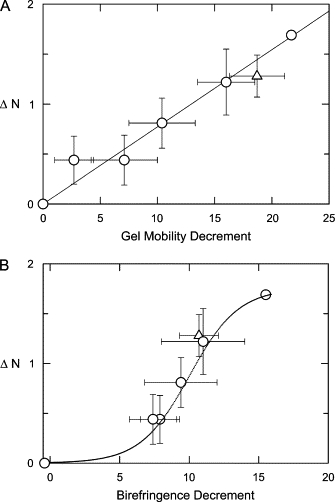
The average number of cations bound by SV40 (○) and M13 (▵) sequence variants containing the same number of A-tracts is plotted as a function of (A) the average polyacrylamide gel mobility decrements, Δμ/μ, and (B) the average τ-decrements, Δτ/τ, observed for the same fragments. The error bars represent the average deviation of the ΔN, Δμ/μ, and Δτ/τ values observed for sequence variants containing the same number of A-tracts. The straight line in (A) was drawn by linear regression (r² = 0.96). The dotted line in (B) is a sigmoidal fit of the data points.

Preferential cation binding to DNA A-tracts is not directly correlated with the curvature of the helix backbone, as shown in Fig. 4 B where the average number of cations bound to sequence variants containing the same number of A-tracts is plotted as a function of the average τ-decrements observed for the same fragments. The data appear to be well fitted by a sigmoidal function, suggesting that stable curvature of the DNA helix axis requires the cooperative binding of monovalent cations to two or more closely spaced A-tracts. Studies of the fluorescence anisotropy of cationic residues tethered in the A-tract minor groove have also indicated that curvature of the DNA helix backbone requires the presence of adjacent positive charges (44). The combined results suggest that fractional occupancy of the A-tract major/minor groove(s) by the first cation facilitates occupancy by additional cation(s) in adjacent A-tracts. Hence, the number of cations bound in the SV40 curvature module increases linearly with the number of A-tracts (Figs. 3 and 4 A), whereas curvature depends on the cooperative binding of two or more cations to adjacent A-tracts (Fig. 4 B).

Conclusion

The results in this study have shown that DNA A-tracts bind monovalent cations about one-third of the time, reducing the effective charge of A-tract-containing DNAs by about one-third charge per A-tract. Preferential cation binding to the A-tracts is linearly correlated with the gel mobility decrements observed for the same fragments (Fig. 4 A); however, stable curvature of the helix axis requires the cooperative binding of monovalent cation(s) to two or more closely spaced A-tracts (Fig. 4 B). The exact sequence and spacing of the A-tracts affects preferential counterion binding to some extent, leading to the error bars reported in Figs. 3 and 4. Quantitative studies of monovalent cation binding to various types of A-tracts will be described in a future communication (Q. Dong, E. Stellwagen, and N. C. Stellwagen, manuscript in preparation).

Appendix A.

Data Supplement 1

Data Supplement 1