Abstract
The means by which extracellular matrix density regulates three-dimensional capillary morphogenesis is unclear. To study this phenomenon, we utilized a fibrin-based in vitro assay in which a fibroblast monolayer is plated atop a fibrin gel ∼2.5 mm away from endothelial cell-coated beads within the matrix. Increasing fibrin density from 2.5 to 10 mg/ml resulted in a threefold reduction in capillary network formation. However, distributing fibroblasts throughout the matrix completely eliminated this inhibitory effect, resulting in robustly vascularized matrices suitable for in vivo applications, as functional anastomoses formed between the implanted tissues and host vasculature when implanted into immune-compromised mice. Dense matrices did not stimulate fibroblast-mediated matrix remodeling: differentiation into myofibroblasts, matrix production, and protease secretion were not enhanced by the dense condition. Instead, quantifying diffusivity of FITC-dextran (molecular mass 10, 40, 70, and 150 kDa) through fibrin revealed a two- to threefold decrease within the 10 mg/ml matrices. Thus, distributing a proangiogenic source (fibroblasts) throughout the matrix stimulates capillary network formation by overcoming this diffusion restriction due to significantly reduced diffusion distances. Although roles for matrix stiffness and ligand binding density have previously been identified, our results emphasize the importance of diffusion restrictions in limiting capillary morphogenesis.
Introduction
Changes in extracellular matrix (ECM) density occur in a variety of pathologies. In cancer, tumors recruit nascent vasculature that leaks the plasma protein fibrinogen into the interstitial space (1). The accumulation and clotting of this protein coupled with a fibrotic response elicited from interstitial cells (2) result in increased ECM density, which in turn alters tissue mechanical properties, integrin adhesion sites, matrix porosity (3,4), and ultimately vascular homeostasis.
For certain therapies, enhancing tissue vascularization is desirable. For instance, the field of tissue engineering has been limited to relatively thin tissues (<2 mm) because of inadequate delivery of oxygen and nutrients to the core of thicker tissues (5). One strategy to overcome this limitation is to form a network of capillaries in vitro that, once implanted, would rapidly anastamose with the host vasculature and enhance nutrient delivery (6). However, a limitation of using natural biomaterials is the requirement that they be compliant enough to facilitate robust network formation yet stiff enough to retain a desired three-dimensional (3-D) configuration on implantation. Hence, we are interested in achieving thorough vascularization within a dense/stiff matrix environment. Although we and others have shown that enhancing the physical properties of the ECM restricts vascular network formation (7–10), the underlying mechanisms in three dimensions are still poorly understood.
To investigate the role of the ECM in 3-D capillary morphogenesis, we have utilized a tissue culture model of angiogenesis comprised of human umbilical vein endothelial cell (HUVEC)-coated beads polymerized within a fibrin clot and cocultured with a stromal cell (i.e., fibroblasts). Normally, fibroblasts, which serve as a source of proangiogenic factor(s) (11), are grown as a monolayer a fixed distance (2.5 mm) from the HUVEC-coated beads. When the distance between the HUVEC-coated beads and the fibroblast monolayer exceeds a critical threshold, capillary formation is severely attenuated, suggesting that diffusion limitations of fibroblast-derived proangiogenic factor(s) are important (12). Maintaining this distance constant while increasing the fibrin density from 2.5 to 10 mg/ml (thus increasing stiffness sevenfold) significantly reduces capillary morphogenesis as well (8).
We hypothesized that distributing fibroblasts in three dimensions within a dense fibrin matrix would also stimulate angiogenesis and that the mechanism could involve one or more of the following: 1), myofibroblast-mediated matrix remodeling; 2), stimulation of ECM (collagen or fibronectin) production; 3), enhanced fibrinolytic activity; or 4), enhanced diffusive transport of fibroblast-derived proangiogenic factors as a result of reduced diffusion distances. Our data demonstrate that, indeed, distributing fibroblasts in three dimensions significantly enhances angiogenesis and completely eliminates the inhibitory effect of increasing fibrin density. Further, these robustly vascularized tissues inosculate with host vessels when implanted within immune-compromised mice and remain functional nearly 1 month postimplantation.
Distributing the fibroblasts in three dimensions does not enhance myofibroblast differentiation, ECM production, or ECM degradation. Instead, increasing the density of fibrin significantly restricts the effective diffusivity of putative angiogenic factors, demonstrated by the reduced diffusion of fluorescein-labeled dextran (molecular mass range of 10–150 kDa). Our results suggest that changes in the density of structural proteins within the ECM, such as fibrin, may play a critical role in the regulation of capillary morphogenesis by limiting the diffusional transport of proangiogenic macromolecules.
Methods
Fibrin tissue construction
Cytodex microcarrier beads (Sigma-Aldrich, St. Louis, MO) were sterilized and prepared for seeding by washing repeatedly with Endothelial Growth Medium (EGM-2, Cambrex, East Rutherford, NJ). Ten thousand such beads were combined in 5 ml of EGM-2 with 4 × 106 HUVEC (p3) and agitated periodically over 4 h in an inverted T-25 culture flask. HUVEC were obtained freshly from umbilical cords as previously described (12). After 4 h, 5 ml of fresh medium was added to the cell-bead mixture. The total volume was then transferred to a new T-25 and incubated in standard cell culture position.
The next day, bovine fibrinogen (Sigma) solutions of the desired concentrations (2.5, 5, or 10 mg/ml) were prepared in serum-free EGM-2 and sterile filtered. After addition of 5% fetal bovine serum, 500 μl of this solution (with 50K normal human lung fibroblasts used before p10 for distributed fibroblast conditions) was mixed with ∼100 HUVEC-coated beads and polymerized with 10 μl of thrombin (Sigma, 50 U/ml) in a single well of a 24-well plate per tissue. At this point, the tissues were left undisturbed for 5 min at room temperature before incubation for 25 min at 37°C and 5% CO2 to facilitate gelation. For monolayer conditions, 25K fibroblasts/ml were suspended in EGM-2 and plated on top of the fibrin gel. Medium was changed the following day, and every other day thereafter. We have previously shown that 3-D tissue constructs prepared via these methods support the formation of capillary networks with well-defined lumens (8).
Tissue implantation within immune-compromised mouse and immunohistochemistry
Robustly vascularized 7-day-old 10 mg/ml fibrin gels were implanted subcutaneously into mice containing disrupted recombination activating gene 2 (Rag2; Taconic Farms, Oxnard, CA). Rag2 knockouts fail to produce mature T or B lymphocytes and thus are ideal for human cell transplantation. Surgeries were performed according to the NIH guideline for laboratory animal usage and our approved institutional protocol. Mice were anesthetized via abdominal injection of a ketamine/xylazine cocktail. The dorsal area of the animal was shaved and disinfected. An incision was made through the dermis, and a pouch was created between the skin and underlying muscle. Tissue constructs were inserted into the pouch (two per animal). Analgesia was provided abdominally at the completion of surgery. The animals were sacrificed, and the tissues were harvested, 4 weeks after implantation. The fibrin tissues were comprised of HUVECs coated on dextran beads with fibroblasts distributed throughout as described above. The tissue was placed in a PDMS mold (10 mm diameter, 3 mm depth) before implantation to limit diffusion of nutrients to the top surface of the tissue.
After 4 weeks of implantation, animals were sacrificed, and tissue constructs were removed, fixed overnight in 10% neutral buffered formalin, and embedded in paraffin. Hematoxylin and eosin (H&E) and immunohistochemical (IHC) stains were performed on 4-μm tissue sections. IHC stain with antihuman CD31 (1:200) (Dako, Cambridgeshire, UK) was carried out using the DakoCytomation EnVision System-HRP (DAB) followed by a light H&E stain.
Transduction of HUVEC and NHLF
HUVEC and normal human lung fibroblast (NHLF) were transduced with monomeric red fluorescent protein (RFP) or green fluorescent protein (GFP) using the Phoenix Retrovirus Expression System (Orbigen, San Diego, CA). The pBMN-GFP vector was obtained commercially (Orbigen). The RFP vector was constructed by inserting the RFP gene of pCDNA3-mcherry (kindly provided by Dr. Roger Tsien, University of California, San Diego) into the pBMN-Z vector (Orbigen). Stable transduction of HUVEC and NHLF were achieved using methods described previously (13). Daily viral transductions were performed 6 h per day for a total of 4 days. The percentage of cells expressing GFP or RFP was 60–80%, as quantified by fluorescence-activated cell sorting.
Imaging and quantification of total network length
Tissues containing GFP-infected HUVEC were imaged at day 7 postassembly via fluorescence microscopy with an Olympus 1X51 equipped with a 100-W high-pressure mercury burner (Olympus America, Center Valley, PA) and a QImaging QICAM 12-bit Color Fast 1394 camera (QImaging, Surrey, BC). QCapture Pro Software was used for image acquisition (QImaging). Five beads per condition were randomly imaged at low power (4×) for each experiment (over three experiments to generate a sample size of 15).
Methods to quantify total network length have been described previously (8). Briefly, vessel segments for each bead were traced, counted, and quantified using open-source image processing software (NIH ImageJ, National Institutes of Health, Bethesda, MD). The resulting values of total network length and total number of vessel segments for all 15 beads per condition were then tabulated and averaged.
Fibrin gel lysing, zymography, and Western blotting
For each condition, three fibrin tissues, each containing ∼100 HUVEC-coated beads, were pooled together and digested via homogenization and sonication in 300 μl of ice-cold Garner buffer (50 mM Tris, pH = 7.5, 150 mM NaCl, 1 mM phenylmethylsulfonyl fluoride, 1% Triton X-100). Any remaining solids (undigested fibrin and cell membrane) were removed by centrifugation at 14,000 rpm for 10 min at 4°C. Protein concentration of the resulting supernatant was quantified via bicinchoninic acid assay (Pierce Biotechnology, Rockford, IL).
For Western blotting, 40 μg of protein per condition was electrophoresed under reducing conditions and transferred to a PVDF membrane. Blots were probed with either a mouse monoclonal antibody against human α-smooth muscle actin (α-SMA; 1:1000, Sigma) or a mouse polyclonal antibody against human fibronectin extra domain-A (ED-A; 1:450, Abcam, Cambridge, MA), followed by incubation with a horseradish peroxidase-conjugated antimouse secondary antibody (1:10,000, Santa Cruz Biotechnologies, Santa Cruz, CA). Membranes were washed for 1 h before detection via an enhanced chemiluminescence detection system. Bands were identified by comparing to a molecular mass ladder (Santa Cruz).
For gelatin zymography, precast Novex zymogram gels (10% Tris-Glycine gel with 0.1% gelatin, Invitrogen, Carlsbad, CA) were loaded with 25 μg of protein per condition and separated under nonreducing conditions. Gels were renatured overnight in a 50 mM Tris-HCl (pH = 8.0), 5 mM CaCl2, and 2.5% Triton X-100 solution. After renaturing, zymograms were incubated at 37°C for 24 h in enzyme activation buffer (125 mM Tris-HCl, pH = 7.5, with 5 mM CaCl2). Gels were then Coomassie stained for 1 h and destained 15 min twice in 10% acetic acid and 20% ethanol. MMP-2 and MMP-9 bands were identified with an MMP-2/-9 standard (Chemicon, Temecula, CA).
Plasminogen zymography was conducted to assess the activities of urokinase plasminogen activator (uPA) and tissue plasminogen activator (tPA) activities in a fashion nearly identical to gelatin zymography, described above. In this case, gels were cast with 1% plasminogen (1 U/ml, Sigma), and CaCl2 was not added to the renaturing or activation buffers; 5 mM EDTA was added to the activation buffer to chelate divalent cations that typically serve to activate MMPs.
Confocal imaging
Multiphoton images were obtained as previously described (14) using a commercially available laser scanning multiphoton microscope (LSM 510 Meta, Zeiss, Jena, Germany). Briefly, 2.5, 5, and 10 mg/ml fibrin gels containing 100K NHLF/ml (300 μl volume) were polymerized in No. 1 thickness, 8-well borosilicate chamber slides and maintained in EGM-2 until the appropriate time point. Live tissues were then scanned using a 40×, 1.3 numerical aperature oil-immersion objective. Backscattered second harmonic generation (SHG) and two-photon fluorescence (TPF) signals were simultaneously obtained in two separate channels by excitation with a 780-nm wavelength. SHG was collected using a 387- to 398-nm bandpass filter, whereas TPF was collected using a 480- to 520-nm bandpass filter. Reflectance of fibrin was imaged by excitation with a 543-nm laser and use of a linepass filter to collect the resulting signal at 505 nm. Pinhole size and laser power were kept constant throughout the imaging. Three different locations within at least two tissues per condition were scanned at days 7 and 14. Images were then compared to determine whether any significant SHG signal existed extracellularly in any of the conditions probed.
Sircol collagen assay
A Sircol soluble collagen assay (Biocolor, Newtownabbey, Northern Ireland) was performed according to manufacturer's protocol. Briefly, at each time point, three fibrin gels per condition were washed once with PBS, collected in 15-ml centrifuge tubes, weighed (to extrapolate gel volume), and stored at −80°C. At the time of the assay, gels were thawed, and pepsin-soluble collagens were extracted from the gels by overnight incubation at room temperature in 1.5 ml of a 0.5 M acetic acid and 5 mg/ml pepsin solution. The following day, tubes were centrifuged, and 100 μl of the resulting supernatant was added to a 1.5 ml microcentrifuge tube. One milliliter of Sircol dye reagent was added to each tube and mixed for 30 min. The collagen-dye complex was subsequently recovered by centrifuging at 14,000 × g for 10 min, draining the supernatant, and removing any remaining unbound dye solution with an absorbent tissue. Alkaline dye solution (0.5 ml) was added to the isolated pellet and vortexed until well mixed. Collagen standards as well as samples from each time point and condition were added in duplicate to a 96-well plate. Absorbance of each sample at 540 nm was measured (after blanking) and averaged using a Benchmark Microplate Reader (Bio-Rad Laboratories, Hercules, CA). The final amount of collagen (weight) for each sample was obtained from its absorbance values by comparison to a collagen standard curve (R2 > 0.99) with correction for all previous dilutions. For each assay, values obtained were normalized by those obtained for an acellular fibrin gel of equal concentration.
Microfluidic diffusion culture platform fabrication
Diffusion chambers were fabricated with PDMS using soft lithography and replica molding. Photolithography was utilized to pattern one layer of negative photoresist, SU-8, on a silicon wafer, resulting in a master comprised of two wells separated by a number of channels that have a width of 500 μm, a height of 300 μm, and a length of 3 mm. A prepolymer mixture of Sylgard 184 was cast and cured onto the negative replica, as previously described (15). After curing, the PDMS was peeled away from the master, and reservoirs were cut out with a surgical blade. Next, both the diffusion device and a No. 1 cover slip were plasma treated using a Harrick Plasma Cleaner (Harrick Plasma, Ithaca, NY) to bond them together irreversibly.
Fibinogen stocks (2.5 and 10 mg/ml in PBS) were aliquoted and maintained at −20°C to eliminate batch-to-batch variability of the polymerized gels. For each experiment, the appropriate aliquot was thawed, mixed with thrombin, and immediately pipetted near the channel edge of the well. The solution wicked into the neighboring channels. After the fibrinogen was allowed to clot within the channels for 5 min at room temperature and another 25 min at 37°C, 300 μl of PBS was added to each well, and the device was incubated overnight to allow the hydrogel network to swell appropriately.
Diffusion experiments and quantification of Deff
Diffusion experiments were monitored with a Nikon TE300 microscope (Nikon, Melville, NY) equipped with a motorized stage and a xenon lamp. PBS was removed from the microfluidic device before mounting so that equal and accurate volumes could be loaded in each well. After mounting, stage positions were chosen such that the “source” reservoir, the reservoir-channel interface, and a substantial portion of the channel were contained in one low-magnification (4×) field of view. Multiple stage positions were chosen such that diffusion through multiple channels of the device could be monitored. At this point, 300 μl of PBS was added to the “sink” reservoir (not contained in the field of view), and 300 μl of a 100 μg/ml solution of fluorescein-conjugated dextran particles (molecular mass of either 10, 40, 70, or 150 kDa) were carefully pipetted into the “source” well to minimize generation of convective currents. Time-lapse imaging commenced immediately after the addition of the dextran particles using a 488-nm excitation filter, and images were taken every 30 s for a total of 30 or 60 min depending on the observed rate of diffusion.
Image stacks were generated from the described time-lapse experiments using Metamorph software (Universal Imaging/Molecular Devices Corporation, Union City, CA). Three parallel linescans spaced 60 pixels apart situated in the middle of the channel were averaged, and the resulting intensity profiles (over distance) were logged onto a spreadsheet at five equally spaced time points (starting at t = 0). The x position of the source reservoir-channel interface was set as x = 0, and the coordinates throughout the rest of the channel were rescaled appropriately.
The effective isotropic diffusion coefficient, Deff, was extracted from the acquired data by assuming that the channel could be approximated as a one-dimensional, semiinfinite slab and solving Fick's second law:
| (1) |
given the following initial condition and boundary conditions:
| (2) |
| (3) |
| (4) |
The following solution was then obtained:
| (5) |
Differentiating Eq. 5 with respect to t and rearranging gives the following relation at x = x0:
| (6) |
Time derivatives at t = tn (n = 1, 2, 3, or 4) were calculated using a finite difference formula:
| (7) |
where Cn is the measured intensity at time tn. The left side of Eq. 6 was plotted against 1/t, and a straight line was fitted to the data using a least-squares procedure. The diffusivity Deff was estimated from the slope of the line, . This was repeated at m different locations along the length of the channel at which were positive. Deff values from the best-fit range with R2 ≥ 0.99 were averaged to obtain the Deff value for that experiment.
Statistical analysis
Statistical analyses were performed using SigmaStat 3.5 (Systat Software, San Jose, CA). All statistical comparisons were made by performing a one-way analysis of variance (ANOVA), followed by one of the following pairwise multiple comparison procedures: Holm-Sidak method (for vessel network quantification) or Student-Newman-Keuls method (for quantification of Deff). Statistical significance was assumed when p < 0.05. Data are reported as mean ± SD.
Results
Distributing fibroblasts interstitially negates the inhibitory effect of matrix density on capillary network formation
GFP-transduced HUVECs cultured on microcarrier beads within 2.5 mg/ml fibrin gels overlaid with a fibroblast monolayer form extensive capillary networks by day 7 (Fig. 1 A). Although increasing matrix density to 5 mg/ml did not significantly affect network formation (Fig. 1 B), total network length was reduced significantly (about threefold) in 10 mg/ml matrices (Fig. 1, C and G: 5231 ± 1884 μm for 2.5 mg/ml gels versus 1734 ± 842 μm for 10 mg/ml gels). This decrease in total capillary network length is caused primarily by a decrease in the number of vessel segments formed (Fig. 1 H).
Figure 1.
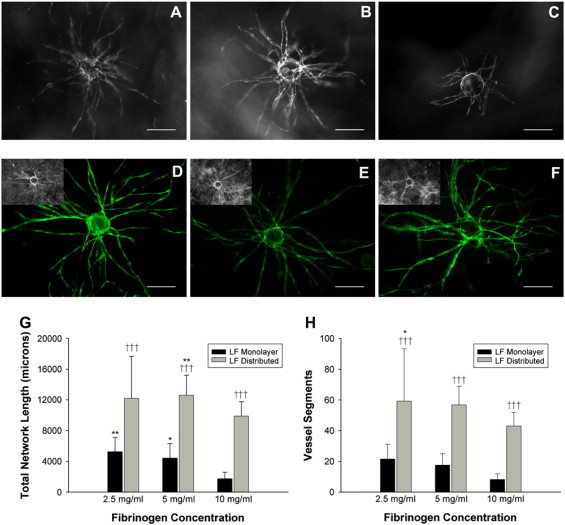
Distributing fibroblasts throughout the matrix abrogates the inhibitory effects of increased fibrin concentration on capillary network formation. Representative images of isolated microcarrier beads initially coated with GFP-transduced HUVEC within (A) 2.5, (B) 5, and (C) 10 mg/ml fibrin matrices (day 7). Cultures contained an overlying fibroblast monolayer. A 488-nm excitation reveals the capillary network in fibrin gels containing distributed fibroblasts instead of a fibroblast monolayer in (D) 2.5, (E) 5, and (F) 10 mg/ml matrices (inset: brightfield imaging was not suitable to distinguish capillaries from fibroblasts). Scale bars = 200 μm. Fifteen beads over three separate experiments were quantified at day 7 for (G) total network length and (H) total number of vessel segments. In G, *p < 0.05 and **p < 0.01 when comparing 2.5 and 5 mg/ml conditions to the 10 mg/ml condition. In H, *p < 0.05 when comparing the 2.5 mg/ml condition to the 10 mg/ml condition. †††p < 0.001 when comparing the distributed condition to the monolayer condition for the respective fibrin density.
A denser matrix may retard the diffusion of soluble mediators (11); thus, we distributed fibroblasts throughout the fibrin matrix (as opposed to a monolayer a fixed distance away) before polymerization to reduce the diffusion distance. Conventional brightfield microscopy did not allow resolution of these networks (Fig. 1, D–F, inset) because of an inability to distinguish fibroblasts from budding vessels. To overcome this, HUVECs were transduced with a GFP-expressing retrovirus (Fig. 1, D–F), facilitating network visualization. Fibroblast distribution led to a drastic upregulation of network formation for all matrix densities, and total network length no longer decreased significantly with increasing fibrin density (Fig. 1 G). Network formation was increased ∼2.3-fold in 2.5 mg/ml matrices, ∼2.9-fold in 5 mg/ml matrices, and ∼5.7-fold in 10 mg/ml matrices (Fig. 1 G). This increase was attributable to a greater number of capillary segments formed (Fig. 1 H). The average segment length did not deviate significantly from those measured for the fibroblast monolayer conditions (e.g., 211.5 μm for 10 mg/ml monolayer gels versus 230.1 μm for 10 mg/ml gels).
Capillary networks formed within dense, fibroblast-distributed gels are functional in vivo
To determine whether the enhanced capillary networks formed within 10 mg/ml fibrin gels are viable, gels initially constructed with HUVEC-coated beads and distributed fibroblasts were cultured for 7 days and implanted subcutaneously on the dorsal surface of immune-compromised mice. Removing these tissues revealed that functional anastomoses had formed between the HUVEC-lined vessels and those of the host. Further, capillaries remained functional for 4 weeks, as evidenced by the presence of red blood cells within vessels near a dextran bead (Fig. 2 A) and human CD31-positive vessels perfused with blood (Fig. 2 B). Vessels in the host tissue surrounding the implant, although perfused, did not stain positive for human CD31, demonstrating that the antibody used did not cross-react (Fig. 2 C). Fibrin tissues containing only HUVEC showed no evidence of perfusion with host red blood cells (Fig. 2 D).
Figure 2.
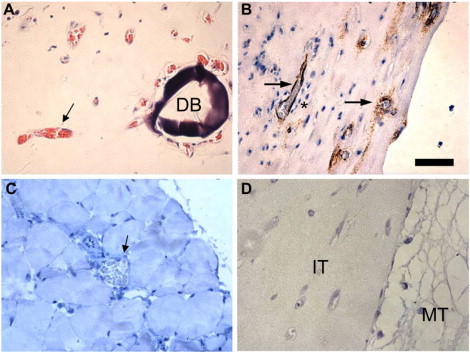
Implanted high-density fibrin tissues with distributed fibroblasts and mature capillaries develops functional anastomoses with mouse. (A) H&E stain of a high-density (10 mg/ml) fibrin tissue with distributed fibroblasts and a developed capillary network originating from HUVEC-coated dextran beads demonstrates capillaries with mouse red blood cells (black arrow) in the lumen near the dextran bead (DB) 28 days postimplant. (B) IHC stain of human CD31 identifies human endothelial cells (HUVEC, in brown) lining vessels perfused with mouse red blood cells (black arrows). Interstitial cells are seen surrounding the mature capillary (*). (C) IHC stain of mouse tissue with antihuman CD31 demonstrates lack of cross-reactivity (black arrow). (D) H&E stain of a negative control tissue comprised of randomly distributed HUVECs in 10 mg/ml fibrin (no fibroblasts). The border between the implanted tissue (IT) and the mouse tissue (MT) is visible.
Fibroblast differentiation into myofibroblasts proceeds independently of fibrin density
To explore the possible mechanisms by which the distribution of interstitial cells reverses the inhibitory effect of increased matrix density on capillary network formation, we first sought to determine whether distributing fibroblasts throughout denser matrices promoted their differentiation into myofibroblasts. A defining characteristic of myofibroblasts is that they express α-SMA (16), and the extent of this expression is directly correlated to the amount of tractional stress the cells can exert to remodel their matrix (17).
Fig. 3, A–C, provides qualitative evidence that fibroblasts (transduced with GFP retrovirus) were intimately interacting with sprouting HUVEC capillaries (transduced with RFP retrovirus) at all fibrin densities. This periendothelial behavior is typical of cells of mesenchymal or smooth-muscle origins, which are characterized by the expression of α-SMA (18). Western blotting for α-SMA and for cellular fibronectin containing the ED-A splice variant, an inducer of myofibroblast maturation (16), demonstrated enhanced myofibroblast differentiation with time in culture (day 14 compared with day 3) but did not show any dependence on fibrin concentration (Fig. 3, D and E). The presence of HUVEC did not appreciably alter these expression patterns (data not shown).
Figure 3.
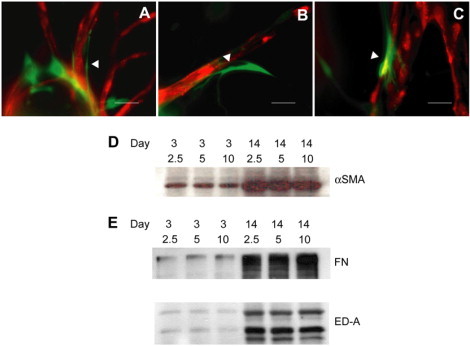
Myofibroblast differentiation is not modulated by fibrin density. RFP-infected HUVECs form capillaries when cocultured with GFP-infected fibroblasts distributed throughout the matrix. At day 7, fibroblasts are in close proximity to the developing capillary (white arrowheads) at (A) 2.5, (B) 5, and (C) 10 mg/ml (representative images). Scale bars = 40 μm. This pericyte-like behavior is indicative of a smooth muscle cell-like phenotype. (D and E) Fibroblasts express markers indicative of myofibroblast differentiation. (D) α-SMA and (E) whole fibronectin (FN) containing the extra domain-A (ED-A) splice variant as well as ED-A fragments for the indicated matrix conditions at day 3 and day 14. Immunoblots are representative of three separate experiments.
Collagen synthesis and secretion of proteins involved in the fibrinolytic cascade are unaffected by increased fibrin density
We next sought to determine whether distributing the fibroblasts enhanced matrix protein secretion and/or degradation, and thus capillary sprouting, within the dense fibrin condition. Fig. 4 A shows a representative image of a single live NHLF at day 14 within a 5 mg/ml fibrin matrix. From comparing the SHG and TPF signals, it is clear that the vast majority of collagen (excited by SHG (19)) is confined pericellularly (shown by the close association of SHG and TPF signals). Reflectance (REF) imaging shows the interaction of this cell with the surrounding matrix. For all fibrin conditions, a signal from collagen, though present, was primarily confined to the pericellular region (data not shown).
Figure 4.
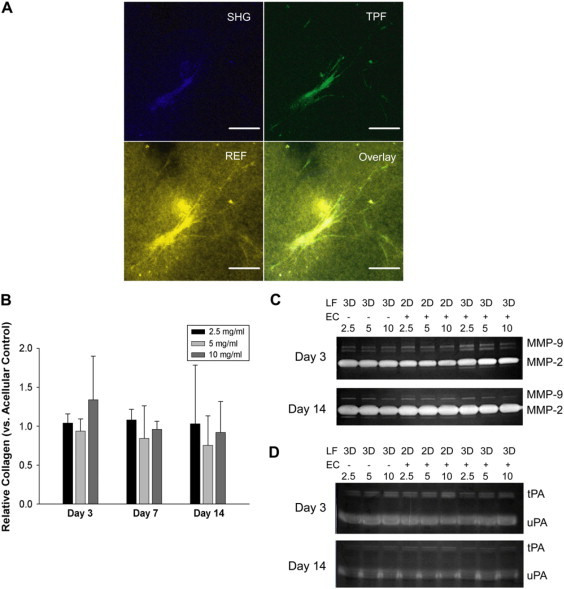
Collagen secretion, gelatinase activity, and plasminogen activator activity do not depend on fibrin density. Representative confocal image of a fibroblast at day 14 within a 5 mg/ml fibrin gel. (A) Second harmonic generation (SHG) reveals an intracellular collagen-laden signal. Two-photon fluorescence (TPF) reveals the fibroblast, whereas the REF image reveals cell-matrix interactions. Scale bars = 50 μm. (B) A quantitative collagen (Sircol) assay demonstrates that levels of newly synthesized (pepsin-soluble) collagen do not significantly change among conditions investigated. (C) Gelatin and (D) plasminogen zymography do not reveal detectable increases in the activities of MMP-9, MMP-2, tPA, or uPA at days 3 or 14 with increasing fibrin density among the indicated conditions. Zymograms shown are representative of three separate experiments.
Quantitative confirmation of this observation was accomplished through the Sircol collagen assay to determine levels of pepsin-soluble collagen. Levels of recently synthesized collagen did not vary significantly from acellular fibrin gels (negative control) for any condition probed and accordingly did not vary significantly with time or fibrin density (Fig. 4 B).
In addition to collagen synthesis, neither fibroblast cultures nor HUVEC-fibroblast cultures demonstrated appreciably altered fibrinolytic capacities in response to increased matrix density. The activities of MMP-2 and -9 were not enhanced early on (day 3) or late (day 14) as fibrin density increased in cultures containing either fibroblasts only, HUVECs with an overlaid fibroblast monolayer, or HUVECs with distributed fibroblasts (Fig. 4 C). Activities of uPA and tPA, which activate plasminogen to the fibrinolytic serine protease plasmin, displayed similar trends (Fig. 4 D).
Dense fibrin matrices restrict diffusive transport of 10-, 40-, 70-, and 150-kDa molecular mass markers
Alterations in the diffusion of soluble mediators represent an alternate mechanism possibly accounting for the enhancements in capillary formation observed when fibroblasts are distributed throughout the interstitial space. To explore diffusive transport, we utilized soft-lithography to construct a two-well, multichannel microdevice within which fibrin gels could be polymerized (illustrated schematically in Fig. 5 A, actual device shown in Fig. 5 B). Fig. 5, C and D, demonstrates that a FITC-conjugated 10-kDa molecular mass marker diffuses markedly faster through channels containing 2.5 mg/ml fibrin (Fig. 5 C) than in channels containing 10 mg/ml fibrin (Fig. 5 D). Intensity profiles versus distance through the channel were generated at separate time points, revealing transport behavior consistent with Fick's second law (Fig. 5 E). Ten mg/ml fibrin matrices yielded a significant decrease in Deff across the entire range of FITC-dextran molecular mass markers tested (represented by their hydrodynamic radius, RH) compared with 2.5 mg/ml gels (Fig. 5 F). The dependence of Deff on RH (extrapolating from the Deff value obtained for the 10-kDa marker) for each fibrin concentration was compared with values predicted by the Wilke-Chang empirical relation and the Stokes-Einstein equation (Fig. 5 F), which state that diffusion through an aqueous medium is inversely dependent on the RH of the diffusing molecule to the power of 1.8 or to the power of 1, respectively (20,21).
Figure 5.
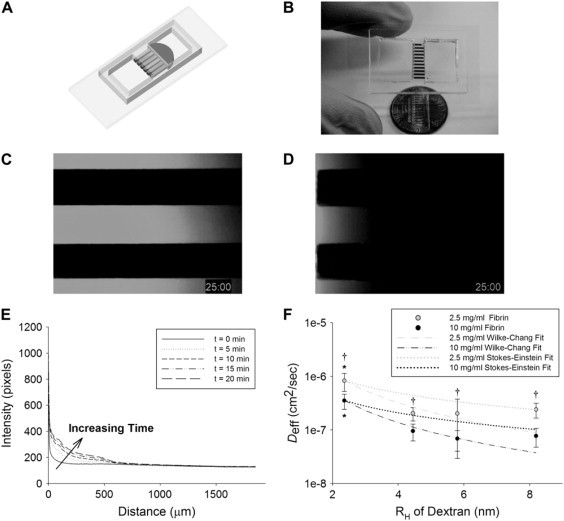
Fibrin density significantly influences molecular diffusivity. (A) Fibrinogen solutions at 2.5 or 10 mg/ml were wicked by capillary action into 500 × 300 × 3000 μm channels and clotted as shown in this SolidWorks representation. (B) The actual device loaded with red dye. Imaging 10 kDa FITC-dextran movement through these channels reveals restricted diffusion of the marker in a (D) 10 mg/ml gel versus a (C) 2.5 mg/ml gel at a sample time point (t = 25 min). Line scanning of fluorescent marker diffusive transport through the channel at discrete time points produced (E) an intensity profile over time similar to that described by Fick's second law. (F) Values of the molecular diffusivity, Deff, for 10-, 40-, 70-, and 150-kDa markers in 2.5 (gray data points) and 10 mg/ml (black) fibrin gels were quantified as described in Methods. Anticipated dependence of the diffusivity on RH was extrapolated from the measured 10-kDa values using the Wilke-Chang empirical model (dashed lines) and the Stokes-Einstein equation (dotted lines). Data points are representative of seven separate experiments quantified in triplicate. Asterisk denotes statistical significance (*p < 0.05) between 10-kDa molecular mass markers and all others within the same fibrin concentration, Dagger denotes significance (†p < 0.05) among different fibrin concentrations for markers with the same molecular mass/RH.
Discussion
The role of the ECM in regulating capillary morphogenesis is only partially understood, and a more complete understanding of its role is necessary to facilitate therapeutic applications to aid tissue engineering approaches and combat pathologic processes such as cancer and fibrosis. Utilizing a truly 3-D in vitro model of angiogenesis, we have demonstrated that increasing the density of fibrin significantly inhibits the formation of capillary networks. This restriction can be overcome by distributing a stromal cell (in this study, fibroblasts) throughout the matrix (Fig. 1).
We previously postulated that 10 mg/ml fibrin matrices, with compressive stiffness values on a par with that of skeletal muscle, would make useful tissue engineering scaffolds (8). The functionality of these dense, vascularized tissue constructs was confirmed by implanting them within immune-compromised mice and demonstrating perfusion within HUVEC-lined vessels as a result of anastomosing with the host vasculature (Fig. 2, A and B). Fibroblasts have previously been shown to support the formation of patent capillaries in vitro (11), and they may help induce vessel penetration in vivo, as tissues lacking these cells provided no evidence of perfusion (Fig. 2 D). In addition, although collagen gels seeded with HUVECs have been shown to anastomose with mouse vasculature (13,22), this is the first study to demonstrate that mature HUVEC capillaries supported by fibroblasts in a dense fibrin gel will inosculate with mouse vasculature as well. Whereas future studies will focus on how prevascularization affects oxygen delivery and the survival of implanted cells, this study focused on the underlying mechanism of how distributing fibroblasts can overcome a dense matrix to stimulate capillary formation in vitro.
We initially hypothesized that increased matrix remodeling by the fibroblasts was responsible for this behavior. Physiologically, fibroblasts differentiate into the highly contractile myofibroblast phenotype in response to a variety of factors during wound healing (16,23), including increases in matrix stiffness (24) and TGF-β1 stimulation (25,26). The extent of this differentiation, marked by levels of α-SMA expression, is directly proportional to the tractional force exerted by myofibroblasts (17), potentially enabling these cells to pull apart the denser matrix and facilitate capillary penetration. However, although fibroblast differentiation into mature myofibroblasts was observed as early as day 3, levels of α-SMA expressed by these cells were not sensitive to changes in fibrin density through day 14 (Fig. 3 D). Furthermore, the ability of fibroblasts to act in a pericyte-like fashion when distributed throughout the matrix (Fig. 3, A–C) is also unlikely to contribute to increases in network lengths, given our evidence that this occurs across all matrix densities. Additionally, pericyte incorporation is a stabilizing mechanism that instead prevents capillary branching at sites of association via local MMP down-regulation (27,28).
In the absence of density-induced upregulation of myofibroblast-mediated matrix remodeling, modification of the fibrin matrix through ECM protein deposition or proteolysis was examined. Fibronectin containing the ED-A fragment is not only an inducer of myofibroblast differentiation, but fibronectin fragments have been shown to enhance endothelial cell proliferation and migration (29). Meanwhile, fibroblast-mediated collagen deposition is a crucial mediator of capillary morphogenesis in other in vitro systems (30). In this system, fibronectin deposition (Fig. 3 E) and collagen secretion (Fig. 4, A and B) were unchanged with fibrin density; in fact, secreted levels of collagen appeared insignificant.
MMP-2 and -9 are soluble members of the MMP family that are secreted by cells in the interstitial space and act in a variety of capacities to promote angiogenesis (31). Specifically, MMP-2 activation by membrane-bound proteases at the endothelial cell surface results in matrix proteolysis and activation of other MMPs, including MMP-9 (32), whereas active MMP-9 itself is fibrinolytic (33) and also liberates matrix-bound VEGF from the matrix (34). In our study, activities of these MMPs were not modulated by fibrin density (Fig. 4 C). Similarly, functions of the soluble serine protease plasmin, activated at the cell surface via uPA and elsewhere by fibrin-bound tPA, include fibrin degradation and MMP activation (35). Levels of uPA and tPA activities were unchanged despite increased fibrin density (Fig. 4 D).
It is important to note, however, that pericellular activity is critical to mediating capillary formation (36,37) and that the amounts of active MMP-2/-9, uPA, and tPA measured in our system reflect bulk levels present throughout the matrix. These measurements are not necessarily indicative of enzyme activity in the immediate vicinity of the capillary. Nonetheless, the notion that robust sprouting takes place in low-density monolayer cultures but not in high-density cultures despite similar levels in activity of these fibrinolytic activators/agents (Fig. 4, C and D) suggests that insoluble cues (e.g., stiffness) derived from increased matrix density are likely not modulating fibroblast secretion of protease precursors. Rather, these data suggest that transport of latent gelatinases and plasminogen/plasmin is hindered in the 10 mg/ml matrices, resulting in reduced levels of these soluble proteins reaching the capillaries.
After obtaining these results, we pursued an alternate hypothesis and chose to focus on limitations in the transport of macromolecules that may result from increasing fibrin concentration from 2.5 to 10 mg/ml. Because interstitial tissue is inherently heterogeneous (38), analyzing diffusion over short length (order of micrometers) and time scales (order of seconds) through interstitial tissue reveals two distinct diffusing populations as a result of their interactions with the aqueous and viscous phases of the tissue (39). We have measured diffusions over length (order of millimeters) and timescales (order of minutes) that capture both of these phases (Fig. 5 E) and as such have termed the measured transport phenomenon Deff. The effective diffusion coefficient (Deff) obtained for each molecular mass marker (10, 40, 70, and 150 kDa) for both fibrin conditions tested was effectively bounded by the Wilke-Chang correlation and the Stokes-Einstein relationship (Fig. 5 F). Both equations describe binary (solute A in solvent B) diffusion in liquids (20,21). The former effectively predicts that D is inversely proportional to solute whereas the latter predicts that D is inversely proportional to RH. D would thus be expected to decrease with increasing molecular mass because increased molecular mass implies increased RH.
The reduced diffusivity when molecular mass (and thus RH) is held constant but fibrin concentration is increased can be attributed to the increased viscosity of the solution. Both the Wilke-Chang and Stokes-Einstein relationships predict that D is inversely proportional to solvent (i.e., fibrin matrix) viscosity. Increasing the fibrin content drastically increases the fiber and branchpoint densities while not significantly altering fiber diameter (4). This increases the viscous component of the hydrogel and is likely responsible for the observed decreases in Deff over all molecular masses tested. As the concentration of fibrin increased from 2.5 to 10 mg/ml (fourfold), dextran Deff was reduced two- to threefold. Because the Stokes-Einstein equation specifies an inverse relationship between D and solvent viscosity, a 10 mg/ml gel is thus expected to be nearly three times more viscous than a 2.5 mg/ml gel. This is indeed the case when the clottable fraction of these gels is considered (40).
There is precedence in the literature for increased matrix density adversely affecting transport properties. A threefold increase in fibrin density decreases the aqueous permeability of the hydrogel by over an order of magnitude (41). Other hydrogels exhibit similar behavior. For example, an increase in collagen concentration of a similar magnitude to the increase in fibrin concentration tested in this study reduces the D by 50% as RH increases (42). Comparable results have also been obtained in vivo with increased collagen content within the tumor interstitium (43) or by comparing transport within neoplastic tissue to that within relatively dense granulation tissue (44). Moreover, variations in structures among discrete hydrogel types can influence measured values of D; relatively broad variations have been measured among agarose, alginate, fibrin, and gelatin (45). Finally, our own research group has demonstrated that capillary formation in this model is significantly reduced when the distance separating the fibroblast monolayers is increased to more than 3 mm (12), suggesting a significant diffusion limitation of a fibroblast-derived mediator.
The observed reduction in molecular-level diffusive transport is significant in our system only if the concentration profile of growth factors was significantly altered in the time and physical dimensions of our experiments. To simulate the functional result of decreasing Deff, Eq. 1 was solved by applying the following initial and boundary conditions to simulate the HUVEC-fibroblast monolayer culture:
| (8) |
| (9) |
| (10) |
These conditions simulate a soluble macromolecule (e.g., a protein), initially at a concentration Co (Eq. 8), produced at a constant rate, Fp, at the gel surface (z = 0) by fibroblasts (Eq. 9) and consumed when it reaches the HUVEC by diffusion at the bottom of the gel (a distance L away, Eq. 10). Solving for these conditions generates the following solution for the concentration profile of a factor:
| (11) |
where m = 1, 3, 5, …, are the eigenvalues, and C is the concentration of the macromolecule in the gel as a function of position and time. Because the identities of the fibroblast-derived factors that facilitate angiogenesis within this system are unknown (11), reasonable values were chosen for the following parameters: L was set at 0.25 cm, Fp = 4.94 × 10−19 mol/s (46), and Co = 0 for a solely fibroblast-derived factor. Fig. 6 plots C as a function of position and time (each line represents a 12-h interval), where Deff = 10−6 cm2/s (Fig. 6 A), Deff = 10−7 cm2/s (Fig. 6 B), and Deff = 10−8 cm2/s (Fig. 6 C). The resulting gradients demonstrate that the time to reach steady state (i.e., achieve a concentration profile that does not vary with time) shifts from hours (Deff = 10−6 cm2/s) to days (Deff = 10−7 cm2/s) to over a week (Deff = 10−8 cm2/s). Although rapidly achieving steady state is not necessarily a requirement for capillary morphogenesis, it is indicative of the time scale over which diffusion of a given macromolecule occurs. Reduced diffusivity in denser matrices thus signifies delayed availability of proangiogenic molecules as a result of hindered transport. Further, in light of recent findings that stable VEGF concentration gradients generated by myoblasts with lower Fp promote far more normalized angiogenesis compared with myoblasts heterogeneously producing more prolific levels of VEGF (46), the time required to achieve a steady state (i.e., stable) concentration gradient for a given factor may be pertinent.
Figure 6.
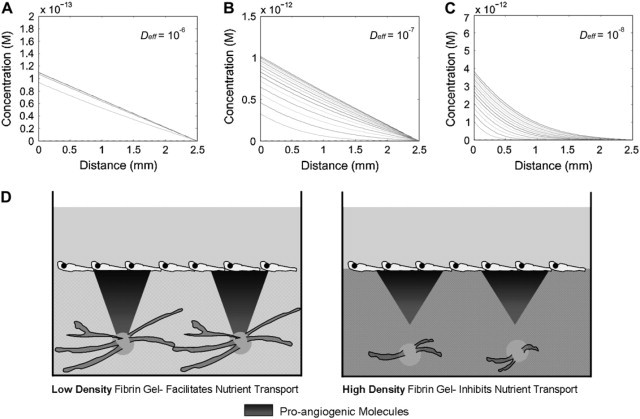
Proposed mechanism by which diffusion limitations imposed by denser matrices restrict angiogenic sprouting. Modeling concentration profiles within the 3-D coculture system reveals that the time to achieve steady state is drastically altered with decreased Deff as shown when (A) Deff = 10−6 cm2/s, (B) Deff = 10−7 cm2/s, and (C) Deff = 10−8 cm2/s. Shaded lines indicate concentration profiles at 12-h intervals up to 1 week (hence, 14 total solid lines). (D) Comparison of these results with those shown in Fig. 5F suggests that a possible mechanism for the observed reduction in angiogenesis is the restricted transport of proangiogenic factors as fibrin density increases. In sparse matrices (e.g., 2.5 mg/ml fibrin, left panel), transport of proangiogenic molecules proceeds rapidly, facilitating robust sprouting, although their transport in denser matrices (e.g., 10 mg/ml fibrin, right panel) is restricted, resulting in reduced capillary morphogenesis.
Fig. 6 D schematically illustrates how the concentration profiles of fibroblast-derived proangiogenic factors could be altered at an early time point (t = 12 h) in a sparse rather than dense matrix. Although transport would be relatively efficient in a 2.5 mg/ml fibrin gel, transport of larger proangiogenic factors such as VEGF165 (38.5 kDa), HGF (85 kDa), and MMP-2 (72 kDa (latent)) would be significantly slower in a 10 mg/ml gel.
One caveat to interpreting the measurements of Deff is that fluorescently conjugated dextran particles were used to approximate physiological proteins. Comparing dextran to proteins of the same molecular mass reveals differences in structure, charge, and susceptibility to matrix binding, which are all likely to affect the transport of physiological proteins. Dextran macromolecules have a very flexible, randomly coiled structure that is easily hydrated, whereas proteins have a more condensed structure. Thus, a protein of a comparable molecular mass to dextran may possess a smaller RH (47). Both the Wilke-Chang correlation and Stokes-Einstein equation predict that molecular diffusivity is inversely related to RH (20,21); however, the relative difference between Deff measured in 2.5 mg/ml and 10 mg/ml fibrin would be unchanged. Furthermore, the potentially smaller RH would likely be countered by charge and binding interactions between a protein and the fibrin matrix, interactions that are not captured by the use of dextran (48). For example, proangiogenic growth factors such as VEGF and bFGF bind specifically to fibrin; greater concentrations of fibrin serve to bind higher amounts of these growth factors and further restrict their net transport through the matrix (49,50). In addition, heparin-mediated binding of these proteins, as well as HGF, to the matrix is also likely to slow transport through the interstitium (51–53). Thus, when all of these factors are taken into account, the overall difference in Deff measured between 2.5 and 10 mg/ml matrices is expected to be even more pronounced.
In summary, we have shown that increasing matrix density reduces capillary network formation and that this effect can be abrogated by distributing fibroblasts throughout the matrix. The robust capillary networks that form in the dense gel as a result of interstitial fibroblast distribution are functional, as evidenced by the fact that on implantation they anastomose with mouse vasculature and carry blood. Network formation within dense gels occurs despite the fact that distributed fibroblasts fail to upregulate their ability to remodel the matrix in response to the denser microenvironment. Instead, enhanced diffusion of fibroblast-mediated factors is likely responsible for the observed effect. Although this result certainly does not rule out the contributions of matrix stiffness and ligand binding density in mediating this morphogenetic process, we believe that our data cast a prominent light on the role of diffusive transport limitations associated with increased matrix density in regulating angiogenesis and potentially other morphogenetic processes.
Acknowledgments
We gratefully acknowledge Dr. Frank Meyskens, Christopher Raub, David Shelley, Dr. Hye-Won Shin, Dr. Jay Unruh, and Carlos Huang for stimulating discussion and/or helpful technical insight. We are also thankful to Dr. Roger Tsien, University of California, San Diego, for the kind gift of the pCDNA3-mcherry vector.
Support for this work was provided by the National Institutes of Health (R01HL085339 to A.J.P. and R01HL067954 to S.C.G.). C.M.G. is partially supported by the Achievement Rewards for College Scientists Foundation and the Arnold and Mabel Beckman Foundation.
Footnotes
Editor: Elliot L. Elson.
References
- 1.Brown L.F., Van de Water L., Harvey V.S., Dvorak H.F. Fibrinogen influx and accumulation of cross-linked fibrin in healing wounds and in tumor stroma. Am. J. Pathol. 1988;130:455–465. [PMC free article] [PubMed] [Google Scholar]
- 2.Kalluri R., Zeisberg M. Fibroblasts in cancer. Nat. Rev. Cancer. 2006;6:392–401. doi: 10.1038/nrc1877. [DOI] [PubMed] [Google Scholar]
- 3.Ingber D.E. Mechanical signaling and the cellular response to extracellular matrix in angiogenesis and cardiovascular physiology. Circ. Res. 2002;91:877–887. doi: 10.1161/01.res.0000039537.73816.e5. [DOI] [PubMed] [Google Scholar]
- 4.Ryan E.A., Mockros L.F., Weisel J.W., Lorand L. Structural origins of fibrin clot rheology. Biophys. J. 1999;77:2813–2826. doi: 10.1016/S0006-3495(99)77113-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mooney D.J., Mikos A.G. Growing new organs. Sci. Am. 1999;280:60–65. doi: 10.1038/scientificamerican0499-60. [DOI] [PubMed] [Google Scholar]
- 6.Levenberg S., Rouwkema J., Macdonald M., Garfein E.S., Kohane D.S., Darland D.C., Marini R., van Blitterswijk C.A., Mulligan R.C., D’Amore P.A., Langer R. Engineering vascularized skeletal muscle tissue. Nat. Biotechnol. 2005;23:879–884. doi: 10.1038/nbt1109. [DOI] [PubMed] [Google Scholar]
- 7.Deroanne C.F., Lapiere C.M., Nusgens B.V. vitro tubulogenesis of endothelial cells by relaxation of the coupling extracellular matrix-cytoskeleton. Cardiovasc. Res. 2001;49:647–658. doi: 10.1016/s0008-6363(00)00233-9. [DOI] [PubMed] [Google Scholar]
- 8.Ghajar C.M., Blevins K.S., Hughes C.C., George S.C., Putnam A.J. Mesenchymal stem cells enhance angiogenesis in mechanically viable prevascularized tissues via early matrix metalloproteinase upregulation. Tissue Eng. 2006;12:2875–2888. doi: 10.1089/ten.2006.12.2875. [DOI] [PubMed] [Google Scholar]
- 9.Ingber D.E., Folkman J. Mechanochemical switching between growth and differentiation during fibroblast growth factor-stimulated angiogenesis in vitro: role of extracellular matrix. J. Cell Biol. 1989;109:317–330. doi: 10.1083/jcb.109.1.317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Urech L., Bittermann A.G., Hubbell J.A., Hall H. Mechanical properties, proteolytic degradability and biological modifications affect angiogenic process extension into native and modified fibrin matrices in vitro. Biomaterials. 2005;26:1369–1379. doi: 10.1016/j.biomaterials.2004.04.045. [DOI] [PubMed] [Google Scholar]
- 11.Nakatsu M.N., Sainson R.C., Aoto J.N., Taylor K.L., Aitkenhead M., Perez-del-Pulgar S., Carpenter P.M., Hughes C.C. Angiogenic sprouting and capillary lumen formation modeled by human umbilical vein endothelial cells (HUVEC) in fibrin gels: the role of fibroblasts and angiopoietin-1. Microvasc. Res. 2003;66:102–112. doi: 10.1016/s0026-2862(03)00045-1. [DOI] [PubMed] [Google Scholar]
- 12.Griffith C.K., Miller C., Sainson R.C., Calvert J.W., Jeon N.L., Hughes C.C., George S.C. Diffusion limits of an in vitro thick prevascularized tissue. Tissue Eng. 2005;11:257–266. doi: 10.1089/ten.2005.11.257. [DOI] [PubMed] [Google Scholar]
- 13.Schechner J.S., Nath A.K., Zheng L., Kluger M.S., Hughes C.C., Sierra-Honigmann M.R., Lorber M.I., Tellides G., Kashgarian M., Bothwell A.L., Pober J.S. vivo formation of complex microvessels lined by human endothelial cells in an immunodeficient mouse. Proc. Natl. Acad. Sci. USA. 2000;97:9191–9196. doi: 10.1073/pnas.150242297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Raub C.B., Suresh V., Krasieva T., Lyubovitsky J., Mih J.D., Putnam A.J., Tromberg B.J., George S.C. Noninvasive assessment of collagen gel microstructure and mechanics using multiphoton microscopy. Biophys. J. 2007;92:2212–2222. doi: 10.1529/biophysj.106.097998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Taylor A.M., Blurton-Jones M., Rhee S.W., Cribbs D.H., Cotman C.W., Jeon N.L. A microfluidic culture platform for CNS axonal injury, regeneration and transport. Nat. Methods. 2005;2:599–605. doi: 10.1038/nmeth777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tomasek J.J., Gabbiani G., Hinz B., Chaponnier C., Brown R.A. Myofibroblasts and mechano-regulation of connective tissue remodelling. Nat. Rev. Mol. Cell Biol. 2002;3:349–363. doi: 10.1038/nrm809. [DOI] [PubMed] [Google Scholar]
- 17.Chen J., Li H., SundarRaj N., Wang J.H. α-smooth muscle actin expression enhances cell traction force. Cell Motil. Cytoskeleton. 2007;64:248–257. doi: 10.1002/cm.20178. [DOI] [PubMed] [Google Scholar]
- 18.Armulik A., Abramsson A., Betsholtz C. Endothelial/pericyte interactions. Circ. Res. 2005;97:512–523. doi: 10.1161/01.RES.0000182903.16652.d7. [DOI] [PubMed] [Google Scholar]
- 19.Zoumi A., Yeh A., Tromberg B.J. Imaging cells and extracellular matrix in vivo by using second-harmonic generation and two-photon excited fluorescence. Proc. Natl. Acad. Sci. USA. 2002;99:11014–11019. doi: 10.1073/pnas.172368799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Welty J.R., Wicks C.E., Wilson R.E. John Wiley & Sons; Hoboken, NJ: 1984. Fundamentals of momentum, heat, and mass transfer. [Google Scholar]
- 21.Cussler E.L. Cambridge University Press; Cambridge, UK: 1999. Diffusion: mass transfer in fluid systems. [Google Scholar]
- 22.Tremblay P.L., Hudon V., Berthod F., Germain L., Auger F.A. Inosculation of tissue-engineered capillaries with the host's vasculature in a reconstructed skin transplanted on mice. Am. J. Transplant. 2005;5:1002–1010. doi: 10.1111/j.1600-6143.2005.00790.x. [DOI] [PubMed] [Google Scholar]
- 23.Gabbiani G. The myofibroblast in wound healing and fibrocontractive diseases. J. Pathol. 2003;200:500–503. doi: 10.1002/path.1427. [DOI] [PubMed] [Google Scholar]
- 24.Arora P.D., Narani N., McCulloch C.A. The compliance of collagen gels regulates transforming growth factor-β induction of α-smooth muscle actin in fibroblasts. Am. J. Pathol. 1999;154:871–882. doi: 10.1016/s0002-9440(10)65334-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Desmouliere A., Geinoz A., Gabbiani F., Gabbiani G. Transforming growth factor-β 1 induces α-smooth muscle actin expression in granulation tissue myofibroblasts and in quiescent and growing cultured fibroblasts. J. Cell Biol. 1993;122:103–111. doi: 10.1083/jcb.122.1.103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Vaughan M.B., Howard E.W., Tomasek J.J. Transforming growth factor-β1 promotes the morphological and functional differentiation of the myofibroblast. Exp. Cell Res. 2000;257:180–189. doi: 10.1006/excr.2000.4869. [DOI] [PubMed] [Google Scholar]
- 27.Saunders W.B., Bohnsack B.L., Faske J.B., Anthis N.J., Bayless K.J., Hirschi K.K., Davis G.E. Coregulation of vascular tube stabilization by endothelial cell TIMP-2 and pericyte TIMP-3. J. Cell Biol. 2006;175:179–191. doi: 10.1083/jcb.200603176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yana I., Sagara H., Takaki S., Takatsu K., Nakamura K., Nakao K., Katsuki M., Taniguchi S., Aoki T., Sato H., Weiss S.J., Seiki M. Crosstalk between neovessels and mural cells directs the site-specific expression of MT1-MMP to endothelial tip cells. J. Cell Sci. 2007;120:1607–1614. doi: 10.1242/jcs.000679. [DOI] [PubMed] [Google Scholar]
- 29.Grant M.B., Caballero S., Bush D.M., Spoerri P.E. Fibronectin fragments modulate human retinal capillary cell proliferation and migration. Diabetes. 1998;47:1335–1340. doi: 10.2337/diab.47.8.1335. [DOI] [PubMed] [Google Scholar]
- 30.Berthod F., Germain L., Tremblay N., Auger F.A. Extracellular matrix deposition by fibroblasts is necessary to promote capillary-like tube formation in vitro. J. Cell. Physiol. 2006;207:491–498. doi: 10.1002/jcp.20584. [DOI] [PubMed] [Google Scholar]
- 31.Page-McCaw A., Ewald A.J., Werb Z. Matrix metalloproteinases and the regulation of tissue remodelling. Nat. Rev. Mol. Cell Biol. 2007;8:221–233. doi: 10.1038/nrm2125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Visse R., Nagase H. Matrix metalloproteinases and tissue inhibitors of metalloproteinases: structure, function, and biochemistry. Circ. Res. 2003;92:827–839. doi: 10.1161/01.RES.0000070112.80711.3D. [DOI] [PubMed] [Google Scholar]
- 33.Sternlicht M.D., Werb Z. How matrix metalloproteinases regulate cell behavior. Annu. Rev. Cell Dev. Biol. 2001;17:463–516. doi: 10.1146/annurev.cellbio.17.1.463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bergers G., Brekken R., McMahon G., Vu T.H., Itoh T., Tamaki K., Tanzawa K., Thorpe P., Itohara S., Werb Z., Hanahan D. Matrix metalloproteinase-9 triggers the angiogenic switch during carcinogenesis. Nat. Cell Biol. 2000;2:737–744. doi: 10.1038/35036374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.van Hinsbergh V.W., Engelse M.A., Quax P.H. Pericellular proteases in angiogenesis and vasculogenesis. Arterioscler. Thromb. Vasc. Biol. 2006;26:716–728. doi: 10.1161/01.ATV.0000209518.58252.17. [DOI] [PubMed] [Google Scholar]
- 36.Hiraoka N., Allen E., Apel I.J., Gyetko M.R., Weiss S.J. Matrix metalloproteinases regulate neovascularization by acting as pericellular fibrinolysins. Cell. 1998;95:365–377. doi: 10.1016/s0092-8674(00)81768-7. [DOI] [PubMed] [Google Scholar]
- 37.Hotary K.B., Yana I., Sabeh F., Li X.Y., Holmbeck K., Birkedal-Hansen H., Allen E.D., Hiraoka N., Weiss S.J. Matrix metalloproteinases (MMPs) regulate fibrin-invasive activity via MT1-MMP-dependent and -independent processes. J. Exp. Med. 2002;195:295–308. doi: 10.1084/jem.20010815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gehrke S.H., Fisher J.P., Palasis M., Lund M.E. Factors determining hydrogel permeability. Ann. N. Y. Acad. Sci. 1997;831:179–207. doi: 10.1111/j.1749-6632.1997.tb52194.x. [DOI] [PubMed] [Google Scholar]
- 39.Alexandrakis G., Brown E.B., Tong R.T., McKee T.D., Campbell R.B., Boucher Y., Jain R.K. Two-photon fluorescence correlation microscopy reveals the two-phase nature of transport in tumors. Nat. Med. 2004;10:203–207. doi: 10.1038/nm981. [DOI] [PubMed] [Google Scholar]
- 40.Roberts W.W., Kramer O., Rosser R.W., Nestler F.H., Ferry J.D. Rheology of fibrin clots. I. Dynamic viscoelastic properties and fluid permeation. Biophys. Chem. 1974;1:152–160. doi: 10.1016/0301-4622(74)80002-5. [DOI] [PubMed] [Google Scholar]
- 41.Rosser R.W., Roberts W.W., Ferry J.D. Rheology of fibrin clots. IV. Darcy constants and fiber thickness. Biophys. Chem. 1977;7:153–157. doi: 10.1016/0301-4622(77)80008-2. [DOI] [PubMed] [Google Scholar]
- 42.Ramanujan S., Pluen A., McKee T.D., Brown E.B., Boucher Y., Jain R.K. Diffusion and convection in collagen gels: implications for transport in the tumor interstitium. Biophys. J. 2002;83:1650–1660. doi: 10.1016/S0006-3495(02)73933-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Netti P.A., Berk D.A., Swartz M.A., Grodzinsky A.J., Jain R.K. Role of extracellular matrix assembly in interstitial transport in solid tumors. Cancer Res. 2000;60:2497–2503. [PubMed] [Google Scholar]
- 44.Nugent L.J., Jain R.K. Extravascular diffusion in normal and neoplastic tissues. Cancer Res. 1984;44:238–244. [PubMed] [Google Scholar]
- 45.Leddy H.A., Awad H.A., Guilak F. Molecular diffusion in tissue-engineered cartilage constructs: effects of scaffold material, time, and culture conditions. J. Biomed. Mater. Res. B Appl. Biomater. 2004;70:397–406. doi: 10.1002/jbm.b.30053. [DOI] [PubMed] [Google Scholar]
- 46.Ozawa C.R., Banfi A., Glazer N.L., Thurston G., Springer M.L., Kraft P.E., McDonald D.M., Blau H.M. Microenvironmental VEGF concentration, not total dose, determines a threshold between normal and aberrant angiogenesis. J. Clin. Invest. 2004;113:516–527. doi: 10.1172/JCI18420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Arrio-Dupont M., Cribier S., Foucault G., Devaux P.F., d’Albis A. Diffusion of fluorescently labeled macromolecules in cultured muscle cells. Biophys. J. 1996;70:2327–2332. doi: 10.1016/S0006-3495(96)79798-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Luby-Phelps K., Taylor D.L., Lanni F. Probing the structure of cytoplasm. J. Cell Biol. 1986;102:2015–2022. doi: 10.1083/jcb.102.6.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sahni A., Francis C.W. Vascular endothelial growth factor binds to fibrinogen and fibrin and stimulates endothelial cell proliferation. Blood. 2000;96:3772–3778. [PubMed] [Google Scholar]
- 50.Sahni A., Odrljin T., Francis C.W. Binding of basic fibroblast growth factor to fibrinogen and fibrin. J. Biol. Chem. 1998;273:7554–7559. doi: 10.1074/jbc.273.13.7554. [DOI] [PubMed] [Google Scholar]
- 51.Ferrara N., Gerber H.P., LeCouter J. The biology of VEGF and its receptors. Nat. Med. 2003;9:669–676. doi: 10.1038/nm0603-669. [DOI] [PubMed] [Google Scholar]
- 52.Whitelock J.M., Murdoch A.D., Iozzo R.V., Underwood P.A. The degradation of human endothelial cell-derived perlecan and release of bound basic fibroblast growth factor by stromelysin, collagenase, plasmin, and heparanases. J. Biol. Chem. 1996;271:10079–10086. doi: 10.1074/jbc.271.17.10079. [DOI] [PubMed] [Google Scholar]
- 53.Zioncheck T.F., Richardson L., Liu J., Chang L., King K.L., Bennett G.L., Fugedi P., Chamow S.M., Schwall R.H., Stack R.J. Sulfated oligosaccharides promote hepatocyte growth factor association and govern its mitogenic activity. J. Biol. Chem. 1995;270:16871–16878. doi: 10.1074/jbc.270.28.16871. [DOI] [PubMed] [Google Scholar]


