Role of Exchange and Dipolar Interactions in the Radical Pair Model of the Avian Magnetic Compass

Abstract

It is not yet understood how migratory birds sense the Earth's magnetic field as a source of compass information. One suggestion is that the magnetoreceptor involves a photochemical reaction whose product yields are sensitive to external magnetic fields. Specifically, a flavin-tryptophan radical pair is supposedly formed by photoinduced sequential electron transfer along a chain of three tryptophan residues in a cryptochrome flavoprotein immobilized in the retina. The electron Zeeman interaction with the Earth's magnetic field (∼50 μT), modulated by anisotropic magnetic interactions within the radicals, causes the product yields to depend on the orientation of the receptor. According to well-established theory, the radicals would need to be separated by >3.5 nm in order that interradical spin-spin interactions are weak enough to permit a ∼50 μT field to have a significant effect. Using quantum mechanical simulations, it is shown here that substantial changes in product yields can nevertheless be expected at the much smaller separation of 2.0 ± 0.2 nm where the effects of exchange and dipolar interactions partially cancel. The terminal flavin-tryptophan radical pair in cryptochrome has a separation of ∼1.9 nm and is thus ideally placed to act as a magnetoreceptor for the compass mechanism.

Introduction

It has been suggested that the ability of migratory birds to extract compass information from the geomagnetic field (reviewed in (1–4)) is derived from a magnetic field-sensitive chemical reaction (5–8). Behavioral (9,10), biological (11,12), theoretical (13–17), and other (18) evidence is steadily accumulating to support this hypothesis, the idea being that a photochemical reaction in the retina produces an immobilized transient radical pair whose subsequent chemical fate is influenced by the orientation of the bird's head with respect to the Earth's magnetic field (8). The other principal proposed mechanism of avian magnetoreception centers on magnetic iron minerals in the beak that appear to act as a magnetometer, allowing birds to determine their geographic position (19,20). Here we focus on the mechanism of compass orientation.

Ritz et al. have proposed that a radical pair magnetoreceptor is formed by photoinduced intramolecular electron transfers in a cryptochrome (8). Cryptochromes are 50–90 kDa blue-light photoreceptor flavoproteins that regulate a variety of processes in organisms ranging from bacteria to humans (reviewed in (21)). They exhibit high sequence-homology and structural similarity to DNA photolyases, which are light-dependent flavoenzymes that repair DNA damaged by ultraviolet light (reviewed in (22,23)). Relatively little is known about the photocycle of cryptochromes; however, there are similarities (24,25) to the photoactivation reaction of photolyases (26) and it has been suggested that excitation of the fully oxidized flavin adenine dinucleotide (FAD) chromophore leads to sequential intraprotein electron transfer along a chain of three tryptophan residues, the Trp triad (23,27,28). Although no effects of applied magnetic fields on the photoresponses of photolyases have yet been reported, time-resolved electron paramagnetic resonance (EPR) spectroscopy has clearly shown that the light-induced flavin-tryptophan and flavin-tyrosine radical pairs formed in photolyases possess the electron spin-correlation that is a necessary but not sufficient condition for magnetosensitivity (29,30). A well-established precedent for comparatively large magnetic field effects on photoinduced radical pairs in proteins, and for the conservation of spin correlation in sequential steps along an electron transport chain, is provided by the photosynthetic reaction center proteins of both bacteria and plants (29,31–33).

In plants, two cryptochromes, Cry1 and Cry2, mediate a number of photoresponses, including blue-light inhibition of hypocotyl (stem) elongation and entrainment of the circadian clock (21). Very recently, Ahmad and colleagues (18) have observed enhanced cryptochrome-mediated hypocotyl growth inhibition in Arabidopsis thaliana in a 500 μT magnetic field under blue-light irradiation but not under red light (where the mediating photoreceptors are phytochromes), nor in total darkness. No magnetic field effects were found in Cry-deficient mutants. Blue-light-induced degradation of Cry2 and blue-light-dependent anthocyanin accumulation—another cryptochrome-dependent process—were also enhanced at 500 μT (18). These observations have been interpreted in terms of a radical pair model, by analogy with photolyase.

The ability of a magnetic field to affect the product yields of a free radical process may be understood by reference to the simple reaction shown in Scheme 1. A spin-conserving electron transfer reaction (not shown) from a donor molecule D to an acceptor molecule A creates a spin-correlated radical pair [D^·+ A^·−], either in a singlet state S (with total electron spin angular momentum quantum number S = 0) or a triplet state T (with S = 1), depending on the spin states of the precursors, D and A. The relative yields of the products, ^SP and ^TP, formed by reaction of ^S[D^·+ A^·−] and ^T[D^·+ A^·−], respectively, are controlled by the rate constants of those reactions (k_S and k_T in Scheme 1) but also by the coherent interconversion of ^S[D^·+ A^·−] and ^T[D^·+ A^·−] (indicated by curved arrows in Scheme 1). S ↔ T interconversion is mediated by the various magnetic interactions within and between the two radicals, including the Zeeman interaction of the two electron spins with an external magnetic field, in this case, the Earth's magnetic field. Thus, if the external field enhances the efficiency of S ↔ T interconversion the result, for a radical pair initially in the S state, is an increase in the yield of ^TP and a corresponding decrease in that of ^SP. This model, known as the radical-pair mechanism, accounts for a wide range of magnetic effects on the chemistry of free radicals (33–40). However, to act as a compass, the radical pair must respond to the direction of the external field as well as to its amplitude. This can be achieved with a spatially ordered array of donor-acceptor molecules (1), at least in principle, if the radicals are immobilized and the electron spins have anisotropic local magnetic interactions, the most likely being the hyperfine couplings to high-abundance magnetic nuclei (e.g., ¹H and ¹⁴N). Thus, the S ↔ T interconversion and therefore the reaction yields should depend on the orientation of the radical pair and, by extension, the orientation of the bird's head, with respect to the direction of the external field (5–8,14).

Scheme 1.

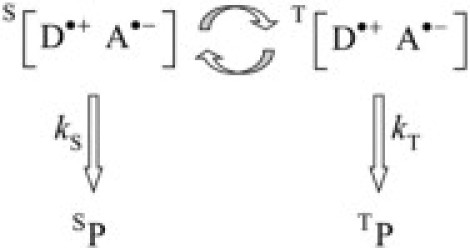
The chemical effects of weak external magnetic fields, including the radical pair model of avian magnetoreception, have been explored extensively by means of quantum mechanical simulations of simple reaction schemes (e.g., Scheme 1). These take into account the spin evolution described above, together with the spin-selective formation and disappearance of the S and T states of the radical pair (8,14–16,41–44). A number of simplifying approximations are commonly employed in these calculations, either to render the problem computationally tractable or to enable general trends and principles to be extracted. In the context of magnetoreception, typical assumptions are that the hyperfine interactions are isotropic or axially anisotropic; that the S and T states of the pair recombine at equal rates; that the two radicals are completely immobile; that spin relaxation is negligibly slow; and that the spin-spin interactions between the two radicals are negligible. This last assumption, which appears to be universal in theoretical treatments of avian magnetoreception, is the most likely to be misleading.

Interradical exchange and dipolar interactions can have a profound effect on the response of a radical pair to an applied magnetic field (31,45–49). For a radical pair magnetoreceptor, one can anticipate that the neglect of exchange and dipolar interactions will only be valid if the two radicals are far enough apart that both interactions are weak, not only in comparison with the major hyperfine couplings (typically 100–1000 μT) but also, more stringently, with respect to the geomagnetic field strength (25–65 μT). The dipolar coupling, D(r), usually has the longer range and dominates the exchange interaction, J(r), except at small radical-radical separations, r < 0.5–1.0 nm (50,51). The strength and distance dependence of D(r) are given exactly by

$$D(r)=-\frac{3}{2}\frac{{\mu }_0}{4\pi }\frac{{\gamma }_e^2{\hslash }^2}{r^3};\text{i}.\text{e}.,D(r)/\mu T=-\frac{2.78\times {10}^3}{{(r/\text{nm})}^3}\text{,}$$ (1)

assuming the electron spins to be point magnetic dipoles, generally a good approximation for radical pairs (see below). Thus, D(r) = −500 μT at a separation r = 1.77 nm and −50 μT at r = 3.82 nm. When the Zeeman interaction with the external magnetic field is sufficiently strong, the effect of the dipolar coupling is to produce energy-level splittings proportional to D(r)[3cos²ξ − 1] where ξ is the angle between the vector connecting the two dipoles and the magnetic field direction; in fields whose amplitudes are comparable to or smaller than D(r) and/or the hyperfine interactions, the dependence on ξ is both less straightforward and less pronounced (50). The exchange interaction parameter, J(r), has a complex dependence on the electronic properties of the radicals, their separation, and the nature of the intervening medium. J(r) is usually assumed to fall off exponentially with r and to be independent of ξ (52)

$$J(r)=J_0\text{exp}(-\beta r),$$ (2)

where J₀ may be positive or negative and β > 0.

A prerequisite for a radical pair reaction to respond significantly to an applied magnetic field whose strength is weak compared to some or all of the hyperfine interactions (the so-called low-field effect (44,53–59)) is that there are degenerate spin energy-levels in zero field which become nondegenerate in a weak field as a result of the electron Zeeman interaction (43,44). An exchange interaction comparable to or larger than the Zeeman interaction lifts the zero-field degeneracies and suppresses the effect of the external magnetic field (44). A dipolar interaction is likely to produce a similar result (50). Thus, if |D(r)| or |J(r)| is too large, the S ↔ T interconversion that would otherwise be driven by the weak Zeeman interaction will be blocked. To permit a ∼50 μT external magnetic field to influence significantly the spin dynamics of a radical pair, both |D(r)| and |J(r)| would need, in general, to be <∼50 μT, i.e., the radicals should be >∼3.5 nm apart. Such large separations are difficult to reconcile with some of the other conditions that a radical pair must satisfy to act as a magnetoreceptor. For example, r > 2.5 nm is unlikely to be compatible with an efficient spin-selective radical recombination, presumably by long-range electron transfer, at a rate that competes favorably with electron spin relaxation.

At first sight, therefore, the inevitable presence of exchange and dipolar interactions within a radical pair would seem to exclude the possibility of a strong response to an external magnetic field as weak as that of the Earth. A possible resolution of this quandary, which has not been considered hitherto, is that the exchange and dipolar interactions are of appropriate size and sign for their effects to be approximately equal and opposite. In this situation, the radical pair might, to some extent, evolve under the Zeeman and hyperfine interactions as if in the absence of interradical spin-spin interactions. That this is, in principle, possible can be seen from the matrix elements of the exchange and dipolar Hamiltonians (${\widehat{H}}_{\text{J}}$ and ${\widehat{H}}_{\text{D}}$) in the S, T₀, and T_±1 basis (60):

$$\begin{array}{l}\langle \text{S}\left|{\widehat{H}}_{\text{J}}\right|\text{S}\rangle =J;\langle {\text{T}}_{\text{m}}\left|{\widehat{H}}_{\text{J}}\right|{\text{T}}_{\text{m}}\rangle =-J;m=0,\pm 1\\ \langle \text{S}\left|{\widehat{H}}_{\text{D}}\right|\text{S}\rangle =0;\langle {\text{T}}_{\text{m}}\left|{\widehat{H}}_{\text{D}}\right|{\text{T}}_{\text{m}}\rangle =D(m^2-\frac{2}{3});m=0,\pm 1\text{.}\end{array}$$ (3)

The effect of ${\widehat{H}}_{\text{J}}$ and ${\widehat{H}}_{\text{D}}$ in the absence of Zeeman and hyperfine interactions is to produce a singlet-triplet splitting of 2J and to split the three triplet sublevels into a doubly degenerate pair at $+\frac{1}{3}$ D and a nondegenerate level at $-\frac{2}{3}$ D. The condition for partial cancellation of the effects of exchange and dipolar interactions is that which reintroduces degeneracies among the zero-field states of the radical pair. From Eq. 3, the S and T_m states have equal energy when

$$D=\frac{2}{m^2-\frac{2}{3}}J;m=0,\pm 1\text{.}$$ (4)

As shown in Fig. 1, S and T_±1 are degenerate when D = +6J, while S and T₀ are degenerate when D = −3J. Since D is negative for a radical pair, the former can occur when J₀ < 0 and the latter when J₀ > 0.

Figure 1.

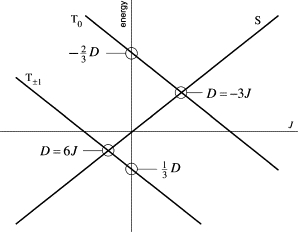
Energy levels for a radical pair as a function of the exchange parameter J for a fixed value of the dipolar coupling parameter D. The figure is appropriate for a radical pair with D < 0, with no hyperfine couplings and in the absence of an external magnetic field. The S and T_m states are degenerate when D = −3J (m = 0, J > 0) and at D = 6J (m = ±1, J < 0).

The purpose of this article is to demonstrate that such “J/D cancellation” can indeed take place and that a ∼50 μT field can have a significant effect on reaction product yields in the presence of radical-radical interactions that would otherwise preclude the operation of the radical pair as a compass sensor. Numerical simulations are presented, the results of which are discussed in the context of the proposed cryptochrome magnetoreceptor.

Theoretical methods

We consider an immobilized radical pair able to recombine to form distinct chemical products from its S and T states with equal first-order rate constants, k_S = k_T = k = 10⁶ s⁻¹ (Scheme 1). The initial state is a pure singlet and we calculate the dependence of the yield, Φ_S, of the singlet-product ^SP (Scheme 1) on the direction of the applied magnetic field, which is specified by the polar angles θ and φ defined in the molecular frame (44)

$${\Phi }_{\text{S}}(\theta ,\phi )=\frac{1}{M}\sum _{\text{n}=1}^{4\text{M}}\sum _{\text{m}=1}^{4\text{M}}\frac{k^2}{k^2+{({\omega }_{\text{n}}-{\omega }_{\text{m}})}^2}|\langle n|{\widehat{P}}^{\text{S}}|m\rangle {|}^2\text{.}$$ (5)

M is the number of nuclear spin configurations (M = 2^N for a radical pair containing N spin-½ nuclei), ω_n and ω_m are eigenvalues, and |n〉 and |m〉 eigenstates, of the radical pair spin Hamiltonian $\widehat{H}$, and ${\widehat{P}}^{\text{S}}$ is the singlet projection operator. Note that $\widehat{H}$, and therefore ω_n, ω_m, |n〉, and |m〉 are all, in general, functions of θ and φ when anisotropic spin interactions are present in the radical pair. The use of identical reaction rates (k_S = k_T) considerably simplifies the calculation (44) but is unlikely to be a feature of any real radical pair magnetoreceptor. However, this approximation does not obscure the essential physics and is therefore harmless for the present purposes.

The spin Hamiltonian contains terms for the Zeeman interactions of the two electron spins with the applied magnetic field, ${\widehat{H}}_{\text{Z}}(\theta ,\phi )$, the various hyperfine interactions in the two radicals, ${\widehat{H}}_{\text{HFI}},$ and the exchange and dipolar interactions,

$$\widehat{H}={\widehat{H}}_{\text{Z}}(\theta ,\phi )+{\widehat{H}}_{\text{HFI}}+{\widehat{H}}_{\text{J}}(r)+{\widehat{H}}_{\text{D}}(r)\text{.}$$ (6)

We omit the nuclear Zeeman interaction, which is extremely small for the weak applied magnetic fields under consideration. For simplicity, all nuclei are spin-½ with the consequence that nuclear quadrupolar interactions need not be considered.

The isotropic Zeeman Hamiltonian (in angular frequency units) may be written

$${\widehat{H}}_{\text{Z}}(\theta ,\phi )={\gamma }_{\text{e}}{B}_0\left[{\widehat{S}}_x\text{sin}\theta \text{cos}\phi +{\widehat{S}}_{\text{y}}\text{sin}\theta \text{sin}\phi +{\widehat{S}}_{\text{z}}\text{cos}\theta \right],$$ (7)

where B₀ is the strength of the external magnetic field and $\widehat{S}={\widehat{S}}^{(1)}+{\widehat{S}}^{(2)}$ is the total electron spin operator (1 and 2 label the two electron spins). We make the reasonable assumption that B₀ is small enough that the difference between the isotropic g-values of the two radicals and the anisotropic parts of their g-tensors may safely be omitted.

The hyperfine Hamiltonian is given by

$${\widehat{H}}_{\text{HFI}}=\sum _{\text{i}=1}^2\sum _{\text{k}=1}^{\text{N}}\left[a^{(\text{i,k})}{\widehat{S}}^{(\text{i})}\cdot {\widehat{I}}^{(\text{k})}+{\widehat{S}}^{(\text{i})}\cdot {\text{A}}^{(\text{i,k})}\cdot {\widehat{\text{I}}}^{(\text{k})}\right],$$ (8)

where a^{(i, k)} is the isotropic hyperfine coupling constant and A^{(i, k)} is the anisotropic part of the hyperfine interaction tensor of nucleus k coupled to electron i. Taking all hyperfine tensors to be axial, A^{(i, k)} (in the molecular frame) is related to A′^{(i, k)} (in the principal axis system of the tensor) by the co-latitude, γ^(i,k) and azimuth, δ^(i,k). The axialities of the hyperfine interactions are defined as ${\alpha }^{(\text{i,k})}={A^{\prime }}_{\text{zz}}^{(\text{i,k})}/2a^{(\text{i,k})}$ with ${A^{\prime }}_{\text{xx}}^{(\text{i,k})}={A^{\prime }}_{\text{yy}}^{(\text{i,k})}=-\frac{1}{2}{A^{\prime }}_{\text{zz}}^{(\text{i,k})}$. (9)

The exchange and dipolar Hamiltonians whose matrix elements were given in Eq. 3 are

$${\widehat{H}}_{\text{J}}(r)=-J(r)({\widehat{S}}^2-\widehat{1}),$$ (9)

$${\widehat{H}}_{\text{D}}(r)=D(r)\left[{({\widehat{S}}_{\text{z}}\text{cos}\epsilon +{\widehat{S}}_{\text{x}}\text{sin}\epsilon )}^2-\frac{1}{3}{\widehat{S}}^2\right],$$ (10)

where ɛ specifies the orientation of the dipolar axis in the molecular frame. Although D < 0 for a radical pair, the calculations reported below were performed with both positive and negative values of D to explore the full range of behavior of the various radical pairs studied. Note that Φ_S is unchanged if the signs of all of J, D, a^{(i, k)}, and A^{(i, k)} are reversed.

The anisotropy of the singlet-yield

$$\Gamma =\frac{\text{ma}{\text{x}}_{\theta ,\phi }[{\Phi }_{\text{S}}]-\text{mi}{\text{n}}_{\theta ,\phi }[{\Phi }_{\text{S}}]}{\text{ma}{\text{x}}_{\theta ,\phi }[{\Phi }_{\text{S}}]}\times 100\%$$ (11)

was obtained by computing Φ_S for several thousand combinations of θ and φ. The spherically averaged singlet-yield was calculated using a trapezium rule approximation to the integral

$$\langle {\Phi }_{\text{s}}\rangle =\frac{1}{4\pi }{\int }_0^{2\pi }{\int }_0^{\pi }{\Phi }_{\text{s}}(\theta ,\phi )\text{sin}\theta \text{d}\theta \text{d}\phi \text{.}$$ (12)

The dipolar coupling parameters D (axiality) and E (rhombicity) for radical pairs in A. thaliana Cry1 were calculated from the crystal structure (61) in two ways. Approximate values were obtained using the point-dipole approximation, Eq. 1, with r equal to the center-to-center separation of the two radicals. The center of each radical (the reduced flavin or an oxidized tryptophan) was determined as the mean of the crystallographic coordinates of all the ring carbon and nitrogen atoms (i.e., 14 atoms for the flavin and 9 for a tryptophan). The rhombicity E is zero for point dipoles. More accurate values of D and E were obtained by explicit numerical integration over the distributions of spin density (ρ₁(r) and ρ₂(r)) in the semioccupied molecular orbitals (SOMOs) of the two radicals. The nine components of the dipolar coupling matrix (in Tesla; p,q = x,y,z) were calculated according to

$$D_{\text{pq}}=\frac{1}{2}\frac{{\mu }_0}{4\pi }\hslash {\gamma }_{\text{e}}\int {\rho }_1({\text{r}}_1){\rho }_2({\text{r}}_2)\left[\frac{r_{12}^2{\delta }_{\text{pq}}-3p_{12}{q}_{12}}{r_{12}^5}\right]\text{d}{\tau }_1\text{d}{\tau }_2,$$ (13)

with obvious notation. This 3×3 matrix was diagonalized to give eigenvalues D_X > D_Y > D_Z from which D and E were calculated as D = 3D_Z/2 and E = (D_X − D_Y)/2. The SOMOs were obtained from Gaussian 03 (62) at the DFT B3LYP EPR-II level of theory.

Results

Exchange and dipolar interactions that are comparable to or stronger than the hyperfine interactions in a radical pair are expected to block S ↔ T interconversion. This effect may be seen in Fig. 2 A where the singlet-yield Φ_S is plotted against D for a radical pair containing a single proton with an isotropic hyperfine interaction (a = 500 μT) with and without a modest exchange interaction (J = 500 μT), in the absence of an applied magnetic field. As either J or D is changed away from zero, the singlet product yield rises toward 1.0, consistent with the anticipated inhibition of S ↔ T mixing in this singlet-born radical pair. For example, the triplet yield (Φ_T = 1 − Φ_S) drops by 84% (from 0.38 to 0.06) when |J| = 0.5 mT and D = 0 or J = 0 and |D| = 3.0 mT. The observation that |J/a| ≥ 1 or |D/a| ≥ 6 is sufficient significantly to suppress S↔T interconversion is also borne out by inspection of the relative sizes of the diagonal and off-diagonal matrix elements of the spin Hamiltonian. As expected, an exchange or a dipolar interaction on its own only has a negligible effect when |J| ≪ |a| or |D| ≪ |a|, respectively.

Figure 2.

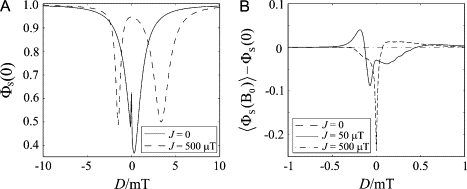
(A) Calculated singlet-yield, Φ_S(0), at zero field as a function of D for J = 0 (solid line) and J = 500 μT (dashed line). (B) Calculated change in the spherically averaged singlet-yield [〈Φ_S(B₀)〉 − Φ_S(0)] produced by an external 50 μT magnetic field as a function of D for J = 0 (dashed line), J = 50 μT (solid line), and J = 500 μT (dash-dot line). In both cases: a = 500 μT, α = 0, and k = 10⁶ s⁻¹.

It is clear from the minima in the dashed curve (J = 500 μT) in Fig. 2 A that a substantial fraction of the S ↔ T interconversion can be restored when one of the matching conditions (D ≈ 6J and D ≈ −3J) is met. It is also evident that the cancellation conditions do not have to be satisfied exactly for this to happen: the dips in Φ_S are not centered exactly at D = 6J or D = −3J and they have finite widths, determined in this case by the magnitude of the isotropic hyperfine coupling constant, a.

It is also important to see how J and D affect the response of the singlet-yield to a weak applied magnetic field. Fig. 2 B shows the change in 〈Φ_S〉 produced by a 50 μT applied field as a function of D for three exchange interactions (0, 50 μT, and 500 μT). It is clear that once J or D becomes larger than B₀, the S↔T interconversion induced by the Zeeman interaction is quenched. The condition for interradical interactions to have a negligible influence on the magnetic field effect (i.e., |J| ≪ B₀ and |D| ≪ B₀) can thus be very restrictive in the case of weak external fields.

Although Fig. 2 A shows that J/D cancellation can restore significant S ↔ T interconversion, this is not a sufficient condition for a pair of interacting radicals to act as a magnetoreceptor. To be able to detect the direction of the Earth's magnetic field, the radical pair must contain anisotropic magnetic interactions that cause the singlet-yield to vary with the orientation of the receptor in the magnetic field. Fig. 3 shows the anisotropy of the singlet-yield for various combinations of J and D in the case of a one-proton radical pair with an axial hyperfine tensor, for two values of the hyperfine anisotropy parameter. The large singlet-yield anisotropies found for D = J = 0 (Fig. 3, A and C) are greatly attenuated when either J or D is changed to a value large compared to the applied magnetic field strength (50 μT). When both J and D are nonzero the anisotropy is severely attenuated except when D ≈ 6J (for α ≈ 0.02) or when D ≈ −3J (for α ≈ −1.0). Only weak cancellation effects are found for D ≈ −3J when α ≈ 0.02 or for D ≈ 6J when α ≈ −1.0, showing that Eq. 4 is a necessary but not sufficient condition for a weak Zeeman interaction to be able to induce a significant degree of S ↔ T mixing. Fig. 3 also shows the shapes of the singlet-yield anisotropies, Φ_S(θ,φ) − 〈Φ_S〉, for the indicated values of J, D, and α. In Fig. 3, A and C, where J = D = 0, the orientation dependence of Φ_S(θ,φ) is ∼3cos² θ − 1, and the symmetry is that of the hyperfine interaction (the z axis), as expected (14). For Fig. 3, B and D, where the polar plots refer to nonzero values of both J and D, the (θ,φ)-dependence is more complex and reflects the symmetry of the dipolar coupling (the x axis) as well as of the hyperfine interaction.

Figure 3.

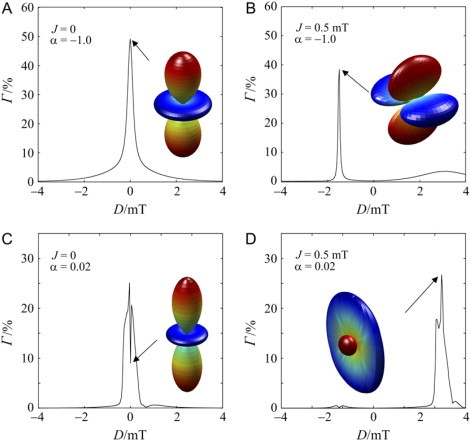
Calculated singlet-yield anisotropies (Γ, Eq. 11) as a function of D for various combinations of J and α. (A) J = 0, α = −1.0; (B) J = 500 μT, α = −1.0; (C) J = 0, α = 0.02; and (D) J = 500 μT, α = 0.02. The polar plots represent the anisotropy of the singlet-yield for four combinations of J, D, and α. In each case, Φ_S(θ,φ) was calculated for 6400 combinations of θ and φ. The distance of the surface from the origin in the direction (θ,φ) is proportional to Φ_S(θ,φ) − 〈Φ_S〉. The color scale is a spectrum in which the maximum value (i.e., most positive) is red and the minimum (most negative) blue. The symmetry axes of the hyperfine and dipolar interactions lie along the z and x directions, respectively. In all cases: a = 500 μT, ɛ = π/2, k = 10⁶ s⁻¹, and B₀ = 50 μT.

To explore more extensively the conditions required for J/D cancellation to take place, we have calculated the singlet-yield anisotropy for large ensembles of radical pairs in which a selection of the parameters for each member of the ensemble were assigned values at random from within predefined ranges. The aim is to judge whether cancellation is a rare occurrence, expected only for very particular combinations of interaction strengths, or whether it is a more general phenomenon. Such a Monte Carlo approach was used because the alternative—a systematic coverage of the whole parameter space—would have been computationally prohibitive.

Singlet-yield anisotropies Γ were calculated for an ensemble of 10⁶ one-proton radical pairs. The results are summarized in Fig. 4 A in which each dot represents a radical pair with Γ > 10%. One sees that the radical pairs with significant anisotropy are clustered around the lines D = 6J and D = −3J. Away from these lines, extremely few radical pairs have anisotropy >15%.

Figure 4.

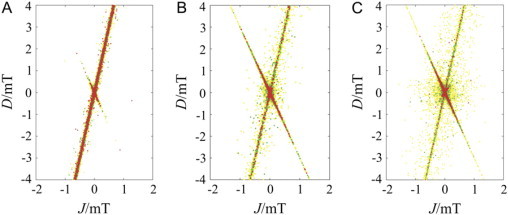
Calculations of singlet-yield anisotropies Γ for radical pairs with (A) 1, (B) 2, and (C) 3 protons on one radical and none on the other. For each member of the ensemble of radical pairs, parameters were assigned values at random from within the ranges: −4 mT < D < 4 mT; −2 mT < J < 2 mT; −1 mT < a^(i,k) < 1 mT; −3 < α^(i,k) < 3; and 0 < γ^(i,k) < π; 0 < δ^(i,k) < 2π, with k = 10⁶ s⁻¹. Each singlet-yield was calculated for a grid of 900 values of θ and φ, from which Γ was determined using Eq. 11. The colored dots represent values of Γ in the ranges 10–15% (yellow), 15–20% (green), and >20% (red).

Fig. 4, B and C, show the outcomes of similar calculations for 10⁶ two-proton and 10⁷ three-proton radical pairs (all protons on the same radical) in which the parameters of the second and third hyperfine couplings (a^{(i, k)}, α^{(i, k)}, γ^{(i, k)}, δ^{(i, k)}; k = 2,3) were added to the list of randomly chosen variables. As in Fig. 4 A, the radical pairs with >15% anisotropy are found close to the lines D = 6J and D = −3J, but less tightly clustered than in Fig. 4 A. Evidently, for more complex radical pairs, there is greater scope for hyperfine interactions to compensate for a slightly nonideal match between J and D.

Further evidence that J/D cancellation does not require special combinations of hyperfine interactions was obtained by calculating Φ_S for ensembles of multinuclear radical pairs with fixed values of J and D and randomly chosen values of the hyperfine parameters in the ranges: −1 mT < a^{(i, k)} < 1 mT; −3 < α^{(i, k)} < 3; 0 < γ^{(i, k)} < π; 0 < δ^{(i, k)} < 2π; and up to a total of four nuclear spins. The other parameters had fixed values: B₀ = 50 μT, k = 10⁶ s⁻¹. The results are given in Table 1.

Table 1.

Percentages of radical pairs that have singlet-yield anisotropy Γ > 5%

J/mT	D/mT	(1,0)	(2,0)	(1,1)	(3,0)	(2,1)	(4,0)	(3,1)	(2,2)
0	0	94.9	97.5	66.8	99.4	68.3	99.2	45.4	69.3
−0.333	0	0.0	2.5	0.1	3.8	0.7	2.3	0.3	0.2
−0.333	+1.0	8.5	45.9	6.5	15.9	6.3	20.1	3.0	4.2
+0.167	+1.0	42.5	30.0	29.3	8.9	7.1	1.8	1.2	1.1

The value (n,m) signifies n spin-½ nuclei in radical 1 and m in radical 2. Singlet-yields were calculated for 64,000–117,000 radical pairs for each combination of J and D. See text for further details. Although singlet-yield anisotropies were calculated for an ensemble of ∼10⁵ radical pairs, the parameter space for the n + m = 4 case is so large that the coverage is rather sparse; the entries in this table are therefore underestimates of the percentages of pairs that have Γ > 5%.

It can be seen from Table 1 that with J = D = 0 (first row), the anisotropy of the singlet-yield is generally rather large and a high proportion of radical pairs have Γ > 5%. When |J| is increased (second row), Γ usually drops quickly toward zero. However, when D and J satisfy one of the cancellation conditions (third and fourth rows), the anisotropy can remain large even though J and D are comparable to the isotropic hyperfine interactions and are larger than B₀. Table 1 shows that J/D cancellation is not restricted to small regions of the parameter space, and that Γ is consistently larger when all the nuclei are confined to a single radical rather than being more uniformly distributed. For example, (4,0) radical pairs have larger entries in the table than do either (3,1) or (2,2) pairs for all four combinations of J and D. This behavior mirrors that reported for multinuclear radical pairs with isotropic hyperfine interactions (42).

Discussion

Exchange-dipolar cancellation

The simulations described here demonstrate that while a modest exchange or dipolar interaction efficiently quenches the effects of an ∼50 μT external magnetic field, these changes may be at least partially restored when one of the cancellation conditions D ≈ 6J or −3J is satisfied. We now explore the consequences of this conclusion for the proposal that the radical pair magnetoreceptor is formed in a cryptochrome.

By analogy with the photoactivation reaction of DNA photolyase, it has been suggested that a long-lived flavin-tryptophan radical pair, with properties suitable for magnetoreception, is formed in an avian cryptochrome by a sequence of electron transfers involving three tryptophan residues and the photoexcited, fully oxidized form of the FAD cofactor (17). This process is shown in Scheme 2 using the sequence numbers for A. thaliana Cry1; the protonation of the excited state FAD* (63) is not shown explicitly, and the deprotonation of the cation radical of the terminal tryptophan W324^·+ (64) is omitted. The first electron transfer (W400 → FAD*) occurs in 38 ps in E. coli photolyase (27); the second (W377 → W400^·+) and third (W324 → W377^·+) have been estimated to be faster than 10 ns, also in E. coli photolyase (26). The primary (FADH^· W400^·+) and secondary (FADH^· W377^·+) radical pairs are therefore much shorter-lived than the tertiary pair (FADH^· W324^·+), which has a lifetime of ∼1 ms in A. thaliana Cry1 (24), and for this reason has been suggested as the most likely candidate for the magnetoreceptor.

Scheme 2.

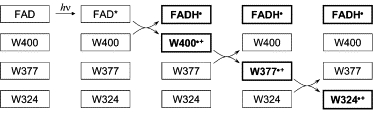
To judge the extent to which the spin evolution of these three radical pairs is likely to be affected by radical-radical interactions, we start by estimating the dipolar parameters. Table 2 gives the center-to-center distances, from the crystal structure of A. thaliana Cry1 (61), and the corresponding point-dipole values of D obtained using Eq. 1. Also included in the table are values of D and E (the rhombicity) determined by averaging over the appropriate electronic wavefunctions of the two radicals using Eq. 13. As expected, the values of E are small (<3% of |D|), justifying the neglect of the rhombicity in the calculations reported above. The differences (< 20%) between the two estimates of D for each radical pair illustrate the approximate nature of the point-dipole approach, especially for the primary radical pair, which has the smallest radical-radical separation. It is clear from Table 2 that all three values of D(r) are >50 μT and so cannot be considered to have a negligible effect on the spin dynamics.

Table 2.

Radical pair separations and dipolar coupling parameters

	FAD-W400	FAD-W377	FAD-W324
r/nm*	0.85	1.32	1.90
D(r)/μT (approximation)†	−4500	−1200	−400
D(r)/μT‡	−5350	−1180	−380
|E(r)|/μT‡	110	30	2

^*Center-to-center distance.

^†Point dipole approximation.

^‡Integral over SOMOs of flavin and tryptophan radicals.

We now turn to the exchange interactions. Although J₀ and β in Eq. 2 have been determined for bi-radicals in solution (65), these values are unlikely to be appropriate for radicals in the largely nonpolar interior of a protein where the extent of electron delocalization and the relative orientation of the relevant molecular orbitals are likely to play an important role. From an analysis of electron transfer rates in photosynthetic reaction center proteins, Moser et al. (66) found that V²(r_e), the matrix element that couples the electronic wavefunctions of the reactants and the products of the electron transfer reaction, depends exponentially on r_e, the edge-to edge donor-acceptor separation

$$V^2(r_{\text{e}})\propto \text{exp}(-\beta r_{\text{e}}),$$ (14)

with β ≈ 14 nm⁻¹ (66). It is reasonable to assume (67) that the exchange interaction J(r) has the same exponential distance-dependence, i.e., that we may use a value of 14 nm⁻¹ for β in Eq. 2. An estimate of J₀ may therefore be obtained from Eq. 2 using the exchange interaction (|J| = 900 μT) for the primary radical pair in the reaction center of the purple photosynthetic bacterium Rb. sphaeroides R26 (68–70), for which the center-to-center separation is r = 1.8 nm (71). Thus, one finds |J₀| ≈ 8 × 10¹³ μT. Given the assumptions involved in this estimate, this value could well be in error by an order of magnitude: we therefore estimate 8 × 10¹² μT ≤ |J₀| ≤ 8 × 10¹⁴ μT.

Fig. 5 shows the dependence on r of J(r) (Eq. 2 with β = 14 nm⁻¹ and 8 × 10¹² μT ≤ |J₀| ≤ 8 × 10¹⁴ μT), |D(r)|/3, and |D(r)|/6 (Eq. 1). It is evident that the exchange interaction dominates at small r and falls off with increasing separation much more rapidly than does the dipolar interaction. With the above range of |J₀| values, Fig. 5 shows that the matching condition for cancellation of the two interactions (|J(r)| ≈ |D(r)|/3 or |J(r)| ≈ |D(r)|/6) is satisfied for radical-radical separations between ∼1.8 and 2.2 nm.

Figure 5.

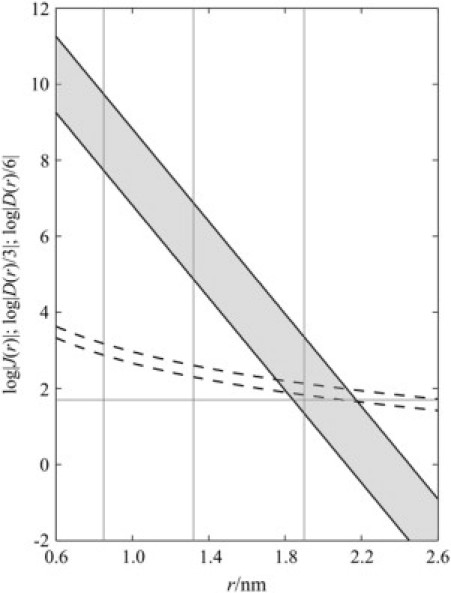
Dependence of the exchange and dipolar interactions in a radical pair on the center-to-center separation of the two radicals. The shaded area corresponds to log[|J₀/μT|exp(−βr)] with 8 × 10¹² μT ≤ |J₀| ≤ 8 × 10¹⁴ μT and β = 14 nm⁻¹. The dashed lines represent log|(D(r)/3)/μT and log|(D(r)/6)/μT|, calculated using the point-dipole approximation. The vertical lines indicate the separations of the radicals in the primary, secondary, and tertiary FAD-tryptophan radical pairs. The horizontal line drawn at 50 μT is the approximate strength of the Earth's magnetic field.

It can be seen from Fig. 5 that both the primary (FADH^· W400^·+) and secondary (FADH^· W377^·+) radical pairs are expected to have strong dipolar and very strong exchange interactions which are not of appropriate amplitudes to cancel one another. Neither pair should be able to undergo any appreciable S ↔ T interconversion, and still less respond to a 50 μT magnetic field. As a consequence, the tertiary pair (FADH^· W324^·+) should be formed in a pure (singlet or triplet) spin state with maximum spin correlation (ignoring spin relaxation). Were this not the case, the tertiary pair would be formed in a coherent superposition of singlet and triplet states and would display a reduced sensitivity to an external magnetic field.

Fig. 5 also shows that J(r) and D(r) are far from negligible compared to 50 μT for the tertiary radical pair, and would therefore severely attenuate the influence of the geomagnetic field were it not for the fact that its radical-radical separation falls within the range of r for which J/D cancellation can be expected. We therefore predict that FADH^· W324^·+ is particularly well suited as a magnetoreceptor not because J(r) and D(r) are negligible (as previously assumed), but because their effects may cancel one another.

Electron transfer kinetics

A further consideration is whether the 2.0 ± 0.2 nm range of radical-radical separations that is optimum for magnetoreception is consistent with a sufficiently rapid back-electron transfer reaction. A crucial requirement for a magnetic field effect is that the radical pair is able to recombine spin-selectively at a rate that competes with spin relaxation and other spin-independent reactions. Given that the relaxation of a protein-bound radical could be as slow as 10–100 μs (30), a reasonable lower limit for the rate constant k of back electron transfer (i.e., FADH^· W324^·+ → FAD + W324 + H⁺) would be 10⁴ s⁻¹. To see whether this is compatible with a center-to-center separation r of 2.0 ± 0.2 nm, we turn to Marcus theory (72,73). Moser et al. have shown that for electron transfer reactions in proteins, k is given by the expression

$$\text{log}(k/{\text{s}}^{-1})=15-6r_{\text{e}}/\text{nm}-3.1\left[\frac{{(\Delta G+\lambda )}^2}{\lambda }\right]/\text{eV},$$ (15)

where ΔG and λ are, respectively, the Gibbs energy and the reorganization energy of the electron transfer reaction (66). For a given edge-to-edge distance, the optimum electron transfer rate occurs when ΔG = −λ, so that

$$\text{log}(k/{\text{s}}^{-1})\le 15-6r_{\text{e}}/\text{nm}\text{.}$$ (16)

From Eq. 16, it may be seen that k ≥ 10⁴ s⁻¹ implies r_e ≤ 1.8 nm. For the flavin-tryptophan radical pairs considered above, the center-to-center separation is ∼0.4 nm larger than the edge-to-edge distance, from which we obtain r ≤ 2.2 nm. It therefore appears that the range of separations required for J/D cancellation is indeed consistent with a sufficiently rapid back electron transfer reaction.

Hyperfine interactions

Another issue concerns how and whether the results obtained using model radical pairs with small numbers of nuclei can be extrapolated to a real radical pair such as FADH^· W^·+ which contains 16 nuclei with isotropic hyperfine couplings, |a|, larger than ∼0.1 mT. It is impossible to simulate spin systems this large with currently available computers, and so it is difficult to predict precisely the extent of J/D cancellation in such a pair. In addition, it may be misleading to attempt to extrapolate from small model systems with randomly chosen hyperfine parameters to real systems which may have correlated, symmetry-related (and possibly evolutionarily optimized) hyperfine interactions. For example, simulations of a flavin-tryptophan pair containing eight nuclei (14) suggest that the anisotropy of the singlet-yield is dominated by two nitrogens in the flavin radical which have relatively large, axial, and collinear hyperfine tensors and whose effects appear to reinforce one another. It is possible, therefore, that the behavior of a FADH^· W^·+ radical pair is well modeled by a system containing only a few nuclear spins.

Reaction yield anisotropy

Finally, how large would Γ need to be to allow a bird equipped with a radical pair magnetoreceptor to sense its orientation in the Earth's magnetic field? Far too little is known about the signal transduction of any magnetic field-dependent reaction yield to give a convincing answer, but some insight may be obtained by assuming that the radical pair reaction leads directly or indirectly to the production of neurotransmitter molecules in amounts that depend on the orientation of the magnetoreceptor in the magnetic field. Thus, Weaver et al. (13) have estimated the number of receptors R and the minimum total detector volume V required to overcome stochastic fluctuations in the number of ligand-receptor complexes. Adapting their arguments, which focus on detection of small changes in the intensity of the external field, to the detection of its direction, it is straightforward to show that

$$R\approx \frac{4}{{[\Gamma \Delta \theta ]}^2}\text{and}V/{\text{m}}^3\approx {10}^{-19}R,$$ (17)

where Δθ is the change in orientation to be detected. Thus, to detect a 0.1 radian change in orientation using a reaction with a 10% singlet-yield anisotropy (Γ = 0.1), the number of receptors must be >∼4 × 10⁴ and the total detector volume would need to be at least ∼4 × 10⁻¹⁵ m³ or ∼(20 μm)³. Judged by the arguments presented by Weaver et al. (13), both figures seem plausible.

Conclusion

We conclude that in several respects the radical pair consisting of FADH^· and the radical derived from the terminal tryptophan residue of the cryptochrome Trp-triad has properties that make it a favorable candidate for the proposed avian compass magnetoreceptor.