Predicting the Folding Pathway of Engrailed Homeodomain with a Probabilistic Roadmap Enhanced Reaction-Path Algorithm

Abstract

To predict a protein-folding pathway, we present an alternative to the time-consuming dynamic simulation of atomistic models. We replace the actual dynamic simulation with variational optimization of a reaction path connecting known initial and final protein conformations in such a way as to maximize an estimate of the reactive flux or minimize the mean first passage time at a given temperature, referred to as MaxFlux. We solve the MaxFlux global optimization problem with an efficient graph-theoretic approach, the probabilistic roadmap method (PRM). We employed CHARMM19 and the EEF1 implicit solvation model to describe the protein solution. The effectiveness of our MaxFlux-PRM is demonstrated in our promising simulation results on the folding pathway of the engrailed homeodomain. Our MaxFlux-PRM approach provides the direct evidence to support that the previously reported intermediate state is a genuine on-pathway intermediate, and the demand of CPU power is moderate.

Introduction

Predicting a protein-folding pathway is an important step toward solving the protein-folding problem. Explicit-solvent molecular dynamics (MD) simulations of protein folding with all-atom models, e.g., CHARMM22 (1) and AMBER parm94 (2), remain challenging, although some exciting successes have been reported (3–5). Here, we present an alternative to the time-consuming dynamic simulation of atomistic models. We replace the actual dynamic simulation with variational optimization of a reaction path connecting known initial and final protein conformations in such a way as to maximize an estimate of the reactive flux (j) or minimize the mean first passage time (MFPT) at a given temperature, referred to as MaxFlux (6). The dynamics of biomolecular conformational transitions can be approximated as an overdamped diffusive process in configuration space subject to the Smoluchowski equation (7),

$$\frac{\partial p(r,t)}{\partial t}=-\nabla \cdot j$$

$$j(r,t)=-e^{-\beta \text{U}(r)}D(r)\cdot \nabla [p(r,t)e^{\beta \text{U}(r)}],$$

where p(r,t) is the probability distribution. If γ is the isotropic and spatially independent friction coefficient, the diffusion tensor D(r) = (k_BT/mγ)I, where I is the identity matrix. Because the temperature effect is included, the obtained reaction path can be considered to be an approximate classical MD trajectory. How representative is the optimized reaction path of the experimentally measured overall reaction mechanism? For simple conformational transitions, e.g., those of organic compounds, there is only one dominant path; as a consequence, the optimal path with the shortest MFPT is the best representation of the actual reaction mechanism. However, for proteins, DNA, and RNA, there may be a large number of paths (with different probabilities) thermally available for the transition, and the experimental observation is the average of all thermally available paths according to their probability. But this does not mean that there is no most probable path. As we have shown in the conformational reorganization within aggregates (8), there is a most populated path. And the most populated path is the one corresponding to the optimal path that overcomes the lowest (free) energy barrier or takes the shortest time.

For a one-dimensional bistable potential under stationary conditions, the approximate forward-reacting MFPT obtained by solving the Smoluchowski equation reproduces the classical Arrhenius formula (6). For the system that moves in a multidimensional potential of mean force U(r), further assumptions are needed—1), the friction coefficient is isotropic in space; 2), the reactive flux along the pathway is constant—before one defines the optimal pathway as the one that minimizes the MFPT (9),

$$P={\int }_{r_{\text{R}}}^{r_{\text{P}}}{e}^{\beta \text{U}(r)}dl(r),$$ (1)

where β = 1/k_BT and k_B is the Boltzmann constant. In this work, T = 300 K. U(r) was the effective energy for a given conformation calculated with the CHARMM19 (10) force field together with the EEF1 (11) implicit solvation model. The dl(r) was defined as the C_α RMSD between two conformations. This definition of optimal pathway is consistent with the fact that a conformation of low effective energy is favored with the probability proportional to exp (βΔU) where ΔU is the difference in effective energy between two conformations. Herein, the objective is to minimize the line integral in Eq. 1.

By minimizing the line integral of Eq. 1 using the self-avoiding walk method (12), one can obtain an optimal pathway corresponding to the fastest reaction rate (6). The MaxFlux algorithm has been successfully applied to study the conformational change of peptides (13,14). However, searching for the global optimized folding pathway for a protein, even a medium-sized protein, using an atomistic model is computationally demanding. So far, the applications of MaxFlux or its alternative MaxFlux-NEB (15) to beyond peptide folding are seldom seen. The difficulties in finding the global optimized path start from the initial guess, which is usually a linear interpolation between the reactant and the product. If the initial guess happens to be close to the optimal pathway, a local minimization method, such as conjugate gradient, is good enough to find the optimal pathway as shown in the MaxFlux application to alanine dipeptide (6). Unfortunately, in most of the cases, the initial guess is far away from the final path; as a result, a global optimization procedure is indispensable. However, the traditional global minimization methods in the path space, such as simulated annealing, are extremely time consuming. We solve the MaxFlux global optimization problem with an efficient graph-theoretic approach, the probabilistic roadmap method (PRM), originally developed for robot motion planning (16) and further adapted in our group (17) based on the pioneer application of PRM to protein folding (18–21).

Imagining that the conformation space and the transition between conformations are encoded in a graph, one can query the graph to obtain useful information. In general, the PRM approach builds a graph, the so-called roadmap, to reflect the connectivity between roadmap nodes (or transitions between conformations) in the part of the conformation space relevant to the study of protein-folding pathways. And for any two conformations (or nodes) that are sufficiently close based on some similarity measure, an edge between them is created with the edge weight reflecting the cost of the transition between the nodes. After constructing a roadmap that has the reactant and product in one connected component, the shortest (or minimum edge weight) path between the reactant and product can be computed by Dijkstra's algorithm (22). The difference between MaxFlux-PRM and Amato and co-workers’ PRM approach (18,19) lies in the edge definition. Instead of using potential energy, MaxFlux-PRM uses the approximate MFPT as edge weight. The comparisons between MaxFlux-PRM and PRM on Müller potential and three-hole potential have shown that MaxFlux-PRM is able to identify an on-pathway intermediate state, whereas PRM fails to do so on these model potentials (17). We also employed the MaxFlux-PRM method to search for the folding pathway of the second β-hairpin of the B1 domain of streptococcal protein G (17). Our folding mechanism is in excellent agreement with the recent experimental results (23,24). However, this β-hairpin contains only 16 residues. Can MaxFlux-PRM be applied to larger systems?

Here, we report the application of further improved MaxFlux-PRM to engrailed homeodomain (EnHD) (PDB entry: 1ENH (25)). This protein adopts a three-helix bundle conformation with 56-amino acid-containing helix 1 (H1: residues 10–22), helix 2 (H2: residues 28–37), and helix 3 (H3: residues 42–56). H1 and H2 align antiparallel, while H3 lies on top of them and runs from the C-terminal of H2 to the C-terminal of H1. The ultrafast kinetic measurements have revealed a two-step folding mechanism at 25°C: a fast phase with a half-life of 1.5 μs to give an intermediate state and a slow phase with a 15-μs half-life to fold to the native state (26). An on-pathway intermediate state has been modeled by unfolding simulations (26), protein engineering (27), and ab initio folding using a reduced all-atom model (28). Our reaction path-based approach is able to provide the direct evidence regarding whether the reported intermediate state is a genuine on-pathway intermediate or not. The wealth of existing experimental and computational data in turn can test the robustness of our MaxFlux-PRM (17) approach.

Materials and methods

The flow chart of our MaxFlux-PRM algorithm is shown in Fig. 1. We employed several innovative techniques to address the conformation space sampling, roadmap connection, and numerical precision issues, which are important for the computational efficiency and the quality of roadmaps and folding pathways. An iterative approach was employed to overcome the difficulties of sampling. Our roadmap in earlier iterations has more relaxed edge connection criteria and encodes coarse-grained conformational transitions. The seeds are considered conformations that show promise for further exploration and generation of more refined roadmaps. The effective energy of each conformation is calculated using a CHARMM19 force field and EEF1 solvation model (10,11). In the first iteration, we generated a set of Gaussian distributions around the backbone dihedral angles of the seed conformations, which are the extended state and the native state with a set of standard deviations (STDs) of (5°, 10°, 20°, 40°, 80°, 160°). The small STDs focus on the sampling in the vicinity of the seeds, whereas the larger STDs allow broader roadmap coverage of the conformation space. To remove some bad contacts, 100 steps of minimization were performed after the side chains were built by CHARMM with the backbone dihedral angles restrained. To sample the side-chain conformation, 15,000 steps of Monte Carlo (29) were carried out in the side-chain dihedral angle space. Finally, the generated conformation was minimized again with the backbone dihedral angles restrained for 3000 steps or ΔU < 0.005 kcal/mol, whichever came first. The nodes with higher effective energy than a threshold (−1300 kcal/mol) were removed. Only conformations with the effective energies lower than the threshold value were saved as roadmap nodes. As a result, 29,533 nodes were in the roadmap during the first iteration.

Figure 1.

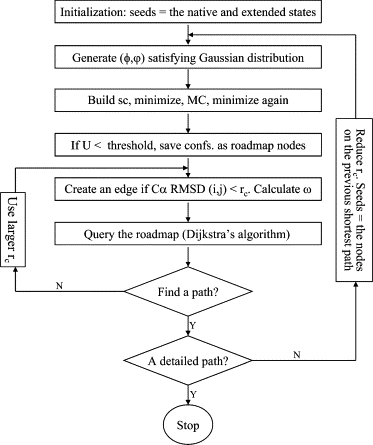
Flow chart of the MaxFlux-PRM algorithm: (sc) side chain; (ω) edge weight.

To build a neighbor list, we used C_α RMSD as a similarity measure. If the C_α RMSD between two roadmap nodes is below certain cutoff values (r_c), our method creates an edge between the two. In general, the smaller r_c value, the fewer the roadmap edges, the more connected components are in the roadmap, and the more detailed the folding pathways (if they exist). Because the C_α RMSD between adjacent conformations along the folding path is ≤r_c, one can think of r_c as the resolution of the folding pathway. Therefore, ultimately, we need to obtain folding pathways with r_c to be sufficiently small, at least in the areas of interest. Typical roadmap algorithms use one r_c for all edge constructions. But our algorithm uses different r_cs in different areas of the conformation space and different iterations. Larger r_c was used in earlier iterations to identify coarse-grained paths along which the conformations were used as seeds for subsequent computations. For the folding pathway results presented here, we wanted to focus on the arrangement of the three helices after the secondary structure formation because 1), the initial nonspecific collapse from the extended state to a random coil (unfolded state) is not the concern of this work, and 2), because the α-helix formation has been extensively studied (30), it is not our aim to reinvestigate it. Hence, the edges close to the native state were set to satisfy a smaller threshold than those close to the extended state. By trial and error, we adopted the following cutoff values in the four iterations of the roadmap constructions used in the study: iteration 1: r_c = 10 Å everywhere; iteration 2: r_c = 10 Å if R_g (radius of gyration) > 32 Å and 6 Å elsewhere; iteration 3: r_c =10 Å if R_g > 32 Å and 5 Å elsewhere; iteration 4: r_c =10 Å if R_g > 32 Å, 3 Å if R_g < 22 Å, and 5 Å elsewhere. Thus, the final path has 3 Å resolution in the compact state. In general, the iteration numbers and the cutoff values could vary: see the Discussion section for the convergence criteria. Edges connect neighboring nodes with a weight defined as $w=\text{exp}(\beta (U(r_1)+U(r_2))/2)\Delta l,$ which means that the graph is undirected with the physical meaning of equal forward and backward reaction rates at equilibrium. In this work, Δl is the C_α RMSD between the neighboring nodes. The summation of the edge weights along the path is a discretized form of Eq. 1. To query the roadmap, we employed Dijkstra's algorithm (22). The total numbers of nodes in the roadmap in iterations 1–4 were 29,533, 181,635, 211,480, and 236,631, respectively.

For our iterative sampling process, we decided to investigate the effect of the choices of seeds on the roadmaps and folding pathways. In our preliminary study in this regard, we also used a different seed generation method from the first roadmap, which was to first merge similar roadmap nodes (those with very small C_α RMSD) and then generate 15 node-disjoint shortest paths, with all these path nodes as seeds for the second iteration. These node-disjoint paths do not share common nodes with each other and can be computed by repeatedly removing the intermediate nodes in the shortest path so far and applying Dijkstra's shortest-path algorithm. In our study, we did not observe any significant difference between the final folding pathway generated from such a larger set of seeds, which in general would have a better coverage of phase space, and that generated using the approach illustrated in Fig.1. In Results, we present the paths generated with the approaches illustrated in Fig. 1.

In the implementation of Dijkstra's shortest-path algorithm, we took special care to deal with the numerical precision issue. For a roadmap edge between two nodes having effective energies U(r₁) and U(r₂), our edge weight function includes an exponential term as mentioned above. With the fast growth rate of an exponential function, the weight difference among our roadmap edges could be very large, which could cause some problem if it were not processed carefully. For example, once the weight of one partial path reached 10⁵⁰, adding 10¹⁰ by taking one subpath or 10²⁰ by taking another subpath could not be distinguished for double precision computation as in C++ (15 bits of decimals). To address this issue, we used infinite-precision computation for path weights and stored at each node the weight of the shortest path from the first path node to the current node. Of course, when the edge weight difference in a roadmap is small, double-precision computation becomes acceptable and is more economical than infinite-precision computation.

Results

Coarse-grained path obtained in the first iteration

In the first iteration, we could not find any path connecting the extended to the native state if we set a small r_c because the sampling of the space far away from the seeds was very poor. Therefore, r_c = 10 Å was applied to build the neighbor list. Fig. 2 a shows the effective energy (molecular mechanics potential plus solvation free energy) as well as the C_α RMSD with respect to the native state as a function of the folding path during the first iteration. Representative conformations along the path are labeled and depicted in Fig. 2 b. Note that the only preknowledge factors were the extended state and native state conformations, which were used as the seeds in the first iteration. Our search gave rise to a path with C_α RMSD between the adjacent conformations along the path ranging from 5.9 Å to 9.8 Å, which could be considered as a low-resolution path or a coarse-grained path. However, it already contained essential information regarding the sequence of events and the folding mechanism. The extended chain first nonspecifically collapses to a random coil with 25 Å C_α RMSD from the native state (point a in Fig. 2 a and conformation a in Fig. 2 b). Then the α-helices start to form in the three α-helical regions concurrently (point b in Fig. 2 a and conformation b in Fig. 2 b) and optimize subsequently. Most importantly, in conformation c (Fig. 2 b) at step 13 (Fig. 2 a), H2 and H3 start to contact with each other, whereas H1 is still further away. This structural feature is in good agreement with the characteristics of intermediate state observed in the thermal unfolding simulations (26), experimental intermediate state analog (27), L16A EnHD, and Monte Carlo folding simulations using a minimalistic all-atom model (28). The C_α RMSD of residues 28–53 (in H2, H2-H3 loop, and H3) between this conformation and L16A EnHD (model 1 of the NMR structure (27)) is 2.9 Å with the main difference in the N-terminal of H2 and the C-terminal of H3 (Fig. 2 b). Conformation d in Fig. 2 b is the near native state.

Figure 2.

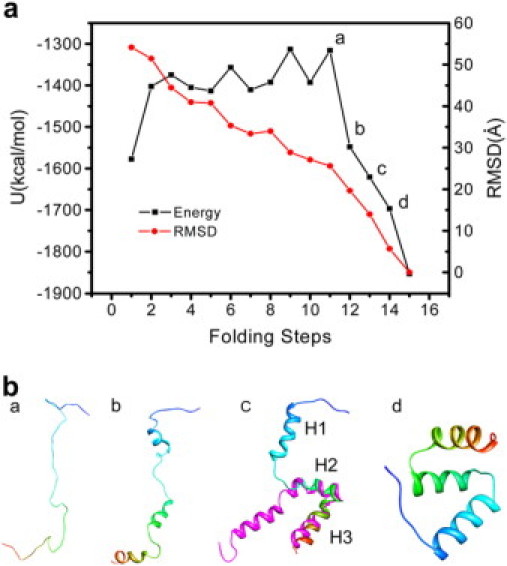
(a) Effective energy (potential energy plus solvation free energy) as well as the C_α RMSD with respect to the native state as a function of the folding path during the first iteration. (b) Representative conformations (a–d) along the path in a. The N-terminal is in blue, and the C-terminal is in red. H1-H3 denotes the three helices. The C_α RMSD of residues 28–53 (in H2, H2-H3 loop, and H3) between conformation c and L16A EnHD (model 1 of the NMR structure (27) in magenta) is 2.9 Å.

Detailed folding pathway obtained in the fourth iteration

To obtain the details of the folding path, as shown in the flow chart (Fig. 1), we started the second iteration using the conformations along the coarse-grained path as seeds to generate more nodes. Again, the only preknowledge were the conformations along the coarse-grained path obtained in the first iteration, which in turn relied only on the known conformations of the extended state and the native state. No experimental intermediate state has been used as the preknowledge. The effective energy as well as the C_α RMSD with respect to the native state as a function of the folding path during the second and third iterations is shown in Supplementary Material. The representative conformations along the path are also presented in Supplementary Material. Until the fourth iteration, we obtained a path with 41 nodes in the roadmap of 236,631 nodes. As illustrated in Fig. 3 a, the C_α RMSD from the native state changes gradually along the folding pathway compared with that of the first iteration shown in Fig. 2 a. The initial drop in R_g from the extended state to R_g = 32 Å corresponds to the nonspecific collapse. A random coil state (step 17 in Fig. 3 a and conformation a in Fig. 3 b) was reached, which can be considered an unfolded state. As in the first iteration, the α-helices subsequently start to form in the three α-helical regions and optimize (steps 18–28 in Fig. 3 a and conformations b and c in Fig. 3 b). The helical content as a function of folding steps is shown in Fig. 4 a. Before step 18, the helical content is zero. The three helices form simultaneously from step 18 to step 22, where R_g falls in the region of 32 Å to 22 Å, and the r_c was set to 5 Å. As mentioned in Materials and Methods, our aim was not to investigate the mechanism of helix formation; therefore, r_c was large in this stage, which means that the path in this range is medium coarse-grained.

Figure 3.

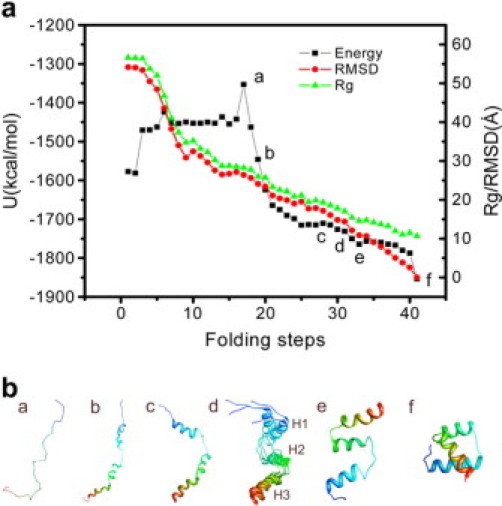
(a) Effective energy (potential energy plus solvation free energy), radius of gyration (R_g), and the C_α RMSD with respect to the native state as a function of the folding path during the fourth iteration. (b) Representative conformations (a–f) along the folding path. a–f correspond to folding steps 17, 19, 28, 29–32, 33, and the native state in a, respectively. (d) Superposition of the conformations from step 29 to 32. H1-H3 denotes the three helices.

Figure 4.

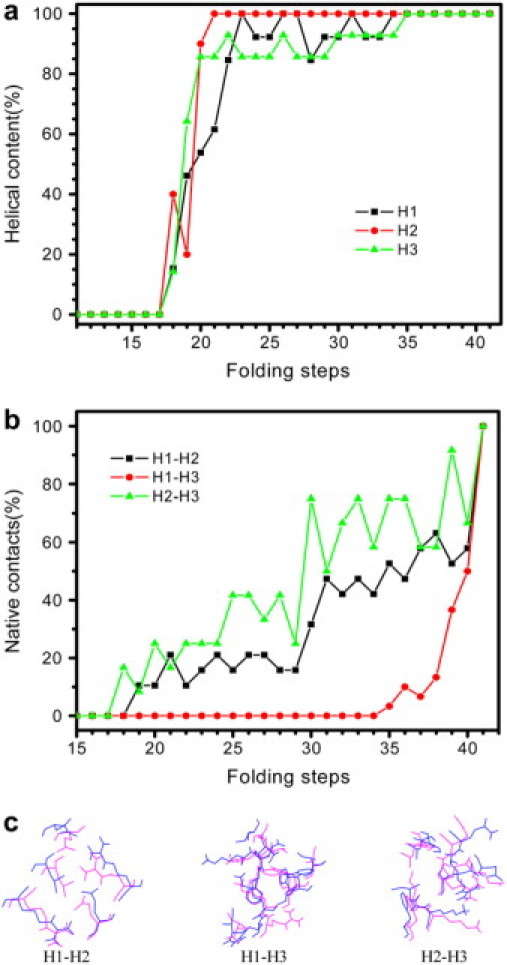
(a) Helical content as a function of folding steps for the fourth iteration. H1-H3 denotes the three helices. (b) Native contact (%) between helices as a function of folding steps for the fourth iteration. Two residues are considered to contact each other if any heavy atom (C, N, O, S) of one residue is within 4.5 Å of any heavy atom of the other residue. (c) Superposition of the native state (magenta) and the conformation at the second-last step (blue) in the fourth iteration. Native contacts between helices are shown. Nonnative contacts as well as native contacts a little bit further away from the 4.5 Å threshold in the second-last conformation lead to the jump in native contact content, as shown in b.

Our focus is the sequence of events of helix formation versus tertiary structure development. Starting step 22, R_g falls <22 Å (Fig. 3 a). Accordingly, after this point, the nodes along the path are obtained using r_c = 3 Å. As a result, the path after step 22 can be considered a fine detailed path with the C_α RMSD between the adjacent conformations along the path <3 Å. At step 22, the helical contents of all three helices reach >80%; thereafter, they fluctuate before the helices are completely formed (at step 35 in Fig. 4 a). However, the native contacts between the helices at step 22 are only 28%, 10%, and 0% for H2-H3, H1-H2, and H1-H3, respectively (Fig. 4 b). Obviously, the helices form independently before the assembly of tertiary structure. Until step 30, H2 and H3 dock with each other (percentage native contact = 75%), whereas H1 is still floating around (H1-H2: 30%, and H1-H3: 0%). Because the H1-H2 loop can adopt various conformations, which in turn results in different orientations of H1 with respect to H2, the configurational entropy of the protein in this stage of folding may lead to lower free energy. The conformations shown in panel d of Fig. 3 b seem very similar to the ensemble description of an on-pathway obligate intermediate state captured in the folding simulation using a minimalistic all-atom model (Fig. 5 I of Hubner et al. (28)). Experimentally, L16A EnHD is an analog of the wild-type intermediate state (27), in which the packing between H2 and H3 is near native, whereas H1 lacks significant contacts with H2 and H3. Along our path, the conformations from step 29 to 32 gradually approach the experimentally modeled intermediate state in which the C_α RMSDs of residues 28–53 (in H2, H2-H3 loop, and H3) between these conformations and L16A EnHD (model 1 of the NMR structure (27)) are 4.6 Å, 3.9 Å, 3.3 Å, and 2.5 Å, respectively. When the L16A mutant is compared with the wild-type, the helical contents of H1, H2, and H3 in the intermediate state are 100%, 100%, and 80%, respectively. Along our path, steps 29–32 in Fig. 4 a, the helical contents are in excellent agreement to the experimental intermediate state analog.

Figure 5.

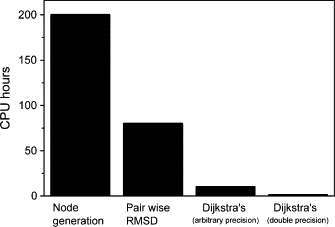
Computational cost based on a 64-bit AMD 1.6 GHz Opteron CPU per 100,000 conformations. The pairwise RMSD is also for 100,000 conformations. For the roadmap query (Dijkstra's algorithm), a hypothetical graph contains 100,000 conformations and 100,000,000 edges.

After the intermediate state, a near-native state (steps 33–40) forms, in which H1 starts to contact H2 and H3. The conformation at step 33 (conformation e in Fig. 3 b) has 15 nonnative contacts and is a local minimum in the effective energy surface (Fig. 3 a). This conformation appears very similar to the near-native state reported by Shakhnovich and co-workers (conformation NN in Fig. 5 of Hubner et al. (28)). After step 33, the protein tries to rearrange the helical contacts. The conformation just before the native state deviates from the x-ray structure (Fig. 3 b) by 2.6 Å C_α RMSD, mainly because there is less contact between H1 and H3 (Fig. 4 b). When the flexible termini (residues 1–7 and residues 55–56) are not included in the calculation, the C_α RMSD for residues 8–54 of the conformation at step 40 with respect to the native state is 1.2 Å, whereas the all-atom (including polar H) RMSD for these residues is 3.0 Å. By visualizing the superposition of the second-last conformation along the path and the last one, which is the native state, we found nonnative contacts as well as native contacts a little bit further away from the 4.5 Å threshold in the second-last conformation (as shown in Fig. 4 c), leading to the jump in the content of native contacts as shown in Fig. 4 b. The potential energy component and the solvation free energy for the conformations at the last two steps are presented in the Supplementary Material.

Discussion

Our sequence of the folding event is close to the limit of the framework (31) or diffusion-collision mechanism (32), in which the native-like secondary structures form first and the development of the tertiary structure is a rate-limiting step. The recent success in protein structure prediction using the AMBER parm96 and GB/SA model for nine proteins also proves the mechanism that local structure happens first at independent sites along the chain followed by either zipping or assembly with other structures (33). Note that there is no intrinsic bias in the MaxFlux-PRM toward the diffusion-collision mechanism against the nucleation-condensation model (34), where the secondary and tertiary structures form concurrently. The fact that our folding path is in line with the recent experimental and computational results (26–28) proves that the MaxFlux-PRM method has the ability to locate the folding pathway beyond the two-state folding. It is important to point out that our model and analysis are subject to a number of limitations. First, the MaxFlux-PRM path provides the sequence of events. Consequently, as shown above, we can verify whether an intermediate state is on-pathway or not, but we cannot predict which event results in an intermediate state and/or transition state with the current version of MaxFlux-PRM. To obtain the free energy profile along the path and locate the transition state(s) and the intermediate state(s), the ΔD_rmsd method (35) can be used after MaxFlux-PRM. Second, we employed an implicit solvation model. The reason we did so is that in Berkowitz's description of reactive flux (9), which is based on the Smoluchowski equation of stochastic processes, U(r) is the potential of mean force of the system with an average over all solvent degrees of freedom at a given temperature. The solvation free energy (ΔG_solvation) can be calculated with the implicit solvation model, whereas the explicit water model is not practical to give ΔG_solvation; nevertheless, the water expulsion in protein folding cannot be addressed with such implicit solvation. To compensate for this, the global optimized MaxFlux-PRM path can be used as an initial guess for transition path sampling (36), or one can add the explicit water in the free energy profile calculation using the ΔD_rmsd method (35).

In our previous work on the folding pathway of the β-hairpin (17), we did not employ the iterative approach because the system was small, and the initial generated 93,886 nodes gave rise to a path with a 1.6 Å mean C_α RMSD between adjacent conformations. In this work, the criterion of the convergence of iteration, the C_α RMSD between adjacent conformations along the path is ≤3 Å in our region of interest (R_g < 22 Å), which in turn depends on the cutoff of the neighbor list, the r_c value. In the first iteration, this RMSD value ranges from 5.9 Å to 9.8 Å. These large RMSDs are not absolutely satisfied, although the sequence of events is consistent with the experimental results. The reason the coarse-grained path can capture the characteristic of the intermediate state is likely a result of our importance sampling strategy. Although the C_α RMSD between the experimental intermediate analogy (L16A mutant) and the native state is 13.4 Å, in the φψ space, these two conformations are actually very similar to each other (only the φ and ψ angles in the H1-H2 loop are significantly different). Our sampling strategy has ensured that, in the φψ space, the proximity of the native state is sampled intensively. As a result, it is not surprising to see that the conformations similar to the reported intermediate state are the nodes in our roadmap even in the first iteration. In the folding process from unfolded state to native state, the C_α RMSD between adjacent conformations along the path is not uniform in the last iteration; in steps 1–12, the C_α RMSD between adjacent conformations along the path ≤ 10 Å; in steps 13–22, the C_α RMSD ≤ 5 Å; and in steps 23–41, the C_α RMSD ≤ 3 Å. If one starts an MD simulation from an NMR structure, it is reasonable to obtain a trajectory with around 2 Å C_α RMSD from the native state. Thus, we believe that a path with the C_α RMSD between adjacent conformations ≤ 3 Å is an acceptable convergence criterion. For a given graph, Dijkstra's algorithm is a global minimization method that can guarantee the location of the shortest path (see Cormen et al. (22) for the proof), given that the neighbor list and edge weight calculation are accurate.

Recently, network and graph analyses have been applied in the protein-folding field (for a recent review see Caflisch (37)). The differences between our graph-theoretic approach and those of others are basically twofold. First, unlike other approaches (28,38–40), which generate the nodes using either MC or MD simulations, we create the nodes using PRM without detailed simulations so that the system can avoid being trapped in a local minimum, and the computational cost is low (see the details on the computational cost in the following discussions). Second, our definition of edge weight is different from others. Our edge weight along the path has clear physical meaning, which is the MFPT. The correct physical meaning of the edge weight is the key advantage of MaxFlux-PRM compared with other PRM approaches in protein folding (see Yang et al. (17) for the comparison on model systems). The uniqueness of MaxFlux-PRM is that it is a graph-theoretic approach enhanced reaction-path algorithm, which distinguishes it from other reaction-path algorithms such as the original MaxFlux (6), MaxFlux-NEB (15), NEB (41), conjugate peak refinement (42), self-avoiding walk (12), string method (43), milestoning (44), and transition path sampling (36). The combination between MaxFlux and PRM allows us to overcome the long-lasting global optimization problem in the application of the reaction-path algorithm. Thus, we hope that we have convinced the reader that MaxFlux-PRM can find the global optimized path. Moreover, in each step of the iteration, we tried to find the k-shortest node-disjoint paths instead of the shortest path; however, the k-shortest paths gave very similar routes to the one presented here.

We show the computational cost of our MaxFlux-PRM method in Fig. 5. Apparently, the cost is moderate. In addition, for node generation and pairwise C_α RMSD calculations, the scale-up on parallel computing is perfect with no need of communication between CPUs. For the first iteration to locate the coarse-grained path of EnHD, we generated ∼3 × 10⁴ nodes which took ∼6 h of running time on six CPUs. Probably, the cost of thermal unfolding simulations in explicit water is comparable to that of our MaxFlux-PRM approach. Although it has been shown that the unfolding simulation can successfully interpret the folding mechanism for several proteins including EnDH (45), it is not clear whether this is a general rule or not. There is also experimental evidence against this generalization: for example, the rate-limiting steps of the β-hairpin folding and unfolding are different (23). Therefore, care must be taken when one uses the thermal unfolding simulation to interpret the folding mechanism. However, the β-hairpin may not be typical because it is small. To conclude, MaxFlux-PRM is a general tool to study protein folding and conformational transition pathway with moderate computational cost.

Supplementary material

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Appendix A.

Data Supplement 1

Data Supplement 1