Role of a critical water in scytalone dehydratase-catalyzed reaction

Abstract

Scytalone dehydratase (EC 4.2.1.94) catalyzes the dehydration of two important intermediates in the biosynthesis of melanin, and it functions without metal ions or any cofactors. Using molecular orbital theory, we have examined the role of a critical water molecule in the mechanism of scytalone dehydratase. The water, together with an internal hydrogen bonding, contributes significantly to the stabilization of the transition state (or the enolate intermediate). The role of two active site tyrosines (Tyr-50 and Tyr-30) is (i) to hold the critical water in place so that it may stabilize the transition state without much structural rearrangement during the catalytic reaction, and (ii) to polarize the water, making it a better general acid. The stereochemistry of the scytalone dehydratase-catalyzed dehydration is also discussed.

Rapid enzyme-catalyzed proton abstractions from carbon acids have attracted great interest. In view of the basicities of protein bases, these proton abstraction might be expected to be slow owning to low acidities of carbon acids. The mechanism by which enzymes accomplish such a difficult task has been a matter of continuing debate (1–4). One proposal invokes the formation of short strong hydrogen bonds during the catalytic process (2). This concept has been used to explain many enzymatic reactions. Our interest here is scytalone dehydratase.

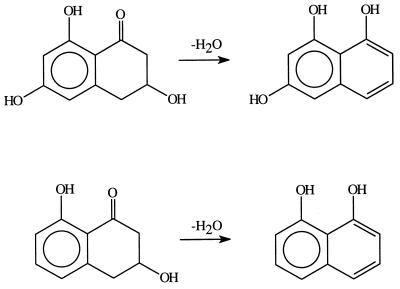
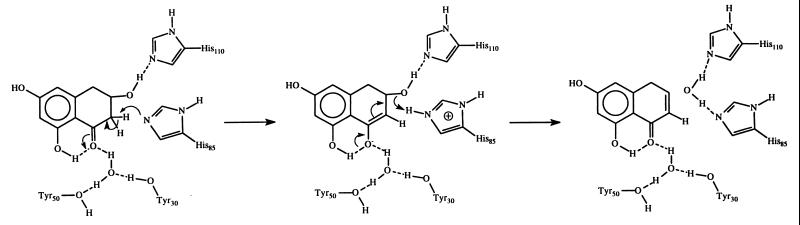
Scytalone dehydratase (EC 4.2.1.94) catalyzes the dehydration of two intermediates in the biosynthesis of melanin (Scheme S1) (5); it has been an important target for fungicides that control rice blast disease. Scytalone dehydratase is a trimeric enzyme consisting of three identical subunits, each unit having 129 amino acid residues. The x-ray crystal structure of scytalone dehydratase with a bound competitive inhibitor has been solved recently (6). Even at 2.9-Å resolution, two tightly bound water molecules were visible in the active site. On the basis of the crystallographic study, a catalytic mechanism was proposed as shown in Scheme S2 (6). According to this proposal, a water acts as a general acid to activate the carbonyl, making the α–C–H sufficiently acidic to be abstracted by a protein base, such as His-85, in the active site. As revealed by the x-ray crystallographic structure, the water is held in place by two tyrosine residues (Tyr-50 and Tyr-30). This dehydratase requires no metal ion or cofactors, so it is an especially interesting system.

Scheme 1.

Scheme 2.

Recently, quantum mechanical methods have been used to examine enolization reactions pertaining to enzyme-catalyzed proton abstraction from weak carbon acids (7–9). Here we decided to employ quantum mechanical theory to investigate the role of the critical water in stabilizing the enolate intermediate and the role of these two active site tyrosine residues (Tyr-50 and Tyr-30) in scytalone dehydration catalyzed by scytalone dehydratase.

THEORETICAL PROCEDURE

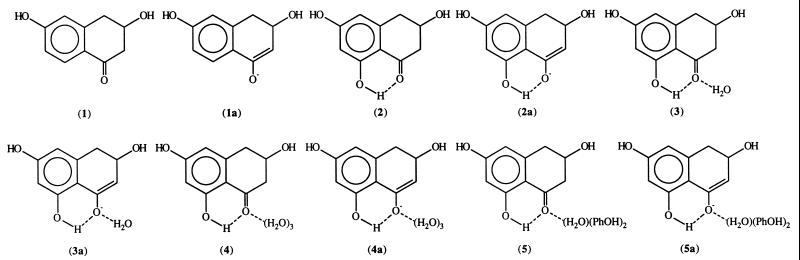
All calculations were carried out with the gaussian 94 program (10). For the ab initio molecular orbital calculations, geometry optimization was done at the Hartree–Fock (HF)/6–31G(d) level of theory, which is the standard method used for force field parameterization related to hydrogen bonding. It generally gives reasonable energetics concerning hydrogen bonding interactions. As a further check, we also performed energy calculations using the second-order Møller-Plesset (MP) perturbation (11) theory with 6–31+G(d) basis set. Previous study has demonstrated that the MP2/6–31+G(d) is a very reasonable method for studying hydrogen bonding interactions involving anions (12). Because we are interested in the relative hydrogen bonding strength, not the absolute values, even HF/6–31G(d) should be adequate for our purpose. Semiempirical PM3 (13) molecular orbital calculations were also carried out. This latter method is necessary for examining the role of tyrosine because the model including two phenols is too large to be treated by ab initio molecular orbital methods at a reasonable level of theory. Scheme S3 lists the compounds investigated.

Scheme 3.

RESULTS AND DISCUSSION

The interconversion of a carbonyl-containing molecule with its enol is a fundamental process in organic and biological chemistry, which has been much studied (14, 15). Normally, reactions of this kind can take place by one of the three possible reaction pathways, the choice between them depending on the reaction conditions, in particular the pH of the solution. In the first pathway, in acid solution, protonation at the carbonyl C=O group occurs first, followed by loss of a proton from an adjacent carbon atom. The second pathway involves deprotonation of an adjacent C—H group by hydroxide and protonation of the resulting enolate ion. The third possible reaction pathway is a concerted deprotonation/protonation. For reactions occurring in the active sites of enzymes, the first pathway looks less likely. However, pathways similar to the second and third are both possible. As proposed by Gerlt and Gassman (2), for an enzymatic reaction to use the third pathway, the transition state is probably a late one with much enolate character. If it is so, hydrogen bonding interactions in the active site would be extremely important for enzyme-catalyzed enolization reactions. In the case of scytalone dehydratase, the dehydration reaction can occur via either a stepwise or a concerted mechanism. For the stepwise mechanism, an enolate intermediate is involved, whereas for the concerted mechanism, the departure of hydroxide is concerted with the deprotonation of the C—H adjacent to the carbonyl group. However, it is very likely that even if the reaction is concerted, it may not be synchronous, meaning that the deprotonation occurs ahead of the elimination of the hydroxide ion. In any case, the initial step in scytalone dehydration, to some extent, resembles the enolization process discussed above. In the present study, we used ab initio and semiempirical molecular orbital theory to examine the differential hydrogen bonding strength in the enolate intermediate relative to the ketone reactant (Scheme S2).

Structure of the Reactant.

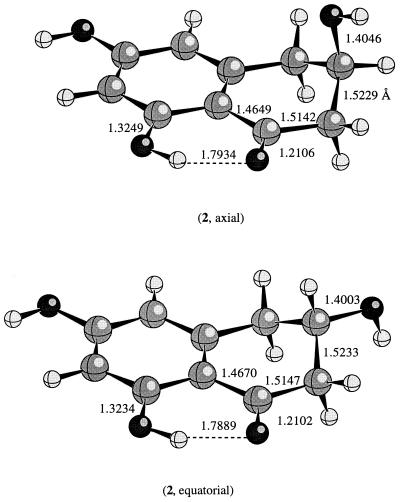
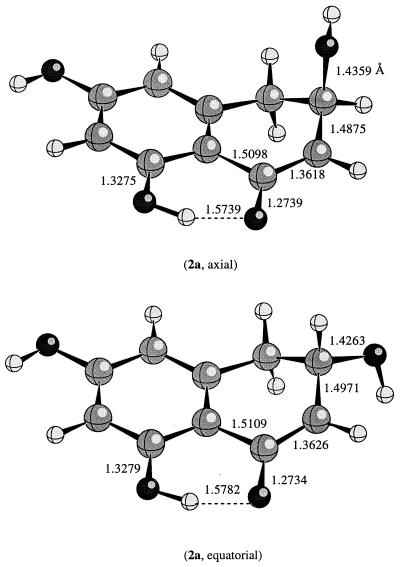
The calculated structure for the reactant scytalone at the HF/6–31G(d) level of theory is shown in Fig. 1. Both PM3 and HF/6–31G(d) methods predict a puckered geometry. The hydroxyl group can be either axial or equatorial. According to the ab initio molecular orbital calculations, the equatorial and the axial conformers are energetically the same in the gas phase. The semiempirical PM3 method favors the equatorial hydroxyl over the axial hydroxyl conformation by about 2 kcal/mol (1 kcal = 4.18 kJ). As indicated by Fig. 1, the bond distances remain essentially the same regardless of whether the hydroxyl is in an axial or equatorial position. For instance, the internal hydrogen bond distance is about 1.79 Å in both conformers of scytalone and the C—O(—H) distance remains around 1.40 Å.

Figure 1.

The calculated conformations for 2 at the HF/6–31G(d) level of theory.

Deprotonation at a methylene group can involve loss of either of the hydrogen atoms, and the factors that control the choice between them remain uncertain. Most interpretations have invoked the so-called stereoelectronic effect, originally proposed by Corey and Sneen (16) to account for the fact that deprotonation of 13-acetoxycholestan-7-one by loss of axial hydrogen is faster than deprotonation by loss of equatorial hydrogen. However, recent studies (17, 18) have cast doubt on the existence of such an effect, and it is in any case uncertain whether it is large enough to account for the observed stereochemistry of base-catalyzed enolizations. In the case of scytalone, the two methylene hydrogens adjacent to the carbonyl group are unequivalent because the ring is puckered; one of the hydrogen atoms is in an axial-like position with a HC—CO dihedral angle closer to 88.2° and the other in an equatorial-like position with a HC—CO dihedral angle of 26.6° (in the axial conformer). In the corresponding enolate intermediate, the HC—CO angle should be close to ≈0° because the carbanionic carbon is planar. Obviously, deprotonation of the axial hydrogen requires much less structural reorganization and the carbanion generated would be in a much more favorable state. The breaking C—H bond (or the doubly occupied atomic orbital) and the carbonyl molecular orbital would have a better overlap, for the dihedral angle between them is smaller. This is true regardless of whether the leaving hydroxide group is in axial or equatorial position.

It is expected that the elimination is faster when the leaving hydroxide group is in the axial position for two reasons. First, the leaving of an axial hydroxide can be assisted by the good overlap between the highest occupied molecular orbital (HOMO) of the enolate molecular orbital and the lowest unoccupied molecular orbital (LUMO) of the C—O(—H) (see below for further discussion). Second, there is less structural reorganization for an axial hydroxyl than for an equatorial hydroxyl. The question is for the enzymatic reaction to be efficient, does the enzyme preselect the conformation of scytalone (e.g., preferentially binding the axial conformation). At the present time, this question cannot be addressed satisfactorily without further structural information such as the crystal structure of an enzyme/substrate complex (see below for further discussion).

Structure of the Enolate Intermediate.

The calculated structures for the enolate are shown in Fig. 2. Again, the hydroxyl group can be in either axial or equatorial position. According to the calculations, the equatorial one is favored by 4.5 kcal/mol at the HF/6–31G(d) level of theory. In the enolate (the axial conformation), the H—C—C—O dihedral angle is very close to ≈0° (in the axial conformer, the angle is 4.1°). The intramolecular hydrogen bonding interaction becomes stronger as indicated by the very much shorter hydrogen bonding distance of 1.57 Å. The hydrogen bonding angle increases by about 10°. The C—O(—H) distance is about 0.01 Å longer for the axial conformation. However, as discussed above, for the equatorial conformation, a large structural reorganization (distortion) is required for the elimination of hydroxide. The activation barrier for the elimination step will be bigger for the equatorial conformation of the enolate even though it is more stable. Thus, if the scytalone-catalyzed dehydration reaction follows a concerted pathway, the leaving hydroxide will likely be in the axial position, suggesting that the enzyme preselects the axial conformation of scytalone before the chemical reaction (e.g., during the binding process). However, if the deprotonation step is ahead of the elimination step, the enzyme may not necessarily preselect the conformation of scytalone. A kinetic study using isotopically labeled scytalone may provide further insight into the mechanism of scytalone dehydratase.

Figure 2.

The calculated conformation for 2a at the HF/6–31G(d) level of theory.

As shown in Fig. 2, the C—O(—H) distance is slightly longer (about 0.01 Å) in the axial conformer than in the equatorial one, whereas the C^α—C^β distance is slightly shorter (about 0.01 Å) in the axial conformer than in the equatorial conformer. The longer C—O(—H) bond and the shorter C^α—C^β bond in the axial conformer are clear indication of stereoelectronic effect caused by the interaction between the LUMO of the C—O(—H) and the HOMO of the enolate. This, again, reveals that the leaving hydroxyl group prefers an axial position.

Hydrogen Bonding Interaction.

To examine the role of the critical water in stabilizing the enolate, we investigated the differential hydrogen bonding in the enolate compared with that in the reactant in the presence of one and three water molecules. For the present calculations, geometry of each complex is fully optimized without any geometrical constraint, using both PM3 and HF/6–31G(d) methods. Additional energy calculations were done at the MP2/6–31+G(d) level of theory.

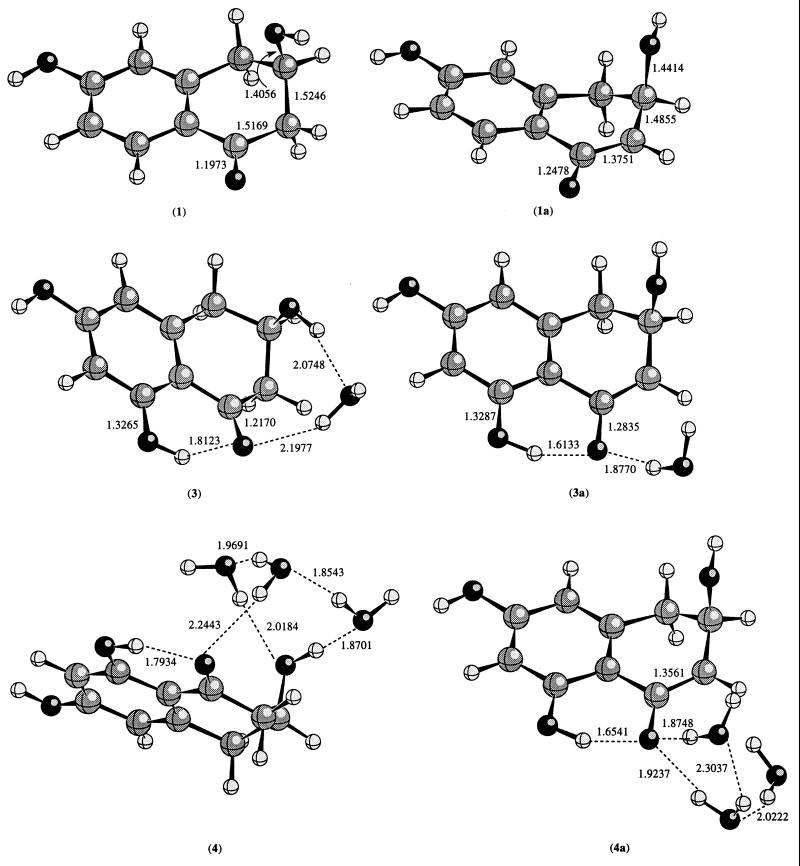
The calculated geometries at the HF/6–31G(d) level are given in Fig. 3 and the PM3 geometries are in Fig. 4. The differential hydrogen bonding stabilization of the enolate intermediate relative to the reactant is taken as the relative energy difference between the intermediate and the reactant in the presence and absence of the hydrogen bonding interaction. For instance, the internal hydrogen bonding stabilization of the intermediate 2a is calculated as the energy difference between ΔE_1–1a and ΔE_2–2a. ΔE_1–1a is the energy difference between 1a and 1; it also reflects the acidity of the methylene C—H hydrogen adjacent to the carbonyl group in the gas phase. Table 1 lists the calculated acidity for 1-4 at HF/6–31G(d), HF/6–31+G(d), and MP2/6–31+G(d) levels of theory. The calculated acidities at the MP2 level are consistently smaller than the corresponding values at the HF levels; however, the relative trend remains the same for compounds 1–4. In the following discussions, only the axial conformations are considered.

Figure 3.

The calculated geometries for 1, 1a, 3, 3a, 4, and 4a at the HF/6–31G(d) level of theory.

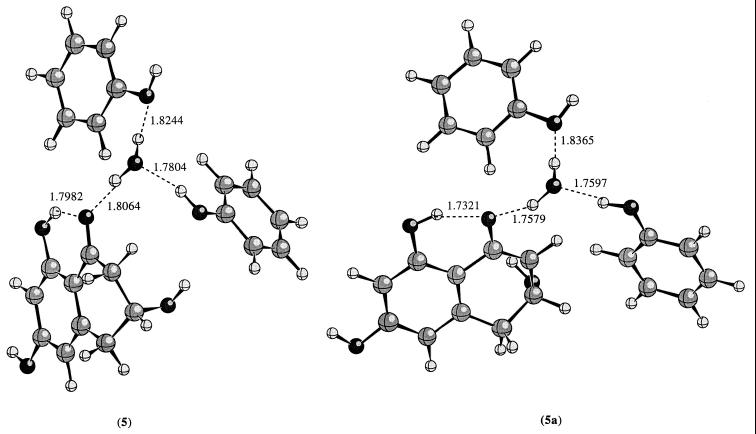
Figure 4.

The PM3 calculated geometries for 5 and 5a.

Table 1.

The calculated deprotonation energies for compounds 1–4 at the HF/6-31G(d), HF/6-31+G(d), and MP2/6-31+G(d) levels of theory

Compound	Deprotonation energy, kcal/mol
	HF/6-31G(d)	HF/6-31+G(d)	MP2/6-31+G(d)
1	389.8	380.1	363.9
2	380.5	371.8	354.0
3	374.0	365.4	349.0
4	369.2	361.6	347.4

As calculated from the data in Table 1, the differential hydrogen bonding stabilization of intermediate 2a is about 10 kcal/mol. The presence of a water molecule in 3a further stabilizes the intermediate by about 5 kcal/mol. The presence of three waters (as a model of the active site: one water and two tyrosines) has a larger effect on the stabilization of the intermediate than the presence of one water, but according to the present calculation, the difference is less significant. However, it should be pointed out that this could be an underestimation owning to the mobility of the water molecules in our calculations. In the present calculations, the water molecules are free to move, whereas in the enzyme active site the position of the critical water is fixed. In 4, the positions of the three water molecules are such that in addition to the hydrogen bonding interaction between the carbonyl oxygen and hydrogen of one water, these water molecules and the axial hydroxyl group form a cyclic hydrogen bonding network. However, in 4a, this cyclic hydrogen bonding network with the axial hydroxyl group becomes impossible because of the strong interaction of the enolate oxygen anion with these water molecules. As a result, additional hydrogen bonding interaction due to the mobility of the water molecules is seen in 4, but not in 4a. Clearly, the role of the two active site tyrosines is (i) to hold the critical water in the correct position relative to the carbonyl oxygen of the substrate, restraining the mobility of this water; and (ii) to further polarize the water molecule, making it a better general acid. From Table 1, it is clear that the presence of the hydrogen bonding interaction stabilizes the enolate intermediate considerably (by 16.5 kcal/mol at the MP2 level of theory).

We also carried out semiempirical PM3 calculations on compounds 1–4 and 5. In general, the PM3 method predicts a larger stabilization than the ab initio molecular orbital method. According to PM3 calculations, the internal hydrogen bonding stabilizes the enolate intermediate by 15.1 kcal/mol, which is about 5.9 kcal/mol larger than the MP2 value. In 4a, the PM3 calculated differential stabilization is about 27.9 kcal/mol, which is about 11.4 kcal/mol higher than the ab initio value at MP2 level. In 5a, the PM3 value is about 30.9 kcal/mol. If we take the difference between the PM3 and the MP2 values in 4a as the error of the PM3 results, then in 5a, the stabilization is probably about 19.5 kcal/mol (30.9 − 11.4 = 19.5 kcal/mol).

Stereochemistry of Dehydration.

The stereochemistry of enzymatic β-elimination reactions can be either syn or anti (19). For the enolase-catalyzed dehydration of 2-phospho-d-glycerate, the reaction follows a stepwise mechanism involving an enolate intermediate (20, 21) and the hydrogen being abstracted and the leaving hydroxide are anti to each other (22). The presence of metal ions and hydrogen bonding interactions are responsible for the facile proton abstraction (23). On the other hand, the dehydration catalyzed by enol-CoA hydratase has a syn stereochemistry (24). This latter reaction appears to be concerted (25–27). The stereochemistry for scytalone dehydration is unclear at the present time, as is the question of whether the reaction is stepwise or concerted. Further study is required to address these questions. However, because the substrate scytalone is a cyclic compound, for a concerted reaction pathway to be operative, the anti stereochemistry should be preferred because large geometrical reorganization is required for the syn elimination. For the stepwise mechanism, either syn or anti stereochemistry is reasonable even though the syn elimination may require considerable conformational change.

CONCLUSIONS

In the present study, we examined the recently proposed mechanism for scytalone dehydratase-catalyzed dehydration of scytalone by using molecular orbital theory. It is clear from the molecular orbital studies that the differential hydrogen bonding interaction is sufficiently strong to make the proposed mechanism feasible. On the basis of this investigation, the role of the two active site tyrosines are twofold: (i) holding the general acid water in the correct position so that during deprotonation of the methylene C—H hydrogen, the developing negative charge on the carbonyl oxygen can be effectively stabilized by the water molecule and the internal hydrogen bond without much structural reorganization; and (ii) polarizing the water molecule, making it a better general acid. It is also suggested that the enzyme probably favors the conformation of the substrate with an axial hydroxyl group over the one with an equatorial hydroxyl group.

ABBREVIATIONS

HF

Hartree–Fock

MP

Møller–Plesset

HOMO

highest occupied molecular orbital

LUMO

lowest unoccupied molecular orbital