Abstract
Healthcare cost-effectiveness analysis (CEA) often uses individual patient data (IPD) from multinational randomised controlled trials. Although designed to account for between-patient sampling variability in the clinical and economic data, standard analytical approaches to CEA ignore the presence of between-location variability in the study results. This is a restrictive limitation given that countries often differ in factors that could affect the results of CEAs, such as the availability of healthcare resources, their unit costs, clinical practice, and patient case-mix.
We advocate the use of Bayesian bivariate hierarchical modelling to analyse multinational cost-effectiveness data. This analytical framework explicitly recognises that patient-level costs and outcomes are nested within countries. Using real life data, we illustrate how the proposed methods can be applied to obtain (a) more appropriate estimates of overall cost-effectiveness and associated measure of sampling uncertainty compared to standard CEA; and (b) country-specific cost-effectiveness estimates which can be used to assess the between-location variability of the study results, while controlling for differences in country-specific and patient-specific characteristics.
It is demonstrated that results from standard CEA using IPD from multinational trials display a large degree of variability across the 17 countries included in the analysis, producing potentially misleading results. In contrast, ‘shrinkage estimates’ obtained from the modelling approach proposed here facilitate the appropriate quantification of country-specific cost-effectiveness estimates, while weighting the results based on the level of information available within each country.
We suggest that the methods presented here represent a general framework for the analysis of economic data collected from different locations.
Keywords: Cost-effectiveness analysis, Statistics, Generalisability, Clinical trials
1. Introduction
Healthcare economic evaluation studies benefit considerably from access to individual patient data (IPD) from randomised controlled trials (RCTs) [1]. In the context of some healthcare interventions - in particular, pharmaceuticals - RCTs are often multinational in design. Such studies offer several advantages over single-country counterparts. These include the opportunity to reach rapidly the required target sample size, and meeting the needs of regulatory agencies in different jurisdictions. Furthermore, because these studies enrol patients from a wide range of countries, multinational trials are thought to have the potential to increase the geographical generalisability of clinical and cost-effectiveness estimates [2].
However, there are two sets of arguments that suggest this viewpoint many not be totally defensible. The first relates to the fact that policy-makers are essentially jurisdiction-specific and, in most instances, this accords with being country-specific. An increasing number of healthcare systems now require economic evidence to make country-specific decisions regarding the reimbursement of specific health technologies [3], which suggests that trial-wide cost-effectiveness results may not be relevant to any specific jurisdiction. Countries in fact will inevitably differ in factors such as availability of healthcare resources, clinical practice, patients’ case-mix and the costs of delivering healthcare. These factors can cause the value for money of a healthcare intervention to vary between different countries in a multinational study [2], leaving country-specific policy-makers uncertain about the extent to which trial-wide (i.e. pooled) cost-effectiveness results are relevant to their own jurisdiction.
The second set of arguments relates to the appropriateness of the methodology used to analyse IPD alongside multinational trials. Patients are often recruited and treated (in a particular centre) in a given country, hence cost-effectiveness data take on a natural hierarchical structure. Failure to acknowledge these features of the data may lead to misleading conclusions with regard to the generalisability of the study results. In other words, it can be argued that there is likely to be statistical heterogeneity in the country-specific cost-effectiveness results between different jurisdictions participating in a multinational RCT, and that it is implausible to assume a priori that differential costs and health outcomes are the same in each country.
There are three important questions that must be addressed when assessing the geographical generalisability of the conclusions of the economic component of any health technology assessment (HTA). First, what are the appropriate methods to analyse IPD relating to cost-effectiveness data from multinational RCTs? Second, how should we assess the extent to which trial-wide results are generalisable between countries participating in the same study? Finally, how to produce country-specific cost-effectiveness estimates that are directly relevant to local decision-makers?
Various analytical strategies - most of which use regression methods - have been proposed to address the above questions [1]. Early approaches ignored the natural clustering in the data and failed to implement methodologies that could facilitate the estimation of the between-country variability in the results [4]. A series of recent papers advocated the use of hierarchical modelling to analyse cost-effectiveness IPD from multi-location trials, while simultaneously allowing for (potential) between-location variability in the data [5-8]. Pinto et al [5] recently explored alternative estimation methods to obtain country-specific estimates of cost-effectiveness, conducting a simulation exercise based on summary estimates of country-level differential costs and effects from a large multinational RCTs. Grieve et al [7] compared OLS and hierarchical models in the analysis of cost data from 11 European countries, and proposed a generalised linear mixed model to address the skewed nature of the length of stay and cost data. Finally, Manca et al [8] extended the net benefit regression [9] to accommodate the hierarchical structure of economic data in multi-location trials, showing how hierarchical models can be used to obtain trial-wide and location-specific estimates of incremental cost-effectiveness, while correctly quantifying the measures of sampling uncertainty around these mean estimates [8].
This paper advocates the use of Bayesian bivariate hierarchical models (BHLM) for the analysis of multinational cost-effectiveness data. In view of the need to investigate potential between-country differences in cost and health outcomes, it is demonstrated that BHLM can be used to accommodate information at subject- and country-level to facilitate robust estimation of overall (i.e. trial-wide) and country-specific differential mean costs and effects. The proposed approach is illustrated using data from the Assessment of Treatment with Lisinopril and Survival (ATLAS) study, a large multinational trial comparing low versus high doses of the ACE inhibitor Lisinopril in patients with chronic heart failure [10, 11].
The paper begins by briefly summarising existing approaches for RCT-based cost-effectiveness analysis (CEA). Section 3 describes the bivariate non-hierarchical regression methods for CEA proposed in the literature. Section 4 outlines the rationale for extending the use of BHLM techniques to the analysis of IPD from multinational cost-effectiveness data. The case study is presented in Section 5. The next provides a discussion of the results from the application of non-hierarchical and hierarchical bivariate models to the case study. The final section summarises the contributions of paper contextualising these in the light of the current methodological debate in medical economic evaluation.
2. Analytical strategies for CEA using individual patient data from multinational trials
Despite the existence of factors that could potentially affect the between-location variability of the study results, most CEAs using IPD collected alongside multinational RCTs have been conducted assuming that the clinical effectiveness of the intervention does not differ greatly (at least in relative terms) across countries [12, 13], and that pooling clinical data across countries (and centres) to assess the effect of treatment on clinical outcomes is an acceptable strategy.i Similarly, on the cost side the standard method has been to apply a single set of unit costs (typically taken from one country) to all patient-specific resource use data collected in the study, regardless of where this resource use had taken place. Pooled costs are related to pooled outcomes to obtain a trial-wide (or pooled) measure of cost-effectiveness. Results for another jurisdiction are then obtained by multiplying the pooled trial-wide resource use data by resource-specific unit costs taken from this other jurisdiction. The above practice implicitly assumes that resource use and effectiveness data are perfectly transferableii between countries/jurisdictions [14]. Despite the popularity of this approach, the proliferation of country-specific re-assessments of previously published trial-wide CEAs suggests that local decision-makers are often uncertain about the ‘transferability’ of the trial-wide results to their own jurisdiction.iii
An alternative approach, sometimes adopted in multinational studies, assumes that resource use data are not at all transferable between locations while effectiveness data are. Analyses for a particular country/jurisdiction would produce cost estimates by multiplying unit costs for a given country by resource use of patients recruited in the same country, while relating these costs to trial-wide effectiveness data (see for instance Bjorholt et al [15]). The two main limitations with this approach are that, first, it is only feasible for trials which recruited a reasonably large number of patients in the country of interest, and second, it ignores the fact that IPD on costs and effects are naturally correlated. Analysing two different samples for costs and effects will introduce bias in the estimation of the joint distribution of the mean differential costs and effects, influencing the analyst’s ability to correctly quantify the sampling uncertainty surrounding the measure of cost-effectiveness [14].
A third and less commonly utilised approach to the analysis of multinational cost-effectiveness IPD is to focus on only one of the countries/jurisdictions in the trial, estimating mean costs and effects solely using patient data from such a country (examples can be found in Liljias et al [16] and Mark et al [17]). While overcoming the limitation of the previous approach, this strategy implicitly assumes that country-specific data are not at all transferable between locations. Most of the time this is impracticable for countries with low recruitment rate in the trial. Furthermore, it makes a sub-optimal use of the data, by discarding potentially relevant information from other countries.
In practical terms it is likely that IPD from multinational trials will be partially transferable. That is, some components of resource use and health outcomes will be common between locations, while others will be more country-specific. Analytically, the problem is to disentangle the extent to which CEA data for one country/jurisdiction are generalisable to another. Attempts to address the issue have focussed on the analysis of individual-patient resource use and cost data only, rather than full cost-effectiveness.
Willke et al were the first to use regression methods for the simultaneous analysis of cost and effects data collected alongside multinational RCTs [18]. To explore the between countries variability in the results, their regression model included country-by-treatment and country-by-outcome interaction terms, which facilitated country-specific estimation of mean differential costs and effect. The regression estimates were then used to calculate incremental cost-effectiveness ratios (ICERs) uing (i) own-country costs and effectiveness results, (ii) own-country costs and trial-wide effectiveness results; or (iii) own-country costs, but trial-wide resource utilisation and effectiveness. The authors found that greatest variation in the country-specific ICER was in case (i), where country-specific resource utilisation, unit prices and outcome levels were all taken into account.
In a recent paper, Willan et al [6] used hierarchical modelling to obtain empirical Bayes estimates of country-specific differential costs from summary data derived from a large multinational trial. The authors compared and contrasted (i) overall random effect estimate, (ii) the country-level estimates obtained from a stratified analysis (i.e. similar to having a dummy variable for each country), and (iii) the empirical Bayes estimates obtained from a random effect model, finding that estimates obtained with (iii) to be more informative for the Canadian decision maker. The method in (i) and (iii) are essentially similar to a random effect meta-analysis [19], which assumes that study-specific (country-specific, in the case of the models applied to multinational IPD) estimates are drawn from a distribution of possible realisations of the study-specific treatment effect (country-specific differential cost) which follows a normal distribution. Using the same summary data, Pinto et al [5] conducted a simulation exercise to explore the validity of univariate and bivariate shrinkage models for differential costs and effects derived using an empirical Bayes approach.
Grieve et al [7] and Manca et al [8] have recently proposed the use of hierarchical modelling to analyse, respectively, individual-level cost and cost-effectiveness data collected alongside multi-location trials. The authors justify the proposed approach on the basis of two main considerations. First, patients treated in the same site are expected to be more similar (in terms of resource use and clinical outcome) than those treated in other locations [20, 21]. Second, locations may vary markedly in factors that influence the resource use, unit costs and outcome data observed in trials [1, 2]. Manca et al showed how to use hierarchical regression analysis to obtain trial-wide and location-specific estimates of cost-effectiveness, using centre-specific predictions to explore the between-location variability in the results. This approach was developed in the context of a univariate model for net benefit and did not use any patient- or centre-specific covariates to explain the observed between centres variability in the results.
This paper extends the approach proposed by Manca et al in two ways. It develops a Bayesian bivariate hierarchical regression model for the analysis of individual patient level cost-effectiveness data collected alongside multinational trials, showing how to incorporate patient- and country-specific information in the model.
3. Bivariate (non-hierarchical) modelling approaches for trial-based CEA
Willan et al [22] recently extended the net benefit regression framework proposed by Hoch et al [9] using of a system of seemingly unrelated regression (SUR) equations for IPD on costs and health outcomes. This (bivariate) approach has three main advantages. Firstly, it facilitates explicit modelling of both costs and effects while allowing the inclusion of a set of covariates in the two equations. Secondly, it exploits the existence of correlation, at patient level, between costs and effects, thereby improving the efficiency of the estimation process when this correlation is different from zero. Thirdly, unlike the standard (univariate) net benefit regression, SUR does not require a new regression to be estimated for every value of the cost-effectiveness threshold (i.e. λ). Using a fully parametric approach, the authors showed how the ‘treatment effect’ (in terms of differential mean costs and effects) is estimated from a regression model in which the error terms for the cost and effects equations are assumed to follow a bivariate normal (BVN) distribution with (zero) mean and a given covariance matrix.iv
A more flexible formulation of the non-hierarchical bivariate model for cost-effectiveness IPD, has been proposed by O’Hagan et al within a Bayesian statistical framework [23]. Their model can be illustrated as follows. Let the vector of individual-specific costs (Cti) and effects (Eti), receiving the treatment t = (0, 1) be described as follows,
| (1) |
where IPD on cost and effects are assumed to follow a BVN distribution, with the parameters , and representing respectively the sample mean estimates for effects and costs in the two arms of the trial (0=standard intervention; 1=new intervention). The parameters , and are, respectively, the variance of the mean effects, the variance of the mean cost, and their covariance in treatment arm t. Notice that unlike the SUR model, this formulation does not require the covariance matrix to be the same in each treatment group.
In each treatment arm, mean cost and effects were assigned a non-informative joint multivariate normal prior distribution, while the covariance matrix was characterised by a Wishart distribution. The estimation of the model parameters was carried out using Markov chain Monte Carlo (MCMC) methods, deriving the information of interest from the posterior distribution of the differential mean costs and effects .
Model (1) can be re-parameterised using the, so-called, product normal formulation which reinterprets the multivariate model into a series of related (univariate) linear models [24-27], as followsv
| (2) |
which assumes (for each treatment arm) a Normal distribution for effects and a Normal distribution for costs, with the latter being conditional upon the departure of the individual-specific effectiveness (i.e. ) from its treatment-group specific overall mean (Etg). The quantities α and γ represent, respectively, the trial-wide mean cost and effect for the control arm.
When IPD on costs and effects follow a BVN distribution, expressions in (2) can be back-transformed to obtain the parameters in (1) as follows
| (3) |
This formulation captures the correlation between costs and effects at patient level through the terms θ0 and θ1 assuming that in each arm, the mean cost is linearly related to the departure of the patient-specific effectiveness from its group mean (i.e. ). The differences in mean cost (Δc) and mean effects (Δe) are subsequently combined as follows to estimate the incremental net benefit:
| (4) |
A Bayesian formulation of (1) requires the specification of prior distributions for both the vector of mean cost and effects and the covariance matrix. The ‘textbook’ definition of a prior distribution for the latter is in the form of a Wishart distribution [25, 26]. However, several authors have commented on the fact that the definition of a non-informative Wishart prior distribution for variance parameters is not a trivial task [25, 26, 28]. One of the advantages of adopting the product-normal formulation in (2) is that more standard non-informative priors [26] for variance parameters can be used.
The models discussed so far assume no differences between countries, and it is reasonable to expect some degree of clustering in multinational economic trials.vi
4. Bivariate hierarchical linear model in trial-based CEA
The model described in the previous section can be extended in two ways. Firstly, by formally recognising the hierarchical structure of the cost-effectiveness data, and secondly, by incorporating subject and country specific covariates to explain observed between-country variability in the economic results. The standard implicit assumption underpinning the validity of this class of models relates to the concept of exchangeability between the units conveying information on the parameter of interest (i.e. country-specific differential costs and effects). The implications of this assumption are considered in the discussion section of this paper. For a full discussion of the concept of exchangeability in Bayesian hierarchical models see Gelman et al [25] (Section 5) and Spiegelhalter et al. [26] (Section 3.17).
4.1 Accounting for hierarchical data structure
We start by reformulating (1) to take into account the nested structure of the cost-effectiveness data (i.e. patients clustered within countries) as follows
| (5) |
where Etij and Ctij represent respectively, the observed effect and cost of the ith patient receiving treatment t(= 0,1) in country j. Note that (5) is the same as (1) except that we have now introduced a subscript to indicate that we are interested in the country j estimates of the mean costs and effects in each arm, as well as their differential mean estimates.
It is assumed for simplicity that the covariance matrix is not country-specific, i.e. in each arm, the variance of costs and effects between subjects is the same in each country, as is their covariance.vii This is another important feature of the modelling framework proposed here compared to the approaches described in section 3.
As before, (5) can be re-expressed using the product-normal formulation
| (6) |
where αj and γj are treated as fixed effects within each country, while the jth country-specific differential mean effects (Δej) and costs (Δcj) are assumed to follow a BVN distribution and to be correlated with each other, as showed in (7),
| (7) |
where and represent the between-country variance in the (country-specific) difference in mean costs and effects, δc and δe are the overall differences in mean costs and effects, and is the departure of the country-specific mean differential effects from the trial overall mean.
This formulation differs from the model proposed by Manca et al. [8], in that the random effects in (7) are specified only for the differential mean costs and effects. In this sense, this model resembles a Bayesian (random effects) IPD meta-analysis [26]..
The parameters (Δcj) and (Δej) can be combined to calculate the country-specific incremental net benefit as showed in (8).viii
| (8) |
For the jth country, the expressions in (6) can be back-transformed to the parameters in (5), as before
| (9) |
The choice of a truly non-informative prior for variance parameters of the random effects in BHLM is an area of ongoing methodological research [25, 26, 29]. Following Lambert et al. [30], a range of several non-informative prior distributions for the variances ( and ) of the ‘random effects’ has been investigated here, and uniform priors on the standard deviation scale have been selected in the final model. This choice was consistent with recent recommendations [25, 26]. For the other parameters in (9) standard non-informative prior distributions were used.
4.2 Patient and country covariates
An important feature of the framework presented in equations (6) to (9) is its ability to accommodate explanatory variables at patient and country level. There are several reasons for wanting to do so in RCT-based statistical CEA modelling.
4.2.1 Subject level covariates
The selection of patient-level covariates in clinical trials is usually a choice dictated by clinical considerations. There are however three main justifications for including subject-level covariates in the cost-effectiveness modelling of IPD. Firstly, adjustment for baseline imbalance of important prognostic factors between groups [31]. This improves the efficiency of the estimation process and ensures that ‘treatment effects’ estimates are unbiased. The second reason is to obtain robust country-specific outcome measures. If there is between countries variation in a given covariate - say age - considered to be an important predictor of cost (effect) differences, then although age may be balanced between treatment groups within each country, part of the between-country variation in the cost-effectiveness results could be ascribed to by-country variation in mean age. A final argument for including subject-level covariates is to look at effect modification [31]. If the researcher believes that differential costs and effects may differ between sub-groups of patients (e.g. by gender) then it is important to look at treatment-covariate interactions. For simplicity, this paper does not explore treatment-covariate interaction at the patient level, but the models presented here could be easily extended to this purpose. For an application of these models to the case of patient and centre sub-group analysis see the recent work by Nixon and Thompson [32].
4.2.2 Country/jurisdiction level covariates
Country-specific variables could also be important predictors of between countries difference in costs and effects and it is reasonable to expect that their role and selection will vary depending on the context of the study. There are two main reasons for including country-level covariates in the type of models proposed here. The first is to investigate if certain ‘contextual factors’ can help explain the observed between-country variability in the results. Between-country difference in clinical treatment protocols for the same condition, for instance, may explain between-country difference in observed resource use and health outcomes. The same can be said for differences in country-specific level of public expenditure in healthcare. Once these factors have been factored in, they can improve the model’s predictions for those countries sharing the same mix of contextual factors. A note of caution is due here. The researcher must be careful when selecting these covariates as there are usually few countries in a typical multinational study and statements about transferability of the results to countries outside the set of those participating in the trial requires careful consideration. The second reason for including country-level covariates is to look at covariate-treatment and cross-level covariates interaction. The former should usually be used for exploratory work, as there are typically very few observations at country level. The cross-level interaction can be used to explore between-country variation of the treatment effect on costs and health outcome for specific patient subgroups. This type of analysis would also be useful in single country multicentre trials to explore whether the treatment effect for the more severe patients, for example, is better in teaching hospitals than district general hospitals. Unfortunately the literature on methods used to identify country-level characteristics that are expected to impact on costs and effects in CEA is sparse. Grieve et al have explored the role of national Gross Domestic Product (GDP) in explaining between country differences in differential cost estimates in an observational study of stroke patients. In a recent study Drummond et al. [33] suggested three types of variables that could characterise a country in the context of CEA: the percentage of national GDP spent on healthcare, the reimbursement system for hospitals in a given healthcare system, and the payment method used for physicians.
The second extension of the analytical framework proposed in this paper is aimed at showing how to incorporate subject and country specific covariates in the modelling strategy proposed so far. The model described in (6-9) can therefore be extended as follows
| (10) |
where and are patient-specific variables (e.g. age, gender, smoking status, etc.). These variables are centred with respect to their trial-wide mean to improve the efficiency of the estimation procedure [34].
Country-level covariates can be included in the expression for the difference in costs and effects. The distinction here is important in that this incorporates an ‘effect modifier’, i.e. the treatment effects vary according to the level of the covariate(s). Therefore the random effects on the difference in mean costs (δcj) and survival (δej) between countries in (7) can be modified as follows to include country-specific information
| (11) |
where and are country-level covariates, and η’s are the coefficients associated with the country-level regressions. The country-level covariates are centred with respect to the trial overall mean, and are not weighted by the number of subjects in each centre. Notice that the country-specific variable used in the cost equation can be different from that use in the effects equation . Non-informative priors are given to ϕ,γ,α,η, and θ assuming normal distribution with mean zero and large variances, while a uniform prior on the standard deviation scale was chosen for parameters τ in (11) as in (7).
4.3 Exploring the variability of the results between countries
The flexibility of BHLM for CEA using IPD facilitates the estimation of country-specific measures of cost-effectiveness in a way that overcomes the limitations of a stratified analysis, where each country is analysed independently from the others. This is achieved through shrinkage estimation, which implements the idea that although different, country-specific data might share some degree of similarity and as such, country-specific estimates of treatment effect (on costs and effects) can borrow strength from each other. In other words, country-specific estimates will be more or less pulled (i.e. shrunken) towards the trial-wide treatment effect depending on the number of observations in each country and the sampling variability around each country-specific estimate. The amount of shrinkage will also depend on the size of the estimated between country variance.
The BHLM proposed in this paper are estimated via Bayesian MCMC methods, using the freely available software package WinBUGS [35] and the code for the models described in section 4.2 are reported in the appendix. A Bayesian approach allows inclusion of pre-existing evidence in the form of prior information [36], and of the use of MCMC has the benefit of producing the output in a convenient format for calculating cost-effectiveness acceptability curves (CEACs). These curves represent the probability that the intervention is cost-effective for a given level of decision maker maximum willingness to pay for additional unit of outcome, given the available information. In the models presented in this paper, the probability that the intervention is cost-effective in country j is simply the probability that the INMBj in (8) is greater than zero (at a given λ value), which can be obtained directly from the posterior distribution of the INMBj. For an extensive discussion of the reasons for adopting a Bayesian perspective in CEA have see Luce and O’Hagan [37].
5. Motivating example: the ATLAS trial
The Assessment of Treatment with Lisinopril and Survival (ATLAS) study is a multinational trial which enrolled 3164 patients in 19 countries, comparing low dose (n=1596) and high dose (n=1568) of the ACE inhibitor lisinopril in patients with chronic heart failure. Details of the main economic and clinical analyses have been reported elsewhere [10, 11]. The case study makes use of a total of 3061 observations (low dose, n=1545; high-dose, n=1516) from 17 countries; 2 countries have been excluded having recruited a very low number of patients and/or an extremely unequal allocation of patients between the two arms. Furthermore, from the end of year 3 patients were subject to administrative censoring. Currently there are no methods in the literature that illustrate how to deal with censored cost-effectiveness data in a bivariate hierarchical modelling framework. Therefore, for simplicity, the analysis uses data observed during the first three years of the study. Due to these assumptions, the specific results of the analyses presented here are not the same as in the main study report [10] and should not be interpreted as definitive.
5.1 Trial-wide results
The starting point is to quantify the trial-wide cost-effectiveness results. Table 1 reports the trial-wide results for the three models discussed in sections 3 and 4, that is the non-hierarchical bivariate model (column 1) estimated implementing the methodology proposed by O’Hagan, Stevens and Montmartin [23], the BHLM with no covariates (column 2) and with the addition of subject- and country-level covariates (column 3).
Table 1.
Trial-wide CEA results in the ATLAS trial§
| Bayesian bivariate non-hierarchical model | BHLM no covariates | BHLM with covariates | |
|---|---|---|---|
| Differential cost (UK pounds): | 8.2 (-32.9 to 50.1) | 11.9 (-192.8 to 217.1) | 10.3 (-200.4 to 222.1) |
| Mean life expectancy#: | — | — | 11.7 (-74.8 to 98.7) |
| Survival gain (days): | 24.9 (0.2 to 51.2) | 40.2 (-50.9 to 132.8) | 35.2 (-64.8 to 136.6) |
| Public expenditure in health*,#: | 52.6 (-18.9 to 124.7) | ||
| Between-country variance in differential cost: | — | 61 (42 to 117) | 71 (42 to 155) |
| Between-country variance in survival gain: | — | 31 (18 to 73) | 12 (7 to 31) |
Results are reported for four different models: Coefficients and 95% confidence (credibility) intervals (in parentheses). N = 3061. MCMC estimates are obtained after 40,000 iterations and a 20,000 iterations burn-in period
As percentage of the GDP
Expressed as departure from the overall mean
As expected, the presence of a hierarchical structure in the data means that the differential costs and survival gain estimates obtained using the non-hierarchical model have excessively narrow credibility intervals (CrI). The 95% CrI estimated using the BHLM for the differential cost are approximately five times wider. Similarly, the 95% CrI for the trial-wide survival gain are 3.5 times wider than those obtained using the non-hierarchical approach. These results are in line with those found by Manca et al. [8]. That is, analytical approaches which ignore the hierarchical structure in multinational trial-based cost-effectiveness data can generate inaccurate estimates of the differential mean costs, effects, and of their credibility intervals.
In the BHLM with covariates, the patient-level cost and survival equations (eq. 10) use patient’s age as covariate, whereas country-level cost and survival equations (eq. 11) employ respectively the country’s mean life expectancy and the public expenditure in healthcare, where the latter is expressed as percentage of the national GDP. It should be noted that (10) assume that patient-level covariates affect the differential costs and survival estimates indirectly, through its impact on the mean cost and survival in each arm of the trial. In model (10) the effect of mean age on the mean cost (ϕc) and survival (ϕe) in the trial are respectively 4.5 (95% CrI: 2.4 to 6.5) and -4.6 (95% CrI:-5.8 to -3.3), suggesting that the mean cost and survival estimates in each country are clearly affected by the patient’s age, and that on average a patient that is one year older than the overall trial mean would be expected to cost £4.5 more and to live 4.6 days less than the average patient in the study (results not reported in the table).
Similarly, country-specific variables seem to affect the estimated differential mean cost and survival in the trial. Mean life expectancy has a positive impact on the differential cost, indicating that those countries with mean life expectancy greater than the trial average will experience an increased per patient cost (for those patients treated with high dose lisinopril) of £11.7 (95% CrI: -74.8 to 98.7). On the survival side of the cost-effectiveness equation the results reported in the last column of Table 1 suggests that those countries with higher (than the overall mean) public expenditure in healthcare as % of national GDP can expect on average a survival gain of 52.6 days (95% CrI: -18.9 to 124.7) in patients treated with high dose lisinopril.
Finally, it should be noted that the inclusion of patient- and country-level covariates in the BHLM model allows us to explain the between-country variability in the estimated difference in survival. The estimate of in fact, is reduced (by more than half) from 31 in the BHLM with no covariates to 12 when adding explanatory variables. The opposite occurs in the cost difference equation, where the addition of mean life expectancy actually increases the between-country variation of the country-specific estimated differential cost. We will come back to this latter result in section 5.2.3.
5.2 Country-specific cost-effectiveness estimates
As mentioned in section 4, an additional advantage of using BHLM is that this methodology facilitates the quantification of country-specific cost-effectiveness estimates, through shrinkage estimation. To illustrate this point Figures 1 and 2 provide a graphical representation of the country-specific differential cost and survival gain estimates (together with their credibility intervals) obtained under the three models discussed above. The marker and the horizontal bars represents respectively the posterior mean estimate and 95% CrI of differential mean costs (Figure 1) and survival (Figure 2) obtained from MCMC estimation, running 3 chains for 20,000 iterations following a burn-in period of 10,000 iterations. Convergence was checked using the Gelman-Rubin convergence criteria [38], as implemented in WinBUGS.
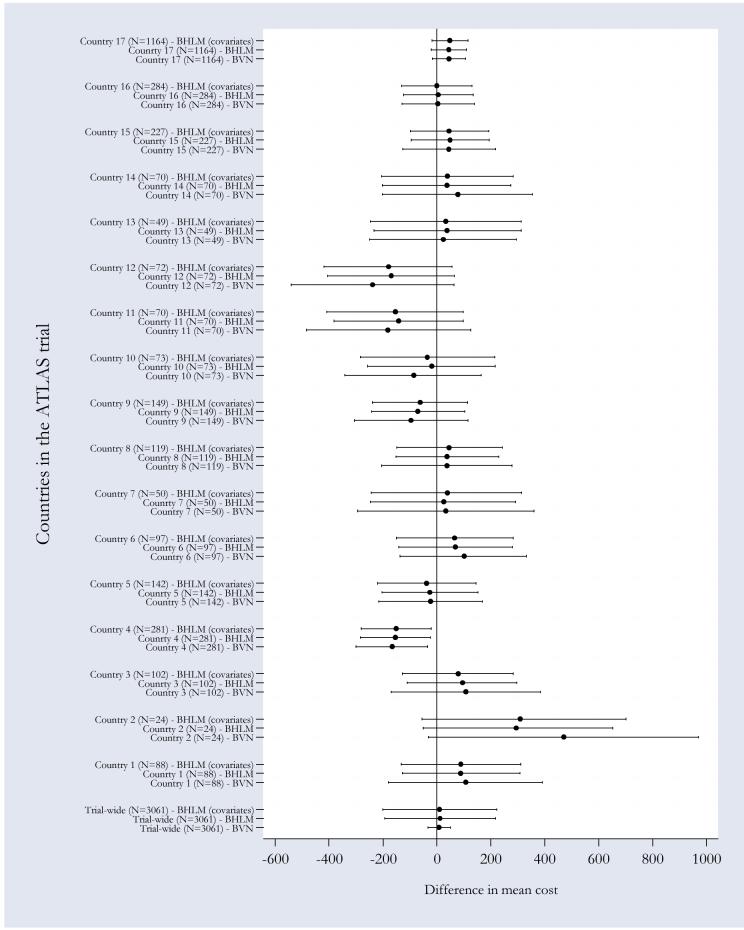
Figure 1. Pooled and country-specific cost differences obtained using alternative modelling strategies.
Markers indicate country-specific mean differential cost estimates, horizontal bars across the markers represent 95% credibility intervals. The covariates used in the cost difference equation are patient’s age and country-specific mean life expectancy, both expressed as departure from the overall mean.
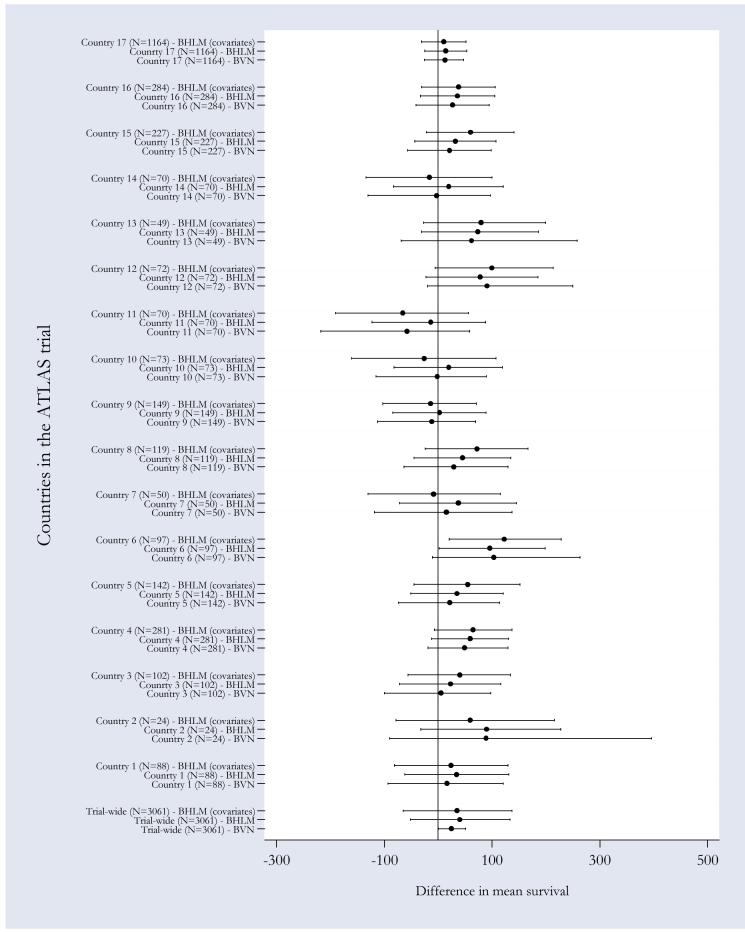
Figure 2. Pooled and country-specific survival gains obtained using alternative modelling strategies.
Markers indicate country-specific mean differential cost estimates, horizontal bars across the markers represent 95% credibility intervals. The covariates used in the survival equation were patient’s age expressed as departure from the overall mean and public expenditure in health expressed as percentage of the GDP.
5.2.1 Non-hierarchical bivariate model
There are a number of interesting considerations that can be made when comparing country-specific versus trial-wide CEA results obtained under a non-hierarchical bivariate model, the most obvious relating to the degree of within-country variability. Larger sampling uncertainty in country-specific estimated differences in cost and survival gain is observed in those countries that recruited a smaller number of patients into the trial (e.g. countries 2, 7, 11, and 14). This is to be expected as some of these countries recruited a very small number of patients (e.g. country 2). Notice, though, that the sample size itself is not always a predictor of the degree of sampling uncertainty around the estimated mean differences. The country-specific estimated difference in costs for country 13 for instance (where n=49), has a narrower CrI than the estimate for country 12 (where n=70). The same consideration can be made with respect to the sampling uncertainty surrounding the differential survival estimates between countries 13 and 10. This phenomenon may be due to several factors. One is the degree of correlation between observations within the same country, where the higher the correlation the narrower the CrI and the variability of the observed cost (and survival) seen in the different countries. Another explanation may be the fact that more expensive countries may have higher costs and larger spread of costs.
More interestingly for the purpose of this paper is the between-country variability of the CEA results, which leads to potentially different country-specific recommendations regarding the value for money of the ‘intervention’ (i.e. high dose). For example, high-dose (strictly) dominatesix low-dose in countries 4, 5, and 12, but is dominated by low-dose in country 14. The question for the policy makers in these two countries is, therefore, whether to consider the trial-wide results as the most valid results in their own context, or instead, to rely only on the results obtained analysing data collected in their own jurisdictions.
5.2.2 Bivariate hierarchical model results without covariates
A comparison of the above results with those obtained from a BHLM with no covariates suggests that, in most cases thanks to the effect of the shrinkage estimation, jurisdictions-specific differential cost and survival are much closer to their trial-wide counterparts. Countries 2, 4, and 12, for example, display particularly large point estimates with correspondingly wide credibility intervals using the non-hierarchical model. By explicitly modelling the hierarchical structure in the data, the BHLM exploits similarities in the subject level data between countries (i.e. they borrow strength), hence obtaining efficiency gains. A direct result is that the mean country-specific estimates of differential costs and survival gains are shrunken towards the trial-wide mean. Furthermore, country-specific estimates are more precise than those obtained using a non-hierarchical modelling, as indicated by their 95% CrIs.
5.2.3 Bivariate hierarchical model CEA results, with subject- and country-level covariates
There might be important factors that, if considered, could contribute to partially explain the observed between-country variability in cost-effectiveness. The argument in favour of their inclusion in CEA of multinational IPD is that, if left unaccounted for, these factors could inflate the between-country unobserved variability in the results leading to potentially erroneous conclusions concerning the transferability of the study findings. In this sense, it is reasonable to expect that a more realistic country-specific estimate will lie between the two extremes results obtained with the (stratified) non-hierarchical bivariate model and the BHLM with no covariates.
The application of the latter assumes perfect exchangeability between the information conveyed by the 17 countries included in the analysis. However, it could be argued that assuming perfect exchangeability may in some occasions be unreasonable. Additional information available at country and patient level could be used to re-assess the between-country variability in the cost-effectiveness results. Table 2 reports the mean values of a selection of patient and country-specific variables that might be important to consider in the ATLAS trial. These are variables that could be expected, a priori, to affect the country-specific mean differential mean estimates of cost and survival gain, their sampling uncertainty, and their between-country variability. Unfortunately, the country-specific variables reported in this table were not collected as part of the ATLAS trial but have been obtained ex post from published OECD health data [39].
Table 2.
Patients and country specific baseline mean values for a sample of covariates in the ATLAS trial
| Patient-level covariates | Country specific covariates1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Centre | nj | Age | LVEF2 | % Male | Life expectancy3 | Private exp. in health care as % of the GDP4 | Public exp. in health care as % of the GDP5 | Alcohol consumption6 | Tobacco consumption7 |
| 1 | 88 | 65.53 | 0.4945 | 81.32 | 79.7 | 2.6 | 5.7 | 9.8 | 1265 |
| 2 | 24 | 57.24 | 0.5200 | 84.00 | 78.8 | 2.0 | 5.4 | 11.3 | 2210 |
| 3 | 102 | 64.34 | 0.5794 | 71.03 | 77.7 | 2.0 | 6.2 | 10.2 | 2310 |
| 4 | 281 | 63.84 | 0.4542 | 79.58 | 79.4 | 2.8 | 6.5 | 7.7 | 1432 |
| 5 | 142 | 61.15 | 0.6081 | 81.76 | 75.3 | 0.6 | 6.4 | 11.8 | 2500 |
| 6 | 97 | 62.32 | 0.5600 | 80.00 | 76.7 | 1.5 | 6.8 | 11.4 | 1527 |
| 7 | 50 | 57.44 | 0.5192 | 78.85 | 78.1 | 1.7 | 5 | 9 | 992 |
| 8 | 119 | 63.88 | 0.4919 | 81.45 | 79.3 | 2.3 | 7 | 10.5 | 2037 |
| 9 | 149 | 67.11 | 0.5033 | 76.82 | 78.2 | 2.9 | 5.7 | 10 | 2319 |
| 10 | 73 | 56.76 | 0.5676 | 82.43 | 72.4 | 1.7 | 4.8 | 12.3 | 1809 |
| 11 | 70 | 63.37 | 0.4722 | 88.89 | 76.2 | 1.3 | 4.5 | 14.5 | 1834 |
| 12 | 72 | 64.39 | 0.5526 | 82.89 | 78.7 | 1.2 | 6.5 | 5.5 | 1433 |
| 13 | 49 | 60.44 | 0.3654 | 90.38 | 76.9 | 2.8 | 6.1 | 13 | 2010 |
| 14 | 70 | 59.84 | 0.4861 | 76.39 | 79.3 | 2.1 | 5.2 | 11.7 | 2670 |
| 15 | 227 | 67.92 | 0.5259 | 83.19 | 79.8 | 1.2 | 7.1 | 6.5 | 1710 |
| 16 | 284 | 63.77 | 0.4414 | 84.83 | 78.1 | 1.2 | 6 | 10.5 | 1225 |
| 17 | 1,164 | 63.60 | 0.5156 | 76.58 | 76.8 | 7.6 | 6.1 | 8.4 | 1542 |
Source: OECD Health Data [41]
Left Ventricular Ejection Function
Life expectancy total population at birth (Years)
Total private expenditure on health (% GDP)
Total public expenditure on health (% GDP)
Alcohol consumption in litres per capita (15+)
Tobacco consumption in grammes per capita (15+)
An examination of the country-level summary statistics for the patient in the trial and of the country-specific variables from OECD, indicates some degree of between-country variability in these covariates. Mean age at randomisation for instance, ranges from a minimum of 56.76 in country 10 to a maximum of 67.92 in country 15. Similarly, the mean left ventricular ejection function (LVEF) varies from 0.3654 in country 13 to 0.6081 in country 5.
Inter-country variability can also be detected when looking at variables such as life expectancy (LE) in the total population at birth. This ranges from a minimum of 72.4 years in country 10 to a maximum of 79.7 in country 1. Similarly, the total private (public) expenditure on healthcare as a percentage of the national GDP varies respectively between 0.6% in country 5 (4.5% in country 11) and 7.6% in country 17 (7.1% in country 15). Finally, the per-capita level of alcohol and tobacco consumption in the population over 15 years of age display a remarkable between-country variation with alcohol consumption ranging from 5.5 units in country 12 to a maximum of 14.5 in country 11, and tobacco consumption varying from 992 grams per capita in Country 7 to 2670 in country 14.
In the attempt to account for some of these between-country differences in factors that could help explaining the between-country variability in cost-effectiveness results, we run the BHLM with the addition of patient- and country-specific covariates. Results have been already reported in Table 1 (with regard to the trial-wide estimates of differential costs and survival) and Figures 1 and 2 (with regard to the country-specific shrunken estimates).
For simplicity of exposition this model used patient-specific age at randomisation (for both costs and survival) as explanatory variable in the patient-level cost and survival equations, public expenditure on healthcare as percentage of the national GDP in the country-specific differential survival equation, and mean LE of the total population at birth in the country-specific differential cost equation. The trial wide results have been discussed in section 5.1 and indicate that age has a positive impact on mean costs and survival in both arms. Furthermore the greater the life expectancy in a specific country compared to the overall trial-mean the greater the incremental cost. On the other hand, the higher the public investment in healthcare with respect to the overall mean in the countries participating in the ATLAS trial, the higher the expected survival benefit that one can expect. It is important to notice that the inclusion of subject- and country-specific variables helps to reduce the between-country variability in the differential survival. This does not occur for the cost side. A closer look at the between-country distribution of the variables used for the cost equation at patient (i.e. age) and country level (i.e. LE) may help to shed light on this apparently contradicting result. Patients recruited in the trial from country 10 tend are in fact the oldest in the trial sample as well as having (on average) the lowest life expectancy at birth, and these factors will set country 10 somewhat apart from the others when estimating country-specific differential costs conditional on these variables, therefore increasing the between-country variation in the estimated mean difference in cost.
Figures 1 and 2 show the impact of including patient- and country-level covariates in the model, by plotting the country-specific treatment effects on costs and survival. The level of shrinkage, now conditional on the covariates included in the model, is more attenuated for some jurisdictions thereby capturing potentially important differences between countries. Results for countries 7 and 14, for example, are now different from those obtained using the BHLM without covariates suggesting that low-dose lisinopril dominates high dose. Similarly, results suggest that in countries 9 and 10 high-dose no longer dominates low-dose, while in some other countries (e.g. 4 and 5) the conclusions remain the same regardless of the model choice. Like in the case of the BHLM with no covariates, the impact of shrinkage is both qualitative and quantitative and varies across countries in the trial.
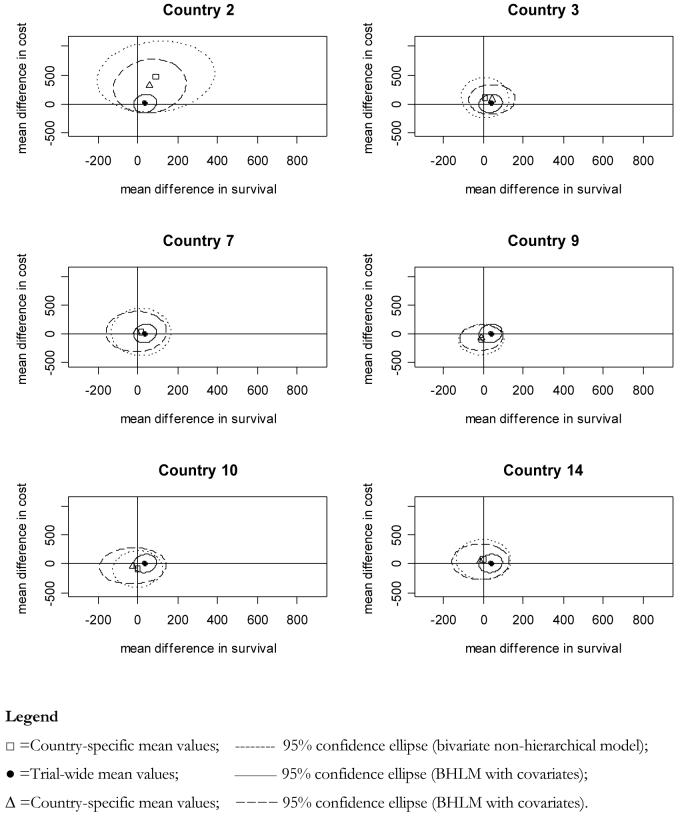
Figure 3, plots the country-specific cost-effectiveness planes for a selection of countries in the trial.
Figure 3. Shrinkage on the cost-effectiveness plane.
The y-axis and x-axis represent, respectively, the estimated difference in mean survival and difference in mean costs. The markers represent the country specific mean estimate of the point with co-ordinates (Δcj,Δsj), together with the relative 95% confidence ellipse.
These graphs show the country-specific confidence ellipses obtained from (i) the non-hierarchical bivariate model, (ii) the BHLM with covariates, and contrasting these against the (iii) trial-wide confidence ellipse derived from the BHLM with covariates trial-wide results. For some countries, the application of a BHLM in combination with patient and country covariates affects both, the joint sampling uncertainty and the point estimates of differential mean costs and survival, leading in some cases to opposite recommendations regarding the cost-effectiveness of high dose lisinopril. Country 2 for instance is shrunken towards the overall mean obtained from the BHLM with covariates. Similar behaviour is observed in countries 3 and 9. On the other hand countries 10 and 14 show that the addition of covariates to their specific cost-effectiveness estimates slightly increases the joint variability of (Δc,Δe), for the reasons discussed earlier in this section. Figure 4 plots the CEACs for the same set of countries inspected in figure 3.
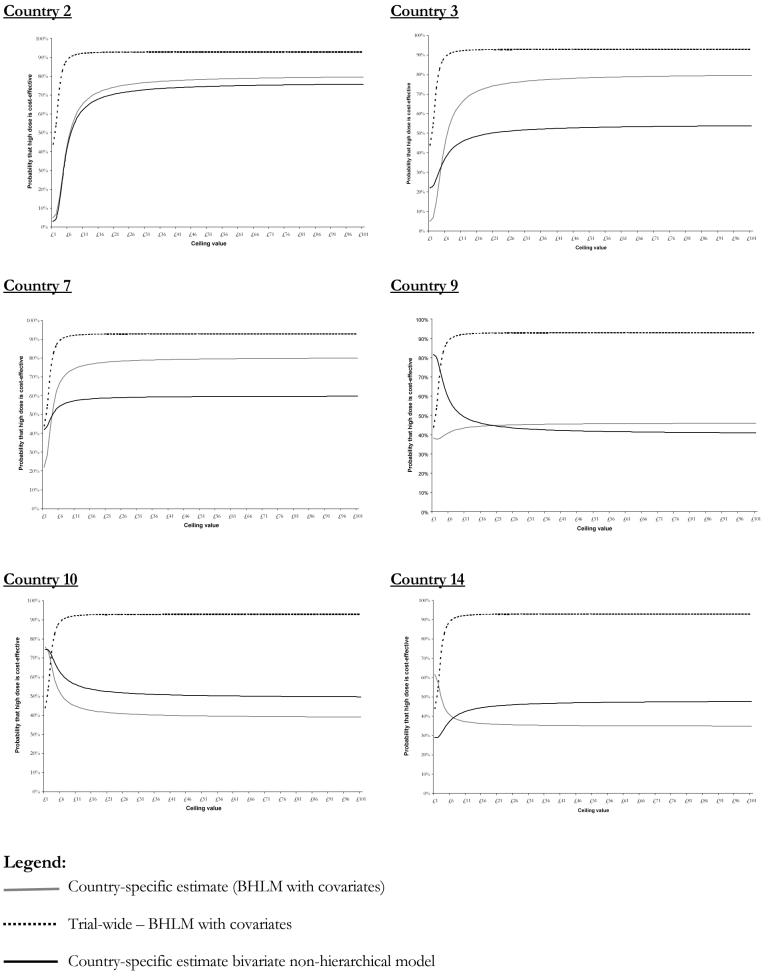
Figure 4. Country-specific cost-effectiveness acceptability curves obtained using alternative modelling strategies for selected countries.
A brief inspection of the CEACs confirms that the use of the trial-wide result does hide an important piece of information for location-specific policy makers. In fact, not only there is clearly variation in the cost-effectiveness by country but there is also considerable variation in the decision uncertainty at a given λ level, represented by the probability that the intervention (i.e. high-dose) is cost-effective. These results suggest that it is impossible to predict the impact on the results deriving from the explicit consideration of patients- and country-specific covariates. In country 2 for instance, where the sample size was very small (n=24) the probability of high dose being cost-effective is still considerably low despite the country-specific results had been heavily shrunken towards the trial-wide BHLM estimate. In other words, although the treatment effects are shrunken towards the trial overall mean in country 2, the probability that the intervention is cost-effective is still penalised.
6. Discussion
This paper proposes a novel approach to the analysis of individual patient-level cost-effectiveness data collected in multinational RCTs, by extending the use of Bayesian bivariate hierarchical modelling for healthcare economic evaluation purposes.
Two recent contributions [5, 32] have proposed methods somewhat similar to those advocated in this manuscript. Nixon and Thompson [32] have used Bayesian modelling for cost-effectiveness IPD to illustrate ways in which alternative research questions could be investigated (i.e. sub-groups CEA at patient and centre level) while relaxing basic assumptions often made in regression analysis (i.e. common variance between treatment arms for costs and effects, alternative parametric assumptions for costs and effects). There are three main differences between the methods proposed in this paper and those advocated by Nixon and Thompson. First, we consider the inclusion of explanatory variables at both patient and country level. Second, our example includes a much larger number of higher level units (i.e. 17) compared to the Nixon and Thompson example which was based on 5 units only. We feel this is an important distinction as a greater confidence can be placed on our country specific random effects being draws from an appropriate distribution; this also allows us to correlate the country specific effects across the two equations. This leads us to the third difference between the two papers, that is, unlike Nixon and Thompson who only consider a bivariate model by linking individual level random terms across the equations (due to the small number of higher level units in their case study), we consider a bivariate model where both the country and the individual level terms are each correlated across equations.
Pinto et al [5] recently explored alternative shrinkage estimation methods presenting a simulation exercise based on summary country-level cost-effectiveness estimates from a large multinational RCTs. The authors explore the impact of univariate versus bivariate shrinkage, for costs and effects as well as exploring the impact of different distributions for the random effects at country level. We take a different approach by using individual patient-level cost-effectiveness data. In addition, while Pinto et al. obtained shrinkage estimates through an empirical Bayes estimation procedure we chose to implement a fully Bayesian analysis. The advantages of our approach compared to empirical Bayes are outlined in section 4.3 above. A final difference relates to the fact that, unlike the methods proposed here, the methods proposed by Pinto et al. did not include covariates at patient and country level. While the inclusion of these variables is still possible in their model, such an analysis based on summary data only would be subject to a number of issues (e.g. aggregation bias [40-42], patient sub-group analysis [43]) which have been well rehearsed in the meta-regression literature.
It could be argued that knowing ‘which country is which’ will convey some information about the costs in a given country, hence violating the exchangeability assumption. While this may be true for absolute costs in each treatment arm, knowing that one country has higher costs than another may not tell us much about the differential costs (and indeed the differential health outcomes). The approach proposed here is standard methodology in many Bayesian random effects meta-regression models, where the knowledge of the characteristics of the trials which enter the model does not prevent the analyst from making a prior assumption of exchangeability. Gelman et al. [25] (chapter 5, section 5.2) argue that “In virtually any statistical application, it is natural to object to exchangeability on the grounds that the units actually differ. [...] The fact that the experiments differ implies that θj [the parameter of interest in the unit j] differ, but it might be perfectly acceptable to consider them as drawn from a common distribution”. The authors continue saying “Objecting to exchangeability for modelling ignorance is no more reasonable than objecting to an iid model for samples from a common population, objecting to regression models in general, or, for that matter, objecting to displaying points in a scatter plot without individual labels. As with regression, the valid concern is not about exchangeability, but encoding relevant knowledge as explanatory variables where possible.” (p. 124). In essence, “...the usual way to model exchangeability with covariates is through conditional independence [...]. In this way exchangeable models become almost universally applicable, because any information to distinguish different units should be encoded ....” (p. 123).
The models presented and discussed in this paper assume joint bivariate Normality of costs and effects at patient and country-level. Although the ‘Normal’ case is a very general framework in multivariate statistical modelling, it can be argued that especially for CEA data one may need to use alternative parametric distributions that describe the data more appropriately. In this sense, the product normal formulation facilitates a more flexible modelling process which allows the use of different distributions for costs (i.e. Gamma) [32, 44] and effects (i.e. Binomial, Poisson). However, Bayesian modelling outside the bivariate normality framework is highly complex. Future work will explore the impact of alternative distributional assumptions.
A further issue concerns the selection of country specific variables for the economic analysis. Unfortunately, when country-level data are not collected as part of the study, as is the case in the vast majority of multinational and multicentre RCTs, the selection of country (centre)-specific variables must rely on some judgment regarding which readily available statistics can be used as proxy to explain between-country variability in costs (and effects). In the present study, the country-specific variables reported in Table 2 were chosen among those suggested to be factors that might affect the cost-effectiveness of a health technology between countries [1], and it is recognised that their explanatory power may be limited. The issue of which variable to use to adjust for factors that may have an impact on the difference in cost and effects is both a theoretical and an empirical one, and it deserves further research.
Should we be concerned about whether there is statistically significant difference between country-specific estimates? Cook et al. have advocated a prior approach, based on a test for homogeneity [45], in which multinational economic RCT data are analysed to assess the appropriateness of a ‘pooled’ CEA. The general idea is to follow the methods used to analyse clinical data from such trials, where tests of homogeneity are typically performed before pooling the data. The authors suggest that if there is no evidence of treatment-by-centre interaction the data can be pooled for analysis across centres/countries, thus offering improved precision of cost-effectiveness ratios for each country. The authors takes a strong statistical inferential view stressing that their interest is “...not in whether the countries differ with respect to their average clinical or economic outcome but rather whether there are important differences in their effect of treatment among the countries” [45]. While this is one possible way to explore the variability of the results between countries, it could be argued that decisions based on the test of interaction could be misled by the fact that this test is often underpowered, and that non-statistically significant between-country differences in the treatment effect may still lead to different decisions in each jurisdiction. More importantly, policy-makers are clearly interested in jurisdiction-specific results, and as argued above results from pooled analyses might not be as informative as they could be.
Finally, as decision makers’ information needs increase, requiring cost-effectiveness evidence comparing all available treatment strategies, in many circumstances cost-effectiveness studies will need to synthesise both IPD and summary data from trials (and other sources) to reflect all available evidence relating to all relevant management options [46]. In this sense, the framework outlined in this paper is highly suitable for evidence synthesis for cost-effectiveness modelling as it can be used to incorporate not only prior information regarding the treatment strategies compared in the trial, but also information on the clinical and cost-effectiveness of alternative treatment strategies in any form this may be available (i.e. summary or IPD).
Appendix: WinBUGS code for BHLM with country and patient covariates
Footnotes
The validity of this assumption is sometimes assessed using formal hypothesis tests of heterogeneity, despite the fact that these are typically underpowered [45]. In fact, Pinto et al. recently showed that the between-country variability in differential effects was even greater than the corresponding variability in differential cost. [5]
The terms ‘transferability’ and ‘generalisability’ are used here interchangeably. Strictly speaking the former should be interpreted as “the extent to which results from a given setting also apply to other settings”, whereas the term generalisability should be used to indicate the extent to which results can be adapted to apply in other settings, or can be interpreted for other settings”.
The economic data collected in the ATLAS trial, for instance, have been analysed from the US perspective with respect to cost differences [47], and in the UK [10], Switzerland [48] and Italy for cost-effectiveness [49]. A similar practice is observed for other multinational studies such as the PURSUIT [50-52], HOPE [15, 53], and SOLVD [54, 55] trials.
In the SUR approach the cost and effects equations are therefore related through their error terms. As Willan et al. point out this method brings efficiency gains over unrelated OLS regression if different sets of covariates are used in each equation. The authors show how to extend the SUR approach in presence of a set of patient-specific covariates. It is important to note that in this formulation the variances for costs (and effects) are assumed to be the same in both treatment arms.
Multivariate normality has the following property [26]. Let X and Y follow a BVN, X, Y ∼ BVN[θX,θY,σX,σY,ρ], where the distribution has the following properties , , , , . It can be showed that the conditional distribution of , where and .
This is an important consideration even in trials where individual patients are the unit of randomisation [56-58].
This assumption can be relaxed to incorporate between-country differences in the covariance matrix, but it’s relevance it’s likely to depend on the data.
It could be argued that different decision makers may have different maximum willingness to pay to achieve one additional unit of effectiveness. In this case equation (8) can be rewritten as INMBj = (Δej ·λj - Δcj)
Strategy A strictly dominates strategy B when the former costs less and produces more benefits.
References
- 1.Sculpher MJ, Pang FS, Manca A, Drummond MF, Golder S, Davies LM, et al. Generalisability in Economic Evaluation Studies in Health Care: a Review and Case-Studies. Health Technology Assessment. 2004;8(49):1–206. doi: 10.3310/hta8490. [DOI] [PubMed] [Google Scholar]
- 2.Drummond MF, Pang F. Transferability of economic evaluation results. In: Drummond MF, McGuire AL, editors. Economic evaluation of health care: merging theory with practice. Oxford: Oxford University Press; 2001. [Google Scholar]
- 3.Hjelmgren J, Berggren F, Andersson F. Health economic guidelines - similarities, differences and some implications. Value in Health. 2001:4, 225–250. doi: 10.1046/j.1524-4733.2001.43040.x. [DOI] [PubMed] [Google Scholar]
- 4.Goeree R, Burke B, Manca A, Sculpher MJ, Willan AR, Blackhouse G, et al. CCOHTA HTA Capacity Building Grants Program. Toronto: Canadian Coordinating Office for Health Technology Assessment; 2005. Generalizability of economic evaluations: using results from other geographic areas or from multinational trials to help inform health care decision making in Canada. Report No.: Grant N. 67. [Google Scholar]
- 5.Pinto EM, Willan AR, O’Brien BJ. Cost-effectiveness analysis for multinational clinical trials. Statistics in Medicine. 2005;24:1965–1982. doi: 10.1002/sim.2078. [DOI] [PubMed] [Google Scholar]
- 6.Willan AR, Pinto EM, O’Brien BJ, Kaul P, Goeree R, Lynd L, et al. Country specific cost comparisons from multinational clinical trials using empirical Bayesian shrinkage estimation: the Canadian ASSENT-3 economic analysis. Health Economics. 2005;14:327–338. doi: 10.1002/hec.969. [DOI] [PubMed] [Google Scholar]
- 7.Grieve R, Nixon R, Thompson SG, Normand C. Using multilevel models for assessing the variability of multinational resource use and cost data. Health Econ. 2005;14(2):185–96. doi: 10.1002/hec.916. [DOI] [PubMed] [Google Scholar]
- 8.Manca A, Rice N, Sculpher MJ, Briggs AH. Assessing Generalisability by Location in Trial-Based Cost-Effectiveness Analysis: the Use of Multilevel Models. Health Economics. 2005;14(5):471–85. doi: 10.1002/hec.914. [DOI] [PubMed] [Google Scholar]
- 9.Hoch JS, Briggs AH, Willan AR. Something old, something new, something borrowed, something BLUE: a framework for the marriage of health econometrics and cost-effectiveness analysis. Health Economics. 2002;11(5):415–430. doi: 10.1002/hec.678. [DOI] [PubMed] [Google Scholar]
- 10.Sculpher MJ, Poole L, Cleland J, Drummond MF, Armstrong PW, Horowitz JD, et al. Low doses vs. high doses of the angiotensin converting-enzyme inhibitor lisinopril in chronic heart failure: a cost-effectiveness analysis based on the Assessment of Treatment with Lisinopril and Survival (ATLAS) study. European Journal of Heart Failure. 2000;2:447–454. doi: 10.1016/s1388-9842(00)00122-7. [DOI] [PubMed] [Google Scholar]
- 11.Paker M, Poole-Wilson PA, Armstrong PW, Cleland J, Horowitz JD, Massie BM, et al. Comparative effects of low and high doses of the angiotensin converting-enzyme inhibitor, lisinopril, on morbidity and mortality in chronic heart failure. Circulation. 1999;100:2312–2318. doi: 10.1161/01.cir.100.23.2312. [DOI] [PubMed] [Google Scholar]
- 12.Caro JJ, Huybrechts KF, De Backer G, De Bacquer D, Closon MC. Are the WOSCOPS clinical and economic findings generalizable to other populations? A case study for Belgium. Acta Cardiologica. 2000;55(4):239–246. doi: 10.2143/AC.55.4.2005746. [DOI] [PubMed] [Google Scholar]
- 13.Drummond MF. Comparing cost-effectiveness across countries. The model of acid-related disease. Pharmacoeconomics. 1994;5(S3):60–67. [Google Scholar]
- 14.Reed SD, Anstrom KJ, Bakhai A, Briggs AH, Califf RM, Cohen DJ, et al. Conducting economic evaluations alongside multinational clinical trials: toward a research consensus. Am Heart J. 2005;149(3):434–43. doi: 10.1016/j.ahj.2004.11.001. [DOI] [PubMed] [Google Scholar]
- 15.Bjorholt I, Andersson FL, Kahan T, Ostergren J. The cost-effectiveness of ramipril in the treatment of patients at high risk of cardiovascular events: a Swedish sub-study to the HOPE study. Journal of Internal Medicine. 2002;251(6):508–517. doi: 10.1046/j.1365-2796.2002.00990.x. [DOI] [PubMed] [Google Scholar]
- 16.Liljas B, Stahl E, Pauwels RA. Cost effectiveness analysis of a dry powder inhaler (Turbuhaler) versus a pressurised metered dose inhaler in patients with asthma. Pharmacoeconomics. 1997;12(2):267–277. doi: 10.2165/00019053-199712020-00017. [DOI] [PubMed] [Google Scholar]
- 17.Mark DB, Harrington RA, Lincoff AM, Califf RM. Cost-effectiveness of platelet glycoprotein IIb/IIIa inhibition with eptifibatide in patients with non-ST-elevation acute coronary syndromes. Circulation. 2000;101(4):366–371. doi: 10.1161/01.cir.101.4.366. al. e. [DOI] [PubMed] [Google Scholar]
- 18.Willke RJ, Glick HA, Polsky D, Schulman KA. Estimating country-specific cost-effectiveness from multinational clinical trials. Health Economics. 1998;7:481–493. doi: 10.1002/(sici)1099-1050(199809)7:6<481::aid-hec353>3.0.co;2-k. [DOI] [PubMed] [Google Scholar]
- 19.Sutton AJ, Abrams KR, Jones DR, Sheldon TA, Song F. Methods for Meta-Analysis in Medical Research. Chichester: John Wiley & Sons; 2000. [Google Scholar]
- 20.Localio AR, Berlin JA, Ten Have TR. Confounding due to cluster in multicenter studies - Causes and cures. Health Services & Outcomes Research Methodology. 2002;3(3-4):195–210. [Google Scholar]
- 21.Localio AR, Berlin JA, Ten Have TR, Kimmel SE. Adjustment for center in multicenter studies: an overview. Annals of Internal Medicine. 2001;135:112–123. doi: 10.7326/0003-4819-135-2-200107170-00012. [DOI] [PubMed] [Google Scholar]
- 22.Willan AR, Briggs AH, Hoch JS. Regression methods for covariate adjustment and subgroup analysis for non-censored cost-effectiveness data. Health Economics. 2004;13:461–475. doi: 10.1002/hec.843. [DOI] [PubMed] [Google Scholar]
- 23.O’Hagan A, Stevens JW, Montmartin J. Bayesian cost-effectiveness analysis from clinical trials data. Statistics in Medicine. 2001;20:733–753. doi: 10.1002/sim.861. [DOI] [PubMed] [Google Scholar]
- 24.Greene WH. Econometric Analysis. Third ed. Upper Saddle Riven, New Jersey: Prentice-Hall, Inc; 1997. [Google Scholar]
- 25.Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian Data Analysis. New York: Chapman & Hall/CRC; 2004. [Google Scholar]
- 26.Spiegelhalter DJ, Abrams KR, Myles JP. Bayesian Approaches to Clinical Trials and Health-Care Evaluation. Chichester: John Wiley & Sons; 2003. [Google Scholar]
- 27.Spiegelhalter DJ. Bayesian graphical modelling: a case-study in monitoring health outcomes. Journal of the Royal Statistical Society - Series C (Applied Statistics) 1998;47(1):115–133. [Google Scholar]
- 28.Lambert PC, Abrams KR, Jones DR, Halligan AW, Shennan A. Analysis of ambulatory blood pressure monitor data using a hierarchical model incorporating restricted cubic splines and heterogeneous within-subject variances. Stat Med. 2001;20(24):3789–805. doi: 10.1002/sim.1172. [DOI] [PubMed] [Google Scholar]
- 29.Gelman A. Prior distributions for variance parameters in hierarchical models. Bayesian Analysis. 2005;1(2):1–19. [Google Scholar]
- 30.Lambert PC, Sutton AJ, Burton LC, Abrams KR, Jones AM. How vague is vague? A simulation study of the impact of the use of vague prior distributions in MCMC using WinBUGS. Statistics in Medicine. 2005;24:2401–2428. doi: 10.1002/sim.2112. [DOI] [PubMed] [Google Scholar]
- 31.Pocock S, Assmann SE, Enos LE, Kasten LE. Sub-groups analysis, covariate adjustment and baseline comparisons in clinical trials reporting: current practice and problems. Statistics in Medicine. 2002;21:2917–2930. doi: 10.1002/sim.1296. [DOI] [PubMed] [Google Scholar]
- 32.Nixon RM, Thompson SG. Methods for incorporating covariate adjustment, subgroup analysis and between-centre differences into cost-effectiveness analysis. Health Econ. 2005;14(12):1217–29. doi: 10.1002/hec.1008. [DOI] [PubMed] [Google Scholar]
- 33.Drummond MF, Manca A, Sculpher MJ. Increasing the Generalisability of Economic Evaluations. Recommendations for the Design, Analysis and Reporting of Studies. International Journal of Technology Assessment in Health Care. 2005;21(2):165–71. [PubMed] [Google Scholar]
- 34.Hox JJ, Kreft IGG. Multilevel Analysis Methods. Sociological Methods and Research. 1994;22(3):283–299. [Google Scholar]
- 35.Spiegelhalter DJ, Thomas A, Best N, Lunn D. WinBUGS User Manual. Version 1.4 ed. Cambridge, UK: MRC Biostatistics Unit; 2003. [Google Scholar]
- 36.O’Hagan A, Stevens JW. Bayesian methods for design and analysis of cost-effectiveness trials in the evaluation of health care technologies. Stat Methods Med Res. 2002;11(6):469–90. doi: 10.1191/0962280202sm305ra. [DOI] [PubMed] [Google Scholar]
- 37.Luce BR, O’Hagan A. A Primer on Bayesian Statistics in Health Economics and Outcomes Research. London: Medtap; 2003. [Google Scholar]
- 38.Brooks SP, Gelman A. Alternative methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics. 1998;7:434–455. [Google Scholar]
- 39. OECD. OECD Health Data. In: OECD; 2003.
- 40.Sheppard L. Insights on bias and information in group-level studies. Biostatistics. 2003;4(2):265–78. doi: 10.1093/biostatistics/4.2.265. [DOI] [PubMed] [Google Scholar]
- 41.Berlin JA, Santanna J, Schmid CH, Szczech LA, Feldman HI, Group A-LAITS. Individual patient-versus group-level data meta-regressions for the investigation of treatment effect modifiers: ecological bias rears its ugly head. Stat Med. 2002;21(3):371–87. doi: 10.1002/sim.1023. [DOI] [PubMed] [Google Scholar]
- 42.Greenland S. Ecologic versus individual-level sources of bias in ecologic estimates of contextual health effects. International Journal of Epidemiology. 2001;30:1343–50. doi: 10.1093/ije/30.6.1343. [DOI] [PubMed] [Google Scholar]
- 43.Thompson SG, Barber JA. How should cost data in pragmatic randomised trials be analysed? British Medical Journal. 2000:1197–1200. doi: 10.1136/bmj.320.7243.1197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Thompson SG, Nixon R, Grieve R. Addressing the issues that arise in multicentre cost data, with application to a multinational study. Journal of Health Economics. 2006 doi: 10.1016/j.jhealeco.2006.02.001. forthcoming. [DOI] [PubMed] [Google Scholar]
- 45.Cook JR, Drummond MF, Glick H, Heyse JF. Assessing the appropriateness of combining economic data from multinational clinical trials. Statistics in Medicine. 2003;22(12):1955–1976. doi: 10.1002/sim.1389. [DOI] [PubMed] [Google Scholar]
- 46.Manca A, Willan AR. “Lost in translation”: accounting for between country differences in the analysis of multinational cost effectiveness data. Pharmacoeconomics. 2006 doi: 10.2165/00019053-200624110-00007. (accepted for publication) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Schwartz JS, Wang YR, Cleland JG, Gao L, Weiner M, Poole-Wilson PA, et al. High- versus low-dose angiotensin converting enzyme inhibitor therapy in the treatment of heart failure: an economic analysis of the Assessment of Treatment with Lisinopril and Survival (ATLAS) trial. Am J Manag Care. 2003;9(6):417–24. [PubMed] [Google Scholar]
- 48.Ess SM, Luscher TF, Szucs TD. High dose lisinopril in heart failure: economic considerations. Cardiovascular Drugs Therapy. 2002;16(4):365–71. doi: 10.1023/a:1021794229020. [DOI] [PubMed] [Google Scholar]
- 49.Scalone L, Mantovani LG. Economic evaluation of high vs low dosage lisinopril in patients with chronic heart failure. Pharmacoeconomics - Italian Research Article. 2002;4(2):45–55. [Google Scholar]
- 50.Brown R, Armstrong PW. Cost effectiveness in Canada of eptifibatide treatment for acute coronary syndrome patients using PURSUIT subgroup analysis. Canadian Journal of Cardiology. 2003;19(2):161–166. [PubMed] [Google Scholar]
- 51.Brown R, Henderson RA, Koster D, Hutton J, Simoons ML. Cost effectiveness of eptifibatide in acute coronary syndromes; an economic analysis of Western European patients enrolled in the PURSUIT trial. European Heart Journal. 2002;23(1):50–58. doi: 10.1053/euhj.2001.2711. [DOI] [PubMed] [Google Scholar]
- 52.Henderson RA, Brown R. The costs of routine eptifibatide use in acute coronary syndromes in Western Europe: An economic substudy of the PURSUIT trial. European Heart Journal (Supplements) 1999;1(N):N35–N41. doi: 10.1053/euhj.2001.2711. [DOI] [PubMed] [Google Scholar]
- 53.Smith MG, Neville AM, Middleton JC. Clinical and economic benefits of ramipril: An Australian analysis of the HOPE study. Internal Medicine Journal. 2003;33(9-10):414–419. doi: 10.1046/j.1445-5994.2003.00455.x. [DOI] [PubMed] [Google Scholar]
- 54.Butler JR, Fletcher PJ. A cost-effectiveness analysis of enalapril maleate in the management of congestive heart failure in Australia. Aust N Z J Med. 1996;26(1):89–95. doi: 10.1111/j.1445-5994.1996.tb02912.x. [DOI] [PubMed] [Google Scholar]
- 55.Szucs TD, Schwenkglenks M, Paschen B, Follath F. Economic efffeciency of Bisoprolol in the treatment of congestive heart failure in Germany - An analysis on the basis of the CIBIS-II trial. Medizinische Klinik. 2000;95(12):663–671. doi: 10.1007/pl00002083. [DOI] [PubMed] [Google Scholar]
- 56.Moerbeek M, Breukelen GJP, Berger MPF. A comparison between traditional methods and multilevel regression for the analysis of multicenter intervention studies. Journal of Clinical Epidemiology. 2003;56:341–350. doi: 10.1016/s0895-4356(03)00007-6. [DOI] [PubMed] [Google Scholar]
- 57.Skene AM, Wakefield JC. Hierarchical models for multicentre binary response studies. Statistics in Medicine. 1990;9:919–29. doi: 10.1002/sim.4780090808. [DOI] [PubMed] [Google Scholar]
- 58.Roberts C. The implication of variation in outcome between health care professionals for the design and analysis of randomised controlled trials. Statistics in Medicine. 1999;18:2605–2615. doi: 10.1002/(sici)1097-0258(19991015)18:19<2605::aid-sim237>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.