RNA backbone: Consensus all-angle conformers and modular string nomenclature (an RNA Ontology Consortium contribution)

Abstract

A consensus classification and nomenclature are defined for RNA backbone structure using all of the backbone torsion angles. By a consensus of several independent analysis methods, 46 discrete conformers are identified as suitably clustered in a quality-filtered, multidimensional dihedral angle distribution. Most of these conformers represent identifiable features or roles within RNA structures. The conformers are given two-character names that reflect the seven-angle δεζαβγδ combinations empirically found favorable for the sugar-to-sugar “suite” unit within which the angle correlations are strongest (e.g., 1a for A-form, 5z for the start of S-motifs). Since the half-nucleotides are specified by a number for δεζ and a lowercase letter for αβγδ, this modular system can also be parsed to describe traditional nucleotide units (e.g., a1) or the dinucleotides (e.g., a1a1) that are especially useful at the level of crystallographic map fitting. This nomenclature can also be written as a string with two-character suite names between the uppercase letters of the base sequence (N1aG1gN1aR1aA1cN1a for a GNRA tetraloop), facilitating bioinformatic comparisons. Cluster means, standard deviations, coordinates, and examples are made available, as well as the Suitename software that assigns suite conformer names and conformer match quality (suiteness) from atomic coordinates. The RNA Ontology Consortium will combine this new backbone system with others that define base pairs, base-stacking, and hydrogen-bond relationships to provide a full description of RNA structural motifs.

INTRODUCTION

While base-pairing and -stacking are the dominant determinants of RNA 3D structure, specific RNA backbone conformation and interactions are crucial for RNA catalysis, for drug and aptamer binding, and for protein/RNA interactions. All-atom detail is much more difficult to achieve for the backbone than for the bases, but it is a result much to be desired: Interacting molecules see the RNA backbone in full atomic detail, whether our experimental techniques can manage to do so or not.

In both X-ray and NMR structure determination of RNA molecules, the bases can be accurately located as large rigid units whose placement is aided by quite reliable secondary structure prediction. Both structural techniques have trouble with the backbone, however, (except for very high-resolution crystal structures, seldom attainable for RNA molecules of biologically interesting size) due to the complex variability of the numerous torsion angles per residue, as can be appreciated in Figure 1. Despite the best efforts of structural biologists, this level of difficulty leads to errors in the detailed backbone conformations and therefore to a high level of noise and even systematic errors in the database of observed conformations, plaguing structural bioinformatics of the RNA backbone. (Note that although many of the above issues also apply to DNA structure, the narrower conformational range but greater flexibility of DNA backbone mean that it would need to be treated by somewhat different procedures and certainly does not adopt the same conformers identified here.)

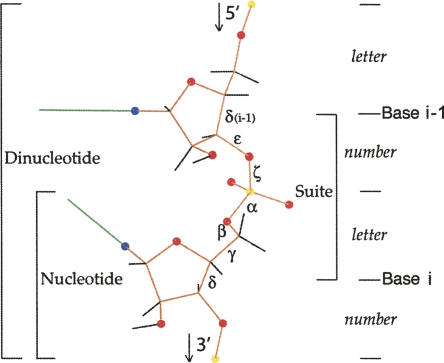
FIGURE 1.

RNA backbone with dihedral angles labeled and divisions into suite, nucleotide (residue), and dinucleotide marked. The modular heminucleotide units are shown along the right edge, which receive letter or number designations in the new nomenclature.

Analysis of RNA backbone conformations is a very hard problem to solve satisfactorily by automated cluster analysis, because of the three-orders-of-magnitude population differences among clusters and the varied cluster shapes and overlaps, as well as the noisy, high-dimensional data. Even after the revolution in information content provided by the ribosome structures (Ban et al. 2000; Schluenzen et al. 2000; Wimberley et al. 2000), most RNA backbone analyses have depended on some form of simplification: on plots for pairs of dihedrals (Kim et al. 1973; Murthy et al. 1999), on reduced dimensionality methods (Sims and Kim 2003), or on use of few parameters insensitive to the most common errors, such as the η,θ virtual-angle system (Malathi and Yathindra 1980; Olson 1980; Duarte and Pyle 1998; Wadley and Pyle 2004), which is still the method most often used for identifying or comparing backbone motifs in an unfiltered general database.

Recently, several research groups have responded to this combined challenge and opportunity by developing classifications of RNA backbone in full or almost full atomic detail. Hershkovitz et al. (2003) analyzed the rr0033/1JJ2 ribosomal RNA by binning values of the individual α, γ, δ, and ζ torsion angles within the chemical unit of the phosphate-to-phosphate nucleotide, or residue; they pioneered the idea of single-character conformation names that could be handled as search strings and defined an alphabet of 37 nucleotide (nt) conformations. That group has also developed a multiresolution approach (Hsiao et al. 2006), where resolution is varied by reducing natural groups of RNA atoms (bases/riboses/phosphates/residues/groups of residues/motifs, etc.) to pseudo-objects with locations and orientations. Murray et al. (2003) proposed the sugar-to-sugar “suite” unit (see Fig. 1), which relates successive bases and within which fitting errors are more easily diagnosed; they developed a large RNA database filtered at the suite level by resolution, crystallographic B-factor, and all-atom steric clashes, then studied the multidimensional dihedral-angle distribution and defined 42 backbone suite rotamers. Schneider et al. (2004) studied the dinucleotide unit of three phosphates and two bases, including the χ base torsions for a total of 14 dihedral-angle parameters, and developed a smoothing method based on multiple 3D Fourier transforms to locate peaks in the data distribution; they defined 32 dinucleotide conformations.

The most common backbone conformations identified in those three studies agreed well, despite the different methods and units of analysis. The groups have now collaborated to re-examine and reconcile their previous definitions and results into a single consensus system. Since the units of analysis previously used were different and overlapping—nucleotide, dinucleotide, or suite (as shown in Fig. 1)—a new modular nomenclature was developed jointly, based on naming the heminucleotides (half-nucleotides) that constitute the units of overlap among the three previous systems. The new nomenclature emphasizes the concise, parsable, and explicitly defined attributes necessary for computational use and database interchange, and it also allows backbone conformation to be expressed as a linear string of two-character conformer names. The empirical data was then reanalyzed in the multidimensional dihedral space and a list of favorable backbone conformers agreed upon. The resulting consensus nomenclature and conformation list are presented here under the auspices of the ROC RNA Ontology Consortium (Leontis et al. 2006). The Results section includes a description of this new system, sufficient for its use in practice, while the Materials and Methods section covers more detailed definitions, reasons behind the various choices made, and relationships to previous work.

RESULTS

Modular nomenclature

The new modular consensus nomenclature is designed for both descriptive and computational usability by assigning a two-character name (a number, then a letter) to each all-dihedral RNA backbone conformer empirically found to occur robustly and frequently. As shown in Figure 1, these conformations are primarily described for the “suite” division from sugar to sugar, within which the angle correlations are stronger than within the traditional nucleotide residue from phosphate to phosphate. The number (or number-like character) represents the combination of mean δ, ε, and ζ dihedral angles for the first half of the suite conformer, while the letter (or letter-like character) represents the combination of mean α, β, γ, and δ dihedral angles in the second half of the suite conformer. The first nucleotide residue that forms part of a suite is referred to as i−1 and the second as i (as shown in Fig. 1); thus, “suite 32” means that residue 32 is the second residue (residue i) of that suite.

The two-character designations should be considered simply as concise, semiarbitrary names for regions in the 7D dihedral-angle space; those regions are elliptical rather than rectangular, and when clusters are close together, their outlines can have more complex shapes (see Materials and Methods). The specific number and letter of each suite conformer name reflect the approximate mean values of all seven dihedral angles for the instances within its region, by rules explained in the text and Table 2, below.

TABLE 2.

Components of the modular consensus nomenclature

For convenience, the conformer names directly reflect the puckers of the two sugars in the suite. An odd number in a suite conformer name signifies a mean δ value for the i−1 ribose consistent with C3′-endo pucker (mean δ between 78° and 90°) and an even number signifies a mean δ value consistent with C2′-endo pucker (mean δ between 140° and 152°). (Note that the values of δ vary more widely for individual instances than for conformer means.) The specific odd or even numbers partition the δεζ heminucleotide space in ζ, and sometimes also in ε. For the second character of the names, letters in the first half of the alphabet (a, c–n) signify 3′ pucker and b, o–z, and [ signify 2′ pucker of the second (i) ribose. For example, 1a is the name of the suite backbone conformer found in A-form helices (with both puckers 3′), while 5z, 4s, and #a conformers form the S shape in S-motifs and contain 3′2′, 2′2′, and 2′3′ puckers, respectively.

For a given conformer name, mean dihedral values can be looked up in Table 1 or in the Web resources (see Web Resources section below). For a given RNA structure, the conformer names for each of its suites are determined by running the Suitename program (see Materials and Methods and below), which applies the defined boundary rules for each of the regions in the 7D parameter space; it also assigns a conformer match quality parameter called suiteness to each input suite, varying from 1.0 at the mean conformer angles to 0.01 at the boundary, to 0 for an outlier beyond the boundary. The observed and named conformers cover most of the data, but only a very small part of the 7D dihedral space. Instances outside of those defined regions are assigned as conformer outliers (named “!!”); most outlier instances result from local errors in fitting backbone conformation, but some represent valid conformations too rare to have yet been identified and named as robust conformer clusters.

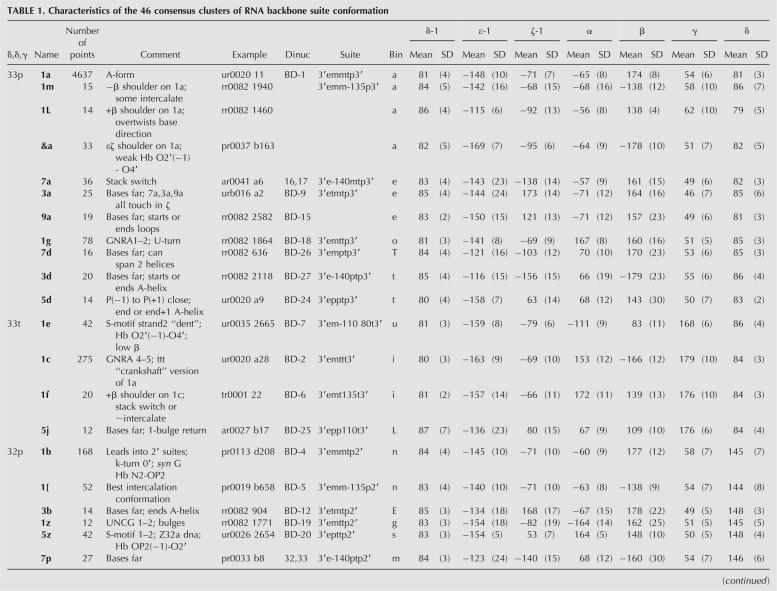
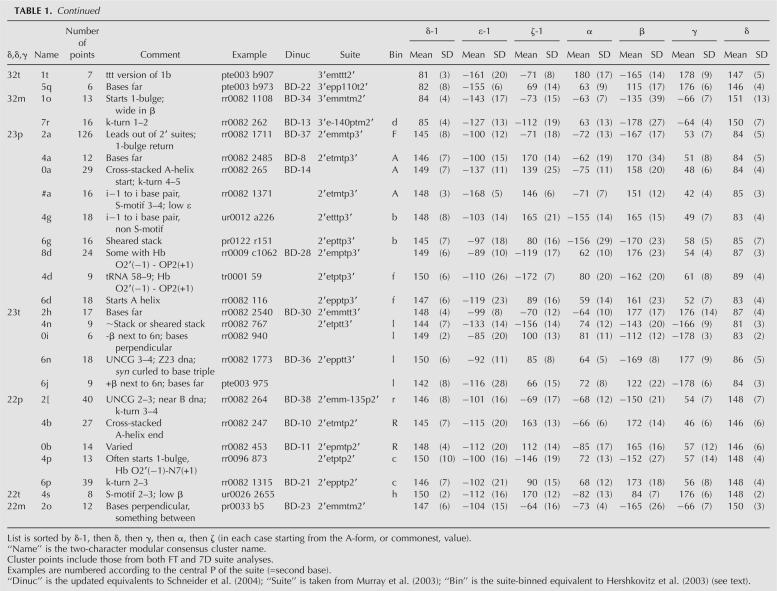
TABLE 1. Characteristics of the 46 consensus clusters of RNA backbone suite conformation

Consensus clusters and means

Table 1 displays the 46 consensus clusters of RNA backbone suite conformations, named by the two-character modular nomenclature. The total number of points in each cluster is given, combining the points from both Fourier and 7D suite analyses. Comments describe the structural roles or characteristic features of the conformer examples. A representative example is listed for each conformer, chosen by stringent combined criteria described in the Materials and Methods section. Columns 6–8 give the equivalent cluster identifiers from the Fourier-averaging update of Schneider et al. (2004), the all-angle suite name from Murray et al. (2003), and the binned-angle names from the suite-based reworking of Hershkovitz et al. (2003); see the “Updates and reanalyses of empirical clustering” section in the Materials and Methods for details. The 7D dihedral-angle mean values for each cluster are given in degrees, with standard deviations in parentheses. An electronic, uncommented version of this information is available in the Web resource data, including the eight “wannabe” clusters that failed but came closest to satisfying the consensus selection criteria. Complete lists of all data points in each cluster can easily be extracted from Web-resource 7D kinemage files (plain text). See the Web Resources section for a description of the content and location of the additional on-line data.

One striking overall result is that the analyses agreed well from studies done with entirely different methodologies and somewhat different data sets, implying that they are reporting real phenomena. Thirty-one clusters were initially in common, and the rest were reconciled with a small number of merges, deletions from each list, and redefinitions of cluster boundaries. These modifications were based on collaborative analysis of superpositions, cluster size and shape in 7D, parallel-axis and virtual-angle spaces, correlation with structure quality parameters, and consideration of structural roles in molecular context (see Materials and Methods for details). Multidimensional kinemage graphics files showing the final consensus cluster assignments are available in the Web resources; they can be viewed on-line by uploading them into the MolProbity section of the kinemage Web site (http://kinemage.biochem.duke.edu) or off-line in the Mage or KiNG software available at that Web site.

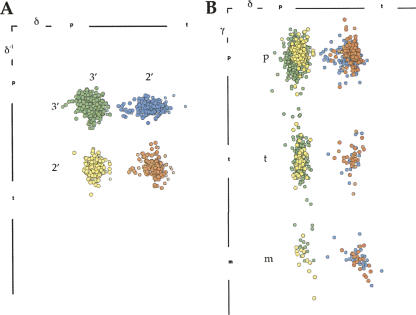
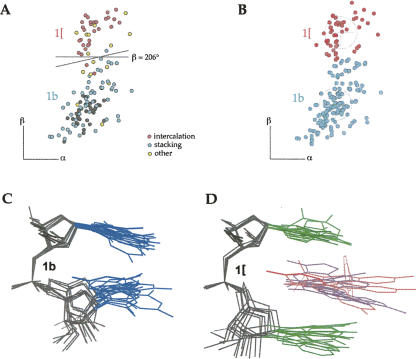
These analyses have shown that the δ values are almost cleanly bimodal and γ values trimodal (see Fig. 8, below). Although high-dimensional techniques were essential to the analyses, the results can be approximately shown by the 12 2D slices of Figure 2, A and B, divided by δ(i−1)δγ class and plotted in ζα, in which nearly all clusters can be seen separated. Mean ε varies quite significantly between clusters (from −169° to −85°) and is generally closer to trans for C3′ puckers (see vertical offset in Fig. 7, below), but it was only twice found to constitute the definitive distinction between clusters (#a/0a/4a and &a/1a, in Fig. 3A). Mean β is most commonly trans, but some combinations of the other angles have highly unusual low values of β (1e and 4s). A number of cluster pairs or triples are distinct only in the β dimension (Fig. 3A, 6j/6n/0i, 1a/1m,/1L, 1f/1c; Fig. 9B, 1b/1[, see below), but can have quite different xyz conformations and structural roles (Fig. 9A–D, 1b/1[ stack versus intercalation example, see below). All remaining suite conformers are distinct in the ζα slices of Figure 2, A and B. Figure 3B shows a selection of atomic models for consensus conformers, varying from base-stacked (Fig. 3B, 1a,1c,5z) to widely extended arrangements (Fig. 3B, 8d,6p) and including many of the conformers discussed below. The first (A) base and ribose are in an approximately constant orientation to facilitate comparison among pairs.

FIGURE 8.

The δ(i−1)δγ separation of the ε-filtered RNA05 data into 12 discrete groups of data points, colored by both δ values. (A) Separation in δ(i−1)δ projection. (B) Separation in δγ projection.

FIGURE 2.

Datapoint clusters in dihedral-angle space for the 46 suite conformers, with a circle and cross marking each mean and standard deviation. Each individual panel shows the ζα projection of one of the δ(−1)δγ groups, in A for δ(−1) C3′ puckers and in B for δ(−1) C2′ puckers. Each point cluster is colored distinctively and labeled with its two-character modular name; names are in parentheses for clusters that are offset in another dimension (those offsets are shown in Fig. 3A).

FIGURE 7.

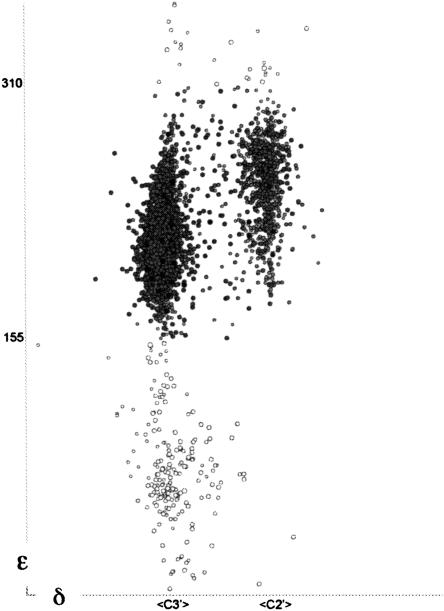
Unfiltered δ versus ε plot for the RNA05 data, with ε outliers shown as open circles. Those occur mainly at + values of ε with C3′ pucker, and are believed to nearly all represent sugars that should have been fit with C2′ pucker.

FIGURE 3.

Comparisons of suite conformers. (A) Dihedral-angle space separation of dominant vs. satellite clusters, which are offset either mainly in ε (top) or mainly in β (bottom; see Fig. 9B for the 1b versus 1[ pair). (B) Atomic models of eight suite conformers. Three are dominant clusters from A above (1a,1c,6n), three are from later motif examples (1g,1e,5z), and two have widely extended bases (8d,6p). All are AU sequence, with the first sugar approximately in the plane of the paper and the A base to the right. Atoms are half-bond colored: (N) blue, (O) red.

FIGURE 9.

Analysis of conformer clusters 1b and 1[. (A) Dihedral-space data points for the RNA05 data set, with examples that stack colored cyan and examples that intercalate colored pink. (B) Final cluster assignments for 1b and 1[. (C) Stacked conformation of cluster 1b. (D) Intercalated conformation of cluster 1[. They differ only in β angle, which swings the second base down to make room for an intercalated base (lilac) or small molecule (pink).

As an additional means of confirming the validity of separating closely spaced clusters in dihedral space, we have investigated the patterns of base preference for each conformational cluster. Absolute sequence preferences are both fairly weak and quite difficult to define quantitatively for three reasons: (1) base preferences are almost always due to tertiary interactions rather than inherent properties of the suite-local backbone conformation; (2) it is difficult to defend a specific reference set for calculating expected preferences, since base composition is known to vary significantly between biological kingdoms, and especially between stems and loops (Schultes et al. 1999); and (3) over half of the defined conformers have fewer than 20 examples, for which only the most extreme biases reach statistical significance. In the RNA05 overall data set, preferences are ∼0.3 for C and G and 0.2 for A and U, while for all conformations other than 1a, preferences are in contrast ∼0.3 for A and G and 0.2 for C and U. In other words, the classified noncanonical conformations show a modest preference for purine nucleotides, while the 1a conformation used in classic A-form helix prefers G and C.

Nine of the 54 backbone conformers reach a 3σ difference from both of the above reference expectation values. 4s prefers an AG sequence and #a prefers GU because of their role in the tertiary interactions of the S-motif. 1c prefers _G and 1[ prefers _A. 1g prefers U_, although similar numbers of U and G occur in that position, which forms a base-backbone H-bond within the U-turn/GNRA tetraloop motif family. 1e and 0a prefer GA and 7a and 4b prefer _A, because A bases are uniquely good at the various noncanonical base-pair geometries (Leontis and Westhof 2001) needed in the second position of those four stack-switch conformations; those base pairs usually use Hoogsteen/WC edges in 1e or 7a, but Hoogsteen/sugar edges in 0a or 4b.

As the above examples suggest, we have found that the complete patterns of base preference for a suite conformer reflect its structural roles. Figure 4A compares base-preference patterns among the four major stack-switch conformers (1e, 7a, 0a, 4b), which use very different dihedral-angle conformations; the four preference profiles match extremely closely. In contrast, Figure 4B compares base preference patterns beween 1a and its three satellite clusters (Fig. 4B, 1m,1L,&a). Each profile is extremely different, confirming that the satellites are separate conformers. Indeed, for all of the groups of close-neighbor clusters illustrated in Figures 3A or 9B, below, base preferences differ by at least 3σ in one or more positions.

FIGURE 4.

Profiles of base preference. (A) Comparison of similar profiles seen for four suite conformers that all produce stack switches, but have very different backbone dihedrals. (B) Comparison of very different profiles seen for the 1a conformer and its three satellite conformers close in dihedral space.

The Web resources also include a set of atomic coordinates for each of the 46 defined suite conformers (plus the eight “wannabe” conformers described in the Materials and Methods), with close to ideal bond lengths and angles (Gelbin et al. 1996; Parkinson et al. 1996). Their construction is described in the Materials and Methods section, producing clash-free models with dihedral angles very close to the mean values and conformations within the main grouping of typical examples for each suite conformer. The representative experimental examples given in Table 1 are best for viewing a suite conformer in its structural context, while the ideal-geometry models are to be preferred as the starting points for model building.

Automated suite name assignment results

The Suitename program instantiates the rules defining conformer cluster boundaries in dihedral-angle space (see Materials and Methods). It was tested by running the entire set of manually assigned cluster points and then comparing its automated assignments with the manual results reported in Figure 2. Of the 6093 manually clustered points, only 11 were declared as outliers by Suitename. Another nine data points were assigned to different clusters by the two methods, most cases involving satellites of the 1a cluster. These disagreements were confirmed by inspection to be borderline cases below our threshold of uncertainty. Thus Suitename reproduced 99.7% of the manual assignments, with no serious disparities.

To check the level of cluster coverage, Suitename was run on the full RNA05 data, both unfiltered and as filtered by backbone steric clashes and B-factor <60. The unfiltered data had 5% triaged suites, 9% outliers, and 86% of the suites assigned consensus conformer names. The filtered data had 2.3% triaged, 6.2% outliers, and 91.5% assigned conformers. Including the eight “wannabe” future clusters adds a bit less than 1% in either case, so that 87% of the total data or 92.4% of the well-ordered data was assigned conformer names for bioinformatic analyses.

Suitename is available both within the MolProbity validation Web site (Davis et al. 2007) and for stand-alone use, for assigning the consensus backbone conformer names of an input RNA structure. It produces either tabular output with one line per suite (including the conformer-match quality parameter called suiteness), or a multidimensional kinemage graphics file of the data points in dihedral space, or a string of two-character suitenames either colon separated or alternating with base sequence, like the GNRA example described and illustrated in the Discussion.

Structural roles of specific conformers

Most of the conformer clusters represent local backbone conformations that play identifiable roles within the RNA molecules. Just over 75% of RNA is in 1a conformation, primarily in long runs of A-form double helix. Changing a single dihedral from the 1a conformation produces a variety of diverse local conformations, such as 3a, 1g, or 7d (Fig. 2A, dihedrals on panel 3′3′p; Fig. 3B, atomic models). These deviations from 1a move the adjacent bases quite far apart and typically end an A-form strand; for instance, 1g starts GNRA tetraloops or U-turns, usually stabilized by reciprocal base-backbone H-bonds between i−1 and i+1. Compensating changes in two dihedrals can be much less drastic, as for the 1c “crankshaft” conformation, which has ttt (all-trans) values for αβγ rather than the mtp of 1a, but retains approximate base-stacking (see Fig. 3B) and other global conformational attributes. 1c suites occur as a rather common but subtle difference within A-form, for instance, just past the end of GNRA tetraloops as at G2663 in the 1.04 Å resolution sarcin–ricin loop of ur0035/1Q9A (Correll et al. 2003), or to accommodate a synG-antiA noncanonical base pair as at G6 and G22 of the ar0006/420D helix (Pan et al. 1999). (Note: Coordinate files are designated here by their six-character NDB code followed by their four-character Protein Data Bank code.) However, 1c shows quite different properties than 1a: 1c only rarely occurs for two suites in a row, it has a straighter backbone shape, it has a different pattern of base preferences, and it puts P(i) and P(i+1) about 1 Å further apart than in A-form, a difference that can be confidently identified even at moderate resolution. U2650 of the sarcin/ricin loop (ur0035/1Q9A) has one alternate conformation in 1c and the other in 1a, showing the different P-P distances clearly and forming a hinge that shifts the three preceding residues by as much as 4 Å.

The vast majority of bases in the data set have their torsion angle χ in the anti orientation (O4′-C1′-C2/4 angle near or above 180°), and none of the suite conformers show a consistently syn χ angle (<120°) for either base. Several conformers do, however, have subclusters that use a syn base in a distinctive role. In general, bases attached at sugars with the minority C2′-endo pucker (where the base is equatorial to the ribose ring) have a higher disposition to adopt syn χ orientation than bases at C3′ sugars (with the base axial, and therefore closer, to the ribose ring). For instance, 1b syn G i bases form a stabilizing H-bond from N2 of the base to its OP2, as in Gb71 of the ar0023/1CSL rev-binding site (Ippolito and Steitz 2000). 6n syn i bases can curl under to join a base triple stacked under the base-paired i−1 base, as in Ud206 of the kink-turn in the pr0113/1SDS complex with L7Ae protein (Hamma and Ferre-D'Amaré 2004). 7r also has a significant subcluster of syn bases at i (used in kink-turns), while 2a, 4p, and 6p can be syn at i−1. Only one data set example, in the relatively rare 5q conformer, was observed to have syn χ for both bases (rr0016/1FJG 30S ribosomal subunit, suite 109) (Wimberley et al. 2000) (also in the later rr0096/1XMQ); the two bases touch perpendicularly at their tips. Sugar pucker correlates with χ value even within the major anti orientation, where χ >240° (“high-anti”) is more prevalent at C2′-endo ribose. Some conformers have consistently high-anti χ at C2′ pucker positions: #a, 4d, 4n, and often 0a and 4b at position i−1 and 4s at position i, while the intercalated majority of 1[ are high-anti at position i.

Several conformations that were quite surprising when first seen in early oligonucleotide structures are now members of sizable clusters. For instance, the open form of UA seen on one chain of urb008 (Sussman et al. 1972) and urb016 (Rubin et al. 1972) is in the 3a suite conformation with bases far apart, while the closed form of UA on the other chain has the 5d conformation, which often starts loops and has P(i−1) and P(i+1) quite close together.

The 2b conformation of B-form DNA is shifted in β for RNA into the 2[ cluster, and forms double helices only under very unusual circumstances (such as RNA/DNA chimeric molecules). Two of the four common suite conformations found in Z-form DNA occur in RNA, although usually singly rather than sequentially in alternation, nor do their bases show the syn/anti alternation of Z-form double helix. 6n (a Z2′3′ conformer) occurs as suites 3–4 of UNCG tetraloops and past other A-helix ends. 5z (a Z3′2′ conformer) is suite 1–2 of S-motifs and in RNA has a characteristic H-bond of OP2(i−1) to O2′ (i) that makes its backbone conformation very reproducible there and elsewhere, as shown by the tight 5z cluster in the 3′2′p panel of Figure 2A. Comparison of 5z to 1a in Figure 3B shows that the second sugar is “upside down” in 5z, as occurs for alternate sugars in Z-DNA. Another characteristic conformer H-bond is O2′ (i−1) to OP2(i+1) in 4d, which helps turn the corner in tRNAs from the TΨC loop to the CCA stem, as at U59 of tr0001/1EHZ tRNA-Phe (Shi and Moore 2000).

Suite 1[ separates the consecutive bases (see Fig. 9, below), allowing intercalation of a drug or another base in between. Other conformers can also sometimes allow intercalation (e.g., 5j, 1m, 7r), but 1[ occurs most frequently and in many high-resolution drug and aptamer complexes. Suites 3–4 of S-motifs use #a conformation (low in ε) to form an i−1 to i base pair. The other common suite with adjacent base-pairing is 4g, as described in Murray et al. (2005). 4g is the only assigned conformer with α and ζ both trans, so its data points appear in the center of panel 2′3′p of Figure 2B.

RNA structural motifs are characterized by a consensus sequence of specific suite conformers (allowing for occasional substitutions, insertions, or deletions). For example, the classic S-motif (Leontis and Westhof 1998; Correll et al. 2003) shows a well-conserved pattern of suites by this analysis, as illustrated in Figure 5A. The strong S-shape of strand 1 is the most distinctive feature of S-motifs, formed by suites 1a, 5z, 4s, #a, and 1a, while suites 1a, 1e, and 1a form the inward-dented backbone and switch between base stacks characteristic of strand 2. Suites 4s and 1e cluster at unusually low β values (see Table 1), both 5z and 1e form specific backbone H-bonds, and #a forms an i−1 to i adjacent base pair. 1e helps form the conserved S-motif GUA base triple, in combination with the #a adjacent base pair on strand 1.

FIGURE 5.

Motif examples. (A) An S-motif; front (S-shaped) strand has bases in blue and 5z, 4s, #a suites in gold, back strand has bases in green, and 1e suite in pink. (B) Stereo of stack switches and dented backbones produced by two 1e suite conformations on opposite strands of the ar0038/1KD5 duplex (Kacer et al. 2003). The 1e suites are highlighted, and all-atom contact dots (Word et al. 1999) show van der Waals contacts for the base stacking (blue and green) and H-bonds for the base pairs (brown). Note the two positions where one base stack ends and the other divides.

Virtual-dihedral analysis has identified a distinct variant designated the S2 motif (Wadley and Pyle 2004); the type specimen is from the large ribosomal subunit rr0082/1S72 around 0 894. This distinction can be confirmed and further characterized by examining the backbone suites. In the S2 motif, the strong S shape of strand 1 is typically formed by 5z, 6p, and 8d suites. Additionally, the classic S1 motif's characteristic base triple is absent in S2: The G base that starts that triple and forms an adjacent base pair in S1 motifs is completely flipped out in all S2 motifs (and is not always a G). The S1 base triple involves an inward dent in the backbone of strand 2, where the conserved 1e suite switches between base stacks. Strand 2 is more variable in S2 motifs, but one example uses 1[ intercalation and one uses a 7a rather than 1e dent and stack switch (50S subunit rr0082/1S72 at 0 1767). Both S1 and S2 motifs can occur within somewhat variable contexts, including even noncontinuous strands (Sarver et al. 2007), but both types are usually flanked by regular A-form double helix on both sides.

The S-shape of strand 1 is not present in the fragment crystal structure of isolated 5S rRNA loop E in url064/354D (Correll et al. 1997). However, the dented stack switch of 1e survives in the fragment, with an additional 1e now seen on strand 1; the region between the two 1e stack-switches has noncanonical base pairs, in a trans rather than the usual cis relationship. A similar, elegant double stack switch is shown in Figure 5B, produced by opposite, but offset 1e conformers on each strand of the ar0038/1KD5 metal-free RNA duplex (Kacer et al. 2003). Conformer 7a can also create a stack switch and an inward-dented backbone within double helices as in ar0049/1SAQ (Jang et al. 2004), and its pattern of base preferences is similar to 1e (see above and Fig. 4A), but its overall conformation in context is different enough that the 1e and 7a clusters are nonoverlapping in a θ/η virtual dihedral plot.

DISCUSSION

This work has defined a library of discrete RNA backbone conformers that cluster in the quality-filtered, multidimensional distribution for the seven backbone dihedral angles of the suite sugar-to-sugar unit. Approximate values for all seven torsion angles in the suite are implied by the two-character modular conformer name (δεζ from the number, αβγδ from the letter). The string of names can be assigned automatically by the Suitename program for an individual RNA structure and should be very useful for descriptive, comparative, or other bioinformatic purposes. Means and standard deviations for each angle in each conformer cluster are listed in Table 1. Structural biology or modeling, however, requires the use or generation of specific atomic coordinates. The idealized-geometry coordinates for each cluster (available in the Web resources) can constitute a library of specific, empirically validated RNA backbone conformations for use in modeling new RNA structures either experimentally or computationally.

This RNA backbone library provides the best set of starting points so far described: high coverage, with most of the common systematic errors removed. However, not every possible and correct local conformation is represented, and most modular strings for specific RNA structures will contain !! wild-card names for unusual suite conformations that are either incorrect or especially interesting. As more experimental data and further methods of analysis become available, this initial list of backbone conformer clusters will be updated.

For RNA structural bioinformatics, the two-character backbone conformer names can be alternated with the base sequence to provide an information-rich string description of the combined linear sequence and 3D structure in RNA molecules. The GNRA tetraloop is perhaps the most classic example of an RNA structural motif, identified by comparative sequence analysis (Woese et al. 1990), characterized structurally by NMR (Heus and Pardi 1991), later defined in high-resolution detail (Correll et al. 2003), and recently reanalyzed (Hsiao et al. 2006). Figure 6A labels the modular backbone annotation on three superimposed examples of GNRA tetraloops, and Figure 6B compares the GNRA modular string N1aG1gN1aR1aA1cN1a with translated equivalents in the earlier nucleotide, dinucleotide, and suite nomenclatures. For the UNCG tetraloop (Cheong et al. 1991; Ennifar et al. 2000), the modular string is N1aU1zN2[C6nG1aN. For the classic S-motif (Fig. 5A), the modular backbone/sequence strings are N1aN5zA4sG#aU1aA1aN for strand 1 and N1aG1eA1aA1aN1aN for strand 2. Such a motif string can also be translated into an atomic model that provides the detailed consensus 3D structure for each suite of a motif recognized in the process of fitting an experimental RNA crystal or NMR structure.

FIGURE 6.

Uses of the modular backbone nomenclature. (A) Stereo of three superimposed GNRA tetraloops (from ur0007, pr0037, and rr0082), with modular two-character names for the backbone suite conformations and with H-bonds shown in gray. (B) Layout of the modular backbone nomenclature (in blue) for the GNRA tetraloop, aligned with equivalent annotations from the earlier dinucleotide, suite, and residue systems. Below is the modular sequence/backbone string that describes the GNRA motif conformation.

The ROC RNA Ontology Consortium will combine this new modular consensus backbone description with other systems that define base-pairing, base-stacking, virtual angles, and hydrogen-bond relationships, to provide full descriptions of currently recognized and newly discovered RNA structural motifs.

MATERIALS AND METHODS

Definition of a consensus modular nomenclature

The new consensus nomenclature consists of concise symbols that name the combinations of heminucleotide conformations experimentally found to occur most often. This new system is designed to provide the concise and cleanly defined nomenclature needed for database and computational uses and to allow translation and comparisons with the previous residue, suite, and dinucleotide systems, as illustrated in Figure 6.

A numeral or number-like single character (that is, a character in the 002–003 “basic Latin” range of Unicode symbols, as at http://www.unicode.org/charts/) is assigned to each δεζ heminucleotide combination, odd for C3′-endo puckers and even for C2′-endo. For the purposes of this system, an individual ribose with δ between 55° and 110° is treated as C3′-endo, and one with δ between 120° and 175° as C2′-endo. It is possible for other sugar puckers (as described by the pseudorotation phase/amplitude system) (Altona and Sundaralingam 1972; Cremer and Pople 1975) to occur within those δ values, but there are so few well-authenticated examples at high resolution (Altona and Sundaralingam 1972; Olson 1982; Gelbin et al. 1996) that they could not be analyzed separately here. C3′-endo or C2′-endo sugar puckers, as diagnosed by their δ values, are referred to here in abbreviated form as C3′ or C2′. Currently, 12 numerical characters are used in the suite names, as tabulated in Table 2 (note that none of the dihedrals can adopt values near zero). 1, 3, and 5 for C3′ puckers and 2, 4, and 6 for C2′ puckers represent mean ζ values within ±35° of minus, trans, and plus, respectively; 7 and 9 for C3′ or 8 and 0 for C2′ represent eclipsed mean ζ values (within ±25° of −120° or 120°); & or # represent heminucleotides with specific unusual mean values of ε.

A lowercase letter or similar character (i.e., Unicode symbols >005A, which codes Z) is assigned to each αβγδ heminucleotide combination: currently a,c-n for C3′ pucker and b,o-z,[ for C2′, leaving uppercase letters for specifying the base sequence. Currently 12 letter characters are used for heminucleotides ending with a δ that indicates C3′ pucker and nine letters for C2′ heminucleotides, as tabulated in Table 2. Each letter specifies a certain combination of αβγδ values, but letters have been chosen to provide mnemonic associations when feasible (such as a for A-form or [ to suggest the intercalation shape), explained by comments in Table 2.

For either heminucleotide, two other characters are used to denote special situations: “_” in suites without all dihedral angles defined (at chain ends or gaps where the 3D structure was disordered) and “!” for unusual conformations currently not classified (dihedral combinations not in the consensus list, bad ε values, etc.), which are therefore either wrong or especially interesting.

Thus, each suite cluster has a two-character name, such as 1a for A-form and 1c for the “crankshaft” variant; for clarity, these names are shown in boldface here. Since αβγδ and δεζ heminucleotides share a δ value, successive suites are logically required to specify compatible ribose puckers. For the same reason, if these symbols are combined in letter-number order to name nucleotide conformations, they constitute well-formed names only if a,c–n is followed by an odd number or b,o–z,[ is followed by an even number. Empirically, only a small fraction of the possible two-character combinations of presently defined number and letter symbols represent clusters identified in the filtered data distribution.

Each number or letter represents specified ranges of the mean dihedrals, but actual mean values vary somewhat in the context of different suite clusters; for instance, the mean ζ is near +50° for 5z and near +80° for 5j, but both are assigned as “5” for plus ζ (approximately +60° or gauche+). All ζ values are shifted away from zero at the −,+ and +,− corners of the ζ,α plot because of steric clashes between atoms separated by four covalent bonds; this is analogous to the “syn-pentane” effect (Dunbrack and Cohen 1997; Lovell et al. 2000) seen for sidechain rotamers in proteins. Thus, there are no 1d or 5a clusters, since they are shifted toward the eclipsed values enough to be named as 7d or 9a instead. (Please note that these ranges for the cluster-mean dihedrals do not act as bins for classifying individual conformations; the conformer regions in the 7D dihedral space are of complex and nonrectangular shapes, as explained below in the section on their automated assignment.)

A specific suite within a given RNA structure may be referred to by giving both included residue numbers (e.g., the 1[ intercalation suite which allows for proflavin binding in drb005 can be called a1–2); if a single number is used, it should be that of the second residue, which contributes the phosphate and the αβγδ heminucleotide (e.g., 1[ suite drb005 a2). That second residue of the suite is here designated as i, while the first residue is i−1. Each suite spans two δ's, two χ dihedrals, and two bases; when referred to individually these must be distinguished as i−1 or i. Since the individual ε, ζ, α, β, and γ angles and the δεζ and αβγδ heminucleotides are unique within a suite, they will not be numbered here except when used within a broader context such as a dinucleotide or a nonlocal H-bond pattern.

Updates and reanalyses of empirical clusterings

Before arriving at a modular consensus system, it was necessary to update and cross-validate the three initial analyses to assure consistent results. The Rutgers/Prague group used the clash and B-factor filtered database of 132 PDB files (here called RNA03) from Murray et al. (2003) in a reanalysis by their Fourier averaging methods (FT) from Schneider et al. (2004). After removal of dinucleotides with missing angles (such as at chain termini), the data set had 3751 dinucleotide data points from 101 structures, 2869 of them “A-like” (with dihedral values at the phosphodiester link for both ζ and α near −60°) and 882 “non-A-like”. To smooth the data distribution, Fourier transforms and inverse transforms were taken for 17 3D combinations of the 14 torsion angles within the dinucleotide [from α(i−1) through ζ, plus χ(i−1) and χ], and peaks were identified in each contoured 3D plot. A data point was assigned membership in each peak for which it lies within a certain distance limit. Data points were sorted and clustered as before (Schneider et al. 2004) by their overall set of peak memberships, emphasizing dihedrals within the central suite unit of the dinucleotide, especially δ(i−1), ζ(i−1), α, β, γ, and δ. The resulting 38 clusters with three or more dinucleotide data points (named as BD-1 to BD-38) were compared in mean suite dihedral values with the closest of the 32 clusters from Schneider et al. (2004) and the 42 suites from Murray et al. (2003). The new analysis agreed in most but not all instances, and provided a number of new clusters with convincing parameters and examples. Atomic RMSD values in Cartesian space were analyzed within each cluster and between close clusters. Cluster conformations were also compared with those that have been observed in an additional sample of high-accuracy oligonucleotide structures.

The Georgia Tech group analyzed the RNA03 filtered data by their binning torsion angle method from Hershkovitz et al. (2003), using both the original nucleotide set of αγδζ and the suite set of ζ(i−1)αγδ. The degree of torsion angle correlation was found to be greater for the suite division. Adding another bin division of β values was tested, but not adopted. An extended set of bins with single-character names was determined for five-angle suites δ(i−1)ζ(i−1)αγδ, with two bins for δ and ζ and three bins for α and γ, plus “other” bins in each angle. A total of 27 binned suites without “other” dihedrals were seen to be populated for the rr0033/1JJ2 large ribosomal subunit. One of these binned suites usually corresponds to several of the consensus conformer clusters, but their total coverage is very good (see Table 1).

The Duke group constructed an expanded database (here called RNA05), with similar criteria for near-duplicate chains or structures as were applied in building RNA03, and with the replacement or addition of new structures at ≤3 Å resolution deposited in the NDB (Nucleic Acid Database) (Berman et al. 1992) between June 2003 and February 2005; it contains 9486 nt in 171 files; the list of RNA05 files is available in the Web resources. For the ribosomal structures, rr0033/1JJ2 was replaced by rr0082/1S72 and rr0016/1FJG by rr0096/1XMQ, and a number of other files were also updated; thus, RNA03 and RNA05 have relatively few identical data points, though they include residues from different structures of the same RNA molecule. (Note: Coordinate files are designated here by their NDB code followed by their Protein Data Bank code [Berman et al. 2000].) The larger size of RNA05 allows suites to be filtered by serious all-atom steric clashes between local base and backbone as well as within local backbone (i±1), giving 3811 suite data points for analysis in the 7D dihedral-angle space.

Conformational clusters for the suites in RNA05 were analyzed in the Mage display program (Richardson and Richardson 1992, 2001) using a new functionality for visualization in high dimensions: All seven backbone dihedrals (or nine with χ's) are read in for each data point and any three can be interactively chosen for display at a given time; point clusters can be selected, colored, regrouped, followed in other sets of dimensions, edited where needed, and written out. An alternative parallel-coordinate display of the sort described by Inselberg (2007) of all seven (or nine) dimensions is toggled with a single keystroke. Cluster means and standard deviations can be calculated and displayed as cluster membership is adjusted. These 7D kinemage graphics files, with the consensus clusters identified, are available in the Web resources.

Even for the unfiltered data shown in δε projection in Figure 7, δ is strongly bimodal, and 97.5% of ε values lie between 155° and 310°; the mean ε is near 215° for C3′ pucker and 250° for C2′. Points with δ or ε far outside of the primary ranges were not used in the cluster analysis, since they are preferentially removed at least three times more frequently than average by each quality filter, and since in the other dimensions they spread widely without forming clusters. Many ε outliers result from incorrectly fitting what should be a C2′ pucker as the more common C3′, which could explain why almost no ε outliers occur at C2′ δ values (Fig. 7). Only one cluster with δ offset from the C3′- or C2′-endo ranges was detected. This cluster, with δ(i−1) in the O4′-endo region, seen in the Fourier averaging, was not included in the final set of clusters because it had a wide spread of ε(i−1) values and several individual cases were diagnosed as probable fitting errors rather than real conformations.

A small number of ε or other outliers are probably valid, representing important strained conformations at functional sites, especially in ribozymes such as HDV (Ferre-D'Amaré et al. 1998) or group I introns (Adams et al. 2004; Golden et al. 2005), but they still do not belong to the set of favored backbone conformers. In the clash- and B-filtered data, only 85 outlier points on ε and δ remained for removal at this stage. δ is cleanly bimodal, as seen for both nucleotides of the suite in Figure 8A. γ is cleanly trimodal, as shown in Figure 8B, with only 14 data points removed as γ outliers. α is trimodal, but less cleanly so. Thus, all clusters are clearly separated in δ(i−1), δ, and γ, and so those variables were used to make preliminary separations of the data points.

Clusters of suite data points within a δ(i−1)δγ category were analyzed primarily in ζαγ, ζαβ, and αβγ dimensions, with checks of δεζ(i−1). χ(i−1) and χ were also available in the kinemages and were examined, but were not used to distinguish backbone conformers. Clusters with few points or with atypical spread in any of the dimensions were evaluated by whether they included any examples from high-resolution structures with unambiguous electron density (e.g., tr0001/1EHZ A59 in cluster 4d), whether the examples appeared to fill similar structural roles in context (e.g., the S-motif 2–3 suites of 4s), whether the superimposed suites in x,y,z formed a coherent atomic conformational cluster, and whether few examples had deviant bond angles. Cluster extent and membership were also evaluated and some outlying points were omitted at this stage. Pairs of neighboring potential clusters that touch in their most distinct dimension (such as 9a, 3a, and 7a in ζ, or 2b and 2[ in β) were split or merged depending on the distinctness of their roles in context and of their conformational clustering when superimposed. Fifty 7D suite clusters were identified, nine of them considered marginal at that stage; all were designated by the new modular two-character names.

Construction of a consensus cluster list

The primary comparison was a reconciliation between the current Fourier averaging analysis and 7D suite cluster analysis, each described above, although agreement with the three previously published conformation lists was also taken into account. Where the same conformation was identified as well populated and clustered in both FT and 7D analyses, it was accepted. The FT peaks generally include fewer data points, because the Fourier peak identification results in lower tolerance for widely spread points, but equivalents of 80%–100% of the FT data points were found also in the matching 7D clusters. In the 7D suite analysis, over 90% of the initial quality-filtered data points were assigned to consensus clusters. (A trivial but essential conversion for this comparison was that the nominal sequence numbers differed as originally published, because the dinucleotides were naturally numbered by their first residue, while the suites were naturally numbered by the second residue, which contributes the most atoms and the most angles to the suite and includes the central P atom of the suite.)

Both analyses flagged cases where the data distribution was continuous and especially broad, or where two FT peaks were close but separate in one dimension (usually β or ζ), but not different in any other dimensions (as in Fig. 9A,B). Sometimes one analysis identified one peak in such a region, while the other analysis identified two. These cases were individually examined and either merged or split based on RMSD or overlap appearance for superpositions within and between the potential subgroups, on their distinctness in a θ/η version of the virtual-dihedral backbone plot from Duarte and Pyle (1998) (see below), on differences in structural roles in the molecular context (Fig. 9A), and on consistent treatment of similar data patterns in ζαβ between different δγδ subsets. The clusters initially identified as 2b and 2[ were found to be highly similar, and thus, 2b was merged into 2[, while 1b and 1[ (Fig. 9B) were judged to be clearly distinct because the two bases stack in 1b (Fig. 9A,C), whereas the β shift in 1[ spreads them apart while maintaining parallel base planes, usually with an intercalated distant base or small molecule (Fig. 9D). Isolated clusters identified in only one analysis were accepted if: (1) they included a reasonably large number of examples (or some at high resolution), or represented a defined structural role, and (2) their superimposed atoms clustered adequately in x,y,z space. Cluster 9a was identified only in the FT analysis, 1t only in the 7D analysis, and 1L suggested by the binned-suite reanalysis, but all three were convincing enough to end up in the consensus list. The final consensus clusters include the data points from both the Fourier and the 7D suite analyses.

As mentioned above, a θ/η virtual-dihedral plot was used to help differentiate similar conformers. This approach allows the suite data to be approximately visualized in two dimensions, which complements the 7D view offered by the standard torsions and aids in assessing the similarity of suite clusters. While the η/θ virtual-dihedral analysis has previously been centered on the residue division of the backbone (Duarte and Pyle 1998; Wadley and Pyle 2004), the θ/η plot instead centers on suites, facilitating a closer correspondence with the consensus conformers. This simpler 2D approach helps quantify overall backbone shape and also local context of the suite, as the virtual dihedrals involve atoms from the previous and following suites. Specifically, θ measures the torsional angle defined by the atoms P(i−1)-C4′(i−1)-P-C4′, so its central virtual bond spans the δ, ε, and ζ angles. The η angle measures the torsion defined by C4′(i−1)-P-C4′-P(i+1) and its central virtual bond thus spans the α, β, and γ angles.

Finally, among the potential clusters that did not satisfy the above requirements for number of examples, low spread, resolution, or structural role, we have identified eight that seem most likely to attain official status in the future when more data is available. They do, however, run more risk than the consensus 46 of turning out to be incorrect. All eight use heminucleotide combinations already defined, so they can be identified concisely as 5n, 5p, 5r, 3g, 2g, 0k, 2z, and 2u. These eight “wannabe” clusters are not listed in Table 1, but their mean values and coordinates are provided in the Web-resource table and data files, and they are by default included in output from the Suitename program.

Automated assignment of modular suite names

The above determination of conformer clusters was done by a consensus of manual examination and evaluations, aided by a variety of software for smoothing, sorting, and displaying the multidimensional data. Now that those definitions are on hand, there is need for an automated algorithm that can closely approximate those suite name assignments given the list of consensus clusters and the specific dihedral-angle values for a new structure. The software developed to do that is called Suitename, and the input dihedrals can be provided by Dangle (both available from http://kinemage.biochem.duke.edu). The dihedral-space cluster sizes and shapes are anisotropic, vary greatly, and are mostly not Gaussian; many include only a small number of data points; and some of the cluster pairs change conformational roles at a boundary whose location is not readily predictable by formula. Therefore, at the current stage of data and understanding, the assignment algorithm and parameters are primarily chosen to fit the manual consensus clusters rather than determined by underlying theory.

For the general case, outer cluster boundaries are treated as axially oriented ellipsoids, generous enough to include any plausible data points without danger of entering an entirely different bin. Each ellipsoid is the same size and shape, but is centered on the mean of its cluster. The ellipsoid semi-axis in each coordinate direction is taken as 3〈σ〉 + 15°, where 〈σ〉 is the average of all cluster standard deviations in that dimension. The first term effectively scales each dimension according to its typical range of variation, while the constant term allows for underlying measurement uncertainties. The ellipsoid half-widths are 28° in δ, 35° in γ, 50° in α, 55° in ζ, 60° in ε, and 70° in β.

As noted above, data points segregate into δ and γ bins nearly independently of other angles, so the first step of the algorithm is to place the data point in one of the 12 δ(i−1)δγ groups or else declare it an outlier. Two ranges are accepted in δ: 55°–110° (C3′) or 120°–175° (C2′), and three in γ: 20°–95° (p), 140°–215° (t), or 260°–335° (m), jointly defining the 12 groups. δ values near zero have been found to signify incorrect ribose stereochemistry (at C3′ for dr0004/1ET4 a212 and dr0010/1NTB b112 in the RNA05 data set), while values of ε outside the range 155°–310° are usually found to signify a misfit sugar pucker; both of these cases are noted specifically by Suitename, as well as being named outliers. Outliers are also declared for β outside 50°–290° or for α or ζ outside 25°–335°. These single-angle outliers are referred to as triaged.

Given the data point's δ(i−1)δγ group, the next step operates in the remaining four dimensions ε, ζ, α, and β, to find all clusters of which the data point could potentially be a member (that is, for which it lies within that cluster's ellipsoid); there may be zero, one, or several. The scaled four-dimensional distance of the data point from a cluster mean is zero at the mean and 1.0 anywhere on the surface of the ellipsoid. In our initial version it was computed as a Euclidean distance, with each component normalized by the semi-axis in that dimension. In most cases, a data point belongs to the cluster to which it is nearest by scaled 4D distance; this is equivalent to drawing a boundary plane halfway between cluster means, perpendicular to the line joining them in the scaled εζαβ space. The point was given that nearest cluster's suite name.

In order to capture more of the clearly positive manual assignments, we found it desirable for Suitename to include points more generously near the diagonal directions than along the coordinate axes. This is done using a superellipsoid, the multidimensional generalization of the superellipse (Gielis 2003) or Lamé oval (Gridgeman 1970). This figure bulges smoothly outward progressively more from an ellipse into the corners of the superscribed rectangle as the exponent increases from 2. Suitename uses an exponent (n) of 3, in the superellipsoid equation:

where a, b, c, and d are the half-widths for the relevant dihedral angles. The data point clusters, even in the clash and B-filtered data, show significant diagonal spread (usually in more than just two dimensions, but not always the same ones) for highly populated clusters such as 1a, 1c, or 1g, an effect presumably produced either by real correlated motions or by correlated errors. Adding the superellipsoid functionality to Suitename is still an approximation to the probable form of the distribution in dihedral-angle space, but it significantly improves the coverage of what seem to be the genuine cluster boundaries.

A few very close cluster groupings require an additional modification as well: Five dominant clusters (1a, 1c, 1b, 0a, and 6n), each in a different δ(i−1)δγ group, have satellite clusters with more than half-overlapped superellipsoids. The estimated boundary plane that was found to divide conformational types can lie as much as four times farther from the dominant than from the satellite cluster mean (e.g., for 1a vs. 1L). Point membership between such pairs is decided by comparing 4D distances further scaled in the relevant dimension (or occasionally two dimensions) by the same ratio as of the two distances from the cluster means to the boundary plane. If a data point is potentially a member of more than two clusters, first its closest nondominant cluster is found using the standard-case algorithm with default scalings, and then the asymmetric comparison is made with the dominant cluster if there is one. Each non-outlier suite in the input structure is thus assigned a modular name.

To evaluate the match quality of a data point to its assigned conformational cluster, a scaled 7D superellipsoid distance (analogous to the 4D formula above) is now computed in all seven dihedral dimensions of the suite, including δ(i−1), γ, and δ as well as ε, ζ, α, and β. That distance d is then converted into a “suiteness” match quality s, according to s = (cos πd + 1)/2, which varies sinusoidally from 1.0 at the cluster mean to zero at the surface of the superellipsoid. A floor of 0.01 is imposed so all non-outlier points have non-zero suiteness. All outliers have suiteness=0. The suiteness is a measure of how well the detailed local backbone conformation fits one of the most commonly observed (and thus presumably most favorable) conformational clusters.

Representative examples and idealized models

A single representative example was chosen from each suite conformer cluster. Visualization of an example's 3D structure provides a good instance of the given suite conformation within a representative context. Criteria were that the representative example should have a high suiteness value and relatively high resolution, show the cluster-typical conformational features (such as base-stacking, a specific H-bond, etc.), lie near the center of cluster examples as superimposed on their backbone atoms using the LSQMAN utility (Kleywegt and Jones 1994), and be free of all-atom steric clashes >0.4 Å and bond-length or bond-angle outliers >4σ (evaluated by Dangle). Some preference was also given to including examples from a wide variety of structures. Those representative examples are listed in Table 1.

For fitting and modeling purposes, it is very desirable to have a library of ideal-geometry coordinates for each backbone suite conformer. However, simply setting bond lengths and angles to accepted values (Parkinson et al. 1996) and dihedral angles to their cluster-mean values (Table 1) gives acceptable models for only a minority of the conformers. Some conformer clusters spread only slightly in backbone dihedrals or backbone atom positions, but show subclusters in base positioning; for instance, 7r suites can have the second base either at a 70° angle to the first (as in the kink-turn rr0082/1S72 0 262 representative example) or parallel to it (as in the intercalated rr0082/1S72 0 776). Other conformer clusters are quite tight even for base positions, but simply constructed ideal models either clash or fail to match the examples. For instance, 1b has intractable steric clashes of about 1 Å overlap at the base tips, uncorrectable by any combination of χ angles when modeled with single-value ideal bond lengths and angles (Parkinson et al. 1996) and with cluster-mean dihedral-angle values. Individual database examples avoid that clash in a variety of ways, sometimes by distorting bond angles or ring planarity. However, a rotatable ideal model can produce 1b conformations excellent by every measure in at least three different ways: either by coupled shifts of about 3° in the α and γ dihedrals, by 3° in the ε and β dihedrals, or by using pucker-specific bond angles at the C3′ atom (Gelbin et al. 1996) and 1° dihedral changes. This fine-scale multiplicity of equally effective but distinct solutions helps explain why mean dihedral values do not by themselves solve the modeling problem. Therefore, we have added a very conservative level of such flexibility to our modeling process, both by allowing small changes from the mean dihedral angles and also by producing a library of riboses optimized with standard bond lengths and specific integer δ values across the two ranges of means in Table 1. Each ribose has a pucker phase close either to C3′-endo (phase 18°) or to C2′-endo (phase 162°), a pucker amplitude between 35° and 40° (Altona and Sundaralingam 1972; Brameld and Goddard 1999), and bond angles close to pucker-specific ideal values (Gelbin et al. 1996).

The final step was manual dihedral-angle adjustment for each suite conformer to satisfy the clash, feature, and superposition-fit criteria. This process used a dockable suite model with rotatable dihedral angles, in the MAGE display software (Richardson and Richardson 2001), with a hypertext menu of starting values for each suite conformer. This system was illustrated in Murray et al. (2005) for RNA structure correction, but now includes choices from the library of optimized riboses and also the option of pucker-specific external bond angles at the tetrahedral C3′ and C4′ atoms, where influential angle differences (up to 4°) between C3′-endo and C2′-endo riboses occur (Gelbin et al. 1996). Nearly all suite conformers could now be acceptably modeled to quite stringent standards, even with our simplified approximation of allowing only C3′-endo or C2′-endo ribose puckers. A few suite conformers (most notably, 4s and #a from the S-motif) required a larger pucker amplitude (45°) and somewhat larger deviations from ideal bond angles in order to position the bases acceptably, suggesting that these suites may have somewhat more strained conformations than the rest.

The resulting idealized conformer models represent base as well as backbone positions for the main grouping of examples in each of the conformers while maintaining closely classic ribose puckers, base ring planarities, bond lengths (deviations <1σ), bond angles (<2σ from Gelbin et al. [1996] values) and all-atom sterics (clashes <0.3 Å). The idealized-geometry atomic coordinates for each suite conformer (including hydrogens) are available in the Web resources, in PDB v3.0 format. Most conformers are given an arbitrary base sequence of AU, but if the subcluster had a nearly unanimous sequence then those bases were used in the idealized model.

WEB RESOURCES

The RNA Ontology Consortium (ROC) Web site is at http://roc.bgsu.edu and the Richardson laboratory Web site is at http://kinemage.biochem.duke.edu. Both sites host the RNA backbone table, list, graphics, and coordinate files on pages linked from this study on their publication lists, and will update and maintain them as the set of ROC-defined suite conformers are modified and expanded in the future. In addition, the kinemage site distributes the free, open-source, multiplatform software used in this work (Suitename, Dangle, Mage, and KiNG) and operates the MolProbity server which now includes on-line analysis of backbone suite conformers for input RNA coordinate files.