Abstract
Pseudoknots are abundant in RNA structures. Many computational analyses require pseudoknot-free structures, which means that some of the base pairs in the knotted structure must be disregarded to obtain a nested structure. There is a surprising diversity of methods to perform this pseudoknot removal task, but these methods are often poorly described and studies can therefore be difficult to reproduce (in part, because different procedures may be intuitively obvious to different investigators). Here we provide a variety of algorithms for pseudoknot removal, some of which can incorporate sequence or alignment information in the removal process. We demonstrate that different methods lead to different results, which might affect structure-based analyses. This work thus provides a starting point for discussion of the extent to which these different methods recapture the underlying biological reality. We provide access to reference implementations through a web interface (at http://www.ibi.vu.nl/programs/k2nwww), and the source code is available in the PyCogent project.
Keywords: RNA, RNA structure, pseudoknot, algorithm
INTRODUCTION
Pseudoknots, RNA structures in which the base pairs are not fully nested, are biologically important but cannot be handled by many computational procedures. Pseudoknots began as a theoretical prediction (Studnicka et al. 1978; Waterman 1978) but were found in viral RNAs a few years later (Rietveld et al. 1982; Pleij et al. 1985). They are now known to be critical for the structure and function of many RNAs, and evolutionarily conserved pseudoknots are involved in processes that include ribosomal frameshifting, self-cleavage, and self-splicing (Pleij 1994; Hilbers et al. 1998; Staple and Butcher 2005; Rødland 2006). The pseudoknotted region can be substantial: for example, at least 36% (8 out of 22) of the base pairs in the hepatitis delta virus (HDV) ribozyme structure must be removed to eliminate pseudoknots. In longer structures, pseudoknots often make up a relatively small but critical part of the molecule. For example, in the Escherichia coli 16S rRNA structure (Cannone et al. 2002), as few as 1.88% (9 out of 478) of the base pairs can be removed to produce a nested structure, but these regions include two pseudoknots that are universally conserved and essential for translation (Vila et al. 1994; Poot et al. 1996).
Removing pseudoknots from structural models is a relevant problem for a growing group of RNA researchers using computational tools. Because of limitations in software or algorithms, it is often necessary to work with nested structures. Pseudoknot elimination can be necessary, for example, to use the growing repository of RNA crystal structures (Ponty 2006; Tyagi and Mathews 2007), to compare different RNA structures (Andronescu et al. 2007), to classify structures into structural components (Smit et al. 2006), to create RNA covariance models (Eddy 2002), or to search for RNA homologs (Chang et al. 2006). Pseudoknots also increase the computational complexity of RNA structure prediction (Rivas and Eddy 1999; Lyngsø and Pedersen 2000) and visualization (Han and Byun 2003; Jossinet and Westhof 2005).
To make a knotted structural model pseudoknot-free, one or more base pairs must be “broken,” treating the corresponding part of the sequence as unpaired. The subtleties of this process are often underestimated. Which criteria should be used to designate one group of base pairs as “the helix” and another group as “the pseudoknot”? In the RNA molecule there may be no physical distinction between the conflicting helices that make up a pseudoknot at a structural level. Consequently, the decision about which helix to leave out can be arbitrary, undocumented, and difficult to reproduce. Pseudoknots are often removed manually or with unspecified computational methods (for example, Xayaphoummine et al. 2003; Smit et al. 2006; Andronescu et al. 2007; Metzler and Nebel 2008; Tyagi and Mathews 2007). An algorithm to calculate a nested structure containing the maximum number of base pairs has been described (Ponty 2006). In addition, related work has been done on computing the number of locally optimal secondary structures with respect to the Nussinov-Jacobson energy model (Clote 2005, 2006). Some information about pseudoknots is also available in the SSTRAND database (http://www.rnasoft.ca/sstrand). Progress is also being made in prediction and visualization of pseudoknotted structures, including a recent method for choosing pseudoknotted helices that minimize the sum of the stacking energies of the individual stems (Huang and Ali 2007).
The existing methods for pseudoknot removal are limited in their underlying assumptions: keeping the maximum number of base pairs is just one possibility and is not necessarily related to the RNA folding process. Other properties of the RNA that have been used to designate pseudoknots include the strength of a helix (either length or free energy), the folding pathway (which helix forms or melts first?), historical considerations (which helix was discovered first?), or ease of visualization. The manual approach is not feasible for large-scale analyses, and the computational approaches are often unspecified or not available to the wider community. The static pseudoknot information in a database is useful, but researchers need to be able to apply methods to their own structures as they are determined.
Current practices lead to duplicated efforts in automating the process of pseudoknot removal, inconsistent nomenclature, and difficulties reproducing analyses that require pseudoknot removal. Because the decision about how to unknot an RNA structure can have significant effects on structure-based downstream analyses, there is a need for explicit descriptions and user-friendly implementations of the possible algorithms.
We present a variety of algorithms for pseudoknot removal. We explore the use of different criteria to define pseudoknots: given a specific goal, each method points out the most critical base pairs that have to be removed. We demonstrate that different methods applied to the same initial structure lead to different results, indicating that pseudoknot removal affects structure-based analyses and that researchers should document their methods to improve reproducibility of their studies.
Our effort is in line with the goals of the RNA Ontology Consortium (Leontis et al. 2006), which aims to construct an ontology of RNA-related concepts to facilitate the integration of data flows in bioinformatics analyses (Jossinet et al. 2007). We intend to begin building a common vocabulary and set of reference software implementations for the removal process, such that pseudoknots can be removed in a consistent matter when the initial set of base pairs and removal method are specified. To make our software available to a wide audience, we provide not only the source code under the PyCogent project (Knight et al. 2007) but also a web interface (see Supplemental Data) and a standalone implementation offering command line control over the methods.
RESULTS
The main result of this study is the development and implementation of several methods to make knotted RNA structures pseudoknot-free. When pseudoknots are present in a structural model, different criteria can be used to remove them. Keeping the maximum number of base pairs ensures the least amount of information is lost. From a biological perspective, however, other criteria might come into play, such as the length of a helix or the distance between its upstream and downstream regions. We have implemented several heuristics with different underlying assumptions about what is important in the structure and a formal optimization approach that calculates all optimal solutions given some scoring function. All methods find saturated structures (Clote 2006), in which no base pair can be added without introducing a pseudoknot. This section begins with a short technical introduction outlining necessary concepts and definitions. We then describe the methods and their performance.
RNA structure and pseudoknots
In this study, we use the term “RNA structure” for a collection of base pairs, where one base can pair with at most one other base. The single-interaction restriction is common in the context of RNA secondary structure. However, we consciously avoid the term “secondary structure,” because traditionally this has been used to describe a pseudoknot-free structure (Waterman 1978). A base pair is denoted as a pair of an upstream and downstream position (i,j) (where i < j), and a structure is a list of these pairs (as in Waterman 1978). A structure is pseudoknotted if for any pair (i,j) there is a base pair (k,l) (i < k) such that i < k < j < l (for definitions, see, for example Studnicka et al. 1978; Waterman 1978; Rivas and Eddy 1999; Lyngsø and Pedersen 2000; Rødland 2006; Rastegari and Condon 2007). A saturated structure is a nested structure to which no base pair (out of the base pairs in the knotted structure) can be added without introducing a pseudoknot (Clote 2006). We call an uninterrupted stretch of base pairs with positions [(m,n),(m+1,n–1),(m+2,n–2),…] a “paired region” (also known as a “helical region” or “ladder”) (Studnicka et al. 1978; Waterman 1978; Rødland 2006). A paired region may contain many base pairs or just a single base pair. Each paired region has an upstream half (closest to the 5′ end of the RNA sequence) and a complementary, antiparallel downstream half (closest to the 3′ end). Two regions are said to be conflicting if they are involved in a knot. A pseudoknot-free structure corresponds to a collection of paired regions that are organized in a nested fashion. The “length” of a paired region is the number of base pairs it contains. The “range” of a paired region is the distance between the highest upstream position and the lowest downstream position. For a region that conflicts with one or more other regions we can define the region's “gain” as the length of the region minus the cumulative length of all of its conflicting regions. The gain of a region expresses how many base pairs are gained if that region is chosen and thus all of its conflicts have to be eliminated (a positive gain means it is favorable to keep the region; a negative gain, to remove it). For example, if region A (2 base pairs) conflict with region B (4 pairs), the gain of region A is −2 and the gain of region B is +2.
Heuristic approaches
The heuristics are split into two groups: conflict elimination methods and incremental methods. The conflict elimination methods start with all paired regions and remove conflicting regions successively. In contrast, the incremental methods all start with an empty list of paired regions and then add nonconflicting regions one at a time. The order in which the regions are eliminated or added differs in each method, and the nested structure that will be reached differs accordingly.
EC (elimination, conflicts)
The EC method tries to reach a nested structure as fast as possible. It removes paired regions from the whole set beginning with the one with the most conflicts. If two regions have an equal number of conflicts, the region's gain and starting position are used to determine which region is processed first. This simple strategy might remove too many regions, resulting in an unsaturated structure, so nonconflicting regions are optionally added back (see the supplemental materials for details).
EG (elimination, gain)
The EG heuristic eliminates conflicting paired regions on the basis of their “gain” (see RNA Structure and Pseudoknots). The algorithm processes the regions from the one with the smallest gain to the one with the largest gain, which means that the most unfavorable regions are removed first. It uses the number of conflicts and the starting position in case of equal gain. To prevent finding unsaturated structures, this method adds back nonconflicting regions (see the EC method).
IO (incremental, order)
The IO method starts with an empty list and adds paired regions that do not conflict with any region that has already been added. It takes the most simplistic approach, which is to add paired regions one by one, from the 5′ end to the 3′ end or the other way around. The order of the regions is controlled by a parameter: the default order is from 5′ to 3′. This method is currently used by INFERNAL (E. Nawrocki, pers. comm.).
IL (incremental, length)
The IL method operates under the idea that longer regions are more important than shorter regions. Thus, it adds nonconflicting paired regions one by one, starting with the longest region and working toward the shortest region. In case of equal lengths, the region starting closest to the 5′ end is added first (preferred end is controlled by a parameter).
IR (incremental, range)
The IR method prefers short-range interactions over long-range interactions, thus in this scenario the structure is built-up starting with the formation of the hairpin loops. Paired regions are added to the list from short to long-range. If ranges are equal, the region starting closest to the 5′ end is added first (preferred end is controlled by a parameter).
Optimization approach
The pseudoknot removal problem can also be solved by formal optimization. A dynamic programming (DP) algorithm (Bellman 1957) can efficiently calculate a solution that is optimal under some scoring function. A modification of the Nussinov–Jacobson algorithm (Nussinov and Jacobson 1980), restricting it to the base pairs in the pseudoknotted structure, has been used to find a nested structure containing the maximum number of base pairs (Xayaphoummine et al. 2003; Ponty 2006; Tyagi and Mathews 2007).
Our optimization approach (OA) differs from the known DP algorithm in two respects. First, it calculates all optimal solutions rather than a single one. Second, it can handle arbitrary scoring functions, incorporating sequence or alignment information in addition to the structure. We have implemented the traditional scoring function to maximize the number of base pairs in the nested structure and a sequence-dependent function that maximizes the number of hydrogen bonds in Watson–Crick base-paired regions, where each GC base pair scores 3 points and each AU or GU pair scores 2 points (Mathews et al. 1999). A detailed description of the optimization approach can be found in the supplemental materials (see Supplemental Data).
A dynamic programming method is preferred to an exhaustive approach despite the relatively low complexity of many natural RNA structures in terms of pseudoknots. Although most collections of canonical base pairs in biological structures belong to a class called bisecondary structures (Haslinger and Stadler 1999), in which the topology of the pseudoknots is restricted, the number and size of the knot components increases rapidly in more exotic base pair collections. Even among sets of canonical base pairs, the complexity varies widely. For example, there are only 14 possibilities for the HDV ribozyme structure (Protein Data Bank [PDB] ID: 1DRZ) (Ferré-D'Amaré et al. 1998), but 3.8 × 1029 possible nested structures for the E. coli large-subunit (LSU) rRNA structure (PDB: 2AW4) (Schuwirth et al. 2005).
Implementation and availability
All methods are implemented in Python. The source code is available as part of the PyCogent library (Knight et al. 2007) distributed through SourceForge.net. In addition, we provide a standalone implementation in combination with a script that gives the user command-line control over the methods, and we have set up a web interface that controls this script through the web. Both the script and the web interface are available as supplemental materials (see Supplemental Data). The code can easily be adjusted to incorporate the user's preferences or extended to support other pseudoknot removal strategies.
Method behavior
A legitimate question is which method should be used; however, the answer likely depends on the situation. We are explicitly not trying to advocate the use of a single method: Different methods produce different results precisely because they have different goals, for example, preserving the longest helices or preserving the most base pairs. Different methods may be more or less suited to different applications. Rather, the description of these methods and their behavior acts as a framework for users to make informed decisions about the following issues: Which methods are available? Is there a method that suits my needs? Should I develop a new method and add it to the collection? Should I combine several existing methods?
Several factors influence the pseudoknot removal process. First, the chosen method is of major importance, because different criteria could all produce different solutions for the same knotted structure (Fig. 1). Second, the selection of base pairs forming the initial structure can lead to different conclusions under the same criterion. For example, in the set of canonical base pairs from the RNaseP structure (PDB ID: 2A64) (Kazantsev et al. 2005), the EC and IR methods found a nested structure containing 82 base pairs (helix P2 broken), while the EG, IO, and IL methods reached a solution of 81 base pairs (helix P4 broken). When adding the immediate helix extensions, there were two optimal solutions containing 95 base pairs each, indicating that P2 and P4 were of equal importance in terms of the number of base pairs. The fact that multiple optimal solutions for the same knotted structure might exist is also illustrated in Figure 2. Finally, we show (in Fig. 2) that applying a different scoring function will change the outcome of the optimization approach. Detailed information about the performance of the methods on biological and artificial structures can be found in Supplemental Tables 1 and 2.
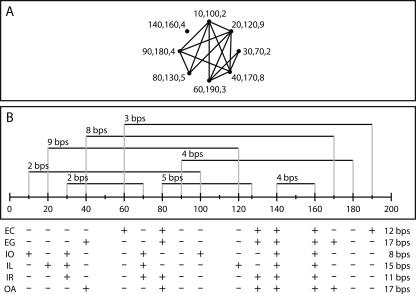
FIGURE 1.
Different behavior of pseudoknot removal methods. All algorithms can find different nested structures for a single knotted structure. This figure shows two different representations of a set of paired regions as found in a randomly generated artificial RNA structure. (A) A graph representation of a collection of paired regions. Each node is a paired region (the start point, end point, and length are specified). Each edge indicates that the two paired regions it connects are conflicting. (B) Start and end points of the paired regions along a sequence. The number of base pairs in each region is specified at the start point. The bottom part of the figure reports which regions are removed (−) or kept (+) by each of the methods (symbols repeated at the start and end points of the regions), and how many base pairs the solution contained. The OA method optimized the number of base pairs, and, in this case (but not generally), produced the same result as the EG method.
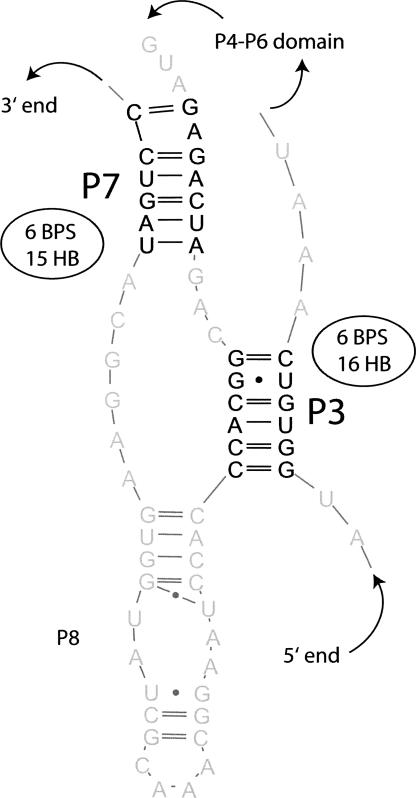
FIGURE 2.
Different criteria for pseudoknot removal lead to different results for a pseudoknot in the group I intron structure (PDB ID: 1ZZN) (Stahley and Strobel 2005). Helices P3 and P7 are involved in a pseudoknot. There are two possible solutions to create a nested structure: Keep P3 and break P7 or keep P7 and break P3. In terms of the number of base pairs (BPS), both solutions are equivalent and optimal (both have 6 BPS). In terms of hydrogen bonds (HB), keeping P3 is optimal, because it has 16 hydrogen bonds where P7 has only 15. The image of the structure is made with the S2S software (Jossinet and Westhof 2005).
DISCUSSION
We have presented a collection of automated methods for pseudoknot removal from RNA structures. This collection will be useful to the RNA community for two reasons. First, it allows pseudoknots to be removed in a consistent manner across different studies, so that analyses can be reproduced exactly. This consistency is especially important for benchmarking of new software that predicts or otherwise uses structural information. Second, it makes explicit the implicit assumptions that underlie the different methods, facilitating discussion of the pros and cons of the different methods for specific biological situations. In their role as operational definitions of pseudoknots, the presented methods can also spark a more informed discussion of which base pairs must be broken to form a nested structure.
The results demonstrate that there are many ways to remove pseudoknots and that, in general, these different methods give different results. For many pseudoknotted structures, all of the methods produce distinct solutions. The optimization method provides a formally optimal solution in terms of optimization of some score function, but this solution is often not unique. Therefore, we recommend that analyses are performed either by using each optimal solution and averaging the results or by using additional biologically informed criteria that are applied in a well-described and consistent manner to choose an optimal solution.
One important, but unresolved, question is how to decide which method is best in a given situation. Both the helices that contribute to a pseudoknot are usually standard A-form RNA helices: because designation of one group of base pairs as “the helix” and the other as “the pseudoknot” has often been performed manually in different families of sequences with no explicit justification—leading to the comment that “pseudoknots are pseudointeresting” (N. Pace, pers. comm.), comparison with existing nomenclature is likely to produce inconsistent results. This will be an important area of investigation for automatic use of structural information in databases such as Rfam (Griffiths-Jones et al. 2003) but can only be addressed with additional data. In particular, which nested structure is the best may depend on the goal: we can ask, for example, which of the methods is most likely to preserve conserved interactions, or which of the methods is most likely to produce covariance models that maximize the number of additional homologs found in the databases. However, these are empirical questions that require empirical studies to resolve.
In conclusion, the availability of a variety of pseudoknot resolution algorithms, along with reference implementations of these methods, fills an important and previously unappreciated need in the field. Because the procedure for pseudoknot removal often seems intuitively obvious, but because intuition differs between different researchers, the explicit rules and motivations for the different procedures have often been hidden. By making this information explicit and by providing a common vocabulary for describing the different methods, we now have a starting point for determining which of the various methods are optimal in specific cases and provide a platform on which more advanced methods can be constructed.
MATERIALS AND METHODS
Crystal structure data
The crystal structure data files were downloaded from the Research Collaboratory for Structural Bioinformatics (RCSB) Protein Data Bank (Berman et al. 2000). For each crystal structure, the set of canonical base pairs was extracted by selecting all Watson–Crick and standard G-U wobble pairs found by RNAview (Yang et al. 2003). Occasional conflicts in this list, where RNAview annotates two bases, x and y, as a standard base pair and also y and z as another conflicting base pair, were removed manually by visual inspection of the crystal structure in the program PyMOL (http://pymol.sourceforge.net/). The helix-extension data set was created by taking the canonical pairs and adding all additional base–base interactions identified by RNAview (excluding stacked bases and tertiary interactions) for which the direct neighbor was already in the collection. This means each base pair (i,j) was added if both i and j were still unpaired and if either (i + 1, j – 1) or (i –1, j + 1) were already in the set.
Artificial structure generation
We generated an artificial RNA structure by inserting the requested number of paired regions in a sequence of a specified length. The minimum number of base pairs in a region was two, the maximum was 10. The algorithm randomly picked an upstream and a downstream position (smaller than the sequence length) and calculated what the possible region lengths were, respecting the surroundings and a three-base distance between the upstream and downstream half of a region. If the chosen sequence positions allowed for the insertion of a region, it randomly chose an available length and added the base pairs to the list. If they did not allow for a region, for example, because the positions were too close to each other or to an already-inserted region, the algorithm simply picked two new positions and checked the criteria again. This process was repeated until the requested number of regions was inserted.
SUPPLEMENTAL DATA
Supplemental material can be found at http://www.ibi.vu.nl/programs/k2nwww.
ACKNOWLEDGMENTS
This work has been strongly motivated by discussions at the 2007 meeting of the RNA Ontology Consortium (NSF Grant No. 0443508) in Madison, WI. We are also grateful to Robin Dowell, Sébastien Lemieux, Michael Yarus, and Norman Pace for their contributions to the discussion. The comments of two anonymous reviewers have greatly helped us to improve this manuscript. This work is supported by the Centre for Medical Systems Biology. The Centre for Medical Systems Biology is supported by a Genomics Centre of Excellence grant from the Netherlands Genomics Initiative, which is funded by the Dutch government.
Footnotes
Article published online ahead of print. Article and publication date are at http://www.rnajournal.org/cgi/doi/10.1261/rna.881308.
REFERENCES
- Andronescu, M., Condon, A., Hoos, H., Mathews, D., Murphy, K. Efficient parameter estimation for RNA secondary structure prediction. Bioinformatics. 2007;23:i19–i28. doi: 10.1093/bioinformatics/btm223. [DOI] [PubMed] [Google Scholar]
- Bellman, R.E. Dynamic programming. Princeton University Press; Princeton, NJ: 1957. [Google Scholar]
- Berman, H.M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T.N., Weissig, H., Shindyalov, I.N., Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannone, J.J., Subramanian, S., Schnare, M.N., Collett, J.R., D'Souza, L.M., Du, Y., Feng, B., Lin, N., Madabusi, L.V., Muller, K.M., et al. The comparative RNA web (CRW) site: An online database of comparative sequence and structure information for ribosomal, intron, and other RNAs. BMC Bioinformatics. 2002;3:2. doi: 10.1186/1471-2105-3-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang, T.H., Huang, H.D., Chuang, T.N., Shien, D.M., Horng, J.T. RNAMST: Efficient and flexible approach for identifying RNA structural homologs. Nucleic Acids Res. 2006;34:W423–W428. doi: 10.1093/nar/gkl231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clote, P. An efficient algorithm to compute the landscape of locally optimal RNA secondary structures with respect to the Nussinov–Jacobson energy model. J. Comput. Biol. 2005;12:83–101. doi: 10.1089/cmb.2005.12.83. [DOI] [PubMed] [Google Scholar]
- Clote, P. Combinatorics of saturated secondary structures of RNA. J. Comput. Biol. 2006;13:1640–1657. doi: 10.1089/cmb.2006.13.1640. [DOI] [PubMed] [Google Scholar]
- Eddy, S.R. A memory-efficient dynamic programming algorithm for optimal alignment of a sequence to an RNA secondary structure. BMC Bioinformatics. 2002;3:18. doi: 10.1186/1471-2105-3-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferré-D'Amaré, A.R., Zhou, K., Doudna, J.A. Crystal structure of a hepatitis delta virus ribozyme. Nature. 1998;395:567–574. doi: 10.1038/26912. [DOI] [PubMed] [Google Scholar]
- Griffiths-Jones, S., Bateman, A., Marshall, M., Khanna, A., Eddy, S.R. Rfam: An RNA family database. Nucleic Acids Res. 2003;31:439–441. doi: 10.1093/nar/gkg006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han, K., Byun, Y. PSEUDOVIEWER2: Visualization of RNA pseudoknots of any type. Nucleic Acids Res. 2003;31:3432–3440. doi: 10.1093/nar/gkg539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haslinger, C., Stadler, P.F. RNA structures with pseudoknots: Graph-theoretical, combinatorial, and statistical properties. Bull. Math. Biol. 1999;61:437–467. doi: 10.1006/bulm.1998.0085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilbers, C.W., Michiels, P.J., Heus, H.A. New developments in structure determination of pseudoknots. Biopolymers. 1998;48:137–153. doi: 10.1002/(SICI)1097-0282(1998)48:2<137::AID-BIP4>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- Huang, X., Ali, H. High sensitivity RNA pseudoknot prediction. Nucleic Acids Res. 2007;35:656–663. doi: 10.1093/nar/gkl943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jossinet, F., Westhof, E. Sequence to structure (S2S): Display, manipulate and interconnect RNA data from sequence to structure. Bioinformatics. 2005;21:3320–3321. doi: 10.1093/bioinformatics/bti504. [DOI] [PubMed] [Google Scholar]
- Jossinet, F., Ludwig, T.E., Westhof, E. RNA structure: Bioinformatic analysis. Curr. Opin. Microbiol. 2007;10:279–285. doi: 10.1016/j.mib.2007.05.010. [DOI] [PubMed] [Google Scholar]
- Kazantsev, A.V., Krivenko, A.A., Harrington, D.J., Holbrook, S.R., Adams, P.D., Pace, N.R. Crystal structure of a bacterial ribonuclease P RNA. Proc. Natl. Acad. Sci. 2005;102:13392–13397. doi: 10.1073/pnas.0506662102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight, R., Maxwell, P., Birmingham, A., Carnes, J., Caporaso, J., Easton, B., Eaton, M., Hamady, M., Lindsay, H., Liu, Z., et al. PyCogent: A toolkit for making sense from sequence. Genome Biol. 2007;8:R171. doi: 10.1186/gb-2007-8-8-r171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontis, N.B., Altman, R.B., Berman, H.M., Brenner, S.E., Brown, J.W., Engelke, D.R., Harvey, S.C., Holbrook, S.R., Jossinet, F., Lewis, S.E., et al. The RNA Ontology Consortium: An open invitation to the RNA community. RNA. 2006;12:533–541. doi: 10.1261/rna.2343206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyngsø, R.B., Pedersen, C.N. RNA pseudoknot prediction in energy-based models. J. Comput. Biol. 2000;7:409–427. doi: 10.1089/106652700750050862. [DOI] [PubMed] [Google Scholar]
- Mathews, D.H., Sabina, J., Zuker, M., Turner, D.H. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J. Mol. Biol. 1999;288:911–940. doi: 10.1006/jmbi.1999.2700. [DOI] [PubMed] [Google Scholar]
- Metzler, D., Nebel, M. Predicting RNA secondary structures with pseudoknots by MCMC sampling. J. Math. Biol. 2008;56:161–181. doi: 10.1007/s00285-007-0106-6. [DOI] [PubMed] [Google Scholar]
- Nussinov, R., Jacobson, A.B. Fast algorithm for predicting the secondary structure of single-stranded RNA. Proc. Natl. Acad. Sci. 1980;77:6309–6313. doi: 10.1073/pnas.77.11.6309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pleij, C.W.A. RNA pseudoknots. Curr. Opin. Struct. Biol. 1994;4:337–344. [Google Scholar]
- Pleij, C.W., Rietveld, K., Bosch, L. A new principle of RNA folding based on pseudoknotting. Nucleic Acids Res. 1985;13:1717–1731. doi: 10.1093/nar/13.5.1717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponty, Y. Modélisation de séquences génomiques structurées, génération aléatoire et applications. Laboratoire de Recherche en Informatique, Université Paris-Sud XI; Paris, France: 2006. Ph.D. thesis, [Google Scholar]
- Poot, R.A., Pleij, C.W., van Duin, J. The central pseudoknot in 16S ribosomal RNA is needed for ribosome stability but is not essential for 30S initiation complex formation. Nucleic Acids Res. 1996;24:3670–3676. doi: 10.1093/nar/24.19.3670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rastegari, B., Condon, A. Parsing nucleic acid pseudoknotted secondary structure: Algorithm and applications. J. Comput. Biol. 2007;14:16–32. doi: 10.1089/cmb.2006.0108. [DOI] [PubMed] [Google Scholar]
- Rietveld, K., Van Poelgeest, R., Pleij, C.W., Van Boom, J.H., Bosch, L. The tRNA-Uke structure at the 3′ terminus of turnip yellow mosaic virus RNA. Differences and similarities with canonical tRNA. Nucleic Acids Res. 1982;10:1929–1946. doi: 10.1093/nar/10.6.1929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivas, E., Eddy, S.R. A dynamic programming algorithm for RNA structure prediction including pseudoknots. J. Mol. Biol. 1999;285:2053–2068. doi: 10.1006/jmbi.1998.2436. [DOI] [PubMed] [Google Scholar]
- Rødland, E.A. Pseudoknots in RNA secondary structures: Representation, enumeration, and prevalence. J. Comput. Biol. 2006;13:1197–1213. doi: 10.1089/cmb.2006.13.1197. [DOI] [PubMed] [Google Scholar]
- Schuwirth, B.S., Borovinskaya, M.A., Hau, C.W., Zhang, W., Vila-Sanjurjo, A., Holton, J.M., Cate, J.H.D. Structures of the bacterial ribosome at 3.5 Å resolution. Science. 2005;310:827–834. doi: 10.1126/science.1117230. [DOI] [PubMed] [Google Scholar]
- Smit, S., Yarus, M., Knight, R. Natural selection is not required to explain universal compositional patterns in rRNA secondary structure categories. RNA. 2006;12:1–14. doi: 10.1261/rna.2183806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stahley, M.R., Strobel, S.A. Structural evidence for a two-metal-ion mechanism of group I intron splicing. Science. 2005;309:1587–1590. doi: 10.1126/science.1114994. [DOI] [PubMed] [Google Scholar]
- Staple, D.W., Butcher, S.E. Pseudoknots: RNA structures with diverse functions. PLoS Biol. 2005;3:e213. doi: 10.1371/journal.pbio.0030213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Studnicka, G.M., Rahn, G.M., Cummings, I.W., Salser, W.A. Computer method for predicting the secondary structure of single-stranded RNA. Nucleic Acids Res. 1978;5:3365–3387. doi: 10.1093/nar/5.9.3365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyagi, R., Mathews, D.H. Predicting helical coaxial stacking in RNA multibranch loops. RNA. 2007;13:939–951. doi: 10.1261/rna.305307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vila, A., Viril-Farley, J., Tapprich, W.E. Pseudoknot in the central domain of small subunit ribosomal RNA is essential for translation. Proc. Natl. Acad. Sci. 1994;91:11148–11152. doi: 10.1073/pnas.91.23.11148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waterman, M.S. Secondary structure of single-stranded nucleic acids. In: Rota G.C., editor. Studies in foundations and combinatorics. Vol. 1. Academic Press; NY: 1978. pp. 167–212. [Google Scholar]
- Xayaphoummine, A., Bucher, T., Thalmann, F., Isambert, H. Prediction and statistics of pseudoknots in RNA structures using exactly clustered stochastic simulations. Proc. Natl. Acad. Sci. 2003;100:15310–15315. doi: 10.1073/pnas.2536430100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, H., Jossinet, F., Leontis, N., Chen, L., Westbrook, J., Berman, H., Westhof, E. Tools for the automatic identification and classification of RNA base pairs. Nucleic Acids Res. 2003;31:3450–3460. doi: 10.1093/nar/gkg529. [DOI] [PMC free article] [PubMed] [Google Scholar]