Abstract
Hydrogen–deuterium exchange experiments have been used previously to investigate the structures of well defined states of a given protein. These include the native state, the unfolded state, and any intermediates that can be stably populated at equilibrium. More recently, the hydrogen–deuterium exchange technique has been applied in kinetic labeling experiments to probe the structures of transiently formed intermediates on the kinetic folding pathway of a given protein. From these equilibrium and nonequilibrium studies, protection factors are usually obtained. These protection factors are defined as the ratio of the rate of exchange of a given backbone amide when it is in a fully solvent-exposed state (usually obtained from model peptides) to the rate of exchange of that amide in some state of the protein or in some intermediate on the folding pathway of the protein. This definition is straightforward for the case of equilibrium studies; however, it is less clear-cut for the case of transient kinetic intermediates. To clarify the concept for the case of burst-phase intermediates, we have introduced and mathematically defined two different types of protection factors: one is Pstruc, which is more related to the structure of the intermediate, and the other is Papp, which is more related to the stability of the intermediate. Kinetic hydrogen–deuterium exchange data from disulfide-intact ribonuclease A and from cytochrome c are discussed to explain the use and implications of these two definitions.
Protein folding pathways traditionally have been described as a series of kinetic intermediates that occur before the formation of the native state (1–4). Intermediates that are of most interest are those that form early in the pathway, because they provide insight into the forces that restrict the conformational space of the unfolded protein at the earliest points in the folding process. These conformational preferences are thought to direct folding along a preferred pathway and thus may contribute to the final native structure attained by that protein. However, the structural properties and kinetic roles of these marginally stable structures are a matter of controversy (3–10).
Evidence for early folding events often is based on spectral changes occurring during the dead time of a fast-mixing experiment (typically a few milliseconds), which can be attributed to the rapid formation of an ensemble of compact states. Although optical spectroscopy can provide useful information on the stability and overall conformational properties of these so-called burst-phase intermediates (11–14), their transient nature and dynamic properties have made it difficult to obtain more detailed structural information. The most promising approach makes use of hydrogen–deuterium exchange labeling on a quenched-flow apparatus with subsequent NMR analysis to probe the formation of hydrogen-bonded structure during folding (15–17). Such hydrogen-exchange competition and pulse-labeling experiments have been the main source of structural information on folding intermediates (reviewed in refs. 18–21).
In a typical pulse labeling experiment, the protein is unfolded in D2O and allowed to refold under conditions where hydrogen exchange is slow (relatively low pH). After a given refolding time, the protein is briefly exposed to H2O buffer at basic pH, where accessible amide groups are rapidly protonated while protected ones remain deuterated. The exchange reaction is then quenched by lowering the pH, and the protein is allowed to refold to the native state. The degree of protonation for individual amide sites is determined by two-dimensional NMR analysis of the refolded protein. By performing a series of such labeling experiments at variable refolding times, it is possible to follow the time course of hydrogen-bond formation during folding for many individual amide groups (all those that are well protected from exchange under native conditions). The pulse-labeling protocol also can be extended to measure protection factors in folding intermediates, which provides unique insight into (local) structural stability (22, 23). Exchange rates in transient intermediates can be measured by systematic variation of the labeling conditions (e.g., a short exchange period at variable pH) at a constant refolding time, and protection factors can be estimated by comparison with the corresponding free-peptide exchange rates (24). In a modified version of this protocol, the labeling pulse is applied directly without a refolding delay, which makes it possible to characterize marginally stable structures that accumulate during the dead time of a quenched flow experiment (25). As in the original competition experiment (15, 26), this burst-phase (or dead-time) labeling method makes use of the competition between refolding and H/D exchange to probe structure formation during early stages of folding.
Protein hydrogen exchange results usually are expressed in terms of protection factors, P = kex(U)/kex(N), where kex(N) and kex(U) represent the rates of exchange for a given amide proton under folded and unfolded conditions, respectively. The exchange rates of fully solvent-exposed amide protons, kex(U), and their dependence on primary structure and solvent conditions are well understood on the basis of model peptide studies (24, 27) and direct measurements on unfolded proteins (28, 29). Although the definition and interpretation of protection factors for conventional exchange studies on folded proteins under equilibrium conditions are straightforward, this concept is less clear-cut in the case of transient states observed in nonequilibrium labeling experiments. In this communication, we discuss the use and definition of protection factors as applied to burst-phase intermediates.
Definition of Protection Factor
For a general discussion of protection factors, we will assume that the refolding pathway of a hypothetical protein can be described by a simple sequential mechanism in which one burst-phase intermediate is populated. Hence, we can write
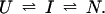 |
1 |
U and N are the unfolded and the native states of the protein, respectively, and I represents an ensemble of intermediate states sequentially populated on the refolding pathway. Without making any assumptions concerning the relative rates of exchange and folding, the most general mechanism for the exchange during the labeling pulse of a hydrogen-exchange labeling experiment can be described as follows,
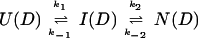 |
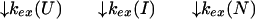 |
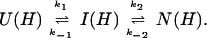 |
2 |
The upper row of the kinetic model represents the refolding of the deuterated protein [indicated by (D)], and the lower row represents the refolding of the protonated protein [indicated by (H)]. The rate constants kx and k−x represent the forward and backward kinetic rates, and the rate constants kex(X) represent the rates for direct exchange from the deuterated species X(D) to the protonated species X(H), probably through local unfolding events.
In describing the protection factors in the burst-phase intermediate I, we define the following two quantities: a structural protection factor,
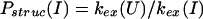 |
3 |
and an apparent protection factor,
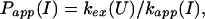 |
4 |
where kapp(I) represents the apparent rate for the appearance of label in I(H) from I(D) through all available pathways including direct exchange and unfolding processes and excluding subsequent folding reactions from the burst-phase intermediate. In other words, exchange can take place from the intermediate or from any other state that is more unfolded than the intermediate. Hence, kapp(I) is derived from the following part of the mechanism of Eq. 2,
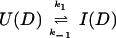 |
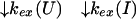 |
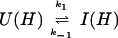 |
5 |
using the following equation,
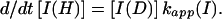 |
6 |
The following general relation can be helpful in calculating kapp when dealing with burst-phase intermediates that are in rapid preequilibrium,
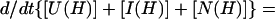 |
7 |
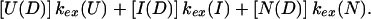 |
Pstruc describes the structure in the intermediate irrespective of the state from which the intermediate folded or toward which the intermediate is proceeding. In other words, Pstruc provides information about the structural stability of a hypothetical equilibrium analogue of the intermediate that is removed from its folding/unfolding pathway. On the other hand, Papp more appropriately describes the structural stability of the intermediate in the context of its folding/unfolding pathway. For the case of a protein in an equilibrium state, a protection factor is simply defined as the ratio of the intrinsic (statistical coil or unfolded) exchange rate to the net exchange rate through all available pathways, including global and local unfolding events. Hence, the apparent protection factor for kinetic intermediates is most similar to the protection factor as defined for equilibrium states. We point out that Pstruc will always be larger than Papp.
Specific Example 1: Ribonuclease A
To provide further understanding of the two definitions of protection factors for kinetic intermediates, we will use the data of Houry and Scheraga (30) as an example. The refolding pathway of the very-fast phase of disulfide-intact ribonuclease A (RNase A) can best be described by the following model,
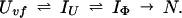 |
8 |
Uvf is the very-fast refolding species, whereas IU is a largely unfolded intermediate and IΦ is a hydrophobically collapsed intermediate. Both IU and IΦ are burst-phase intermediates that are formed within the dead-time of the stopped-flow instrument. We have carried out pulse-labeling experiments on the refolding pathway of Uvf to determine the structure present in IU and in IΦ. The experiment is mainly a competition between folding and exchange. The kinetic model that was used to fit the exchange data is as follows,
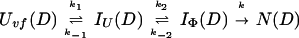 |
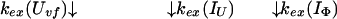 |
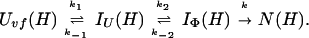 |
9 |
No direct exchange from N is assumed to occur within the time scale of the labeling pulse (which was 20 ms). Furthermore, any back reactions from N are assumed to be negligible under the conditions of the experiment.
By fitting the above model (Eq. 9), we calculated the exchange rates with respect to that of the unfolded species (Uvf), and we defined the protection factor as being the ratio of the exchange rate from Uvf [kex(Uvf)] to that from the intermediate [kex(IU) or kex(IΦ)]. Such a definition would give the structural protection factor (Pstruc, Eq. 3) and not the apparent protection factor (Papp, Eq. 4).
We now derive the relation between Pstruc and Papp for the case of refolding of Uvf (Eq. 9). As discussed by Houry and Scheraga (30), the rapid equilibrium between Uvf, IU, and IΦ is established before formation of N. In other words, k1, k−1, k2, and k−2 ≫ k. Hence, we can write at any time during the labeling pulse,
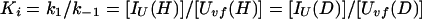 |
10 |
and
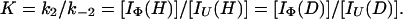 |
11 |
In addition, we have argued that Ki ≫ 1 and that Ki ≫ K. We also calculated that Pstruc(IU) ∼ 1. kapp(IU) is derived from the following part of Eq. 9,
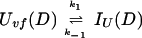 |
 |
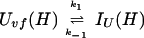 |
12 |
using the equation,
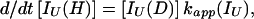 |
13 |
and kapp(IΦ) is derived from the following part of Eq. 9,
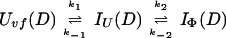 |
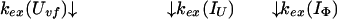 |
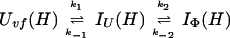 |
14 |
using the equation,
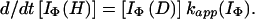 |
15 |
Hence, by using Eqs. 12–15 and the relevant form of Eq. 7, together with the above approximations, it can easily be shown that Papp(IU) = Pstruc(IU) = 1, and
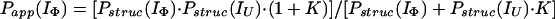 |
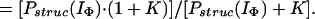 |
16 |
If we consider the limiting case in which there is no direct exchange from IΦ, i.e., Pstruc(IΦ) → ∞, then
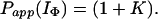 |
17 |
If we consider the other limiting case in which there is no protection in IΦ, i.e., Pstruc(IΦ) = 1, then Papp(IΦ) = 1.
In Houry and Scheraga (30), four categories of protected amides were found in IΦ. As mentioned earlier, the protection factors used were defined as Pstruc and not as Papp. Under the conditions of the experiment, K = 1.3. Hence, by using Eq. 16 to relate Pstruc and Papp, the four categories are:
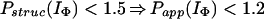 |
18 |
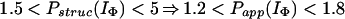 |
18a |
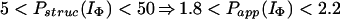 |
18b |
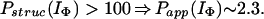 |
18c |
It is important to note that, according to Eq. 17, the maximum value for Papp(IΦ) is 2.3. The range of values for Pstruc is much wider than that for Papp. Consequently, from Eqs. 18a–18d, it can be observed that the information about the structure in IΦ is less clear when presented in terms of Papp.
As can be seen from the above treatment, the mathematical interpretation of Papp is much more involved than that of Pstruc. When the values of kex(I) can be obtained directly, as in the case of the study by Houry and Scheraga (30), then it is easier to use Pstruc to gain insight into the structure present in the intermediates. However, in experiments in which the proton occupancies for the amide protons for a well defined intermediate are measured at different refolding times, the exchange rates obtained are those of kapp and, consequently, Papp is usually calculated to gain insight into the stability of the structure in that intermediate.
Specific Example 2: Cytochrome c
In a recent hydrogen-exchange labeling study on horse cytochrome c (cyt c), J. M. Sauder and H.R. (unpublished data) measured protection factors for about 40 individual amide groups in an early folding intermediate by using the burst-phase competition protocol (25, 31). The competition between hydrogen–deuterium exchange and structure formation during the 2-ms dead time of the quenched-flow experiment was measured as a function of labeling pH under two sets of conditions: (i) strongly native conditions (0.3 M GuHCl, 0.4 M Na2SO4) favoring accumulation of early intermediates (32, 33), and (ii) marginally native conditions (2.5 M GuHCl, 0.4 M Na2SO4) in which intermediates are destabilized and the native state is formed in an approximate two-state transition. The latter was confirmed by fluorescence-detected stopped-flow measurements of the kinetics of folding, which further showed that the stability of the burst-phase intermediate was essentially independent of pH over the range of 7–11 despite significant destabilization of the native state at alkaline pH.
The burst-phase labeling results were interpreted on the basis of a three-state folding mechanism (Eq. 2), where formation of the native structure (or more structured late intermediates) is preceded by a rapid (<ms) preequilibrium involving a marginally stable intermediate, I. Apparent protection factors in I, Papp(I), were calculated according to Eq. 4, by using the parameters of Bai et al. (24) to estimate kex(U). Under destabilizing conditions (2.5 M GuHCl), the pH profiles for 37 of the 40 amide protons observed were in close agreement with the behavior predicted for a statistical coil, yielding Papp(I) = 1. However, the pH profiles for three amide protons (Cys-14, Ala-15, and His-18) were shifted toward basic pH by 1–2.5 pH units, indicating apparent protection factors in the range of 10–300. This observation is consistent with earlier evidence for the presence of residual structure in the vicinity of the His-18 iron ligand and the heme attachment site (Cys-14 and Cys-17), which persists even in the fully denatured state (34). The same three amides also showed unusually high protection under stable conditions (0.3 M GuHCl). To correct for this residual structure effect, the apparent protection factors at 0.3 M GuHCl were divided by those at 2.5 M GuHCl. These corrected protection factors are a measure of the net stabilization from formation of intermediates within the first 2 ms of refolding, independent of residual structure in the unfolded state.
Amide groups with significant protection, Papp(I) ≥ 2, were found primarily in three segments of the backbone (residues 9–14, 60–70, and 94–101), which span the major α-helices of the native structure (35). Several helical core residues (F10, M65, L96, K99, A101) showed protection factors in the range of 5–7, which corresponds closely to the maximum protection, Papp(I) = K + 1 [assuming kex(I) = 0; see Eq. 17], predicted on the basis of the I ↔ U equilibrium constant, K ∼ 4, obtained from the fluorescence-detected burst-phase amplitude (J. M. Sauder and H.R., unpublished data). These observations are consistent with the rapid (<2 ms) formation of a marginally stable intermediate with persistent hydrogen-bonded structure limited to three mutually interacting α-helices. A number of amide groups (especially at the ends of α-helical segments) showed intermediate protection factors in the range of 2–5, indicating that exchange at these sites can occur without complete unfolding of the intermediate. According to Eq. 2, these correspond to sites where kex(I) > 0 [finite Pstruc(I)]. Alternatively, such intermediate protection factors might be interpreted in terms of an expanded mechanism containing additional, less structured intermediates. However, a unique mechanism cannot be obtained, because it is unclear whether such intermediates should be placed on a direct path toward U or off-pathway (36).
The comparison of apparent protection factors with preequilibrium measurements relies on the assumption that k1 ≫ kex(U) (EX2 exchange; ref. 37), which is consistent with the sigmoidal pH dependence for most amide protons observed in the study of J. M. Sauder and H.R. (unpublished data). Moreover, M. C. R. Shastry and H.R. (unpublished data) recently were able to measure the initial rate of folding in cyt c directly, by using a continuous-flow mixing method with submillisecond time resolution (38). The rate observed (2 × 104 s−1) indicates that the EX2 condition should be satisfied up to pH 11.
Conclusions
The definition of protection factors for transient kinetic intermediates is much more involved than that for well defined equilibrium states. We have elucidated mathematically the definition and use of two different types of protection factors for kinetic intermediates, Pstruc and Papp. Pstruc relates more directly to the structure of the intermediates independent of the folding/unfolding processes, and Papp is more closely related to the stability of the intermediates. The relation between Pstruc and Papp can easily be derived for the case of burst-phase intermediates in rapid preequilibrium with the unfolded species.
The definition of Pstruc implies the presence of direct-exchange mechanisms from the intermediate of interest. The exchange mechanisms are not well understood at this time and most probably involve local unfolding events. By varying the time, pH, and solvent conditions of the pulse, more insight might be gained about these exchange mechanisms. Such information may provide insight into the question of whether protein folding proceeds along well defined pathways populating well defined intermediates, or whether protein folding is better described by funnel-shaped energy landscapes (39, 40). In the latter case, Pstruc would reflect the exchange from an ensemble of structures present along a folding funnel. Because it would be less clear-cut to define a stability for those structures, the Pstruc would be a more useful parameter to use than Papp.
Acknowledgments
This work was supported by National Institutes of Health Grants GM-24893 (to H.A.S.), and GM-35926 and CA-06927 (to H.R.), and by an appropriation from the Commonwealth of Pennsylvania to the Institute for Cancer Research.
References
- 1.Kim P S, Baldwin R L. Annu Rev Biochem. 1990;59:631–660. doi: 10.1146/annurev.bi.59.070190.003215. [DOI] [PubMed] [Google Scholar]
- 2.Matthews C R. Annu Rev Biochem. 1993;62:653–683. doi: 10.1146/annurev.bi.62.070193.003253. [DOI] [PubMed] [Google Scholar]
- 3.Roder H, Colón W. Curr Opin Struct Biol. 1997;7:15–28. doi: 10.1016/s0959-440x(97)80004-8. [DOI] [PubMed] [Google Scholar]
- 4.Rothwarf, D. M., Li, Y.-J. & Scheraga, H. A. (1998) Biochemistry, in press.
- 5.Scheraga H A, Konishi Y, Rothwarf D M, Mui P W. Proc Natl Acad Sci USA. 1987;84:5740–5744. doi: 10.1073/pnas.84.16.5740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Baldwin R L. Chemtracts Biochem Mol Biol. 1991;2:379–389. [Google Scholar]
- 7.Fersht A R. Proc Natl Acad Sci USA. 1995;92:10869–10873. doi: 10.1073/pnas.92.24.10869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Creighton T E. Trends Biochem Sci. 1997;22:6–11. doi: 10.1016/s0968-0004(96)20030-1. [DOI] [PubMed] [Google Scholar]
- 9.Eaton W A, Muñoz V, Thompson P A, Chan C-K, Hofrichter J. Curr Opin Struct Biol. 1997;7:10–14. doi: 10.1016/s0959-440x(97)80003-6. [DOI] [PubMed] [Google Scholar]
- 10.Sosnick T R, Shtilerman M D, Mayne L, Englander S W. Proc Natl Acad Sci USA. 1997;94:8545–8550. doi: 10.1073/pnas.94.16.8545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Houry W A, Rothwarf D M, Scheraga H A. Biochemistry. 1994;33:2516–2530. doi: 10.1021/bi00175a022. [DOI] [PubMed] [Google Scholar]
- 12.Roder H, Elöve G A. In: Mechanisms of Protein Folding: Frontiers in Molecular Biology. Pain R H, editor. New York: Oxford Univ. Press; 1994. pp. 26–54. [Google Scholar]
- 13.Evans P A, Radford S E. Curr Opin Struct Biol. 1994;4:100–106. [Google Scholar]
- 14.Kuwajima K. In: Circular Dichroism and the Conformational Analysis of Biomolecules. Fasman G D, editor. New York: Plenum; 1996. pp. 159–182. [Google Scholar]
- 15.Roder H, Wüthrich K. Proteins. 1986;1:34–42. doi: 10.1002/prot.340010107. [DOI] [PubMed] [Google Scholar]
- 16.Udgaonkar J B, Baldwin R L. Nature (London) 1988;335:694–699. doi: 10.1038/335694a0. [DOI] [PubMed] [Google Scholar]
- 17.Roder H, Elöve G A, Englander S W. Nature (London) 1988;335:700–704. doi: 10.1038/335700a0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Roder H. Methods Enzymol. 1989;176:446–473. doi: 10.1016/0076-6879(89)76024-9. [DOI] [PubMed] [Google Scholar]
- 19.Baldwin R L, Roder H. Curr Biol. 1991;1:218–220. doi: 10.1016/0960-9822(91)90061-z. [DOI] [PubMed] [Google Scholar]
- 20.Baldwin R L. Curr Opin Struct Biol. 1993;3:84–91. [Google Scholar]
- 21.Englander S W, Mayne L. Annu Rev Biophys Biomol Struct. 1992;21:243–265. doi: 10.1146/annurev.bb.21.060192.001331. [DOI] [PubMed] [Google Scholar]
- 22.Elöve G A, Roder H. ACS Symp Ser. 1991;470:50–63. [Google Scholar]
- 23.Udgaonkar J B, Baldwin R L. Proc Natl Acad Sci USA. 1990;87:8197–8201. doi: 10.1073/pnas.87.21.8197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bai Y, Milne J S, Mayne L, Englander S W. Proteins. 1993;17:75–86. doi: 10.1002/prot.340170110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gladwin S T, Evans P A. Folding Des. 1996;1:407–417. doi: 10.1016/S1359-0278(96)00057-0. [DOI] [PubMed] [Google Scholar]
- 26.Schmid F X, Baldwin R L. J Mol Biol. 1979;135:199–215. doi: 10.1016/0022-2836(79)90347-4. [DOI] [PubMed] [Google Scholar]
- 27.Connelly G P, Bai Y, Jen M-F, Englander S W. Proteins. 1993;17:87–92. doi: 10.1002/prot.340170111. [DOI] [PubMed] [Google Scholar]
- 28.Roder H, Wagner G, Wüthrich K. Biochemistry. 1985;24:7407–7411. doi: 10.1021/bi00346a056. [DOI] [PubMed] [Google Scholar]
- 29.Robertson A D, Baldwin R L. Biochemistry. 1991;30:9907–9914. doi: 10.1021/bi00105a014. [DOI] [PubMed] [Google Scholar]
- 30.Houry W A, Scheraga H A. Biochemistry. 1996;35:11734–11746. doi: 10.1021/bi961085c. [DOI] [PubMed] [Google Scholar]
- 31.Roder H, Wand A J, Milne J S, Englander S W. Biophys J. 1986;49:57a. [Google Scholar]
- 32.Elöve G A, Chaffotte A F, Roder H, Goldberg M E. Biochemistry. 1992;31:6876–6883. doi: 10.1021/bi00145a003. [DOI] [PubMed] [Google Scholar]
- 33.Colón W, Elöve G A, Wakem L P, Sherman F, Roder H. Biochemistry. 1996;35:5538–5549. doi: 10.1021/bi960052u. [DOI] [PubMed] [Google Scholar]
- 34.Elöve G A, Bhuyan A K, Roder H. Biochemistry. 1994;33:6925–6935. doi: 10.1021/bi00188a023. [DOI] [PubMed] [Google Scholar]
- 35.Bushnell G W, Louie G V, Brayer G D. J Mol Biol. 1990;214:585–595. doi: 10.1016/0022-2836(90)90200-6. [DOI] [PubMed] [Google Scholar]
- 36.Clarke J, Itzhaki L S, Fersht A R. Trends Biochem Sci. 1997;22:284–287. doi: 10.1016/s0968-0004(97)01087-6. [DOI] [PubMed] [Google Scholar]
- 37.Hvidt A, Nielsen S O. Adv Protein Chem. 1966;21:287–386. doi: 10.1016/s0065-3233(08)60129-1. [DOI] [PubMed] [Google Scholar]
- 38.Shastry, M. C. R., Luck, S. D. & Roder, H. (1998) Biophys. J., in press. [DOI] [PMC free article] [PubMed]
- 39.Baldwin R L. J Biomol NMR. 1995;5:103–109. doi: 10.1007/BF00208801. [DOI] [PubMed] [Google Scholar]
- 40.Dill K A, Chan H S. Nat Struct Biol. 1997;4:10–19. doi: 10.1038/nsb0197-10. [DOI] [PubMed] [Google Scholar]


