Behavioral Economic Analysis of Drug Preference Using Multiple Choice Procedure Data

Abstract

The Multiple Choice Procedure has been used to evaluate preference for psychoactive drugs, relative to money amounts (price), in human subjects. The present re-analysis shows that MCP data are compatible with behavioral economic analysis of drug choices. Demand curves were constructed from studies with intravenous fentanyl, intramuscular hydromorphone and oral methadone in opioid-dependent individuals; oral d-amphetamine, oral MDMA alone and during fluoxetine treatment, and smoked marijuana alone or following naltrexone pretreatment in recreational drug users. For each participant and dose, the MCP crossover point was converted into unit price (UP) by dividing the money value ($) by the drug dose (mg/70 kg). At the crossover value, the dose ceases to function as a reinforcer, so “0” was entered for this and higher UPs to reflect lack of drug choice. At lower UPs, the dose functions as a reinforcer and “1” was entered to reflect drug choice. Data for UP vs. average percent choice were plotted in log-log space to generate demand functions. Rank of order of opioid inelasticity (slope of non-linear regression) was: fentanyl > hydromorphone (continuing heroin users) > methadone > hydromorphone (heroin abstainers). Rank order of psychostimulant inelasticity was d-amphetamine > MDMA > MDMA + fluoxetine. Smoked marijuana was more inelastic with high-dose naltrexone. These findings show this method translates individuals’ drug preferences into estimates of population demand, which has the potential to yield insights into pharmacotherapy efficacy, abuse liability assessment, and individual differences in susceptibility to drug abuse.

1. Introduction

For more than a decade, the Multiple Choice Procedure (MCP; Griffiths et al., 1993) has been used in human behavioral pharmacology studies to assess the reinforcing potential of various psychoactive drugs, including pentobarbital (Griffiths et al., 1993), sedative-hypnotics (Mumford et al., 1995; Mintzer and Griffiths, 1998), cocaine (Jones et al., 1999; Lile et al., 2004), methylphenidate (Stoops et al., 2003), d-amphetamine (Alessi et al., 2003), MDMA (Tancer and Johanson, 2007), caffeine (Garrett and Griffiths, 1998; Schuh and Griffiths, 1997), nicotine (Jones et al., 1999), marijuana (Greenwald and Stitzer, 2000), and mu-opioid agonists (Greenwald, 2005; Greenwald, 2006; Greenwald et al., 1999; Greenwald and Hursh, 2006). Using this procedure, participants – who, in part, are selected because they report having used the test drug or similar compound – are administered a dose of the test drug. After experiencing the drug’s effects, each participant completes a structured questionnaire, involving a series of choices between receiving the drug dose (held constant across choices) and a range of money amounts, from near zero to higher money values that are likely to reflect the maximum “street value” of the drug.¹

Using the standard format of the MCP, choices on the questionnaire are followed by at least one reinforcement occasion, in which participants randomly select one of the choices they have made. This provides an actual consequence for the participant’s choices. In other studies, choices are evaluated using self-report but not consequated; in such cases, the money values offer only a proxy measure of a drug’s reinforcing efficacy. Regardless of whether a reinforcement opportunity is provided or whether choices remain hypothetical, the MCP yields an estimate of a drug’s value. At low money values, participants tend to choose drug over money but, as the money alternative values increase, participants switch from choosing drug to selecting money thereafter. This “crossover point” is the money value at which the drug dose ceases to be preferred, and can be conceptualized as the opportunity cost of foregoing drug for the next best available option (Bickel et al., 1993; Bickel et al., 1998).

It may be useful to conceptualize the crossover point within the framework of behavioral economics, which applies consumer demand theory to the experimental analysis of behavior – in this case, drug self-administration (Bickel et al., 1993; Bickel et al., 2000; Hursh, 1993). The behavioral economic approach uses demand curve analysis to examine the relationship between a range of drug unit prices (abscissa) and drug consumption (ordinate) in log-log coordinates. Unit price (UP) provides an overarching, parsimonious independent variable that integrates changes in response requirement and drug dose:

$$\mathrm{UP}=\text{Response Requirement}÷\mathrm{Dose}$$ (Equation 1)

Demand curve analyses show that, as drug price increases, consumption remains relatively constant until a certain point is reached, beyond which consumption decreases more steeply, i.e., becomes positively decelerating. Two slope values characterize the curve: the initially shallow slope at low UPs indicates that the decrease in consumption is proportionally smaller than the increase in UP (demand-inelastic), whereas the steeper slope at higher UPs indicates that the decrease in consumption is proportionally larger than the increase in UP (demand-elastic) (Bickel et al., 1993; Bickel et al., 2000). Hursh and Winger (1995) first developed a normalized exponential regression equation to quantify this positively decelerating function of log₁₀–transformed percent consumption on UP, which was simplified (Greenwald and Hursh, 2006) to be:

$${log}_{10}(C)={log}_{10}(L)\ast exp(-A\ast P)$$ (Equation 2)

In this equation, parameter P is the unit price; parameter L (initial level of consumption) is set to 100% for all experimental conditions (normalized, because participants always chose drug at the lowest UPs); and parameter A (rate of change in slope, or elasticity) is allowed to vary.

An MCP questionnaire that is devised for any given study contains a range of money amounts that function as a non-drug alternative exchange medium, thereby providing a continuum of drug prices. Response requirement is not relevant to calculation of UP in this context; rather, the monetary value of foregoing drug choice becomes an opportunity cost:

$$\mathrm{UP}=(\text{MCP questionnaire money amount})÷\text{Drug dose}\hspace{0.17em}(\mathrm{mg}/70\hspace{0.17em}\mathrm{kg})$$ (Equation 3)

Thus, it is simple to transform MCP money amounts into UPs to generate the range of values of the independent variable. For each MCP questionnaire value for a given dose, the drug is chosen or not, relative to the alternative money amount. Thus, at each UP for each participant, the dependent measure is binary. A central principle in this analysis is that the crossover point is analogous to the UP at which the participant’s consumption of the drug becomes elastic, such that drug choice probability equals one at MCP questionnaire values below the crossover point (i.e., lower UPs) and choice probability equals zero at MCP questionnaire values at and above the crossover point (i.e., higher UPs). If the participant is afforded repeated opportunities to choose a drug at the same UP under differing combinations of doses and money values, then a more finely graded within-subject choice probability measure (ranging from 0 to 1) can be generated. Participants’ choice probability data can then be aggregated to obtain group-average demand curves.

The aim of this study was to determine whether MCP data from disparate behavioral pharmacology studies could be integrated within a behavioral economic framework of drug vs. money preference. It was hypothesized that Equation 3 would be a valid method for transforming MCP questionnaire values into corresponding UPs, and that Equation 2 would provide acceptable logarithmic curve fits of the UP vs. population demand curves. Elasticities of the normalized curves were directly compared across drug conditions from selected studies (which used varying MCP and dosing parameters) to assess whether this method can detect variations in abuse liability of drugs, medication effects, and individual response to the same drug.

2. Methods

2.1 Study Selection

To perform these analyses, it was necessary to have access to the raw data of each study. The author selected several published MCP studies conducted in our laboratory. All studies used within-subject designs and were conducted under double blind conditions. In these experiments, up to three active doses of each drug were administered, and assessed with at least ten MCP money values, so that a large range of UPs could be examined. Variation in the number of UPs across studies enabled an examination of this factor on demand curve fit (R² values). Data for placebo (0 mg) were excluded from analyses because UPs cannot be calculated when the denominator is zero. The studies extend across drug classes (opioids, marijuana and psychostimulants), routes of drug administration (i.e., oral, intramuscular, intravenous and smoked), dosing protocols (i.e., discrete vs. cumulative), subject populations (i.e., dependent and non-dependent), and different numbers of MCP money choices (from 10 to 50) and amounts of money choices (from $0.25 to $100), providing an opportunity to assess the robustness of this procedure and findings across these pharmacological and methodological factors.

Tables 1 and 2 list parameters of the studies that were subjected to analysis. Four experiments tested opioid-dependent research volunteers who were not seeking treatment (see Table 1). In two studies, buprenorphine-maintained volunteers were exposed to different doses of the mu-agonist hydromorphone (HYD; 4, 8 and 16 mg IM in Greenwald et al., 1999; 12 and 24 mg IM in Greenwald and Hursh, 2006) on separate test days; the MCP was completed 3 hr after each injection, i.e., after the peak effect and return to baseline following each dose. In a third experiment (Greenwald, 2005), methadone-maintained volunteers were administered the short-acting mu-agonist fentanyl (0.25, 0.75 and 1.5 mg/70 kg IV) within a single cumulative-dosing session; the MCP was completed 15 min after each infusion, i.e., following the peak effect of each cumulative dose. In a fourth experiment (Greenwald, 2006), outpatient volunteers were administered oral methadone once daily during a two-week induction period. Two groups received different sequence of doses but received some of the same doses on different days (28, 56 and 84 mg); the MCP was completed the morning after the previous day’s dose.

Table 1.

Summary of Opioid Studies Analyzed

Study	N	Drug/Doses/Route	MCP Range (# money values)	UP Range (df)	A parameter Mean (95% CI)	Computed Pmax	R2
1. Greenwald et al. (1999)	14	Hydromorphone 4, 8 and 16 mg IM (during maintenance on 2-8 mg/day SL buprenorphine)	$0.25 – $20.00 (30)	0.016 – 5.0
Heroin User	6			(32)	0.436 (0.396 – 0.477) b	0.665	0.92
Heroin Non-User	8			(18)	1.772 (1.587 – 1.958) d	0.164	0.89
2. Greenwald and Hursh (2006)	13	Hydromorphone 12 and 24 mg IM (during maintenance on 8 mg/day SL buprenorphine)	$0.25 – $25.00 (44)	0.010 – 2.08 (50)	0.518 (0.451 – 0.586) b	0.560	0.80
3. Greenwald (2005)	7	Fentanyl 0.25, 0.75 and 1.5 mg/70 kg IV (during maintenance 60-70 mg/day oral methadone)	$0.50 – $30.00 (18)	0.33 – 120.0 (31)	0.031 (0.028 – 0.033) a	9.355	0.95
4. Greenwald (2006)	34	Methadone 28, 56 and 84 mg/day oral	$1.00 – $100.00 (20)	0.012 – 3.57 (32)	0.871 (0.759 – 0.983) c	0.333	0.88
Rapid Induction	18			(32)	0.846 (0.761 – 0.931) c	0.343	0.92
Stepwise Induction	16			(30)	0.812 (0.718 – 0.905) c	0.357	0.90

Note: Different superscripts indicate that the “A” parameter values significantly differed (p < .05) based on F test.

Table 2.

Summary of Other Studies Analyzed

Study	N	Drug/Doses/Route	MCP Range (# money values)	UP Range (df)	A parameter Mean (95% CI)	Computed Pmax	R2
5. Alessi et al. (2003)	20	d-Amphetamine 5, 10 and 20 mg oral	$0.25 – $20.00 (30)	0.013 – 4.0 (30)	1.382 (1.233 – 1.531) a	0.210	0.84
6. Tancer and Johanson (2007)	8	MDMA 1.5 mg/kg (105 mg/70 kg) oral	$0.50 – $5.00 (10)	0.005 – 0.05 (9)	3.518 (2.517 – 4.520) b	0.082	0.45
	8	MDMA 1.5 mg/kg + fluoxetine 20 mg/day	$0.50 – $5.00 (10)	0.005 – 0.05 (9)	11.070 (7.767 – 14.370) c	0.026	0.44
7. Greenwald and Stitzer (2000)	5	Marijuana 3, 9 and 18 puffs from 3.5% Δ9-THC cigarettes	$0.25 – $64.51 (50)	0.014 – 21.50
		+ naltrexone placebo		(121)	0.308 (0.294 – 0.322) §	0.942	0.94
		+ naltrexone 50 mg		(113)	0.294 (0.275 – 0.313) §	0.986	0.89
		+ naltrexone 200 mg		(132)	0.161 (0.154 – 0.167) †	1.801	0.95

Note:Different superscripts indicate that the “A” parameter values significantly differed (p < .05) based on F test.

Three other studies (see Table 2) involved recreational drug users who did not meet psychiatric criteria for abuse or dependence on any psychoactive substance. In one study (Alessi et al., 2003), individuals consumed d-amphetamine (5, 10 and 20 mg orally) on three separate test days; the MCP was completed 5 hr after each dose. In a second study (Tancer and Johanson, 2007), only one active dose of MDMA was administered (1.5 mg/kg or 105 mg/70 kg orally); however, it was administered on two separate weeks, either following short-term maintenance on fluoxetine (20 mg oral) or its placebo. The MCP was completed 7 hr after MDMA administration. This latter study served as a comparator to d-amphetamine as well as to test the hypothesis that fluoxetine would reduce elasticity of the MDMA demand curve. In another study (Greenwald and Stitzer, 2000), regular marijuana users smoked cumulative doses from 3.5% Δ⁹-THC cigarettes (3, 9 and 18 controlled puffs interspersed with puffs from 0% Δ⁹-THC cigarettes); the MCP was completed about 15 min after smoking each cumulative marijuana dose. In this study, 0, 50 or 200 mg oral naltrexone (administered on different days) preceded these same cumulative marijuana doses.

2.2 Data Analysis

For each study, individual MCP crossover points were converted to UPs using Equation 3. For each participant, the MCP monetary value (dollars) was divided by the drug dose (mg/70 kg), producing the UP at which the dose was no longer chosen. Thus, “0” was entered for this UP and higher UP values to reflect lack of choice. For all lower UP values, the drug was preferred over money and “1” was entered to reflect positive drug choice. For each participant this process was repeated for each drug dose, generating a UP vs. choice probability curve. For duplicate UPs, a within-subject choice probability measure served as the unit of analysis. In some studies analyzed here, there were sometimes two identical UPs, so this probability measure reflected whether the subject chose drug both times (1.0), half the time (0.5), or never (0.0). In the other studies analyzed here, there were sometimes three identical UPs, so this measure reflected whether the subject chose drug over money all three times (1.00), twice (0.67), once (0.33), or never (0.0). Individual-subject data were averaged and multiplied by 100 to obtain mean percent drug choice at each UP.

To re-analyze data from the Greenwald and Stitzer (2000) study, further assumptions were required to estimate the actual smoked Δ⁹-THC dose. Participants smoked puffs from 3.5% Δ⁹-THC-containing cigarettes supplied by the National Institute on Drug Abuse. Using publicly available data on drug extraction from marijuana cigarettes (http://www.druglibrary.org/schaffer/Library/studies/nc/nc1d.htm), each 1.0% Δ⁹-THC cigarette has 5 mg Δ⁹-THC, of which roughly 40% (2 mg) would be extracted if smoked entirely, i.e., accounting for drug lost to side-stream smoke and burning during inter-puff intervals. Thus, it was assumed that each 3.5% Δ⁹-THC cigarette contains 17.5 mg Δ⁹-THC, of which roughly 7 mg would be extracted if smoked entirely. If one assumes there are about 7 puffs per cigarette, then each puff would yield approximately 1 mg. Following these assumptions, there would be a 1:1 correspondence between the number of puffs and the Δ⁹-THC dose (mg) that is delivered when smoking 3.5% Δ⁹-THC-containing cigarettes. Thus, the UP for smoked marijuana doses in this study equaled the MCP value ÷ the number of active cigarette puffs.

GraphPad Prism^® version 4.0 software (www.graphpad.com; GraphPad Software, Inc., San Diego, CA) was used to analyze the data. Unit price (abscissa) and mean percent consumption (ordinate) were plotted on log-log coordinates. Exponential regression (Equation 2) was used to fit the demand curve of mean percent consumption data on UP. When mean percent consumption equaled zero (i.e., by design, none of the subjects chose drug at the highest UPs), data were not analyzed or plotted for these UPs because log₁₀ (0) is not defined. For this reason and due to duplicate UPs (see above), the number of MCP questionnaire money values (i.e., number of unduplicated prices) could differ from the degrees of freedom (i.e., equal to the number of UPs minus 1) in the exponential regressions; see Tables 1-2.) As noted for Equation 2, the parameter L – which is the intercept at low UPs – was held constant at 100% (i.e., all subjects initially chose drug over money at the lowest UP). The parameter A, reflecting rate of change in slope of the curve, was left to vary; thus, each regression solved for this parameter. With parameter L set to 100, the price at unit elasticity (at which slope in log-log space equals −1) – referred to here as computed P_max – is approximated by the simple expression: P_max = 0.29 ÷ A (Greenwald and Hursh, 2006).

Analyses of variance (ANOVAs) in GraphPad Prism^® were used to conduct planned comparisons of the A parameters for selected drugs/conditions. The goal in each case was to determine whether the curve fits were explained by a single parameter (accept null hypothesis) or not (reject null hypothesis) based on goodness-of-fit criteria, i.e., sums of squares of the vertical distances of the data points from the curve. The following planned comparisons were conducted for the opioid studies: (1) between response to HYD in two groups, both maintained on the same buprenorphine doses, that differed in achieving heroin abstinence (Greenwald et al., 1999); (2) between two studies involving different HYD doses and MCP (standard vs. hypothetical) formats (Greenwald et al., 1999; Greenwald and Hursh, 2006); (3) between intramuscular HYD (two buprenorphine studies just noted) and intravenous fentanyl during methadone maintenance (Greenwald, 2005); and (4) between fentanyl during methadone maintenance (Greenwald, 2005) and methadone itself (Greenwald, 2006). Further planned comparisons were conducted for the non-opioid studies: (5) between oral MDMA alone and following fluoxetine pretreatment (Tancer and Johanson, 2007); (6) between MDMA alone (Tancer and Johanson, 2007) and oral d-amphetamine (Alessi et al., 2003); and (7) for smoked marijuana following acute pretreatment with 0, 50 or 200 mg oral naltrexone (Greenwald and Stitzer, 2000). The minimum level of statistical significance was p < .05 for all comparisons.

3. Results

Table 1 and Figure 1 summarize the behavioral economic analytic results for opioid drug condition comparisons (# 1-4). Table 2 and Figure 2 summarize findings for the remaining drug condition comparisons (# 5-7).

Figure 1.

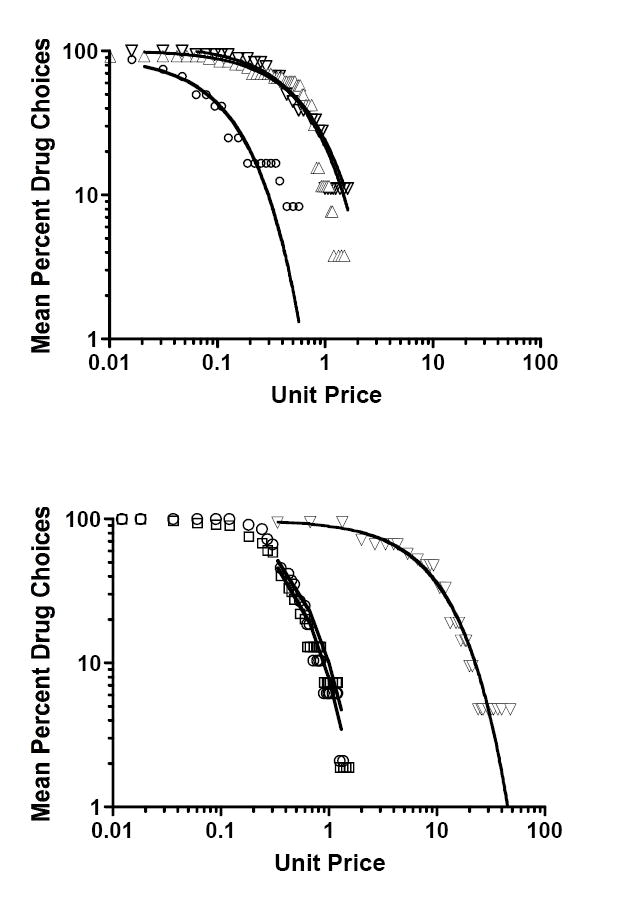
Upper panel: Demand curves based on MCP drug/money choices for intramuscular hydromorphone (HYD) among opioid-dependent outpatient volunteers who either abstained from heroin (○) or continued using heroin (▽) while maintained on buprenorphine (Greenwald et al., 1999); and a second study of IM HYD among buprenorphine-maintained volunteers who continued using heroin before their inpatient admission and experimental testing (▲; Greenwald and Hursh, 2006). Lower panel: Demand curves based on MCP drug/money choices for intravenous fentanyl among methadone-maintained volunteers (▼; Greenwald, 2005), and for oral methadone doses among volunteers who received rapid (□) or stepwise (○) schedules of methadone induction (Greenwald, 2006). See Table 1 for study and analysis parameters and statistically significant differences.

Figure 2.

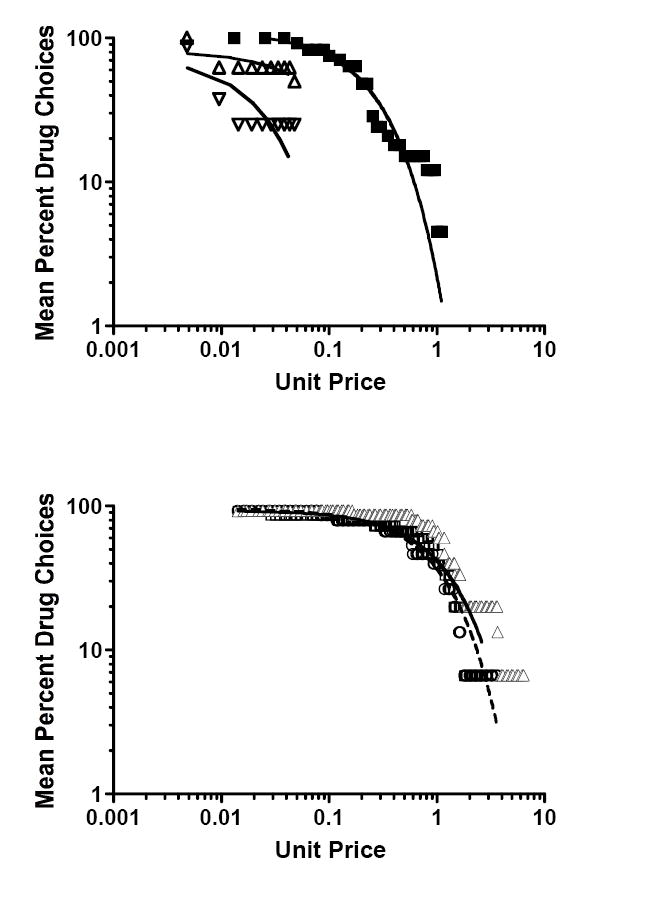
Upper panel: Demand curves based on MCP drug/money choices for oral d-amphetamine (■; Alessi et al., 2003), oral MDMA alone (△) and MDMA during fluoxetine treatment (▽) (Tancer and Johanson, 2007) among volunteers with limited lifetime recreational substance use. Lower panel: Demand curves based on MCP drug/money choices for smoked marijuana in the same volunteers pretreated on separate occasions with 0 mg (--○--), 50 mg (□) or 200 mg (–▲–) oral naltrexone (Greenwald and Stitzer, 2000). See Table 2 for study and analysis parameters and statistically significant differences.

Comparisons 1-2

Demand for hydromorphone (HYD) across a 2.5-log unit range of UPs was much more elastic among outpatient volunteers who stopped using heroin compared to volunteers who continued to use heroin while maintained on buprenorphine (Greenwald et al., 1999), resulting in significantly larger A parameter (F[1,50] = 329.5, p < .0001) and smaller computed P_max values for the non-user group. In a second study of heroin-dependent, buprenorphine-maintained volunteers who did not quit heroin use as outpatients (Greenwald and Hursh, 2006), HYD demand during an inpatient stay was slightly more inelastic but statistically the same (F[1,82] = 3.88, p < .06) as the heroin user group in the Greenwald et al. (1999) study, and significantly more inelastic than the heroin non-users in the earlier study (F[1,68] = 105.7, p < .0001).

Comparisons 3-4

Demand for IV fentanyl in methadone-maintained volunteers (Greenwald, 2005) was the most inelastic of all opioid conditions examined (i.e., very small A parameter and high computed P_max), significantly more so than for all heroin users responding for HYD in the above studies, e.g., relative to Greenwald and Hursh, 2006), F[1,80] = 484.6, p < .0001. Demand elasticity for oral methadone did not significantly differ between the two groups that were randomly assigned to receive different induction dose sequences (Greenwald, 2006), F[1,62] = 0.33, p = .57. Intravenous fentanyl administered to methadone-maintained volunteers (Greenwald, 2005) was significantly more demand-inelastic than methadone alone (Greenwald, 2006).

Comparisons 5-6

Demand for oral MDMA was significantly more elastic (i.e., higher A parameter and smaller computed P_max) compared to d-amphetamine, F[1,39] = 6.34, p < .02. Short-term maintenance on fluoxetine significantly increased elasticity of demand for MDMA, F[1,18] = 29.67, p < .0001.

Comparison 7

Demand for smoked marijuana was statistically similar following pretreatment with placebo or 50 mg oral naltrexone. The high naltrexone dose (200 mg) significant decreased marijuana demand elasticity relative to pretreatment with placebo, F[1,253] = 436.7, p < .0001, and 50 mg naltrexone, F[1,245] = 242.4, p < .0001.

Factors potentially related to curve fit

Due to variation in methodological parameters across studies (see Tables 1-2), Pearson correlations were computed to determine whether the number of subjects (or log₁₀ sample size), number of MCP money values, number of UPs, the difference or sum of MCP money values and UPs, or a product of sample size and degrees of freedom ([log₁₀ sample size] X [number of MCP + UP values]), was related to curve fit (R²) values. To avoid repeat observations (i.e., subgroups within a study that have similar parameters) that could lead to range restriction, only a subset of data in Tables 1-2 was used. While there were no significant correlations with curve fit, the most closely related factor was the number of MCP values (r = 0.49, p = 0.22), followed by the product score above (r = 0.44, p = 0.27).

4. Discussion

The present study offers a novel method to convert drug vs. money choices from the Multiple Choice Procedure (Griffiths et al., 1993) or from similar procedures into behavioral economic demand curves, and compares findings from previous studies to establish the utility of this method. The technique developed here maps each subject’s MCP crossover point into a choice probability measure at each unit price (a ratio of the MCP questionnaire money value divided by the drug dose). Choice probability data are averaged across participants to yield a normalized population demand curve that is analyzed using non-linear regression, as first described by Hursh and Winger (1995).

In a recent study of heroin-dependent, buprenorphine-maintained volunteers (Greenwald and Hursh, 2006), the present analysis shows that HYD demand elasticity was not statistically different from the heroin-using, buprenorphine-maintained subgroup in the Greenwald et al. (1999) study. This replication is noteworthy because – like the heroin-using subgroup in that study – none of the participants in the Greenwald and Hursh (2006) study achieved drug abstinence as outpatients before being admitted to an inpatient unit to complete the drug vs. money choice procedure. Because similar groups of individuals from independent studies responding to the same drug produced the same behavioral economic profile, this adds confidence to the usefulness of this data-analytic procedure. Interestingly, these two studies used different HYD doses (see Table 1), so these overlapping curve fits attest that HYD demand is functionally equivalent, i.e., drug consumption is the same at a given UP, regardless of the cost (numerator) and doses (denominator) that comprise UP (Bickel et al., 1991; DeGrandpre et al., 1993; Greenwald and Hursh, 2006). This same functional equivalence was also found in the present analysis for methadone, when comparing two groups of subjects who received different induction dose sequences (Greenwald, 2006).

Furthermore, in the Greenwald et al. (1999) study, individuals who stopped using heroin while receiving buprenorphine relative to those who continued using heroin demonstrated significantly greater HYD demand elasticity. In that original study, analysis of variance revealed a significant Group X HYD dose interaction for MCP crossover points, such that the groups showed different HYD dose-response sensitivities. Indeed, a linear interaction from ANOVA would be expected to produce differences in normalized demand elasticity (different slope parameters) in behavioral economic analyses, due to the manner in which linear functions are mapped into non-linear (log-log) space and because the intercept at low UPs is constrained to 100 percent. The present finding thus confirms this expected pattern and provides a statistical context for converting MCP values into UP/consumption space. Furthermore, this finding is important because it establishes that this data conversion method may be used to interpret individual differences in response to drugs of abuse, e.g., individual differences in vulnerability to drug use such as family history, behavioral traits, and genetic polymorphisms.

The present analysis compared normalized demand for hydromorphone (Greenwald and Hursh, 2006) with fentanyl (Greenwald, 2005), a mu-opioid with at least 10 times greater analgesic potency than HYD (Reisine and Pasternak, 1996). Normalized demand curves remove differences in Y-intercept (demand intensity) between drugs due to differences in relative potency (Hursh and Winger, 1995). However, there were two other parametric differences between these studies. First, the route of HYD administration was intramuscular whereas fentanyl was intravenous. Second, each HYD dose was administered as a bolus injection on separate days, whereas fentanyl doses were infused during a single session using a cumulative-dosing protocol. The present analysis found that HYD demand was far more elastic than for fentanyl. Due to the methodological differences across studies, it is not yet possible to conclude whether the pharmacokinetics of these two drugs and/or the different routes of administration account for this finding. Specifically, the rapid onset of fentanyl and its IV delivery could each potentiate its inelasticity, relative to HYD given intramuscularly. Interestingly, Abreu et al. (2001) found that faster IV infusion rates of HYD produced greater self-reported estimates of the street value of the drug; however, because a drug vs. money choice procedure was not used in that study, those data could not be subjected to the behavioral economic analysis described here. In preclinical studies it has been shown that ketamine, an NMDA antagonist with a rapid onset of action, produces more inelastic demand than dizocilpine, another NMDA antagonist with a slower onset of action (Winger et al., 2002). This issue of rate of drug onset influencing abuse liability is an important theme, and could be addressed by conducting a study that directly compares MCP data or behavioral economic demand for the same drug when given by different routes of administration. This method could also be used to evaluate different formulations of the same drug that are expected to have more rapid versus slower rates of onset (Mansbach and Moore, 2006; McColl and Sellers, 2006).

The present method was shown to be useful in detecting changes in elasticity in drug demand as a function of pretreatment with putative medications. Specifically, fluoxetine increased MDMA elasticity, which is the desired treatment effect; in contrast, high-dose (but not low-dose) naltrexone decreased marijuana elasticity, which is an undesirable treatment effect. Interestingly, analysis of variance of the MCP crossover points in the latter study did not produce a significant Marijuana dose X Naltrexone dose interaction (Greenwald and Stitzer, 2000). This demonstrates that the procedure is sensitive to both positive and negative pharmacotherapy outcomes, can detect dose-related differences (perhaps more so than ANOVA), and thus has the ability to complement other assessment methods as part of medication development studies.

Further applications of this approach include the following. First, the present analysis included three studies that employed the standard format of the MCP involving one or more “lottery” sessions of intermittent reinforcement of questionnaire choices (Alessi et al., 2003; Greenwald et al., 1999; Tancer and Johanson, 2007) and four studies that assessed hypothetical choices without an associated lottery reinforcement session (Greenwald, 2005; Greenwald, 2006; Greenwald and Hursh, 2006; Greenwald and Stitzer, 2000). These methodological differences preclude a systematic evaluation of the influence of MCP format (standard vs. hypothetical) on the nature of the demand curve. This is a limitation of the present analysis because one cannot assume that verbal reports of drug choices correspond to reinforced behavioral choices. On the other hand, this raises the opportunity to compare these two modes of MCP administration to determine whether elasticity estimates for the same drug are similar. This would provide data pertaining to the utility of this analytic method. On the other hand, the present analysis demonstrated functional equivalence of HYD demand (i.e., statistically similar elasticity) across two studies that used different HYD doses and different MCP formats (Greenwald et al., 1999; Greenwald and Hursh, 2006). While these preliminary data suggest the potential for these different MCP formats to be consistent with one another, it remains to be seen whether this would hold true across a range of experimental parameters. Second, the MCP has been used in some abuse liability studies and could be incorporated as part of a standard assessment battery (Griffiths et al., 2003). Namely, one could convert MCP data as described here to measure a drug’s price-elasticity and whether the A parameter captures its abuse liability profile relative to other compounds, and/or predicts abuse of the drug as determined in post-marketing surveillance studies. Third, clinical interventions such as take-home medication doses or dose increases have been evaluated using the MCP (Kidorf et al., 1995). Accordingly, it would be possible to use the MCP to measure the value of a clinical intervention (e.g., voucher), and whether it modifies drug price-elasticity. It is hoped that these and other uses of this procedure could improve the analytic strength of human laboratory models and our understanding of multiple processes involved in drug dependence.