The theoretical limits of DNA sequence discrimination by linked polyamides

Abstract

Linked polyamides bind in the minor groove of double-stranded DNA in a partially sequence-specific manner. This report analyzes the theoretical limits of DNA sequence discrimination by linked polyamides composed of two to four different types of heterocyclic rings, determining (i) the optimal choice of base-binding specificity for each ring and (ii) the optimal design for a polyamide composed of these rings to target a given DNA sequence and designed to maximize the fraction of the total polyamide binding to the specified target sequence relative to all other sequences. The results show that, fortuitously, polyamides composed of pyrrole, a naturally occurring G-excluding element, and imidazole, a rationally designed G-favoring element, have features similar to the theoretical optimum design for polyamides composed of two different rings. The results also show that, in polyamides composed of two or three types of heterocyclic rings, choosing a nonspecific “placeholder” ring, which binds equally strongly to each of the four bases, along with one or two base-specific rings will often enhance sequence specificity over a polyamide composed entirely of base-specific rings.

Linked polyamides are currently the most promising compounds for the creation of bioavailable sequence-specific DNA-binding molecules for use in chemotherapy and biosensing (1). These compounds are composed of two linked polyamide chains, analogous to the antibiotics netropsin and distamycin, running side-by-side and antiparallel down a widened minor groove of B-DNA, with a polyamide ring packed tightly against each DNA base, as diagrammed in Fig. 1. Pyrrole-imidazole polyamides, with either a hairpin linkage (2) or a central “stapled” linkage (3), bind in the minor groove of DNA in a partially sequence-specific manner. Pyrrole is the naturally occurring G-excluding element of netropsin and distamycin (4, 5), and the imidazole ring was first proposed as a G-reading element based on the structures of 1:1 polyamide:DNA complexes (6–8). Footprinting analysis has demonstrated the pairing rules for these rings in hairpin-linked polyamides: imidazole–pyrrole pairs bind strongly to GC bp and, by symmetry, pyrrole–imidazole pairs bind to CG, whereas pyrrole–pyrrole pairs are degenerate, binding strongly to both AT and TA (9). NMR (10–12) and crystallographic (13–15) analyses have revealed the specific steric and hydrogen bonding interactions that mediate this specificity.

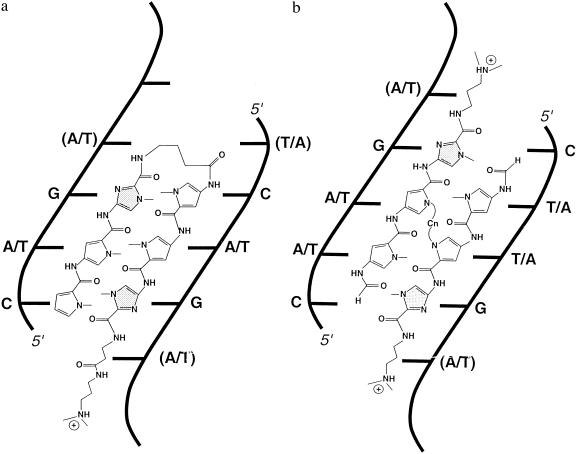
Figure 1.

Linked polyamides comprised of imidazole and pyrrole rings have been synthesized by using two methods: with a hairpin linkage (a) or stapled through a central linkage (b). When bound in the DNA minor groove, the amide groups form hydrogen bonds with the bases, positioning the heterocyclic rings directly adjacent to the edges of the bases. Hydrogen bonding and steric contacts between the rings and the bases give each ring its particular base specificity. The molecules shown here contain two imidazole rings (stippled) and four pyrrole rings (unstippled). The hairpin-linked polyamide binds to sequences of the form C-A/T-G, where A/T refers to degenerate binding to either adenine or thymine. The stapled polyamide with the same rings will bind with a shifted phasing of the rings to sequences of the form C-A/T-A/T-G. In both cases, the actual target sequence will include an additional A/T bp at each end (in parentheses), which is recognized by atoms in the tails and linkers of the polyamides.

This report analyzes the theoretical limits of DNA sequence discrimination by linked polyamides composed of two to four different types of rings, each preferentially binding to a different base. An ideal sequence-reading polyamide, or “lexitropsin” (6–8), with full base-reading ability would be built from four different types of rings, each binding specifically to one of the four DNA bases. Unfortunately, such hyper-specific rings have not been discovered and given the close similarity of the minor groove faces of the two pyrimidines, may never be discovered. This report examines the optimal design of polyamides composed of less than this perfect complement of rings, which were chosen to maximize the fraction of polyamide bound to the target DNA sequence. Two design issues are addressed: (i) the optimal choice of base-binding specificity for each ring, and (ii) the optimal polyamide composed of these rings designed to target a given DNA sequence. A full mathematical analysis will be presented in a separate publication; this report presents the major implications for polyamide design.

METHODS

Linked polyamides bind in the minor groove of DNA such that each ring contacts primarily a single base. Each base pair is thus contacted by two polyamide rings, one from each of the two side-by-side polyamide chains (see Fig. 1). An individual ring will be denoted as R_N with the subscript denoting the particular specificity of the ring, such as R_A for an adenine-specific ring. It will be assumed that these rings bind strongly to their target base, and equally poorly to the three nontarget bases, with the difference in binding free energy denoted as δ_N, where N again denotes the specific base. Thus, for an adenine-specific ring R_A:

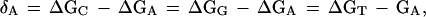1

where ΔG_N is the free energy of binding of a given ring to base N. The notation R_NR_N will refer to a pair of rings that bind side-by-side in the minor groove to a given base pair; for instance, R_AR_T is a pair of rings that bind preferentially to an AT bp. The representation (R_N1,...,R_Nm) will refer to an entire polyamide composed of a given set of m base-specific rings; for instance, an (R_G, R_A) polyamide is composed of two types of ring, one specific for G and one specific for A.

The sequence discriminatory ability of each polyamide will be evaluated using three assumptions. First, the binding free energy will be approximated as a linear sum of binding energies for each individual ring with a single DNA base. This approximation has worked well in a study of experimentally determined binding constants of polyamides with pyrrole and imidazole rings (16). In long pyrrole–imidazole polyamides, however, a slight mismatch between the contour length of the polyamide and the contour length of the DNA minor groove causes the rings to get “out of phase,” and binding does not improve for polyamides with greater than ≈5 units (17). This issue has been addressed previously in connection with polyamide design (18), and methods have been reported to restore proper phasing by incorporating spacers into long polyamides (19). Hence, the effects of phasing mismatch will be neglected in this work. Second, any interference from competitive binding of overlapping binding sites will be neglected. Third, all sequences will be assumed present with equal frequency in the genome.

Given these assumptions, the fractional occupancy of the i^th n-bp DNA site (θ_i,n, where i ranges from 1 to 4ⁿ and i = 1 corresponds to the target sequence) is calculated with the following Hill equation:

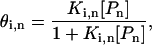2

where K_i,n is the binding constant and [P_n] is the concentration of polyamide with length n. (Note: polyamides are denoted by the length of DNA contacted by the rings; a P_n polyamide is comprised of 2n rings that bind to n consecutive base pairs. As seen in Fig. 1, the charged tails and linkers, which are not addressed in the current work, will recognize an additional AT bp at each end of the linked polyamide.). The binding fraction ψ_n, the ratio of the occupancy of the target site relative to that of all possible n-bp sites, is calculated as:

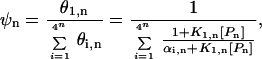3

where α_i,n = K_1,n/K_i,n = exp[−(ΔG_1,n − ΔG_i,n)/RT] and ΔG_i,n is the free energy of binding of the polyamide to the i^th n-bp site. The parameter α_i,n is a function of the relative number of mismatches between the polyamide with the target sequence compared with the number of mismatches with the i^th nontarget sequence and is a function of the energetic cost (δ_N) of each of these mismatches. The binding fraction ψ_n ranges between 0 and 1 and larger values indicate more specific binding to the target sequence relative to the nontarget sequences.

In cases where the target sequence is bound at least as favorably as all other sequences, two limits on the binding fraction may be evaluated. As the ligand concentration increases, ψ_n decreases monotonically to a value of ¼ⁿ, and all of the DNA sequences become equally saturated. Conversely, at low polyamide concentrations, the binding fraction approaches the upper limit:

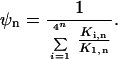4

RESULTS AND DISCUSSION

The analysis below examines three increasingly complex cases: case 1 analyzes an A/T DNA target with polyamides containing only two types of rings; case 2 analyzes a general sequence A/T/C/G DNA target and a polyamide with two types of rings; and case 3 analyzes a general-sequence target with polyamides composed of three types of rings. In each case, there are two design issues. First, the optimal choice of base-binding specificity for each ring is determined by exhaustive search of the unique combinations. Second, the optimal design for a polyamide composed of these rings to target a given DNA sequence is determined by deriving upper bounds on the binding fraction (ψ_n) for specified target sequences and then determining relationships among the binding specificities (δ_N) of the chosen set of rings that permit these bounds on ψ_n to be achieved. Where possible (as in case 1), the obvious design choice is made, associating each base along the target DNA sequence with the polyamide ring that it prefers. But when the number of ring choices is less than the number of unique bases in the target sequence (as in cases 2 and 3), then one or more bases will lack a preferentially binding ring. Strategies developed for placement of rings adjacent to these bases turn out to be nonobvious and even counter-intuitive.

Because of the assumption that each polyamide ring interacts with a single DNA base, the unique characteristic for each target sequence in this study is its base content—the number of AT bp and the number of GC bp—and not its specific base sequence. Reshuffling a base sequence would only require a concomitant reshuffling of the polyamide ring sequence. Thus, an optimal choice of rings to target a sequence composed of 1-GC and 4-AT bp will apply equally well to the target sequences AGAAA, TACAT, ATATG, and others, assuming the proper rearrangement of rings within each polyamide. For brevity, a sequence such as AAAAG will represent the 2⁵ × 5 = 160 different target sequences with 1-GC and 4-AT bp.

Case 1: A/T Target and Polyamides with Two Types of Rings.

The simplest case limits the target to a sequence composed of only AT bp, within a mixed sequence genome, and limits the design of the polyamides to two types of ring. Ring specificity can be chosen in three different ways: (i) One ring binds preferentially to adenine and the other to thymine; (ii) One ring recognizes one of the bases in an AT bp, and the other ring prefers one of the bases in a GC bp; and (iii) One ring prefers cytosine and other prefers guanine.

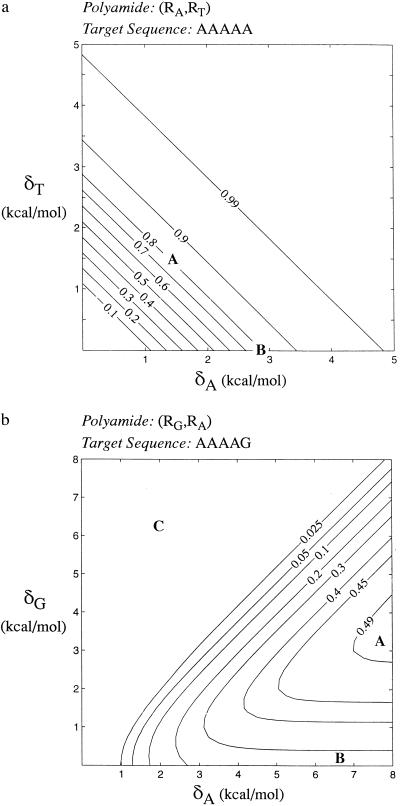
The third choice may be discarded outright given the A/T DNA target. The first choice, an (R_A, R_T) polyamide, obviously is preferable. A polyamide with R_A next to each adenine and R_T next to each thymine will bind more tightly to the target sequence than to any nontarget sequence. Provided that the base specificity of the two rings is high enough (i.e., both δ_A and δ_T are large), ψ_n approaches one and near perfect base discrimination is possible. Fig. 2a shows isocontours of the binding fraction for different values of binding strengths δ_A and δ_T. Points along the δ_A = δ_T diagonal indicate an ideal choice of rings, providing a maximal fraction of binding to the target sequence given minimal base specificities for each polyamide ring.

Figure 2.

Binding fraction for polyamides composed of two different types of rings. (a) For polyamides composed of a ring that recognizes adenine and a ring that recognizes thymine, target sequences composed of only AT bp may be recognized with a binding fraction close to one for rings with strong base specificity. A given level of binding may be obtained with an adenine-specific ring and a thymine-specific ring of identical specificity (point marked “A”) or with a placeholder and an adenine-specific ring of twice that strength (“B”). (b) For polyamides composed of a ring that recognizes adenine and a ring that recognizes guanine, binding to a sequence with 4-AT and 1-GC bp, the maximal binding fraction is 0.5. To achieve this fraction, the polyamide must be designed from a strong adenine-specific ring and a weaker guanine-specific ring (“A”). If the guanine-specific ring is replaced by a placeholder, the maximal binding fraction drops to 0.25 (“B”). If the guanine-specific ring is stronger than the adenine-specific ring, the binding fraction drops to close to zero (“C”).

Surprisingly, strong base discrimination also is possible with the second choice of rings, with one ring recognizing one of A or T and the other recognizing one of C or G, given particular values of the binding specificities. Consider an (R_A, R_G) polyamide, composed of rings specific for adenine and rings specific for guanine. Near perfect target recognition is possible if the specificity of R_A for adenine is much stronger than the specificity of R_G to guanine. The optimal polyamide design would place R_AR_G at each AT bp, with R_A adjacent to the adenine. Target discrimination improves as the binding specificity of the R_G ring is reduced to zero, effectively becoming an R₀-placeholder ring that binds equally well to all four bases. One of the surprising findings of this work, also encountered in the two following cases, is that the optimal choice of rings will often include a placeholder in place of a base-specific ring. The performance of a polyamide composed of R_A and a completely nonspecific placeholder R₀ may be seen in Fig. 2a as points along the horizontal axis (that is, changing R_T into R₀ by setting δ_T to zero). It is apparent that, to achieve the same binding fraction, each ring in an (R_A, R_T) polyamide need only have one-half the binding specificity of the R_A ring in an (R_A, R₀) polyamide.

Case 2: General Sequence Target and Polyamides with Two Types of Rings.

Now consider a target containing a mixed sequence of AT bp and GC bp and polyamides with two different types of rings. Again, there are three ways of matching rings to bases: (i) an (R_A, R_T) combination, (ii) the four mixed combinations (R_A, R_G), (R_A, R_C), (R_T, R_G), and (R_T, R_C), and (iii) an (R_C, R_G) combination.

When faced with a general sequence target containing some GC bp, (R_A, R_T) polyamides provide only limited specificity. The optimal polyamide design places the ring pair R_AR_T at each AT bp in the target, but the choice of rings to bind to GC bp is not obvious. Any choice for pairing of these rings with GC will result in a polyamide that binds to many nontarget sequences as least as favorably as to the target sequence. The best compromise is to choose the ring with the minimum specificity, for instance, R_T if δ_T < δ_A, and place two of these next to each GC bp. Indeed, the binding fraction is maximized when the specificity of this weaker ring is reduced to zero, becoming a placeholder unit. An effective design places R_AR₀ with each AT and R₀R₀ with each CG in the target sequence. Because R₀R₀ binds to all base pairs equally, the upper bound on ψ_n is ¼^n_G, where n_G is the number of GC bp in the sequence. This discussion applies similarly to (R_C, R_G) polyamides, which will be compromised by the number of AT bp in the target sequence.

Mixed polyamides, with one ring recognizing one of adenine or thymine and the other recognizing one of cytosine or guanine, fare better. For example, consider an (R_A, R_G) polyamide with δ_A > δ_G. The highest binding fractions are obtained with a strongly base-specific R_A and a weaker R_G, such that δ_A-δ_G is large, but δ_G is also large. The best design places R_AR_G with each AT bp, where the R_G acts as a placeholder on the thymine side, because δ_A is significantly larger than δ_G. A pair of R_G rings is placed next to each GC bp. Because δ_G is large, the R_GR_G rings exclude AT bp, but the two identical rings cannot distinguish GC from CG bp. This redundancy leads to an upper limit of the binding fraction of ½^n_G. The target sequence AAAAA would be recognized perfectly. One-half of the polyamides designed to target AAAAG would bind correctly, the other one-half binding erroneously to AAAAC. Targets with additional GC bp diminish the binding fraction still further, until the worse case of GGGGG, in which only ≈3% of the polyamide binds to the target sequence in the best possible case.

Fig. 2b presents isocontours of the binding fraction for various values of R_A and R_G to a 5-bp sequence with 1-GC bp, AAAAG in our shorthand notation. Note that this discussion applies to many other mixed combinations: for example, a polyamide with a strong G discriminator and a weaker A discriminator would have symmetrically similar behavior, binding to G/C-rich sequences with greater specificity than A/T-rich sequences with an upper limit of the binding fraction of ½^n_A.

Serendipitously, the imidazole and pyrrole rings currently used in polyamides are similar to the (R_G, R₀) combination. The imidazole ring acts as the R_G ring, showing a binding energy ≈1.1 kcal/mol stronger to guanine than to adenine, cytosine, or thymine. Pyrrole acts like a placeholder, binding to adenine, cytosine, and thymine with similar affinity, but has a guanine-excluding ability, disfavoring binding to guanine by 1.9 kcal/mol (16). Pyrrole might be termed an R_ACT ring. Pyrrole/imidazole polyamides show improved discrimination relative to a true (R_G, R₀) combination, because of the GC-excluding ability the pyrrole–pyrrole pairs, but still show poor discriminatory ability with A/T-rich sequences, caused by the ambiguity of AT bp recognition by pyrrole–pyrrole pairs.

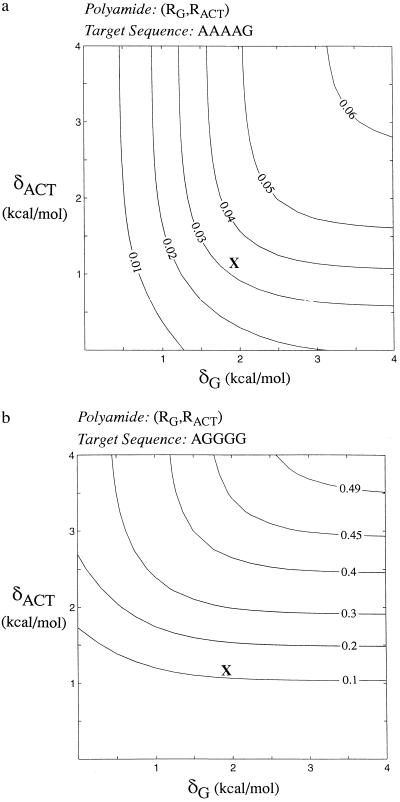
For an (R_G, R_ACT) polyamide with strongly specific rings, the upper bound of the binding fraction is ½^n_A. Pyrrole and imidazole rings, however, do not have binding strengths high enough to reach this limit. Based on binding constants from Walker et al. (16), only ≈3% of the polyamide will bind specifically to a target sequence composed of 4-AT and 1-GC bp, at a concentration that saturates one-half of the target sites, as compared with the theoretical upper limit of 6.25%. This situation is plotted in Fig. 3a. Pyrrole/imidazole polyamides perform better with G/C-rich sequences: for a sequence with 1-AT and 4-GC bp, 12% of the polyamide will bind to the target sequence (upper limit: ψ_n = ½¹ = 50%), as seen in Fig. 3b. For sequences composed entirely of GC bp, the percentage rises to 18% (upper limit: 100%).

Figure 3.

Binding fraction for polyamides composed of imidazole- and pyrrole-type rings. (a) Binding to a sequence with 4-AT and 1-GC bp. (b) Binding to a sequence with 1-AT and 4-GC bp. The value for the optimal polyamide composed of pyrrole and imidazole rings, with imidazole placed next to each guanine and pyrrole next to adenine, cytosine, or thymine in the target sequence, is shown with an “X.”

Case 3: General Sequence Targets and Polyamides with Three Types of Rings.

Polyamides composed of only two types of rings, as discussed above, cannot provide the specificity needed to bind selectively to a given mixed sequence DNA target. A third type of ring must be added to allow design of polyamides to bind to any arbitrary sequence with a maximal binding fraction approaching one. For analysis of polyamides composed of three types of rings, the specificity of the three rings is ordered such that δ₁ ≥ δ₂ > δ₃ > 0. There are two unique ways to choose the rings: (i) the two most specific rings recognize bases in the same base pair, such as the combination δ_A ≥ δ_T > δ_G > 0; and (ii) the two most specific rings recognize bases in different base pairs, such as δ_A ≥ δ_G > δ_T > 0.

For the first of these two choices, in which the two most specific rings recognize bases in the same base pair, consider the combination (R_A, R_T, R_G) where δ_A ≥ δ_T > δ_G > 0. The rings R_AR_T can be used to recognize AT bp in the target sequence with strong specificity, but the choice for GC bp is not as obvious. The best choice is to place an R_GR_G pair at each GC bp, giving some specificity of GC over AT bp, but failing to discriminate GC vs. CG inversions. Using R_GR_A or R_GR_T to bind to GC bp is a poorer strategy because these ring choices will bind to AT bp with higher affinity than GC bp. The upper limit of ψ_n with this design is ½^n_G, in which n_G is the number of GC bp in the target sequence. Thus, surprisingly enough, the addition of a third ring in this combination does not add specificity over an optimal two-ring combination.

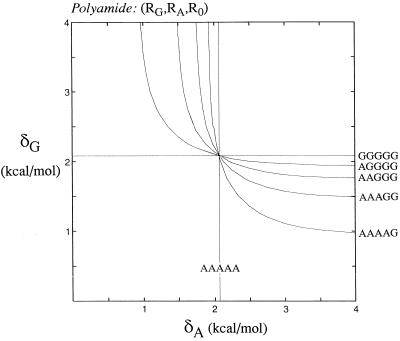
For the second of the two choices of rings, in which the two most specific rings bind to bases in different base pairs, consider an (R_G, R_A, R_T) polyamide where δ_G ≥ δ_A > δ_T > 0. The optimal design pairs R_AR_T with AT and pairs R_GR_T with GC. For values where δ_G > δ_A ≫ δ_T, the binding fraction approaches one, and near perfect discrimination is possible. Note that the R_GR_T ring pair will bind strongly to GC and also weakly to AT bp; this nonspecific binding may be minimized by keeping δ_T low. This is a surprising result: the use of a placeholder and two base-specific rings substantially improves the specificity over a polyamide composed of three different base-specific rings. Fig. 4 plots ψ_n = 0.5 contours for binding of an (R_G, R_A, R₀) polyamide to five different sequences with different base content, from all A/T to all G/C. The curves cross at the δ_A = δ_G diagonal, indicating the design for an ideal multifunctional polyamide comprised of an effective adenine-discriminating ring, an equally effective guanine-discriminating ring, and a placeholder ring. This design will allow the creation of polyamides to target A/T-rich sequences as well as G/C-rich sequences. Note that this discussion also applies to the other choices possible in this second case, including three other polyamide designs (R_G, R_T, R₀), (R_C, R_A, R₀), and (R_C, R_T, R₀).

Figure 4.

Performance of polyamides composed of an adenine-specific ring, a guanine-specific ring, and a placeholder ring. Contours of 0.5 for the binding fraction are shown for sequences with different AT and GC content. The best choice for a multifunctional set of rings is at the point where the curves cross, with adenine- and guanine-specific rings of equal strength.

The addition of a placeholder ring significantly improves the sequence specificity of a polyamide design. Comparing the (R_G, R_A, R₀) polyamide in Fig. 4 with the (R_G, R_A) polyamide in Fig. 2b illustrates some of the advantages. To bind to the target sequence AAAAG with a binding fraction of ≈0.5, the rings in the (R_G, R_A) polyamide must have strong specificity: specificity for adenine must be >7 kcal/mol, and specificity for guanine must be >3 kcal/mol. Upon adding a placeholder ring, however, the specificity needed to achieve the same binding fraction drops to ≈2 kcal/mol for both rings. Moreover, the (R_G, R_A, R₀) polyamide also may approach perfect target recognition, given strong enough base specificity, whereas the upper limit of specificity for the (R_G, R_A) polyamide is 0.5. But perhaps the most attractive feature of the (R_G, R_A, R₀) polyamide is its generality: with these three rings, effective polyamides may be designed to target sequences with widely different base content.

Polyamide Length and DNA Sequence Discrimination.

An additional design issue involves the optimal polyamide length for targeting a given DNA sequence. Assume that there is a specific sequence to be targeted in a genome, such as AAAGAAAA. Two opposing considerations affect the choice of polyamide length. On one hand, a short sequence will have far fewer competing sequences of the same length: a 4-bp sequence has 4⁴–1 = 255 competing sequences, whereas a 5-bp sequence has 4⁵–1 = 1,023. A small affinity for nonspecific sites will have a greater harmful effect with longer sequences. On the other hand, longer sequences add additional specificity to the target: if the target is AGAAAA, a short polyamide targeted to AGAAA will bind to the target but also to AGAAAC, AGAAAT, and AGAAAG, whereas the longer polyamide will bind specifically only to the target. Taking this second consideration—that longer sequences are found less frequently in a given genome—into account, the shorter polyamide will be preferred if ψ_n/ψ_n+1 > 4.

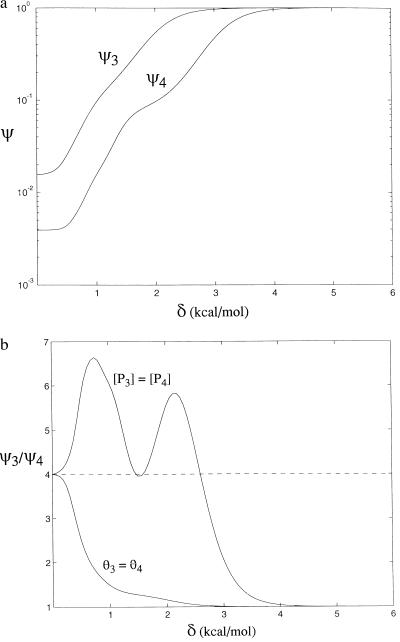
Surprisingly, when comparing equal concentrations of polyamides of two different lengths, a shorter polyamide will often perform better. Compare the case of two ideal polyamides, P₃ and P₄, that are composed of four different types of rings, R_A, R_T, R_G, and R_C, such that δ_A = δ_T = δ_G = δ_C = δ. Each ring is placed next to its preferred base in the target sequence and the binding fractions are calculated at equal concentrations. Fig. 5a includes values for ψ₃ and ψ₄ as a function of δ, and Fig. 5b plots ψ₃/ψ₄. For polyamides composed of strong base discriminators, at high values of δ in the graphs, both ψ₃ and ψ₄ become arbitrarily close to one so the longer polyamide performs best, binding tightly to the target sequence and binding to fewer sites in the genome. At low δ values, similar to the values observed for imidazole and pyrrole rings, the fraction ψ₃/ψ₄ is greater than four in nearly all cases, indicating that the shorter polyamide shows better specificity at the given concentration. As δ increases from right to left in Fig. 5a, the value of ψ₃ increases from zero to one sooner than ψ₄ because of the smaller number of competing sequences with the shorter polyamide.

Figure 5.

Effect of polyamide length on binding fraction. A polyamide with three pairs of rings is compared with a polyamide with four pairs of rings. (a) Values of ψ₃ and ψ₄ for different values of the base specificity δ. (b) Values of ψ₃/ψ₄ for two comparisons: with equal concentrations of the two polyamides, [P₃] = [P₄], with values chosen such that the saturation of the target site θ₃ is 0.97 (at this concentration, θ₄ = 0.999); and at equal saturation of target sites, θ₃ = θ₄ = 0.97. Values of ψ₃/ψ₄ greater than four indicate that the shorter molecule is the optimal choice in the comparison. The complex nature of the equal concentration ψ₃/ψ₄ graph at low δ values, where ψ₃ and ψ₄ are close to zero, is due to a set of stepwise increases of ψ₃ and ψ₄ with very small magnitude. These points are not relevant to polyamide design, as the polyamides would have very low specificity.

This comparison, however, is not entirely fair when approached from the therapeutic standpoint. At equal concentrations, the longer polyamide will occupy a greater fraction of its target sites than the shorter polyamide because it has the stronger binding constant. It is fairer to compare the performance of the polyamides at the same saturation of binding sites, choosing concentrations, for example, that will ensure occupancy of 90% of the target sites in a given genome. In this case, the longer polyamide is always the best choice. It gives a better binding fraction and requires lower concentrations to give the same site saturation as the shorter polyamide. Thus, for use as an antibiotic or in chemotherapy, the longer polyamide is the better choice. The equal-concentration comparison warns, however, that the longer polyamides are sensitive to increases in concentration: high concentrations of the longer polyamides will significantly compromise their specificity as more and more nonspecific sites are also targeted.

Implications for Rational Design of Linked Polyamides.

A polyamide of the form (R_G, R_A, R₀), which complements two rings recognizing components of different base pairs with a placeholder ring, is the best choice for design of a multifunctional lexitropsin, allowing the flexibility to target any given sequence using a single set of three rings. Two elements for this optimal design are available in current polyamides: imidazole acts like a moderately specific guanine-reader and pyrrole acts like a placeholder but adds G-excluding ability for extra gains in specificity. The missing element is an adenine-specific ring or a thymine-specific ring. Rational design of one of these rings is a difficult prospect because of the similar steric and hydrogen-bonding properties of the minor groove-accessible faces of adenine, thymine, and cytosine. Based on the crystallographic structure of an imidazole lexitropsin bound to DNA, Kopka et al. (15) have proposed that rings with a bulky group at the base edge contact, such as thiazole or methylpyrrole, might favor adenine over thymine because of the different placement of the adenine N3 and the thymine O2 atoms in the minor groove. Such differences apparently are used by the TATA-binding protein to differentiate TA from AT at the beginning of the TATA-box sequence (20). If thiazole, methylpyrrole, or a similar ring does indeed discriminate in this manner, the degeneracy of AT binding in the current imidazole–pyrrole polyamides would be broken, allowing synthesis of true lexitropsins.