Ion binding in the Open HCN Pacemaker Channel Pore: Fast Mechanisms to Shape “Slow” Channels

Abstract

I_H pacemaker channels carry a mixed monovalent cation current that, under physiological ion gradients, reverses at ∼−34 mV, reflecting a 4:1 selectivity for K over Na. However, I_H channels display anomalous behavior with respect to permeant ions such that (a) open channels do not exhibit the outward rectification anticipated assuming independence; (b) gating and selectivity are sensitive to the identity and concentrations of externally presented permeant ions; (c) the channels' ability to carry an inward Na current requires the presence of external K even though K is a minor charge carrier at negative voltages. Here we show that open HCN channels (the hyperpolarization-activated, cyclic nucleotide sensitive pore forming subunits of I_H) undergo a fast, voltage-dependent block by intracellular Mg in a manner that suggests the ion binds close to, or within, the selectivity filter. Eliminating internal divalent ion block reveals that (a) the K dependence of conduction is mediated via K occupancy of site(s) within the pore and that asymmetrical occupancy and/or coupling of these sites to flux further shapes ion flow, and (b) the kinetics of equilibration between K-vacant and K-occupied states of the pore (10–20 μs or faster) is close to the ion transit time when the pore is occupied by K alone (∼0.5–3 μs), a finding that indicates that either ion:ion repulsion involving Na is adequate to support flux (albeit at a rate below our detection threshold) and/or the pore undergoes rapid, permeant ion-sensitive equilibration between nonconducting and conducting configurations. Biophysically, further exploration of the Mg site and of interactions of Na and K within the pore will tell us much about the architecture and operation of this unusual pore. Physiologically, these results suggest ways in which “slow” pacemaker channels may contribute dynamically to the shaping of fast processes such as Na-K or Ca action potentials.

INTRODUCTION

I_H pacemaker channels activate upon hyperpolarization and carry a mixed Na and K current that is depolarizing at resting potentials but which becomes a repolarizing outward flux at voltages positive to the physiological reversal potential of ∼−34 mV (Santoro and Tibbs, 1999; Accili et al., 2002; Robinson and Siegelbaum, 2002). Gating of these channels is slow with respect to many physiological processes, a finding that has influenced the way in which the channels are conceived to contribute to cellular physiology. Thus, while opening and closing of channels formed predominantly from HCN2 and 4 are thought to provide a drive for slow rhythmic events (such as the cardiac action potential and thalamocortical delta and spindle oscillations; McCormick and Bal, 1997; Accili et al., 2002; Biel et al., 2002; Robinson and Siegelbaum, 2002), the contribution of I_H to fast nonrhythmic processes (as exemplified by the role of HCN1 and 2 in normalization of the somatic time course of proximal and distal synaptic inputs) is generally considered with respect to the resting input resistance and slow changes therein (Hausser et al., 2000; Reyes, 2001; Robinson and Siegelbaum, 2002; Magee and Johnston, 2005; Ying et al., 2007). By analyzing the behavior of expressed HCN2 channels we show that pacemaker channels undergo rapid changes in conductance that seem poised to allow these slow channels to help shape the fastest cellular processes.

Architecturally, HCN channels are members of the voltage-gated K (K_V) channel superfamily. Thus, they have six transmembrane helices (S1–S6) and cytoplasmic amino and carboxy termini. S1–S4 form the voltage sensor while S5, S6, and the intervening loop form the ion conducting pore (Santoro and Tibbs, 1999; Robinson and Siegelbaum, 2002). Functionally, hyperpolarization increases the intracellular accessibility of S4 in both HCN and K_V channels (Bell et al., 2003; Vemana et al., 2003), albeit this is linked to opening of the helical bundle at the cytoplasmic end of S6 in HCN channels but closing in other K_V channels (Shin et al., 2001; Rothberg et al., 2002, 2003).

HCN2 activation gating is slow due, in part, to the presence of a slow, voltage-independent opening transition (see the representative activation records herein and Shin et al., 2004; Bruening-Wright et al., 2007; Chen et al., 2007) but deactivation is faster than would be expected based on return along such a reaction path (Bruening-Wright et al., 2007; Chen et al., 2007). Further complexity in channel gating is revealed by the finding that the kinetics of deactivation of both native (DiFrancesco, 1984; Maruoka et al., 1994) and expressed (Mannikko et al., 2005; Elinder et al., 2006; Bruening-Wright and Larsson, 2007) channels change as a function of the strength and duration of the hyperpolarizing step used to open the channels. Mechanistically, the origin of this hysteresis was originally ascribed to the existence of multiple closed and open states linearly coupled by voltage-dependent reactions (Maruoka et al., 1994). However, the ability of cAMP binding to the C-terminal gating ring to increase the fully activated open probability, (Shin et al., 2004; unpublished data), of anesthetics to lower this (Lyashchenko et al., 2007), and the observation that the rate of opening of HCN2 saturates at very negative voltages (Chen et al., 2007) argues against this. More recently, HCN channel gating has been interpreted within models wherein the voltage sensors are decoupled from opening such that they can deactivate before the pore closes (Bruening-Wright et al., 2007; Chen et al., 2007) and they can undergo a modal shift in their gating energetics such that activation and/or opening makes gating easier (Mannikko et al., 2005; Elinder et al., 2006; Bruening-Wright and Larsson, 2007).

Architectural conservation between HCN and other K channels extends to the selectivity filter (where HCN channels have a canonical K-selective sequence of CIGYG) but not to the pore helix, S5, or S6, and differences in these regions presumably account for the physiologically critical weak K selectivity (P_K:P_Na ∼4:1). Despite these differences, the behavior of native I_H and expressed HCN channels suggest their pores, like those of other K channels, contain multiple ion binding sites and are plastic. First, increasing K or lowering Na externally increases the permeability of Na relative to K in native I_H (Hestrin, 1987; Frace et al., 1992; Ho et al., 1993; Solomon and Nerbonne, 1993) and expressed HCN channels (Moroni et al., 2000; unpublished data). Second, in the limiting case when K is absent, the ability of I_H (Edman and Grampp, 1989; Frace et al., 1992; Wollmuth and Hille, 1992; Solomon and Nerbonne, 1993) and HCN channels (data presented herein) to carry an inward Na current appears to be lost. Third, kinetic and equilibrium parameters describing voltage-dependent gating of both native I_H (Hart, 1983; McCormick and Pape, 1990; Wollmuth and Hille, 1992; Maruoka et al., 1994; Wollmuth, 1995) and expressed HCN channels (Azene et al., 2003; Mannikko et al., 2005; Elinder et al., 2006; Lyashchenko et al., 2007; see also data reported herein) are generally, though not universally (Hestrin, 1987), reported to be sensitive to changes in K and Na concentrations. While the effects on ion selectivity could be attributed to anomalous mole fraction effects of permeant ions, the other behaviors indicate plastic coupling of the pore to the energetics of opening or to intrinsic or extrinsic conductance blocking mechanisms. Indeed, it has been suggested that the K dependence of current flow and/or of gating could represent rearrangements of the pore analogous to P/C-type inactivation in K_V channels (Kurata and Fedida, 2006), but the relationships between the architecture and operation of the pore in HCN channels remains poorly understood.

Here we show that the current carried by open HCN channels is shaped by at least two distinct ion sensitive mechanisms: (1) a submillisecond block by intracellular Mg that has a similar voltage dependence to that observed in Shaker K channels and (2) a K depletion–mediated collapse of conduction that is asymmetrical with respect to flux and that occurs with kinetics close to the maximal K ion transit rate through the HCN channel pore. The former mechanism indicates that the architecture of the inner face of the selectivity filter of HCN and Shaker channels may be similar while the latter observation helps define the origin of the small, K-dependent conductance of pacemaker channels. The relationship between these processes and ion-sensitive modifications of activation and deactivation gating reactions remains to be explored.

MATERIALS AND METHODS

Molecular Biology

1–50 ng of HCN2 cRNA, transcribed from pGHE-cDNA (amplified in STBL2 cells and linearized with SphI; from Invitrogen Life Technologies and New England Biolabs, respectively) using Message Machine T7 RNA polymerase (Ambion) was injected per Xenopus oocyte. Oocytes were maintained in L-15 media without ficoll (Specialty Media) at 17°C.

Animal procedures

Xenopus oocytes were harvested according to a Columbia University approved protocol (PI#366G CU#2928) (Lyashchenko et al., 2007).

Electrophysiology

Two-electrode voltage clamp (TEVC) and excised inside-out patch clamp (IOPC) recordings were made at 22–25°C using a Warner Instruments OC-725C amplifier and an Axon Instruments Axopatch 200B amplifier (in the resistive mode), respectively. In both configurations, the amplifier gain was kept below the point where the fastest transients would be internally clipped and signals were digitized (at 20 kHz in TEVC and 20, 100, or 200 kHz in IOPC) using an ITC-18 interface (Instrutech Corporation) controlled by Pulse software (HEKA Elektronik). In IOPC, but not TEVC, analogue compensation of linear ionic and capacitive currents was applied. In initial experiments the Axopatch 200B stimulus filter was set to 20 μs but in wide bandwidth experiments this was routinely set to 2 μs. If IOPC currents exceeded 500 pA at the most extreme voltages, we applied analogue series resistance compensation (90% correction, 20 μs lag, resistance set to that of the electrode before seal formation). In TEVC, the wide bandwidth output from the clamp was filtered at 1 kHz using a Frequency devices 902 8-pole Bessel low pass filter while in IOPC the 100 kHz four-pole amplifier output was sampled directly or following additional filtering through a Warner Instruments LPF-8 eight-pole low pass Bessel filter. Sampling and filter corner frequencies are indicated in each figure legend.

Microelectrodes (V-sensing, 1–4 MΩ; I-passing, 0.1–0.4 MΩ) and patch electrodes (1–2 MΩ) were fabricated from 1B120-F4 (World Precision Instruments) and Kimax-51 (Kimble Glass) borosilicate glass, respectively. Patch electrodes were coated with Sylgard (Dow Corning Corporation). Ag-AgCl ground wires were connected to the bath by 3 M KCl-2% agar salt bridges placed close to, but downstream of, the oocyte. Patch electrodes were moved upstream of the cell after excision.

In all experiments, the extracellular solution was (in mM) 112 MCl, 1 MgCl₂, 1 CaCl₂, 10 HEPES-free acid, pH 7.4. In IOPC the intracellular solution was (in mM) 112 MCl, 1 EGTA-free acid, 10 HEPES-free acid, pH 7.4 with either MgCl₂ (at 1 or 2 mM) or 1 EDTA-free acid, as indicated. The alkali metal (M) salts and the hydroxide used to pH the solutions were chosen to achieve the ion concentrations indicated on each figure. Unless otherwise indicated, 30 μM cAMP was included in intracellular IOPC solutions to saturate cyclic nucleotide enhancement of activation gating as this permitted use of higher voltages and shorter times to fully activate the channels.

To prevent contamination of the patch pipette solution, cells were bathed in the pipette solution during seal formation and the bath was switched to the appropriate intracellular solution before patch excision. As HCN channel activation shifts hyperpolarized upon patch excision, we waited at least 4 min before acquiring IOPC data to allow gating to stabilize to the cell free level.

Paradigms and Analysis

In TEVC, cells were held at −30 mV while the holding potential in IOPC was −40 mV. The voltage paradigms used to collect data are depicted on each figure or described in the appropriate legend. In pilot experiments, we confirmed that the activation voltages were adequate to saturate gating under the indicated conditions (not depicted).

The kinetics of Mg block were analyzed within the context of the model shown in Scheme 1. Within this framework, activation of the voltage sensors is represented by the equilibrium between closed resting (CR) and closed activated (CA) states and is defined by the equilibrium constant, K_(V) (all equilibrium constants are reported in the forward direction).

(SCHEME 1)

Opening of the channel is represented by the reaction from CA to O and is defined by the equilibrium constant L. In keeping with the results from several groups, we assume that the opening and closing transitions underlying L are voltage independent (Shin et al., 2004; Bruening-Wright and Larsson, 2007; Bruening-Wright et al., 2007; Chen et al., 2007; Lyashchenko et al., 2007). For simplicity, we further assume that Mg ions (B) associate with a single class of binding sites and do so only when the channel is open such that this association is defined by the equilibrium constant K_a, that the Mg bound state, OB, is nonconducting, and that channels do not significantly redistribute between closed and open states in the intervals where Mg block is examined at depolarized potentials. The validity of these assumptions is considered further in the Discussion. Within this framework, we can ignore changes in the open probability (as defined as the sum of being either open or open blocked) and treat the reaction between O and OB as a simple two state process. Accordingly, the kinetics of block and unblock can be described according to Eqs. 1–3 .

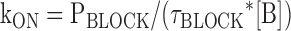1

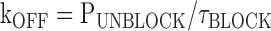2

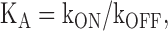3

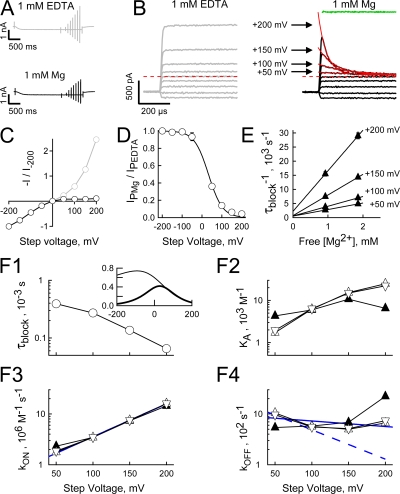
where P_block is the fraction of the outward tail that is blocked according to I_t/(I_t + I_p), P_unblock is the fraction of the outward tail that is not blocked according to I_p/(I_t + I_p), τ_block is the single exponential time constant of the decay of the transient component of the predeactivation tail current, and [B] is the free concentration of Mg (0.924 and 1.859 mM) in our standard solutions wherein we add 1 or 2 mM MgCl₂ and 1 mM EGTA (determined using WebmaxC http://www.stanford.edu/%7Ecpatton/webmaxc/webmaxcE.htm). I_t and I_p represent the amplitudes of the transient and plateau components of the predeactivation phase of the tail currents with I_t determined from the zero time extrapolation of the block exponential (see Fig. 4 B and Fig. 5 B) or from the current in the absence of internal Mg (I_-Mg) minus I_p determined in the presence of internal Mg (see Fig. 5 B).

Figure 4.

The transient outward current is carried by the HCN2 channels. (A1) HCN2 currents obtained before (black), during (blue), and after (gray) application of 300 μM ZD7288 (ionic conditions and voltage paradigms as in Fig. 3). Each trace is the average of eight sweeps evoked in response to the 3-ms “active” protocol before subtraction of the interlaced “leak” sweeps (records not shown for simplicity). Currents were filtered and sampled at 20 and 100 kHz, respectively. (A2) Expanded views of the +80 mV sojourn following subtraction of the appropriate “leak” records before (raw) and after (scaled) scaling each trace to the amplitude of the preZD7288 −135 mV current (I _–135). (A3) ZD7288-sensitive component of the current (obtained as the difference between the leak-subtracted pre and plus ZD7288 records in “A2, raw”) is shown before (subtracted) and after (subtracted and scaled) scaling the blocked component (blue traces) to the preZD7288 I _–135 amplitude. (B) Outward transient in the absence of ZD7288 (black line) with superimposed fit of a single-exponential function (red line). Residuals from the fit (green line) are offset from zero for clarity. Arrows show the amplitudes of the plateau (I_p) and transient (I_t) components of the outward current. (C) Fractional ZD7288 inhibition of I _–135, I_t, and I_p, where I_C is the control amplitude and I_Z the 300 μM ZD7288-resistant amplitude, respectively. Data are mean ± SEM from three recordings acquired and analyzed as described in A and B. (D and E) Linear regressions (superimposed lines) show the amplitudes of I_t (R² = 0.955) and I_p (R² = 0.986) are highly correlated with that of I _–135 (D) and with each other (E; R² = 0.945). Data are from seven independent patches. (F) Time constant of current decay at +80 mV as a function of the I _–135 amplitude. The black line is a linear regression (R² = 0.070) across the control data from seven independent recordings. Red lines connect data acquired in three independent recordings before, during, and after cut down of the current by inclusion of ZD7288 (data points obtained before and after washout of ZD7288 in the same patch are ringed by a red ellipse).

Figure 5.

Inward rectification of the open HCN2 channel current arises from a voltage-dependent block by intracellular Mg. (A and B) HCN2 currents activated at 2140 mV in the presence of 300 μM cAMP with either 1 mM EDTA plus 1 mM EGTA or 1 mM Mg plus 1 mM EGTA in the intracellular solution (records are from the same patch). In all panels K was the only alkali metal on either side of the membrane ([K]_OUT 117 mM; [K]_IN 119 mM or 121 mM when EDTA replaced MgCl₂). After allowing activation to equilibrate (2 s), the patch was stepped to potentials between −200 and +200 mV in 50-mV intervals with test steps applied at 10 Hz (records were filtered at 100 kHz and sampled at 200 kHz). To ensure steps were long enough to determine the time constant of block but short enough to prevent deactivation, the durations of the steps were increased from 1 ms at +200 mV to 3 ms at 0 mV in 0.5-ms increments and then held at 3 ms for all negative potentials. Collection of such “active” sweeps was interlaced with “leak” sweeps wherein the patch was stepped to −140 mV for 5 ms before and after each test step (not shown for simplicity). For each condition, four averaged “leak” records were subtracted from the average of the four cognate “active” records (shown in A) and the subtracted currents aligned to the beginning of each test step (B). Activation at −155 mV with test steps applied at a lower frequency (4 Hz) gave identical results so data from these two paradigms were combined. Records collected at depolarized potentials in the presence of Mg are well fit (red lines) with a single exponential function (residuals from the fits shown as green lines offset from zero for clarity). Arrows show the correspondence between the zero time extrapolation of the fitted exponentials and the amplitudes of currents acquired in the absence of Mg. (C) Plateau tail currents (determined at the end of test steps as shown in B) in the presence (I_{P Mg}) and absence (I_{P EDTA}) of 1 mM Mg (mean ± SEM from nine separate recordings for each condition) plotted versus the corresponding test potential. (D) Equilibrium voltage dependence of the block by 1 mM Mg was determined by fitting Eq. 6 (smooth line) to the ratio of I_{P Mg}/I_{P EDTA} (same data as shown in C). The 95% confidence interval of this quotient was smaller than the symbol size at all voltages except −50 mV. The ratio is undefined at the reversal potential of 0 mV. (E) Plot of the inverse time constant of block at the indicated potentials as a function of the free Mg concentration. Data for low and high concentrations of Mg are mean ± SEM of eight and four recordings acquired and analyzed as described in A–D. (F) Kinetic parameters of Mg block plotted as a function of the test potential. Parameters were determined from τ_block (such as shown for 1 mM Mg in B and F1) and the steady-state current inhibition (D) according to Eqs. 1–3 based on the zero time extrapolation of the block exponential (upright open triangle) or the instantaneous current predicted from scaled amplitudes determined in the absence of internal Mg (inverted open triangle) and from 1/τ_BLOCK versus free Mg concentration (E) (upright filled triangles). Solid blue lines are regressions to the data represented by the inverted open triangles. The dashed blue line represents the predicted value of k_OFF based on δ_OFF = 0.17 (from δ-δ_ON where δ and δ_ON are 0.36 and 0.19, respectively) and k_OFF ⁰ = 1848 s⁻¹ (from the 0 mV version of Eq. 3 where k_on ⁰ = 7.97 × 10⁵ M⁻¹s⁻¹ and K_A ⁰ = 431 M⁻¹). The inset in F1 shows relationship of τ_BLOCK to membrane voltage at 0.924 mM free Mg when k_OFF ⁰ and δ_OFF are 1848 s⁻¹ and 0.17 (thick line) or 936 s⁻¹ and 0.03 (thin line). The ordinates are logarithmic in the main panels but linear in the inset.

The relationships of k_on and k_off to the applied membrane voltage were fit with Eqs. 4 and 5, respectively, while the fractional block at equilibrium was fit with Eq. 6.

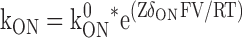4

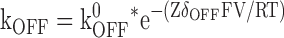5

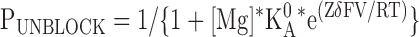6

In these equations Z is the valence of the Mg ion, k_on ⁰ and k_off ⁰ are the on and off rate constants in the absence of an applied field, K_a ⁰ = k_on ⁰ / k_off ⁰, δ_on and δ_off are the effective electrical distance Mg travels across the field (V) to the transition state in the on and off reactions assuming that all the effect of the field arises from a discrete effect on the Mg ion, δ = δ_on + δ_off, while R, T, and F have their usual meaning.

To facilitate comparison between the IV relationships under different conditions, we superimposed the normalized inward (I_{M INWARD} in Eq. 7), outward (I_{M OUTWARD} in Eq. 8) and net fluxes (sum of inward and outward components) predicted by the GHK current equation. To do so, we let P_M equal the relative permeability of ion M with respect to K and then scaled the results such that the net flux was equal to the flux observed at the extreme positive (Fig. 8 E) or negative (all other IV plots) potential of the particular paradigm. Z_M is the valence of ion M, while [M]_O and [M]_I are the external and internal concentrations of M, respectively. In TEVC, we assumed that the internal concentrations of Na and K were 14 and 122 mM, respectively (Zeuthen et al., 2002).

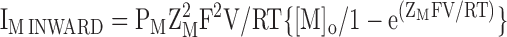7

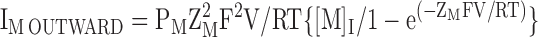8

Figure 8.

Na sensitivity of Mg block does not account for the collapse of conduction in a K-depleted pore. (A and D) Unblocked HCN2 currents (intracellular solution contained 1 mM EDTA and 1 mM EGTA and no added divalent cations) were collected and processed as described in Fig. 5, A and B, except the cAMP concentration was 30 μM and Na and K were presented biionically (with the direction of the gradients reversed in the two records as indicated). Red circles indicate a small transient present in the current collapse time course that is absent in the recovery time course. Data are representative of four and three similar recordings for A–C and D–F, respectively, with records in A–C from the same patch shown in Fig. 5, A and B. (B and E) Plateau tail current amplitudes (measured 1 ms after the beginning of each test step) plotted versus the corresponding step potential. (C and F) Expanded views of the collapse (black lines) and recovery (blue lines) of current observed when the potential was stepped between −140 mV and test potentials of +50 to +200 mV (thicker lines represent steps to more depolarized voltages). In each panel the currents have been normalized to change from 0 to 1 for both the step to, and the return from, the depolarized test potentials and each phase of the sweep shifted on the time axis so its beginning is aligned with respect to its onset.

Data analysis was performed in PulseFit (HEKA Elektronik) and IgorPro (Wavemetrics Corporation). Data are presented as mean ± SEM or range except for quotients, which are reported with respect to their 95% confidence interval.

Reagents

ZD7288 (Tocris bioscience) solutions were prepared fresh each day by dilution of a 100 mM stock solution (deionized water) that was stored at −20°C for no longer than 1 mo. Spermine and spermidine (obtained as Ultra grade, >99.5% purity, hydrochloride salts from Fluka) solutions were prepared from 30 mM stock solutions (deionized water) that were prepared fresh each day. Other electrophysiology reagents were of the highest purity from Sigma-Aldrich.

RESULTS

Ion-dependent Conductance Asymmetry in HCN2 Channels

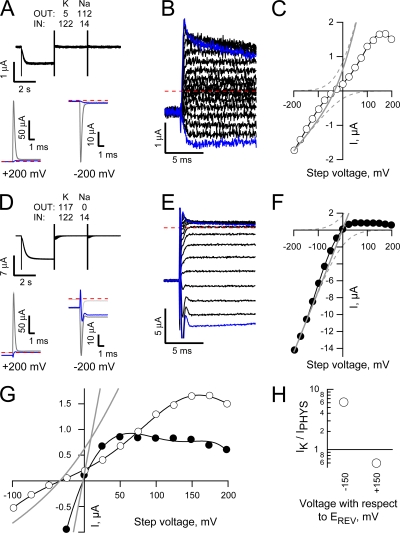
Fig. 1 (A and D, top) shows superimposed TEVC currents recorded from a Xenopus oocyte stepped briefly (50 ms) to potentials ranging between ±200 mV (in 25-mV increments) in the presence of physiological ion gradients (Fig. 1 A) or elevated external K (Fig. 1 D) when the expressed HCN2 channels were fully activated (by preconditioning at −115 mV for 3 s, left half of sweeps) or closed (stepped from the holding potential to −115 mV for 5 ms, a time sufficient to allow the voltage clamp and capacity transients to settle but not evoke any channel opening, right half of the sweeps). The lower records in each panel show the “activated” (dark gray) and “closed” (light gray) currents recorded at +200 (left) and −200 mV (right) with the sweeps aligned with respect to the onset of the step to the test potential. In each case, the blue line shows the difference between these “active” and “leak” responses. Fig. 1 (B and E) shows the full family of subtracted records with the plus and minus 200-mV responses again highlighted in blue. With physiological ion gradients, the difference currents settle relatively quickly and smoothly while in the presence of elevated K there is a greater distortion immediately following the voltage step. However, as the shape of the early phase of both records will be impacted by differences in the time constant of the clamp in the presence and absence of channel activation (particularly under the high conductance elevated K condition), we do not consider the initial 2.5 ms of the records further. Inspection of these records and the IV plots derived there from (Fig. 1, C, F, and G) shows that elevating external K modestly slows activation and enhances the inward current amplitude (see also Fig. 1 H, left) while the difference in the reversal potentials (−34.9 ± 0.8 mV and −1.3 ± 0.8 mV, n = 5 with physiological concentrations of ions and elevated K, respectively) accords with the accepted selectivity.

Figure 1.

Permeant ion-dependent rectification in the IV relationship of fully activated HCN2 channels. (A and D) HCN2 TEVC currents (from a single Xenopus oocyte) obtained in response to 50-ms steps to potentials ranging from −200 to +200 mV following channel activation at −115 mV for 3 s or after a 5-ms step to −115 mV (left and right parts of sweeps in top panels and dark and light gray sweeps in bottom panels, respectively) and the difference currents (blue lines) at test potentials of +200 mV (bottom left) and −200 mV (bottom right). In this and subsequent figures, text insets indicate the Na and K concentrations in the intracellular (IN) and extracellular (OUT) solutions (see Materials and methods for estimations of internal concentrations in TEVC) while the red dashed line shows the zero current level. Sweeps were filtered at 1 kHz and sampled at 20 kHz. (B and E) Expanded views of the difference current families (from recordings shown in A and D, respectively) with −200 and +200 mV sweeps highlighted in blue. (C and F) Difference current amplitudes (determined by averaging records in B and E between 2.5 to 5 ms after the onset of the voltage step) plotted versus observed voltages. E_REV and current amplitudes with respect thereunto were determined from fits of an eighth order polynomial (thin black line). In this and subsequent IV plots, superimposed gray lines show component (dashed) and net current (solid) predictions of the GHK current equation assuming a 4:1 K:Na selectivity. (G) Expanded view around zero current of the IV plots shown in C and F. (H) Ratio of the currents recorded in elevated external K (I_K) with respect to those obtained in physiological concentrations of Na and K (I_PHYS) 150 mV negative (left) or positive (right) to E_REV. Data are mean ± SEM from five cells recorded as shown in A–G.

However, closer consideration of the data reveals that the open HCN2 channel conductance has a complex relationship with the applied voltage and the identity and concentration of the permeant ions. Thus, in neither ionic condition do the plots conform to simple predictions assuming independence of ion movement within the pore (gray lines in Fig. 1, C, F, and G, represent appropriate solutions of the GHK current equation). Rather, under physiological ion gradients, the IV behavior is almost linear and not outwardly rectifying as expected from the ionic selectivity while, in the presence of high external K, the IV relationship is strongly inwardly rectifying rather than linear. Furthermore, the observed relationships are clearly not monotonic, requiring a high order polynomial for an adequate fit.

Fig. 1 H provides a further demonstration of the complexity of the conductance behavior. Here, the relative amplitude of the inward and outward currents carried in the presence of elevated external K are plotted as a function of the currents carried when physiological levels of Na and K are presented externally. In each case the currents are determined 150 mV positive and negative to the observed reversal potential. These results show that while the inward current shows the strong (∼6.1-fold) enhancement of the inward flux in the presence of elevated K, the outward flux (which should, in both cases, be dominated by the high internal K concentration) is markedly (∼0.6 times) smaller when external K is elevated.

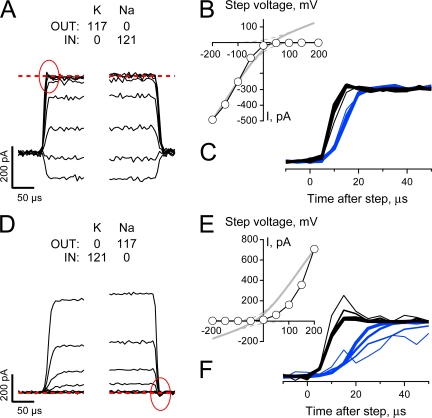
Fig. 2 (A, C, and E) shows superimposed representative HCN2 channel currents (left) and expanded views of the tail currents (right) collected from IOPC recordings wherein patches were first stepped to −145 mV for 1.5 s and then stepped to a series of tail potentials between −100 and + 80 mV in 20-mV increments (as indicated next to select tail current traces). In these recordings, currents were acquired in the presence of quasi-physiological gradients of Na and K (Fig. 2 A), symmetrical high K (Fig. 2 C), or in the presence of an inverted Na and K gradient (Fig. 2 E). Fig. 2 (B, D, and F) plots the IV relationships for the three representative recordings with current amplitudes determined during the plateau phase of the tails.

Figure 2.

Ion-dependent asymmetry in the IV relationship of fully activated HCN2 channels is maintained in excised inside-out patches. (A, C, and E) HCN2 currents obtained in response to activation at −145 mV for 1.5 s (left) and expanded views of tail currents upon depolarization to potentials between −100 and + 80 mV (right) when K was the only alkali metal presented to the channels (C) or Na and K were presented with quasi-physiological (A) and inverted (E) gradients. Each record is a single sweep filtered at 5 kHz and sampled at 20 kHz with no post hoc digital correction for uncompensated linear ionic or capacitive components. (B, D, and F) Plateau tail currents (determined by averaging current amplitudes between 7 and 9 ms after the test step) plotted versus the corresponding tail potential. Data are from records shown in A, C, and E, respectively. Data are representative of 4 (A and B), 6 (C and D), and 4 (E and F) similar recordings.

With 5 mM K and 112 mM Na in the external solution and 119 mM K as the only internal monovalent alkali metal, the channels activate relatively quickly and carry both inward and outward currents. As observed in TEVC, the IV relationship is essentially linear and not outwardly rectifying as would be expected based on the observed K:Na selectivity (E_REV = −44.1 ± 2.6 mV, n = 5).

Further paralleling the findings shown in Fig. 1, elevation of external K results in a slowing of the activation time course, enhancement of the inward current (though, in these experiments, this is only qualitatively demonstrated by comparison across patches), depolarization of the reversal potential (to E_REV = -2.7 mV ± 0.4, n = 13), and, most significantly, an emergence of a clear inward rectification of the open channel current.

To explore the role of Na and K in altering channel function in general and influencing alterations in conductance in particular, we inverted the gradients of these ions. If the only effects of Na and K on HCN2 channels arise as a result of a mole fraction–determined occupancy within a static, modestly K-selective selectivity filter, inverting the Na and K ion gradients should result in an enhancement of the inward current amplitude, a slowing of activation gating, and generation of a linear (based on the behavior observed with quasi-physiological concentrations of Na and K, see Fig. 2 B) or modestly inwardly rectifying (according to the GHK equation, gray lines in Fig. 2 F) IV relationship that reverses around +44 mV. Inspection of the current records and the plateau IV plot (Fig. 2, E and F, respectively) reveals that the HCN2 conductance does not hew to the above predictions. Thus, while gating and the current amplitude at negative potentials appear to follow the external K concentration, the channel becomes strongly inwardly rectifying such that it carries no detectable current positive to the anticipated reversal potential. Together, these findings indicate that open channel rectification is influenced by both permeant ions and other mechanisms.

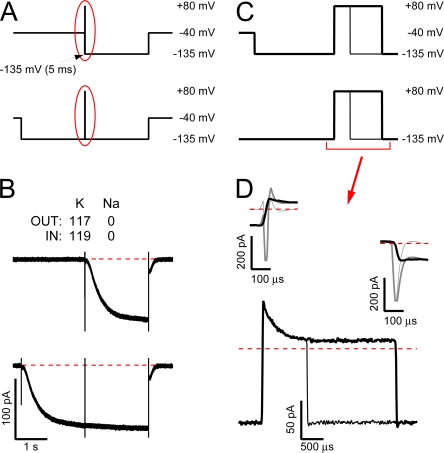
Inward Rectification of the HCN2 Channel Current in Symmetric Elevated K Is Accompanied by a Rapidly Decaying Outward Transient

During the course of the experiments with symmetrical K, we observed, at depolarized potentials, a transient component of the initial phase of the tail current that did not appear to arise from uncompensated capacity transients (this component is not well resolved in recordings such as those in Fig. 2 so was omitted there for clarity). We hypothesized that this transient may arise from a rapid deactivation, inactivation, or block of the HCN2 channels and such a process could account for the emergence of inward rectification.

To address these possibilities, we recorded HCN2 currents at a wide bandwidth and incorporated an interleaved leak subtraction protocol to eliminate any linear capacitive or ionic components that were not excluded from the recordings by analogue compensation. Fig. 3, A and C, shows the voltage paradigm while Fig. 3, B and D, shows a representative recording. In this paradigm, the patch was stepped to −135 mV for 2 s (Fig. 3, A and B, bottom “active” paradigm and record, respectively) or 5 ms (Fig. 3, A and B, top “leak” paradigm and record) and then stepped to + 80 mV for 1 or 3 ms before returning to −135 mV. The longer preconditioning step in the “active” paradigm was sufficient to fully activate the channels while the shorter step in the “leak” paradigm was sufficient to allow the uncompensated capacity transients to decay without evoking channel opening.

Figure 3.

Rectification of the hyperpolarization-activated current is associated with a submillisecond outward transient that does not arise from HCN2 channel deactivation. (A and C) Schematic representation of the complete voltage paradigms (A) and expanded views of the interval during the middle of the record (C, as indicated by the red ovals in A). In the top “leak” paradigm, the patch was stepped to −135 mV for 5 ms (a duration sufficient to allow uncompensated capacity transients to decay but insufficient to permit channels to open) and then stepped to +80 mV for 1 or 3 ms before being returned to −135 mV for 2 s. In the bottom “active” paradigm, channels were first opened at −135 mV for 2 s before the 1- or 3-ms sojourn at +80 mV and the return to −135 mV. Each sweep was filtered at 20 kHz and sampled at 100 kHz with “leak” and “active” sweeps recorded interlaced. (B) Averages of seven “leak” sweeps (top) and their cognate interleaved “active” sweeps (bottom) recorded with K as the only alkali metal. (D) Expanded views of the total current (including uncompensated capacity and ionic components) observed during the step to (top left) and return from (top right) +80 mV in the presence (dark gray lines) and absence (light gray lines) of activated HCN2 channels and of the “active” minus “leak” subtracted records before, during, and after the step to +80 mV for 1 ms (thin black line, bottom panel only) or 3 ms (thick black lines). Data are representative of five similar recordings of which three were collected at the widest bandwidth (filtered at 100 kHz and sampled at 200 kHz).

Comparison of the records in Fig. 3 B shows that a brief sojourn at +80 mV did not result in emergence of a reactivation phase that proceeded with the slow kinetics of channel opening (as reported by the apparently uninterrupted inward current trace at −135 mV either side of the +80-mV step; Fig. 3 B, bottom record) while conditioning at +80 mV did not noticeably alter the activation either (compare openings trajectories in top and bottom records). To explore the behavior of the open HCN2 current before, during and after the step to +80 mV, we subtracted the averaged “leak” sweeps (Fig. 3 B, top, and light gray sweeps in the top of Fig. 3 D) from the averaged “active” records (Fig. 3 B, bottom, and the dark gray sweeps in the top of Fig. 3 D). The black traces in Fig. 3 D show the resulting difference currents obtained from the 3-ms (thick traces) or 1-ms (thin trace in the bottom of Fig. 3 D) steps to +80 mV. These records indicate that the paradigm isolates a transient outward current that flows only after a prolonged sojourn at −135 mV before the step to +80 mV. On return to −135 mV, the full amplitude of the inward current is restored very rapidly.

The Transient Outward Current in Symmetric Elevated K Is Carried by the Expressed HCN2 Channels but Does Not Arise from Fast Deactivation or Restricted Diffusional Access of Permeant Ions to the Pore

As a first test of the origin of the outward transient, we asked if it was sensitive to HCN channel blockade and if its suppression correlated with the efficacy of the blocker on the plateau tail current and the inward HCN2 ionic current. Fig. 4 A1 shows averaged, but not otherwise post hoc processed, HCN2 currents (recorded with voltage paradigms as described in Fig. 3 A, bottom) before, during, and after inclusion of the HCN-selective inhibitor, ZD7288, in the bath. It is apparent that both the inward current at −135 mV and the tail currents on return to the holding potential were reversibly inhibited by ZD7288. Importantly, the stability of the −135-mV current trajectory either side of the brief sojourn (3 ms) at +80 mV reveals that there was no significant change in channel block during the depolarizing interval. Fig. 4 A2 (left) shows, on an expanded time scale, the leak-subtracted currents recorded before, during, and after the step to + 80 mV in the absence, presence, and following washout of ZD7288. These records show that in addition to suppressing the steady-state current at −135 mV and the inward tail currents at −40 mV (Fig. 4 A1), ZD7288 also reduced the amplitudes of both the fast transient and the plateau phases of the outward +80-mV tail current. Fig. 4 A2 (right) shows that a scaled version of the ZD7288 unblocked transient (normalized with respect to the current amplitudes at −135 mV preceding each +80-mV step) superimposed with the control current (and with a scaled version of the ZD7288-washout current). Similarly, Fig. 4 A3 shows the time course of the ZD7288-sensitive component of the outward current (obtained by subtraction of the ZD7288-unblocked current from the control current) and a scaled version plotted with respect to the outward transient obtained in the absence of ZD7288 (Fig. 4 A3, left and right, respectively). Together, these results show that the ZD7288-blocked and unblocked components of the outward transient had identical time courses, indicating that a homogenous population of channels carries the transient.

To quantitatively explore the relationship between the amplitudes and ZD7288 sensitivity of the inward and outward current components, we estimated the amplitudes of the transient (I_T) and plateau (I_p) phases of the outward current by fitting the falling phase of the current with a single exponential function (Fig. 4 B shows a representative fit for a control current). Fig. 4 C shows that all three components of the current (the steady-state inward current at −135 mV and both I_t and I_p) are equally diminished by the HCN-specific antagonist while Fig. 4, D and E, shows that the amplitudes of I_t and I_p are linearly correlated with the amplitude of the inward current at −135 mV determined immediately before the step to + 80 mV (Fig. 4 D) and with each other (Fig. 4 E).

These findings confirm that the transient is carried by the expressed HCN2 channels and does not represent a gating current or ionic current arising from recruitment of an endogenous channel.

The data obtained in the experiments reported in Figs. 3 and Figs.4 also serve to eliminate fast deactivation or ion accumulation and/or depletion as mechanisms underlying or contributing to the outward transient based rectification of the HCN2 current.

With respect to gating, several lines of evidence suggest HCN channels display hysteresis in gating such that (a) deactivation is faster than would be anticipated if this were to proceed by reversal of the slow, voltage-independent opening transition of activated channels, a finding that has been interpreted to mean that open channels can deactivate permitting them to close rapidly (Chen et al., 2007); (b) movement of the voltage sensors is thought to be dependent on the holding potential such that open channels activate more readily than closed channels (Mannikko et al., 2005; Elinder et al., 2006; Bruening-Wright and Larsson, 2007). However, in the former canon, deactivated open channels would remain conducting at +80 mV while any channels that closed would be obliged to reopen along the original, slow path. As the channels reestablish the full conductance at −135 mV without the emergence of slow reactivation (see, for example, Fig. 3, B and D), this route can be discounted. Similarly, a key effect of the modal shift in activation gating is that tail currents develop a sigmoidicity upon prolonged or strong activation, that is, closing slows down, an effect that is opposite to the observed fast loss of conduction on depolarization.

Does ion accumulation and/or depletion in the unstirred layers outside of the channel contribute to the observed current decline? This hypothesis predicts that the time constant of decay should be faster when the current flow is larger. To explore this, we plotted the time constants of current decay at +80 mV against the amplitude of the current determined at −135 mV immediately before the depolarizing step. Inspection of Fig. 4 F shows that there was no marked dependency of the time constant of decay at +80 mV in seven patches wherein the control current amplitude varied between 98 and 1120 pA (black regression line). To eliminate the possibility that differences in patch geometry were occluding observation of a negative correlation between the time constant and the current density, we examined the time constants obtained in the absence and presence of ZD7288 within three separate recordings (symbols linked by red regression lines represent data from each separate patch). In two out of three such experiments inclusion of intracellular ZD7288 suppressed the maximal current by 90% but had no marked effect on the time constant. Although, in a third recording, the time constant accelerated upon wash on of the inhibitor, this response is the inverse of that predicted by the ion accumulation/depletion model.

Together, the above results indicate the mechanism for rectification of the K conductance is an intrinsic property of the channel but is distinct from voltage-dependent closing of the S6 activation gate. Accordingly, we hypothesized that the inward rectification could arise as a consequence of intrinsic conductance asymmetry, an ion-dependent collapse of conduction (perhaps akin to P/C-type inactivation) or a voltage-dependent block by an internal cation. Below, we present evidence that suggests each of these processes may contribute to the behavior of open HCN2 channels as a function of permeant ion concentrations.

Inward Rectification of the HCN2 Channel K Current Arises as a Result of a Fast, Voltage-dependent Block by Internal Mg

To explore the possibility that current rectification arises from a voltage-dependent block by internal polyvalent cations, we asked what effect the presence or absence of internal divalent ions or polyamines would have on the current carried by symmetrical elevated K. To do so, we used a hybrid of the paradigms described in Figs. 1 and Figs.3. Thus, we recorded interleaved “active” and “leak” IV families (wherein the patch was stepped to voltages between ±200 mV for 1–3 ms with steps applied at 10 or 4 Hz in 50-mV increments) that were distinguished by the duration of the conditioning steps to the activation voltage. In the “active” paradigm the patch was held at the activation voltage for 2 s and returned to this potential between test steps, while in the “leak” paradigm the patch was held at −40 mV and stepped to the activation voltage for only 5 ms before (and after) each test step.

Fig. 5 A shows the averaged but unsubtracted records obtained in response to the “active” protocol when the internal solution contained 1 mM EDTA (top) or 1 mM Mg (bottom) in addition to 1 mM EGTA in both cases.Fig. 5 B shows the same records following subtraction of the cognate averaged leak records (in each case the current responses have been aligned according to the onset of the test step for clarity). In the presence of internal Mg, the outward currents decay with a monoexponential time course (solid red lines) that accelerates upon depolarization (note the crossover of the currents recorded at the more depolarized potentials with respect to those obtained at the less positive voltages). In the absence of internal divalent ions this current decay is abolished. The close correspondence of the zero time intercept of the exponential fit of the currents obtained in the presence of Mg to the amplitudes observed in the absence of internal Mg supports the conclusion that the decay of the current under these conditions is due to Mg block.

Fig. 5 C shows plateau IV relationships of open HCN2 channels in the absence or presence of internal Mg. It is apparent that the robust inward rectification in the presence of internal Mg arises from the block of an open channel current that shows strong outward rectification in the ion's absence.

To determine the equilibrium voltage dependence of the internal Mg block, we plotted the ratio of the current available in the presence versus the absence of internal Mg and fit this relationship with Eq. 6 (Fig. 5 D). Under conditions of symmetrical K, a fit of Eq. 6 yielded a value of the equilibrium constant in the absence of an applied field (K_a ⁰) of 431 M⁻¹ and an effective electrical distance δ of ∼0.36, suggesting that Mg crosses a significant fraction of the electric field to reach its binding site (but see also the Discussion with respect to K_IR channels).

We next examined the origin of the voltage dependence by determining k_on and k_off at depolarized potentials. We performed this analysis in two ways. First, we evaluated the rate constants and the association constant (K_a) from the values of τ_block (Fig. 5, B and F1) and the unblocked fraction of the current (Fig. 5 D) by solution of Eqs. 1–3 (see Materials and methods). We performed this analysis with values of I_t determined from either the extrapolated amplitude of the exponential fits or from scaled versions of the Mg-free IV relationships. These two approaches yielded essentially identical estimates of each parameter (compare open upright and inverted triangles in Figs. 5, F2–4). Second, we determined the rate constants from linear regression to plots of 1/τ_block versus the free Mg concentration (Fig. 5 E), where k_on at each voltage is the slope of the appropriate line and k_off its zero concentration intercept. These estimates of k_on and k_off (and the derived value of K_a) are plotted as upright filled triangles in Fig. 5 (F2–4).

Several things are apparent. First, all approaches yielded similar measures of k_on, k_off, and K_a. Second, the variation of k_on with voltage is well described by Eq. 4 (solid blue line in Fig. 5 F3, R² = 0.9997), yielding values for k_on ⁰ and δ_on of 7.97 * 10⁵ M⁻¹s⁻¹ and 0.19, respectively. Third, k_off is only poorly described by Eq. 5 (solid blue line in Fig. 5 F4, R² = 0.246), suggesting the derived values of k_off ⁰ and δ_off (936 s⁻¹ and 0.03, respectively) are unlikely to be accurate.

We considered two possibilities for the deviation in behavior of k_off from a simple exponential relationship. First, that this arises from an experimental error in estimation of the blocking parameters. Second, that this reflects complexity in the blocking mechanism.

The most likely sources of experimental error are (a) contamination of τ_block as a consequence of the finite clamp response time and (b) errors in the determination of P_unblock. Although τ_block is fast, 66 μs at +200 mV, it is only at this potential that it approaches the clamp response kinetics (10–90% rise time is on the order of 10–20 μs, see Fig. 8 and discussion thereof), suggesting the clamp kinetics should not have a marked impact at lower voltages. However, not only is k_on well behaved across all voltages, the deviations in k_off are marked at lower potentials. Accordingly, we consider the clamp kinetics to be a relatively minor factor. Similarly, while modest errors in P_unblock (which is a small value at very depolarized potentials, see Fig. 5 D) could translate into a significant error in the estimation of k_off based on Eq. 2, this will not impact estimation of k_off based on regression to the inverse of the time constants at different free Mg concentrations (which relies only on τ_BLOCK). As k_off determined by these two approaches shows close correspondence, we conclude that errors in P_unblock are unlikely to fully account for the deviant behavior of k_off.

In light of the above arguments, we conclude that the concave relationship of k_off with voltage represents true deviation of the Mg block reaction from that shown in Scheme 1. Accordingly, we have used our measures of k_on and of K_a ⁰ and δ (as obtained from the fit to the equilibrium block) to reevaluate k_off ⁰ and δ_off (estimated to be 1848 s⁻¹ and 0.17 based on the 0 mV solution of Eq. 3 and δ − δ_on, respectively) and then explored the predicted behavior of k_off to consider the reasonableness of these new parameter estimates. Two observations suggest these estimates may be more reasonable. First, the predicted values of k_off correspond very closely to the values observed at +50 to +100 mV with deviations becoming marked only at higher field strengths (compare the blue dashed line and open symbols in Fig. 5 F4). Second, the value of τ_block at negative potentials predicted from these estimates of the k_off parameters (83 μs at −140 mV) is an order of magnitude faster than that estimated if the voltage dependence follows the shallow relationship determined by the regression analysis (when τ_block at −140 mV is estimated to be 718 μs, see the inset in Fig. 5 F1 for a full comparison of the predicted voltage dependence of τ_block for the two k_off parameter sets). The faster unblock accords more closely with the very fast reversal of block observed at such potentials (see, for example, Fig. 3 D). The origin of the nonexponential behavior of k_off and the implications of k_off kinetics on the physiological impact of Mg block are considered further in the Discussion.

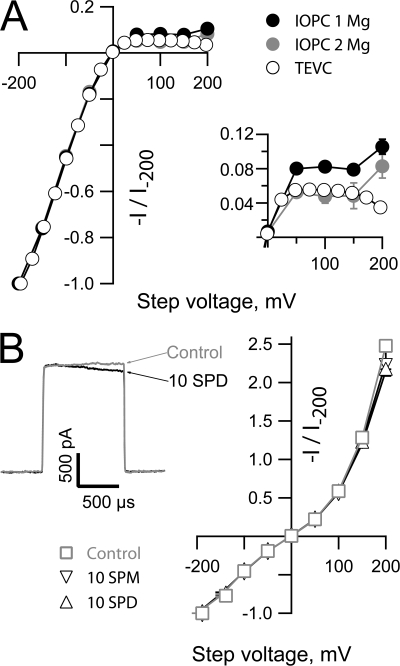
Does Mg block account quantitatively for the rectification observed in TEVC? A comparison of the normalized IV relationships obtained in IOPC and TEVC (Fig. 6 A) reveals that while inclusion of Mg in the internal solution in IOPC can largely recapitulate the rectification observed in the whole cell currents obtained in TEVC there are two notable discrepancies between the datasets (see inset in Fig. 6 A for an expanded view of the IV relations at depolarized potentials). First, an increase in the IOPC current at extreme positive potentials is not observed in the whole cell current. Second, the extent of rectification observed in TEVC is only quantitatively reproduced in IOPC when the free Mg concentration is increased to ∼1.9 mM while the bulk free concentration in an oocyte is estimated to be closer to 0.3 mM (Gabriel and Gunzel, 2007). These observations suggest that either block by other polyvalent cations contributes to the shape of the whole cell current or the action of Mg is modified in the context of an intact cell. Given that polyamines act as important blockers of other classes of Mg sensitive channels, we asked whether the open HCN2 current was sensitive to spermine or spermidine when these ions were presented in the absence of Mg. Although both ions exerted a weak slow block at very depolarized potentials (see left panel of Fig. 6 B for an example of the effect of 10 μM spermidine on the HCN2 current at +200 mV) neither ion had any noticeable effect on the current amplitude at lower voltages. Thus, while block by polyamines may account for the divergence in the TEVC and IOPC IV relationships above 150 mV, these molecules are not responsible for the suppression of the whole cell current at lower potentials. We consider possible explanations for the quantitative discrepancy between the effectiveness of Mg in IOPC and suppression of the TEVC current further in the Discussion.

Figure 6.

Spermine and spermidine are inefficient blockers of the HCN2 current. (A) Plateau tail currents obtained from the TEVC and IOPC experiments shown in Figs. 1 and Figs.5 were normalized with respect to the amplitudes of the currents observed at −200 mV and plotted with respect to the observed (TEVC) and the command potential (IOPC). Data are plotted as mean ± SEM. The errors around the voltage in TEVC were always smaller than the symbols. The inset shows an expanded view of the IV relations at depolarized potentials. (B) Representative recording obtained upon stepping to +200 mV in the absence and presence of 10 μM spermidine (SPD) and normalized open channel IV relationships in the absence (n = 6) and presence of 10 μM SPD (n = 3) or spermine (SPM, n = 5) determined using the protocol described in Fig. 5 and plotted as mean ± SEM versus the command potential. Test steps were applied at 4 Hz from an activation potential of −155 mV in the absence of added divalent ions and the presence of 1 mM EGTA, 1 mM EDTA, and 30 μM cAMP with K as the only alkali metal on either side of the membrane ([K]_OUT 117 mM; [K]_IN 121 mM).

Mg Block Reshapes the HCN2 Current in the Presence of Physiological Ion Gradients

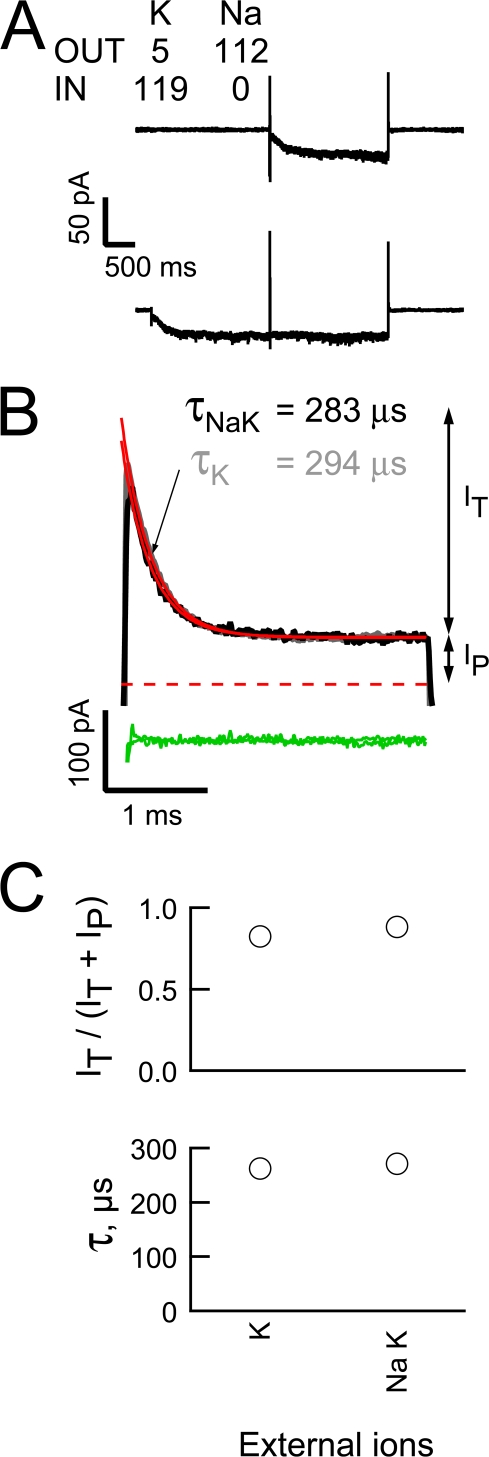
In TEVC, the open HCN2 channel current shows an unanticipated linearity in the presence of physiological concentrations of Na and K consistent with Mg acting as a blocker under these ionic conditions (Fig. 1). However, as suppression of outward flux is weaker than is observed when external K is elevated (in a manner not simply accounted for by the shift in the reversal potential, Fig. 1 H), we wondered if internal Mg block is sensitive to the identity of external ions such that it is weaker or lost when Na is the major external alkali metal.

Fig. 7 A shows averaged “active” and “leak” records collected using the voltage paradigm described in Fig. 3 but with our quasi-physiological ion gradients. As observed when elevated concentrations of K were present on both the internal and external face, elimination of uncompensated linear leakage currents (by subtraction of the “leak” from the “active” records) isolates the outward HCN2 current and reveals that this has a clear predeactivation transient component (Fig. 7 B, black trace). Importantly, this record superimposes on a scaled version of a predeactivation tail obtained in the presence of elevated K (Fig. 7 B, gray trace) while the relative amplitudes of I_t and I_p (Fig. 7 C, top) and the time constant of the predeactivation decay (Fig. 7 C, bottom) under the two ion conditions are indistinguishable. These findings demonstrate that Mg block contributes to shaping the HCN2 current under physiological ion gradients. Interestingly, the close correspondence of the IOPC-determined block parameters (Fig. 7 C) suggests that the dissonance in the strength of rectification observed in the data shown in Fig. 1 has a different origin to Na and K sensitivity of the Mg block but we have not explored this further.

Figure 7.

Mg blocks the outward HCN2 current in the presence of physiological gradients of Na and K. (A and B) Averaged sweeps (A) and subtracted predeactivation HCN2 channel +80-mV tails (B) (three and two “leak” and “active” records collected as described in Fig. 3 except for the use of quasi-physiological gradients of Na and K, black lines). In B, the gray line is the K tail shown in Fig. 4 B scaled to the amplitude of I_p of the mixed ion tail. The red and green lines represent fits of a single exponential function and the resultant residuals for the two transients. (C) Plot of the extent (top) and time constant (bottom) of block at +80 mV in the presence of elevated K or physiological levels of Na and K in the extracellular solution. Data are mean ± SEM and range from five and two recordings, respectively.

K Dependence of the HCN Channel Current Emerges from K Occupancy of a Permissive Site within the Pore and Not K Suppression of a Na Sensitivity of the Mg Block

Does the K dependence of conduction arise from K binding to a site within the pore or at some regulatory site outside of the permeation pathway? Does this K dependence arise because Mg is only efficiently displaced from its blocking site when K occupies the regulatory site?

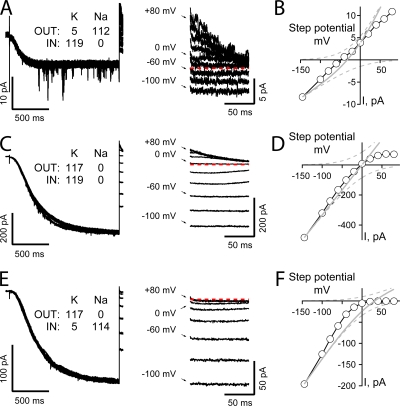
To explore these questions, we adopted the same protocol as shown in Fig. 5 with the exception that K was present only on the external (Fig. 8, A–C) or internal (Fig. 8, D–F) face with Na as the only alkali metal ion on the opposite side and EDTA replacing Mg in the intracellular solution. Inspection of the “on” and “off” phases of the steps to ±200 mV (Fig. 8, A and D, wherein records have been averaged, subtracted, and temporally aligned with respect to the onset of each step) and the current voltage plots obtained there from (Figs. 8, B and E) shows that, even in the absence of internal Mg, Na does not carry a detectable current when K was only present on the trans face irrespective of the orientation of the ion gradients. These results reveal that the loss of Na flux does not arise because Na cannot displace the block by internal Mg but, rather, K association with a control site within the pore of the channel permits the passage of Na.

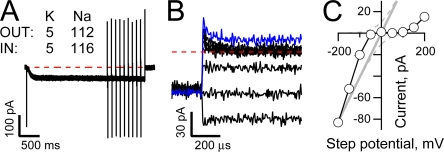
Interestingly, the ability of K to support a Na flux is asymmetrical such that a low external concentration of K supports an inward Na current but an equivalent concentration of K presented to the internal face supports outward flux of Na only poorly, if at all (Fig. 9). These findings demonstrate that inherent asymmetries in the energetics underlying inward and outward movements of Na and K also contribute to the conductance asymmetry of the HCN2 pore.

Figure 9.

Asymmetry in the ability of low concentrations of K to support Na conduction gives rise to a Mg-independent form of inward rectification. (A) Unblocked HCN2 currents were collected and processed as described in Fig. 8 except the major charge carrier in both internal and external solutions was Na with K included at only 5 mM. Records are averages of 10 “active” sweeps before subtraction of the averaged cognate “leak” sweeps (not shown for simplicity). (B) Leak-subtracted records obtained in response to steps from −140 mV to potentials ranging from −200 to +200 mV with the later sweep highlighted in blue. (C) Plateau tail current amplitudes (measured 1 ms after the beginning of each test step) plotted versus the corresponding step potential.

The Kinetics of Collapse and Recovery of Unidirectional K Fluxes Are Rapid

Inspection of the current records in Fig. 8 (A and D) suggest that the collapse of conduction and its recovery may occur with rapid, but different, kinetics. To what extent do these kinetics report on ion movements in the channel rather than on the effects of the finite response properties of the clamp? To examine this in more detail, we inverted the leak-subtracted current obtained at the end of each test step and, after normalizing the amplitudes with respect to the equilibrium level at each potential, we superimposed these “off” records onto the normalized “on” records such that zero time represents the beginning of both the “on” and “off” voltage transients. Consideration of these normalized plots (Fig. 8, C and F) shows two things: (1) current recovery (blue traces) is slower than the rate of loss of channel function as K exits the pore (black traces) but (2) the anticipated oppositely directed transients as the channels become nonconducting are poorly (see red circled part of traces in Figs. 8, A and D) if at all detectable on top of the rising phase that takes ∼10 μs to evolve. The later observation suggests that the rising phase of the black traces is predominantly accounted for by the clamp's kinetics. Does this mean that the slower rate of rise of the blue traces informs us that the rate of restoration of the channel function as K reenters the pore is slow? We suspect not. It seems probable that this simply reflects the longer time constant of the system when the channels are initially nonconducting (and the patch resistance high). Nonetheless, these records show that current recovery cannot be slower than 10–20 μs. That is the rate of reentry of K and/or any conformational changes required to reestablish flux is not markedly different from the optimal ion transit time observed when the pore is multiply occupied by K (∼0.5 to 3 μs based on the single channel conductance determined at negative potentials).

DISCUSSION

Here, we have analyzed the mechanistic basis of ion-dependent control of conduction in HCN pacemaker channels. Our results show that inward current rectification arises because the open HCN channel pore undergoes a voltage-dependent block by internal Mg, a collapse of conduction when the pore is not occupied by K ions combined with an inherent asymmetry in ion movements in the conducting pore. Since each of these processes occurs in the submillisecond time domain our findings suggest changes in the conductance profile of pacemaker channels are fast enough to allow these “slow” channels to influence the fastest of cellular events. Below we discuss the mechanistic and physiological implications of these findings in greater detail.

Biophysical Properties of Internal Cation Block in HCN Channels and Comparison with K_IR and K_V Channels

Where is the Mg site located and what do the results tell us about the shape of the field in an open HCN channel pore? To explore this question, it is instructive to consider the behavior of other channels that are sensitive to cation block.

In K_IR channels, polyvalent cations interact with at least two sites, one formed from S6 residues lining the inner vestibule and a second formed from residues in the cytoplasmic extension of S6. However, these sites are thought to lie outside the field per se such that the voltage dependence of block (which resides predominantly in the off rate) arises from coupling of blocker occupancy to the inward K flux (Bichet et al., 2003; Lu, 2004). In contrast, in ShakerB and K_V3.1 (where Mg appears to cross 0.41 and 0.37 of the electric field to reach its blocking site) the distance from the intracellular solution to the barrier is determined by the identity of the amino acid at the second position of the selectivity filter (TVGYG versus TLGYG) (Harris and Isacoff, 1996) rather than more cytoplasmic structures.

While the available data do not provide definitive insights into the location of the Mg site(s) in HCN channels, we consider them to be most readily reconciled with Mg penetrating deeply into the pore and binding to a site within the field, that is, close to, or within, the selectivity filter (Jiang et al., 2002). First, mutation of critical residues within the central core of the post-S6 cyclic nucleotide gating ring does not restrict ion flow (Johnson and Zagotta, 2005), suggesting Mg binding here will not be able to restrict flux either. Second, k_on is robustly voltage dependent in HCN channels, a finding that distinguishes block here from block in K_IR channels. Within this canon, the Mg site would be close to that of externally presented Cs, which appears to cross ∼0.7 of the electric field of native and expressed pacemaker channels (DiFrancesco, 1982; Moroni et al., 2000).

What does the deviation of k_off from exponential behavior tell us? If we are correct and this does not arise from sensitivity of parameter estimation to experimental error then it suggests that either Mg can permeate through the HCN pore at positive potentials (such that the deviation of k_off from the simple exponential relationship is a consequence of Mg obtaining access to this additional path) or that Mg does not fully occlude the channel (as retention of a small conductance in the presence of bound Mg would tend to overestimate P_unblock in the high voltage range). While the former interpretation is consistent with Mg entering the filter, the later explanation is difficult to reconcile with such a mechanism. Clearly, further analysis of the location, stoichiometry, and efficacy of Mg (and, potentially, other polyvalent cation) binding is warranted as this will not only yield insight into the physical and electrostatic architecture of the pore but will better define how this process dynamically shapes I_H across the physiological voltage range.

Are the Kinetics of Mg Block Contaminated by Gating?

This question has two elements. First, are the experimental measures of block influenced by gating and, second, does the choice of model used as a framework for analysis influence parameter estimation? The second issue is important as Scheme 1 cannot simultaneously account the sigmoidicity of gating, the prepulse-dependent nature of HCN channel tail current kinetics, a maximal open probability less than 1, and slow opening combined with relatively fast closing (rather, such observations require use of a model that incorporates multiple closed and open states, see Introduction and Results) while it also explicitly ignores closed state binding. Despite these limitations in the model, we think our measures and our parameter estimations are reasonable for the following reasons.

First, redistribution from closed to open and open-blocked states is unlikely to influence our findings because the observed, model independent gating kinetics are at least two to four orders of magnitude slower than the block kinetics. Thus, at depolarized potentials (e.g., +50 to +200 mV as used experimentally), τ_block in the presence of 0.924 mM free Mg is 100–600 times faster than the limiting rate of the exponential phase of deactivation (time constant of ∼40 ms; Chen et al., 2007) while at hyperpolarized potentials the rate of Mg unblock is 700–6,000 times faster (at −140 mV depending on the parameters assumed for estimating k_off) than opening (∼2 s⁻¹, Chen et al., 2007) (see Figs. 3, B and D, Fig. 4 A, and Fig. 5).

Second, redistribution between open states during the depolarized blocking step is unlikely to be significant as (a) block is well described by a single exponential, suggesting it involves a single site (although this would also be observed if the architecture of the Mg site is similar in the different open states), and (b) the times and voltages we use to activate the channels are long enough and hyperpolarized enough to not only fully activate the channels but permit equilibration across the open states before the onset of the blocking step (Mannikko et al., 2005; Elinder et al., 2006; Bruening-Wright and Larsson, 2007).

Third, the primary effect of closed state binding would be to bias activation rather than alter our measures of open state block. Moreover, as opening at very negative voltages in the presence of cAMP appears to be very favorable (such that all preopen activated states such as CA and a “voltage sensor desensitized” state not shown in Scheme 1 for simplicity should be largely depleted under our conditions; Shin et al., 2004; Johnson and Zagotta, 2005; Dekker and Yellen, 2006; Lyashchenko et al., 2007), the effect of closed state binding should be largely eliminated from our data.

Finally, it is relevant to ask to what extent channel opening at voltages that are nonpermissive for voltage-dependent activation may contribute to the data reported here. Although our experiments were not designed to detect flux through open-resting channels, we noted no systematic difference in the seal resistance as a function of the density of active channels in the patch, an impression that accords with recent reports wherein the contribution of these open-resting states to flux has been progressively revised downward such that it appears to represent no more than 2 × 10⁻² (Proenza and Yellen, 2006) and maybe less than 2 × 10⁻⁴ (Chen et al., 2007; Lyashchenko et al., 2007) of the open-activated current. Moreover, as our digital leak subtraction does not rely on P/N type scaling but our “leak” records differ from the “active” records only in the time at the activating potential (1.5–3 s for “active” current versus 5 ms for the “leak”), the leak and active records would each have the same open-resting component such that any component not eliminated by use of the analogue “leak” circuit on the clamp will, presumably, be eliminated upon digital subtraction.

Is Mg the Endogenous Blocker that Gives Rise to Suppression of the Outward HCN2 Current in Intact Cells?

Suppression of the outward HCN2 whole cell current is mimicked by inclusion of Mg in IOPC. However, the concentration of Mg required to fully recapitulate the TEVC IV relationship is approximately six times higher than the estimated free concentration of the alkaline earth in Xenopus oocytes (Gabriel and Gunzel, 2007). Does this mean that Mg is not the endogenous regulator of the open channel current or do these results indicate the effectiveness of intracellular Mg is plastic? Although we have not exhaustively explored these questions we suspect that the later explanation is correct. Thus, neither polyamines nor Ca appear likely candidates for the endogenous blocking particle; polyamines are ineffectual blockers of the HCN2 current in IOPC recordings (see above) while the effects of Ca on pacemaker channels appear to involve a cAMP-mediated increase in the current amplitude (Hagiwara and Irisawa, 1989; Luthi and McCormick, 1998, 1999). Accordingly, we suggest that either the effective concentration of Mg at the internal mouth of HCN channels is elevated in intact cells due to the presence of labile anionic lipids (such as free fatty acids or phosphatidylinositols) or the interactions with such messengers raises the Mg affinity of the channel due to lipid-sensitive changes in the architecture of the pore, a mechanism that appears to predominate in the phosphatidylserine enhancement of BK channel K conductance (Park et al., 2003).

Locus of K Binding Site(s) that Control Ion Flux and Gating in HCN Channels

Our results directly address the question of the location of the “permissive” K site that allows HCN channels to carry a Na current. In the absence of internal divalent ion block, HCN channels do not support a measurable Na flux when K is present only on the trans face. Thus, HCN channels require K to occupy one or more sites within the pore to maintain significant Na conduction.

Is this the same site or sites that allow permeant ions to control gating kinetics? Although we have not explored the kinetic behavior of the channels under our conditions, two lines of evidence suggest that this is likely to be the case. First, Larsson and colleagues have shown that lowering K occupancy of the pore (by using a low external K concentration coupled with a physiological level of Na or partially blocking the inward flux of elevated external K by inclusion of 1 mM Cs) alters the kinetics of the redistribution between open states, a change that they suggest reflects a stabilization of the voltage sensor in the activated conformation and is therefore a reflection of the ion control of gating per se. Second, mutation of A352 (Azene et al., 2003), A354 (Azene et al., 2005), and C347 (Bell et al., 2002), residues that lie at either end of the selectivity filter (CIGYGAQA), suppresses the K sensitivity of HCN1 channel gating and, at the external locations, do so without altering ion selectivity. These findings are in keeping with gating-coupled flexibility of the filter being an important determinant of selective ion binding (Noskov and Roux, 2007). However, it should be noted that it has not been established whether these residues contribute to the ion binding site or indirectly alter coupling of ion binding to gating nor has it been determined whether such channels can carry a substantial Na current in the absence of K as might be anticipated.

Is Conductance Collapse in the Absence of K due to a Loss of Ion–Ion Coupling that Promotes Conduction or a Rapid Equilibration between a Conducting and a Nonconducting State?

Our results indicate that the recovery (and possibly collapse) of conduction occurs within a time interval of 10–20 μs or faster, a rate that is close to that at which K ions transit the pore when K is the sole charge carrier and is presented at a high concentration (∼0.5–3 μs with a driving force of between 50 and 200 mV and a single channel conductance of 1–2 pS, DiFrancesco, 1986; Johnson and Zagotta, 2005; Dekker and Yellen, 2006; Lyashchenko et al., 2007). These observations raise an interesting question. Is conduction slow because ion-–ion repulsion is not efficient even in a pore occupied by multiple K ions or because the pore undergoes a fast equilibrium between conducting and nonconducting configurations but with the conducting state very unstable even in the presence of K?

While resolution of this question will require an independent measure of the rate at which the last K leaves the pore (which in higher conductance K channels is slow with a time constant of ∼150 μs, Baukrowitz and Yellen, 1996) and of the architecture of the openings of single HCN channels, it is interesting to note that functional, structural, and molecular dynamics simulation studies in K channels show that (a) in low K, the pore of K-selective channels adopts a nonconductive arrangement wherein sites 2 and 3 are effectively lost and are replaced by an enlarged vestibule in the middle of the filter (Zhou and MacKinnon, 2003; Lockless et al., 2007) and this “collapsed” arrangement of the K channel pore is similar to the architecture of the presumptive conducting configuration of a bacterial NaK channel pore (Shi et al., 2006); (b) if collapse of the K channel filter is prevented by mutation of one of the filter glycines to d-alanine, the channel can carry Na in the absence of K (Valiyaveetil et al., 2006); (c) the pore of K channels undergo marked rearrangements during ion transport, changes that may underlie fast flickering as the open channel transiently “blocks” itself (Noskov et al., 2004; Berneche and Roux, 2005; Noskov and Roux, 2006); and (d) rearrangements of the filter appear to underlie voltage gating in KcsA (Blunck et al., 2006; Cordero-Morales et al., 2006a,b) and the emergence of brief sojourns in subconductance states during opening of Shaker channels (Zheng et al., 2001).

Physiological Function of Permeant and Impermeant Ion Control of HCN Channels

We hypothesize that the fast changes in conductance we have characterized may allow “slow” pacemaker channels to help shape cellular physiology in a temporal domain where heretofore the channels were thought to be passive players. Thus, the onset of block by Mg may serve to limit the outward flux of K during depolarizing sojourns while alterations in ion concentrations in restricted diffusional spaces (such as a dendrite where intracellular Na can rise to 100 mM; Rose, 2002) may lead to ion-sensitive collapse of the I_H conductance and modification of the electrical properties of the compartment. The hypothesis that the conductance as well as the gating (Pian et al., 2006; Zolles et al., 2006; Fogle et al., 2007) of HCN channels is sensitive to lipid messengers suggests additional ways in which “slow” pacemaker channels may influence cellular excitability.