Asymmetry of Reinforcement and Punishment in Human Choice

Abstract

The hypothesis that a penny lost is valued more highly than a penny earned was tested in human choice. Five participants clicked a computer mouse under concurrent variable-interval schedules of monetary reinforcement. In the no-punishment condition, the schedules arranged monetary gain. In the punishment conditions, a schedule of monetary loss was superimposed on one response alternative. Deviations from generalized matching using the free parameters c (sensitivity to reinforcement) and log k (bias) were compared in the no-punishment and punishment conditions. The no-punishment conditions yielded values of log k that approximated zero for all participants, indicating no bias. In the punishment condition, values of log k deviated substantially from zero, revealing a 3-fold bias toward the unpunished alternative. Moreover, the c parameters were substantially smaller in punished conditions. The values for bias and sensitivity under punishment did not change significantly when the measure of net reinforcers (gains minus losses) was applied to the analysis. These results mean that punishment reduced the sensitivity of behavior to reinforcement and biased performance toward the unpunished alternative. We concluded that a single punisher subtracted more value than a single reinforcer added, indicating an asymmetry in the law of effect.

Behavior analysts have debated the symmetrical nature of reinforcement and punishment, specifically, whether a punisher and a reinforcer have equal, though opposing, effects on behavior (e.g., Balsam & Bondy, 1983; Farley & Fantino, 1978; Smith, 1971). The subtractive (i.e., direct-suppression) model of punishment suggests that a punisher directly subtracts value from the reinforcer earned from performing a response (see deVilliers, 1980). What is unclear, however, is how much value a single punisher subtracts from a reinforcer. One possibility is that a single punisher subtracts the value equivalent to a single reinforcer; another is that punishment may also have side effects, such as elicited responses that are incompatible with the operant (see Sidman, 1989), amplifying its impact such that a single punisher subtracts more value than a single reinforcer adds (see Epstein, 1985).

Schuster and Rachlin (1968) attempted to separate the subtractive properties of aversive stimuli from their side effects on key-pecking in pigeons by using contingent and noncontingent shock. They reasoned that contingent shock could capture both properties of punishment, but noncontingent shock would capture only the side effects. If a noncontingent aversive stimulus reduced behavior, then an argument could be made that the side effects produce an additional suppressive effect, deeming punishment more potent than reinforcement. In their study, food and shock were delivered under a concurrent chains schedule. The initial links were presented as a concurrent variable-interval (VI) 2-min VI 2-min (conc VI 2-min VI 2-min) schedule of terminal link access. The terminal links were identical VI 1-min schedules that differed with regard to shock programming and the stimuli that accompanied each schedule. For one terminal link, responses also produced response-contingent shocks under an FR 1 schedule of reinforcement. In the other terminal link, shocks were delivered independently of responding under a variable-time schedule that ranged between 0 and 120 shocks per min. Responses in the terminal link of the contingent-shock key were suppressed, but little change was exhibited in responses in the terminal link that contained noncontingent shock. The authors concluded that (a) the contingency between response and punisher is essential in order to reduce behavior, and (b) as behavior did not decrease in the noncontingent shock condition, the putative side effects of aversive control were negligible. Hence, the authors argued that punishment is symmetrical to reinforcement, because, as with punishment, side effects are unnecessary to describe a reinforcer's influence on behavior. It is noteworthy, however, that in this study, behavior under reinforcement and punishment conditions was not analyzed for asymmetry. To determine symmetry directly, for example, a second concurrent chains schedule, in which behavior is arranged under contingent and noncontingent reinforcer deliveries, would be needed. In the absence of such, any conclusions about symmetry between reinforcement and punishment must be considered tentative.

Direct comparisons of the relative effects of reinforcers and punishers on behavior are often difficult to make because the punishers and reinforcers (e.g., food vs. shock) are qualitatively different stimuli that cannot be easily compared using a common metric (see deVilliers, 1980; Schuster & Rachlin, 1968). One way to standardize a reinforcer–punisher comparison is to use a reinforcer and punisher with the same dimension. Critchfield, Paletz, MacAleese, and Newland (2003) arranged gain and loss of money under concurrent schedules of reinforcement and punishment. After demonstrating that monetary loss and monetary gain could function as a punisher and a reinforcer, respectively, the authors used the point-loss punisher to compare two models of punishment. One was an additive model, in which punishment adds to the reinforcing efficacy of other, unpunished behavior. The second was a subtractive model in which punishment subtracts from the reinforcing value of the targeted operant. The authors found strong support for the subtractive model of punishment. We used Critchfield et al.'s approach in the present study to address the issue of symmetry in a subtractive model of punishment. Specifically, the question addressed in the present study was whether one cent lost was equivalent to one cent gained in terms of its effects on behavior.

Under a conc VI VI schedule, two alternatives are available simultaneously. Behavioral allocation to the two alternatives has been described quantitatively using the generalized matching relation (Baum, 1974), a power-law formulation that captures two sources of deviation: bias and sensitivity. The generalized matching relation is described as:

1

where the ratio of behavior allocated to two alternatives (B_a and B_b) is related to the ratio of reinforcers earned under those two alternatives (R_a and R_b). The two free parameters, log k and c, describe bias and sensitivity, respectively. Bias in behavioral allocation may come from historical factors or characteristics of the experimental setting, such as hedonic preference for one reinforcer over another (Miller, 1976) or difficulty operating one response device, that appears as disproportionate responding on one alternative, irrespective of reinforcer frequency (Davison & McCarthy, 1988). If log k > 0, a bias toward the numerator (alternative a in equation 1) is evident; if log k < 0, a bias toward the denominator (alternative b) is evident. Sensitivity refers to the degree to which the ratio of responding on the two alternatives tracks the reinforcer ratio, i.e., the sensitivity of behavior to reinforcement. When c  =  1, matching is obtained so that an increase in the reinforcer ratio results in an equivalent increase in behavior allocation. If c < 1, then a change in the response ratio is less than a change in the reinforcer ratio. This is called undermatching, meaning behavior is less sensitive to reinforcer ratios, and is a common finding with humans and nonhumans (Kollins, Newland, & Critchfield, 1997). When c > 1, changes in response ratios will be greater than changes in reinforcer ratios. This is called overmatching and implies that behavior is relatively more sensitive to reinforcer ratios. Overmatching may occur, for example, if there is a high cost for changing alternatives or if changing from one alternative to another is punished (Todorov, 1971).

If a schedule of punishment is superimposed on one alternative (or both alternatives, as in Critchfield et al., 2003) of a concurrent schedule, then more behavior is allocated toward the no-punishment alternative despite the continued availability of reinforcers under the punished alternative (Deluty & Church, 1978; deVilliers, 1980; Farley & Fantino, 1978; Todorov, 1977.) Few studies have examined matching with human participants and punishment, but in those studies, the punisher tends to subtract value from the reinforcers earned on an alternative, changing the value associated with that alternative and, therefore, the proportion of behavior allocated to the punished alternative (e.g., Bradshaw, Szabadi, & Bevan, 1979; Critchfield et al., 2003; Katz, 1973; Wojnicki & Barrett, 1993.)

If two consequences with a common metric, such as money lost or money earned, function as a punisher and as a reinforcer, respectively, then log k can be used to determine whether reinforcement and punishment are symmetric in their effects. Consider the two alternatives under a conc VI VI schedule in which no punisher is used. Under the richer alternative 10¢ may be earned per unit time, and, under the leaner alternative, 5¢ may be earned per unit time. The generalized matching relation predicts that slightly less than twice as many responses should occur on the richer alternative (assuming slight undermatching) compared to the leaner alternative. If a punishment schedule is then superimposed on the richer alternative, such that 5¢ are lost and 10¢ gained, then the net value of reinforcement would likely be reduced from its baseline of 10¢. The question is: By how much will it be reduced? If a cent lost is equal to a cent gained, then the loss can be calculated easily: 10¢ earned minus 5¢ lost equals 5¢ and there should be no preference of one condition over the other. This prediction holds, however, only if the punisher affects behavior in a manner symmetrical to the reinforcer, i.e., if, behaviorally, 10 minus 5 equals 5. Conversely, if a punisher is weighted more heavily than a reinforcer, then more behavior is predicted to be distributed to the unpunished alternative under the concurrent schedule than such simple subtraction would predict. Applying this reasoning to the generalized matching relation, if the weight of a punisher is equal to the weight of a reinforcer, then bias (log k) should equal 0 when net reinforcers (money earned minus money lost) are used. However, if a punisher is weighted more than a reinforcer, then log k should move in the direction associated with the unpunished alternative.

To examine the symmetry of reinforcement and punishment, we compared net reinforcers (money delivered minus money lost) with obtained reinforcers (money delivered) using Equation 1. If the use of net reinforcers in a punishment condition results in no bias beyond that seen in the no-punishment condition, then matching may be said to be based solely on relative net reinforcement rates, including what point loss subtracts from the obtained number of reinforcers. In this case, symmetry is supported. If there is additional bias, however, in the punishment condition, then this contradicts the claim of symmetry between reinforcers and punishers.

It was hypothesized that undermatching would occur under the no-punishment schedules as has been reported previously for humans (see Kollins et al., 1997, for review), and that no bias would be observed. Under the punishment schedules, however, it was hypothesized that a bias toward the unpunished alternative would be observed, indicating that a punisher was more heavily weighted than a reinforcer. In addition, it was hypothesized that punishment would also reduce sensitivity to reinforcement, as other punishment studies using concurrent schedules have shown (Bradshaw et al., 1979; deVillers, 1980.)

Method

Participants

Five male undergraduate students enrolled in psychology courses at Auburn University were recruited to participate in up to five 2-hr blocks of time in exchange for money.

Materials

An IBM-compatible computer was used to present visual images, transduce responses from the participants, arrange monetary loss and gain, and record data. All code was written in VisualBasic®. Participants were placed individually in small, separate, office-sized rooms containing a desk, chair, computer monitor, mouse, and mouse pad.

Procedure

The procedure was similar (though not identical) to that reported by Critchfield et al. (2003). Each participant completed a consent form and was given a set of instructions to read before beginning the experiment:

In front of you is a computer monitor. Click your mouse on the START box, and a new screen will appear. You will now see a screen with two moving targets on it. Clicking the mouse on these targets can cause you to earn or lose money. When this happens, a flashing message will show how many cents you gained or lost. The two targets may differ in terms of how clicking affects your earnings. It is your job to figure out how to earn as many points as possible.

After the participant mouse-clicked a START icon on the monitor, an 8-min session commenced. First, a setup screen appeared that was split vertically in half. A small colored box appeared in the middle of each half of the screen. For each participant, the right box (alternative A) and left box (alternative B) were different colors, though the same two colors were associated with the same boxes for the same participant throughout the experiment. A mouse-click on either box set both boxes in motion in separate random patterns at a constant rate over each box's respective half of the screen. Each box was associated with a VI schedule of reinforcement (described below). The reinforcing stimulus was a white, flashing “+4¢” icon that appeared on the screen for 2 s, indicating that four cents had been earned. No cumulative money counter was associated with either alternative, nor was there a counter that tallied total earnings. Participants could switch from one side of the screen to the other throughout the session. A 2-s changeover delay was imposed for each switch. During this delay, mouse clicks had no scheduled consequences. Participants completed 10–12 sessions in a 2-hr block and completed no more than five blocks.

No-punishment Condition

Table 1 summarizes the experimental conditions for each participant. Each participant responded under three conc VI_A VI_B schedules (“A” represents the schedule value on alternative A, the left side of the screen, as represented in Equation 1. “B” represents the value on alternative B, the right side). VI schedules were arranged using Fleshler and Hoffman's (1962) constant probability distributions. Sessions continued until stability occurred under each schedule. Stability was defined as three consecutive sessions in which response allocation (percent of responses on alternative A) differed by no more than ±0.05 of the mean of the last three sessions, and no trends were observable. The following schedules were used: conc VI 12-s VI 60-s, conc VI 20-s VI 20-s, and conc VI 60-s VI 12-s. For example, under conc VI 12-s VI 60-s, the first mouse click on alternative A produced the reinforcer after an average of 12 s had elapsed; for alternative B, the first mouse click after an average of 60 s had elapsed, on an independent but concurrently running clock, produced a reinforcer. These three schedules collectively will be referred to as the no-punishment condition. The programmed reinforcer ratios for these schedules were 5∶1, 1∶1, and 1∶5, respectively.

Table 1.

Sequence of concurrent schedules for each participant. PUN indicates a schedule that had a superimposed VI schedule of punishment, as explained in the text.

Participant 02	Participant 04	Participant 05	Participant 06	Participant 08
VI 20-s VI 20-s	VI 60-s VI 12-s	VI 12-s VI 60-s	VI 20-s VI 20-s	VI 12-s VI 60-s
VI 60-s VI 12-s	VI 12-s VI 60-s	VI 60-s VI 12-s	VI 12-s VI 60-s	VI 20-s VI 20-s
VI 12-s VI 60-s	VI 20-s VI 20-s	VI 20-s VI 20-s	VI 60-s VI 12-s	VI 60-s VI 12-s
VI 60-s VI 12-s	VI 12-s VI 60-s	VI 20-s VI 20-s	VI 20-s VI 20-s	VI 12-s VI 60-s
VI 60-s (PUN)VI 12-s	VI 12-s VI 60-s (PUN)	VI 20-s VI 20-s (PUN)	VI 20-s (PUN) VI 20-s	VI 12-s (PUN) VI 60-s
VI 20-s VI 20-s	VI 20-s VI 20-s	VI 60-s VI 12-s	VI 12-s VI 60-s	VI 60-s VI 12-s
VI 20-s (PUN) VI 20-s	VI 20-s VI 20-s (PUN)	VI 60-s VI 12-s (PUN)	VI 12-s (PUN) VI 60-s	VI 60-s (PUN)VI 12-s
VI 12-s VI 60-s	VI 60-s VI 12-s	VI 12-s VI 60-s	VI 60-s VI 12-s	VI 20-s VI 20-s
VI 12-s (PUN) VI 60-s	VI 60-s VI 12-s (PUN)	VI 12-s VI 60-s (PUN)	VI 60-s (PUN)VI 12-s	VI 20-s (PUN) VI 20-s

Punishment Condition

After behavior stabilized under the no-punishment schedules, one no-punishment condition was reinstated until stability occurred. Then a VI schedule of point loss was superimposed on one of the alternatives (alternative A for 3 participants, alternative B for 2—see Table 1) of the concurrent schedule. The length of the punishment schedule was 1.25 times the length of the reinforcement schedule. For example, a VI 15-s schedule of punishment was superimposed on the VI 12-s reinforcement schedule. The value of the punisher was −4¢. A red flashing “−4¢” icon was the stimulus associated with monetary loss. For each participant, the punishment schedule was always superimposed on the same alternative. The three concurrent schedules with a conjoint punishment schedule superimposed on one alternative will be referred to as the punishment condition. Each punishment schedule was in effect until stable responding occurred. Once stability was observed, another no-punishment schedule was reintroduced until stability occurred. Then the conjoint punishment schedule was superimposed on one response alternative. In this way the implementation of each punishment schedule alternated with the implementation of each no-punishment schedule (see Table 1). All participants received each of the six concurrent schedules (three with punishment, three without). The experiment was approved by the Auburn University Institutional Review Board.

Data Analysis

Data from the last three stable sessions of each concurrent schedule were used in the analysis. Data from the no-punishment replication conditions were not included in the analysis, as they did not differ from the initial no-punishment conditions (see also Figure 2, which will be introduced later). Measures included the number of responses on alternatives A and B, the net number of reinforcers (the total number of reinforcers obtained on one alternative minus the total number of punishers obtained on the same alternative) under alternatives A and B, the obtained total number of reinforcers (total number of reinforcers only) under each alternative, and the obtained total number of punishers under each alternative per session. From these, response ratios (B_A/B_B) and net reinforcer ratios (R_A/R_B) were employed for analysis. The side on which punishment was superimposed was on the left for 3 participants (alternative A) and on the right for 2 participants (alternative B), though all data will be reported as though the punisher was superimposed on alternative A for ease of explication.

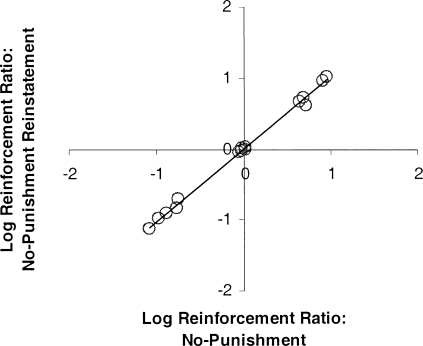
Fig 2.

Mean log reinforcement ratio in the reinstated no-punishment condition plotted as a function of the mean log reinforcement ratio of the initial no-punishment condition. Each point represents the mean of the last three sessions of each schedule for each participant.

The generalized matching relation (see Baum, 1974; Davison & McCarthy, 1988) formed the basis of the analysis of choice (see Equation 1). Briefly, the ratio of net reinforcers on alternative A to those on alternative B, and the ratios of responses on A to responses on B were log-transformed. The log of the response ratio was then expressed as a function of the log net-reinforcer ratio, and these data were fitted using linear regression applied to the log ratios. Functions were fitted using response and reinforcer ratios from the last three sessions of each concurrent schedule for each participant, so nine data points from the no-punishment schedules (three from each schedule) as well as nine data points from the punishment schedules were analyzed for each participant.

Results

No-punishment Schedules

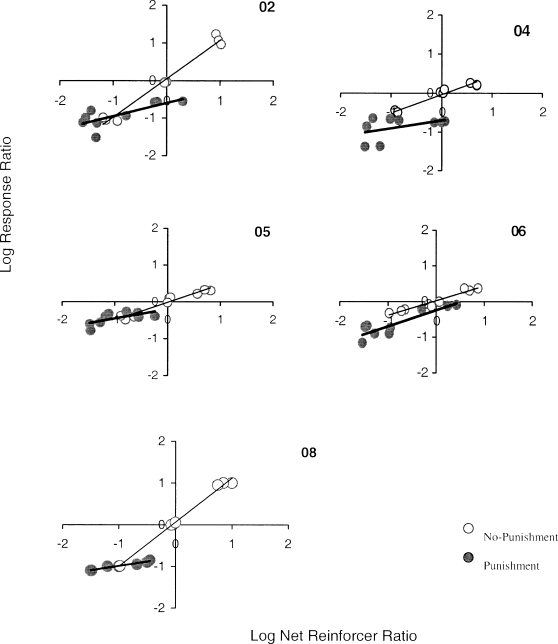
Appendix A shows the mean responses, obtained reinforcers, and obtained punishers on each alternative for the last three sessions of all six schedules for each participant. Figure 1 shows log response ratios (y-axis) plotted against log net-reinforcer ratios (x-axis) for all 5 participants. Open circles represent the no-punishment conditions, and closed circles represent the punishment conditions. Bias (log k) and sensitivity (c) as estimated from Equation 1 for the no-punishment condition are summarized in Table 2. Linear functions described all of the participants' data adequately, accounting for 94 to 99% of the variance. Note that 3 participants (04, 05, and 06) showed undermatching (slopes less than 1). The other 2 participants (02 and 08) demonstrated response allocation approximating ideal matching, i.e., their slopes were near 1. Bias in the no-punishment condition ranged between −0.04 and 0.05. As has been reported in other studies (e.g., Baum & Rachlin, 1969; Brownstein & Pliskoff, 1968), response allocation and time allocation (data not shown) correlated highly (r  =  0.98).

Fig 1.

Log response ratios (y-axis) plotted against log net-reinforcer ratios (reinforcers delivered minus reinforcers removed; x-axis) for the 5 participants under no-punishment (open circles) and punishment (closed circles) conditions.

Table 2.

Slope (c) and bias (log k) estimates for each participant under no-punishment and punishment conditions.

Participant	No punishment			Punishment
	c	Log k	r2	c	Log k	r2
02	1.02	0.05	0.98	0.35	−0.50	0.58
04	0.47	−0.04	0.95	0.20	−0.70	0.20
05	0.49	−0.01	0.94	0.25	−0.20	0.48
06	0.41	0.01	0.95	0.46	−0.25	0.80
08	1.06	0.03	0.98	0.31	−0.76	0.87
Mean (SEM)	0.69 (0.14)	0.01 (0.01)	0.96 (0.008)	0.32 (0.04)	−0.50 (0.12)	0.59 (0.12)

Figure 2 shows matching functions from the reinstated no-punishment conditions that were implemented before each punishment schedule as a function of log reinforcement ratios of the initial no-punishment conditions. Each data point represents the mean log reinforcement ratio for the last three stable sessions for each participant for each schedule. The reinstatement conditions were indistinguishable from the initial reinforcement conditions (y  =  1.02x − 0.001; r²  =  0.99), indicating that behavioral allocation in the initial no-punishment condition was recaptured after the punishment condition was imposed. Punishment's effects were confined to the punishment condition and did not affect choice in subsequent conditions.

Punishment Schedules

The regression equations for the punishment conditions for each participant are listed in Table 2. The variance accounted for ranged between 20% and 87% across all participants. With the exception of Participant 04, the functions were roughly linear. Each participant exhibited a slope less than 1 (undermatching) in the punishment conditions. In addition, each participant demonstrated bias toward the unpunished alternative, with values ranging from −0.20 to −0.76. Response allocation and time allocation correlated highly in the punished condition (r  =  0.98).

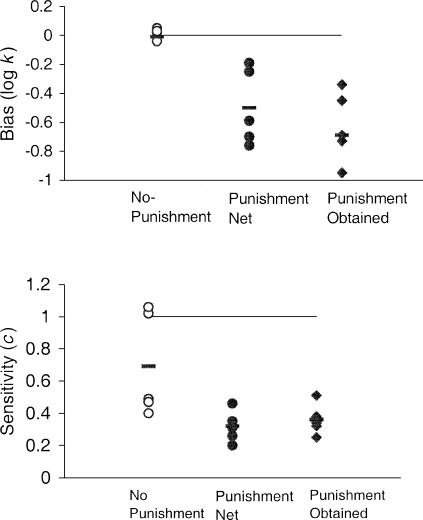
Figure 3 compares bias (top panel) and sensitivity (bottom panel) parameters in the no-punishment and the punishment conditions. Each data point represents a participant. Net reinforcers (punishment-net) and obtained reinforcers (punishment-obtained) are displayed for the punishment conditions. Dashes represent the means for each condition. In the top panel, note that the bias values are clustered tightly around 0 (M  =  −0.01, SEM  =  0.01) in the no-punishment condition, indicating the absence of bias. In the punishment-net analysis, the mean bias was −0.50 (SEM  =  0.12). A paired-samples t test revealed a significant difference between the bias parameter values in the no-punishment and the punishment-net analyses [t(4)  =  4.26, p  =  0.01].

Fig 3.

Values for bias (log k; top panel) and sensitivity to reinforcement (c; bottom panel) parameters for the no-punishment (open circles), punishment-net (closed circles), and punishment-obtained analyses (closed diamonds). In the top panel, the horizontal line represents the bias value under perfect matching (log k  =  0); in the bottom panel, the horizontal line represents the sensitivity value under perfect matching (c  =  1). Dashes represent means.

Figure 3 also shows the bias values from the punishment-obtained analysis using obtained reinforcers (punishers were not subtracted from earned reinforcers). The mean bias parameter was −0.63 (SEM  =  0.11). The bias values in this analysis differed significantly from those in the no-punishment analysis [t(4)  =  5.98, p < 0.01]. However, the bias values from the punishment-obtained analysis did not differ from those from the punishment-net analysis [t(4)  =  1.08, p  =  0.34].

The bottom panel in Figure 3 shows the sensitivity parameter, c, for the three analyses. In the no-punishment analysis, the mean was 0.69 (SEM  =  0.14). The punishment-net analysis produced a mean of 0.32 (SEM  =  0.04). A paired-samples t test showed that the difference between these two conditions was not statistically significant using the conventional criterion [t(4)  =  2.48, p  =  0.07]. The spread in the data in the no-punishment condition suggests a dichotomy in the effect of punishment on slope. Two of the participants who matched in the no-punishment condition (Participants 02 and 08) undermatched in the punishment condition. The other 3 participants showed little change in sensitivity parameter values between the analyses. The mean in the punishment-obtained analysis was 0.36 (SEM  =  0.04), which did not differ significantly from that in the punishment-net analysis [t(4)  =  −1.37, p  =  0.24] or from the no-punishment condition net analysis (t(4)  =  1.92, p  =  0.13).

Discussion

Monetary gain functioned as a reinforcer for all participants, and unbiased matching or undermatching was observed when participants earned money under the no-punishment conditions. This finding replicates other data on matching in humans (see Kollins et al., 1997; Pierce & Epling, 1983.) This performance was stable and insensitive to a history of punishment as it could be recaptured when no-punishment conditions were restored between punishment conditions. Performance was nearly identical to that seen during the initial baseline. This is important because it shows that monetary loss in the punishment conditions did not disrupt choice in subsequent no-punishment conditions.

Monetary loss functioned as a punisher for all participants. This was demonstrated as a reduction in response rate when responding on one alternative resulted in the occasional, response-contingent loss of money. Punishment's effects were demonstrated by shifts in response allocation away from the alternative associated with punishment under all punishment conditions (see Appendix A). An exception was Participant 02, who made an almost equal number of responses in the no-punishment and punishment conditions under the conc VI 60-s (PUN) VI 12-s schedule. This may be due to a floor effect in response allocation to alternative A that occurred because so few reinforcers were delivered in both no-punishment and punishment conditions.

Punished behavior could be modeled using the generalized matching relation, and this enabled the quantification of punishment's effects as a change in bias and sensitivity to reinforcement. Bradshaw et al. (1979) also showed that bias toward an alternative was created by punishing behavior under another alternative. Some investigators have reported that punishment changes reinforcer sensitivity (c) in the direction of undermatching (e.g., Bradshaw et al., 1979; deVillers, 1980.) In the present study, too, reinforcement sensitivity under the punishment condition was lower than that under the no-punishment condition for all but one participant (Participant 06; see Table 2). For two of the participants, this difference was large—Participant 02's c parameter changed from 1.02 in no-punishment to 0.35 under punishment; Participant 08's changed from 1.06 to 0.31.

Because the punisher (monetary loss) and reinforcer (monetary gain) were measured using a common metric, the present experiment can be used to address the issue of symmetry in the behavioral effects of reinforcement and punishment. A shift in bias as seen under the net analysis indicates that, if the money earned under the reinforcement condition is weighted the same as money lost under the punishment condition, then there is still a strong preference for the condition that does not involve punishment. Based on these data, then, reinforcers and punishers are not symmetrical in their behavioral effects. In fact, the degree of asymmetry can be quantified. The mean value of the bias parameter under the no-punishment condition was about 0, so the bias that appeared under the punishment condition can be attributed to the punishment contingency. The mean value of the bias parameter under the punishment condition was approximately −0.5, which represents a 3-fold (10^0.5) shift in responses toward the unpunished alternative over what would be predicted by the generalized matching relation on the assumption of symmetry of punishment and reinforcement.

The shallow lines representing the punishment condition in Figure 1 illustrate how powerfully punishment degrades the impact of a reinforcer. The combined effects of a change in bias and diminished sensitivity can be interpreted graphically by comparing the lines representing the punishment and no-punishment conditions in that figure. The alternative associated with punishment is represented in the numerator of the matching function (Equation 1) for the lines representing the punishment condition. Therefore, the low slopes can be interpreted as reduced sensitivity to reinforcement by monetary gain when monetary loss sometimes occurs. In the left hemiplane, the punished alternative is relatively lean in terms of the reinforcers earned, and the response ratios were similar in the punishment and no-punishment conditions: most responding occurred on the rich, unpunished alternative in the punishment condition, and, of course, on the richer alternative in the no-punishment condition. The similarity between the two conditions is indicated by the convergence of the lines representing the two conditions in the left hemiplane. In contrast, in the right hemiplane, the punished alternative is relatively rich, yet the response rate on the punished alternative remains quite low (log response ratio less than 0 or ratio less than 1.0). The lines representing the two conditions diverge sharply here. The shallow slope representing the punishment condition means that a sizable increment in obtained reinforcers would be required to overcome this loss of sensitivity. Thus, the relatively greater effect of punishment is especially prominent in the right hemiplane, where the punished alternative is relatively rich.

Finally, it is of interest that the bias and sensitivity parameters produced in the punishment-obtained analysis were indistinguishable from those produced in the punishment-net analysis. We offer two hypotheses about this. The first is that the “side effects” of punishment are negligible in estimating preference, as noted by Schuster and Rachlin (1968). To see how this might be applicable, consider the y-intercept of the matching functions in Figure 1 and Equation 1. The y-intercept represents preference when the reinforcer ratios are equal. For the punishment-obtained analysis, this point, log k, might be viewed as the combined effects of reinforcer loss plus side effects. In the punishment-net analysis, this point can only represent side effects, as reinforcer loss has been accounted for. The value of log k is the same for both conditions, so, insofar as the side effects are unrelated to this quantitative loss of value, they must be negligible.

The second hypothesis is that the reduced sensitivity induced by punishment prevents the detection of a difference in bias across the two conditions. The difference lay only in how reinforcer ratios were calculated. Total net reinforcers in the numerator for the punishment-net condition was simply the total number obtained minus the total number lost while that for the punishment-obtained condition was the total number obtained. This difference would skew the reinforcer ratio slightly, but since behavior was so insensitive to reinforcement ratios when punishment was delivered on one alternative, this skewing produced only a negligible shift in behavior over the range of reinforcer ratios in the experiment. This hypothesis, then, is that punishment of one alternative so degrades sensitivity to changes in reinforcement density that subtle differences in bias are difficult to detect. Further studies are required to clarify these possibilities.

To summarize the current experiment, when humans are offered a choice between two response alternatives, the allocation of behavior is captured well by the generalized matching relation, and sensitivity to reinforcer ratios resembles that seen in other studies with human and nonhuman species. Punishing one alternative reduces the sensitivity of behavior to reinforcer ratios and produces a significant bias toward the unpunished alternative, even when the two alternatives deliver the same net reinforcer amount. In fact, when monetary gain is the same on the alternatives, it appears that losing a penny is three times more punishing than earning that same penny is reinforcing.

Appendix

Mean responses, obtained reinforcers, and punishers (with ranges) for each alternative of the conc VI VI schedules. The alternative (A or B) on which the punishment schedule was superimposed differed across participants, though for ease of interpretation, the table presents alternative A as the one on which the punishment schedule was superimposed.

Partic.	Concurrent Schedule	Mean responses on A	Mean responses on B	Mean reinforcers from A	Mean reinforcers from B	Mean Punishers on A
02	VI 12-s VI 60-s	207.67 (198–218)	17.67 (12–24)	30.67 (28–33)	3.33 (3–4)
	VI 12-s (PUN) VI 60-s	40 (31–45)	146 (118–161)	7.33 (7–8)	4.33 (2–6)	3.67 (3–4)
	VI 20-s VI 20-s	77.3 (74–83)	85 (81–89)	12 (11–13)	12.6 (12–13)
	VI 20-s (PUN) VI 20-s	16 (8–22)	231 (188–261)	3.33 (2–5)	19.33 (17–21)	1.67 (1–2)
	VI 60-s VI 12-s	20.3 (18–24)	218.33 (201–228)	2.33 (2–3)	27.67 (25–31)
	VI 60-s(PUN) VI 12-s	24.33 (20–29)	225 (182–260)	2.33 (2–3)	32 (26–37)	1.33 (1–2)
04	VI 12-s VI 60-s	578.33 (563–600)	343.67 (307–367)	25.33 (25–26)	5.67 (5–7)
	VI 12-s (PUN) VI 60-s	166.33 (158–173)	926 (903–956)	10.67 (10–12)	6.33 (6–7)	4.66 (4–5)
	VI 20-s VI 20-s	429.33 (361–486)	391 (361–486)	16.67 (15–18)	16 (15–18)
	VI 20-s (PUN) VI 20-s	110.33 (102–122)	515 (467–541)	8.67 (8–9)	21.67 (21–23)	6.67 (6–7)
	VI 60-s VI 12-s	230.33 (209–268)	701.33 (667–716)	4.33 (4–5)	33.67 (30–37)
	VI 60-s(PUN) VI 12-s	40.33 (25–69)	701.33 (667–746)	2.33 (2–3)	32 (30–33)	1 (1–1)
05	VI 12-s VI 60-s	386 (358–441)	199 (168–214)	24.3 (22–26)	5 (4–6)
	VI 12-s (PUN) VI 60-s	163.67 (150–184)	370.33 (339–389)	9.33 (7–12)	6.67 (6–7)	7 (5–8)
	VI 20-s VI 20-s	332.67 (150–184)	280.33 (265–290)	15.33 (14–17)	14.33 (14–15)
	VI 20-s (PUN) VI 20-s	167.67 (157–175)	365 (320–394)	7.33 (7–8)	13 (11–15)	5.67 (4–7)
	VI 60-s VI 12-s	121 (109–130)	319.33 (310–332)	3.67 (3–4)	21.67 (17–25)
	VI 60-s(PUN)VI 12-s	116.35 (84–133)	501.67 (481–522)	3.67 (2–5)	26 (19–30)	2.67 (1–4)
06	VI 12-s VI 60-s	143.67 (133–150)	64.33 (63–65)	26 (23–30)	5 (4–6)
	VI 12-s (PUN) VI 60-s	64 (60–71)	89.67 (80–101)	13 (11–15)	4.33 (3–6)	7 (6–8)
	VI 20-s VI 20-s	79 (56–100)	93 (67–110)	11.3 (7–15)	12.67 (10–15)
	VI 20-s (PUN) VI 20-s	32 (29–36)	225.33 (200–246)	6.33 (6–7)	18.67 (18–19)	4.67 (4–5)
	VI 60-s VI 12-s	95.67 (83–103)	178 (170–189)	4 (2–6)	22.33 (19–27)
	VI 60-s (PUN) VI 12-s	58.33 (28–96)	378 (235–489)	3.67 (2–5)	26 (27–34)	2 (2–2)
08	VI 12-s VI 60-s	643.33 (626–668)	66.33 (58–77)	29.67 (28–31)	3.67 (3–4)
	VI 12-s (PUN) VI 60-s	76 (65–86)	609 (603–617)	8.33 (8–9)	6.33 (6–7)	6 (5–7)
	VI 20-s VI 20-s	364.67 (340–382)	343 (320–387)	14.33 (14–15)	15 (14–16)
	VI 20-s (PUN) VI 20-s	50 (44–53)	642.67 (605–682)	5.33 (5–6)	20.33 (19–22)	4 (4–4)
	VI 60-s VI 12-s	61 (58–67)	619.67 (601–652)	3.33 (3–4)	31.33 (29–33)
	VI 60-s (PUN) VI 12's	34 (32–36)	558.33 (529–590)	2.33 (2–3)	30 (30–32)	1 (1–1)