Quantification of Drug Choice with The Generalized Matching Law in Rhesus Monkeys

Abstract

The generalized matching law provides precise descriptions of choice, but has not been used to characterize choice between different doses of drugs or different classes of drugs. The current study examined rhesus monkeys' drug self-administration choices between identical drug doses, different doses, different drugs (cocaine, remifentanil, and methohexital), and between drug and drug-paired stimuli. The bias parameter of the generalized matching law was used to quantify preference for one reinforcer over another. Choice between identical drug doses yielded undermatching. Choices between 0.3 µg/kg/injection remifentanil and either 0.1 µg/kg/injection remifentanil or saline plus drug-paired stimuli revealed bias for the 0.3 µg/kg/injection dose. Choice was relatively insensitive to differences in random interval schedule value when one reinforcer was replaced with drug-paired stimulus presentations. Bias for 0.3 µg/kg/injection remifentanil over 10 µg/kg/injection cocaine was seen in one subject, and indifference was generally observed between 0.1 µg/kg/injection remifentanil and 56 µg/kg/injection cocaine and between 30 µg/kg/injection cocaine and 320 µg/kg/injection methohexital. These findings suggest the bias parameter may be useful in quantitatively measuring level of preference, which would be an advantage over concurrent FR procedures that often result in exclusive choice.

The generalized matching law provides a framework for quantitatively describing choice. The proportion of behavior allocated to each of two response alternatives generally matches the relative rates of reinforcement available on those alternatives (Herrnstein, 1961). This observation has been formally stated as the matching law (Herrnstein, 1970), which was later extended to the generalized matching law (Baum, 1974):

1

where B₁/B₂ is the ratio of behavior allocated toward response alternatives 1 and 2, R₁/R₂ is the ratio of reinforcement obtained on alternatives 1 and 2, and a and b are free parameters representing the slope and y-intercept of a best-fit regression line fitted to experimental data, respectively. The a parameter quantifies sensitivity to differences in rates of reinforcement, while b provides a measure of bias toward one response alternative independent of schedule parameters.

The bulk of research on the matching law has focused on food-maintained behavior on concurrent variable interval (VI) or random interval (RI) schedules of reinforcement where the first response after a variable amount of time has passed produces an identical reinforcer regardless of response alternative. Less frequently the matching law has been used to quantify choices maintained by drug reinforcers (Anderson, Velkey, & Woolverton, 2002; Anderson & Woolverton, 2000; Iglauer & Woods, 1974; Llewellyn, Iglauer, & Woods, 1976; Woolverton, 1996; Woolverton & Alling, 1999). In general, these studies demonstrate that drug choice is well described by the matching law. No systematic bias is typically found, and sensitivity parameters have been reported ranging from near matching (a ≈ 1.0) (Iglauer & Woods, 1974; Llewellyn et al., 1976) to undermatching (a range 0.2 to 0.8; Anderson et al., 2002; Anderson & Woolverton, 2000; Woolverton, 1996; Woolverton & Alling, 1999). Sensitivity does not appear to be correlated with the unit dose of drug being self-administered (Anderson & Woolverton, 2000; Woolverton, 1996) or with drug class, including stimulants (cocaine), barbiturates (methohexital), and opiates (alfentanil) (Anderson & Woolverton, 2000).

When qualitatively or quantitatively different reinforcers are programmed across response alternatives, the bias parameter (log b) quantifies preference for one reinforcer over the other (Anderson et al., 2002; McLean & Blampied, 2001; Miller, 1976). The bias parameter has been used to quantify pigeons' preferences between different types of grain (Miller, 1976), rhesus monkeys' preferences between cocaine and food reinforcers (Anderson et al., 2002), and pigeons' preferences between different durations of food access (McLean & Blampied, 2001). Each of these studies found biases for specific reinforcer alternatives independent of reinforcer rate, indicating that bias could be used to quantify relative preference for qualitatively different reinforcers.

A great deal of effort has been allocated to measuring relative reinforcing efficacy of different drugs using choice procedures (for recent review, see Bergman & Peronis, 2006). Concurrent fixed-ratio (FR) schedules are usually employed in drug choice experiments. A shortcoming of this procedure is that it typically yields near-exclusive preference for one drug over the other (e.g., Galuska, Winger, Hursh, & Woods, 2006; Johanson & Schuster, 1975; Manzardo, Stein, & Belluzzi, 2002; Wang, Brown, Grabowski, & Meisch, 2001). Occasionally, graded curves are found demonstrating dose-specific intermediate levels of choice (e.g., Woolverton & Johanson, 1984), but this is rare.

The present experiment was designed to determine if the bias parameter of the generalized matching law could be used to quantify preferences between nonidentical drug or drug-paired consequences. To our knowledge, no prior studies have examined choice when different drug doses, drug classes, or drug-paired stimuli are arranged according to concurrent VI or RI schedules. Therefore, this study constitutes a test of the utility of these procedures and quantitative methods for the study of relative reinforcer efficacy, as applied to drug self-administration. Choice between drug and drug-paired stimuli were included as a control expected to produce strong bias favoring the drug reinforcer. In addition, choice between drugs and drug-paired stimuli may prove interesting as another pairing of qualitatively different reinforcers that has received little attention in studies of choice.

Method

Subjects

Three male rhesus monkeys (Macaca mulatta) with varied experimental histories including drug self-administration served as subjects. At the start of the experiment, monkeys PA, FO, and SC were 13, 10, and 11 years old and weighed 12.5, 14.5, and 9.0 kg, respectively. Subjects were given fresh fruit and other edible treats each day and fed Purina® monkey chow to maintain healthy weights (determined by veterinary staff and somewhat less than ad lib weights). Water and environmental enrichment toys were continuously available, both in and out of session.

Apparatus

Monkeys were housed in stainless steel cages (83.3 cm high by 76.2 cm wide by 91.4 cm deep) in visual contact with other monkeys of the same species. Located on one side of the cage was an instrument panel containing three depressible levers (Model 121-07, BRS-LVE) each requiring 10 to 15 g (0.10 to 0.15 N) of downward force to operate. The levers were separated by 0.3-cm thick stainless steel dividers extending 8 cm from the response panel. A stimulus light was positioned above each lever. Experimental events were controlled by computers in an adjacent room running Med-PC IV® (Med-Associates, Georgia, VT, USA) software.

Monkeys were implanted with intravenous catheters in an internal jugular, external jugular, femoral, or brachial vein. Catheters were routed subcutaneously out the back of the monkey and through a flexible stainless steel tether held in place by a Teflon mesh jacket (Lomir, Quebec, Canada). Catheters were implanted under ketamine (10 mg/kg, intramuscular) and xylazine (2 mg/kg, intramuscular) anesthesia. Three injection pumps (one for each of the drug alternatives and one for saline flush) were located behind the cages and were also operated by Med-PC IV® software.

Procedure

Sessions were conducted twice daily (6:00 AM and 12:15 PM), seven days per week, each lasting two hours. Independent RI schedules were concurrently available on the center and right levers and these schedules were signaled by orange and red stimulus lights, respectively. The center and right levers are referred to as left and right, respectively, throughout this paper. On each RI schedule, a probability gate was assessed once every 100 msec and probabilities were set so that average programmed interreinforcer intervals would equal the RI schedule value. After a reinforcer became available according to a RI schedule, the first response on that lever produced a 5-s injection period during which an injection pump was activated, lights above both levers were turned off, and a green light above the associated lever was illuminated. RI timers were not active during this period. After the 5-s injection, the green light went out, the stimulus lights associated with the schedules were illuminated, and the RI schedules were reactivated. To avoid drug mixing in the intravenous catheter, 1 ml of saline was injected over 5 s after each drug injection. This occurred without any overt stimulus change other than the sound of the injection pump. There was no timeout after drug injections.

To decrease the probability of rapid switching between alternatives or responding on both levers simultaneously, a 3-s changeover delay (COD) was programmed (Herrnstein, 1961). The COD ensured that after switching from one lever to the other, responding had no programmed consequences for 3 s. Consequences made available by the RI schedules prior to or during the COD were delivered for the first response on the same lever following the COD. For 2 of the subjects (PA and FO), an additional contingency required them to hold down the leftmost, “holding” lever throughout the session, thereby occupying one hand (the third subject responded exclusively with one hand). If the holding lever was released, the stimulus lights above the other two levers were turned off, the RI schedules were deactivated, and the stimulus light above the holding lever flashed white. While the holding lever was released, responses on the left and right levers had no scheduled consequences and were not included in data analyses. Releasing the holding lever during a drug injection did not affect the sequence of programmed events until the injection period finished.

Because of their experimental histories monkeys did not require lever-press training; however, they completed several preliminary sessions in which the RI schedule durations were gradually increased until a concurrent RI 300 s RI 300 s schedule was reached. At this point, the experimental conditions shown in Table 1 were initiated.

Table 1.

The order of conditions assessed and the total number of sessions required to meet stability for all six, or all three, RI schedule combinations. All doses are µg/kg/injection(inj).

	PA		FO		SC
	Left / Right	Sessions	Left / Right	Sessions	Left / Right	Sessions
1	10 coc / 10 coc	115	10 coc / 10 coc	123	0.3 remi / 0.3 remi	61
2	0.3 remi / 10 coc	69	10 coc / 0.3 remi	68	0.3 remi / 0.1 remi	69
3	0.1 remi / 0.3 remi	68	0.3 remi / 0.1 remi	70	0.3 remi / saline	63
4	0.3 remi / saline	97	0.3 remi / saline	76	saline / 0.3 remi	111
5	saline / 0.3 remi	70	saline / 0.3 remi	83	0.1 remi / 0.3 remi	68
6	0.3 remi / 0.3 remi	66	0.3 remi / 0.3 remi	75	10 coc / 0.3 remi	65
7	0.3 remi / 0.1 remi	75	0.1 remi / 0.3 remi	74	0.3 remi / 10 coc	77
8	10 coc / 0.3 remi	76	0.3 remi / 10 coc	67	10 coc / 10 coc	75
9	0.1 remi / 56 coc	74	0.1 remi / 56 coca	47	0.1 remi / 56 coca	30
10	56 coc / 0.1 remia	32	56 coc / 0.1 remia	36	56 coc / 0.1 remia	31
11	320 met / 30 coca	36	30 coc / 320 meta	42	320 met / 30 coca	30
12	30 coc / 320 meta	44	320 met / 30 coca	48	30 coc / 320 meta	31

Note: coc  =  cocaine, remi  =  remifentanil, met  =  methohexital.

^aThree RI schedule combinations assessed instead of six.

The consequences of responding on the left and right levers were changed across conditions. For each pair of consequences, either three or six different RI schedule combinations were assessed, each with the same overall programmed rate of consequences (1 per 150 s). When six schedule combinations were assessed, the schedule pairings were RI 900 s RI 180 s, RI 600 s RI 200 s, RI 400 s RI 240 s, RI 240 s RI 400 s, RI 200 s RI 600 s, and RI 180 s RI 900 s. When three schedule combinations were assessed they were RI 600 s RI 200 s, RI 300 s RI 300 s, and RI 200 s RI 600 s. These three or six different schedule combinations were completed in an unsystematic order with one pair of RI schedule values in effect until choice stabilized.

Stability was assessed after 10 sessions were completed and required that none of the left/right response ratios obtained in each of the last five sessions deviated by more than 10% from the mean response ratio across those sessions. Table 1 shows the number of sessions individual monkeys completed before meeting these stability criteria; values are summed across all RI schedule pairs at each drug combination. The minimum number of sessions per condition was 60 when six RI schedule combinations were assessed and 30 when three RI schedule combinations were assessed.

Drugs

Cocaine hydrochloride (National Institute on Drug Abuse, Rockville, MD, USA), remifentanil hydrochloride (Glaxo-Wellcome, Research Triangle Park, NC, USA), and methohexital sodium (Ace Surgical Supplies, Brockton, MA, USA) were used. Cocaine and remifentanil were dissolved in sterile saline and methohexital was dissolved in sterile water. Doses refer to the salts.

Data Analysis

Descriptive and inferential statistical analyses were always based on data collected in the last five stable sessions of each drug/schedule combination. Time allocated to each lever was defined as the sum of the intervals initiated by a response on that lever and terminated by a response on the other lever. Time during drug injections or while the holding lever was released (PA and FO only) was not counted in these time-allocation data.

Mean log response- and time-allocation ratios were plotted against mean log obtained reinforcer ratios. Linear regression analyses of individual subjects' behavior were conducted using GraphPad Prism® v. 4 software. Sensitivity (a) and bias (log b) parameters of the generalized matching equation (corresponding to the slope and y-intercept, respectively) were derived from these regression analyses.

When the levers to which the two drugs or doses were assigned were reversed (e.g., conditions 2 and 8 for monkeys PA and FO), regression lines from each condition were compared to assess changes in bias and sensitivity. This was done using Prism software, which employs a method equivalent to an Analysis of Covariance (Motulsky & Christopoulos, 2003). Briefly, this method calculates the total error variance of two regression lines when the slope of each line is free to vary. Then, the error variance of a single line fitted to both data sets is calculated. Significant differences in error variance across the one- and two-line analyses reveals a significant change in slope (for a detailed description of this method see Zar, 1999, chap. 18). If no significant difference in slope is detected, then y-intercepts (bias) may be similarly compared for statistically significant changes across lever reversals. To determine if y-intercepts differ significantly, the error variance of parallel lines fitted to each data set is compared to the error variance of a single line fitted to all the data. Because bias was of primary interest in the current experiment, separate linear regression analyses were conducted with parallel lines sharing a common slope forced through the two data sets of interest, even when slopes differed significantly. These lines were then compared for significant differences in bias using the method described above.

Unlike programmed injection ratios, obtained injection ratios that are partially determined by subjects' responding are not entirely independent of behavior ratios. As a result, it should be noted that statistical analyses are somewhat more likely to find a significant correlation between these factors than if they were completely independent. This interdependence has been discussed elsewhere (see Herrnstein, 1970), and was not considered a major limitation of the current set of statistical analyses because the ratio of responses to injections was very large, limiting the extent to which behavior ratios determine injection ratios.

Local response rate on each lever was defined as the number of responses on that lever divided by the time allocated to that lever, as defined above. Local rates were compared using an Analysis of Variance (ANOVA) using Systat SigmaStat© v. 3.5 software.

Results

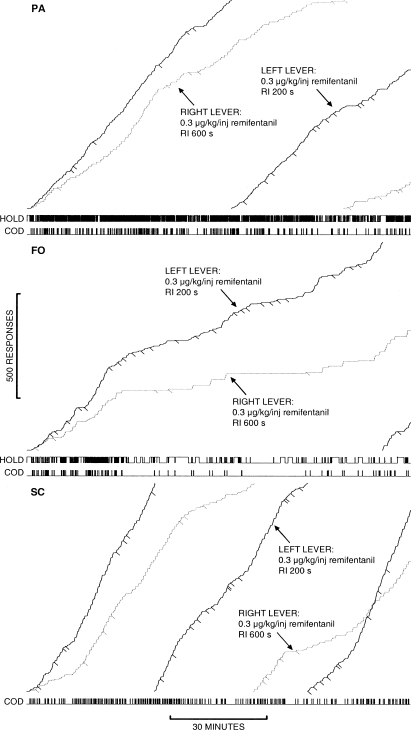
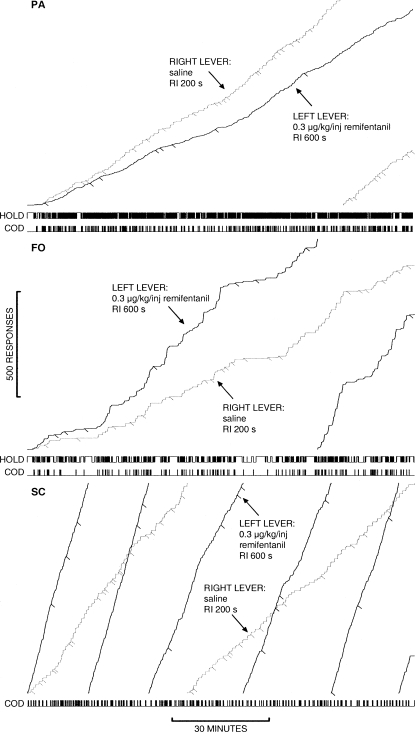
Response- and time-allocation measures were sensitive to both changes in RI schedule values and programmed consequences. Figures 1 and 2 show representative cumulative response records from the last stable session of two sets of conditions illustrating the effects of relative RI schedule values and reinforcer type on left- and right-lever responding. The top two records are those of monkeys required to depress the holding lever throughout the session (Monkeys PA and FO; note the event records at the bottom of these panels) while the bottom panel is that of the monkey responding without this contingency (Monkey SC). Figure 1 shows that when the drug and dose were identical across levers but the RI schedules differed, overall response rates were higher on the richer alternative. Responding on each lever tended to occur in bouts. Bout duration and the number of responses emitted in a bout differed across reinforcers, resulting in differences in overall response allocation on the two levers. As illustrated in Figure 2, when one lever produced saline and drug-paired stimuli (i.e., sound of the injection pump, green light above the lever), responding on that lever persisted, albeit at a lower overall rate than was observed on the drug lever in 2 of the 3 monkeys. This occurred despite the programmed injection rate being three times higher on the saline lever.

Fig 1.

Cumulative response records for each subject generated on concurrent RI 200 s RI 600 s schedules. The consequence for responses on both levers was 0.3 µg/kg/inj remifentanil, and the records depict the last stable session at this set of contingencies. Left- and right-lever responses are represented by black and gray response traces, respectively. Pip marks below the traces indicate the delivery of drug injections for that response alternative. The event line labeled “HOLD” (PA and FO only) depicts the state of the holding lever; when the line is down, the subject was holding the lever and the schedule contingencies were active. The event line labeled “COD” shows periods when the 3-s changeover delay was active, precluding any responses from resulting in a drug injection.

Fig 2.

Cumulative response records for each subject generated on concurrent RI 600 s RI 200 s schedules. Injections of 0.3 µg/kg/inj remifentanil were contingent on left lever responses and saline injections were contingent on right lever responses. Other details are as in Figure 1.

Local rates of individual monkeys are shown in Table 2 and were compared across RI schedule pairings, and independent of scheduled consequences, with one-way ANOVAs. These analyses revealed no significant effect of RI schedule value. By contrast, two-way ANOVAs comparing local response rates across levers and drug conditions (and independent of RI schedule value) showed that each monkey responded more rapidly on the right lever [significant main effect of lever: PA, F(1, 102)  =  589, p < .001; FO, F(1, 96)  =  102, p < .001; SC, F(1, 96)  =  321, p < .001]. When the generalized matching equation was applied to response-allocation ratios, this local response rate difference was reflected in systematically lower log b values. A significant main effect of drug condition on local response rates was also observed [PA, F(11, 102)  =  8.99, p < .001; FO, F(11, 102)  =  7.06, p < .001; SC, F(11, 96)  =  36.6, p < .001], although there was no consistency across subjects for which drug produced the highest and lowest local response rates. A larger proportion of the variation seen in local response rates occurred on the right lever and this was reflected in a significant interaction between lever and drug condition [PA, F(11, 102)  =  6.65, p < .001; FO, F(11, 96)  =  6.65, p < .001; SC, F(11, 96)  =  14.4, p < .001].

Table 2.

Mean (± SEM) local response rates (responses per second) averaged across all RI schedule values on each lever during each drug condition, calculated by dividing the left and right responses by the left and right time allocation measures, respectively.

Left Drug:		0.3 remi	10 coc	0.1 remi	0.1 remi	0.1 remi	56 coc	0.3 remi	10 coc
Right Drug:		0.3 remi	10 coc	0.3 remi	0.3 remi	56 coc	0.1 remi	10 coc	0.3 remi
PA	Left Lever	0.333 (0.041)	0.408 (0.041)	0.201 (0.041)	0.359 (0.041)	0.387 (0.041)	0.419 (0.057)	0.331 (0.041)	0.386 (0.041)
	Right Lever	0.987 (0.041)	0.835 (0.041)	0.607 (0.041)	0.936 (0.041)	0.738 (0.041)	0.685 (0.057)	1.096 (0.041)	0.961 (0.041)
FO	Left Lever	0.591 (0.059)	0.489 (0.059)	0.540 (0.059)	0.620 (0.059)	0.614 (0.083)	0.308 (0.083)	0.648 (0.059)	0.475 (0.059)
	Right Lever	0.474 (0.059)	0.811 (0.059)	1.111 (0.059)	0.712 (0.059)	0.720 (0.083)	1.009 (0.083)	1.128 (0.059)	0.540 (0.059)
SC	Left Lever	1.100 (0.080)	0.708 (0.080)	0.880 (0.080)	0.818 (0.080)	1.154 (0.114)	1.119 (0.114)	1.032 (0.080)	0.856 (0.080)
	Right Lever	2.223 (0.080)	0.762 (0.080)	1.204 (0.080)	1.098 (0.080)	2.741 (0.114)	2.623 (0.114)	1.816 (0.080)	1.666 (0.080)

Note: coc  =  cocaine, remi  =  remifentanil, met  =  methohexital.

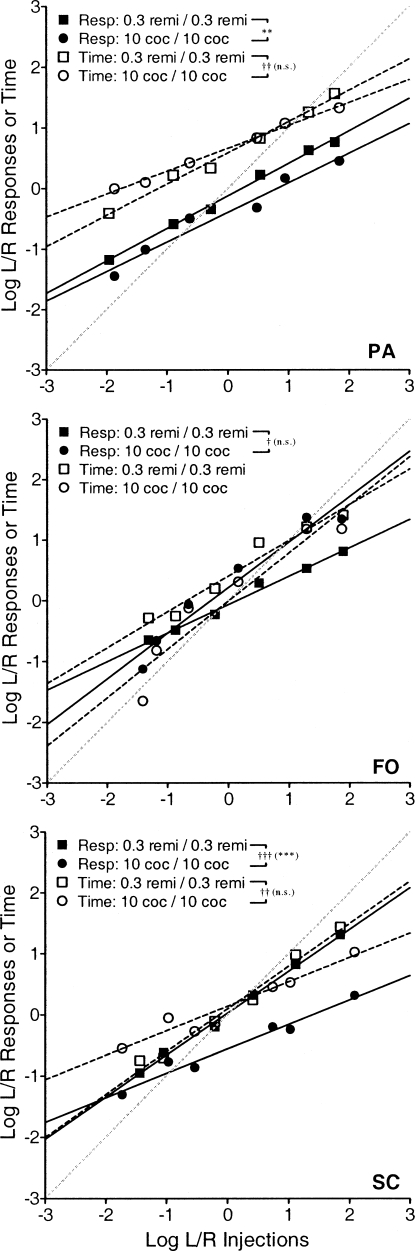
As illustrated in Figure 3, and by the parameters shown in Table 3, when the same drug and dose were arranged on both levers, response allocations were well described by the generalized matching law, with r² values for both response- and time-allocation functions all exceeding 0.9. Response and time allocations generally undermatched relative rates of reinforcement in these equivalent drug and dose conditions, with schedule-sensitivity parameter (a) values ranging from 0.377 to 0.794. Thus, the proportion of behavior allocated to the lever arranging fewer reinforcers was more than would be predicted based on the proportion of reinforcers obtained on those alternatives. Some differences were noted in sensitivity and bias values between the 0.3 µg/kg/inj remifentanil and the 10 µg/kg/inj cocaine conditions, although these differences were not consistent across subjects. Sensitivity significantly differed between remifentanil and cocaine with PA's time data [F(1, 8)  =  22.5, p  =  .001], FO's response data [F(1, 8)  =  9.10, p  =  .017], and SC's response [F(1, 8)  =  41.6, p < .001] and time [F(1, 8)  =  21.5, p  =  .002] data. The bias parameter (log b) differed between remifentanil and cocaine for PA's [F(1, 9)  =  15.1, p  =  .004] and SC's [F(1, 9)  =  23.7, p < .001] response data.

Fig 3.

Log response- and time-allocation ratios plotted as a function of log injection ratios when the drug reinforcer was the same for both response alternatives. Both 0.3 µg/kg/inj remifentanil (squares) and 10 µg/kg/inj cocaine (circles) are plotted for each subject. Filled symbols and solid linear regression lines represent log response-allocation ratios and open symbols and dotted lines represent log time-allocation ratios. Symbols represent the average of the last five sessions of stable performance. The dotted gray line indicates perfect matching. Asterisks signify a significantly different y-intercept (log b) between the cocaine and remifentanil data (* p < .05; ** p < .01; *** p < .001). Crosses signify a significantly different slope (a) between the cocaine and remifentanil data († p < .05; †† p < .01; ††† p < .001). If slopes differed, log b was compared by using a common slope for each data set determined by drawing a regression line through all the data. Asterisks in parentheses after crosses indicate any significant difference in log b when regression lines were forced through a common slope (these parallel regression lines are not shown).

Table 3.

Sensitivity (a), bias (log b), and r² values for the equal dose comparisons of 0.3 µg/kg/inj remifentanil and 10 µg/kg/inj cocaine and the unequal dose comparison and lever reversal of 0.3 and 0.1 µg/kg/inj remifentanil.

	Left:	0.3 remifentanil		10 cocaine		0.1 remifentanil		0.3 remifentanil
	Right:	0.3 remifentanil		10 cocaine		0.3 remifentanil		0.1 remifentanil
		Resp	Time	Resp	Time	Resp	Time	Resp	Time
PA	a	0.536	0.515	0.488	0.377	0.531	0.496	0.595	0.612
	log b	−0.123	0.591	−0.391	0.665	−0.878	0.230	−0.123	0.830
	r2	0.995	0.990	0.960	0.994	0.994	0.959	0.943	0.970
FO	a	0.468	0.589	0.750	0.794	0.339	0.403	0.573	0.580
	log b	−0.064	0.407	0.216	−0.006	−0.535	0.201	0.315	0.652
	r2	0.989	0.959	0.949	0.904	0.892	0.953	0.983	0.989
SC	a	0.686	0.699	0.400	0.400	0.428	0.362	0.580	0.572
	log b	0.027	0.096	−0.557	0.414	−0.579	−0.269	0.343	0.625
	r2	0.996	0.983	0.967	0.953	0.940	0.848	0.980	0.929

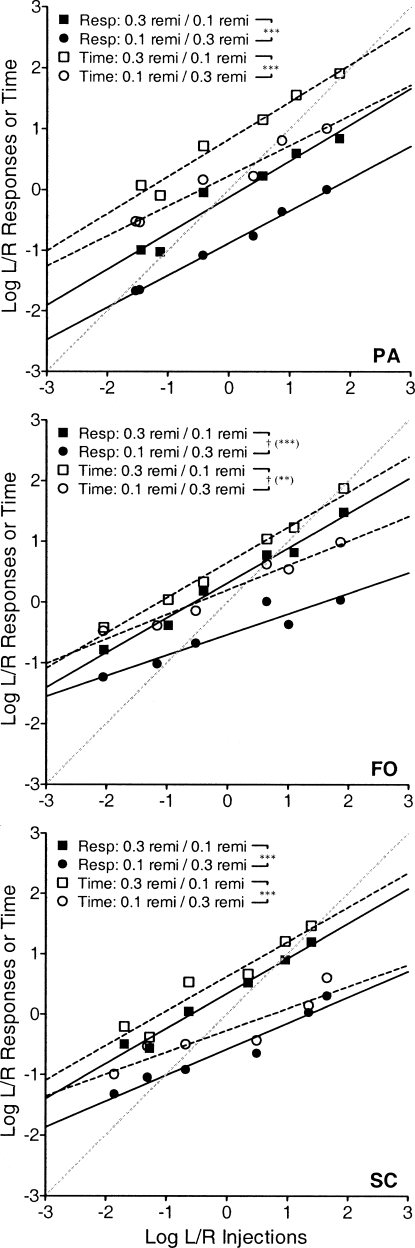
As illustrated in Figure 4 and Table 3, changing the lever to which the higher dose of remifentanil was assigned always resulted in large shifts in response- and time-allocation bias indicative of a systematic preference for the larger dose not accounted for by relative rates of reinforcement. For Monkeys PA and SC, this shift was quite clear as no significant differences in sensitivity were observed, and bias was shifted toward the larger dose in both response [PA, F(1, 9)  =  73.6, p < .001; SC, F(1, 9)  =  80.0, p < .001] and time [PA, F(1, 9)  =  40.5, p < .001; SC, F(1, 9)  =  32.3, p < .001] allocation. For Monkey FO, slopes differed significantly for response [F(1, 8)  =  11.2, p  =  .010] and time [F(1, 8)  =  10.5, p  =  .012] measures, but a shift in bias in favor of the higher dose of remifentanil was revealed when linear regression lines were forced through a common slope [response, F(1, 9)  =  39.0, p < .001; time, F(1, 9)  =  19.0, p  =  .002]; these forced regression lines are not shown in Figure 4.

Fig 4.

Log response- and time-allocation ratios plotted as a function of log injection ratios with concurrent 0.3 and 0.1 µg/kg/inj remifentanil. Squares represent log ratios of behavior with 0.3 µg/kg/inj remifentanil on the left lever and 0.1 µg/kg/inj remifentanil on the right and circles represent the lever reversal. Asterisks and crosses indicate significant differences in bias (log b) and sensitivity (a), respectively, following a lever reversal. Other details are as in Figure 3.

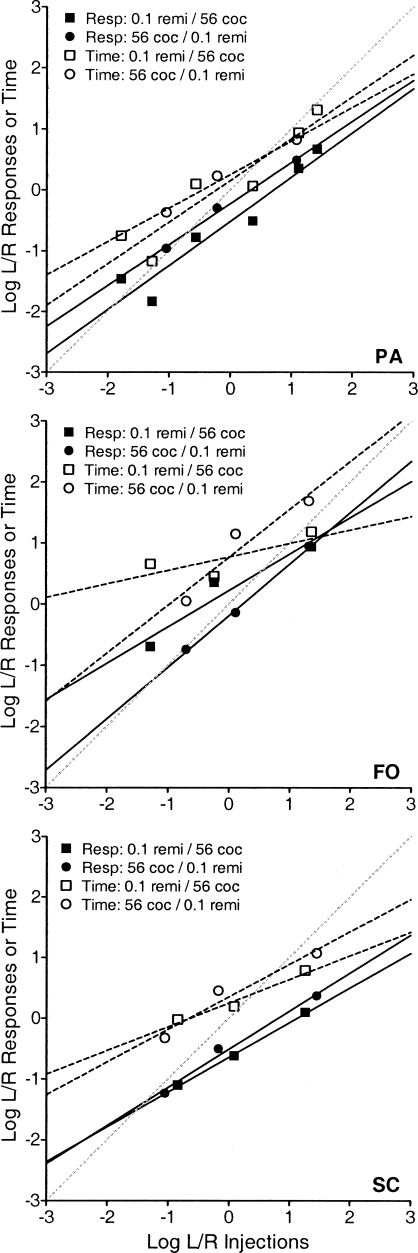
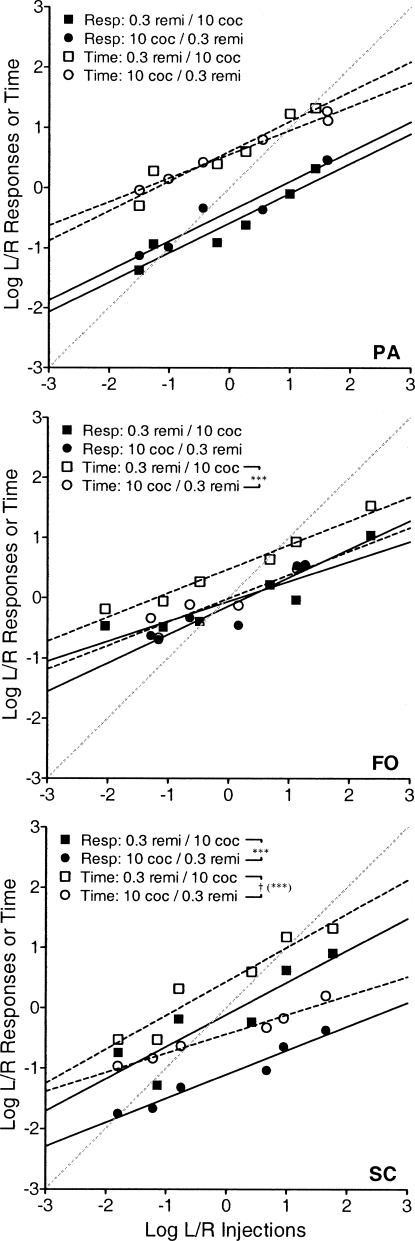
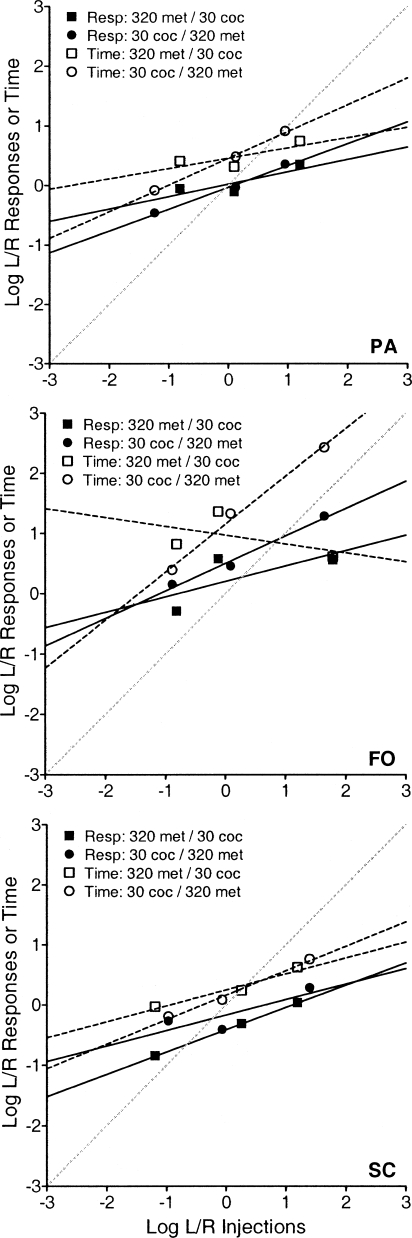
Choices between drugs from different classes were also examined to see if systematic shifts in bias would be observed. Drug combinations included 0.1 µg/kg/inj remifentanil and 56 µg/kg/inj cocaine (Figure 5, Table 4); 0.3 µg/kg/inj remifentanil and 10 µg/kg/inj cocaine (Figure 6, Table 4); and 320 µg/kg/inj methohexital and 30 µg/kg/inj cocaine (Figure 7, Table 5). Despite the sensitivity of the bias parameter to differences in dose, few systematic shifts in this parameter were observed when the choice was between different drugs. The only significant shifts may be observed in Figure 6 (Table 4). When Monkey SC chose between 0.3 µg/kg/inj remifentanil and 10 µg/kg/inj cocaine, response- [F(1, 9)  =  30.1, p < .001] and time-allocation data [F(1, 9)  =  34.5, p < .001] revealed a bias shift toward the 0.3 µg/kg/inj remifentanil alternative. A similar bias shift was observed in Monkey FO's time-allocation data [F(1, 9)  =  33.3, p < .001], but this was not seen in response allocations. A sensitivity difference was seen with SC's time-allocation data [F(1, 8)  =  7.86, p  =  .023] with these drugs.

Fig 5.

Log response- and time-allocation ratios plotted as a function of log injection ratios with concurrent 0.1 µg/kg/inj remifentanil and 56 µg/kg/inj cocaine. Squares represent log ratios of behavior with 0.1 µg/kg/inj remifentanil on the left lever and 56 µg/kg/inj cocaine on the right and circles represent the lever reversal. Other details are as in Figure 3.

Table 4.

Sensitivity (a), bias (log b), and r² values for the comparisons of 0.1 µg/kg/inj remifentanil v. 56 µg/kg/inj cocaine and 0.3 µg/kg/inj remifentanil v. 10 µg/kg/inj cocaine and their lever reversals.

	Left:	0.1 remifentanil		56 cocaine		0.3 remifentanil		10 cocaine
	Right:	56 cocaine		0.1 remifentanil		10 cocaine		0.3 remifentanil
		Resp	Time	Resp	Time	Resp	Time	Resp	Time
PA	a	0.725	0.684	0.673	0.550	0.495	0.495	0.495	0.395
	log b	−0.518	0.155	−0.226	0.253	−0.587	0.607	−0.390	0.559
	r2	0.920	0.876	0.994	0.982	0.897	0.914	0.937	0.989
FO	a	0.750	0.794	0.842	0.784	0.331	0.400	0.473	0.391
	log b	0.216	−0.006	−0.189	0.764	−0.060	0.477	−0.138	−0.010
	r2	0.949	0.904	0.997	0.909	0.808	0.971	0.897	0.880
SC	a	0.571	0.390	0.627	0.536	0.531	0.562	0.396	0.317
	log b	−0.445	0.249	−0.512	0.352	−0.113	0.437	−1.104	−0.436
	r2	0.998	0.962	0.986	0.946	0.789	0.919	0.955	0.970

Fig 6.

Log response- and time-allocation ratios plotted as a function of log injection ratios with concurrent 0.3 µg/kg/inj remifentanil and 10 µg/kg/inj cocaine. Squares represent log ratios of behavior with 0.3 µg/kg/inj remifentanil on the left lever and 10 µg/kg/inj cocaine on the right and circles represent the lever reversal. Asterisks and crosses indicate significant differences in bias (log b) and sensitivity (a), respectively, of response- or time-allocation ratios obtained after a lever reversal. Other details are as in Figure 3.

Fig 7.

Log response- and time-allocation ratios plotted as a function of log injection ratios with concurrent 320 µg/kg/inj methohexital and 30 µg/kg/inj cocaine. Squares represent log ratios of behavior with 320 µg/kg/inj methohexital on the left lever and 30 µg/kg/inj cocaine on the right and circles represent the lever reversal. Other details are as in Figure 3.

Table 5.

Sensitivity (a), bias (log b), and r² values for the comparisons of 30 µg/kg/inj cocaine v. 320 µg/kg/inj methohexital and 0.3 µg/kg/inj remifentanil v. saline and their lever reversals.

	Left:	30 cocaine		320 methohexital		0.3 remifentanil		saline
	Right:	320 methohexital		30 cocaine		saline		0.3 remifentanil
		Resp	Time	Resp	Time	Resp	Time	Resp	Time
PA	a	0.366	0.449	0.208	0.173	0.112	0.142	0.073	0.132
	log b	−0.031	0.457	0.023	0.460	0.933	1.545	−0.491	0.298
	r2	0.987	0.996	0.701	0.597	0.158	0.185	0.035	0.154
FO	a	0.455	0.795	0.256	−0.147	0.261	0.651	0.438	0.434
	log b	0.499	1.152	0.203	0.971	0.892	1.060	−0.005	0.363
	r2	0.983	0.993	0.485	0.262	0.590	0.651	0.808	0.799
SC	a	0.257	0.406	0.370	0.265	0.115	0.216	0.298	0.146
	log b	−0.165	0.165	−0.411	0.252	1.364	1.623	−0.480	−0.039
	r2	0.697	0.989	1.000	0.946	0.245	0.581	0.598	0.140

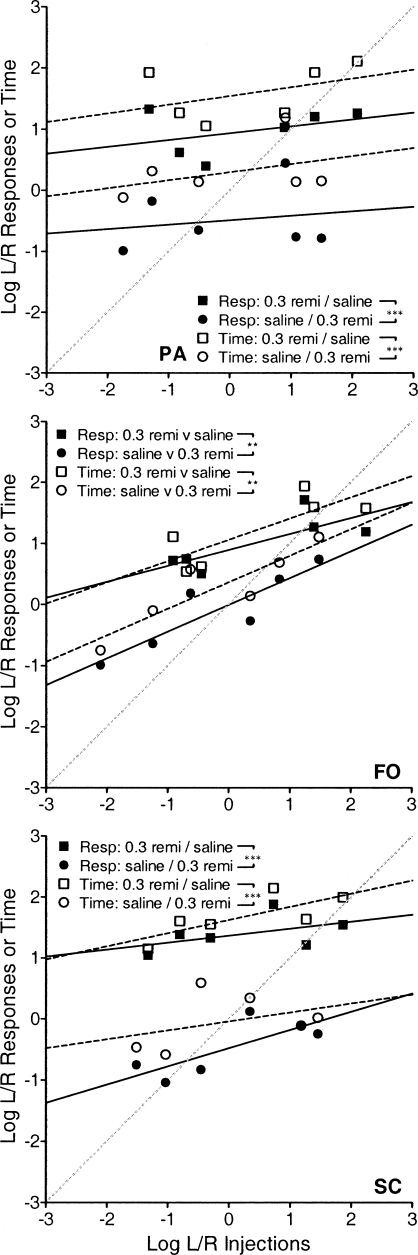
Choices between 0.3 µg/kg/inj remifentanil and saline plus drug-paired stimuli are shown in Figure 8 and parameters of the linear functions are provided in Table 5. Schedule sensitivity was notably lower in this situation with sensitivity parameter values ranging from 0.073 to 0.651 (mean  =  0.251). Despite poor control by the schedules, large and consistent bias shifts were noted with more responding on the 0.3 µg/kg/inj remifentanil alternative relative to saline. This was true for both response-allocation [PA, F(1, 9)  =  27.5, p < .001; FO, F(1, 9)  =  19.7, p  =  .002; SC, F(1, 9)  =  102, p < .001] and time-allocation [PA, F(1, 9)  =  24.6, p < .001; FO, F(1, 9)  =  11.3, p  =  .008; SC, F(1, 9)  =  64.6, p < .001] measures.

Fig 8.

Log response- and time-allocation ratios plotted as a function of log injection ratios with concurrent 0.3 µg/kg/inj remifentanil and saline plus drug-paired stimuli. Squares represent log ratios of behavior with 0.3 µg/kg/inj remifentanil on the left lever and saline plus drug-paired stimuli on the right and circles represent the lever reversal. Asterisks and crosses indicate significant differences in bias (log b) and sensitivity (a), respectively, following a lever reversal. Other details are as in Figure 3.

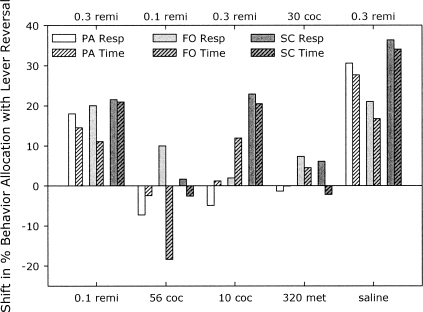
Figure 9 summarizes the shifts in bias observed as changes in percent of behavior allocated toward one alternative over another following a lever reversal. This was calculated for each drug by taking the percentage of behavior allocated on the left lever when that drug was available on the left lever and subtracting percentage of behavior allocated toward the left lever after a lever reversal. Independent of RI schedules, response- and time-allocation percentages sometimes tracked lever reversals to reveal preferential responding for one drug alternative. Clear shifts were observed when the monkeys chose between different doses of remifentanil and between remifentanil and saline. Less reliable differences were observed when drugs of two different classes were compared.

Fig 9.

Shift in percentage of responses or time allocated, independent of schedule pairing, to one drug when levers were reversed. Downward deflected bars indicate a shift toward the drug alternative on the lower horizontal axis, and upward deflections indicate a shift toward the alternative on the upper horizontal axis. Solid bars represent response allocations and hatched bars represent time-allocation data. Data are averaged from stable conditions for all RI schedule combinations. All doses are µg/kg/inj. Note: remi  =  remifentanil; coc  =  cocaine; met  =  methohexital.

Discussion

The current study examined choice on concurrent RI schedules between nonidentical drug reinforcers. The bias parameter of the generalized matching law was used to quantify a systematic preference for one reinforcer over the other that was not accounted for by differences in the relative rates of reinforcement. Consistent and sizeable shifts in bias were observed that favored large (0.3 µg/kg/inj) over small (0.1 µg/kg/inj) doses of remifentanil. Likewise, large bias shifts in favor of 0.3 µg/kg/inj remifentanil over saline plus drug-paired stimuli were observed, and these shifts were greater in magnitude than with 0.3 and 0.1 µg/kg/inj remifentanil. No systematic shift in bias was observed in conditions that compared two drugs from different drug classes. The only hint of bias was observed when 0.3 µg/kg/inj remifentanil and 10 µg/kg/inj cocaine were concurrently available. SC showed biased responding toward the remifentanil alternative with both response and time allocation measures, while FO showed a similar bias in time allocation only.

The current study found different local response rates on the left and right levers that were consistent and statistically significant between subjects. This tendency to respond at higher rates on the right lever, irrespective of experimental conditions, may simply be due to the tendency of each monkey to respond with his right hand. The holding-lever contingency used with Monkeys PA and FO strongly encouraged right-hand responding and casual observations of Monkey SC indicated predominant right-hand responding as well. In addition, the stainless steel dividers between the levers may have made the left lever less accessible. Together these factors may have increased the response cost of left-lever responding. Finally, each of the subjects had an experimental history of responding on FR schedules on the right lever while responding was extinguished on the other levers, potentially adding to a bias for the right lever. Nonetheless, the right-lever biases did not inhibit shifts in bias from being observed when lever reversals were conducted.

A potential advantage of using the bias parameter of the generalized matching law as a measure of preference is that it may provide a graded level of preference. In the current experiment, bias was most extreme with choices between remifentanil and saline, less extreme with choices between 0.3 and 0.1 µg/kg/inj remifentanil, and largely did not differentiate choices between different classes of drugs. In contrast, concurrent FR schedules typically result in exclusive choice for one reinforcer, regardless of any underlying level of preference. For example, Galuska et al. (2006) showed that when rhesus monkeys chose between self-administered doses of 0.3 and 0.1 µg/kg/inj remifentanil on a discrete-trials FR schedules procedure, they exclusively selected the larger dose. Subjects in that experiment defended this choice until the FR response requirement for the larger dose was more than 100 times greater than for the smaller dose. The current study found a bias for the same dose, although responding was not exclusively maintained by the larger dose. Thus the bias parameter of the generalized matching law may provide a more graded, quantitative measure of preference.

To date, no reports have been published on self-administration of different drug doses arranged on concurrent VI or RI schedules. However, researchers have compared reinforcer magnitude of appetitive reinforcers in this context. By parametrically manipulating reinforcer magnitude (varying durations of access to grain) instead of reinforcer rate, a in Equation 1 becomes a measure of sensitivity to magnitude instead of sensitivity to rate. To obtain a measure of bias for a reinforcer size or type as in the current experiment, VI or RI schedule combinations must be manipulated while holding reinforcer magnitude or type constant. Parametric magnitude manipulations in the absence of rate manipulations (e.g., Catania, 1963; Chelonis & Logue, 1996; Davison & Baum, 2003; Davison & Hogsden, 1984) or with too few rate manipulations to obtain meaningful bias values (e.g., Keller & Gollub, 1977; Todorov, Hanna, & Bittencourt de Sá, 1984) have all led to the conclusion that responding is sensitive to reinforcer magnitude, although with no specific measure of reinforcer preference or bias. Only a study by McLean and Blampied (2001) used the bias parameter in a manner similar to the current study to measure preferential responding maintained by access to different durations of grain presentation across many RI schedule combinations. They found a bias for 6-s access over 2-s, with intermediate levels of bias when both alternatives were 4-s access. Davison (1988) implemented a similar procedure and showed response ratios consistently favoring a larger reinforcer duration, but did not report bias values.

The current study found no significant bias between 0.1 µg/kg/inj remifentanil and 56 µg/kg/inj cocaine or between 30 µg/kg/inj cocaine and 320 µg/kg/inj methohexital. FO (time allocation only) and SC did show a bias for 0.3 µg/kg/inj remifentanil over 10 µg/kg/inj cocaine. For both of these monkeys, time-allocation bias for 0.3 µg/kg/inj remifentanil over 10 µg/kg/inj cocaine approximately equaled that shown for 0.3 over 0.1 µg/kg/inj remifentanil, but was less than that for 0.3 µg/kg/inj remifentanil over saline plus drug-paired stimuli. This capacity to order biases may be an advantage of concurrent RI schedule choice over discrete-choice procedures.

When responses on one of the levers produced saline plus drug-paired stimuli, matching behavior was disrupted in each of the monkeys. To date, no published accounts of concurrent VI or RI performance comparing a primary reinforcer to a stimulus paired with primary reinforcement have been reported. Davison and Baum (2006) recently reported conditions in which some food reinforcers were replaced with food-paired stimuli under concurrent VI schedules. With up to 42% of the food reinforcers replaced on both response alternatives with food-paired stimuli alone, schedule sensitivity as described by the generalized matching law remained unaffected. In the current experiment, sensitivity to the RI schedules was dramatically reduced when one response alternative exclusively produced saline plus drug-paired stimuli, despite responding being maintained on both levers for the duration of the exposure to these conditions (see Table 1 for exposure duration and Figure 2 for an example of response patterns under these conditions). Even though the sensitivity parameter of the generalized matching law did not describe variation in responding under these conditions, the bias parameter still revealed a substantial and statistically significant bias toward the response alternative that arranged injections of 0.3 µg/kg/inj remifentanil.

Reduced schedule sensitivity seen with the 0.3 µg/kg/inj remifentanil and saline plus drug-paired stimuli comparison, also seen to a lesser degree with the 30 µg/kg/inj cocaine and 320 µg/kg/inj methohexital comparison, may be indicative of the degree of economic substitutability of these consequences. The matching law was developed to describe choice between identical reinforcers (Herrnstein, 1970), and while matching has been observed with qualitatively different reinforcers, the substitutability of these reinforcers seems to influence the observed sensitivity parameter (Rachlin, Kagel, & Battalio, 1980). Rachlin and colleagues indicate that a sensitivity parameter approaching indifference (a  =  0) may be indicative of an economic independent relation between the commodities and that matching (a  =  1) can only be expected with economic substitutes. If this interpretation of a is correct, then the results of the current experiment suggest that cocaine and remifentanil are substitutes (mean a  =  0.550; range 0.317 to 0.842). While these values are less than 1.0, they are comparable to those from conditions measuring choice between equal doses of remifentanil or cocaine (mean a  =  0.559; range 0.377 to 0.794). Consistent with this interpretation, Wade-Galuska, Winger, and Woods (in press) have demonstrated a substitute relation between cocaine and remifentanil when arranged on concurrent FR schedules. As the response requirement for either drug was increased, consumption of that drug decreased while consumption of the other (substitute) drug increased.

In the current experiment, sensitivity values were low (mean a  =  0.251; range 0.073 to 0.651) with concurrent 0.3 µg/kg/inj remifentanil and saline plus drug-paired stimuli which, according to the Rachlin et al. (1980) analysis, is indicative of an economic independent relation. Sensitivity was also low with concurrent 30 µg/kg/inj cocaine and 320 µg/kg/inj methohexital (mean a  =  0.321; range −0.147 to 0.795), suggesting these commodities are relatively poor economic substitutes. It should also be noted that, compared to cocaine, Anderson and Woolverton (2000) did not find consistently lower schedule sensitivity with concurrent injections of methohexital available on RI schedules, suggesting schedule insensitivity is not a byproduct of methohexital intoxication.

The current study found that the bias parameter of the generalized matching law can provide a measure of choice between concurrently available drug alternatives. Biases were seen for some subjects when drugs from different classes were compared, although there was variability among subjects with these comparisons. Clear biases in all 3 monkeys were seen in conditions where a preference would be expected (0.3 µg/kg/inj remifentanil versus either 0.1 µg/kg/inj remifentanil or saline plus drug-paired stimuli). In addition, bias was generally more extreme in the 0.3 µg/kg/inj remifentanil versus saline plus drug-paired stimuli condition than the 0.3 versus 0.1 µg/kg/inj remifentanil condition. This suggests the bias parameter may be useful in quantitatively measuring level of preference which would be an advantage over concurrent FR procedures that often result in exclusive choice.