Sensor noise suppression

Abstract

We present a method to remove the effects of sensor-specific noise in multiple-channel recordings such as magnetoencephalography (MEG) or electroencephalography (EEG). The method assumes that every source of interest is picked up by more than one sensor, as is the case with systems with spatially dense sensors. To reduce noise, each sensor signal is projected on the subspace spanned by its neighbors and replaced by its projection. In this process, components specific to the sensor (typically wide-band noise and/or ‘glitches’) are eliminated, while sources of interest are retained. Evaluation with real and simulated MEG signals shows that the method removes sensor-specific noise effectively, without removing or distorting signals of interest. It complements existing noise-reduction methods that target environmental or physiological noise.

I Introduction

Modern physiological recording techniques such as magnetoencephalography (MEG) or electroencephalography (EEG) employ arrays of sensors that sample the electric or magnetic fields produced by brain activity. The signal within each channel is typically a combination of brain activity, environmental noise (power lines, machines, etc.), physiological noise (heart, muscle activity, etc) and sensor noise (transducer or or electronic noise) (Vrba, 2000; Baillet et al. 2001). Together, the noise components are often stronger than brain components and may interfere with further analysis and interpretation. Methods to reduce the noise are crucial for scientific and clinical applications. The present paper describes a denoising algorithm that addresses sensor noise.

Recent systems employ relatively large numbers of sensors (up to several hundreds) to maximize spatial resolution and increase processing options. Sensor transductors and electronics are subject to various noise mechanisms that may affect the signal (Hämäläinen et al. 1993; Lounasmaa and Seppä 2004), and a large number of sensors increases the likelihood that a “glitch" (MEG) or momentary variation of skin contact (EEG) occurs during a recording (Junghöfer et al. 2000). Cost constraints may limit the technical options available to minimize such noise, particularly as cost scales approximately linearly with the number of sensors.

The physics of magnetic and electric fields produced by intracranial sources is such that every brain source is usually picked up by several sensors. Furthermore, the number of independent brain sources (at least the number considered in any particular study) is usually much smaller than the number of sensors, and this implies redundancy between channels. The algorithm takes advantage of this property.

The method to be described addresses only sensor noise. It is complementary with methods that address other noise sources such as environmental (e.g. Adachi et al. 2001; Ahmar and Simon 2005; de Cheveigné and Simon 2007), and physiological (e.g. Croft and Barry 2000; Sander et al. 2002) noise, and is compatible with source analysis and modeling procedures (e.g. Baillet et al. 2001; Parra et al. 2005). Simulations show that distortion of brain activity is small, and denoising should not affect the validity of forward models. Sensor noise suppression tends to reduce the dimensionality of multichannel data (inflated by sensor-specific noise sources), and thus it may be a useful preprocessing step for methods such as ICA (e.g. Barbati et al. 2004). We believe that the method is safe to use as a routine preprocessing step in MEG or EEG signal analysis.

II Methods

Signal model

The sensor signals S(t) = [s₁(t),⋯,s_K(t)]^┬ reflect a combination of brain activity and sensor noise:

$$\mathrm{S}(t)=\mathrm{B}(t)+\mathrm{N}(t)$$ (1)

where B(t) represents brain activity in sensor space, and N(t) represents sensor noise. Other sources of noise exist but are not considered here. Brain activity is supposed to reflect multiple sources within the brain:

$$\mathbf{B}(t)=\mathbf{A}\mathbf{X}(t)$$ (2)

where X(t) = [x₁(t),⋯,x_J(t)]^┬ are brain sources and A = [a_kj] is the source-to-sensor mixing matrix.

Assumptions

We make the following two assumptions: (1) Sensor noise is uncorrelated with brain activity and uncorrelated between sensors. (2) Brain activity at any sensor can be reconstructed from its neighbors: for every sensor k there exist coefficients α_k′ such that

$$b_k(t)={\displaystyle \sum _{k\prime \ne k}^K{\alpha }_{k\prime }{b}_{k\prime }(t).}$$ (3)

In other words, for each sensor k the brain component b_k(t) belongs to the span of [b_k′≠k]. For every k, the rank of the complementary set [b_{k′,k′≠k}] of sensor signals is the same as the rank of the entire set.

Intuitively, we expect the second assumption to be met if each sensor picks up small number of brain sources, each of which is also picked up by other sensors. The assumptiuon implies that the K sensor signals are linearly dependent (Eq. 3), but linear dependence is not sufficient for the property to be true. The property is of interest because data that obey it are invariant to the operation that consists of replacing every channel by its regression on the subspace formed by the other channels.

Algorithm

The denoising algorithm is simple: replace each noisy channel by its regression on the subspace formed by the other channels. In practice, for each channel k, the set of signals [s_k′≠k] is orthogonalized by applying PCA to obtain an orthogonal basis of the subspace spanned by the other channels. The channel s_k is projected on this basis and replaced by its projection. These steps are repeated for all channels. For channel k:

$${\mathit{s̃}}_k(t)={\displaystyle \sum _{k\prime =1,k\prime \ne k}^K{\alpha }_{kk\prime }{s}_{k\prime }(t)}$$ (4)

where ${\mathit{s̃}}_k(t)$ represents the denoised sensor signal and [α_kk′] minimize $\Vert s_k(t)-{\mathit{s̃}}_k(t)\Vert$. The algorithm can be formulated in matrix notation:

$$\mathrm{S̃}(t)=A\mathrm{S}(t)$$ (5)

where A = [α_kk′] is a matrix with zeros on its diagonal.

It is easy to guess why the algorithm might reduce sensor-specific noise. The formula that defines the projection of channel k on the span of the other channels does not include the channel itself, and therefore is not sensitive to sensor noise within that channel. It is sensitive to noise components within the other channels, but arguably that sensitivity is weakened by the fact that they add incoherently via Eq. 4. This intuition is confirmed by simulations, that show further that denoising has little effect on brain activity as long it verifies assumption (2) (Eq. 3). Lack of effect on brain activity implies that forward models do not need to be adjusted, distinguishing the algorithm from other forms of spatial filtering. We call this algorithm “Sensor Noise Suppression" (SNS).

The SNS algorithm was implemented in Matlab. A few implementation details are worth mentioning: (a) It is usually sufficient to project channel k on a subset of complementary channels rather than the full set. This saves computation but has little effect on the outcome as long as there more channels than independent brain sources that contribute to channel k. Channels are selected on the basis of correlation with channel k. Physical proximity could be substituted for correlation, but correlation seems to work well and does not require knowledge of sensor layout. (b) The algorithm may be iterated several times: each step reduces the norm which is lower bounded, guaranteeing convergence. In practice the first step removes most noise and subsequent repetitions offer smaller improvement. (c) Exceptionally large signal values should be discounted in the calculation of the projection parameters. This prevents the sums-of-squares that determine these parameters from being dominated by those large values. d) Large files may be treated in several passes to reduce memory requirements. Taking these implementation details into account, data can be denoised in better than real time on a standard PC. The channel subset count (in a) and outlier threshold (in c) introduce arbitrary parameters in an otherwise parameter-less procedure, but their exact values, if reasonable, have little effect on the outcome.

III Results

The method is evaluated with real MEG data to illustrate its practical effectiveness, and with synthetic data to better understand its behavior.

A MEG data

Setup

MEG data were acquired from a 160-channel, whole-head MEG system with 157 axial gradiometers sensitive to brain sources and 3 magnetometers sensitive to distant environmental sources (KIT, Kanazawa, Japan, Kado et al., 1999). Subject and system were placed within a magnetically shielded room. Data were filtered in hardware with a combination of highpass (1 Hz), notch (60 Hz) and lowpass (200 Hz antialiasing) filters before acquisition at a rate of 500 Hz. Environmental noise was suppressed using the TSPCA algorithm (de Cheveigné and Simon 2007). Tests were also performed with data from other systems.

Effect of denoising

Figure 1 present data recorded in an MEG study with auditory stimuli (Chait et al. 2005). Figure 1 (a) shows the time course of a channel that was affected by a “glitch" of unknown origin, before (red) and after (blue) denoising. The glitch is suppressed. Figure 1 (b) and (c) shows two other channels that appear to pick up brain activity in the alpha and theta bands respectively. Denoising has little effect on this activity beyond a slight reduction of high-frequency noise visible in (c).

Fig. 1.

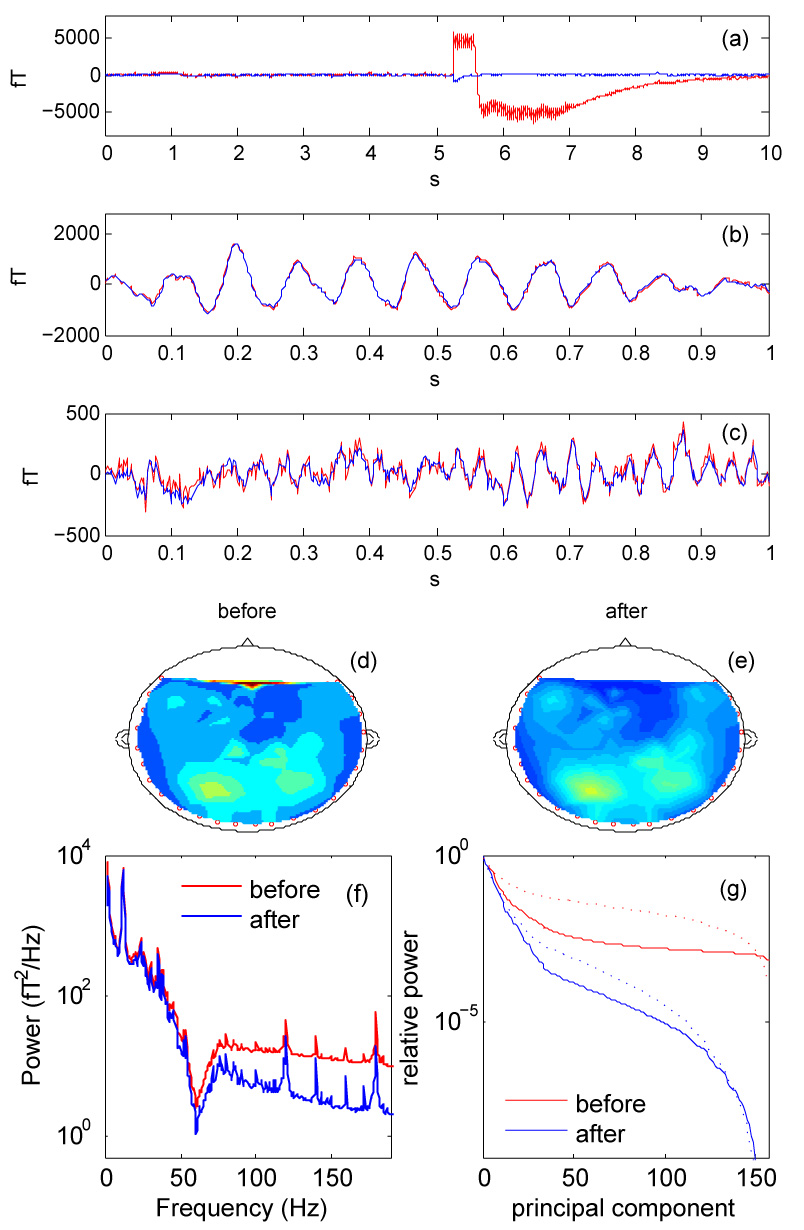
(a, b, c): Waveforms of individual channels of a 157-channel MEG recording, before (red) and after (blue) denoising. In (a) the channel is subject to a “glitch" of unknown origin, that denoising removes. In (b) denoising hardly affects the relatively high-amplitude waveform of what seems to be alpha-band brain activity. In (c), denoising attenuates the high-frequency noise riding on what seems to be theta-band brain activity. (d, e): RMS field distributions before (d) and after (e) denoising. (f): Power spectrum averaged over all channels, before (red) and after (blue) denoising. (g): PCA spectrum (relative power of principal components) before (red) and after (blue) denoising. Dotted line: proportion of power lost by discarding components beyond a given rank before (red) and after (blue) denoising.

Figure 1 (d) and (e) schematize the distribution of RMS magnetic field over the sensor array before (d) and after (e) denoising. The glitch affected a frontal channel (left); after denoising the glitch no longer emerges, and the spatial distribution is smoother. Figure 1 (f) shows the power spectrum averaged over channels, before (red) and after (blue) denoising. The most obvious spectral effect of denoising is to reduce the noise floor at high frequencies by about 10 dB, presumably because that frequency range was dominated by sensor noise.

The “PCA spectrum" (eigenvalue spectrum) is a measure of spatiotemporal complexity of the data set. Figure 1 (g) (full lines) shows the distribution of power over principal components before (red) and after (blue) denoising, normalized by division by the power of the first principal component. After denoising the PCA spectrum drops much faster, presumably because several dimensions were specific to individual channel sensor noise that denoising suppressed. The dotted lines represent the proportion of power that would be lost by truncating the series of principal components beyond a certain rank. For example, to limit power loss to 1% would require keeping about 120 components of the raw data, but only about 20 components after denoising.

The reader may be concerned that strong noise within a channel, for example a glitch, could contaminate other channels via Eq. 4. By the same token that noise is removed from a channel by replacing it by a weighted sum of its neighbors, surely that channel could contaminate those neighbors when they are denoised? The answer lies in the “opportunistic" nature of the algorithm: it always chooses the best-fitting combination of neighbors to reconstruct a channel. A channel with a glitch is automatically discounted from the formulae that reconstruct other channels.

Data from other systems

Figure 2 (a, b) shows data from a 440-channel MEG system (Yodogawa, Japan). Prior to the test, environmental noise was suppressed by applying the TSPCA algorithm (de Cheveigné and Simon 2007). One channel was subject to a glitch [Fig. 2 (a), red], that the algorithm successfully suppressed (blue). The PCA spectra [Fig. 2 (b)] indicate that denoising greatly reduces the dimensionality of the data. The benefit of the algorithm is not specific to the system described previously.

Fig. 2.

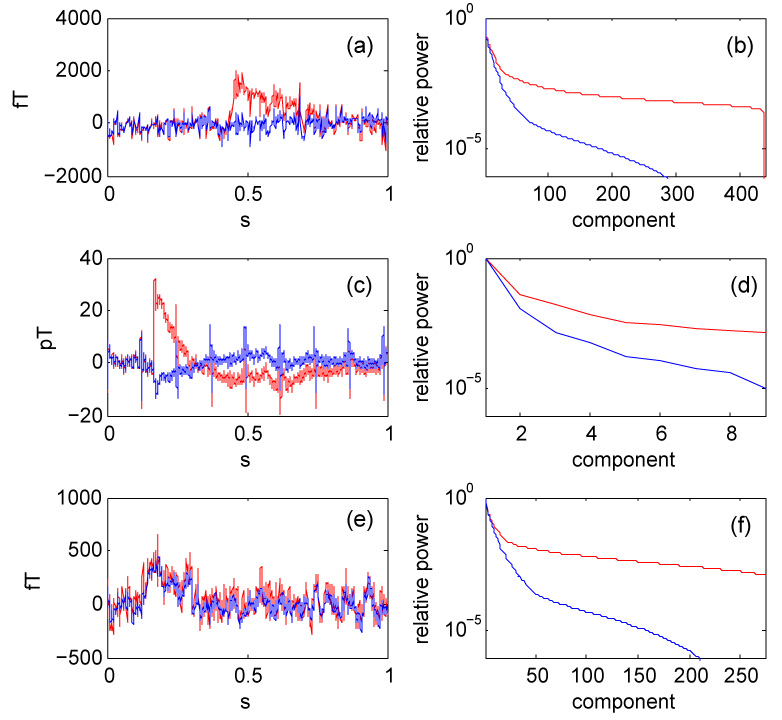
Effect of denoising data from various systems. (a): Time course of one channel of a 440-channel MEG system before (red) and after (blue) denoising. (b): PCA spectra for the the same system. (c): Time-course of one channel of an experimental 9-channel magnetocardiogram system for small animals, before (red) and after (blue) denoising. (d): PCA spectra for the same system. (e): Time course of one particular channel of the 272-channel data set of the IEEE Machine Learning for Signal Processing 2006 MEG denoising competition (MLSP 2006), before (red) and after (blue) denoising. (f): PCA spectra for the same data.

Figure 2 (c, d) shows data from an experimental 9-channel magnetocardiogram system for small animals (KIT, Japan). Prior to the test, environmental noise was suppressed by applying the TSPCA algorithm (de Cheveigné and Simon 2007). One channel was subject to a glitch [Fig. 2 (c), red], that the algorithm successfully suppressed (blue). Note that the heartbeat signal is not suppressed. Denoising again reduced the dimensionality of the data [Fig. 2 (d)]. This example shows that the algorithm can also benefit systems with relatively few channels.

Figure 2 (e, f) shows data from the data set of the IEEE Machine Learning for Signal Processing MEG denoising competition (MLSP 2006). Figure 2 (e) shows the waveform of one of the 274 channels before (red) and after (blue) denoising, and Fig. 2 (f) shows the PCA spectrum before (red) and after (blue) denoising. The dimensionality is again greatly reduced.

To summarize, the SNS method effectively removes sensor-specific noise from MEG data. The power of such noise is usually not very large (typically 10 to 20% the level of brain activity power on average), but glitches can require data to be discarded, and sensor noise inflates the dimensionality of data. Suppressing sensor noise makes it easier for analysis techniques such as PCA or ICA to determine the genuine dimensionality of brain activity (e.g. Kayser and Tenke 2003; Delorme and Makeig 2004). The SNS method is “safe" in that it usually does not distort brain activity. This claim is addressed in detail in the next sections.

B Simulated data

Is brain activity distorted?

An obvious concern is that denoising might affect brain activity. Indeed we can imagine a potential failure scenario: a brain component picked up by only one sensor would be treated as noise and suppressed. However the geometry of MEG arrays is such that this is unlikely to occur: brain activity picked up by one sensor is almost certainly picked up by its neighbors, although possibly with lower signal to noise ratio (SNR). To gain a better grasp of this situation, “sensor noise" was simulated as an array of 157 independent Gaussian noise signals with equal amplitudes, one for each channel, while “brain activity" was simulated as a an independent Gaussian signal in one channel with a large SNR (100 dB). Such an isolated “brain" component is indeed removed by SNS despite its favorable SNR. However, if the same component is added to one or more additional channels, the outcome depends on the SNR within those channels. Comparing target power before and after denoising, the proportion of error is plotted in Fig. 3. (a) for one (full line) or four (dotted line) additional sensors as a function of SNR. Error is negligible for SNR>~ 20dB, whereas for SNR<−20dB the target is essentially suppressed. MEG data tend to have favorable signal-to-sensor-noise ratios (see above), and therefore SNS is unlikely to suppress a brain component.

Fig. 3.

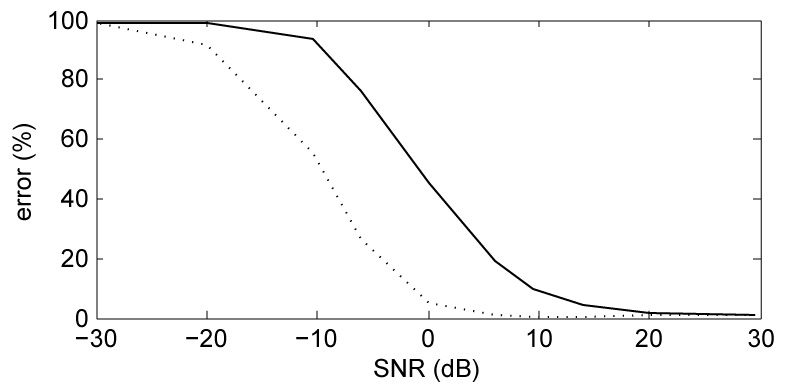
(a): Percentage error for a target component that loads mainly one channel, as a function of the SNR of the same component on one other channel (full line) or four other channels (dotted line).

Aside from the previous unlikely scenario, does denoising affect measured brain activity? The question cannot be tested directly for lack of direct access to real brain activity, but several arguments can be put forward. First, any activity that obeys assumption (2) is invariant to the denoising operation, and it is easy see that that assumption would be verified for a small number of brain sources that each loads several sensors. This assertion was further tested by simulation in two ways. As a first test, a set of 10 independent Gaussian “brain source" signals were projected into sensor space according to a 10 × 157 random “brain-to-sensor mixing matrix". This is a crude (but controlled) model of brain activity observed in sensor space. SNS indeed left this simulated “brain activity" perfectly invariant. As a second test, the SNS algorithm was applied repeatedly to a set of MEG data. After a few iterations, additional applications of SNS left the data unchanged. Brain activity that produced that same pattern in sensor space would obviously not be distorted by application of SNS. While direct verification with real brain activity is impossible, these indirect tests suggest that distortion of brain activity is minimal.

Equation 4 appears to define a spatial filter, and thus the claim that SNS does not distort the spatial properties of the brain signal may seem odd. The explanation is that the algorithm chooses for each channel k the coefficients [α_kk′] that minimize the distance between the original and denoised channel signals, thus minimizing any spatial filtering effect on brain signals. Note that the “filter" is in any event not spatially invariant.

Is SNS always effective?

Again we must consider a potential failure scenario: noise correlated across sensors. Reusing the previous simulation and swapping the roles of “brain" and “noise" component, it appears that a noise component might indeed survive denoising if it appears on one or more additional sensors (Fig. 3 (a)). Sensor noise processes (Hämäläinen et al. 1993) are unlikely to be correlated across sensors, but it is conceivable that crosstalk could arise within the electronics. SNS cannot suppress noise that is correlated across sensor channels (although it will not enhance it either). In particular, denoising is expected to be seriously compromised by spatial smoothing or filtering techniques (such as Laplacian or Signal Space Separation). These should be applied, if necessary, after application of SNS.

Aside from this scenario, what factors affect the effectiveness of denoising? To simulate conditions ideal for denoising, a set of 157 orthogonal (spatially white) Gaussian noise signals was used as “sensor noise". In the absence of any target, SNS reduces noise power to near the floor of the floating point representation. Such orthogonal noise signals are representative of independent noise sources in the limit of infinite duration and/or infinite bandwidth. Over shorter durations, band-limited noise processes usually show residual (chance) correlation. Replacing the orthogonal noise signals by independent Gaussian noise of 20 s duration (10000 samples at 500 Hz), noise power was reduced by a smaller factor of about 23 dB. Residual correlation is likely to increase for shorter noise segments, low pass filtering (in particular as required for sampling), or spatial filtering that introduces correlations among sensors. Ideally, data should be acquired with the widest possible bandwidth. Filtering, if necessary, should be performed after application of SNS.

In the presence of a target, the effectiveness of denoising may also be reduced by chance correlations between target and noise components. To illustrate this point, we simulated synthetic “brain activity" consisting of 10 random components, and projected it to sensor space via a 10 × 157 random matrix. This was mixed with synthetic “sensor noise" consisting of 157 independent Gaussian noise signals at 0 dB SNR. Applying SNS, error power (defined of as the power of the difference between original and cleaned target) dropped from almost 100% before denoising to 12%. This level of residual noise is greater than in previous examples, nevertheless even in this far from ideal situation (MEG data usually have better SNR) denoising is beneficial.

The synthetic signals used in these examples are not typical of MEG signals, but they allow an intuitive understanding of the properties and limitations of the algorithm. To summarize, the SNS method is effective if (a) sensor noise is uncorrelated across channels, and (b) every brain source of interest loads two or more channels with sufficient SNR, (c) spectral and spatial filtering of sensors is minimal.

Dipole simulation

To further illustrate the algorithm we used data from a two-dipole model with parameters derived from the M100 response to an auditory stimulus (GOF 82.5%). Synthetic “brain activity" was obtained by taking the outer product between the model-produced pattern of amplitudes across sensors, and a time series of 100 pulses of duration 50 ms (shaped as an inverted parabola) at 500 ms intervals. Sampling rate was 1 kHz. Gaussian noise with equal amplitude over all sensors was added at SNRs from −45 to +25 dB, and the data were then processed by SNS. Figure 4 (a) shows the topography of instantaneous activity at the “M100" peak before (left) and after (right) denoising, for several values of SNR. Fig. 4(b) plots goodness-of-fit as a function of SNR, before and after denoising. Dipole analysis was performed using MEG160 software (Yokogawa Corporation/Eagle Technology Corporation, Kanazawa Institute of Technology).

Fig. 4.

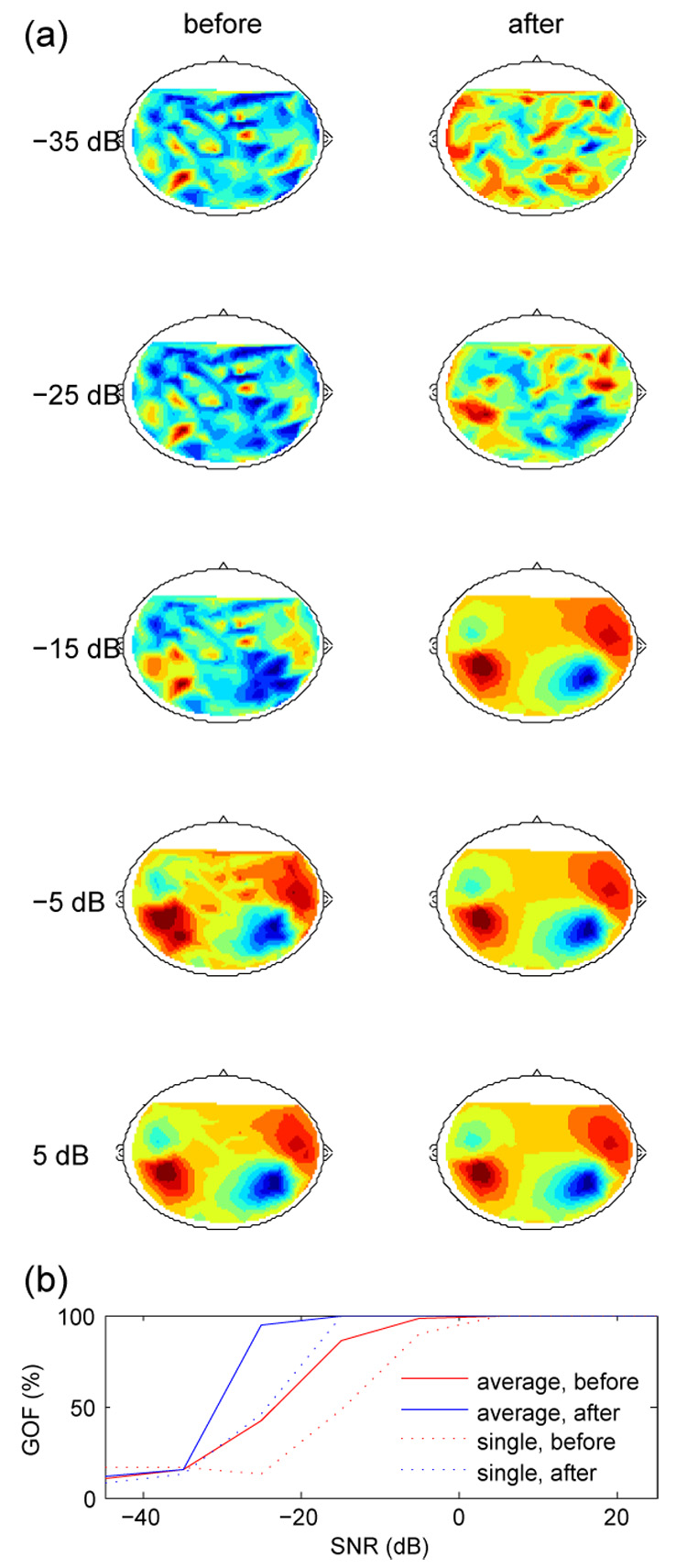
(a): Topographies of synthetic “auditory M100" activity produced by a two-dipole model at various values of SNR, before and after denoising. (b) Goodness-of-fit (GOF) as a function of SNR. Full lines: GOF of average over 10 repeats. Dotted lines: average of GOFs of a single repeat.

At very low SNR, denoising is ineffective whereas at high SNR it is not needed, but in between there is a range of SNRs for which denoising significantly improves the fit of the denoised data to the dipole model. Dipole localization errors (not shown) show a similar trend. The topography of denoised data tends to that of noiseless data: there is no evidence that denoising itself causes distortion.

A final question of practical interest is whether SNS is compatible with algorithms that address other sources of noise, such as our recent TSPCA algorithm that targets environmental noise. With the previous dipole simulation we synthesized a 500 ms interval of data including one “M100" response peak. To this we added a combination of sensor noise (independent gaussian noise with equal amplitudes across sensors) and environmental noise (60 Hz sinusoid with equal amplitudes and random phases) at an SNR of −18 dB. The first row of Fig 5 shows the field distribution at the M100 peak without (left) and with (right) noise. The second row shows the effect of applying either SNS (left) or TSPCA (right) alone, and the bottom row shows the effect of applying both. It is clear that the two algorithms are compatible and complementary. For these data, applying SNS followed by TSPCA (left) works less well than the opposite order, possibly because some of the degrees of freedom of SNS are wasted on preserving environmental noise components. Applying TSPCA followed by SNS (right) is very effective (compare to top left).

Fig. 5.

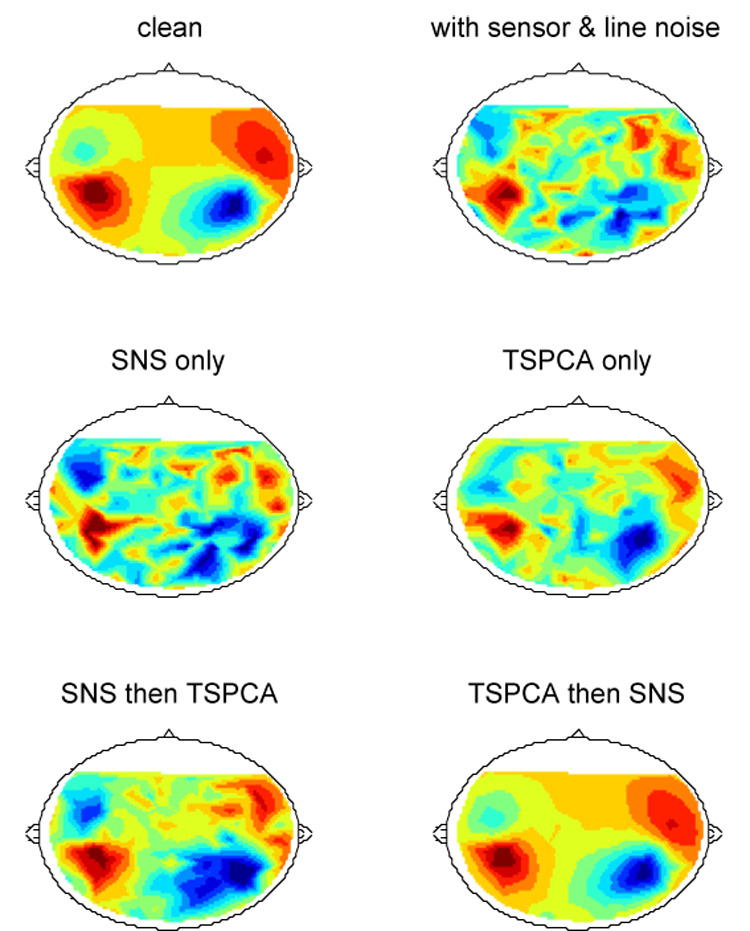
Combining SNS and TSPCA (de Cheveigné and Simon 2007). Top left: field distribution at the peak of a simulated M100 response based on a two-dipole model. Top right: same superimposed on a mixture of simulated environmental noise and sensor noise (in equal proportions) at SNR=−18 dB. Middle: result of applying SNS alone (left) or TSPCA alone (right). Bottom: result of applying SNS followed by TSPCA (left) or TSPCA followed by SNS (right).

C The special case of reference sensors

For MEG systems equipped with reference sensors, the sensor noise of the reference sensors may determine the ultimate level of the noise floor. Reference sensors sample environmental noise and allow it to be stripped from brain sensor channels (Ahmar and Simon 2005; Volegov et al. 2004; Adachi et al. 2001). For example our TSPCA algorithm projects brain channels onto the subspace spanned by time-shifted reference channels, and removes the projection to obtain clean signals. Unfortunately, by the same process reference sensor noise may be injected into brain channels. When both TSPCA and SNS are applied to clean the data, we conjecture that such reference sensor noise components, rather than background brain activity or brain sensor noise, determine the ultimate noise level.

A way to reduce the impact of reference sensor noise is to apply SNS to reference channels prior to using them to remove environmental noise. This is feasable only if there are more reference sensors than the dimension of environmental noise components (usually at least 3). When it comes to system design using limited resources, it would seem prudent to use redundant reference sensors (say, 6 for the three spatial components of environmental noise) and put the best electronics in the reference sensors rather than the (much larger number of) neural sensors. Though this might seem counterintuitive, reducing reference sensor noise may be the most effective step to minimizing the sensor-produced noise of an MEG system.

IV Discussion

The value of recorded data in scientific or clinical applications depends critically on the level of noise. Noise narrows the range of conclusions that can be drawn from experimental data, and makes them less reliable. New applications such as brain-machine interfaces (by which a handicapped person can control a machine) are still limited by noise and artifacts, and significant progress in noise reduction techniques might lead to a breakthrough in those applications. Every effort to reduce noise is worthwhile.

MEG noise may be divided into environmental noise (e.g. power lines), physiological noise (e.g. fields produced by cardiac or muscular activity), and sensor noise. A wide range of techniques may be found in the literature that address the first two kinds of noise. SNS targets the third, and is complementary with methods that target the other two. In our experience, except for large amplitude glitches, sensor noise is relatively mild in terms of overall power (typically 100 times weaker than environmental noise, and 5 to 10 times weaker than brain activity) but it becomes more of a problem as techniques to remove other noise sources improve. Sensor noise suppression makes the job of other denoising methods easier by reducing the part of noise that does not fit their noise models. Removing glitches such as in Fig. 1(a) avoids having to discard the data epoch in which they occur. Removing the extra dimensionality induced by sensor-specific noise eases the task of methods such as PCA or ICA, that must decide on the dimensionality of data based on the rate of decay of the PCA spectrum. Finally, lowering the noise floor in the high frequency region may give better access to phenomena such as very high frequency oscillations (e.g. Edwards et al., 2005; Leutohold et al. 2005; Gonzales et al., 2006) that are usually obscured by noise (or by the low-pass filtering used to minimize that noise).

An important feature of the SNS method is that it does not cause appreciable distortion or loss of information, in contrast to other spatial or spectral filtering techniques. It also does not rely on assumptions about the geometry of brain sources, in contrast to source-modeling techniques. We see every reason to use it systematically as a preprocessing stage for MEG signal analysis.

The project-on-neighbors operation bears a superficial resemblance with the surface Laplacian technique (e.g. Bradshaw and Wikswo, 2001), in which each channel is subtracted from a linear combination of its neighbors (as opposed to replaced by). The surface Laplacian aims at improving spatial resolution by forming a spatial filter that emphasizes high spatial frequencies. The weakness of that method is precisely its sensitivity to the type of noise that our method removes (Bradshaw and Wikswo, 2001). SNS is conceptually related to Local Linear Embedding (Roweis and Saul 2000), to techniques that deal with missing data (e.g. Kondrashov and Ghil, 2006), and to leave-one-out cross-validation techniques in statistics.

SNS may be applicable to a wider range of situations. We have found that it can be applied usefully to EEG data, and it seems that it could be applied it to data from single or multi-unit electrode arrays to facilitate the simultaneous recording of local field potentials (with components shared among electrodes) and fine-grained neuronal activity (specific to individual electrodes). The method might also be of use outside physiology, for example to process data from arrays of geophysical sensors. SNS appears to have the intriguing property of reducing the effective noise of sensor arrays below the level expected by their physics: if so, this property is worth investigating more systematically. We have so far not found any trace of a method similar to SNS in the literature, which is surprising given its simplicity and effectiveness.