Abstract
When subjected to acidic conditions and high temperature, insulin is known to produce fibrils that display the common properties of disease amyloids. Thus, clarifying the mechanisms of insulin fibrillation can help the general understanding of amyloidal aggregation. Insulin fibrillation exhibits a very sharp time dependence, with a pronounced lag phase and subsequent explosive growth of amyloidal aggregates. Here we show that the initial stages of this process can be well described by exponential growth of the fibrillated proteins. This indicates that the process is mainly controlled by a secondary nucleation pathway.
Keywords: insulin, protein aggregation, amyloids, nucleation, Thioflavin T, fluorescence
Protein aggregation processes have been extensively studied in recent years, and are of fundamental relevance in many areas of scientific and technological research. The appearance of ordered protein aggregates (amyloid fibrils) is observed in a number of disorders, such as Parkinson’s, Alzheimer’s, and prion diseases (Harper and Lansbury 1997; Collinge 2001; Dobson 2003; Uversky and Fink 2004). Moreover, the tendency of many proteins to form large aggregates is one of the major problems in protein drug preparation, delivery, and storage (Brange 2000). The phenomenon of protein fibrillation is not limited to disease-related proteins. Rather, it seems to be a generic property of polypeptide chains (Fandrich and Dobson 2002). Under appropriate destabilizing conditions, even globular, otherwise stable, proteins may form amyloid fibrils (Fandrich et al. 2001; Goers et al. 2002).
Insulin is a 51-residue protein hormone involved in glucose metabolism and universally used in diabetes treatment (Brange 1994). It has long been known that, when subjected to acidic conditions and high temperature, insulin forms fibrils (Waugh 1946). These fibrils have been characterized and shown to exhibit the common properties of amyloids (Burke and Rougvie 1972; Yu et al. 1974; Bouchard et al. 2000; Nielsen et al. 2001b). This makes insulin a good model system for the study of amyloidal aggregation. The purpose of the present work is to apply a careful analysis of the fibrillation kinetics to reveal features of the underlying pathway.
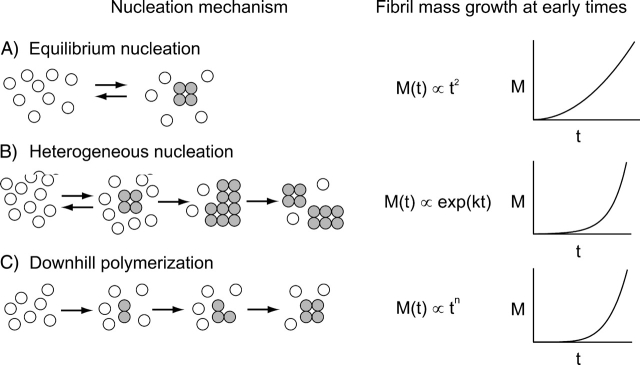
In bulk solutions, and in the absence of agitation, the kinetics of the fibrillation process are characterized by an abrupt time dependence, with a pronounced lag phase (in which nothing apparently occurs) and a subsequent fast fibrillation. This behavior has been ascribed to a nucleation–elongation mechanism, in which the lag phase is the time required for the formation of the nuclei, and the subsequent fast growth is due to simple monomer addition to the ends of pre-existing fibrils (Nielsen et al. 2001a,c). As explained by Ferrone (1999) in an elegant review, this deterministic description of lag-phase phenomena is not fully convincing. In mathematical terms, the simplest possible kinetic scheme describing a nucleation–elongation polymerization is the Oosawa model (Oosawa and Asakura 1975), which applies when the nucleus is in thermodynamic (very unfavorable) equilibrium with the monomeric protein (Fig. 1A ▶; Ferrone 1999). For this class of aggregation processes, the fibril mass should always be proportional to t2 at the beginning of the reaction, with essentially no lag phase. Moreover, the concentration dependence of the effective rate constant should be given by c0(n+1)/2, where c0 is the initial protein concentration and n is the size of the nucleus. In the case of insulin fibrillation, this class of models is ruled out by the abrupt time dependence, which is clearly incompatible with a t2 behavior at the beginning of the kinetics. In addition, the concentration dependence of the effective rate constant is relatively weak, being at maximum no more than linear (Nielsen et al. 2001c), although in some experimental conditions this could be explained by the fact that insulin can associate as dimers or larger oligomers (Nielsen et al. 2001a,c).
Figure 1.
Possible mechanisms in a nucleation–elongation fibrillation. (A) Equilibrium nucleation (Oosawa’s model; Oosawa and Asakura 1975). (B) Heterogeneous nucleation (sickle cell hemoglobin; Ferrone et al. 1980, 1985). (C) Forward nucleation (the figure shows t5; Flyvbjerg et al. 1996).
Within the framework of a nucleation-dependent aggregation process, there are two simple possibilities to explain the sharp time dependence displayed by insulin fibrillation. The first one is that nucleation can be catalyzed by existing aggregates or fibrils (secondary pathway). Initially, nuclei must be formed from monomers, but after the creation of a certain amount of aggregates, this secondary pathway takes control of the growth. The classic case is sickle cell hemoglobin polymerization (Ferrone et al. 1980, 1985; Hofrichter 1986; Ferrone 1999). There are at least three simple mechanisms by which a fibril can catalyze the formation of other fibrils: fragmentation, branching, and nucleation on the fibril surface (Fig. 1B ▶). All of them give rise to an exponential growth of the total mass of fibrillated protein as a function of time, i.e., depending on the actual rate constants, to a pronounced lag phase and a very fast subsequent aggregation (Ferrone 1999). The concentration dependence is determined by the mechanism of creation of the first fibrils and by the nature of the secondary pathway (Ferrone et al. 1985). Padrick and Miranker (2002) used the marked lag phase of islet amyloid polypeptide fibrillation to argue that a secondary pathway was involved.
Alternatively, a lag phase can arise when a nucleus, rather than being in thermodynamic equilibrium with the native protein, is formed in a certain number of slow steps by successive addition of smaller aggregates or monomers (downhill polymerization) (Fig. 1C ▶). In such a case, the kinetics at the beginning of the process will be described by a power law growth, in which the exponent is determined by the number of slow steps necessary for the formation of the nucleus. This mechanism was successfully used for modeling the kinetics of tubulin polymerization (Flyvbjerg et al. 1996). If the exponent in the power law is high enough, a pronounced lag phase will be observed. The concentration dependence is determined by the details of the process and can be as low as linear (Ferrone 1999).
In this work we investigate the early stages of insulin fibrillation, with the aim of ascertaining whether one of the above-mentioned aggregation mechanisms can be employed in the description of the process. In general, the association state of insulin is strongly affected by the details of the external conditions. In order to simplify the problem as much as possible, we performed our study in 20% acetic acid, because in these conditions the protein is reported to be fully monomeric (Nielsen et al. 2001a; Whittingham et al. 2002), implying that all the protein molecules follow a similar kinetic pathway. The progress of the fibrillation was monitored in situ by using Thioflavin T (ThT) fluorescence (see Materials and Methods), and, in order to bring the kinetics in a suitable timescale, the experiments were performed at high ionic strength (0.3 M NaCl) and at a temperature of 60°C. In acetic acid and at high ionic strength insulin is known to form relatively short and thick fibrils (Nielsen et al. 2001a).
Results and Discussion
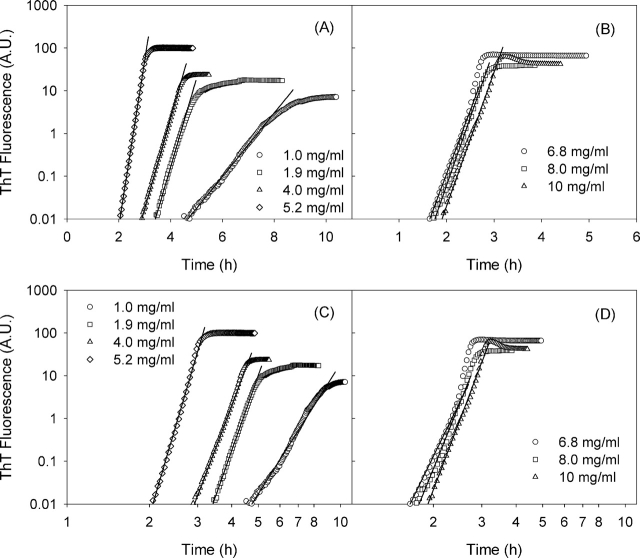
Figure 2 ▶ shows the ThT fluorescence for our samples as a function of time during the fibrillation process, after the subtraction of the value obtained at t = 0. For all the concentrations investigated, data are shown in log–lin (Fig. 2A,B ▶) and log–log (Fig. 2C,D ▶) plots. In agreement with earlier experiments in the literature (Nielsen et al. 2001c), we observe an initial lag phase in which nothing apparently occurs, followed by a sharp progression of the fibrillation process. In this second phase, ThT fluorescence exhibits a very large dynamic range, spanning over three orders of magnitude. In both kinds of plots reported in Figure 2 ▶ (log–lin and log–log), the growth phase exhibits an approximately straight-line behavior, suggesting either (1) heterogeneous nucleation (exponential growth; straight line in log–lin plot) or (2) downhill polymerization (power law growth; straight line in log–log plot). In fact, a high exponent power law is hardly distinguishable from exponential growth, unless very good data are available.
Figure 2.
Time course of insulin aggregation at 60°C at the different concentrations investigated. The same kinetics are shown in a log–lin plot (A,B) and in a log–log plot (C,D).
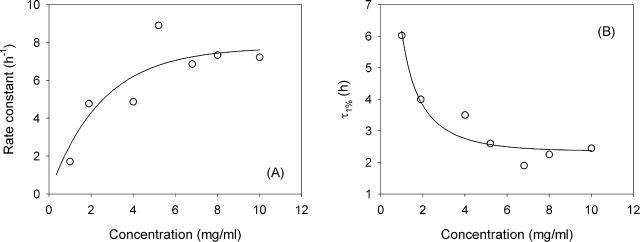
Figure 3A ▶ reports as a function of the protein concentration the apparent rate constants obtained by assuming an exponential process, i.e., the slope of the straight lines reported in Figure 2, A and B ▶. Figure 3B ▶ reports the concentration dependence of the lag time, defined as the time necessary to reach 1% of the maximum value of ThT fluorescence during the fibrillation process. As can be seen and as reported in the literature (Nielsen et al. 2001c), the concentration dependence of both the apparent rate constant (Fig. 3A ▶) and the lag time (Fig. 3B ▶) is very weak and also quite irregular. Moreover, replicate runs of the same experiments show that uncertainty in these parameters is ~50% (data not shown).
Figure 3.
(A) Rate constants obtained from the slopes of the straight lines shown in Figure 2 ▶, A and B. (B) τ1%, defined as the time necessary to reach 1% of the final value in the ThT fluorescence intensity, as a function of the protein concentration. Solid lines are guides for the eye.
From a statistical point of view, the correlation coefficients of the fits shown in Figure 2 ▶ are on the average slightly better for the case of an exponential growth (Fig. 2A,B ▶), and the dynamic range in which a straight line is observed is also slightly wider. The differences, however, are not large enough to be fully convincing.
What is more significant is the fact that the slopes of the straight lines shown in Figure 2, C and D ▶ (i.e., the exponents of the presumed power law dependence) are not the same, spanning from ~10 to 20. As stated by Flyvbjerg et al. (1996), the exponent minus one is the number of slow steps necessary for nucleus formation, a number that is equal to or smaller than the number of monomers in the nucleus. This number should be roughly independent of concentration, as it is for tubulin polymerization (Flyvbjerg et al. 1996). Moreover, it seems unlikely that a nucleus is formed in something like 15 subsequent steps or more (in the case of tubulin, the exponent was 5).
The above observations indicate that the kinetics of insulin aggregation in our conditions can be better described by exponential growth. This means that the aggregation process is significantly affected by a mechanism in which a pre-existing fibril can promote the formation of new fibrils, i.e., by a secondary pathway. This conclusion agrees well with recent Atomic Force Microscopy (AFM) studies of insulin fibrillation. Time-lapse AFM experiments showed that in the very initial stages of the aggregation process, insulin fibrils display the tendency to grow onto each other; i.e., a pre-existing fibril may promote the formation of new fibrils on its surface (Jansen et al. 2005). The investigators in this study concluded that “a single protofilament may act as a lateral template or scaffold” for the formation of new protofilaments, and this process is an alternative pathway to the “otherwise dominating” mere association of separately formed protofilaments. The fact that we observe exponential growth, with the same rate throughout the growth phase, shows that the secondary pathway in fact has a pivotal role in the aggregation process, since it determines the overall kinetic behavior.
Insulin aggregation is much faster in the presence of hydrophobic surfaces (Sluzky et al. 1991; Sharp et al. 2002), presumably because they promote the conformational transition to partially unfolded protein structures. Now an amyloid fibril, especially at the beginning of the aggregation process when the fibrils are not arranged in large ordered units, is a hydrophobic surface by itself. As such it may enhance the formation of new fibrils. Such an effect could be enhanced by specific interactions between the monomers in solution and the already fibrillated proteins (templated nucleation).
The rate constant shows a very modest increase with increasing concentration (Fig. 3A ▶). If the monomer is the reactive species, oligomer formation can blunt the concentration dependence (Lomakin et al. 1996). In our conditions insulin is monomeric at room temperature, but we cannot rule out the presence of oligomers or nonfibrillar aggregates at 60°C. Actually, such aggregates have been observed by Jansen et al. (2005) at the beginning of the kinetics. Another possibility is that the nucleation rate in the secondary pathway is almost independent of monomer concentration. This could correspond to branching or defect formation on the fibril surface being the time-limiting step. In this case, the rate constant is expected to increase proportionally to the square root of the concentration, as we show in the Appendix. In any case, a realistic description of the concentration dependence of the rate constant should probably take into account the spatial nonuniformity of the process and the local depletion of monomers.
We believe that this link between dynamics and fibrillation mechanism is of general utility for proteins whose fibrillation process is characterized by an abrupt time dependence and/or for proteins that form fibrils according to the Hierarchical Assembly Model (Ionescu-Zanetti et al. 1999; Khurana et al. 2003), since this model implies a strong interaction between early aggregates. Moreover, as suggested by Jansen et al. (2005), the existence of heterogeneous nucleation pathways must be taken into account in designing strategies to prevent amyloidosis and can shed new light into the general mechanisms of propagation of amyloids.
Materials and methods
Bovine insulin, acetic acid, and Thioflavin T (ThT) were purchased from Sigma Aldrich and used without further purification. Before each experiment, insulin was dissolved in solutions of acetic acid (20%) and NaCl (0.3 M). The resulting solutions were centrifuged and filtered through 0.22-μm filters. Protein concentration was determined by absorbance at 276 nm, using an extinction coefficient of 1.0 for 1 mg/mL (Nielsen et al. 2001c). A stock solution of ThT (1 mg/mL) was prepared in pure water and stored protected from light exposure at 4°C. This stock solution was diluted 1:40 into the samples before each experiment. As previously reported (Nielsen et al. 2001c), the presence of ThT in solution should not affect the fibrillation process. All glasses were boiled in concentrated alkaline detergent (Sodosil, Riedel-de-Häen) and rinsed with pure water. This point is particularly important, since using glasses cleaned with diluted detergent at room temperature systematically resulted in a sizable shortening of the lag phase in the fibrillation process. The same effect was also observed when samples were not centrifuged and/or filtered.
ThT fluorescence is widely used as a selective probe for the detection of amyloid fibrils (Levine 1999). In the presence of fibrils, ThT fluoresces brightly, with excitation and emission maxima at ~450 and ~482 nm, respectively. Fluorescence measurements were performed on a Perkin Elmer LS55 by using 2.5-nm excitation and emission bandwidth, and 75 nm/ min speed. An excitation wavelength of 450 nm was used, and, in order to improve the signal to noise ratio, the integrated intensity of the whole emission band in the range 460–600 nm was taken as signal. Temperature was controlled by using a circulating water bath. An ultramicro fluorescence cell (Hellma) was used to sample a very small volume (45 μL) of the fluorescent solution. Interestingly, using standard fluorescence cells (1 cm × 1 cm) resulted in much less regular kinetic profiles, thus indicating the existence of some kind of spatial heterogeneity of the fibrillation process in the larger sample volume.
ThT fluorescence response is reported to be proportional to the amount of fibrils present in the sample (e.g., Naiki et al. 1989; Naiki and Geyjo 1999). We verified the linearity of the response by measuring ThT fluorescence intensity in samples obtained by different dilution of a pre-fibrillated insulin solution (10 mg/mL, not shown).
Acknowledgments
We thank R. Carrotta, H. Flyvbjerg, and M. Manno for useful discussions, and M. Leone for the critical reading of the manuscript. This work was supported by a grant from the Danish Technical Research Council.
Appendix: Dimensional analysis of kinetic equations
We consider the following set of differential equations, in which M(t) is the total mass of already fibrillated protein at time t after the beginning of the process, N(t) is the number of fibrils ends, and c0 is the initial protein concentration:
 |
where k1 and k2 are the rate constants for fibril growth and formation of new fibrils, respectively, both second-order. The first equation simply states that the rate of growth of the total mass of fibrillated proteins is proportional to the number of fibril ends and to the monomer concentration (c0 − M(t)). The second one states that new fibril ends (i.e., new fibrils) are created by a spontaneous nucleation mechanism (fsp (c)) as well as by a secondary pathway with a rate proportional to the total mass of already fibrillated protein molecules and to the monomer concentration. Such a mechanism could be templated nucleation on the fibril surface. During the exponential growth phase, the spontaneous nucleation term can be neglected, and we can use the method of dimensionless equations (Goldstein and Stryer 1986; Flyvbjerg et al. 1996). If we use the quantities, m = M / c0, 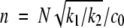 and
and 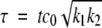 , we can write equation 1, neglecting the spontaneous nucleation term, as the following set of dimensionless equations:
, we can write equation 1, neglecting the spontaneous nucleation term, as the following set of dimensionless equations:
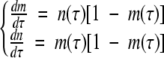 |
(2) |
The solution of equation 2 is independent of the value of c0; the behavior at particular initial concentrations is found by reinserting the definitions of τ, n, and m. Since τ ∞ c0t, it can be seen without actually solving the kinetic equations that the time course speeds up linearly with increasing concentration, so the rate constant is directly proportional to the initial concentration. This is clearly not in agreement with the data in Figure 3 ▶.
Alternatively, we can consider the possibility that heterogeneous nucleation is independent of monomer concentration:
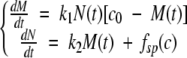 |
(3) |
where k2 is now a first-order rate constant. This could correspond to branching or defect formation on the fibril surface being the time-limiting step. In this case, the dimensionless parameters are m = M / c0, 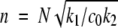 and
and 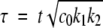 so it can be seen that the rate constant is proportional to the square root of the initial concentration, in better agreement with our data.
so it can be seen that the rate constant is proportional to the square root of the initial concentration, in better agreement with our data.
We note that equation 2 has the well-known solution
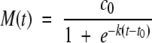 |
(4) |
with 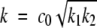 . This form is often used as an empirical fit to fibrillation curves (Nielsen et al. 2001c; Padrick and Miranker 2002). Equation 3 does not have to our knowledge an explicit solution, so the dimensionless approach is necessary in order to understand the concentration dependence.
. This form is often used as an empirical fit to fibrillation curves (Nielsen et al. 2001c; Padrick and Miranker 2002). Equation 3 does not have to our knowledge an explicit solution, so the dimensionless approach is necessary in order to understand the concentration dependence.
Equations 2 as well as 3 in the approximate form, i.e., neglecting the spontaneous nucleation term, lead to kinetic profiles that must display particular scaling properties. However, these properties are not expected really to be observed, since in both cases the lag time is also affected by the spontaneous nucleation term. Accordingly, the dimensionless approach can give information only about the rate constants, and not about the lag times.
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.051692305.
References
- Brange, J. 1994. Stability of insulin. Studies on the physical and chemical stability of insulin in pharmaceutical formulation. Kluwer Academic Publishers, Dordrecht, The Netherlands.
- ———. 2000. Physical stability of proteins. In Pharmaceutical formulation development of peptides and proteins (eds. S. Frokjaer and L. Hovgaard), pp. 89–112. Taylor and Francis, London.
- Bouchard, M., Zurdo, J., Nettleton, E.J., Dobson, C.M., and Robinson, C.V. 2000. Formation of insulin amyloid fibrils followed by FTIR simultaneously with CD and electron microscopy. Protein Sci. 9 1960–1967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burke, M.J. and Rougvie, M.A. 1972. Cross-β protein structures. I. Insulin fibrils. Biochemistry 11 2435–2439. [DOI] [PubMed] [Google Scholar]
- Collinge, J. 2001. Prion diseases of humans and animals: Their causes and molecular basis. Annu. Rev. Neurosci. 24 519–550. [DOI] [PubMed] [Google Scholar]
- Dobson, C.M. 2003. Protein folding and misfolding. Nature 426 884–890. [DOI] [PubMed] [Google Scholar]
- Fandrich, M. and Dobson, C.M. 2002. The behaviour of polyamino acids reveals an inverse side chain effect in amyloid structure formation. EMBO J. 21 5682–5690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fandrich, M., Fletcher, M.A., and Dobson, C.M. 2001. Amyloid fibrils from muscle myoglobin. Nature 410 165–166. [DOI] [PubMed] [Google Scholar]
- Ferrone, F. 1999. Analysis of protein aggregation kinetics. Methods Enzymol. 309 256–274. [DOI] [PubMed] [Google Scholar]
- Ferrone, F.A., Hofrichter, J., Sunshine, H.R., and Eaton, W.A. 1980. Kinetic-studies on photolysis-induced gelation of sickle-cell hemoglobin suggest a new mechanism. Biophys. J. 32 361–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrone, F.A., Hofrichter, J., and Eaton, W.A. 1985. Kinetics of sickle hemoglobin polymerization. II. A double nucleation mechanism. J. Mol. Biol. 183 611–631. [DOI] [PubMed] [Google Scholar]
- Flyvbjerg, H., Jobs, E., and Leibler, S. 1996. Kinetics of self-assembling microtubules: An “inverse problem” in biochemistry. Proc. Natl. Acad. Sci. 93 5975–5979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goers, J., Permyakov, S.E., Permyakov, E.A., Uversky, V.N., and Fink, A.L. 2002. Conformational prerequisite for α-lactalbumin fibrillation. Biochemistry 41 12546–12551. [DOI] [PubMed] [Google Scholar]
- Goldstein, R.F. and Stryer, L. 1986. Cooperative polymerization reactions. Analytical approximations, numerical examples, and experimental strategy. Biophys. J. 50 583–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harper, J.D. and Lansbury, P.T. 1997. Models of amyloid seeding in Alzheimer’s disease and scrapie: Mechanistic truths and physiological consequences of the time-dependent solubility of amyloid proteins. Annu. Rev. Biochem. 66 385–407. [DOI] [PubMed] [Google Scholar]
- Hofrichter, J. 1986. Kinetics of sickle hemoglobin polymerization. III. Nucleation rates determined from stochastic fluctuations in polymerization progress curves. J. Mol. Biol. 189 553–571. [DOI] [PubMed] [Google Scholar]
- Ionescu-Zanetti, C.R., Khurana, R., Gillespie, J.R., Petrick, T.S., Trabachino, L.C., Minert, L.J., Carter, S.A., and Fink, A.L. 1999. Monitoring the assembly of Ig light-chain amyloid fibrils by atomic force microscopy. Proc. Natl. Acad. Sci. 96 13175–13179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansen, R., Dzwolak, W., and Winter, R. 2005. Amyloidogenic self-assembly of insulin aggregates probed by high-resolution atomic force microscopy. Biophys. J. 88 1344–1353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khurana, R., Ionescu-Zanetti, C., Pope, M., Li, J., Nielson, L., Ramirez-Alvarado, M., Regan, L., Fink, A.L., and Carter, S.A. 2003. A general model for amyloid fibril assembly based on morphological studies using atomic force microscopy. Biophys. J. 85 1135–1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levine, H. 1999. Quantification of β-sheet amyloid structures with thioflavin T. Methods Enzymol. 309 256–274. [DOI] [PubMed] [Google Scholar]
- Lomakin, A., Chung, D.S., Benedek, G.B., Kirschner, D.A., and Teplow, D.B. 1996. On the nucleation and growth of amyloid β-protein fibrils: Detection of nuclei and quantitation of rate constants. Proc. Natl. Acad. Sci. 93 1125–1129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naiki, H. and Gejyo, F. 1999. Kinetic analysis of amyloid fibril formation. Methods Enzymol. 309 256–274. [DOI] [PubMed] [Google Scholar]
- Naiki, H., Higuchi, K., Hosokawa, M., and Takeda, T. 1989. Fluorimetric determination of amyloid fibrils in vitro using the fluorescent dye, thioflavin T1. Anal. Biochem. 177 244–249. [DOI] [PubMed] [Google Scholar]
- Nielsen, L., Frokjaer, S., Brange, J., Uversky, N., and Fink, A.L. 2001a. Probing the mechanism of insulin fibril formation with insulin mutants. Biochemistry 40 8397–8409. [DOI] [PubMed] [Google Scholar]
- Nielsen, L., Frokjaer, S., Carpenter, J.F., and Brange, J. 2001b. Studies on the structure of insulin fibrils by Fourier Transform Infrared (FTIR) spectroscopy and electron microscopy. J. Pharm. Sci. 90 29–37. [DOI] [PubMed] [Google Scholar]
- Nielsen, L., Khurana, R., Coats, A., Frokjaer, S., Brange, J., Vyas, S., Uversky, V.N., and Fink, A.L. 2001c. Effect of the environmental factors on the kinetics of insulin fibril formation: Elucidation of the molecular mechanism. Biochemistry 40 6036–6046. [DOI] [PubMed] [Google Scholar]
- Oosawa, F. and Asakura, S. 1975. Thermodynamics of the polymerization of proteins. Academic Press, New York.
- Padrick, S.B. and Miranker, A.D. 2002. Islet amyloid: Phase partitioning and secondary nucleation are central to the mechanism of fibrillogenesis. Biochemistry 41 4694–4703. [DOI] [PubMed] [Google Scholar]
- Sluzky, V., Tamada, J.A., Klibanov, A.M., and Langer, R. 1991. Kinetics of insulin aggregation in acqueous solutions upon agitation in the presence of hydrophobic surfaces. Proc. Natl. Acad. Sci. 88 9377–9381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uversky, V.N. and Fink, A.L. 2004. Conformational constraints for amyloid fibrillation: The importance of being unfolded. Biochim. Biophys. Acta 1698 131–153. [DOI] [PubMed] [Google Scholar]
- Waugh, D.F. 1946. A fibrous modification of insulin. I. The heat precipitate of insulin. J. Am. Chem. Soc. 68 247–250. [Google Scholar]
- Whittingham, J.L., Scott, D.J., Chance, K., Wilson, A., Finch, J., Brange, J., and Dodson, G.G. 2002. Insulin at pH 2: Structural analysis of the conditions promoting insulin fibre formation. J. Mol. Biol. 318 479–490. [DOI] [PubMed] [Google Scholar]
- Yu, N.T., Jo, B.H., Chang, R.C., and Huber, J.D. 1974. Single-crystal Raman spectra of native insulin. Structures of insulin fibrils, glucagons fibrils, and intact calf lens. Arch. Biochem. Biophys. 160 614–622. [DOI] [PubMed] [Google Scholar]