Abstract
Analysis of the conformational distribution of polypeptide segments in a conformational space is the first step for understanding a principle of structural diversity of proteins. Here, we present a statistical analysis of protein local structures based on interatomic Cα distances. Using principal component analysis (PCA) on the intrasegment Cα–Cα atomic distances, the conformational space of protein segments, which we call the protein segment universe, has been visualized, and three essential coordinate axes, suitable for describing the universe, have been identified. Three essential axes specified radius of gyration, structural symmetry, and separation of hairpin structures from other structures. Among the segments of arbitrary length, 6–22 residues long, the conservation of those axes was uncovered. Further application of PCA to the two largest clusters in the universe revealed local structural motifs. Although some of motifs have already been reported, we identified a possibly novel strand motif. We also showed that a capping box, which is one of the helix capping motifs, was separated into independent subclusters based on the Cα geometry. Implications of the strand motif, which may play a role for protein–protein interaction, are discussed. The currently proposed method is useful for not only mapping the immense universe of protein structures but also identification of structural motifs.
Keywords: protein segment universe, structure classification, principal component analysis, local structural motif, helix capping
With growing protein structural database and proceeding structural genomics projects, the importance of protein/peptide structure classification is increasing. Quantifying structural similarities among proteins is the first step to understanding a rule or principle according to which protein architectures are constructed. If the protein structure distribution is visible in a conformational space (i.e., a protein structure universe), this is helpful in investigating the structure similarity.
Exploring the protein structure universe at a fold (or structural domain) level could answer a fundamental question: How are proteins distributed in a conformational space? Holm and Sander (1996) have shown that the conformational space has a biased distribution depending on arrangements and combinations of secondary-structure elements. By visualizing a global representation of the fold universe, Hou et al. (2003) have clearly shown the distribution controlled by essential axes segregating into four major structural classes (α, β, α +β, and α/β). On the other hand, exploring the structure universe of short to medium size segments is also important, because protein folds share a few types of common structural units of short to medium size. Salem et al. (1999) have shown that most of 10 super-folds highly contain supersecondary structural units, such as β-hairpin, α-hairpin, and βαβ. Taylor (2002) has suggested that a variety of protein structures can be simplified by using a periodic table of all possible combinations of α-helices and β-sheets, and that the protein-structure comparison can be automatically done by using the periodic table. Therefore, investigating physicochemical and/or evolutionary principles governing segment structures of short to medium size may be useful for understanding the structural diversity of longer segments and proteins.
For the segment or protein structure classification, the choices of similarity measure and clustering algorithm are the crucial issues. Classification of short (typically four to nine residues long) polypeptide segments embedded in proteins has been attempted as reviewed (Tomii and Kanehisa 1999). Many similarity measures and clustering algorithms have been proposed for different goals of the surveys. The RMSD after structural superposition (Unger et al. 1989; Matsuo and Kanehisa 1993; Unger and Sussman 1993; Micheletti et al. 2000) and the Cα–Cα distances coupled with the pseudotorsion angles along the backbone trace (Rackovsky 1990; Rooman et al. 1990; Prestrelski et al. 1992; Fetrow et al. 1997) are the typical measures for identification of structural motifs or building blocks. The structural pattern of short segments in proteins most dominantly found in these surveys is α-helix. It is possible to detect β-strands and more detailed motifs, such as capping motifs, in high-resolution clustering. Fetrow et al. (1997) employed the Cα–Cα distances and the pseudotorsion angles, developed an autoassociative neural network for identifying structural motifs of seven residues long, and succeeded in distinguishing four capping motifs of helix and strand. Hunter and Subramaniam (2003) developed a hypercosine clustering method based on a geometrical similarity of segments for classifying canonical local shapes with an abundant segment data set. The identified local shapes included some typical motifs with various combinations of β-turns, β-strands, and α-helices, and a particular twisted motif with high frequencies of glycine and proline. A structure comparison method, which used geometric invariants of a tetrahedron generated by four Cα atoms in a segment, detected structural motifs in loop structure, where a large number (1.2 million) of fragments were taken for the structural library (Tendulkar et al. 2004). Recently, the classification results of short segments were applied for protein structure prediction. The backbone dihedral angles were employed for a neural network, which was based on self-organized maps, and local structural motifs of five residues long were identified with significant amino acid preference (de Brevern et al. 2000). The characterized motifs were applied for prediction of protein backbone structures based on a Bayesian probabilistic approach.
Since protein structure should be expressed by a number of degrees of freedom, a technique to reduce the high dimensional space to a lower dimensional one is indispensable. In this study, we used a well-known mathematical method, principal component analysis (PCA). Takahashi and Go (1993) applied PCA on the atomic coordinates of short peptides (i.e., two or three residues long) after the structural superposition, and showed that the short-peptide backbone can be classified into some conformational clusters. Hou et al. (2003) calculated the overall pairwise similarity scores among representatives from SCOP (Murzin et al. 1995) folds using the DALI program (Holm and Sander 1993), and projected the folds on a three-dimensional (3D) PCA space. Moreover, many groups used the PCA method to analyze the trajectories of molecular dynamics simulation (for example, Amadei et al. 1993; Kitao et al. 1998; Kamiya et al. 2002). With applying PCA on a conformational ensemble of a short peptide of about 10 residues long, where the conformations were sampled with a generalized-ensemble method (i.e., multicanonical molecular dynamics simulation), the peptide folding pathways were visualized in the 3D PCA space (Ikeda and Higo 2003; Ikeda et al. 2003).
The purposes of the present study were (1) to uncover the essential structural axes governing the structural variations of protein segments by visualizing a structure universe of short to medium size (6–22 residues long) segments, which were taken from all fold types of globular proteins, and (2) to identify local structural motifs distinguishable in the visualized conformational distribution. For these purposes, we applied PCA for the intrasegment Cα–Cα atomic distances, and attempted to obtain a global representation of the segment structure universe in the PCA space. Although the measure of structural similarity we used was simple, it was efficient and powerful for mapping the segment universe with an extreme density gradient. To address the second purpose, we focused on the structure universe of segments 10 residues long because of its tractability and the profitable results of motif identification.
Results
Visualization of the protein segment universe U10 in PCA space
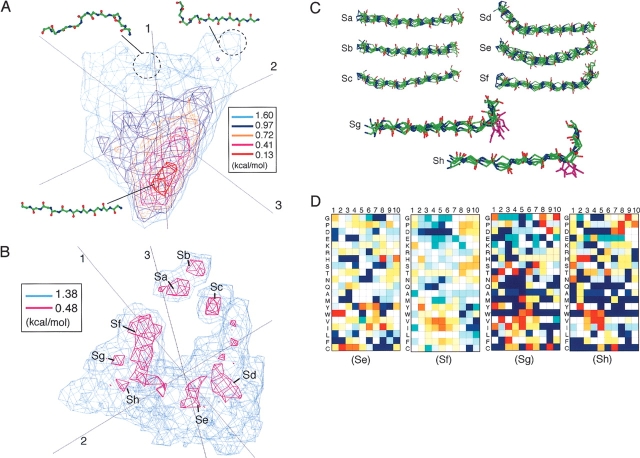
Given an ensemble consisting of segments of arbitrary length, the overall distribution of segments in a conformational space was visualized using PCA: The variance–covariance matrix was calculated from intrasegment Cα–Cα atomic distances, then PCA was applied on the variance–covariance matrix, and the PCA axes constructed the conformational space (see Materials and Methods). Figure 1 ▶ shows a 3D representation of the protein segment universe for 10 residues long, U10, depicted using the first three principal axes (v1, v2, and v3). Segments tended to concentrate in specific regions in the universe. In this analysis, we selected thresholds suitable for separating secondary structure elements. When the potential of mean force (PMF) = 2.84 kcal/mol (magenta line) was used as the threshold, two prominent clusters, characterized well by the secondary structure content (i.e., α-helix and β-strand), were obtained. Helix segments were assigned to the largest cluster in U10 (Pall = 32.07%). The definition of Pall is given in the subsection “Analysis of the protein segment universe” in Materials and Methods. The lowest PMF region (red line; discriminated by PMF = 2.36 kcal/mol) in this cluster consisted of complete helices, and different types of helical segments surrounded the complete-helix region. The strand cluster (Pall = 8.16%) was found on the opposite side of the helix cluster in U10, which mainly originated from β-sheets in the proteins and rarely from extended loops. Our method did not discriminate strands that participate in parallel and anti-parallel β-sheets, since those segments have similar conformations at the level of the Cα-carbon geometry. The populated central region of the strand cluster (PMF < 2.36 kcal/mol) consisted of fully extended strands (Pall = 3.29%), and the surrounding of the central region consisted of partly deformed strands (Pall = 4.87%). We further analyzed both the helix and strand clusters, classifying them into subclusters, as shown later.
Figure 1.
U10 expressed by PMF contour levels. PCA axis numbers (1, 2, and 3) are given near the axes. (A) Overview of U10. Conformational clusters (e.g., helix, strand, and β-hairpin clusters) and segment conformations picked from each cluster are displayed with the names. Eight conformations are taken from each β-hairpin cluster. To make out the difference between HPN and HPN′, hydrogen bonds in conformations are emphasized with solid lines. (B) Side view of A. (C) Subclusters in a hairpin cluster, HPN5,6, at the symmetrical center. Conformations from the two subclusters had different hydrogen-bonding patterns. Hydrogen bonds are represented by bold lines.
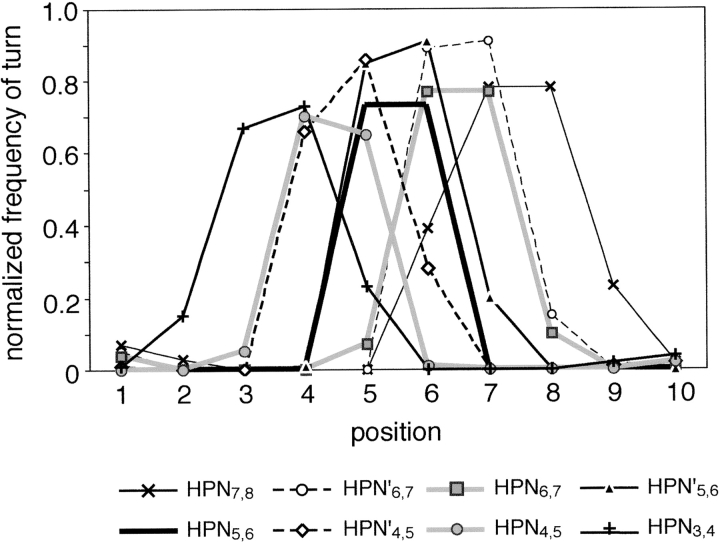
The β-hairpin clusters discriminated by PMF = 3.33 kcal/mol were symmetrically arranged on a semicircle arch around an edge of U10. Those β-hairpin clusters were quantitatively distinguishable from one another by the position of β-turn and the loop conformation characterized by the intrasegment hydrogen-bonding patterns (Fig. 2 ▶). Then, a hairpin cluster, where the majority of segments in the cluster could be characterized by the β-turn at the ith and the (i + 1)th residues, was called HPNi,i+1. The position of β-turn moved from the N/C- to the C/N-terminal side of the segment, when shifting the β-hairpin cluster along the semicircle arch. The HPN3,4, HPN4,5, HPN5,6, HPN6,7, and HPN7,8 had double hydrogen bonds between the (i − 1)th and (i + 2)th residues (Fig. 1A ▶). On the other hand, HPN′4,5, HPN′5,6, and HPN′6,7 had a single hydrogen bond. The cluster HPN5,6 was located at the symmetrical center of the hairpin arch (Fig. 1A ▶). By setting PMF = 3.33 kcal/mol, the central cluster was clearly separated into two subclusters (Fig. 1C ▶) with different hydrogen-bonding patterns. One subcluster frequently had double hydrogen bonds between the fourth and the seventh residues, and the other frequently had a single hydrogen bond between the backbone amide group of the third residue and the carbonyl group of the eighth residue. The two subclusters were clearly separated on a plane by v2 and v3. Thus, our simple method had enough resolution to discriminate the slight main-chain conformational differences.
Figure 2.
Normalized frequencies of turn for each β-hairpin cluster in U10. The frequency was defined as the rate of residues assigned to be “T” at each position of the segment within a β-hairpin cluster by the DSSP program (Kabsch and Sander 1983).
The distribution of segment conformations was shoe-shaped, where mirror symmetry was almost found about a plane constructed by v1 and v3. The strand, helix, and hairpin clusters correspond to toe, heel, and ankle of a shoe, respectively. The symmetrical feature as typically observed in the locations of the hairpin clusters persisted over the whole distribution of U10. From a local viewpoint, however, we found two asymmetrical areas (asym1 and 2 in Fig. 1A ▶) isolated by PMF of 3.27–3.33 kcal/mol. In the asymmetrical areas, five conformational clusters were found (Table 1). Although the structural conversion of the segments in each cluster was low, specific amino acid preferences were identified in each asymmetrical cluster. This implies that the amino acid preference may induce the structural differences between the asymmetrical clusters.
Table 1.
Asymmetrical clusters in the U10
| Cluster | PMF difference (kcal/mol) | Gly/Pro preference | % | Remarks |
| Um | 0.95 | Gly 6 | 0.19 | C-capping helix |
| Un | 0.46 | Gly 6 | 0.13 | C-capping helix |
| Uo | 0.23 | Gly 5, 6; Pro 6 | 0.05 | helix + loop + helix |
| Up | 0.41 | Pro 3, 5 | 0.11 | N-capping helix |
| Uq | 0.39 | Pro 5 | 0.04 | strand + 310-helix |
Column 1 is the name of the cluster described in the text. Column 2 is PMF difference, which indicates the difference in PMF value between the center (v1,v2,v3) of each cluster and that at the opposite position (v1, −v2,v3) on v2. Column 3 is the position where Gly or Pro has a preference of 1.0 or more. Column 4 is Pall for each cluster. Structures picked from the asymmetrical clusters in U10 are shown in Figure 1A ▶.
In asym1, there were three conformational clusters (Um, Un, and Uo). Cluster Um consisted of helix C-capping structures, where the first four residues were α-helical with the helix termination at the fifth residue. Amino acid Gly was favored at the sixth residue: FUm6(Gly) = 1.98. Hydrophobic residues were favored at the second and the ninth residues: FUm2(Cys) = 0.83, FUm2(Leu) = 0.83, and FUm9(Val) = 1.01. The hydrophobic contacts between the two residues were frequently observed in Um. Cluster Un also consisted of helix C-capping structures. The N-terminal helical conformations in Un were similar to those in Um. Amino acid Gly was favored at the sixth residue: FUn6(Gly) = 1.72. The favorable positions for the hydrophobic residues were the second and the seventh residues: FUn2(Leu) = 1.03, FUn2(Trp) = 0.95, FUn2(Met) = 0.81, FUn7(Val) = 0.74, FUn7(Ile) = 0.58, and FUn7(Phe) = 0.56. The side-chain contacts between the two residues were frequently observed, suggesting that Un correlates with the Schellman motif (Schellman 1980; Aurora et al. 1994). Cluster Uo consisted of helix–loop–helix structures. Amino acid Gly was favored at the fifth and the sixth residues: FUo5(Gly) = 1.47 and FUo6(Gly) = 1.10. The segments mostly originated from joint loops connecting two helices. In asym2, there were two conformational clusters (Up and Uq). Cluster Up consisted of helix N-capping structures, where the last five residues were helical with the helix termination at the fifth residue where amino acids Ser and Thr were strongly favored: FUp5(Ser) = 1.37 and FUp6(Thr) = 0.97. The hydrophobic residues were favored at the fourth and the ninth residues: FUp4(Met) = 0.95, FUp4(Ile) = 0.84, and FUp9(Trp) = 0.86. The side-chain contacts between the two residues were frequently observed, suggesting that Up correlates with the box motif (Harper and Rose 1993). Cluster Uq consisted of segments characterized as strand + 310-helix. The N-terminal half formed a strand conformation. The C-terminal half contained a significant amount of 310-helix. The percentage of segments with three or more 310-helical residues in Uq was 37.5%.
General features of the protein segment universe
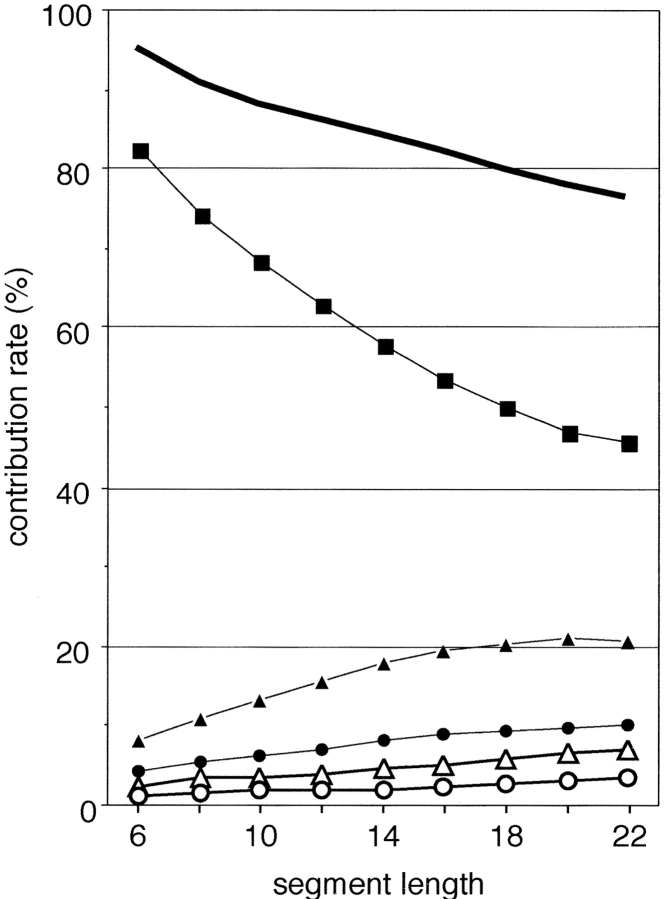
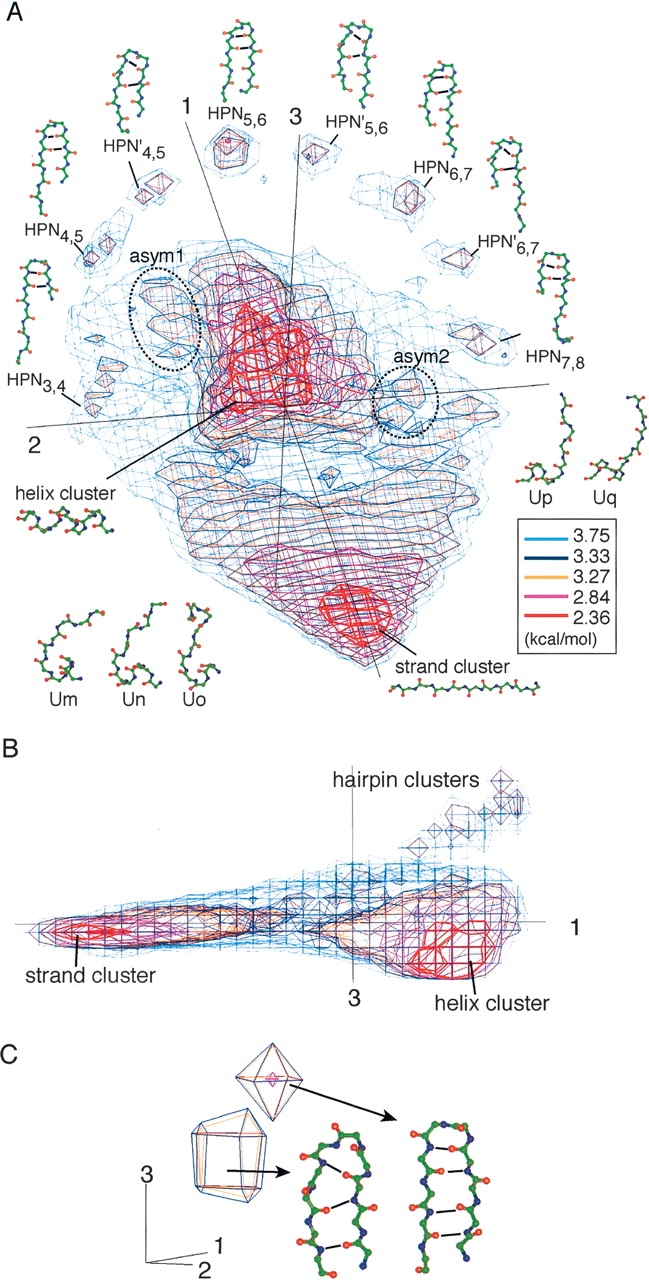
We show, here, the meanings of PCA axes describing the protein segment universe, and the conservation of those axes over segment universes from U6 to U22. Figure 3 ▶ shows a cumulative contribution of the first three axes, S1–3, and individual contributions of the first five axes. Interestingly, up to U16, S1–3 exceeded 80%, and even for U22 it was 76.3%. Thus, only three axes can account for the original structural variations of short to medium size segments. The individual contribution Q1 was especially large compared to those of the other axes, although Q1 remarkably decreased at extension of segment length. Contrarily, Q2 significantly increased up to 21 residues long (maximum contribution rate = 21.06%) and decreased for segments longer than 22 residues long. Other contributions (i.e., Q3–Q5) slightly increased with the segment length, which may be a natural outcome resulting from the decrease in Q1. The image of conformational space was conserved for longer segments. Figure 4 ▶ demonstrates U20. The distribution of conformational clusters (especially helix and β-hairpin clusters) in U20 was similar to that in U10. Although the strand cluster found in U10 diminished in U20, fully extended strands were located on the opposite side of the β-hairpin clusters on v1.
Figure 3.
Contribution rates of principal components for each segment length (6–22 residues long). The first five principal contributions, Q1 (filled squares), Q2 (filled triangles), Q3 (filled circles), Q4 (empty triangles), and Q5 (empty circles), are shown. The bold line indicates the cumulative contribution of the first three principal components, S1–3.
Figure 4.
U20 expressed by PMF contour levels. PCA axis numbers are given near the axes. (A) Overview of U20. β-Hairpin conformations picked from each β-hairpin cluster in U20 are shown in an inset. A fully extended strand found at the tail end of U20. (B) Side view of A.
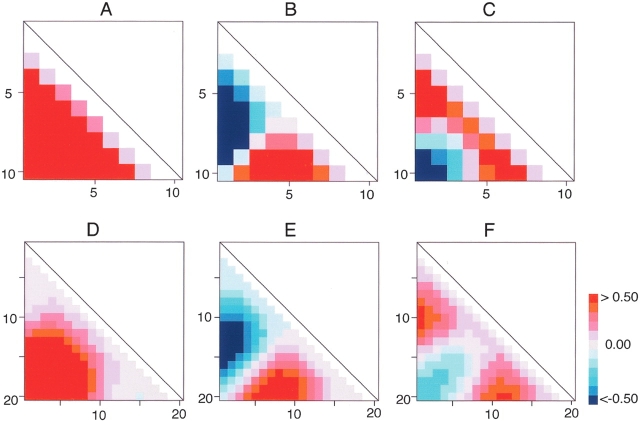
The eigenvectors v1, v2, … can be regarded as collective variables to describe the segment conformation in the PCA space, and each eigenvector may relate to a specific conformational variance of segment. The Δqk = wkλk1/2vk (see Equation 1, below) gives the conformational deviation along the kth eigenvector vk from the average 〈q〉. The deviation Δdi,j (i.e., the deviation of the distance, di,j, between the ith and the jth Cα atoms from the average distance 〈di,j〉) can be obtained by picking up the corresponding element to di,j from Δqk. We expressed Δqk with triangle maps (Fig. 5A–F ▶). The deviations along the major PCA axes, v1, v2, and v3 showed different patterns. Between U10 and U20, the triangle maps of each eigenvector correlated to each other: Figure 5 ▶, A and D, B and E, and C and F were considerably similar. In Figure 5, A and D ▶, the maps show that v1controlled end-to-end distance (Cα–Cα distance between the N-terminal and the C-terminal residues) or the radius of gyration of segments. The correlation coefficient between Δq1 and the end-to-end distance was 0.82, and that between Δq1 and the radius of gyration was 0.94 for U10. In Figure 5, B and E ▶, the maps show clear separation into the positive and negative areas. This means that the N-terminal residue reached (or got away from) the middle of a segment (i.e., the region around the fifth residue in the 10-residue segment), when the C-terminal residue got away from (or reached) the middle. Namely, v2 controlled the structural symmetry of segments. Remember that the shift of turn position in the β-hairpin clusters was controlled by v2(Fig. 1A ▶). In Figure 5, C and F ▶, the maps show clear separation into one negative area and two positive areas. The distances assigned to the negative area correspond to the end-to-end distance, and those assigned to the positive areas correspond to the end-to-middle distances. When a segment formed a hairpin, the end-to-end distance became small and the end-to-middle distance became large. On the other hand, when the segment formed a helix, the end-to-end distance became large and the end-to-middle distance became small. In fact, the hairpin clusters were located on the opposite side of the helix cluster along v3 (see Fig. 1B ▶) and segregated from the other clusters (the helix and strand clusters). Thus, v3 specified the separation of the hairpin conformations from the other structures.
Figure 5.
Triangle maps indicating deviations of Cα–Cα distances along each eigenvector (i.e., each PCA axis) from the mean Cα–Cα distances. Scale bar indicates relative deviation. Red color is anti-phase against blue color. Residue numbers are displayed with horizontal and vertical sides of the triangle maps. (A) v1, (B) v2, and (C) v3 for U10. (D) v1, (E) v2, and (F) v3 for U20.
Helical segment subuniverse
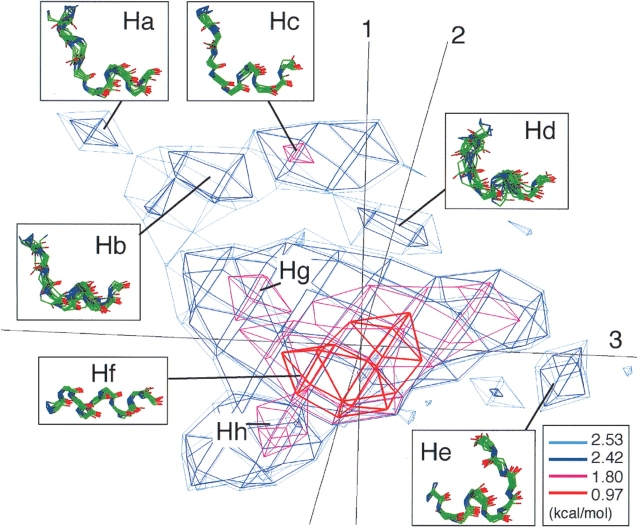
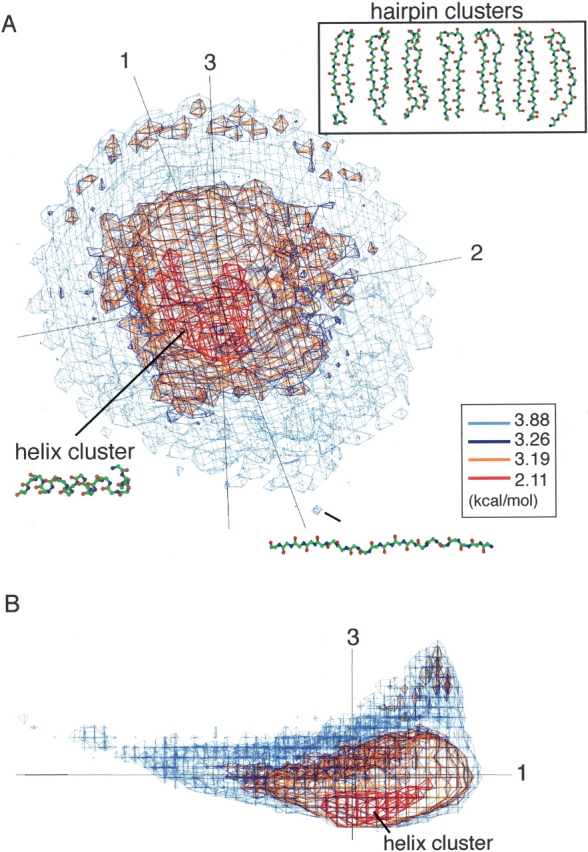
The helix cluster contained 37,261 helical segments. In spite of the fact that the segments in this cluster consisted of various types of helical conformations, they were not separated well as different clusters in the U10. Since three eigenvectors v1, v2, and v3 were calculated from the ensemble of all segments, the three PCA axes were suitable for describing the global conformational distribution, but not necessarily describing well the local region around the helix cluster. Thus, we applied PCA again only on the helical segments, and generated a helical segment subuniverse. The accumulative contribution S1–3 from the second PCA was 52%. It was relatively low, but the obtained distribution was well separated into conformational clusters in the 3D PCA space (Fig. 6 ▶). As a result, the first three principal components expressed the variety of the helical structures. Seven principal components (i.e., v1–v7) covered 80% of the whole distribution in the subuniverse. In the subuniverse, there were five small subclusters (Ha–He) and one large cluster at the level of PMF = 2.42 kcal/mol, as shown in Figure 6 ▶. Conformations randomly picked from each subcluster suggested that the subclusters Ha–Hd are helix N-capping structures and subcluster He is a helix C-capping structure (see insets of Fig. 6 ▶). Compared with the asymmetrical clusters of U10, the structural conversion in each helix subcluster was better and the helical region in the segments was longer. In fact, the helical region of segments in the helix subcluster Ha–Hd was one or two residues longer than that of segments in the asymmetrical cluster Up. Remember that these subclusters (i.e., Ha–Hd and Up) belonged to the helix N-capping structure. This structural conversion enables us to classify the subclusters into specific helix-capping motifs. At the level of PMF = 1.80 kcal/mol, the largest cluster was separated into a further three subclusters (Hf–Hh). Subcluster Hf (Phelix = 45.48%), which corresponded to the dense core region of the largest cluster, consisted of complete α-helices. Subclusters Hg (Phelix = 0.95%) and Hh (Phelix = 1.71%), located near Hf, could be characterized as conformations where helices were broken at the N- or the C-terminal residue, respectively. The definition of Phelix is given in the subsection “Analysis of the protein segment universe” in Materials and Methods.
Figure 6.
Helical segment subuniverse of 10 residues long expressed with PMF levels. Each cluster is labeled with its name. PCA axis numbers are given near axes. Conformations arbitrarily chosen from each subcluster are shown in insets. Mean values of main-chain RMSD among the conformations in subcluster Ha, Hb, Hc, Hd, He, Hf, Hg, and Hh are 1.01, 1.48, 0.74, 1.98, 1.10, 0.60, 1.05, and 1.33 Å, respectively.
Subcluster Ha (Phelix = 0.30%) consisted of helix N-capping segments, which agreed well with the box motif (Harper and Rose 1993; Aurora and Rose 1998). The α-helical region was from the fifth to the 10th residues. The amino acid preferences (Equation 4, below) FXi(A), where X = Ha, …, Hd, are shown in Figure 7B ▶. At the N-terminal helix-breaking point (the fourth residue), Ser and Thr were strongly favored: FHa4(Ser) = 1.44 and FHa4(Thr) = 1.43 (Fig. 7B ▶). In the majority of the Ha segments, the side chain of the fourth residue formed a hydrogen bond with the backbone amide group of the seventh residue, and the 3–8 side-chain contact was observed: A side chain-to-side chain contact between the ith and the jth residues was called the i–j side-chain contact in this study. Subcluster Hc (Phelix = 0.83%) consisted of segments with one residue sliding from those in Ha toward the N-terminal side. Namely, FHc3(Ser) and FHc3(Thr) were high. Furthermore, we observed the hydrogen bond between the side chain of the third residue and the backbone of the sixth residue, as well as the 2–7 side-chain contact. Other conservative amino acid preference between Ha and Hc were also found: FHa3(Met) and FHc2 (Met), as well as FHa7(Gln) and FHc6(Gln). Besides, hydrophobic amino acids had a high preference at the eighth residue in Ha and at the seventh residue in Hc. This high preference of the hydrophobic amino acids correlates well with the observation on the box motif (Harper and Rose 1993).
Figure 7.
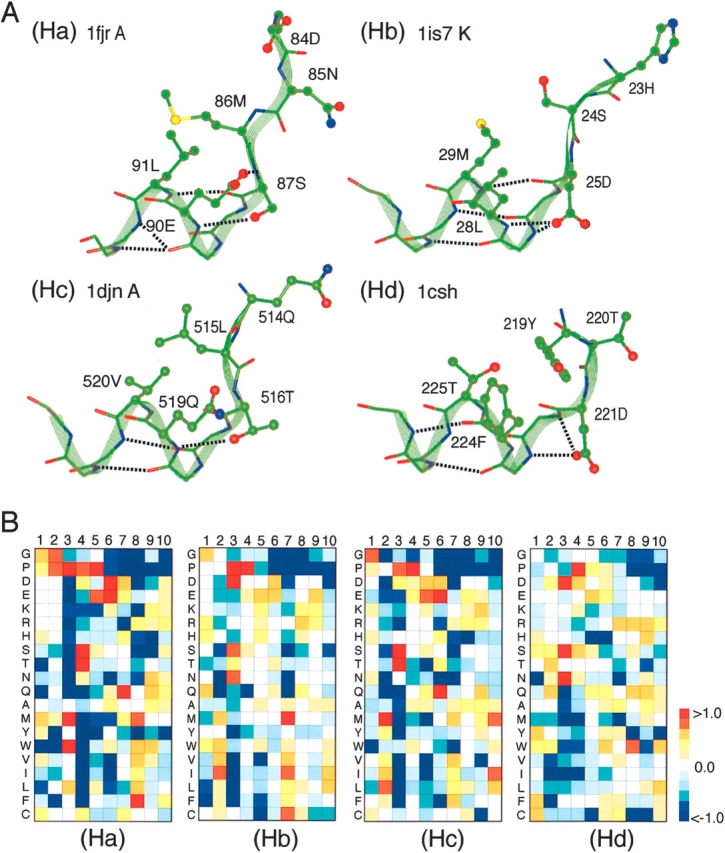
Conformations and amino acid preferences of helical subclusters Ha–Hd. (A) Typical conformations chosen from Ha–Hd are displayed. Each conformation is shown with residue numbers and PDB code of originated protein. Side-chain conformations that participate in helix capping interactions at the N termini of helices are shown. Broken lines represent hydrogen bonds. (B) Amino acid preference at each position of segments of Ha–Hd. Scale bar with colors represents values of the preference.
Subcluster Hb (Phelix= 0.69%) also consisted of helix N-capping segments, and again agreed well with the box motif (Harper and Rose 1993; Aurora and Rose 1998). According to the motif classification by Aurora and Rose (1998), which was made based on the side-chain–side-chain contact patterns, Hb should be equivalent to Hc, because both Hb and Hc involved the 2–7 side-chain contacts. The reason for the separation is because the N-terminal helix-breaking point (third residue for both subclusters) was characterized by different amino acid preferences and hydrogen-bond patterns between the subclusters: In Hb, Asp was strongly favored at the third residue: FHb3(Asp) = 1.23 (Fig. 7B ▶), although Thr/Ser was favored in Hc. The side chain of Asp in Hb was located at a position where a hydrogen bond is formable either with the fifth or the sixth residue (see Hb in Fig. 7A ▶), whereas the side chain of Thr/Ser in Hc was located at a position where a hydrogen bond is formable only with the fifth residue (see Hc in Fig. 7A ▶). These differences resulted in the backbone structural difference at the N-terminal region of the segments. Accordingly, the [ψ2, ψ3] angles were different between the subclusters: [111.4°, 112.8°] for Hb, and [133.0°, 135.2°] for Hc, where the values are the average over segments in each subcluster.
Subcluster Hd (Phelix = 0.52%) consisted of helix N-capping segments, which agreed well with the big-box motif (Seale et al. 1994). The α-helical region was from the 4th to the 10th residues. At the N-terminal helix-breaking point (the third residue), Asp, Ser, and Asn were favored: FHd3(Asp) = 1.14, FHd3(Ser) = 1.06, and FHd3(Asn) = 1.08 (Fig. 7B ▶), and large hydrophobic residues, such as Thr, Phe, and Cys, were favored at the first residue (Fig. 7B ▶): FHd1(Tyr) = 0.78, FHd1(Phe) = 0.64 and FHd1(Cys) = 0.66. The structural conversion of segments in subcluster Hd was relatively wrong compared with that in the other subclusters (see the caption for Fig. 6 ▶). However, the segments frequently formed either the 1–6 or 1–7 side-chain contact, which is a common feature in the big-box motif.
Subcluster He (Phelix = 0.71%) consisted of helix C-capping segments, which agreed well with the Schellman motif (Schellman 1980; Aurora et al. 1994). The α-helical region was from the first to the sixth residues. At the seventh residue, which is one residue after the C-terminal helix-breaking point, Gly was strongly favored: FHe8(Gly) = 2.12. The majority of the He segments contained a turn at the seventh or the eighth residue, and did not form a side-chain-to-backbone hydrogen bond. The 4–9 side-chain contact was frequently formed in He. In the fourth and the ninth residues, nonpolar and hydrophobic residues were favored: FHe4(Cys) = 1.12, FHe4(Leu) = 0.89, FHe4(Met) = 0.85, and FHe9(Trp) = 0.84. On the other hand, polar and hydrophilic residues were disfavored: FHe4(Asn) = −1.76, FHe4(Ser) = −0.80, FHe9(Asp) = −1.63, and FHe9(Gln) = −1.61.
Figure 6 ▶ indicates that the axis v2 separates the helix N-capping segments in subclusters (i.e., Ha–Hd) from the other clusters (i.e., He–Hh), and that the subclusters Ha–Hd are well separated from one another along the axis v3, when the other subclusters are removed. Triangle maps (Fig. S1A–C in Supplemental Material) indicate the changes of Cα–Cα distances along the three essential eigenvectors (i.e., each PCA axis) derived from the helical segment subuniverse.
Strand segment subuniverse
To further investigate the strand cluster (PMF < 2.84 kcal/mol) in U10, we applied PCA again on the cluster, and generated a strand segment subuniverse (S1–3 = 79%. Then the fully extended strands populated again in the central region of the obtained subuniverse, overlapping on the surrounding regions consisting of the partly deformed strands (Fig. 8A ▶). Thus, the strand cluster was not separated into independent subclusters.
Figure 8.
Strand segment subuniverse of 10 residues long. (A) Subuniverse generated by all segments from strand cluster of U10. (B) Subuniverse generated by segments from the surrounding region around the strand core of U10. (C) Segments in strand subclusters Sa–Sh. Conformations arbitrarily chosen from each subcluster, except for Sg and Sh, are shown. Segments with Asp at the ninth or the eighth residue are picked up from subcluster Sg or Sh, respectively, and the Asp side chains are also displayed. (D) Amino acid preference at each position of segments of Se–Sh. See Figure 7 ▶ caption for color to represent the scale of the preference.
To classify the surrounding regions consisting of the partly deformed strands into subclusters, we did the following: First, we collected segments, which distributed in the regions of 2.36 ≤ PMF < 2.84 kcal/mol, from the strand cluster. Thus the collected segments are those remaining after removing the central strand core (a red region at the bottom of Fig. 1A ▶) dominated by the fully extended strands. Remember that the level of PMF < 2.84 kcal/mol was also used to discriminate the helix cluster. Then, we further applied PCA on the picked 5664 segments, and obtained several subclusters. The distribution of the segments is shown in Figure 8B ▶ (S1–3 = 77%, where eight subclusters, named Sa, Sb, …, Sh, were found. Four principal components (i.e., v1–v4) covered more than 80% of the whole distribution in this subuniverse.
Although the majority of the fully extended strands were removed by the procedure explained above, 37 fully extended β-strands still remained in the subuniverse and they formed subcluster Sb (Pstrand = 0.65%). The definition of Pstrand is given in the subsection “Analysis of the protein segment universe” in Materials and Methods. Eighty-nine percent of the segments in Sb originated from anti-parallel β-sheets in proteins. Subcluster Sa (Pstrand = 1.50%) consisted of β-strands broken at the 10th residue. Amino acids Pro, Glu, and Asp were disfavored in the Sa and Sb segments, whereas Val, Ile, Trp, and Phe, which are generally favored in strands, were favored.
Subcluster Sc (Pstrand = 1.48%) consisted of segments whose strand region was from the third to the 10th residues bending around the third residue. Amino acids Gly and Pro were favored at the N-terminal region: FSc1(Gly) = 1.06 and FSc2(Pro) = 0.85. The third residue relatively favored Arg, which is known as a β-strand breaker (Colloc’h and Cohen 1991): FSc3(Arg) = 0.74. Thus, there is a possibility that Sc is a N-capping strand. Subcluster Sd (Pstrand = 2.07%) consisted of segments whose strand region was from the fourth to the 10th residues bending around the fourth residue. We could not find any particular amino acid preference in Sd.
Subcluster Se (Pstrand = 1.40%) consisted of 79 curved strands, which mostly originated from extended loops or strands in β-sheets. The percentage of segments with five or more residues serving strand–strand hydrogen bonds was 58%. Generally, Pro is rarely found in strands. However, the preferences of Pro assigned to the strand region (the fourth to the eighth residues) were relatively high (Fig. 8D ▶). Note that the preference for Pro was not specifically high on a site, but nonspecifically high in the strand region. Twelve Se segments contained two or three Pro residues in the strand region. We named Se the “Pro-rich curved strand motif.” The Se segments were frequently located on the protein (or domain) surface: The average solvent accessible surface area (ASA) assigned to Se was the largest in the strand subclusters (Sa, 403; Sb, 354; Sc, 369; Sd, 415; Se, 554; Sf, 429; Sg, 427; and Sh, 394 Å2), where ASA was calculated on the condition that the segment was embedded in the protein (or domain). In He, segments with large ASA (ASA > 800 Å2) were exposed loops or strands in β-hairpin, whereas all of the segments buried in the interior of the protein (ASA < 200 Å2) were β-sheet strands. We found that 14 Se segments participated in protein–protein interactions (see Discussion).
Subcluster Sf (Pstrand = 6.39%) consisted of strand C-capping segments whose strand region was from the first to the seventh residues. Amino acids Pro, Asp, and Ser were relatively favored in the C-terminal region. Twenty-five percent of the Sf segments had a turn at the ninth residue and 30% at the 10th residue.
Subcluster Sg (Pstrand = 0.53%) consisted of strand C-capping segments whose strand region was from the second to the seventh residues. Amino acids Pro, Asp, and Gly were favored in the C-terminal region: FSg8(Pro) = 1.09, FSg9(Asp) = 1.39, and FSg10(Gly) = 1.15. There were seven segments where Asp existed at the ninth residue, and the side-chain orientations of Asp converged well as displayed in Figure 8D ▶. Six of the seven side chains of Asp formed intraprotein hydrogen bonds. Thus, we named Sg “Asp C-cap strands.”
Subcluster Sh (Pstrand = 0.51%) consisted of strand C-capping segments whose strand region was from the first to the seventh residues. Amino acids Pro, Asp, and Gly were favored in the C-terminal region: FSh8(Pro) = 1.12, FSh8(Asp) = 1.11, and FSh9(Gly) = 1.03. Thus, both Sg and Sh had a high preference for Asp in the C-terminal region. However, the side-chain orientations of Asp did not converge well in Sh compared with those in Sg. Besides, the majority of side chains of Asp in Sh were exposed to solvent without participating in the intraprotein hydrogen bond.
Triangle maps (Fig. S1D-I in Supplemental Material) indicate the changes of Cα–Cα distances along the three essential eigenvectors (i.e., each PCA axis) derived from the strand segment subuniverse.
Discussion
The choice of the measure to discriminate the protein/segment structural differences is critically important for structural classification. The root mean square deviation, widely used as the measure, is meaningful only when the two structures to be compared are similar (Mizuguchi and Go 1995; Koehl 2001). We used the difference of the Cα–Cα atomic distances for the measure. The benefits of using this measure are that the computation of the variance–covariance matrix does not require the structural superposition and that the segment backbone structure can be reconstructed from the Cα–Cα atomic distances. Note that our method is sufficiently rapid for building the structural universe including segment structures with a vast data set. The disadvantages of this measure are that the side-chain conformational differences cannot be directly detected and that the structural chirality is not considered. These disadvantages are due to the fact that the relative position between two atoms was not expressed by a vector but by a scalar (i.e., distance). For instance, right- and left-handed helices are exactly the same in the Cα–Cα atomic distances.
The significance of applying the PCA method to a complicated system, such as protein structure, is to obtain a small number of essential variables that account for a large proportion of the original structural variation, and then to represent the variation in a low dimensional PCA space. In the present study, by using three axes with large contributions, which were able to considerably cover the structural variation of segments (S1–3 of U10 was 87.8%), we clearly showed the overall distribution of segment conformations in the 3D PCA space. On the other hand, even if such essential variables are obtained, it is often difficult with the PCA method to understand what the variables really mean for the given original information. We succeeded in defining the meaning of the three essential elements (i.e., radius of gyration, structural symmetry, and separation of hairpin structures from other structures), which are suitable for describing the structural diversity of protein segments. It is reasonable that the first principal component remarkably correlated with radius of gyration, because the most sensitive quantity to the variety of segment conformations, collected from various proteins, is probably radius of gyration.
By comparing U10 and U20, we showed that the symmetrical distribution is a common feature for the short to medium size segments in the PCA space. This means that two segments, which have conformations similar to each other when the residue numbering of one segment is inversed, appear with an approximately equal frequency in proteins. Thus, we presume that in the short to medium size segments, there is almost no bias acting on the chain direction from the N to C terminus or from the C to N terminus, and that this symmetry is a “property of a string” of short to medium size segments in natural proteins (polypeptide chains). We also observed the asymmetrical areas (asym1 and asym2) in U10. The causal reason for this asymmetry is the structure differences between the N- and C-terminal caps of helices, and this structural difference may be caused by the difference of the hydrogen-bond patterns. In fact, we observed that only the N-terminal cap helix favored the side-chain-to-backbone hydrogen bond, which agrees well with the observation by Aurora and Rose (1998).
We applied PCA two times on the segment ensemble to analyze the helical or strand segment subuniverse. This means that the segment universe is viewed with two different scales. The first PCA made the large-scale structures of the universe visible, where helical, strand, and hairpin clusters distributed. The second PCA made the details of the universe visible, where subclusters distributed. The triangle maps of the first three axes for the helix subuniverse (Fig. S1A–C in Supplemental Material), where some locally restricted conformational deviations were seen, were different from those for the whole segments (Fig. 5A–C ▶). As shown in Results, the axes v2 and v3 from the helix subuniverse described the variety of the helix capping structures. For the strand segments taken from the strand cluster (PMF < 2.84 kcal/mol) in U10, the strand cluster was not separated into independent subclusters unless the central strand core in U10 was eliminated (Fig. 8A ▶). The reason should be addressed that the shape of the strand segment subuniverse was analogous with that of the strand cluster in U10, and that the strand cluster did not show a fine structure in U10. The triangle maps of the first two axes of the strand subuniverse were similar to those of U10 (see Fig. S1D,E in Supplemental Material). The strand segment universe has a continuous distribution whereas the helix segment universe has a discontinuous one.
The helix-capping motifs have been summarized in a previous review (Aurora and Rose 1998). In the helical segment subuniverse, some subclusters corresponded to the helix-capping motifs ever reported (Schellman 1980; Harper and Rose 1993; Aurora et al. 1994; Seale et al. 1994). The two subclusters Hb and Hc should belong to the box motif, according to the classification method of Aurora and Rose (1998). We showed that the separation into the two subclusters resulted from the difference in the side-chain-to-backbone hydrogen-bond patterns between Hb and Hc. Since our classification method is based on the Cα–Cα distances, it cannot directly detect the side-chain conformational differences. However, our method is also useful to detect the side-chain conformational differences, when the side-chain conformation correlates with the main-chain conformation.
One may consider that the structure classification of strands is less important than that of helices, because a strand is not stabilized by the intrastrand interactions but is usually stabilized by interacting with the surrounding strands in the same β-sheet. The majority of the strand cluster consisted of fully extended strands, and the trends of amino acid preferences favorable for β-strand have just been confirmed. This may mean the lesser importance of the strand-cluster classification. However, the deformed strands were classified well into subclusters with the specific amino acid preferences (Fig. 8D ▶). Typically, we could identify a strand subcluster Se, named the Pro-rich curved motif. Based on the status of Se segments participating in protein–protein interactions, we have categorized them into the following three cases:
Segments in a hinge region of a dimer. The dimer, where the constituent proteins are denoted here as proteins A and B, maintains the structure by exchanging an arm (strand) in each protein, and the strand of protein A is interacting with protein B, as well as that of protein B interacting with protein A.
Segments on the interface of an oligomer except for a dimer.
Segments on the interface between the equivalent proteins in crystal.
Three segments with one or two Pro residues (5csc A415–424, 1dqa A529–538, and 1djn A702–711) were identified as case 1. Especially, the two Pro residues (Pro418 and Pro422) in 5csc have been suggested by Bergdoll et al. (1997) as the hinge prolines, which are important for the oligomerization with the arm exchange. They have proposed that the existence of Pro at the root of the exchanged arm induces the oligomerization by imposing the arm to a favorable position. The two remaining segments in case 1 may play the same role for the dimerization, since the Pro residues are located at the root of the arms in the dimer. Five segments (trimer: 1el6 A194–203, 1pya A10–19, 1i9r A199–208; pentamer: 1i9b A48–57, A80–89) were identified as case 2. The arrangements of Se segments in the oligomer vary, such as a triangular or a spherical shape. Six segments (1i4j A70–79, 1g61 A2092–2101, 1d8i A402–411, 1qpa A320–329, A330–339, and 1a9x A985–994) were identified as case 3. Thus, we suggested that Se motifs, which are localized on the protein surface, play an important role for oligomerization or maintenance of protein complexes in various ways. Figure S2 in Supplemental Material displays three cases of Se segments at the protein interface. We found that some segments in cases 2 and 3 did not contain Pro residue, although the common curved conformations were conserved. In the analysis, we used a segment ensemble selected from the current structural database. More analysis should be done, when the structural database becomes more abundant in the feature. Then, we may find Pro residue in a complex that involves a protein homologous with the current one.
A role of edge strands in protein–protein interaction has been studied (Richardson and Richardson 2002). The edge strand was defined as that bordered on only one side by another β-strand in a β-sheet (Minor and Kim 1994), and then the other side of the edge strand may be used for avoiding edge-to-edge aggregation when the strand is located on the protein surface. Richardson and Richardson (2002) have studied a strategy adopted by natural β-sheet proteins to avoid the protein aggregation. A method to distinguish the edge strand from the other strands based on the sequence information was proposed (Siepen et al. 2003). We investigated the relation between the edge strand and the Se subcluster, and found that 19 of 79 Se segments were exposed edge strands. Then, the current study showed that the edge strand is a member of the Se subcluster in the segment universe.
We used the fold representatives to generate the segment ensembles. One may consider that structural representatives should be collected from each superfamily, because the variety of structures in a fold group is larger compared to that in a superfamily. We consider that our result does not change much even though the representatives are collected from each superfamily, because one superfamily often forms one fold group. In fact, in 625/731 of the SCOP folds, which we used in this analysis, one fold group has only one superfamily member. To evaluate the sensitivity of data size and the selection of structural representatives on the structural distribution, we constructed a 3D conformational space using a segment ensemble generated from 100 proteins, which were randomly picked up from the full SCOP folds (i.e., 731 folds). The obtained conformational distribution was highly similar to the original one: Secondary structure clusters (helix, strand, and hairpins) existed as dense cores in the conformational space, and the shape of the whole distribution was again like that of a shoe (data not shown).
The current study showed that the protein segment universe had a symmetrical shape (i.e., shoe-shaped) in the PCA space. It should be noted that the universe 20 residues long, U20, exhibited a shape similar to that of U10. This similarity may reveal a general feature of short to medium size segments. For longer segments (i.e., 30-residue segments), the shape was not similar to those of U10 and U20: The shape changed from the shoe shape to a different one at around 25 residues long, which may indicate that the boundary between the peptide-like structure and the protein-like one in natural proteins is at around 25 residues long (will be reported elsewhere). This discontinuity of the universe shape may reveal the existence of a boundary between segment-like and protein-like structures.
Materials and methods
Preparation of a segment ensemble from representative folds in SCOP
For a comprehensive survey of protein segment conformation, it is desirable that the data set contains a wide range of distinct protein folds. To avoid the biases from structural similarity, we selected one structure from each fold group, referring to the SCOP database (release 1.63): 171, 119, 224, 117, 39, and 61 domains for all-α, all-β, α + β, α/β, multidomain, and small protein classes, respectively. Membrane proteins were excluded. The 731 proteins were selected for preparing a segment ensemble (see http://www.cbrc.jp/~ikeda/psu/list.html). Tertiary structures of the proteins were taken from the Protein Data Bank (Berman et al. 2000) to build the segment ensemble. Then, we cut the protein structures into short to medium size segments (6–22 residues long) with a window sliding by one residue along the sequence. Segments with incomplete coordinate data were excluded. The number of the 10-residue and 20-residue segments in each segment ensemble was 116,182 and 106,324, respectively.
Constructing a protein segment universe using PCA
We calculated all intrasegment Cα–Cα atomic distances for each segment in the ensemble. Denoting di,j as the distance between the ith and jth Cα atoms in a segment, a distance set was expressed for the segment as q = [d1,2, d1,3, d1,4,. . .., dn−1,n] = [q1, q2, q3, … , qn(n−1)/2], where n is the number of residues in the segment. Then, a variance–covariance matrix, C, was calculated as Cij = 〈qiqj〉 − 〈qi〉〈qj〉, where Cij is the (i,j)th element of the matrix. The average 〈…〉 was taken over all segments in the ensemble.
A set of eigenvectors {v1, v2, v3, … ,vn(n − 1)/2} and eigenvalues {λ1, λ2, λ3, … , λn(n − 1)/2} was obtained with diagonalyzing C, where two equations, Cvi = λivi and vi•vj = δij, are satisfied. If the distribution of segments in the conformational space is expressed by a gaussian, λi corresponds to the standard deviation along vi. Although the real distribution cannot be simply expressed by the gaussian, the situation that λi corresponds to the standard deviation is maintained. Thus, eigenvectors with larger eigenvalues are more important to study the conformational variety of the segments. Here, eigenvalues are arranged in the descending order: λi > λj if i < j.
A conformational space constructed by the eigenvectors is called “PCA space,” where an eigenvector corresponds to a PCA axis. The origin of the PCA space is set on the average Cα–Cα atomic distances: 〈q〉 = [〈q1〉, 〈q2〉, 〈q3〉, … , 〈qn(n − 1)/2〉]. Then, any position (i.e., any segment structure) in the PCA space can be expressed by a linear combination of eigenvectors as
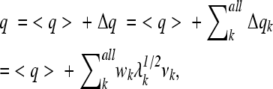 |
(1) |
where Δqk = wkλk1/2vk is the conformational deviation from 〈q〉 along vk, and wk is the amount of deviation along vk (note that vk is normalized). Thus, q can be represented as [w1, w2, w3, … , wn(n − 1)/2], and wi be regarded as the ith coordinate assigned to vi in the PCA space.
To study the segment universe, we used three eigenvectors with the three largest eigenvalues: v1 (the first PCA axis), v2 (the second), and v3 (the third). Thus, the cumulative contribution of the three PCA elements to the whole conformational distribution is assessed by
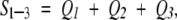 |
(2) |
where Qi = λi/∑k all λk. The larger the Q1–3, the larger the contribution of the three PCA axes to the whole distribution. The three eigenvectors construct a 3D PCA space, and the introduction of the 3D space makes it possible to view the segment universe.
Analysis of the protein segment universe
As described above, the distribution of segments in the 3D PCA space gives an image of the segment universe. We designated the segment universe n residues long as Un. We defined a vector, r, to express the segment position in the 3D PCA space: r = [w1, w2, w3]. After obtaining the density ρ(r) of the distribution at each position r in the space, ρ(r) was converted to the form of the potential of mean force (PMF):
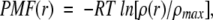 |
(3) |
where R is the gas constant, T = 300 K, and ρmax is the maximum density to set PMF at the maximum position to zero. We expressed the 3D PCA space by the PMF contour map because the segment structure space had an extreme density gradient.
The number of segments involved in each conformational cluster was represented by a ratio (i.e., percentage) to that in the segment universe (or subuniverse): Pall, Phelix, and Pstrand are ratios to U10, the helix subuniverse, and the strand subuniverse, respectively.
Amino acid preference
We calculated a preference, Fxi(Aj), of amino acid Aj at position i in the segments of a cluster (or subcluster) X:
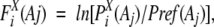 |
(4) |
where PXi(Aj) is the frequency of amino acid Aj at position i in cluster X and Pref(Aj) is the frequency of amino acid Aj in all of the segments of a segment universe (Bystroff and Baker 1998).
Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.04956305.
Supplemental material: see www.proteinscience.org
References
- Amadei, A., Linssen, A.B., and Berendsen, H.J. 1993. Essential dynamics of proteins. Proteins 17 412–425. [DOI] [PubMed] [Google Scholar]
- Aurora, R. and Rose, G.D. 1998. Helix capping. Protein Sci. 7 21–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aurora, R., Srinivasan, R., and Rose, G.D. 1994. Rules for α-helix termination by glycine. Science 264 1126–1130. [DOI] [PubMed] [Google Scholar]
- Bergdoll, M., Remy, M.H., Cagnon, C., Masson, J.M., and Dumas, P. 1997. Proline-dependent oligomerization with arm exchange. Structure 5 391–401. [DOI] [PubMed] [Google Scholar]
- Berman, H.M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T.N., Weissig, H., Shindyalov, I.N., and Bourne, P.E. 2000. The Protein Data Bank. Nucleic Acids Res. 28 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bystroff, C. and Baker, D. 1998. Prediction of local structure in proteins using a library of sequence-structure motifs. J. Mol. Biol. 281 565–577. [DOI] [PubMed] [Google Scholar]
- Colloc’h, N. and Cohen, F.E. 1991. β-breakers: An aperiodic secondary structure. J. Mol. Biol. 221 603–613. [DOI] [PubMed] [Google Scholar]
- de Brevern, A.G., Etchebest, C., and Hazout, S. 2000. Bayesian probabilistic approach for predicting backbone structures in terms of protein blocks. Proteins 41 271–287. [DOI] [PubMed] [Google Scholar]
- Fetrow, J.S., Palumbo, M.J., and Berg, G. 1997. Patterns, structures, and amino acid frequencies in structural building blocks, a protein secondary structure classification scheme. Proteins 27 249–271. [PubMed] [Google Scholar]
- Harper, E.T. and Rose, G.D. 1993. Helix stop signals in proteins and peptides: The capping box. Biochemistry 32 7605–7609. [DOI] [PubMed] [Google Scholar]
- Holm, L. and Sander, C. 1993. Protein structure comparison by alignment of distance matrices. J. Mol. Biol. 233 123–138. [DOI] [PubMed] [Google Scholar]
- ———. 1996. Mapping the protein universe. Science 273 595–602. [DOI] [PubMed] [Google Scholar]
- Hou, J., Sims, G.E., Zhang, C., and Kim, S.H. 2003. A global representation of the protein fold space. Proc. Natl. Acad. Sci. 100 2386–2390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter, C.G. and Subramaniam, S. 2003. Protein fragment clustering and canonical local shapes. Proteins 50 580–588. [DOI] [PubMed] [Google Scholar]
- Ikeda, K. and Higo, J. 2003. Free-energy landscape of a chameleon sequence in explicit water and its inherent α/β bifacial property. Protein Sci. 12 2542–2548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ikeda, K., Galzitskaya, O.V., Nakamura, H., and Higo, J. 2003. β-Hairpins, α-helices, and the intermediates among the secondary structures in the energy landscape of a peptide from a distal β-hairpin of SH3 domain. J. Comput. Chem. 24 310–318. [DOI] [PubMed] [Google Scholar]
- Kabsch, W. and Sander, C. 1983. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 22 2577–2637. [DOI] [PubMed] [Google Scholar]
- Kamiya, N., Higo, J., and Nakamura, H. 2002. Conformational transition states of a β-hairpin peptide between the ordered and disordered conformations in explicit water. Protein Sci. 11 2297–2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitao, A., Hayward, S., and Go, N. 1998. Energy landscape of a native protein: Jumping-among-minima model. Proteins 33 496–517. [DOI] [PubMed] [Google Scholar]
- Koehl, P. 2001. Protein structure similarities. Curr. Opin. Struct. Biol. 11 348–353. [DOI] [PubMed] [Google Scholar]
- Matsuo, Y. and Kanehisa, M. 1993. An approach to systematic detection of protein structural motifs. Comput. Appl. Biosci. 9 153–159. [DOI] [PubMed] [Google Scholar]
- Micheletti, C., Seno, F., and Maritan, A. 2000. Recurrent oligomers in proteins: An optimal scheme reconciling accurate and concise backbone representations in automated folding and design studies. Proteins 40 662–674. [DOI] [PubMed] [Google Scholar]
- Minor, D.L. and Kim P. 1994. Context is a major determinant of β-sheet propensity. Nature 371 264–267. [DOI] [PubMed] [Google Scholar]
- Mizuguchi, K. and Go, N. 1995. Seeking significance in three-dimensional protein structure comparisons. Curr. Opin. Struct. Biol. 5 377–382. [DOI] [PubMed] [Google Scholar]
- Murzin, A., Brenner, S.E., Hubbard, T., and Chothia, C. 1995. SCOP: A structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol. 247 536–540. [DOI] [PubMed] [Google Scholar]
- Prestrelski, S.J., Williams Jr., A.L., and Liebman, M.N. 1992. Generation of a substructure library for the description and classification of protein secondary structure. I. Overview of the methods and results. Proteins 14 430–439. [DOI] [PubMed] [Google Scholar]
- Rackovsky, S. 1990. Quantitative organization of the known protein x-ray structures. I. Methods and short-length-scale results. Proteins 7 378–402. [DOI] [PubMed] [Google Scholar]
- Richardson, J.S. and Richardson, D.C. 2002. Natural β-sheet proteins use negative design to avoid edge-to-edge aggregation. Proc. Natl. Acad. Sci. 99 2754–2759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rooman, M.J., Rodriguez, J., and Wodak, S.J. 1990. Automatic definition of recurrent local structure motifs in proteins. J. Mol. Biol. 213 327–336. [DOI] [PubMed] [Google Scholar]
- Salem, G.M., Hutchinson, E.G., Orengo, C.A., and Thornton J.M. 1999. Correlation of observed fold frequency with the occurrence of local structural motifs. J. Mol. Biol. 287 969–981. [DOI] [PubMed] [Google Scholar]
- Schellman, C. 1980. The α-L conformation at the ends of helices. In Protein folding (ed. R. Jaenicke), pp. 53–61. Elsevier/North Holland, New York.
- Seale, J.W., Srinivasan, R., and Rose, G.D. 1994. Sequence determinants of the capping box, a stabilizing motif at the N-termini of α-helices. Protein Sci. 3 1741–1745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siepen, J.A., Radford S.E., and Westhead, D.R. 2003. β Edge strands in protein structure prediction and aggregation. Protein Sci. 12 2348–2359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi, K. and Go, N. 1993. Conformational classification of short backbone fragments in globular proteins and its use for coding backbone conformations. Biophys. Chem. 47 163–178. [Google Scholar]
- Taylor, W.R. 2002. A ‘periodic table’ for protein structures. Nature 416 657–660. [DOI] [PubMed] [Google Scholar]
- Tendulkar, A.V., Joshi, A.A., Sohoni, M.A., and Wangikar, P.P. 2004. Clustering of protein structural fragments reveals modular building block approach of nature. J. Mol. Biol. 338 611–629. [DOI] [PubMed] [Google Scholar]
- Tomii, K. and Kanehisa, M. 1999. Systematic detection of protein structural motifs. In Pattern discovery in biomolecular data (eds. J.T.L. Wang et al.), pp. 97–110. Oxford University Press, New York.
- Unger, R. and Sussman, J.L. 1993. The importance of short structural motifs in protein structure analysis. J. Comput. Aided Mol. Des. 7 457–472. [DOI] [PubMed] [Google Scholar]
- Unger, R., Harel, D., Wherland, S., and Sussman, J.L. 1989. A 3D building blocks approach to analyzing and predicting structure of proteins. Proteins 5 355–373. [DOI] [PubMed] [Google Scholar]