Abstract
The increasing use of enzymes in industrial processes and the importance of understanding protein folding and stability have led to several attempts to predict and quantify the effect of every possible amino acid exchange (mutation) on the thermostability of proteins. In this article we describe a knowledge-based discrimination function that acts as a fast and reliable guide in protein engineering and optimization. The function used consists of two parts, a pairwise energy function based on a distance- and direction-dependent atomic description of the amino acid environment, and a torsion angle energy function. In a first step a training set of 11 proteins including 646 mutant proteins with experimentally determined thermostability was used to optimize the knowledge-based energy functions. The resulting potential function was then tested using a test mutant database consisting of 918 various point mutations introduced in 27 proteins. The best correlation coefficient obtained for the experimental data and the predicted thermostability for the training set is r = 0.81 (561 data points). A total of 76% of the mutations could be predicted correctly as being either stabilizing or destabilizing. The results for the test set are r = 0.74 (747 data points) and 72%, respectively. The global correlation over the combined data (1308 mutants) obtained is 0.78.
Keywords: protein, thermostability, prediction, knowledge-based, potential
For the prediction of thermostability for proteins (Dill 1990, 1999; Finkelstein 1997; Sippl 1999), a detailed understanding of the forces that are involved in protein folding is essential. Therefore a large number of experimental and theoretical investigations were carried out in recent years to identify factors contributing to the thermal stability of proteins (Matthews 1993; Kannan and Vishveshwara 2000; Kumar et al. 2000; Liu et al. 2000; Bruins et al. 2001). Since the knowledge about these factors is still very limited, the protein engineering process to design efficient enzymes for industrial processes—such as detergent manufacturing, food and starch production, and textile processing—is still mainly based on human experience (Bruins et al. 2001). Presently no general method for an automatic and a fast prediction of the effects of possible mutations on the protein stability is available.
The different theoretical approaches to describe and quantify mutational effects on protein stability can be divided in three categories (Lazaridis and Karplus 2000) that differ in the complexity of the description of the physical forces involved in protein folding. The first approach utilizes physical effective energy functions (PEEF), including molecular dynamics simulations with force fields. Because of the high amount of computational time required for a stability prediction with PEEF, it can only be used on small sets of protein mutants. In order to reduce computational time, implicit terms for the solvation energies and side-chain entropies can be introduced, but the results obtained so far are not suitable for large-scale calculations (Wang et al. 1996, 1998; Moult 1997; Duan and Kollman 1998; Duan et al. 1998; Kollman et al. 2000).
The other two approaches are based on knowledge-based potentials (Sippl 1990, 1993, 1995; Miyazawa and Jernigan 1994; DeBolt and Skolnick 1996; Melo and Feytmans 1997; Koppensteiner and Sippl 1998; Gohlke et al. 2000; Xu et al. 2000; Lu and Skolnick 2001) and can be divided into the statistical energy functions (SEEF) and empirical effective energy functions (EEEF). They are based on pseudo-energies derived either from distributions of structural elements in protein structures or empirical data obtained from experimental results on proteins. The advantage of the SEEF potentials is that they describe complex interactions as entropic effects or many-body interactions which are difficult to separate and quantify (Lazaridis and Karplus 2000). SEEFs usually make use of an empirical approximation for the denaturated state.
The EEEF approach combines a physical description of possible interactions with empirical data determined experimentally (Guerois et al. 2002), resulting in two main drawbacks: A full physical description of all possible forces involved in protein stability is needed, and the free energies used in these methods are approximations derived from accurate models and experimental data associated with errors that are difficult to estimate.
A new approach was recently published by Capriotti et al. (2004) that uses a neural network-based method to describe the direction (stabilizing or destabilizing) of a mutational effect on protein stability.
We decided to develop a knowledge-based discrimination function based on a SEEF approach. The usage of knowledge-based potentials for the prediction of thermostability was shown in papers by Ota et al. (1995), Wang et al. (1998), Gilis and Rooman (1996, 1997), Topham et al. (1997), Guerois et al. (2002), and Zhou and Zhou (2002). Ota et al. (1995) used an empirically derived simple pseudo-energy potential originally developed for the evaluation of 3D-1D compatibility to predict the thermal stability of 96 point mutations introduced in ribonuclease H. Their pseudo-energy potential consists of four terms: side-chain packing, hydration, hydrogen-bonding efficiency, and local conformation. They describe a top and bottom approach to represent interacting directions. Wang et al. (1998) calculated a protein mutant profile based on a mean force field including protein main-chain characteristics and determined the thermal stability of 33 single-mutant proteins. Gilis and Rooman (1996, 1997) developed two knowledge-based potentials: a distance-dependent residue–residue potential and a backbone torsion angle potential. They analyzed stability changes upon mutation for up to 238 single-mutant proteins. The method Topham et al. (1997) used to predict the thermal stability of protein mutants is based on structural environment-dependent amino acid substitution and propensity tables. They analyzed 131 single mutations. Zhou and Zhou (2002) used their DFIRE knowledge-based potential to predict the stabilities of 895 mutants.
Guerois et al. (2002) chose an EEEF approach to predict thermal stability of single-mutant proteins. The developed free energy function has eight elements and was tested on 667 mutants. Recently Bordner and Abagyan (2004) published another EEEF approach to predict the thermal stability of 1816 single point mutations from 81 proteins. Their free energy function consists of seven elements, such as electrostatic, van der Waals, hydrogen bonding, and torsional energies, which were calculated with a force field.
Here, we present a knowledge-based potential function of the SEEF type which consists of a pairwise energy function giving a direction- and distance-dependent atomic description of the amino acid environment and a torsion angle contribution. The computed stabilization energies are compared with the free energy changes of a large number of experimental investigations. The potential was developed and optimized with a training data set (with 646 single mutations) and tested on 946 single mutations. In the following we present the discrimination function, the experimental data sets, and the analysis of our results.
Results
The described discrimination function for the prediction of protein thermostability consists of two parts: a knowledge-based direction- and distance-dependent amino acid–atom potential, and a knowledge-based torsion angle potential. The parameters of this function are optimized with a training set and evaluated with a test set. All possible point mutations (sequence length times 19) are computed, and the predicted stabilization energies are calculated and compared to available experimental results.
There are several ways to analyze the predictive power of the potential function. The most common value in literature used is the correlation coefficient rcor between the predicted and the experimental data (Ota et al. 1995; Gilis and Rooman 1996, 1997; Guerois et al. 2002; Zhou and Zhou 2002; Bordner and Abagyan 2004). Accordingly in most cases potentials are optimized to give maximal correlation coefficients. Other equally important criteria that should be considered are the correct prediction of the direction of the stability change, rv, and the sensibility, Sens (Capriotti et al. 2004). The optimized set of derived parameters for the developed potentials are described in Materials and Methods. A computer program was developed that creates a mutation profile for any given protein with a given 3D structure.
Direction component of the amino acid–atom potential
We expect the distribution of atoms around an amino acid to be dependent on the direction. Therefore we tested whether the inclusion of a direction component into the amino acid–atom potential could improve the results (see Materials and Methods).
The prediction results for the amino acid–atom potential with and without a directional component are presented in Table 1. The differences between the amino acid–atom potentials are minor. This changes when the amino acid–atom potential is combined with the torsion angle potential to our final discrimination function (see Materials and Methods). The correlation coefficient rcor for the discrimination function with a directional component is 0.72 (rv = 75%). These values are slightly better for the discrimination function without directional component (rcor = 0.71 and rv = 73%).
Table 1.
Results of the prediction with and without the directional component for the amino acid-atom function and the discrimination function for the training data set
| Method | rcor (n) | rv [;%]; | Sens |
| Amino acid-atom potential with direction componenta | 0.67 (646) | 65 | 0.67 |
| Discrimination functionb with direction component | 0.72 (646) | 75 | 0.75 |
| Amino acid-atom potential without direction component | 0.67 (646) | 65 | 0.65 |
| Discrimination functionb without direction component | 0.71 (646) | 73 | 0.75 |
aSee Materials and Methods.
bCombined amino acid-atom potential and torsion angle potentials; see Materials and Methods.
n, number of data points.
Prediction of the free energy differences for the training data set
The results for the training data set are shown in Table 2 and Figure 1 ▶. For the discrimination function, rcor is 0.72 (646 data points) with rv at 75% and a standard deviation of 1.44 kcal/mol. The standard deviation σ is calculated from the difference between the predicted and the experimental data. The sensibility reaches a value of 75%. The prediction results are strongly improved by the combination of the amino acid–atom potential with the torsion angle. rcor increases from 0.67 (amino acid–atom potential) and 0.26 (torsion angle potential) up to 0.72. Furthermore, rv increases from 64.7% (amino acid–atom potential) and 67.8% (the torsion angle potential) to 74.5%.
Table 2.
Results of the prediction with the discrimination function for the training data set
| Training data set | |||
| Method | rcor (n) | rv [;%]; (σ [;kcal/mol];) | Sens |
| Amino acid-atom potential function | 0.67 (646) | 64.7 (1.44) | 0.67 |
| Torsion angle potential function | 0.26 (646) | 67.8 (1.48) | 0.75 |
| Discrimination function | 0.72 (646) | 75 (1.44) | 0.75 |
| Discrimination function with outliers >3σa excluded | 0.76 (612) | 75 (1.00) | 0.73 |
| Discrimination function with outliers >2σa excluded | 0.81 (561) | 76 (0.77) | 0.72 |
| Discrimination function with ncalc-σa | 0.72 (646) | 52 (1.37) | 0.96 |
a σ = 1.44 kcal/mol.
ncalc, calculated values; n, number of data points.
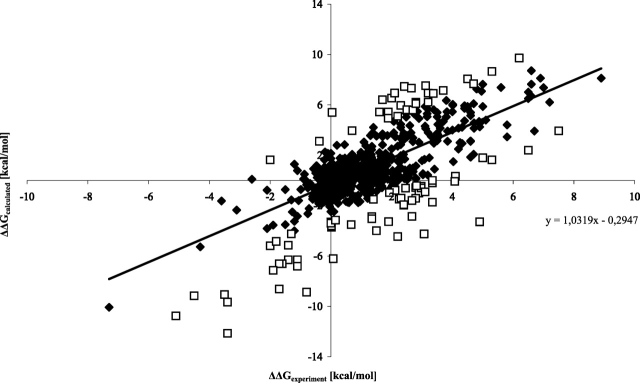
Figure 1.
Calculated stabilization energies Δ ΔGcalculated for the training data set with 646 data points compared to the experimental values Δ ΔGexperiment. The linear regression line was obtained for 561 data points after the outliers (> 2σ) were discarded (the equation is shown in the figure). Its correlation coefficient is rcor = 0.81. The discarded mutations are indicated as squares, and the other mutants are shown with rhombic symbols.
As shown in Figure 1 ▶, there are distinct “outliers” where the difference between calculated and experimental data is much larger than for the average experiments. Excluding those data points with a standard deviation greater than the threefold standard deviation based on the training data set (σ = 1.44 kcal/mol) raises rcor to 0.81 (561 data points, 87% of the data set), rv to 76%, and Sens is 72% (see Discussion for a justification of the exclusion). From the 85 excluded mutations (13% of the original data set), only eight mutations could not be assigned to a secondary structure by the program DSSP (Kabsch and Sander 1983), and 55 (65%) mutations have a solvent accessibility of lower than 20% (see details in Materials and Methods). This indicates that the over- or underestimation of calculated stabilization energies in comparison to the experimental stabilization energies is mostly due to cooperative effects (e.g., many-body interactions, secondary structure interactions), structural rearrangements, or hydrophobic effects. These effects cannot be correctly estimated by any currently published method (Gilis and Rooman 1996, 1997; Topham et al. 1997; Guerois et al. 2002; Capriotti et al. 2004).
Use of the present method as an automatic approach for prefiltering protein engineering experiments requires a high sensibility and a reduction of the number of necessary experiments. Therefore we limited our list of stabilizing candidates to mutants with a predicted stabilization effect larger than the calculated standard deviation. By subtracting the standard deviation from the calculated values, the sensibility increases to 96%, with only six stabilizing mutations falsely predicted as destabilizing (1lyd Gly30Ala, 2ci2 Lys37Ala, 2wsy Glu49Pro, 3lzm Lys60Pro, 4lyz Phe34Tyr, Gly102Arg).
Prediction of the free energy differences for the test set
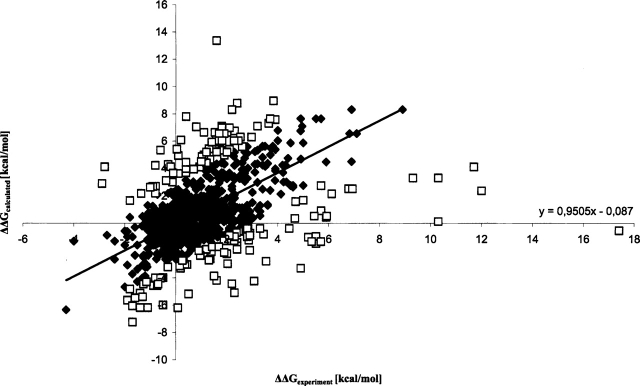
The calculated predictions for the test database are shown in Figure 2 ▶ and Table 3. The test set contains single mutations collected from the ProTherm database (Gromiha et al. 2000; see Materials and Methods for details). The correlation coefficient between calculated and experimental values is 0.46 (918 data points) with rv of 70%; the standard deviation is 1.67 kcal/mol with a sensibility value of 67%. By discarding mutations with a difference between predicted and experimental data greater than two or three times the standard deviation (1.44 kcal/mol), rcor raises to 0.64 (851 data points, 93% of the data set) with rv = 70% (σ = 1.06 kcal/mol) and rcor = 0.74 (747 data points, 81% of the data set) with rv = 72% (σ = 0.75 kcal/mol), respectively. These findings correspond to the results of the training data set.
Figure 2.
Calculated stabilization energies Δ ΔGcalculated for the test data set with 918 data points compared to the experimental values Δ ΔGexperiment. The linear regression line was obtained for 747 data points after the outliers (> 2σ) were discarded (the equation is shown in the figure). Its correlation coefficient is rcor = 0.74. The discarded mutations are indicated as squares, and the other mutants are shown with rhombic symbols.
Table 3.
Results of the prediction with the discrimination function for the test database
| Test database | |||
| Method | rcor (n) | rv [;%]; (σ [;kcal/mol];) | Sens |
| Discrimination function | 0.46 (918) | 69 (1.67) | 0.67 |
| Discrimination function with outliers >3σa excluded | 0.64 (851) | 70 (1.06) | 0.68 |
| Discrimination function with outliers >2σa excluded | 0.74 (747) | 72 (0.75) | 0.67 |
| Discrimination function with ncalc-σa | 0.46 (918) | 59 (1.68) | 0.93 |
a σ = 1.44 kcal/mol.
ncalc, calculated values; n, number of data points.
We can optimize the sensibility to a value of 93% if we subtract the standard deviation of 1.44 kcal/mol from the 918 calculated values. Then up to 50% of all possible candidates for a protein engineering experiment trying to increase the thermostability can be excluded by our discrimination function.
Dependence of the predictive power on the position of the mutation site
In order to analyze the dependence of the results on the mutation site, further investigations were carried out. We describe the mutation site by the solvent-accessible surface and the possible assignment to secondary structure elements of the wild-type amino acid. Results of the analysis are presented in Tables 4 and 5. The best predictions are achieved for mutations located in secondary structure elements or for mutation sites with a solvent-accessible surface < 20%. As expected, results for the training data set are better than for the test set. The discrepancies in the correlation coefficients for the β-strand with nearly the same number of data points are remarkable (see Table 5). The rcor for the training data set is 0.83, while the rcor for the test set is 0.38. Amino acids located in a β-strand for the training data set are frequently buried, with 68% having a solvent-accessible surface of < 20% while being changed to ALA or other hydrophobic amino acids. In the test data set, a total of only 45% of the wild-type amino acids have a solvent accessible surface of < 20%. The majority of these amino acids are located at the surface of the protein and are not as strongly restricted in their movement compared to amino acids located in the interior of a protein. This property makes structural rearrangements more likely. The fact that surface or flexible amino acids located in turns or a random fold are harder to predict is reflected by our results (see Tables 4, 5).
Table 4.
Correlation coefficient rcor for the discrimination function dependent on the solvent accessible surface of the wild-type amino acid
| Training data set | Test set | |||||
| Method | <20% rcor (n,rv [;%];) | <AS< rcor (n,rv [;%];) | 40% rcor (n,rv [;%];) | <20% rcor (n,rv [;%];) | <AS< rcor (n,rv [;%];) | 40% rcor (n,rv [;%];) |
| Discrimination function | 0.76 (239,82) | 0.56 (128,52) | 0.54 (279,71) | 0.58 (401,76) | 0.29 (168,57) | 0.19 (349,65) |
| Discrimination function mutations discarded >3σa | 0.78 (215) | 0.56 (122) | 0.54 (275) | 0.72 (361) | 0.51 (161) | 0.29 (329) |
| Discrimination function mutations discarded >2σa | 0.86 (181) | 0.68 (111) | 0.58 (269) | 0.81 (295) | 0.55 (148) | 0.43 (304) |
a σ = 1.44 kcal/mol.
n is the number of mutations assigned to the given solvent accessible surface, and rv is the number of correctly predicted mutations (for details, see Materials and Methods).
Table 5.
Results of the discrimination function dependent on the secondary structure
| Helices | β-strand | Turns | Random | |
| Method | rcor (n,rv [;%];) | rcor (n,rv [;%];) | rcor (n,rv [;%];) | rcor (n,rv [;%];) |
| Discrimination function (training data set) | 0.72 (296,73) | 0.83 (119,87) | 0.51 (135,70) | 0.27 (96,69) |
| Discrimination function (test data set) | 0.67 (485,70) | 0.38 (110,72) | 0.31 (189,65) | 0.07 (134,66) |
n is the number of mutations assigned to the given secondary structure element, and rv is the number of correctly predicted mutations (for details, see Materials and Methods).
Furthermore, in many cases polar or charged amino acids in the protein interior (solvent-accessible surface < 20%) are substituted by nonpolar amino acids. A buried single charge in the protein nucleus is very uncommon because of the unfavorable interactions with the nonpolar environment (Dill 1990). The charges are paired to salt bridges, and polar groups form hydrogen bonds. If such a group is exchanged by a nonpolar amino acid, a single noncompensated partial or full charge is created. This effect seems to be underestimated by the developed discrimination function: For the training data set 68 mutations are predicted as stabilizing, but in the experiment these mutations had a destabilizing effect. A total of 43 (63%) mutations out of the 68 mutations were exchanges from polar or charged amino acids to nonpolar amino acids.
Dependence of results on the protein
The quality of prediction for single mutations shows a dependence on the proteins analyzed (see Table 6). Correlation coefficients for mutants of a specific protein can vary between 0.4 and 0.8. In many cases it is not obvious whether differences in the prediction quality are due to special structural properties of the protein in question or whether they are connected to experimental circumstances or different calculations of the free energy of folding. The variant thermostabilities reported for T4-lyzozyme mutants from Alber et al. (1987) are such a special case. For this set of mutants we calculated an rcor close to zero, whereas for the other mutants of the T4-lysozyme the rcor is much higher.
Table 6.
Results of the discrimination function dependent on the protein for the training set
| Protein | n | rv [;%]; | rcor |
| 1bgs | 60 | 77 | 0.48 |
| 1l63 | 94 | 69 | 0.80 |
| 1lyd | 78 | 68 | 0.55 |
| 1lz1 | 5 | 100 | 0.84 |
| 1rnb | 118 | 75 | 0.54 |
| 1stn | 83 | 96 | 0.71 |
| 2ci2 | 79 | 80 | 0.57 |
| 2lzm | 16 | 50 | −0.09 |
| 2wsy | 18 | 89 | 0.52 |
| 3lzm | 59 | 59 | 0.39 |
| 4lyz | 36 | 61 | 0.42 |
n is the number of mutations assigned to the given protein, rv is the number of correctly predicted mutations, and rcor is the correlation coefficient (for details, see Materials and Methods).
Discussion
The discrimination function used in our approach consists of two factors: an amino acid/atom-based potential that describes the atomic “environment” of the amino acid to be exchanged, and a torsion angle potential that reflects how well an amino acid fits into the local main-chain topology at the specific position, taking nonbonding and through-bond effects into account. The quality of the results is distinctly improved by the combination of these two factors (see Materials and Methods). Attempts to further improve the results by inclusion of a directional component into the radial-symmetrical mean force did not show a conclusive effect.
Force-field methods for the prediction of mutant protein stability are based on the knowledge of the 3D structure of the native protein and the assumption that the folding of the mutant is not different from that of the native one. This is a requirement of any protein engineering experiment trying to preserve protein function. Nevertheless, this assumption is not correct given that local changes of folding occur in many cases. Our approach analyzes how well a mutant amino acid “fits” into the atomic environment of the wild-type amino acid and how well the new amino acid is able to reproduce the original main-chain torsion angle. This approach is likely to minimize any refolding in the predicted mutants. On the other hand, during the evaluation of the approach we do not know whether the assumption of a structural identity between mutant and native protein for the experimentally determined stabilization or destabilization effects is correct. We can safely assume that local refolding occurs with a higher probability in parts of the protein without a secondary structure as well as on the surface of the protein. Other reasons for failure of the mean force approaches are the loss or the new formation of highly specific interactions such as hydrogen bonds or salt bridges or changes of amino acid side-chain size in the interior of the protein. These effects may cause structural changes or rearrangements. In addition, mutations may alter the properties of the denaturated state (Gilis and Rooman 1996, 1997; Guerois et al. 2002; Zhou and Zhou 2002). In the absence of detailed experimental information regarding the folding of a protein mutant, the only basis for the exclusion of specific values from the experimental data set is the exclusion of mutants that show a behavior distinctly different from that of the rest of the samples. Of course, we see the danger that results can be “improved” by a repeated exclusion of “outliers.” The decision upon exclusion can only be based on the standard deviation of the full data set and must be regarded with care.
Several methods for the prediction of thermostability have been described (Miyazawa and Jernigan 1994; Ota et al. 1995; Gilis and Rooman 1996, 1997; Topham et al. 1997; Wang et al. 1998; Guerois et al. 2002; Zhou and Zhou 2002; Bordner and Abagyan 2004; Capriotti et al. 2004; Khatun et al. 2004). The largest data set used thus far was by Bordner and Abagyan (2004). Capriotti et al. (2004) used a data set consisting of 1615 mutations. Gilis and Rooman analyzed up to 238 mutations (Gilis and Rooman 1996, 1997), while other authors focused on a single protein (Ota et al. 1995) or a few mutations (Miyazawa and Jernigan 1994; Wang et al. 1998). In all these works, so-called outliers were identified and discarded from the test set for basically the same reasons that prompted us to remove some of the values. Furthermore, often only correlation coefficients were reported. Capriotti et al. (2004) used a neural network–based method combined with an energy-based method to predict the stabilizing or destabilizing effect of a mutation upon a protein. They correctly classified > 90% of their mutations, which is even better than with our approach. Since they trained their neural network toward the direction of the stability change, they cannot predict the importance of this change in the form of the correlation coefficient.
Topham et al. (1997) predicted 68 mutations of barnase and 83 mutations of Staphylococcal nuclease, with a correlation coefficient of 0.77 and with 73.3% correctly predicted mutations to be stabilizing or either destabilizing. The drawback of this method is the need for mutant crystal structures; often only the wild-type crystal structures are known. Gilis and Rooman (1996, 1997) analyzed 238 mutations with a combined knowledge-based amino acid–amino acid potential and torsion-angle potential. The best correlation they achieved is for 121 mutations buried in the interior of the protein (solvent-accessible surface < 20%) with a value of 0.8. Guerois et al. (2002) developed an EEEF-potential called FOLD-X. They optimized their potential with several training sets derived from their test set. The best correlation coefficient, 0.8 (323 single mutations) for the training set was achieved by discarding 5% of the mutational data. The correlation coefficient for the test data set was 0.8 (591 single mutations), after discarding 5% of the data. Zhou and Zhou (2002) analyzed the effect on protein stability of 895 single point mutations (DFIRE-based all-atom potential). The best correlation coefficient achieved was 0.62. The solvent-accessible surface distribution of these mutations was not discussed. Bordner and Abagyan (2004) used a data set of 1816 experimental stability values of single point mutations in 81 different proteins. The correlation coefficient for the training set (908 single mutations) was 0.82. For the test set they reported a covariance of 0.59 (removing 26 outliers from 908 single mutations). The correlation coefficient was not reported.
In the discussion of the achieved results, two main aspects will be addressed: (1) the question of why some mutations are falsely predicted to be either stabilizing or destabilizing, and (2) why some of the calculated predictions show a deviation from the experimental values that is significantly higher than the calculated standard deviation. This analysis will be exemplified in detail for the training data set. In addition, the use of the correlation coefficient as a measure of quality for the prediction will be discussed.
Here, 648 mutations being assigned to a secondary structure element were included in the test set with a correlation coefficient of rcor = 0.76. The reason why mutations in secondary elements are discarded or falsely predicted to be either stabilizing or destabilizing is often breakage of hydrogen bonds. The mutations for barnase (1bgs) were discussed in detail by Serrano et al. (1992). In that work, polar and ionic amino acids that are substituted with hydrophobic amino acids (e.g., Tyr24Phe, Asp54Ala, and Tyr99Val) were falsely predicted to be stabilizing and discarded from the training set because the corresponding data points were not within the confidence range of 2σ. These mutations are located in a β-strand and are located additionally in the protein interior. Therefore, the environment is more likely to be hydrophobic and the exchange of polar amino acids to hydrophobic amino acids should result in a more stable protein. But in this case the mutations disrupt up to five hydrogen bonds, resulting in structural changes and unfavorable interactions. Furthermore, distinct structural rearrangements are observed in the crystal structures of some mutations: in the case of the t4-lysozyme1lyd (Glu11Met, correctly predicted but discarded; Shoichet et al. 1995) and 1lyd (Thr157, all possible amino acids, falsely predicted and discarded).
A question that must be addressed is whether the general hydrophobic effect is overestimated in the potential. This would lead to a general prediction of increased thermostability when amino acids in the interior of the proteins are exchanged by others with a higher hydrophobicity, even in those cases where the new amino acid does not fit into the cavity created by the removal of the original one. We had hoped that this effect was smaller for an amino acid/atom-based potential compared to an amino acid/amino acid potential. The results seem to support this. In the training set and the test set, 64% of the discarded mutations have a solvent accessibility lower than 20%, and 90% of those are assigned to secondary structure elements. The 295 mutations with a solvent accessibility of < 20% show a correlation coefficient of rcor = 0.81, indicating that the observed differences between prediction and experiment are not due to a general over- or underestimation of the hydrophobic effect, but probably caused by cooperative effects or structural rearrangements. Limited structural rearrangement leads to a quantitative uncertainty, but the direction of the stability change is often correctly predicted. The mutations Ala31Ile, Ala31Leu, and Ala31Val in chicken egg lysozyme are correctly predicted to be stabilizing, although a structural relaxation is necessary for the introduction of larger amino acids, but only for Ala31Ile, and the Ala31-Leu stabilization effect was overestimated.
The discrepancies between the calculated stabilization energies and the experimental values are most likely due to such cooperative effects (e.g. many-body interactions, secondary structure interactions), which are difficult to handle (Gohlke et al. 2000). Cooperative effects are observed in every unfolding study of proteins (Robertson and Murphy 1997). These effects are not described accurately by the presented discrimination function. On average, the effect of 10% of the buried mutations and ~14% of mutations assigned to secondary structure elements is not sufficiently predicted by the described discrimination function.
To evaluate a prediction function for thermostability, one can choose several criteria. The selection of these criteria naturally depends on the usage of the method. Often the correlation coefficient is not only used to describe the correctness or quality of a method but also as a criterion for the use in protein engineering or enzyme optimization. However, as shown in the Results section, the correlation coefficient can be significantly increased with reasonable criteria (from rcor = 0.46 to rcor = 0.8) (see Tables 3, 5) without an increase in the percentage of correctly predicted mutations to be either stabilizing or destabilizing, nor with an increase in the sensibility.
This indicates that the correlation coefficient is insufficient as the sole criterion to assess the practical value or quality of a method. This was also stated by Capriotti et al. (2004). The correlation coefficient could be further increased artificially to rcor = 0.91 by an additional restriction of included experimental data (393, 61% of the original data points of the training data set), resulting in the best correlation coefficient for this number of data published so far, but the correctly predicted mutations to be either stabilizing or destabilizing would be only 81%. About 20% of all mutations that are used to evaluate these methods are predicted falsely, and we assume that the large majority of these mutations cannot easily be treated by energy functions because of experimental errors, cooperative effects, and/or structural changes (Gilis and Rooman 1996, 1997; Guerois et al. 2002). This resembles the use of mean force methods for the treatment of the inverse protein folding problem, where ~80% of a diverse set of sequences can be correctly assigned to its structure (Dill 1990, 1999; Brady and Sharp 1997; Sippl 1999). In addition, 31% of the 561 mutations have an absolute value of the experimental stabilization energy of < 0.5 kcal/mol, which is in the range of experimental errors (Yutani et al. 1987; Ruiz-Sanz et al. 1995; Shih and Kirsch 1995; Shih et al. 1995; Shoichet et al. 1995; Xu et al. 1998).
In the quality assessment of the results, particular emphasis must be laid on the significance of the predicted effect. For example, for the training set we achieved a sensibility of 96% (see Results). This means that only six of 646 mutations are falsely predicted to be destabilizing, but four of these six mutations have experimental values of ΔΔG < 0.3 kcal/mol (1lyd Gly30Ala, 2ci2 Lys37Ala, 3lzm Lys60Pro, 4lyz Phe34-Tyr).
Conclusion
We have developed a knowledge-based potential that predicts the stability change upon mutation of residues that span most of the structural environments found in proteins. The discrimination function was trained with 646 mutations introduced at 273 sites on 11 different enzymes and finally tested on 918 mutations introduced at 326 sites on 27 proteins
For 83% (1308 out of 1564) of all experimental mutations on 31 different proteins, a correlation coefficient of 0.78 between calculated and experimental data was achieved. Moreover, 76% of the mutations were correctly predicted to be either stabilizing or destabilizing, with an average error < 0.75 kcal/mol as indicated by the standard deviation. The expected quality of the results depends on the localization of the mutation within the protein. If the mutation site occurs in a secondary structure element or in the interior of a protein (solvent accessibility of < 20%), the results for the prediction are much better than for other mutations.
The results indicate that the method is limited to mutations that do not affect the backbone structure of the wild type. Additive effects of mutations are expected for mutations at positions with a large distance to each other.
The presented discrimination function is a fast method to create a mutation profile with possible candidates for point mutations and can be used in protein engineering processes as a prefilter.
The program will be available via a Web interface at http://www.hnb-cologne.uni-koeln.de.
Materials and methods
To estimate the changes in stability upon mutation, we calculated the free energy of folding for the wild-type (WT) ΔGWT and the mutant (MT) ΔGMT. It was stated that the difference of the computed free energies of folding equals the experimental stabilization energy Δ ΔG (Sippl 1990). For the computation of free energies we used a discrimination function consisting of two combined knowledge-based potentials: a direction- and distance-dependent amino acid–atom-potential and a torsion angle energy potential.
The direction- and distance-dependent amino acid–atom potential
The radial distribution of two structure elements in a distinct distance is described by the radial pair distribution function (Gohlke et al. 2000). The distance-dependent pair potentials ΔEij(rij) are derived following an approach developed by Sippl (1990, 1993, 1995):
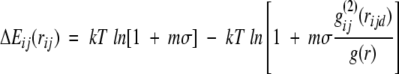 |
(1) |
where g(2)ij(rij) is the radial pair distribution function of a pair i,j separated by a distance rij. g(r) is the description of the reference state. k is the Boltzmann constant, T is a conformational temperature, and m and σ are constants (Gilis and Rooman 1997).
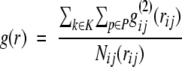 |
(2) |
The reference state is defined as an ensemble of structure elements in a large set of protein structures. Summing the occurrences of the structure elements i,j for one protein, P for all k proteins, in the set of protein structures GP in the interval (r) of rd and rd+dr and in the direction interval (ω) gives the number of structure pairs Nij(rijωij):
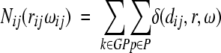 |
(3) |
where δ(dij,r,ω) = ,1 if dij ɛ[rd,rd+dr), otherwise is δ(dij,r,ω) = 0.
As some rarely occurring combinations of structural element pairs may not be sufficiently represented in the data set, the computed frequencies may not be accurate. To avoid the problem of sparse data, Sippl (1990) introduced a correction term with the values m and σ. m is the number of occurrences of the observed pairs, and σ is a parameter with the value of 0.002 (see Equations 1, 4).
In addition to the distance information, a direction- and distance-dependent description of the amino acid environment includes the orientation ω between a pair of structure elements. This changes the pair potential function to:
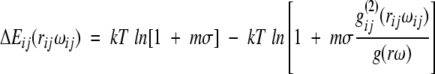 |
(4) |
In this study an amino acid–atom potential was used. For the atomic description of the amino acid environment we defined five classes of atom types: aliphatic carbon, aromatic carbon, nitrogen, oxygen of amino acids, and oxygen of the solvent. We developed an algorithm to fill and surround a protein with solvent water, based on a grid model with a chosen lattice constant of 0.6 Å. All grid space not occupied by protein was defined as free and filled with water (with an approximate volume of 30 Å3) (Richards 1974) when enough free grid space is available (Colonna-Cesari and Sander 1990; Gerstein and Levitt 1998; Lazaridis and Karplus 1999).
The amino acid is represented by three points and a direction. The points are the geometric center CZ, the CB (β-C-Atom), and O (oxygen from the carbonyl group of the backbone) of the amino acid. The direction is defined by the vector CZCB, and a plane was created by CZ, CB, O. The chosen amino acid representation is based in some part on already published approaches (CB, Bryant and Lawrence 1993 and Huang et al. 1995; CZ, Kocher et al. 1994 and Ota et al. 1995; O, Feig et al. 2000) and was enhanced to fit our approach. The vector n of the plane is defined as the vector product CZCBxCZO, whereas CZCB, CZO, CZCBxCZO is a right-handed system. Distances between the amino acid and the atom types are measured from the CZ point. The angle between an atom type and the direction vector determines the relative orientation of the structure element pair. The angle is given in polar coordinates, which are used to describe every point relative to CZCB.
The torsion angle potential
The torsion angles ϕ and Ψ describe the local interactions of an amino acid with its direct sequence neighbors. Every amino acid prefers specific torsion angle pairs and differs in its distribution of (ϕ,Ψ)-pairs. From this distribution of (ϕ,Ψ)-pairs a knowledge-based potential can be derived (Dengler 1998). For this purpose the axis of the Ramachandran ϕΨ map is divided into intervals of 1°, resulting in 129,600 fields. To achieve a steady distribution out of a discrete distribution of (ϕ,Ψ)-combinations, the (ϕ,Ψ)-values are normalized. Values are obtained from the protein structure set. The normalized distribution n(ϕ,Ψ) of (ϕ,Ψ) pair occurrences is used to calculate the potential energy ΔEaa(ϕ,Ψ) for a specific amino acid aa with a distinct torsion angle pair (ϕ,Ψ) via the inverse Boltzmann equation:
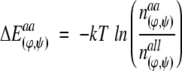 |
(5) |
where all refers to the average values of all 20 amino acids.
The discrimination function
The direction- and distance-dependent amino acid–atom potential Eaap was combined with the torsion angle potential Etp to the discrimination function Eww:
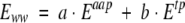 |
(6) |
The best results for the training data set for the discrimination function were achieved with two half spheres up and down the defined plane, a distance of 3–13 Å with an interval length of 0.5 Å, and the weighting factors a, b = 1.
Calculation of the stabilization energy
To estimate the stabilization energy, the folding energies of the wild-type ΔGWT and the mutant ΔGMT were computed using Equations 4–6. For this purpose it was assumed that the wild type and the mutant have the same backbone structure. The stabilization energy Δ ΔG (the difference in folding free energy between mutant and wild type) was determined using the following equation:
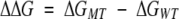 |
(7) |
The stabilization energy is thus negative if the mutated protein is more stable than the wild-type protein.
Evaluation of the predictive power
To evaluate the predictive power of the discrimination function several criteria were chosen, namely the correlation coefficient rcor between the computed and the experimental values, the number of correctly predicted mutations (rv) to be either stabilizing or destabilizing, and the sensibility (Sens) of the prediction:
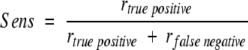 |
(8) |
rtrue positive is the number of mutations correctly predicted to be stabilizing, and rfalse negative is the number of mutations falsely predicted to be destabilizing.
Experimental data sets
Three experimental data sets were used: a protein structure data set, the training set, and the test set.
The knowledge-based potentials were derived from the protein structure data set of 286 well-resolved (<2.5 Å) and refined protein structures with low sequence homology (Berman et al. 2000).
The training set contained 646 Δ ΔG experimental data points from 11 proteins extracted from the literature (Gilis and Rooman 1996, 1997; Topham et al. 1997).The experimentally studied proteins (PDB codes) were barnase (1bgs, 1rnb), t4-lysozyme (1l63, 1lyd, 1lz1, 2lzm, and 3lzm), staphylococcal nuclease (1stn), chymotrypsin inhibitor (2ci2), tryptophan synthase (2wsy), and the hen egg white lysozyme (4lyz).
The experimental Δ ΔG values for the test mutant database were exclusively retrieved from the ProTherm database (Gromiha et al. 2000). Stabilization energies of single mutations measured by thermal denaturation were considered, resulting in 918 data points from 27 proteins (PDB codes 1abm, 1ank, 1bni, 1bpi, 1csp, 1cyo, 3gap, 1lhm, 1lz1, 1mbn, 1myl, 1rn1, 1rop, 1rtb, 1sar, 1stn, 1sup, 1tyu, 1ycc, 2ci2, 2lzm, 2rn2, 2trx, 2wsy, 3ssi, 1dyj, and 4lyz).
A BLAST run (Blossum 62, e-value 1e-3) resulted in 25 independent sequence families, and six of them (two lysozyme classes) were picked for the training set (Altschul et al. 1997). The test set included all 25 sequence families. About 50% of all single point mutations in the combined data set were derived from lysozyme experiments.
Computer programs
For the assignment of secondary structure the program DSSP (Kabsch and Sander 1983) was used (helices [α-helix, π helix, and 3–10 helix], β-strands, turns [bend, hydrogen bonded turn, and residue in isolated β-bridge], and random [nonassignment with DSSP]). The calculation of the solvent accessibility was performed by the program psa (http://www-cryst.bioc.cam.ac.uk/~joy). Similar to the work of Gilis and Rooman (1997), the mutations were sorted in three classes: solvent-accessible surface < 20%, solvent-accessible surface between 20% and 40%, and solvent-accessible surface > 40%.
Abbreviations
ΔG, free energy difference between folded and unfolded protein
ΔΔG, free energy difference between the wild-type (WT) and the mutant protein
SEEF, statistical effective energy function
EEEF, empirical effective energy function
PEEF, physical effective energy function
rcor, correlation coefficient
rv, correctly predicted mutations to be either stabilizing or destabilizing
Sens, sensibility.
Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.04940705.
References
- Alber, T., Sun, D.P., Wilson, K., Wozniak, J.A., Cook, S.P., and Matthews, B.W. 1987. Contributions of hydrogen bonds of Thr 157 to the thermodynamic stability of phage T4 lysozyme. Nature 330 41–46. [DOI] [PubMed] [Google Scholar]
- Altschul, S.F., Madden, T.L., Schaffer, A.A., Zhang, J., Zhang, Z., Miller, W., and Lipman, D.J. 1997. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 25 3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman, H.M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T.N., Weissig, H., Shindyalov, I.N., and Bourne, P.E. 2000. The Protein Data Bank. Nucleic Acids Res. 28 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bordner, A.J. and Abagyan, R.A. 2004. Large-scale prediction of protein geometry and stability changes for arbitrary single point mutations. Proteins 57 400–413. [DOI] [PubMed] [Google Scholar]
- Brady, G.P. and Sharp, K.A. 1997. Entropy in protein folding and in protein–protein interactions. Curr. Opin. Struct. Biol. 7 215–221. [DOI] [PubMed] [Google Scholar]
- Bruins, M.E., Janssen, A.E., and Boom, R.M. 2001. Thermozymes and their applications: A review of recent literature and patents. Appl. Biochem. Biotechnol. 90 155–186. [DOI] [PubMed] [Google Scholar]
- Bryant, S.H. and Lawrence, C.E. 1993. An empirical energy function for threading protein sequence through the folding motif. Proteins 16 92–112. [DOI] [PubMed] [Google Scholar]
- Capriotti, E., Fariselli, P., and Casadio, R. 2004. A neural-network-based method for predicting protein stability changes upon single point mutations. Bioinformatics 20 (Suppl. 1): I63–I68. [DOI] [PubMed] [Google Scholar]
- Colonna-Cesari, F. and Sander, C. 1990. Excluded volume approximation to protein-solvent interaction. The solvent contact model. Biophys. J. 57 1103–1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeBolt, S.E. and Skolnick, J. 1996. Evaluation of atomic level mean force potentials via inverse folding and inverse refinement of protein structures: Atomic burial position and pairwise non-bonded interactions. Protein Eng. 9 637–655. [DOI] [PubMed] [Google Scholar]
- Dengler, U. 1998. “Kristallstruktur der D-2-Hydroxyisocaproat-dehydrogenase aus Lactobacillus casei: Verfeinerung, interpretation und anwendung in einem Verfahren zur Erkennung der Proteinfaltung.” Ph.D. thesis, Technische Universität Carolo-Wilhelmina zu Braunschweig, Braunschweig, Germany.
- Dill, K.A. 1990. Dominant forces in protein folding. Biochemistry 29 7133–7155. [DOI] [PubMed] [Google Scholar]
- ———. 1999. Polymer principles and protein folding. Protein Sci. 8 1166–1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan, Y. and Kollman, P.A. 1998. Pathways to a protein folding intermediate observed in a 1-microsecond simulation in aqueous solution. Science 282 740–744. [DOI] [PubMed] [Google Scholar]
- Duan, Y., Wang, L., and Kollman, P.A. 1998. The early stage of folding of villin headpiece subdomain observed in a 200-nanosecond fully solvated molecular dynamics simulation. Proc. Natl. Acad. Sci. 95 9897–9902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feig, M., Rotkiewicz, P., Kolinski, A., Skolnick, J., and Brooks 3rd, C.L. 2000. Accurate reconstruction of all-atom protein representations from side-chain-based low-resolution models. Proteins 41 86–97. [DOI] [PubMed] [Google Scholar]
- Finkelstein, A.V. 1997. Protein structure: What is it possible to predict now? Curr. Opin. Struct. Biol. 7 60–71. [DOI] [PubMed] [Google Scholar]
- Gerstein, M. and Levitt, M. 1998. Simulating water and the molecules of life. Sci. Am. 279 100–105. [DOI] [PubMed] [Google Scholar]
- Gilis, D. and Rooman, M. 1996. Stability changes upon mutation of solvent-accessible residues in proteins evaluated by database-derived potentials. J. Mol. Biol. 257 1112–1126. [DOI] [PubMed] [Google Scholar]
- ———. 1997. Predicting protein stability changes upon mutation using database-derived potentials: Solvent accessibility determines the importance of local versus non-local interactions along the sequence. J. Mol. Biol. 272 276–290. [DOI] [PubMed] [Google Scholar]
- Gohlke, H., Hendlich, M., and Klebe, G. 2000. Knowledge-based scoring function to predict protein–ligand interactions. J. Mol. Biol. 295 337–356. [DOI] [PubMed] [Google Scholar]
- Gromiha, M.M., An, J., Kono, H., Oobatake, M., Uedaira, H., Prabakaran, P., and Sarai, A. 2000. ProTherm, version 2.0: Thermodynamic database for proteins and mutants. Nucleic Acids Res. 28 283–285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guerois, R., Nielsen, J.E., and Serrano, L. 2002. Predicting changes in the stability of proteins and protein complexes: A study of more than 1000 mutations. J. Mol. Biol. 320 369–387. [DOI] [PubMed] [Google Scholar]
- Huang, E.S., Subbiah, S., and Levitt, M. 1995. Recognizing native folds by the arrangement of hydrophobic and polar residues. J. Mol. Biol. 252 709–720. [DOI] [PubMed] [Google Scholar]
- Kabsch, W. and Sander, C. 1983. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 22 2577–2637. [DOI] [PubMed] [Google Scholar]
- Kannan, N., and Vishveshwara, S. 2000. Aromatic clusters: A determinant of thermal stability of thermophilic proteins. Protein Eng. 13 753–761. [DOI] [PubMed] [Google Scholar]
- Khatun, J., Khare, S.D., and Dokholyan, N.V. 2004. Can contact potentials reliably predict stability of proteins? J. Mol. Biol. 336 1223–1238. [DOI] [PubMed] [Google Scholar]
- Kocher, J.P., Rooman, M.J., and Wodak, S.J. 1994. Factors influencing the ability of knowledge-based potentials to identify native sequence-structure matches. J. Mol. Biol. 235 1598–1613. [DOI] [PubMed] [Google Scholar]
- Kollman, P.A., Massova, I., Reyes, C., Kuhn, B., Huo, S., Chong, L., Lee, M., Lee, T., Duan, Y., Wang, W., et al. 2000. Calculating structures and free energies of complex molecules: Combining molecular mechanics and continuum models. Acc. Chem. Res. 33 889–897. [DOI] [PubMed] [Google Scholar]
- Koppensteiner, W.A. and Sippl, M.J. 1998. Knowledge-based potentials—Back to the roots. Biochemistry (Mosc.) 63 247–252. [PubMed] [Google Scholar]
- Kumar, S., Tsai, C.J., and Nussinov, R. 2000. Factors enhancing protein thermostability. Protein Eng. 13 179–191. [DOI] [PubMed] [Google Scholar]
- Lazaridis, T. and Karplus, M. 1999. Effective energy function for proteins in solution. Proteins 35 133–152. [DOI] [PubMed] [Google Scholar]
- ———. 2000. Effective energy functions for protein structure prediction. Curr. Opin. Struct. Biol. 10 139–145. [DOI] [PubMed] [Google Scholar]
- Liu, R., Baase, W.A., and Matthews, B.W. 2000. The introduction of strain and its effects on the structure and stability of T4 lysozyme. J. Mol. Biol. 295 127–145. [DOI] [PubMed] [Google Scholar]
- Lu, H. and Skolnick, J. 2001. A distance-dependent atomic knowledge-based potential for improved protein structure selection. Proteins 44 223–232. [DOI] [PubMed] [Google Scholar]
- Matthews, B.W. 1993. Structural and genetic analysis of protein stability. Annu. Rev. Biochem. 62 139–160. [DOI] [PubMed] [Google Scholar]
- Melo, F. and Feytmans, E. 1997. Novel knowledge-based mean force potential at atomic level. J. Mol. Biol. 267 207–222. [DOI] [PubMed] [Google Scholar]
- Miyazawa, S. and Jernigan, R.L. 1994. Protein stability for single substitution mutants and the extent of local compactness in the denatured state. Protein Eng. 7 1209–1220. [DOI] [PubMed] [Google Scholar]
- Moult, J. 1997. Comparison of database potentials and molecular mechanics force fields. Curr. Opin. Struct. Biol. 7 194–199. [DOI] [PubMed] [Google Scholar]
- Ota, M., Kanaya, S., and Nishikawa, K. 1995. Desktop analysis of the structural stability of various point mutations introduced into ribonuclease H. J. Mol. Biol. 248 733–738. [DOI] [PubMed] [Google Scholar]
- Richards, F.M. 1974. The interpretation of protein structures: Total volume, group volume distributions and packing density. J. Mol. Biol. 82 1–14. [DOI] [PubMed] [Google Scholar]
- Robertson, A.D. and Murphy, K.P. 1997. Protein structure and the energetics of protein stability. Chem. Rev. 97 1251–1267. [DOI] [PubMed] [Google Scholar]
- Ruiz-Sanz, J., de Prat Gay, G., Otzen, D.E., and Fersht, A.R. 1995. Protein fragments as models for events in protein folding pathways: Protein engineering analysis of the association of two complementary fragments of the barley chymotrypsin inhibitor 2 (CI-2). Biochemistry 34 1695–1701. [DOI] [PubMed] [Google Scholar]
- Serrano, L., Kellis Jr., J.T., Cann, P., Matouschek, A., and Fersht, A.R. 1992. The folding of an enzyme. II. Substructure of barnase and the contribution of different interactions to protein stability. J. Mol. Biol. 224 783–804. [DOI] [PubMed] [Google Scholar]
- Shih, P.P. and Kirsch, J.F. 1995. Design and structural analysis of an engineered thermostable chicken lysozyme. Protein Sci. 4 2063–2072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shih, P., Holland, D.R., and Kirsch, J.F. 1995. Thermal stability determinants of chicken egg-white lysozyme core mutants: Hydrophobicity, packing volume, and conserved buried water molecules. Protein Sci. 4 2050–2062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shoichet, B.K., Baase, W.A., Kuroki, R., and Matthews, B.W. 1995. A relationship between protein stability and protein function. Proc. Natl. Acad. Sci. 92 452–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sippl, M.J. 1990. Calculation of conformational ensembles from potentials of mean force. An approach to the knowledge-based prediction of local structures in globular proteins. J. Mol. Biol. 213 859–883. [DOI] [PubMed] [Google Scholar]
- ———. 1993. Boltzmann’s principle, knowledge-based mean fields and protein folding. An approach to the computational determination of protein structures. J. Comput. Aided Mol. Des. 7 473–501. [DOI] [PubMed] [Google Scholar]
- ———. 1995. Knowledge-based potentials for proteins. Curr. Opin. Struct. Biol. 5 229–235. [DOI] [PubMed] [Google Scholar]
- ———. 1999. Who solved the protein folding problem? Structure Fold. Des. 7 R81–R83. [DOI] [PubMed] [Google Scholar]
- Topham, C.M., Srinivasan, N., and Blundell, T.L. 1997. Prediction of the stability of protein mutants based on structural environment-dependent amino acid substitution and propensity tables. Protein Eng. 10 7–21. [DOI] [PubMed] [Google Scholar]
- Wang, Y., Lal, L., Li, S., Han, Y., and Tang, Y. 1996. Position-dependent protein mutant profile based on mean force field calculation. Protein Eng. 9 479–484. [DOI] [PubMed] [Google Scholar]
- Wang, L., Veenstra, D.L., Radmer, R.J., and Kollman, P.A. 1998. Can one predict protein stability? An attempt to do so for residue 133 of T4 lysozyme using a combination of free energy derivatives, PROFEC, and free energy perturbation methods. Proteins 32 438–458. [PubMed] [Google Scholar]
- Xu, J., Baase, W.A., Baldwin, E., and Matthews, B.W. 1998. The response of T4 lysozyme to large-to-small substitutions within the core and its relation to the hydrophobic effect. Protein Sci. 7 158–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, D., Unseren, M.A., Xu, Y., and Uberbacher, E.C. 2000. Sequence-structure specificity of a knowledge based energy function at the secondary structure level. Bioinformatics 16 257–268. [DOI] [PubMed] [Google Scholar]
- Yutani, K., Ogasahara, K., Tsujita, T., and Sugino, Y. 1987. Dependence of conformational stability on hydrophobicity of the amino acid residue in a series of variant proteins substituted at a unique position of tryptophan synthase α subunit. Proc. Natl. Acad. Sci. 84 4441–4444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou, H. and Zhou, Y. 2002. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci. 11 2714–2726. [DOI] [PMC free article] [PubMed] [Google Scholar]