A novel method reveals that solvent water favors polyproline II over β-strand conformation in peptides and unfolded proteins: conditional hydrophobic accessible surface area (CHASA)

Abstract

In aqueous solution, the ensemble of conformations sampled by peptides and unfolded proteins is largely determined by their interaction with water. It has been a long-standing goal to capture these solute-water energetics accurately and efficiently in calculations. Historically, accessible surface area (ASA) has been used to estimate these energies, but this method breaks down when applied to amphipathic peptides and proteins. Here we introduce a novel method in which hydrophobic ASA is determined after first positioning water oxygens in hydrogen-bonded orientations proximate to all accessible peptide/protein backbone N and O atoms. This conditional hydrophobic accessible surface area is termed CHASA. The CHASA method was validated by predicting the polyproline-II (P_II) and β-strand conformational preferences of non-proline residues in the coil library (i.e., non-α-helix, non-β-strand, non-β-turn library derived from X-ray elucidated structures). Further, the method successfully rationalizes the previously unexplained solvation energies in polyalanyl peptides and compares favorably with published experimentally determined P_II residue propensities.

We dedicate this paper to Frederic M. Richards.

Of the many factors that determine the conformation of polypeptides, the interaction with water is one of the most important. Intrapeptide backbone interactions limit available conformational space (Pappu and Rose 2002), and sidechain interactions specify conformational preferences (Chou and Fasman 1978; Creamer and Rose 1992; Penel and Doig 2001), but neither works in isolation. Rather, such effects act in concert with solvation preferences, which are measured by the free energy of interaction between peptides and water (Luo and Baldwin 1999; Thomas et al. 2001).

It is often assumed, usually implicitly, that protein backbone solvation is uniform in the unfolded state. However, computational studies indicate that the solvation energetics differ among conformations in both peptides (Anderson and Hermans 1988; Pettitt and Karplus 1988; Tobias and Brooks 1992; Brooks and Case 1993; Bartels and Karplus 1997; Resat et al. 1997; Smart et al. 1997; Han et al. 1998; Scarsi et al. 1998; Tazaki and Shimizu 1998; Apostolakis et al. 1999; Smith 1999; Hu et al. 2003; Drozdov et al. 2004) and longer chains (Avbelj et al. 2000; Garcia 2004; Kentsis et al. 2004; Mezei et al. 2004).

Accessible surface area (ASA) (Lee and Richards 1971) has a long and successful history in estimating the energetics of solvation in small molecules and peptides (Ooi et al. 1987; Wimley et al. 1996; Chan and Dill 1997) and desolvation during protein folding, unfolding, and association (Horton and Lewis 1992; Makhatadze and Privalov 1993; Murphy et al. 1993; Privalov and Makhatadze 1993; Hilser et al. 1996; Baker and Murphy 1998; Vallone et al. 1998). Indeed, this method has even been used as a potential function in protein simulations (Ferrara et al. 2002; Rathore et al. 2003).

Unfortunately, the ASA approximation breaks down eventually (Avbelj et al. 2000; Gallicchio et al. 2000; Mezei et al. 2004) because typical ASA calculations assume the entire surface in question is available for solvation simultaneously, and in an undifferentiated way, with no distinction made between one accessible site and another. This is a particularly poor assumption for a chemically heterogeneous moiety like a peptide, which has both polar and apolar sites in close proximity. Given that interactions between water and polar sites are much stronger than the corresponding interactions between water and apolar sites, the Boltzmann-weighted distribution of water-peptide interactions favors solvation of N-H and C = O groups over apolar groups. The residence times of water molecules at polar solvation sites are known to be two to three times longer than those at apolar sites (Russo et al. 2004), and therefore effective apolar solvation will frequently depend on prior polar solvation. In other words, a water molecule hydrogen-bonded to a backbone polar site can inhibit the close approach of other water molecules at nearby apolar sites.

In practice, this distribution can be approximated simply by pre-solvating sterically accessible polar sites. Subsequent calculation of hydrophobic ASA under the prior condition that these polar sites are already solvated provides a method to differentiate among these distinct solvation environments. Here we compare the conventional hydrophobic ASA to the hydrophobic ASA conditional upon prior water occupancy at polar solvation sites.

This conditional hydrophobic accessible surface area, termed CHASA, is a modification of conventional hydrophobic ASA, and it captures experimental propensities effectively. The CHASA modification was validated by comparison of predicted conformational propensities for all residues (except proline) to the experimentally observed natural propensities in the coil library, a data base of non-α-helix, non-β-strand, non-β-turn fragments derived from X-ray crystallographic structures (www.roselab.jhu.edu/coil). This library is thought to represent the unfolded population of proteins (Swindells et al. 1995; Fiebig et al. 1996; Smith et al. 1996).

Results

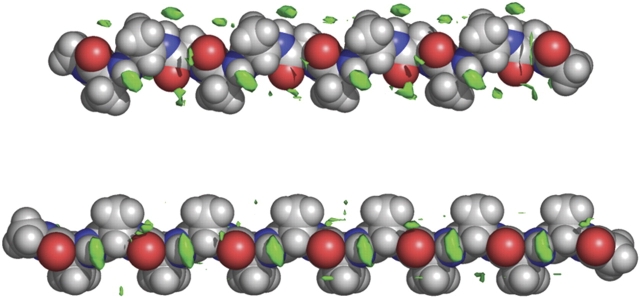
Position-specific solvation sites differ between polar and apolar groups. In Figure 1 ▶, solvation sites around polyalanine, calculated from an all-atom simulation in explicit solvent (Mezei et al. 2004), are displayed as probability density map contours. Both P_II (top) and antiparallel β-strand con-formations (bottom) are shown. Probability densities are contoured at a level of 2.5%, i.e., there is a 2.5% probability that the center of a water oxygen is present in a 0.5 Å cube within these solid green contours. At this probability level, backbone N-H groups already exhibit significant position-specific solvation, and distinct solvation sites around backbone C = O groups are beginning to emerge. Decreasing the probability to 1.5% does not change the N-H contours significantly, but the carbonyl oxygen contours become more pronounced. Conversely, upon increasing the probability, only the N-H contours persist, and these survive to probability levels of 10%. In mean bulk solvent, probability density in the 0.5Å volume element was 0.45%.

Figure 1.

Molecular graphics images of solvation sites around polyalanine as probability density map contours. Top, P_II conformation; bottom, anti-parallel β-strand conformation. The probability densities are depicted as green solid contours at the 2.5% level. The images were created using the program PyMOL (DeLano 2003).

It can be seen from these contours that N-H solvation localizes to a single site, while C= O solvation localizes to multiple positions around the oxygen. Solvation sites around Cβ atoms only emerge at very low contour levels, less than 1.5%; these are seen to be partially localized in antiparallel β-strand but not in P_II conformation.

The position of each N-H solvation site is consistent with an N-H• • •OH₂ hydrogen bond; i.e., the site is situated at a distance of 2.95 Å from the nitrogen and approximately in-line with the N-H bond vector (Taylor and Kennard 1984). At probability density levels between 2.5 and 1.5, C= O groups usually exhibit two predominant solvation sites, situated ~2.95 Å from the carbonyl oxygen and with some dependence on polypeptide conformation. The locations and densities of solvation sites in P_II conformation (Fig. 1 ▶) resemble those found by Garcia (2004) using unconstrained molecular dynamics of a blocked polyalanyl 21-residue peptide and a different force field.

These results, extracted from detailed simulations in explicit water, indicate that solvation is positionally specific for backbone polar atoms in polyalanine but much less so for the nonpolar Cβ group. The observed positional specificities are consistent with water hydrogen bonds to both N-H and C = O groups. Our measure of solvation positional specificity is related to the residence time of solvating water molecules at these sites. A recent study combining quasi-elastic neutron scattering and molecular simulation of a blocked leucinyl peptide concluded that water residence time near polar groups exceeds that of apolar groups by a factor of 2–3 (Russo et al. 2004). The positional specificity of the long-residence, low-energy sites will influence the location of more dynamic solvation positions around the rest of the molecule, especially the high-energy positions around hydrophobic groups.

Estimating solvation free energy using CHASA

Methods that estimate the hydrophobic contribution to solvation free energy by simply summing surface area fail to take site-dependent positional specificity into account. In these methods, the area is calculated as if the entire surface were simultaneously available for interaction with the solvent (Lee and Richards 1971), with all accessible positions treated equivalently. However, both experimental findings (Russo et al. 2004), other computational results (Garcia 2004; Kentsis et al. 2004), and our results (Fig. 1 ▶) indicate that polar and apolar solvent sites are not equivalent. The availability of high-energy hydrophobic solvation positions depends in part on prior solvation of low-energy hydrogen-bonded sites, which have longer water residence times. The CHASA method was developed to take these critical differences into account.

The predictive value of CHASA was tested by using the method to calculate the solvation free energies and resulting preferences of residues in both P_II and β-strand conformations in a polyalanyl host-guest peptide. The calculated P_II/β-strand preferences were then compared to natural preferences in a data set derived from experimentally determined structures.

The difference in CHASA between the two respective conformations in a pure polyalanyl peptide is 59.5 - 38.0 = 21.5 Ų per residue (Table 1 with X = Ala). This difference stands in marked contrast to the conventional, nonconditional difference in hydrophobic ASA, which is almost identical for the two conformations: 68.8 and 68.3 Ų per residue, respectively (data not shown). CHASA distinguishes between these two conformations while conventional hydrophobic ASA fails to measure a difference.

Table 1.

Calculated conformational energetics of host-guest peptides

	β-stranda				PIIa
	CHASAb	Apolar solv. free energy	Polar solv. free energy	Total solv. free energy	CHASAb	Apolar solv. free energy	Polar solv. free energy	Total solv. free energy	PIId pref.	Coil library pref.e
X Res.	Å2	kcal/molc	kcal/molc	kcal/molc	Å2	kcal/molc	kcal/molc	kcal/molc	%	%
ALA	297.4	8.9	−30.0	−21.1	189.9	5.7	−30.0	−24.3	75.0	76.0
ARG	296.5	8.8	−30.0	−21.2	197.2	5.9	−29.8	−23.9	72.3	57.2
ASN	269.5	8.0	−30.0	−22.1	174.5	5.2	−29.2	−24.0	62.5	49.0
ASP	271.1	8.0	−29.9	−22.1	171.9	5.1	−29.1	−24.2	67.0	55.3
CYS	325.5	9.8	−30.0	−20.2	216.8	6.5	−29.3	−22.9	70.9	57.3
GLN	281.3	8.3	−29.8	−21.7	185.4	5.3	−29.1	−23.9	68.2	56.1
GLU	278.4	8.3	−29.9	−21.8	186.5	5.3	−29.1	−24.0	68.1	63.7
GLY	264.5	7.9	−30.0	−22.1	172.6	5.2	−30.0	−24.8	71.9	79.1
HIS	303.2	9.0	−29.8	−20.9	217.4	6.5	−28.7	−22.2	61.0	52.7
ILE	345.0	10.3	−30.0	−19.7	239.4	7.0	−28.5	−21.5	64.6	46.8
LEU	347.3	10.4	−30.0	−19.6	241.1	7.2	−29.8	−22.4	71.9	67.6
LYS	323.9	9.6	−30.0	−20.3	222.1	6.6	−29.8	−23.2	71.1	59.1
MET	324.0	9.5	−30.0	−20.3	220.7	6.5	−29.8	−23.3	73.3	62.3
PHE	357.0	10.6	−29.8	−19.2	261.5	7.8	−29.4	−21.4	67.9	53.0
SER	266.2	7.9	−30.0	−22.1	174.5	5.2	−29.9	−24.8	71.0	63.2
THR	283.7	8.3	−30.0	−21.7	188.8	5.6	−29.2	−23.8	67.3	50.5
TRP	369.4	10.9	−29.8	−18.5	291.7	8.7	−29.2	−20.7	68.2	58.8
TYR	320.7	9.5	−29.8	−20.5	235.5	7.0	−29.4	22.2	64.1	52.1
VAL	325.7	9.8	−30.0	−20.2	215.1	6.4	−28.5	−22.2	66.2	46.6

The host peptide model (Acetyl-ALA₅-X-ALA₆-N-methylamide) was constructed with backbone torsions set to φ= −120°, Ψ = 130° (β-strand) or φ = −78°, Ψ = 149° (P_II). Different guest residues were constructed in the X position with the same backbone conformations. All sterically allowed rotamers were analyzed. The constructed peptide models were tested for accessibility to hydrogen-bonding water oxygens, and solvation free energy was calculated as the Boltzmann-weighted sum of hydrophobic and polar solvation terms as described in the text.

^aValues shown are the sums for 5 residues (4–8) of the peptide.

^bConditional hydrophobic accessible surface area (CHASA) is the hydrophobic accessible surface area calculated conditional upon prior solvation of the backbone N and O atoms.

^cSolvation free energies are Boltzmann-weighted averages according to the number of sterically allowed rotamers.

^dPreference was calculated from the relative solvation free energies taking into account the number of ways (rotamers) that contributed to the energies as described in the text.

^ePreference was calculated from a non-β-helix, non-β-strand, non-β-turn fragment database extracted from the PDB (Berman et al. 2000), as described in the text.

In detailed free energy simulations of polyalanine, the difference in solvation free energy, ΔΔA, between β-strand and P_II is 0.7 kcal/mol/residue (β-strand = −4.0 kcal/mol/residue; P_II = −4.7 kcal/mol/residue) (Mezei et al. 2004). Using these values and assuming the difference in solvation free energies is due entirely to differences in hydrophobic surface, the free energy of nonpolar surface solvation

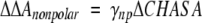(1)

gives γ_np = 0.03 kcal/Ų, remarkably close to both early (Hermann 1972) and recent (Chan and Dill 1997) values in the literature. Furthermore, this value of γ_np is probably an underestimate, owing to the fact that the polar solvation condition would be more realistically derived as a Boltzmann-weighted probability, in which case the effective ΔCHASA would be less than indicated in Table 1.

We can then derive

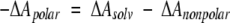(2)

using the above values for ΔA_solv (−4.0, −4.7) together with a calculated ΔA_nonpolar from surface areas in Table 1 and γ_np in Equation 1. Doing so, we obtain a total solvation free energy of −6 kcal/mol/residue for peptide polar groups (ΔA_polar). This estimate compares favorably with the value of −7.9 kcal/mol/residue calculated by Avbelj and Baldwin (Avbelj et al. 2000) using a finite difference Poisson-Boltzmann method. From our analysis, there is no basis on which to separate the respective contributions of N-H and C = O groups to the total polar solvation free energy. Therefore, we have approximated the individual contributions by splitting the difference equally, assigning a value of -3 kcal/mol/residue for the solvation free energy of each polar group that has free access to solvent water within its respective cone of approach, as described in Materials and Methods. Steric limitations in the close approach of water molecules are assessed by attempting to situate a water oxygen at multiple positions within the solvent approach cone of each polar group. That group is assigned to have a favorable solvation free energy if and only if it can form a clash-free hydrogen bond with at least one water molecule, with the solvation free energy becoming increasingly favorable as the cone volume becomes increasingly accessible.

Detailed results of the host-guest peptide solvation free energy and P_II/β-strand preference calculations are listed in Table 1. In every case, hydrophobic solvation free energy favors P_II conformation, i.e., conditional hydrophobic accessible surface area is significantly less in P_II than in β-strand. In contrast, polar group solvation free energy is slightly favored in β-strand conformation for 17 residue types, and equal to P_II conformation in the remaining two. Total solvation free energies, a balance between hydrophobic and polar contributions, favor P_II conformation for all residue types.

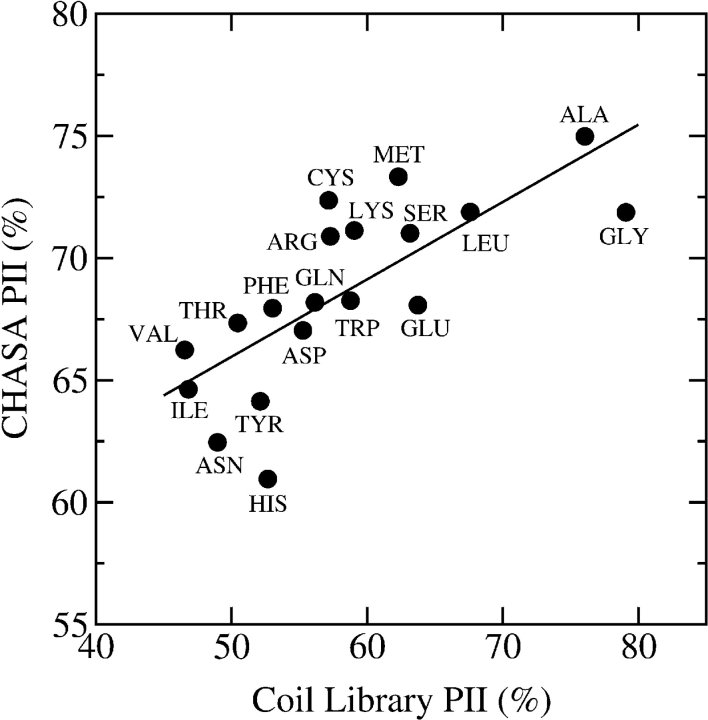
The correlation between our calculated P_II/β-strand preferences and the corresponding P_II/β-strand preferences observed in the coil library is plotted in Figure 2 ▶. Although imperfect, our calculations capture important features that agree with these experimentally observed distributions. First, alanine and glycine have high P_II preferences in both the coil library and model host-guest system. Second, the β-branched residues, valine, isoleucine, and threonine have low P_II preferences in both the coil library and calculations. For these residues, the CHASA values, and thus hydrophobic solvation free energies, are favorable in P_II conformation, but this contribution is partially counterbalanced by less favorable polar solvation. Histidine, tyrosine, and tryptophan have the least favorable CHASA differences between P_II and β-strand (85.7, 85.2, 77.7 Ų per five residues, respectively) with correspondingly low calculated P_II preferences.

Figure 2.

Calculated and natural P_II preferences compared to β-strand for different amino acid residues. Calculated preferences (CHASA P_II) are from Table 1, and natural preferences (Coil Library P_II) were calculated from a coil library derived from the PDB as described in the text. The line represents a linear regression with a correlation coefficient of 0.75.

A more comprehensive exploration of conformational space may change the exact values of these calculated P_II preferences, but the trends seen in the coil library are captured effectively with our straightforward analysis. The P_II/β-strand preferences for the coil library reported here largely agree with previously published coil library preferences (Avbelj and Baldwin 2003), although the two coil libraries are not strictly comparable. Specifically, we have removed β-turn residues, unlike the coil library used by Avbelj and Baldwin (2003); this difference may explain the discrepancy between the low P_II preferences of aspartate and asparagine observed here and those published previously.

Comparison with experimentally determined scales

Additional experimental validation can be seen by comparing the trends in Figure 2 ▶ with recent estimates of P_II preferences in host-guest experiments using circular dichroism (Chellgren and Creamer 2004). In these experiments, ala-nine, glutamine, asparagine, and valine were measured in a proline-based host. In this system, the P_II propensity of alanine is high, glutamine is less, and asparagine and valine are the lowest. The relative order of valine and asparagine is reversed from that in Figure 1 ▶, but the overall trends are consistent. Our results also are in general agreement with those of Eker et al. (2004), who used spectroscopic methods to obtain the dihedral angles of ALA-X-ALA tripeptides, although the relative propensities of TYR and TRP reported here are different. A strict correlation is not expected in either case, because the experimental systems report on the P_II propensities with respect to all available conformational space, while we have singled out the P_II to β-strand preferences.

Discussion

The CHASA method is easily extended to any other range of peptide conformations, such as that shown in Figure 3 ▶. The conformational space examined in the figure represents an area in the upper left quadrant of the Ramachandran plot (Ramachandran et al. 1963), covering the extended strand and P_II regions. The top plot shows that traditional hydrophobic ASA is relatively insensitive to conformation. In contrast, the middle and bottom plots show that the CHASA, conditional upon N-H and C= O solvation, respectively, varies considerably with conformation. In both CHASA plots, the hydrophobic accessible surface is minimal within the region −85° ≤ φ ≤ −55° and 130° ≤ ψ ≤ 180°, which includes P_II but excludes β-strand.

Figure 3.

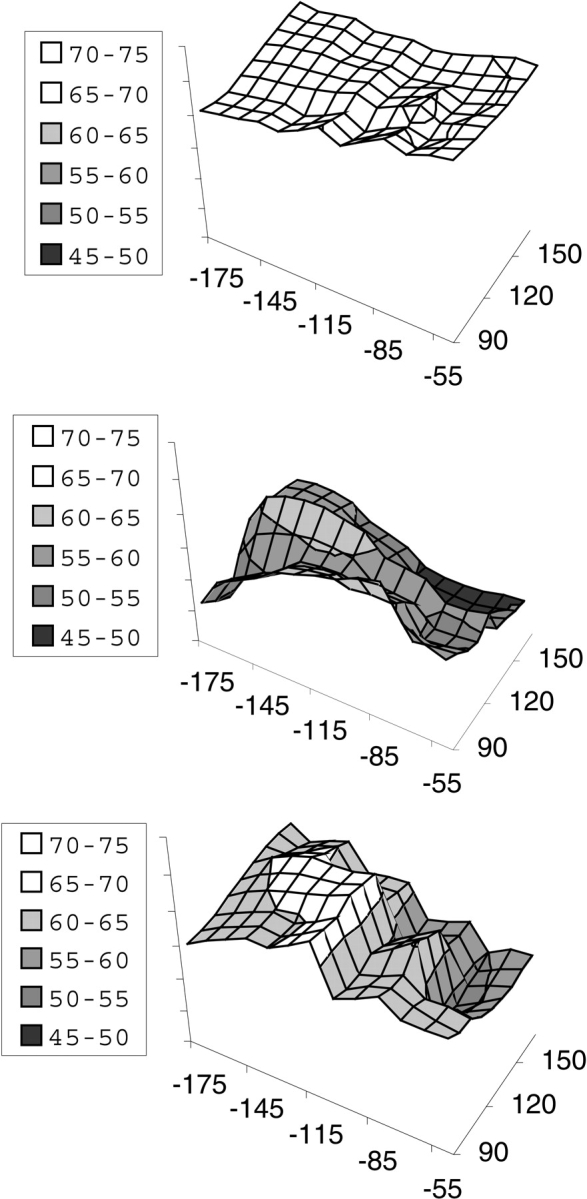
Per residue hydrophobic accessible surface areas as a function of polyalanine φ, ψ values. The surface areas in Ų are indicated in the boxes to the left of each plot; φ is along the bottom axis, and ψ is along the axis on the right in each plot. Conformational distributions of 12-residue polyalanyl peptides were generated as described in Materials and Methods. The nonconditional hydrophobic ASA (top), the CHASA conditional upon N-H solvation (middle), and the CHASA conditional upon C = O solvation (bottom) were calculated for each residue in each polypeptide conformation as described in the text. The surface area values for individual residues in each polypeptide conformation were accumulated into 10° × 10° φ, ψ bins, and the mean hydrophobic ASA or CHASA value within the bin is plotted. The number of residues represented in each 10° × 10° φ, ψ bin is 890 ± 134 (S.D.).

In developing the CHASA method, we started with the simplifying assumption that backbone polar groups are solvated equivalently in both P_II and β-strand conformers of polyalanine, and therefore the main difference in solvation free energy between these two conformations would arise from differences in hydrophobic solvation. Similarly, Av-belj and Baldwin found that the free energy of backbone group solvation is dependent on whether the polar group is solvent-accessible, but not on the extent of polar ASA (Avbelj et al. 2000), earlier findings notwithstanding (Spolar et al. 1992; Makhatadze and Privalov 1993; Privalov and Makhatadze 1993). In both β-strand and P_II, the N-H and C = O are openly available for solvation in a polyalanine peptide (Fig. 1 ▶). Very recently, Petukov et al. (2004) reported that polar group solvation free energies are proportional to polar ASA but with a hyperbolic relationship, based on analysis of molecular dynamics simulations. Their results suggest that after a minimal exposure to solvent is attained (5–10 Ų ASA), solvation free energy becomes only slightly dependent on additional polar ASA. We assess this nonlinear proportionality by probing backbone polar groups with water oxygens at multiple positions and quantifying the number of successful attempts.

In other related work, Hamburger et al. (2004) and Ferreon and Hilser (2004) use an experimental peptide/protein binding system to assess the thermodynamics of P_II formation. For alanine in a proline-based host peptide, they find that P_II conformation is enthalpy-driven, implicating backbone-solvent interactions as the molecular origin of the P_II preference. How can this evidence be reconciled with the fact that such preferences are also predicted by differences in conditional hydrophobic accessible surface areas, an entropy-driven effect at 25°C?

The substantial CHASA-based reduction in apolar surface favors P_II over β-strand in all cases (Table 1). However, once in P_II, individual residue preferences may be dominated instead by differences in polar accessibility to solvent. For example, within P_II an ALA to VAL mutation would increase ΔA_apolar by 0.7 kcal/mol but ΔA_polar by 1.5 kcal/mol. These within-structure differences may predominate in experimental peptide mutation studies.

Clearly, our understanding of these solvation effects is incomplete. The interplay between polar and apolar solvation in an amphipathic molecule like a peptide is complicated by their spatial juxtaposition and the solvation dynamics of water. In a comprehensive thermodynamic analysis of hydration during protein unfolding, Privalov and Makha-tadze used ASA parametized with small-molecule experimental data to successfully calculate hydration enthalpies, entropies, and Gibbs energies on a macromolecular scale for four proteins (Makhatadze and Privalov 1993; Privalov and Makhatadze 1993). Despite this success, the atomic scale contributions—including hydrogen bonding, van der Waals forces, polar and apolar hydration enthalpies and entropies—remain difficult to quantify.

Three recent studies (Drozdov et al. 2004; Garcia 2004; Mezei et al. 2004) found that a significant component of P_II preference is contributed by the fact that this conformation is less disruptive of bulk solvent organization than β-strand. This contribution does not come from backbone:water hydrogen bonding per se; instead, it is manifest indirectly in the energetics of water:water interactions. The success of CHASA may reflect the compensating effects of decreased apolar group–water interaction with increased polar group– water interaction, coincident with β-strand to P_II conformational change. In any event, the fact that differences in hydrophobic solvation can rationalize the preferred conformations of peptides suggests that we must look beyond the backbone to understanding this phenomenon.

Summary

Previous applications of the ASA method assume that the entire solvent-accessible surface is available simultaneously. We challenge this assumption by showing that the accessibility of hydrophobic solvation sites may depend on prior solvation of proximate polar sites. For solutes such as polypeptides, computing the hydrophobic ASA after first pre-solvating backbone polar groups can correct for this dependence. Solvation free energy calculations using CHASA successfully predict individual residue preferences for P_II conformations over β-strand conformations in a coil library derived from known protein structures. To the extent that the coil library represents the unfolded population of proteins, these results add to the growing body of evidence that P_II is a prevalent conformation in unfolded proteins.

Materials and methods

The conditional hydrophobic accessible surface area (CHASA) of model peptides was calculated using modules from the LINUS suite of programs (Srinivasan and Rose 1995; Srinivasan et al. 2004) with an effective probe radius of 1.4 Å after first placing virtual oxygen atoms at suitable positions around backbone N and O atoms, viz., a distance of 2.95 Å from the peptide N or O atom and positioned within a 30° cone around the N-H bond vector or an 80° cone around the C = O bond vector. The algorithm described by Shrake and Rupley (1973) was used with 960 sampling points per atom surface to calculate accessible surface area. Hydrophobic area is defined as the accessible surface area associated with carbon atoms; hydrogen atoms were not included in the calculation.

Conformational preferences of residues were predicted in a model host-guest system. Specifically, each of 19 different residue side chains was modeled at position 6 of a blocked, 12-residue polyalanyl host constructed in either β-strand or P_II backbone conformation. All rotamers described by Lovell et al. (2000) were constructed, and van der Waals overlap was removed, if possible, by varying the χ angles up to 10°. Only models without steric clash were used in the analysis. CHASA was calculated for residues 4–8 in each host-guest model as described above.

CHASA values, together with estimates of polar solvation, were used to calculate a solvation free energy (ΔA_solv) as

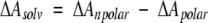(3)

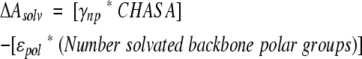(4)

where γ_np is the solvation free energy per Ų of conditional hydrophobic surface area, and ɛ_pol is the free energy contributed by each backbone N-H or C= O group for which a hydrogen bond to water is sterically allowed. As discussed in the Results, values for these parameters (in kcal/mol) were determined to be: γ_np = 0.03 and Δ_pol = 3.0. In addition, placement of a hydrogen-bonded water oxygen was probed at five uniformly distributed positions within each cone of approach. The number of successful, clash-free attempts was used to calculate the final polar solvation free energy, with Δ_pol = (3.0/5) each.

The Boltzmann-weighted P_II preference (P_PII) of each residue type in the guest position of host-guest peptides was calculated from ΔA_solv as:

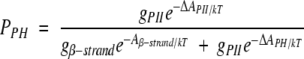(5)

where g_PII is the number of sterically possible rotamers in P_II conformation, ΔA_PII is the Boltzmann-weighted average solvation free energy of the P_II conformation, g_β-strand is the number of sterically possible rotamers in β-strand conformation, and ΔA_β-strand is the Boltzmann-weighted average solvation free energy of the β-strand conformation.

For the flexible backbone calculations shown in Figure 3 ▶, sterically allowed distributions of polyalanine conformations were made by constrained torsion angle Monte Carlo simulations of a blocked 12-residue polyalanyl model using modified modules from the LINUS suite of programs (Srinivasan and Rose 1995; Srinivasan et al. 2004) and www.roselab.jhu.edu/dist/. The region of the Ramachandran plot bounded by −175° ≤φ≤− 45° and 90° ≤ψ≤ 180° was subdivided into 15 equal, 30° × 30° bins. Fifteen separate hard-sphere Monte Carlo simulations were performed, with φ, ψ-values constrained to each respective bin. Conformations were saved after every 300 successful attempts; 1000 conformations were accumulated for each bin. Virtual oxygen atoms were placed at backbone solvation sites only where sterically feasible, as described above. The accessible surface area for residues 3–10 was then calculated with and without virtual oxygens and indexed by conformation, resulting in 8000 × 2 values per bin.

Probability density maps of solvent water oxygen atoms were calculated from previously described molecular simulations (Mezei et al. 2004) using the MMC program (inka.mssm.edu/~mezei/mmc). Briefly, blocked polyalanyl peptides modeled as either β-strand (φ = −139°, ψ = 135°) or P_II (φ = −78°, ψ = 149°) were solvated with ~2600 TIP3P waters (Jorgensen et al. 1983) under periodic boundary conditions and simulated with the CHARMM22 force field (MacKerell et al. 1998) at 300°K. The simulations used the Metropolis algorithm (Metropolis et al. 1953) with force-bias sampling (Rao et al. 1979) scaled down near the solute (Mezei 1991); solute positions were held fixed. Our previous simulations (Mezei et al. 2004) of 10⁸ Monte Carlo steps were extended 5 × 10⁸ steps. Configurations were saved every 25,000 steps; in all, 20,000 configurations were included. Every configuration was embedded in a cubic 0.5 Å grid, and each grid volume element was scored for occupancy by a water oxygen center. Occupancy probabilities were calculated for each grid element and formatted as a CNS density map (Brunger et al. 1998), commonly used in X-ray crystallography. Probability density maps and molecular models were displayed using PyMOL (DeLano 2003).

Natural P_II/β-strand preferences were calculated from the Protein Coil Library (www.roselab.jhu.edu/coil) a non-α-helix, non- β-strand, non-β-turn fragment data base extracted from the PDB (Berman et al. 2000). In this library, secondary structures for each protein model in the PDB are classified solely by dihedral angles (Srinivasan and Rose 1999): an α-helix is defined as having at least five consecutive residues in helical conformation, a β-strand as having at least three consecutive residues in strand conformation, and a β-turn as having two consecutive residues in one of the eight major turn conformations (Rose et al. 1985). Residues not included in these three categories comprise the coil library. In the current study, all coil library residues from a data set of nonhomologous protein X-ray crystallographic structures were classified individually into right-handed helix, left-handed helix, strand, P_II, or coil regions of the Ramachandran map (Ramachandran et al. 1963). A nonhomologous protein data set with sequence identity ≤ 90%, resolution ≤ 2 Å, and R-factor ≤ 0.25 was obtained from the PISCES Web site (Wang and Dunbrack 2003). Residues from this data set found in the coil library ranged from 250,830 for proline to 4889 for tryptophan, with a mean of 30,200.

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.041047005.