Skip to main content
NCBI home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2005 Jul;14(7):1934–1938. doi: 10.1110/ps.051401905

Charge–charge interactions in the denatured state influence the folding kinetics of ribonuclease Sa

Jared M Trefethen 1, C Nick Pace 1,2, J Martin Scholtz 1,2, David N Brems 3
PMCID: PMC2253365  PMID: 15937282

Abstract

Gaining a better understanding of the denatured state ensemble of proteins is important for understanding protein stability and the mechanism of protein folding. We studied the folding kinetics of ribonuclease Sa (RNase Sa) and a charge-reversal variant (D17R). The refolding kinetics are similar, but the unfolding rate constant is 10-fold greater for the variant. This suggests that charge–charge interactions in the denatured state and the transition state ensembles are more favorable in the variant than in RNase Sa, and shows that charge–charge interactions can influence the kinetics and mechanism of protein folding.

Keywords: protein folding, protein stability, folding kinetics, denatured state, charge–charge interactions

Protein stability is an important consideration in protein engineering. There is considerable interest in developing methods to increase the stability of a protein. Two ways this can be achieved are (1) decrease the free energy of the native state, and/or (2) increase the free energy of the denatured state. In an earlier study (Pace et al. 2000), a charge-reversal mutation (D17K) was made to improve electrostatic interactions on the surface of native ribonuclease Sa (RNase Sa) to stabilize the protein. However, the mutant was less stable than the wild-type protein by about 1 kcal/mol. We suggested that this resulted because electrostatic interactions were more favorable in the denatured state of the mutant than in wild-type RNase Sa, and that this might influence the folding kinetics. The results in the present work support this idea, and show that charge–charge interactions in the transition and denatured state ensembles of a protein can exert a substantial effect on the kinetics of protein folding. Recent work on another protein from Raleigh’s lab has reached a similar conclusion (Cho et al. 2004; Horng et al. 2005), and thus these findings may be fairly general.

Results

To monitor the folding and unfolding of WT RNase Sa and the charge-reversal variant, D17R, by fluorescence spectroscopy, a Trp residue was added in place of Tyr 81. The crystal structure of Y81W showed that the Trp is 87% buried, and the variant is 0.4 kcal/mol less stable than WT (Alston et al. 2004). For Y81W RNase Sa, there is a 2.5-fold increase in fluorescence intensity at 319 nm when the protein folds (Alston et al. 2004). Throughout this work, the Y81W variant will be referred to as WT* and the charge-reversal variant as WT*(D17R).

Equilibrium denaturation

Equilibrium urea denaturation experiments showed that both WT* and WT*(D17R) closely approach a two-state folding mechanism, as do all of the mutants ofRNase Sa that we have studied (Pace et al. 2000). The parameters characterizing the urea denaturation curves are (Pace and Scholtz 1997): Cm=4.84±0.01 M, m value=955±70 cal/mol •M, ΔG (H2 O)=4.6±0.4 kcal/mol for WT*(D17R); and Cm=6.01±0.05 M, m value= 960±20 cal/mol •M, ΔG (H2O)=5.7±0.2 kcal/mol for WT*. Thus, WT* (D17R) is about 1.1 kcal/mol less stable than WT*. This is the same as the difference in stability between WT RNase Sa and the D17K variant (Shaw et al. 2001).

Folding kinetics

Since the fluorescent properties of the tryptophan substitution at position 81 are effective in distinguishing between the denatured and native states, the folding and unfolding reactions were monitored using fluorescence spectroscopy. Both proteins were initially equilibrated in solutions that favored the native state (no denaturant) or the denatured state (high denaturant) such that a maximum change in fluorescence intensity could be followed as the protein unfolded or refolded. The progress of the fluorescence change as the folding reaction approached equilibrium was recorded and the data were fit by Equation 1, which describes a first-order reaction,

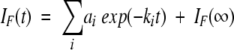graphic file with name M1.gif (1)

where IF (t) is the fluorescence intensity at time t, ai is the amplitude of phase i with rate constant ki, and IF(∞) the fluorescence intensity at infinite time (Matthews 1987). The rate constants from data fitting, kobs, were then plotted as a function of urea concentration to generate the chevron plots for WT* and WT*(D17R) RNase Sa shown in Figure 1 ▶. The chevron plots were then analyzed using Equation 2 (Jackson and Fersht 1991):

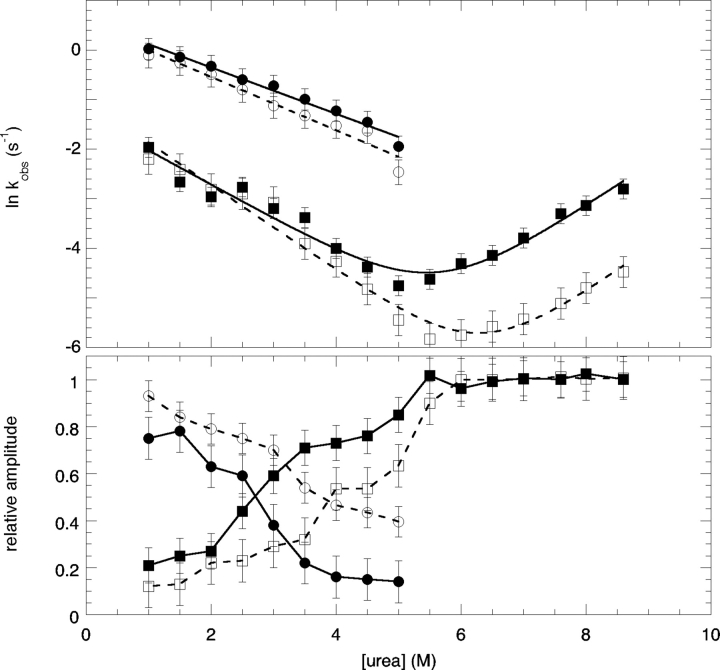
Figure 1.

Figure 1.

Open in a new tab

Chevron plots for WT* and WT*(D17R) at pH 7 in 30 mM MOPS buffer. The upper panel shows the effect of urea on the observed rate constants. The lower panel shows the relative reaction amplitudes for each reaction phase as a function of urea. For both panels, ○ and □ represent WT* data (fast and slow phases, respectively) while • and ▪ represent WT*(D17R) data (fast and slow phases, respectively). Data in both panels include measurements of standard error. No fewer than four experiments were done at each denaturant concentration.

graphic file with name M2.gif (2)

where kobs is the observed rate constant, ksf H2O and ku H2O are the extrapolated slow refolding and unfolding rate constants in water, respectively, msf and mu represent the dependence of the refolding and unfolding rate constants on urea, D is the concentration of urea, R is the gas constant, and T is the temperature. The parameters obtained from fitting Equation 2 to the data for unfolding and the slow folding reaction, and the linear extrapolation for the fast folding (kff and mff) reaction are summarized in Table 1.

Table 1.

Kinetic parameters for the folding and unfolding of WT*and WT*(D17R) RNase Sa

WT* WT*(D17R)
Parameters Refolding Unfolding Refolding Unfolding
kuH2O (s−1)a — 6.5(±10) × 10−6 — 5.4(±6) × 10−5
kffH2O (s−1)b 1.7 ± 0.23 — 1.8 ± 0.15 —
ksfH2O (s−1)c 0.36 ± 0.07 — 0.26 ± 0.06 —
mu (cal mol−1 M−1)d — 520 ± 120 — 490 ± 80
mff (cal mol−1 M−1)e −320 ± 25 — −280 ± 15 —
msf (cal mol−1 M−1)f −510 ± 38 −410 ± 45
mk (cal mol−1 M−1)g 1030 ± 130 900 ± 90
meq (cal mol−1 M−1)h 960 ± 20 955 ± 70
Open in a new tab

a The rate constant at 0 M urea (Equation 2) based on the unfolding phase in Figure 1 ▶.

b The rate constant at 0 M urea (Equation 2) based on the fast refolding phase in Figure 1 ▶.

c The rate constant at 0 M urea (Equation 2) based on the slow refolding phase in Figure 1 ▶.

d The m value characterizing formation of the transition state from the native state (Equation 2). This value is based on the slope of the curve for the unfolding phase in Figure 1 ▶.

e The m value characterizing the slope of the fast refolding phase obtained by linear extrapolation.

f The m value characterizing formation of the transition state from the denatured state (Equation 2). This value is based on the slope of the curve for the slow refolding phase in Figure 1 ▶.

gmk=mu − msf; the error was calculated as the square root of the sum of the square of each individual error, i.e., etot=sqrt(e12+e22), where e is the error.

h This is the m value obtained from an analysis of the equilibrium urea denaturation curves described above. Note that the kinetic m values (mk) and the equilibrium m values (meq) are identical within experimental error.

The presence of two refolding limbs suggests the presence of an intermediate in the folding of WT* and WT*(D17R) RNase Sa. As the denaturant concentration increased, the fast phase could not be detected, probably because the intermediate is unstable at high denaturant concentrations. We are currently studying the folding intermediate, and the results will be described in a future publication. Since the folding kinetics for the two proteins are similar, the presence of the intermediate will not affect the conclusions reached in this paper. The minimum of the chevron plot should correspond to the midpoint of the equilibrium denaturation curve (Cm), and both plots have a minimum at a urea concentration close to the Cm of the corresponding denaturation curves. In addition, the unfolding limb for WT*(D17R) was shifted to a lower urea concentration than WT*, showing again that WT*(D17R) is less stable than WT*. While there were no significant differences between the refolding limbs for the proteins, the unfolding limbs revealed a 10-fold increase in the unfolding rate constant for WT*(D17R) (Table 1).

The position of the transition state relative to the native and denatured states on a reaction coordinate can be estimated using m values (Khan et al. 2003). The m values derived from an analysis of the equilibrium urea denaturation curves reflect the change in accessible surface area (ΔASA) between the native and denatured states upon unfolding (Myers et al. 1995). The m values derived from the unfolding portion of the kinetic chevron plot, mu, represents the ΔASA between the native and transition states. These equilibrium, meq, and kinetic, mu, m values from Table 1 can be combined to give the Tanford β value (βT=mu/meq) (Tanford 1970). A βT close to 1 suggests a highly folded, compact transition state similar to the native state. Alternatively, a βT close to 0 suggests an unfolded transition state similar to the denatured state. WT* and WT*(D17R) RNase Sa have βT values of 0.54 and 0.51, respectively, showing that the transition state ensemble is about half folded.

Discussion

Several recent studies have shown that charge-reversal mutations on the surface of proteins can be used to improve electrostatic interactions and increase protein stability (Grimsley et al. 1999; Loladze et al. 1999; Spector et al. 2000; Pradeep and Udgaonkar 2004). In a previous study (Pace et al. 2000), we showed that the E74K RNase Sa variant was 1.1 kcal/mol more stable that WT RNase Sa, but the D17K variant was 1.1 kcal/mol less stable than WT RNase Sa. The side chains of both Asp 17 and Glu 74 are about 65% solvent exposed, and do not form any intramolecular hydrogen bonds in WT RNase Sa. In addition, both mutations were predicted to increase the stability by over 2 kcal/mol based on a summation of the electrostatic interactions of charged groups on the folded protein using Coulomb’s law with a dielectric constant of 80 (Pace et al. 2000). These results suggested that charge–charge interactions can be more favorable in the denatured state, as in D17KRNase Sa, than they are in the native state, as in E74K RNase Sa, and that this effect in the denatured state ensemble might play an important role in the kinetics and mechanism of protein folding.

Equilibrium studies are important for analyzing the stability of proteins, but they only show the net effect of a mutation on the stability, and provide no information on whether the native state or the denatured state is affected. In contrast, studies of the folding kinetics can reveal folding intermediates not observed under equilibrium conditions and give information on the free energies of the native, denatured, and intermediate states and on the transition states that separate them in the folding pathway (Fersht 1999).

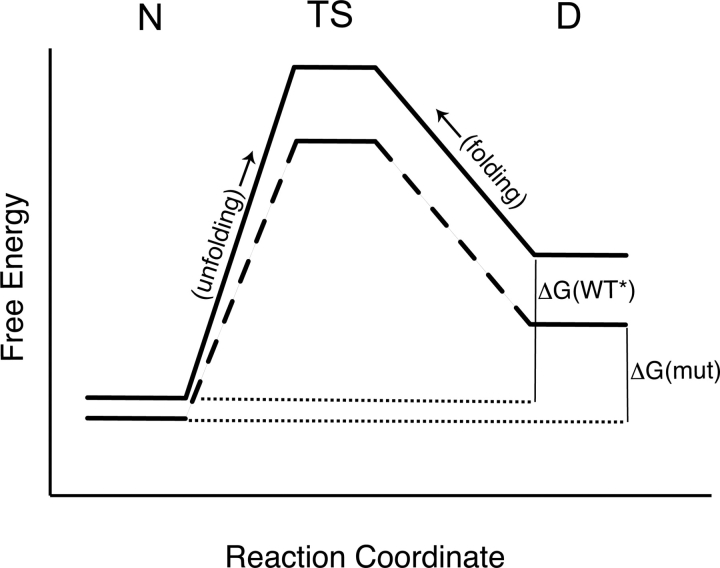
Here, our most interesting finding is that the unfolding rate constant for WT*(D17R) is 10-fold greater than for WT*. Our interpretation of this is illustrated in Figure 2 ▶. Note that the stability of the variant is less than WT* RNase Sa because the energy of the denatured state is decreased more than that of the native state. This is consistent with the equilibrium results (Pace et al. 2000). The effect of these changes on the kinetics of folding will be determined by the effect of the mutation on the energy of the transition state. We suggest that the energy of the transition state is lowered as it is in the denatured state. As a consequence, the energy of activation and the rates for folding will be similar for WT* and WT*(D17R), as observed, but the rate of unfolding of the variant will be greater because the energy of activation is lower than for WT*. In the transition and denatured state ensembles, some of the hydrophobic interactions and intramolecular hydrogen bonds will be disrupted so that the polypeptide chain can rearrange itself to optimize the electrostatic interactions among the charged groups. Electrostatic interactions depend on the distances between charged groups and the dielectric constant of the environment. Because the transition and denatured state ensembles are likely to be compact (Daggett and Fersht 2003), the rearrangement might lead to distances that are shorter than those in the native state, but with an effective dielectric constant that is still less than bulk solvent. The Tanford βvalues suggest that the transition state is just over 50% folded for WT* and the charge-reversal variant. For most proteins, the βvalues are larger, and suggest more compact transition states (Dagget and Fersht, 2003). We suggest that electrostatic interactions in the transition and denatured states are more favorable for WT*(D17R) than they are for WT*, and this leads to a change in the makeup of the denatured state ensemble, which is the cause of the large difference in the rate constant for unfolding.

Figure 2.

Figure 2.

Open in a new tab

Energy diagram illustrating the possible effects of the charge-reversal on the free energy of the native state (N), the transition state (TS), and the denatured state (D). The solid line represents WT* and the dashed line represents WT*(D17R). The proposed effects of the charge-reversal show that the free energy of activation for unfolding is smaller for WT* (D17R) than for WT*, and this accounts for the 10-fold increase in the rate constant for the unfolding of WT*(D17R). The free energy of activation for refolding is similar for WT* and WT*(D17R), resulting in similar folding rates. (We have simplified this diagram by omitting the intermediate observed for both proteins in the folding reaction.)

Raleigh’s group observed similar results with the N-terminal domain of the ribosomal protein L9 (Cho et al. 2004). In their case, the variant K12M was 1.9 kcal/mol more stable than wild-type L9 protein, and refolded 2.3 times faster. They showed that these changes were due to nonnative electrostatic interactions and concluded that the “. . . non-native electrostatic interactions involving K12 persist in the transition state.”

In summary, our results suggest that reversing a single charge on the side chain of a protein can influence the topology of the transition and denatured state ensembles enough to significantly affect the folding kinetics. This provides evidence for residual structure in the denatured state ensemble that is stabilized by charge– charge interactions.

Materials and methods

Protein expression and purification

WT* and WT*(D17R) were expressed and purified as described (Hebert et al. 1997).

Equilibrium denaturation experiments

The conformational stability of WT* RNase Sa and the charge-reversal variant was determined using urea denaturation as monitored by fluorescence spectroscopy on an Aviv 202SF spectropolarimeter. The sample was excited at 280 nm, and fluorescence emission intensity was detected above 320 nm using a cutoff filter. Urea concentrations were determined using refractive index measurements (Pace 1986). Analysis of the denaturation curves was performed using the two-state model and the linear extrapolation method (Pace and Shaw 2000), as previously described (Santoro and Bolen 1988; Pace and Scholtz 1997),

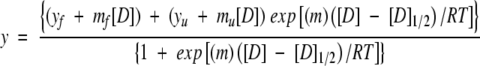graphic file with name M3.gif (3)

where mf=slope of the pretransition baseline; yf=y-intercept of the pretransition baseline; mu=slope of the post-transition baseline; yu=y-intercept of the post-transition baseline; m=the dependence of ΔG on urea; D1/2=midpoint of the unfolding transition curve; and D=denaturant concentration.

Kinetics experiments

All stopped-flow fluorescence measurements were performed at 25°C and pH 7.0 with a PiStar-180 Circular Dichroism Spectrometer (Applied Photophysics). The samples were excited at a wavelength of 280 nm, and emission was detected above 320 nm using a cutoff filter. The refolding reactions were initiated by diluting RNase Sa in 8.8 M urea (in 30 mM MOPS) with varying amounts of urea to give the desired urea concentration and a final protein concentration of 0.01 mg/mL. Refolding progress curves were analyzed and fit by Equation 1 using PiStar software. Two exponential terms were required to fit the refolding results. The unfolding reactions were followed after manual mixing using a PTI spectrofluorimeter equipped with a Peltier temperature control element. RNase Sa was mixed with a concentrated urea solution to give the desired urea concentration and a final protein concentration of 0.06 mg/mL. Unfolding progress curves were analyzed and fit by Equation 1 using Pro Fit and Kaleidagraph analytical software. The observed rate constants, kobs, were used to generate the chevron plots shown in Figure 1 ▶. Chevron plots for both proteins showed contiguous refolding and unfolding phases and these data were fit to Equation 2 to obtain the kinetic parameters given in Table 1. The fast phase for each protein, which has no corresponding unfolding phase, was fit by a linear expression that only considers the parameters for the folding reaction, i.e., kff and mff. These parameters are also found in Table 1.

Acknowledgments

This work was supported by grants GM-37039 and GM-52483 from the National Institutes of Health, grants BE-1060 and BE-1281 from the Robert A. Welch Foundation, and the Tom and Jean McMullin professorship. We thank Douglas Laurents and Siegfried Musser for valuable comments on the manuscript.

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.051401905.

References

  1. Alston, R.W., Urbanikova, L., Sevcik, J., Lasagna, M., Reinhart, G.D., Scholtz, J.M., and Pace, C.N. 2004. Contribution of single tryptophan residues to the fluorescence and stability of ribonuclease Sa. Biophys. J. 87 4036–4047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Cho, J.H., Sato, S., and Raleigh, D.P. 2004. Thermodynamics and kinetics of non-native interactions in protein folding: A single point mutant significantly stabilizes the N-terminal domain of L9 by modulating non-native interactions in the denatured state. J. Mol. Biol. 338 827–837. [DOI] [PubMed] [Google Scholar]
  3. Daggett, V. and Fersht, A.R. 2003. The present view of the mechanism of protein folding. Nat. Rev. Mol. Cell Biol. 4 497–502. [DOI] [PubMed] [Google Scholar]
  4. Fersht, A.R. 1999. Structure and mechanismin protein science:Aguide to enzyme catalysis and protein folding. W.H. Freeman &Co., New York, NY.
  5. Grimsley, G., Shaw, K., Fee, L., Alston, R., Huyghues-Despointes, B., Thurlkill, R., Scholtz, J., and Pace, C. 1999. Increasing protein stability by altering long-range coulombic interactions. Protein Sci. 8 1843–1849. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Hebert, E.J., Grimsley, G.R., Hartley, R.W., Horn, G., Schell, D., Garcia, S., Both, V., Sevcik, J., and Pace, C.N. 1997. Purification of ribonucleases Sa, Sa2, and Sa3 after expression in Escherichia coli. Protein Expr. Purif. 11 162–168. [DOI] [PubMed] [Google Scholar]
  7. Horng, J.C., Cho, J.H., and Raleigh, D.P. 2005. Analysis of the pH-dependent folding and stability of histidine point mutants allows characterization of the denatured state and transition state for protein folding. J. Mol. Biol. 345 163–173. [DOI] [PubMed] [Google Scholar]
  8. Jackson, S.E. and Fersht, A.R. 1991. Folding of chymotrypsin inhibitor 2. 1. Evidence for a two-state transition. Biochemistry 30 10428–10435. [DOI] [PubMed] [Google Scholar]
  9. Khan, F., Chuang, J.I., Gianni, S., and Fersht, A.R. 2003. The kinetic pathway of folding of barnase. J. Mol. Biol. 333 169–186. [DOI] [PubMed] [Google Scholar]
  10. Loladze, V.V., Ibarra-Molero, B., Sanchez-Ruiz, J.M., and Makhatadze, G.I. 1999. Engineering a thermostable protein via optimization of charge–charge interactions on the protein surface. Biochemistry 38 16419–16423. [DOI] [PubMed] [Google Scholar]
  11. Matthews, C.R. 1987. Effect of point mutations on the folding of globular proteins. Methods Enzymol. 154 498–511. [DOI] [PubMed] [Google Scholar]
  12. Myers, J.K., Pace, C.N., and Scholtz, J.M. 1995. Denaturant m values and heat capacity changes: Relation to changes in accessible surface areas of protein unfolding. Protein Sci. 4 2138–2148. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Pace, C.N. 1986. Determination and analysis of urea and guanidine hydrochloride denaturation curves. Methods Enzymol. 131 266–280. [DOI] [PubMed] [Google Scholar]
  14. Pace, C.N. and Scholtz, J.M. 1997. Measuring the conformational stability of a protein. In Protein structure: A practical approach (ed. T.E. Creighton), pp. 299–321. IRL Press, Oxford, UK.
  15. Pace, C.N. and Shaw, K.L. 2000. Linear extrapolation method of analyzing solvent denaturation curves. Proteins Struct. Funct. Genet. 41 1–7. [DOI] [PubMed] [Google Scholar]
  16. Pace, C.N., Alston, R.W., and Shaw, K.L. 2000. Charge–charge interactions influence the denatured state ensemble and contribute to protein stability. Protein Sci. 9 1395–1398. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Pradeep, L. and Udgaonkar, J.B. 2004. Effect of salt on the urea-unfolded form of barstar probed by m value measurements. Biochemistry 43 11393–11402. [DOI] [PubMed] [Google Scholar]
  18. Santoro, M.M. and Bolen, D.W. 1988. Unfolding free energy changes determined by the linear extrapolation method. 1. Unfolding of phenyl-methanesulfonyl alpha-chymotrypsin using different denaturants. Biochemistry 27 8063–8068. [DOI] [PubMed] [Google Scholar]
  19. Shaw, K.L., Grimsley, G.R., Yakovlev, G.I., Makarov, A.A., and Pace, C.N. 2001. The effect of net charge on the solubility, activity, and stability of ribonuclease Sa. Protein Sci. 10 1206–1215. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Spector, S., Wang, M., Carp, S.A., Robblee, J., Hendsch, Z.S., Fairman, R., Tidor, B., and Raleigh, D.P. 2000. Rational modification of protein stability by the mutation of charged surface residues. Biochemistry 39 872–879. [DOI] [PubMed] [Google Scholar]
  21. Tanford, C. 1970. Protein denaturation. C. Theoretical models for the mechanism of denaturation. Adv. Protein Chem. 24 1–95. [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES