Spectrin R16: Broad energy barrier or sequential transition states?

Abstract

A number of models have been proposed to account for nonlinearity in the relation between observed rate constants for folding and/or unfolding and denaturant concentration. Where curvature is seen principally in the arm of a chevron plot, three explanations are proposed: a change in the ground state at increasing concentration of urea, movement of the transition state along a broad energy barrier, and a switch between two sequential transition states separated by an on-pathway high-energy intermediate. Here we demonstrate that the latter two models in particular can be used to describe the data for the all-α protein spectrin R16. Further, whatever the method of analysis, the pattern of Φ-values seen is robust; thus we would draw the same conclusions from our data set independently of the method used for analysis. While this is not a novel observation, this is the first systematic study where a comparison has been made between Φ-values calculated using the broad and sequential transition state models.

We have recently published folding data on a 116-residue, three-helix bundle protein domain from chicken brain spectrin, R16 (Pascual et al. 1997; Grum et al. 1999; Scott et al. 2004a,b). This protein is stable (ΔG_D-N = 6.3 kcal/mol) with an average equilibrium m-value (m_D-N) of 1.9 kcal/mol/M. As for a large number of apparent two-state proteins, the unfolding arm of the R16 chevron plot shows a nonlinear free energy relation between the natural logarithm of the rate constant for unfolding and the concentration of denaturant (summarized in Sanchez and Kiefhaber 2003a). In the literature there has been extensive discussion of how data of this kind can be analyzed (see Walkenhorst et al. 1997^; Oliveberg 1998^{, 2001;} Ferguson et al. 2001^; Otzen and Oliveberg 2002^; Sanchez and Kiefhaber 2003a^; Seeliger et al. 2003). A number of possible interpretations of this type of results can be postulated. Here we consider whether models postulating a change in the unfolding ground state, the presence of a broad energy barrier resulting in movement of the rate limiting transition state along the reaction coordinate, and a switch between transition states separated by an obligatory on-pathway intermediate can describe the data for R16 and its mutants.

The effect of ground state changes

Ground state changes may occur as a function of urea concentration, as a function of protein stability (i.e., on mutation), or both in the same protein. Curvature or kinks in the unfolding arm of the chevron plot can arise from a change in the ground state as the concentration of urea is increased. This can be envisaged either as a continuum of native-like species or as a single native-like state. The simplest scenario to describe is the presence of a single native-like state; in this case the native state (N) reorganizes to a less-structured form or, kinetically equivalent, exists in equilibrium with a highly compact intermediate (N*) (Figure 1A ▶; Otzen and Oliveberg 2002). This is not without precedent, with the unfolding of barstar being the classic example (Zaidi et al. 1997). More recently, the yeast prion protein Ure2 has also shown to populate an unfolding intermediate (Galani et al. 2002). The effect of a continuum of native-like species can be rationalized in a similar manner.

Figure 1.

Schematic free energy profile for models used to account for curvature in unfolding (and possibly also refolding) arms of chevrons. In all panels the profile is shown for folding conditions (solid line, A), mild denaturing conditions (long-dashed line, B), and strongly denaturing conditions (short-dashed line, C). (A) Change in ground state/population of an unfolding intermediate. As the concentration of urea is increased, N* becomes stable relative to N and thus becomes the ground state for folding. (B) Broad transition state model; folding takes place relatively isoenergetically across a broad energy barrier. (C) Sequential transition state model. Folding transition states are narrow along this reaction observable (β_T) (Oliveberg 1998, 2001; Otzen and Oliveberg 2002; Sanchez and Kiefhaber 2003a; Seeliger et al. 2003).

Plasticity in the native state upon mutation has been reported for a number of proteins, including the split β-α-β protein S6 (Otzen and Oliveberg 2002). This is an interesting example as the structural homolog U1A behaves quite differently, as discussed below. For S6 the folding arm is linear for wild type and all mutants, but kinks/curvatures or changes in slope are seen in the unfolding arm of many of the mutants. These changes are proposed to arise from a complex combination of factors, with plasticity in all states along the reaction coordinate for S6 (Otzen and Oliveberg 2002).

Broad transition state model

An alternative to a change in the ground state is a movement of the transition state along the reaction coordinate as a function of concentration of urea. This is analogous to Hammond behavior in small molecule reactions. Hammond (1955) states that “if two states, as for example, a transition state and an unstable intermediate, occur consecutively during a reaction process and have nearly the same energy content, their interconversion will involve only a small reorganization of the molecular structures.” Therefore as the native state and transition state become closer in energy, the transition state should move toward the native state in structure. Hammond effects on protein folding under differing conditions are discussed in references including Matouschek and Fersht 1993^, Matouschek et al. 1995^, Dalby et al. 1998^, Yiu et al. 2000, and Sanchez and Kiefhaber 2003b. It is expected that Hammond effects will occur for all protein folding reactions; however, if the transition state is narrow, the effect may be too small to be distinguished experimentally.

A broad transition state barrier model has been presented by Oliveberg and coworkers to account for the curvature in the S6 homolog U1A (Silow and Oliveberg 1997; Oliveberg et al. 1998; Otzen et al. 1999; Ternstrom et al. 1999; Oliveberg 2001). The protein U1A shows symmetric curvature in both arms of the chevron plot. Oliveberg and coworkers describe the protein folding transition state as a broad ensemble along a reaction coordinate representing structure formation. In this case folding takes place through an isoenergetic ensemble in water. On the addition of denaturant, those transition state structures closer to the native state in structure are destabilized to a greater extent relative to those closer to the denatured state (Fig. 1B ▶). This has the effect of shifting the highest point in the transition state ensemble toward the native state and resulting in the downward curvature of the unfolding arm of a chevron. Changing curvature as a result of mutation can then be envisaged by postulating that the mutation has different effects on different regions of the transition state ensemble.

The data for U1A were fitted to the equation for a two-state chevron with quadratic terms added to account for the curvature in each arm. To account for the fact that mutants have different β_T values at a particular concentration of denaturant, Φ-values were calculated as a function of β_T, providing a picture of which regions of structure were formed at different regions along the reaction coordinate (Ternstrom et al. 1999).

Sequential transition state model

An alternate interpretation to the broad transition state model is the presence of two or more sequential transition states separated by a high-energy intermediate. This has been used to model the behavior of Staphylococcal Nuclease, by Roder and coworkers (Walkenhorst et al. 1997), and the disulfide bonded protein tendamistat, by Kiefhaber and coworkers (Bachmann and Kiefhaber 2001). It has also been discussed as a possible method of analysis by others, including Oliveberg (1998) and Radford and coworkers (Ferguson et al. 2001). This model was used by Sanchez and Kiefhaber (2003b) to reanalyze work previously published by other groups in 2003.

In this model the transition state ensemble is described as encompassing only a small region of the reaction coordinate representing structure formation, with curvature arising due to the switch between discrete transition states separated by one or more obligatory on-pathway high-energy intermediates (Fig. 1C ▶). Where curvature is seen in only one limb of a chevron, the presence of two transition states is the minimal model. The data can therefore be fit to the three-state equation, modified to account for the intermediate being unpopulated. Unlike the quadratic equation used in the previous model, which describes a smooth curvature over the arms of the chevron, the equation used in this model has limiting slopes. Where the switch between two transition states is apparent in the unfolding kinetics, there are two limiting slopes representing unfolding with one or the other transition state being rate limiting. Curvature (or a kink) is seen in the region where the transition states are similar in energy. Whether a curve or kink is seen depends on how close the transition states are both in energy and position along the reaction coordinate and also the range of the experimental data. Thus while this model is clearly appropriate for kinked chevrons (such as tendamistat), it may also be appropriate where smooth curvature is seen.

There has recently been considerable discussion in the literature about the best way to fit curved chevrons. The aim of this work is to assess the importance of the method used to fit the data on the conclusions drawn about the folding mechanism for R16 from protein-engineering Φ-value analysis. We show that either of the latter two models can be used to fit the kinetic data for wild-type R16 and all of the mutants expressed in our laboratory. Further, we emphasize that no matter how the data are analyzed, essentially the same conclusions can be drawn.

Results

R16 mutant kinetics

The analysis of wild-type R16 has been discussed previously (Scott et al. 2004a). In summary, we have shown that the protein folds by a two-state mechanism with two refolding phases, one of which is isomerization limited. There is also some evidence for residual structure in the denatured state, as demonstrated by fluorescence amplitude measurements.

The folding kinetics of 70 R16 mutant proteins were followed using stopped-flow fluorescence. Only one phase was apparent in unfolding traces; however, in refolding two phases were detected. The slower phase typically accounts for 10%–15% of the total amplitude in all fluorescence measurements and exhibits a similar concentration dependence to the wild-type protein. As for wild type, the second phase is attributed to isomerization effects and is not discussed further here. For all mutants curvature is seen in the unfolding arm, with the degree of curvature often differing between wild type and mutant.

Changing ground state model

Does population of a burst phase unfolding intermediate account for the curvature of the unfolding arm of the wild-type chevron? This is of particular concern in an all α-helical protein where mutations or denaturant may cause “fraying” at the ends of helices. If a burst phase intermediate were populated, we would expect to see evidence of this from amplitude measurements (Zaidi et al. 1997; Galani et al. 2002). For wild-type R16 there is no evidence of such a burst phase unfolding intermediate from fluorescence amplitudes (Scott et al. 2004a) or from far UV CD amplitude measurements. Many of the mutants unfolded too rapidly for CD amplitude measurements to be reliable; however, curvature is seen both in mutations that would be expected to stabilize helical structure and at locations away from the ends of the helices, supporting the assertion that native state changes are not sufficient to explain the observed curvature.

Broad transition state model

In this model symmetric curvature is expected in both arms of the chevron plot. Thus at first glance it would seem that the R16 data are not consistent with this model. However, if we assume that the curvature seen in the unfolding arm is reflected in the refolding arm, we find that the predicted curvature in the refolding arm would be too small to distinguish from linearity. This is a consequence of the small curvature term, multiplied by the square of the urea concentration (also small). For the purpose of this analysis, we assume that there is a broad transition state and then compare the kinetic free energy for unfolding and kinetic m-values against the equilibrium data to evaluate how well this modelworks. The value of k_f ^H₂O used was found assuming symmetric curvature in both arms of the chevron plot; however, the value is identical to that found using a linear extrapolation and thus this assumption does not alter the final result.

For the same reason, the value of k_u ^H₂O was determined by using the extrapolation of the quadratic equation used to fit the observed region of the unfolding arm. This also removes the added complication of deciding where the extrapolation should become linear. The values reported here are obtained from an independent fit to each chevron. Attempts to fit the data by using a global curvature parameter were not successful, and it is not clear that this is a sensible approach in any case. Typical chevrons with the appropriate fitted line are shown in Figure 2 ▶. The associated parameters are given in Table 1.

Figure 2.

Typical R16 chevrons. Chevrons fitted using a quadratic term to account for the observed curvature are shown in panels A, C, and E. The same chevrons fitted using a three-state equation with a high-energy intermediate are shown in panels B, D, and F. The fit to the data is shown as a solid black line. A PDF file showing all chevrons for all mutants fitted to both models is available on request (jc162@cam.ac.uk).

Table 1.

Parameters from fit to a broad transition state model

Mutant	kfH2Os−1	kuH2Os−1	mD-N kcal/mol/M	ΔGD-N (H2O) kcal/mol	ΔΔGD-N (H2O) kcal/mol	|ΔGD−N(eq)− ΔGD-N(kin) | (H2O) kcal/mol
WT Core mutants	113	0.0017	2.0	6.5		0.3
F11L	86	0.007*	2.1	5.5	1.0	0.4
F11A	33	0.16	2.0	3.1	3.4	0.5
L11A	33	0.16	2.0	3.1	2.4	0.5
M15A	38	0.020	2.1	4.4	2.1	0.3
W21F	57	0.008	2.1	5.2	1.4	0.5
I22V	77	0.011	2.1	5.2	1.3	0.5
I22A	47	0.15	2.1	3.3	3.1	0.2
V22A	47	0.15	2.1	3.3	1.9	0.2
K25A	381	0.008*	2.0	6.3	0.2	0.0
V29A	80	0.001*	2.0	6.5	0.0	0.4
V41A	110	0.0030	2.0	6.2	0.3	0.3
L44A	110	0.003*	1.9	6.1	0.3	0.04
H48A	93	0.04*	1.8	4.5	1.9	0.4
L51A	59	0.09	2.1	3.8	2.7	0.2
L55A	47	0.50	2.3	2.6	3.9	0.1
H58A	118	0.08	2.0	4.3	2.2	0.3
P60A	362	0.0001*	2.2	8.8	−2.3	2.0
I62V	77	0.005	1.9	5.7	0.8	0.1
I62A	52	0.19	1.9	3.3	3.2	0.2
V62A	52	0.19	1.9	3.3	2.4	0.2
V65A	81	0.052	2.0	4.3	2.2	0.3
L72A	69	0.08	2.0	4.0	2.5	0.04
I83V	72	0.0026	1.9	6.0	0.5	0.3
I83A	52	0.027	2.0	4.4	2.1	0.1
V83A	52	0.027	2.0	4.4	1.6	0.1
L87A	24	0.054	2.0	3.5	2.9	0.03
F90A	29	0.08	2.0	3.4	3.1	0.2
W94F	62	0.031	2.1	4.4	2.1	0.1
L97A	24	0.14	2.3	3.0	3.5	0.5
A101G	42	0.07	2.1	3.7	2.8	0.0
R104A	170	0.0037	1.9	6.3	0.2	0.0
L108A	91	0.039	1.8	4.5	2.0	0.4
Ala/Gly scanning mutants
H9A	147	0.0006*	2.0	7.2		0.4
H9G	76	0.0021	2.0	6.1	1.1a	0.3
R13A	93	0.003	2.0	6.0		0.1
R13G	44	0.018	2.0	4.6	1.4	0.1
D16A	115	0.0023	2.0	6.3		0.2
D16G	75	0.0039	2.1	5.8	0.6	0.6
S20A	150	0.001*	2.0	6.9		0.1
S20G	89	0.0019	2.1	6.3	0.6	0.4
E24A	146	0.001*	2.1	6.8		0.4
E24G	78	0.0028	2.0	6.0	0.8	0.8
T39A	107	0.0007	2.0	7.0		0.4
T39G	105	0.0021	2.0	6.3	0.7	0.1
N43A	132	0.005*	1.8	5.9		0.6
N43G	114	0.0046	1.9	5.9	0.0	0.02
K46A	150	0.0023*	1.9	6.5		0.3
K46G	110	0.010	1.8	5.4	1.0	0.4
R50A	127	0.0011	1.9	6.8		0.2
R50G	87	0.0070	1.9	5.5	1.3	0.2
A53G	73	0.0025	2.2	6.0	0.5	0.8
A57G	82	0.0029	2.1	6.0	0.5	0.7
Q63A	86	0.0052	2.0	5.7		0.02
Q63G	78	0.0062	1.9	5.5	0.2	1.0
D67A	127	0.0020	2.0	6.5		0.2
D67G	83	0.011	2.0	5.2	1.3	0.2
K71A	117	0.002*	1.9	6.4		0.2
K71G	99	0.008	1.9	5.5	0.9	0.6
Q85A	128	0.002	2.1	6.6		0.5
Q85G	50	0.003	2.1	5.7	0.9	0.2
A88G	40	0.004	1.9	5.3	1.2	0.1
D92A	251	0.00070	2.0	7.5		0.4
D92G	103	0.001*	2.1	6.6	0.9	0.5
K95A	65	0.00020	2.0	7.4		1.5
K95G	32	0.0025	2.0	5.5	1.9	0.5
Q99A	140	0.001*	2.0	6.8		0.1
Q99G	61	0.0023	2.1	5.9	0.9	0.3
A103G	35	0.009	2.0	4.8	1.7	0.3
D106A	160	0.0009	2.1	7.1		0.3
D106G	82	0.020	1.8	4.8	2.3	0.2

The error in the rate constant for folding is typically 5% of the reported value. Unless marked with an asterisk, the error in the rate constant for unfolding from the fit to the data is <25% of the reported value, no error is >30% of the reported value. Values for k_u^H₂O are given to the appropriate number of significant figures, based on the error.

Note that the errors in the parameters ΔG_D-N and m can be judged rather well from the scatter in the plots in Fig. 4 ▶.

^a The value for the alanine to glycine mutation is quoted against the appropriate glycine mutant.

Sequential transition state model

Curvature in a single limb of a chevron plot requires a single high-energy intermediate in this model. Wild type and all mutants were fit to a three-state equation, adapted for the presence of a high-energy intermediate (Walkenhorst et al. 1997; Bachmann and Kiefhaber 2001; Ferguson et al. 2001; Sanchez and Kiefhaber 2003b).

Many of the R16 variants approach a limiting slope only at a very high concentration of denaturant, making it difficult to determine the gradient of this line. Although the data for each mutant can be fit individually, the fact that some of the mutants do not define the second slope well leads to a variation in the m-value for this slope. To test whether the data could be fit to a model where the m-values do not vary between mutants, a global fit was carried out. In doing so, it is important to note that we have to make the assumption that the early transition state, the late transition state, and N do not move along the reaction coordinate. When the data are fitted individually, the vast majority of mutants give the same Φ-value for transition state 2, within the experimental error of ±0.1 (the large error is due to long extrapolation and error in the slope), and there is no change in the Φ-value for transition state 1. However, where we use individual fits, there is poorer agreement between the kinetic and equilibrium values for the free energy change on unfolding than when a fixed m value is used. A pair of global unfolding m-values is able to describe all mutants and was used for the rest of the analysis described here. No attempt was made to find a global value for the refolding arm; this can easily be fitted for each data set, and given that we have some evidence for residual structure in the denatured state (Scott et al. 2004a), this value may be expected to change on mutation.

Typical chevrons fit using this method are shown in Figure 2 ▶. For illustration, the hypothetical chevrons for each of the two transition states are also shown for two mutants in Figure 3 ▶. The parameters associated with this fit are given in Table 2.

Figure 3.

Hypothetical chevrons for the sequential transition state model. Two chevrons showing lines corresponding to the hypothetical fit for TS 1 (long-dashed line) and TS 2 (short-dashed line) in the sequential transition state model. The fit to k_obs is shown as a solid line.

Table 2.

Parameters from fit to a sequential transition state model

Mutant	kfH2Os−1	kuH2Os−1a	mD-N kcal/mol/M	ΔGD-N (H2O) kcal/mol	ΔΔGD-N (H2O) kcal/mol	|ΔGD−N(eq)− ΔGD-N(kin) | (H2O) kcal/mol
WT Core mutants	125	0.0032	1.9	6.2		0.02
F11L	90	0.011	2.0	5.2	1.0	0.2
F11A	36	0.39	1.9	2.6	3.6	0.01
L11A	36	0.39	1.9	2.6	2.6	0.01
M15A	37	0.020	2.0	4.4	1.9	0.2
W21F	58	0.02*	1.9	4.6	1.6	0.1
I22V	74	0.017	2.0	4.9	1.3	0.2
I22Aa	47	0.3*	2.0	3.0	3.2	0.6
V22Aa	47	0.3*	2.0	3.0	1.9	0.6
K25A	371	0.012	1.8	6.0	0.2	0.3
V29A	84	0.0028	1.9	6.0	0.2	0.1
V41A	115	0.0051	1.9	5.9	0.4	0.01
L44A	114	0.004*	1.9	6.1	0.2	0.03
H48A	101	0.034	1.8	4.7	1.6	0.2
L51A	64	0.22	1.9	3.3	2.9	0.3
L55A	51	1.51	2.1	2.0	4.2	0.5
H58A	127	0.11	1.9	4.1	2.1	0.1
P60A	390	0.0064	1.8	6.4	−0.2	0.4
I62V	81	0.0054	1.9	5.6	0.6	0.1
I62A	54	0.21	1.9	3.2	3.0	0.2
V62A	54	0.21	1.9	3.2	2.4	0.2
V65A	84	0.075	1.9	4.1	2.1	0.1
L72A	71	0.073	2.0	4.0	2.2	0.1
I83V	79	0.0048	1.8	5.7	0.6	0.1
I83A	53	0.030	1.9	4.4	1.9	0.1
V83A	53	0.030	1.9	4.4	1.3	0.1
L87A	25	0.053	2.0	3.6	2.7	0.04
F90A	30	0.062	2.0	3.6	2.6	0.03
W94F	63	0.048	2.0	4.2	2.1	0.1
L97A	26	0.36	2.2	2.5	3.8	0.1
A101G	44	0.10	2.0	3.5	2.7	0.2
R104A	179	0.0041	1.8	6.2	−0.02	0.1
L108A	98	0.031	1.8	4.7	1.5	0.2
Ala/Gly scanning mutants
H9A	177	0.0023	1.9	6.6		0.3
H9G	85	0.0040	1.9	5.8	0.8b	0.01
R13A	97	0.0043	1.9	5.9		0.2
R13G	46	0.018	2.0	4.6	1.3	0.2
D16A	120	0.0036	1.9	6.1		0.03
D16G	79	0.0063	2.0	5.5	0.6	0.3
S20A	160	0.0027	1.8	6.4		0.4
S20G	95	0.0040	1.9	5.9	0.5	0.02
E24A	155	0.0041	1.9	6.2		0.3
E24G	93	0.0064	1.9	5.6	0.6	0.4
T39A	125	0.0021	1.9	6.4		0.2
T39G	117	0.0038	1.9	6.0	0.4	0.2
N43A	132	0.0034	1.9	6.2		0.3
N43G	119	0.0058	1.9	5.8	0.4	0.2
K46A	152	0.0018	1.9	6.6		0.1
K46G	114	0.0080	1.8	5.6	1.1	0.2
R50A	136	0.0018	1.8	6.6		0.1
R50G	94	0.0098	1.9	5.4	1.2	0.4
A53G	82	0.014	1.9	5.1	1.2	0.1
A57G	92	0.014	1.9	5.1	1.1	0.1
Q63A	95	0.008	1.9	5.4		0.2
Q63G	81	0.051	1.9	4.3	1.1	0.3
D67A	138	0.0040	1.9	6.1		0.1
D67G	87	0.016	1.9	5.0	1.1	0.04
K71A	126	0.0034	1.8	6.1		0.1
K71G	103	0.0094	1.9	5.4	0.7	0.5
Q85A	120	0.0027	1.8	6.3		0.1
Q85G	49	0.0080	1.8	5.1	1.2	0.1
A88G	40	0.0039	1.8	5.4	0.8	0.2
D92A	278	0.0028	1.8	6.9		0.2
D92G	109	0.0032	1.9	6.1	0.8	0.1
K95A	69	0.0033	1.9	5.8		0.2
K95G	34	0.0053	1.9	5.1	0.7	0.1
Q99A	156	0.0028	1.8	6.4		0.3
Q99G	68	0.0061	1.9	5.4	1.0	0.2
A103G	38	0.016	1.9	4.5	1.7	0.02
D106A	168	0.0028	1.9	6.4		0.4
D106G	89	0.020	1.8	4.9	1.5	0.2

The error in the rate constant for folding is typically 5% of the reported value. Unless marked with an asterisk, the error in the rate constant for unfolding from the fit of the data is <15% of the reported value, no error is >25% of the reported value.

^a In the sequential transition state model, k_u^H₂O is calculated as (k₋₁.k₋₂)/k₂.

^b The value for the alanine to glycine mutation is quoted against the appropriate glycine mutant.

Calculation of Φ-values

Parameters from the broad transition state model and the sequential transition state model were used to calculate sets of Φ-values. The Φ-values presented were calculated using the value of Δ G_D-N ^H₂O determined from equilibrium measurements. While this has the disadvantage that 0 M Φ-values calculated from refolding and unfolding data will not give identical values where the equilibrium and kinetic values of ΔG_D-N ^H₂O differ, it eliminates concern over the extrapolation of the unfolding data to 0 M. In fact we find that the pattern of Φ-values is the same whichever value of ΔΔG_D-N ^H₂O we use; generally the Φ-value only changes by 0.1. As Φ-values are best interpreted as “low,” “medium,” and “high,” our interpretation would be the same whether we use the equilibrium or kinetic ΔΔG_D-N ^H₂O. In this discussion we are treating the folding of R16 as being an observable two-state process from a structured denatured state.

Φ-Values from the fit to the broad transition state model were calculated at 0 M from refolding data (Table 3). The value of k_f ^H₂O was from the fit of the data, rather than the measured point; however, none of the proteins show sufficient difference between fit and measured k_f ^H₂O that choice of value significantly changes the results. Φ-Values were also calculated from unfolding data in 9 Murea and at a β_T of 0.85 (a β_T of 0.85 corresponds to the β_T of the second transition state in the sequential transition state model) (Table 3). Oliveberg and coworkers (Ternstrom et al. 1999) have previously used this approach to account for the difference in curvature seen in mutants of U1A.

Table 3.

R16 Φ-values

Mutant	ΔΔ GD−NH2Oeq (kcal/mol)	Φ(TS1)	Φ (TS2)	Φ (0 M)	Φ (9 M)	Φ (βT=0.85)
Core mutants
F11L	1.2a	0.2	0.4	0.2	0.5	0.7
F11A	3.6	0.2	0.4	0.2	0.5	0.7*
L11A	2.4	0.2	0.4	0.2	0.4	0.7*
M15A	2.1	0.4	0.6	0.4	0.7	0.9
I22V	1.5	0.2	0.4	0.2	0.5	0.7
I22A	2.7	0.2	0.4	0.2	0.3	0.5
V22A	1.2	0.2	0.5	0.3	−0.1	0.2
K25A	−0.1b
V29A	0.1b
V41A	0.4b
L44A	0.1b
H48A	1.3	0.1	1.0	0.1	0.8	1.3
L51A	2.7	0.2	0.4	0.2	0.4	0.7
L55A	3.7	0.2	0.4	0.2	0.4	0.6
H58A	2.3	0.0	0.4	0.0	0.5	0.7
I62V	0.5b
I62A	2.8	0.2	0.5	0.2	0.4	0.6
V62A	2.3	0.1	0.3	0.1	0.3	0.5
V65A	2.2	0.1	0.3	0.1	0.3	0.4*
L72A	2.3	0.2	0.5	0.2	0.5	0.6
I83V	0.5b
I83A	2.0	0.3	0.5	0.3	0.5	0.6*
V83A	1.5	0.2	0.4	0.2	0.5	0.5*
L87A	2.7	0.4	0.6	0.4	0.6	0.7
F90A	2.7	0.3	0.7	0.3	0.7	0.8
L97A	3.7	0.3	0.3	0.3	0.3	0.5*
A101G	2.6	0.3	0.5	0.2	0.5	0.6
R104A	−0.1b
L108A	1.3	0.1	1.0	0.1	0.8	1.3
Ala/Gly scanning mutants
A9G	1.1	0.4	0.6	0.4	0.9	0.8
A13G	1.6	0.3	0.5	0.3	0.7	0.6*
A16G	0.9	0.3	0.5	0.3	0.9	0.7
A20G	1.0	0.3	0.3	0.3	0.8	0.6
A24G	1.2	0.2	0.2	0.3	0.7	0.3*
A39G	0.5b
A43G	0.5b
A46G	0.9	0.2	0.9	0.2	0.8	0.9*
A50G	0.9	0.2	1.0	0.3	0.7	1.4*
A53G	1.6	0.2	0.3	0.3	0.4	0.8
A57G	1.0	0.2	0.1	0.2	0.1	0.5
A63G	1.1	0.1	0.8	0.1	1.9	1.8
A67G	1.3	0.2	0.5	0.2	0.6	0.4
A71G	1.3	0.1	0.3	0.1	0.7	0.6
A85G	1.4	0.4	0.5	0.4	0.7	0.7*
A88G	1.0	0.7	0.7	0.7	0.8	−0.1*
A92G	1.0	0.7	0.6	0.5	0.8	0.7*
A95G	0.9	0.5	0.4	0.5	−0.8	0.5
A99G	1.1	0.5	0.4	0.5	0.6	0.6
A103G	1.7	0.4	0.8	0.4	0.9	1.2
A106G	1.7	0.2	0.9	0.2	1.8	1.1*

Φ-Values for TS1 and at 0 M and 9 M (where no extrapolation is made) have an error of ±0.1. The use of global m-values for unfolding in the sequential transition state model also reduces the calculated error in the Φ-values for TS2 to ±0.1. The error in the Φ_(βT=0.85) varies depending on whether a β_T of 0.85 occurs inside the data set in this model. Those Φ-values where β_T = 0.85 occurred outside the measured range are marked with an asterisk (the largest extrapolation outside the measured range was to 9.5 M urea).

^aΔΔG^H₂O_D−N is calculated from equilibrium measurements; the error in these values is typically 0.1 kcal/mol.

^bΔΔG^H₂O_D−N was too small for the calculation of a Φ-value.

From the fit of the data to a sequential transition state model, two sets of Φ-values were calculated from folding rate constants, one for each of the rate limiting transition states Φ _(TS1) and Φ _(TS2) (Table 3).

Discussion

Changing ground state model

We have no evidence that changes in the ground state for unfolding are responsible for the curvature seen in the unfolding arm of wild-type R16; no unfolding burst phase is seen in fluorescence or CD amplitude data. While we cannot rule out fraying in some mutants contributing to curvature, it is clear that this is not the principle mechanism through which curvature arises.

Broad transition state model

As can be seen in Figure 4 ▶, with the exception of P60A, a reasonable agreement (given the long extrapolation and error in fitting the curvature) is seen between the value of ΔG_D-N calculated from equilibrium and kinetic data in this model. The m-values calculated from the kinetic and equilibrium data do not agree well, although the mean over the whole data set, 〈m_D-N〉, shows good agreement between the kinetic and equilibrium values.

Figure 4.

Comparison of kinetic parameters from each of the analysis methods used with the equilibrium parameters. In all panels the line Y=X is shown in black for reference. (A) Kinetic free energy change in water calculated from the fit using a quadratic equation, points with a discrepancy between the equilibrium and kinetic parameters >0.6 kcal/mol are shown as crosses (correlation coefficient of the best fit line r²=0.94). (B) Kinetic free energy change in water calculated using a three-state equation with a high-energy intermediate species (correlation coefficient of the best fit line r²=0.99). (C) m_D-N in water calculated from the fit using a quadratic equation. (D) m_D-N calculated from the fit using a three-state equation with a high-energy intermediate species.

Closer inspection of the deviation between equilibrium and kinetic values of ΔG_D-N, |ΔG_D-N(eq) ^H₂O − ΔG_D-N(kin) ^H₂O | in Table 1 shows that (with the exception of P60A, which does not agree at all well) the values for the core mutants are in better agreement than those for the alanine to glycine scanning mutants. The average deviation for the core mutations is 0.2 kcal/mol, while that for the alanine to glycine scanning mutants is 0.4 kcal/mol (excluding P60A). Those mutants with a deviation >0.6 kcal/mol are A57G, A53G, K95A, N43A, E24G, Q63G, and D16G. Inspection of the chevron plots for the first five mutants shows that the unfolding arms of the alanine and glycine mutants appear to diverge, rather than converge, at high concentration of denaturant. In fact, P60A also shows divergence of the unfolding arm from the wild type at high concentration of urea. There is no obvious reason for the poor agreement between the kinetic and equilibrium ΔG_D-N for Q63G and D16G. (It should be noted that if the refolding armis assumed linear, then the value of |ΔG_D-N(eq) ^H₂O − ΔG_D-N(kin) ^H₂O| is within error of the one reported here in all cases, and thus the conclusions are not affected by this assumption.)

Sequential transition state model

An acceptable fit for all proteins, as judged by the fitting software, can be achieved individually for each data set. However, given the poorly defined nature of the limiting slopes for some mutants, in some cases more than one set of parameters is able to do so. Instead we used the best set of global parameters for data fitting, as judged by the error in the global fit of all data sets.

A good agreement is seen between the kinetic and equilibrium values of ΔG_D-N from this fit, with the mean deviation |ΔG_D-N(eq) ^H₂O − ΔG_D-N(kin) ^H₂O| being 0.2 kcal/mol over the whole data set (and also for the core mutants and scanning mutants as two sets) (Fig. 4 ▶). This is surprisingly good given the nature of the data and the assumptions that we have made in this analysis. The major exceptions are V22A and I22A; this is due to the large error in the fitted value of one of the rate constants (k₂) (see Materials and Methods for description of parameters used in the fit).

As for the broad transition state model, the kinetic m-values do not reproduce the equilibrium values well.

Broad versus sequential transition states compared

Given the uncertainty in the extrapolations and the assumptions made when fitting the data, both models give a surprisingly good agreement between the equilibrium and kinetic values of ΔG_D-N ^H₂O. As shown in Figure 5 ▶, better agreement between kinetic and equilibrium values is seen for the sequential transition state model. This shows that using the value of k_u ^H₂O found using a limiting slope gives better agreement with equilibrium data, as the values of k_f ^H₂O are essentially identical in both cases. If we fit individual chevrons to the sequential transition state model, then this is not the case; one advantage of this model is the use of the global parameters to reduce fitting error due to poorly defined limiting slopes, although care must be taken that a global fit is appropriate. In contrast, an acceptable global solution could not be found using the quadratic equations.

Figure 5.

Graphical illustration of the difference between the kinetic and equilibrium free energy change for each of the models. Differences in Δ G_D-N ^H₂O found when the kinetic free energy is from the fit to a three-state equation are shown as halftone bars extending from left to right. Differences in Δ G_D-N ^H₂O found when the kinetic free energy is from the fit using a quadratic model are shown as black bars extending from right to left. The order of bars is as in Tables 1 and 2, with wild type at the bottom and D106G at the top of the figure.

Comparison of Φ-values

A graphical comparison of Φ-values calculated using the two methods is shown in Figure 6 ▶. The values are obtained for Φ_(TS1) and Φ_(0M) are not shown; both sets of Φ-values are calculated from folding rate constants in water, and these values essentially do not vary between models, as can be seen in Tables 1 and 2.

Figure 6.

Comparison of Φ-values calculated using different analysis methods. Φ-Values for TS2 from the sequential transition state model compared with those calculated at 9 M urea from the moving transition state model. All Φ-values in this figure are calculated using ΔΔG_D-N from equilibrium data; the same pattern of Φ-values is seen for if the kinetic values are used, with few mutants having a difference in Φ-value of >0.1.

Poor numerical agreement is seen between Φ_(TS2) and Φ_(9M); this not a surprising result given the assumptions made in the analysis. Also the choice of 9 M urea was arbitrary with Φ_(9M) representing different β_T values for different proteins. Despite this, both sets of Φ-values give a very similar qualitative picture for folding (Fig. 6 ▶). Several mutations, including A95G, A106G, A63G and V22A, A16G, A20G, E24G, and K71G, have Φ-values differing by >0.4. Of these, A95G, A63G, A16G, and A24G are mutations where one of proteins showed a significantly poorer than average agreement between equilibrium and kinetic values of Δ G_D-N ^H₂O in the broad transition state model, with the others having one protein showing a significantly poorer than average agreement in the sequential transition state model. Therefore where the kinetic and equilibrium data are in good agreement, the two sets of Φ-values show a reasonable agreement, a logical conclusion.

Φ-Values were also calculated where β_T=0.85 in the broad transition state model for comparison with Φ_(TS2); 0.85 is the β_T value for TS2 in the sequential transition state model. The values of Φ _(βT=0.85) are given in Table 3; however, there is a significant error associated with these values. In the broad transition state model, this value of β_T is not reached in the experimental range for about one-third of the proteins studied, and thus we have less confidence in the values. In fact, the large difference in the values of m_ku for different mutants means that there is only a limited range of β_T values that lie in the experimental range for all proteins. This has also been observed in the cell cycle protein CKS1 (Seeliger et al. 2002). Nonetheless, the pattern of Φ-values is again similar to that observed for TS2.

How does this affect our conclusions?

As discussed previously by others, including Oliveberg and coworkers (Otzen and Oliveberg 2002) and Itzhaki and coworkers (Seeliger et al. 2003), conclusions about the order of events in folding are robust to how the data are analyzed. Here we illustrate the point with reference to mutant L108A. Inspection of the folding arm of the chevron shows little change in the folding rate constant, demonstrating that this mutation has little effect upon the rate determining transition state in water. The unfolding limb is then markedly curved. In the first scenario, at high concentration of denaturant this mutation leads to fraying of the native state. In the other two models, this interaction is now formed to a much greater extent in the dominant transition state at high denaturant concentration. In either case this is flagged as residue that makes many of its interactions late on the folding pathway.

Conclusions

For this data set, better agreement is seen between kinetic and equilibrium free energy values when the sequential transition state model is used. However, in this case we do not believe that data fitting can actually distinguish between a broad transition state or sequential transition states separated by a high-energy intermediate. The broad transition state model suffers from being difficult to describe in terms of kinetic equations, with the addition of a quadratic parameter being the best approximation available. On the other hand, in the sequential transition state model we are obliged to assume no movement of the two transition states on mutation or addition of denaturant and to use a global fitting protocol with shared m_ku values. It might be possible to distinguish further between the two models for R16 by carrying out experiments in guanidinium chloride or at different temperatures. However, most importantly, the conclusions drawn from this data set are independent of the method used to analyze the data.

Materials and methods

Production of the wild-type and mutant proteins has been described previously (Scott et al. 2004a,b). All experiments were carried out at 25°C in 50 mM sodium phosphate buffer (pH 7.0). Protein concentration for all experimental work was maintained at 1–2 mM. Both equilibrium and kinetic data were shown to be independent of protein concentration at this level. Equilibrium stabilities and m-values were determined as has been described (Pace 1986), using urea as a denaturant and monitoring protein unfolding by changes in fluorescence at 350 nm. Kinetic experiments were carried out using an Applied Photophysics SX.18MV stopped-flow fluorimeter maintained at a temperature of 25 ± 0.1°C. Rate constants above ~200 sec⁻¹ were measured using both the 5-μL cell (which gives a shorter dead-time) and the 20-μL cell. Between 10 and 15 traces were averaged for typical measurements. An excitation wavelength of 280 nm with a 320-nm cutoff filter was used for all proteins. Refolding traces were fit to an equation describing two exponential processes; unfolding traces, to an equation describing a single exponential process. No linear term was necessary in either case, and the addition of extra phases did not improve the fit as judged by the residual (deviation of the fit from the data).

Data analysis: Broad transition state model

The equation typically associated with this model includes two quadratic terms accounting for curvature in the folding and unfolding arms of the chevron (Oliveberg 1998, 2001). For R16 the curvature was sufficiently small as to not be apparent in the refolding arm of the chevron. Therefore the unfolding arm of the chevron outside the transition region was fit to Equation 1 and the value of m_ku′ used to fix m_kf′ in Equation 2 (Silow and Oliveberg 1997; Oliveberg et al. 1998; Otzen et al. 1999; Ternstrom et al. 1999).

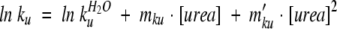(1)

(2)

Where m_ku′ is the term accounting for curvature in the unfolding arm of the chevron (M⁻²), and m_kf′ is the term accounting for curvature in the folding arm of the chevron (M⁻²).

The concentration of urea at which a particular value of β_T occurs can be found using Equation 3:

(3)

Data analysis: Sequential transition state model

The equation used to fit the data is the analytical solution for the eigenvectors and eigenvalues of the rate matrix describing a three-state on-pathway mechanism (Fig. 1C ▶). The resulting equation and method of analysis is given in Comprehensive Chemical Kinetics (Szabo 1969), and (more simply) by Schmidt and coworkers (Kiefhaber et al. 1992). Briefly, two amplitudes, A1 and A2, are defined as:

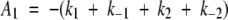(4)

(5)

The observed rate constant is then

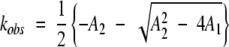(6)

To fit a chevron, the logarithm of Equation 6 is used with each of the rate constants in A₁ and A₂ replaced by the expression showing how it varies with the concentration of denaturant; for example, k₁ is replaced by

(7)

The intermediate is never populated; therefore we cannot know m-values between I and each transition state, nor do we measure rate constants from I experimentally. As a result some alteration of the typical three-state model is necessary (Bachmann and Kiefhaber 2001; Sanchez and Kiefhaber 2003b). First, the value of m₋₁ is set to 0 in all cases; this means that m₂ now represents the change in solvent accessible area between the two transition states and can be fit from the slope of the unfolding arm at low concentration of denaturant. Second, the value of k₋₁ is set to be non–rate limiting (10⁵ sec⁻¹ in this case); as a result, while k₋₁ and k₂ are not the actual rate constants for the system, the ratio of the two rate constants K_TS1-TS2 will represent the nature of the system.

Hypothetical chevrons for each transition state were calculated using the following equations (Bachmann and Kiefhaber 2001; Sanchez and Kiefhaber 2003b):

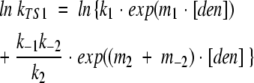(8)

(9)

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.051377105.