Mapping protein energy landscapes with amide hydrogen exchange and mass spectrometry: I. A generalized model for a two-state protein and comparison with experiment

Abstract

Protein amide hydrogen exchange (HDX) is a convoluted process, whose kinetics is determined by both dynamics of the protein and the intrinsic exchange rate of labile hydrogen atoms fully exposed to solvent. Both processes are influenced by a variety of intrinsic and extrinsic factors. A mathematical formalism initially developed to rationalize exchange kinetics of individual amide hydrogen atoms is now often used to interpret global exchange kinetics (e.g., as measured in HDX MS experiments). One particularly important advantage of HDX MS is direct visualization of various protein states by observing distinct protein ion populations with different levels of isotope labeling under conditions favoring correlated exchange (the so-called EX1 exchange mechanism). However, mildly denaturing conditions often lead to a situation where the overall HDX kinetics cannot be clearly classified as either EX1 or EX2. The goal of this work is to develop a framework for a generalized exchange model that takes into account multiple processes leading to amide hydrogen exchange, and does not require that the exchange proceed strictly via EX1 or EX2 kinetics. To achieve this goal, we use a probabilistic approach that assigns a transition probability and a residual protection to each equilibrium state of the protein. When applied to a small protein chymotrypsin inhibitor 2, the algorithm allows complex HDX patterns observed experimentally to be modeled with remarkably good fidelity. On the basis of the model we are now in a position to begin to extract quantitative dynamic information from convoluted exchange kinetics.

It has become clear in recent years that large-scale macro-molecular dynamics are an important determinant of protein function. A growing number of proteins are found to be either partially or fully unstructured under native conditions, and such flexibility (intrinsic disorder) appears to be vital for their function. Proteins that do have native folds under physiological conditions also exhibit dynamic behavior via local structural fluctuations or by sampling alternative (“higher-energy” or “activated”) conformations transiently. Such nonnative states are often functionally important despite their low Boltzmann weight (Tsai et al. 2001). Because of their transient nature, nonnative states present a great challenge vis-à-vis detection and characterization. A potent experimental tool that has been widely used to study protein dynamics is hydrogen deuterium exchange (HDX). According to a commonly accepted model of protein HDX, such measurements for amides shielded from the solvent in the native structure detect virtually no contribution from the protein in the ground state, but provide a wealth of information on transiently populated activated states with distorted structure (Englander 2000; Englander et al. 2002).

While the majority of HDX studies have employed high-resolution NMR as a means to monitor exchange kinetics, electrospray ionization mass spectrometry (ESI MS) is currently enjoying a dramatic surge in popularity in this field (Engen and Smith 2001; Kaltashov and Eyles 2002; Hoofnagle et al. 2003; Konermann and Simmons 2003). The number of applications of the HDX MS methodology to probe both architecture and dynamics of biomolecules continues to expand, catalyzed by spectacular technological improvements in “soft” ionization methods. ESI MS offers several important advantages over NMR as a means of monitoring HDX. These include tolerance to paramagnetic ligands and cofactors as well as much more forgiving molecular weight limitations, and, most important, low sample consumption and superior sensitivity, providing the ability to work at concentrations in many cases close to endogenous levels.

The mathematical formalism primarily used to describe HDX kinetics was introduced several decades ago and is based upon a simple two-state kinetic model (Hvidt and Nielsen 1966). This model is represented below in a slightly modified form (which assumes that the protein is initially deuterated and the exchange is initiated by placing it in a protiated buffer):

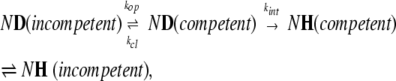(1)

where k_op and k_cl are the rate constants for the opening (unfolding) and closing (refolding) events that expose or protect a particular amide hydrogen to or from exchange with the solvent. The rate constant of intrinsic exchange of an unprotected amide hydrogen atom (from the exchange-competent state) k_int depends on both solution pH and temperature and can be estimated using short unstructured peptides (Bai et al. 1994). The ND→NH transition is essentially irreversible, as HDX experiments are carried out in significant excess (10- to 1000-fold) of exchange buffer. A general expression for the apparent (observed) exchange rate constant for a single amide within this model is given by Hvidt and Nielsen (1966):

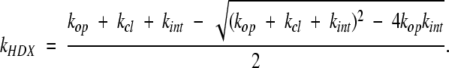(2)

In most HDX studies the exchange-incompetent state of the protein is presumed to be the native state. Since most HDX measurements are carried out under conditions that favor the native state (i.e., the effective unfolding equilibrium constant K_op = k_op / k_cl ≪ 1), the expression for k_HDX can be simplified to

(3)

The latter expression is intuitive, as it presents the exchange rate as a product of frequency of opening events (k_op) and fraction of hydrogen atoms at a particular position that undergo exchange during a single opening event (k_int / (k_cl + k_int)).The exchange-competent state is usually considered to be a nonnative structure that can be either fully unstructured (random coil) or partially unfolded (intermediate states). It can also represent a small-scale structural fluctuation within the native conformation, which exposes an otherwise protected amide hydrogen to solvent transiently, through local unfolding or structural breathing, but without unfolding the entire protein molecule or a significant segment of it (Maity et al. 2003). Sometimes such microstates are treated as substates of the exchange-incompetent conformation (Qian and Chan 1999). Transitions between different nonnative states under equilibrium conditions are usually ignored in mathematical treatments of HDX. One reason for this is that the majority of HDX measurements are carried out under native or near-native conditions. The Boltzmann weight of nonnative states for most proteins (save intrinsically unstructured ones) under these conditions is very low and the transitions between such states do not make any detectable contribution to the overall HDX kinetics.

Two exchange regimes are usually identified as limiting cases in HDX measurements, namely, EX1 (k_int ≫ k_cl) and EX2 (k_int ≪ k_cl). The ability to clearly identify the exchange regime is important, since such knowledge is crucial for correct quantitative interpretation of the results of HDX measurements (EX1 measurements provide kinetic information, while measurements under EX2 conditions yield thermodynamic information). The vast majority of HDX measurements have been carried out in the EX2 exchange regime, which is usually favored under native conditions. However, nonnative HDX is now becoming popular due to renewed interest in structure and dynamics of intermediate protein states, hence increased interest in HDX experiments carried out in the EX1 regime (Ferraro and Robertson 2004). Reliable identification of the exchange regime in HDX NMR experiments requires that a series of measurements be carried out under gradually changing conditions (e.g., pH or denaturant concentration). Invariance of the exchange rate with regards to such variation indicates an EX1 exchange regime, while a linear dependence is expected in the EX2 regime (Qian and Chan 1999). Interpretation of HDX NMR data acquired under intermediate conditions (between the two extremes) is rather difficult and may not necessarily lead to unequivocal conclusions (Kragelund et al. 1998). An important advantage offered by ESI MS is its ability to generate in many cases mechanism-specific exchange patterns. Thus, correlated exchange patterns are often observed in the EX1 regime, which in many cases allows various protein states to be detected distinctly based on the difference in their ²H content (Deng and Smith 1999; Ferraro and Robertson 2004). If, however, exchange occurs under conditions favoring the EX2 regime, direct observation of various protein states becomes impossible. Furthermore, Robertson and coworkers have demonstrated that even under EX1 exchange conditions, different protein conformers may not necessarily be detected distinctly in HDX MS experiments (Arrington et al. 1999; Arrington and Robertson 2000). Further complications arise due to a possibility of deviation from the EX1 regime, which may introduce ambiguity in interpretation of the experimental data (Arrington and Robertson 2000). No attempt has been made so far to carry out systematic HDX MS measurements under conditions favoring neither EX1 nor EX2 exchange regime (i.e., k_int ~ k_cl) and explore utility of such measurements for quantitative characterization of protein dynamics.

The goal of this work is to establish a model of protein amide HDX as a tool to aid quantitative interpretation of HDX MS data acquired within a range of conditions not limited to either EX1 or EX2 regimes. To achieve this goal, we use a probabilistic approach that assigns a transition probability and a residual protection to each equilibrium state of the protein. The initial evaluation of the model is carried out using a small model protein chymotrypsin inhibitor 2 CI2 under a range of conditions favoring different exchange mechanisms. CI2 is one of relatively few proteins that lack both kinetic and equilibrium intermediate states and conform to a classic two-state folding/unfolding scheme. The native state of CI2 comprises a single helix and a mixed parallel and antiparallel β-sheet. The structure is highly stable, with the exception of a long flexible internal loop (Itzhaki et al. 1997; Neira et al. 1997). The denatured state of the protein lacks any detectable residual structure and appears to be a relatively expanded state (Fersht 1999). Although this protein has been recently shown to be able to populate an alternative (nonnative) conformation under rather exotic conditions (Silow and Oliveberg 2003), these conditions have been avoided in the present work to insure conformity to a two-state system. Furthermore, we have previously explored (CI2) unfolding under a variety of mildly denaturing conditions (pH 3–9, methanol content 0%–80%) using a low-resolution technique based on the analysis of protein ion charge state distributions in ESI mass spectra (Mohimen et al. 2003). Only two states of the protein, assigned as native (N) and denatured (U) were detected across the entire range of conditions tested. In neutral and mildly acidic solutions, the U state becomes detectable only when the alcohol content of the solvent exceeds 40%. In the absence of alcohol, protein unfolding is not detected until the solution pH is raised above 8. Further increase of pH leads to progressively more abundant U state in solution. Presence of alcohol in a basic solution exerts some influence on the abundance of the U state, but not nearly as much as does the pH alone. When applied to CI2, the simulation algorithm allows complex HDX patterns observed experimentally under a variety of conditions to be modeled with remarkably good fidelity.

In this work we demonstrate that collective motions within the protein (e.g., cooperative large-scale conformational changes) can be observed and characterized even if the exchange does not follow the EX1 mechanism. The model also defines the limits of HDX MS measurements as far as detection and characterization of partially structured (nonnative) protein states. At the same time, the model provides a framework, which can be used to extract both kinetic and thermodynamic characteristics of various protein equilibrium states from HDX MS data, paving the way toward mapping of protein energy landscapes.

Results

Uncorrelated exchange under native conditions

HDX of CI2 under near-native conditions (10 mM ammonium acetate [pH 6.8], 33°C) is clearly uncorrelated, as suggested by the evolution of the isotopic cluster of the most abundant ion peak in the CI2 mass spectrum (Fig. 1A ▶). The same behavior was observed for other charge states (data not shown). This observation is hardly surprising, since amide exchange under these conditions is expected to occur in the EX2 regime. However, one rather unexpected feature of the observed HDX MS pattern is a nearly constant width of the isotopic cluster of CI2 ions throughout the exchange reaction. The exchange rate (change in the number of deuterium atoms retained by the protein as a function of exchange time) is measured using the apex of the isotopic cluster and appears to follow a biexponential decay (Fig. 1B ▶; Table 1). We note that HDX MS detects significantly higher initial protection compared with HDX NMR experiments carried out under similar conditions (Itzhaki et al. 1997), as several amides exchange too fast to be measured on a timescale of a typical HDX NMR experiment. A stepwise increase of the solution temperature from 8°C to 55°C clearly accelerates the exchange, while the kinetics remains biexponential (Fig. 1B ▶). As the temperature is elevated, the amplitude of the slow phase of the exchange (i.e., the number of amides whose half-life time τ exceeds 200 min) slowly decreases from ~40 to 23, followed by a complete elimination of the slow exchange phase at 60°C (Table 1).

Figure 1.

HDX MS of CI2 under near-native conditions (pH 6.8): evolution of isotopic distributions of CI2 ions (+5 charge state) at 33°C (A) and exchange kinetics at different solution temperatures (B).

Table 1.

HDX kinetics of CI2 under native conditions (pH 6.8)

		Fast exchange		Slow exchange
T, °C	kint, 103 min−1	kHDX (kF), 10−2 min−1	ΔGN*, kcal/mol	kHDX (kS), 10−3 min−1	ΔGU, kcal/mol	Average number of amides unaffected by local fluctuations
8	0.091	32	3.2	1.1	6.3	40.1
23	0.47	12	4.9	0.96	7.7	35.8
28	0.69	7.5	5.5	0.84	8.2	32.4
33	1.1	6.9	5.9	0.57	8.8	30.9
38	—	10	—	1.1	—	31.7
45	—	8.3	—	1.7	—	27.6
55	—	7.2	—	4.9	—	23.0
60	—	5.3	—	—	—	0

Apparent values of ΔG are calculated based on the assumption that the exchange follows EX2 regimen: ΔG = −RTln(k_int/k_HDX). Values of k_int are estimated based on data compiled in Bai et al. (1993, ¹⁹⁹⁴); pH values are uncorrected for temperature changes.

HDX under mildly denaturing conditions favoring EX1 mechanism: Correlated exchange

Correlated exchange can be observed by MS only if it follows EX1 exchange kinetics (k_cl ≪ k_int), a situation that is achieved by either increasing the pH of the exchange buffer or by adding a denaturant to the protein solution. The former increases the intrinsic exchange rate (in proportion to OH^-concentration), while the latter destabilizes the protein and usually decreases refolding rate k_cl. Unfortunately, most strong denaturants (e.g., urea, guanidinium chloride) have a detrimental effect on the quality of ESI measurements. To avoid this problem, we used mild chaotropes (such as methanol) and elevated pH to achieve conditions favoring the EX1 exchange mechanism. While a significant proportion of CI2 becomes unfolded at neutral pH when alcohol concentration exceeds 50% (Mohimen et al. 2003), the exchange remains uncorrelated (data not shown), suggesting that the criterion for EX1 exchange kinetics (k_cl ≪ k_int) is not met. In order to observe correlated exchange of CI2 backbone amides, the solution pH has to be raised above 10, while keeping the methanol content above 50%. HDX MS exchange patterns acquired under these conditions (pH 11, 60% methanol) are shown in Figure 2 ▶, A and B. The isotopic clusters of CI2 ions are clearly bimodal, indicating that the HDX reactions within the unfolded state are correlated (and, therefore, must follow the EX1 mechanism). The early appearance and gradual accumulation of protein ion species whose ¹H content is the same as that of the exchange buffer suggests that each global unfolding event leads to complete amide exchange within the protein. Accumulation of this fully exchanged state follows simple first-order kinetics (Fig. 2C ▶). In addition to this, some exchange also occurs within the folded protein species, as evidenced by a gradual mass shift of the isotopic subcluster corresponding to the protein species with significant deuterium content. Kinetics of this uncorrelated exchange process appears to be pseudo-first order, fitting a simple single-exponential decay (Fig. 2D ▶).

Figure 2.

HDX MS of CI2 under denaturing conditions (pH 11, 60% methanol): evolution of isotopic distributions of CI2 ions (+5 charge state) at 8°C (A) and 35°C (B); kinetics of the N→U transition deduced from the correlated component of the global exchange pattern at different temperatures (C); and kinetics of uncorrelated exchange component caused by local fluctuations within the native state at different temperatures (D). The inset on panel B illustrates resolution of the isobaric protein ions corresponding to an ²H-rich, ²³Na-free protein species (○) and an ²H-depleted ²³Na-adduct species (▾). The latter species has exactly the same isotopic makeup as an ionic species whose peak is marked with an open triangle in the full spectrum, apart from the ¹H/²³Na substitution.

One potential complication in interpreting the data presented in Figure 2 ▶ and extracting quantitative information on HDX kinetics is the presence of sodium adducts of CI2 ions in the spectra.

For example, replacement of a proton with Na within a multiply charged CI2 ion leads to an apparent mass increase of 22 u (or, more precisely, 21.982 u, the mass difference between ²³Na and ¹H). Such adduct ions peaks usually do not interfere with ordinary mass analysis (when the width of the isotopic cluster is <22 u, as is the case in the spectra shown as bottom traces in Fig. 2A,B ▶). However, they may present a serious problem if a protein ion cluster becomes extended and/or bimodal in the course of HDX measurements. This problem has been circumvented in the present work using the high resolving power of an FT ICR mass spectrometer. ²³Na has a negative mass defect, while that of ²H is positive (deuterium mass is 2.014 u). The resulting difference in the exact masses of the isobaric ions, namely, a deuterium-free [CI2+5H⁺+Na⁺] ion and a fully protonated [CI2+6H⁺] ion carrying an extra 22 deuterium atoms is very small (only 0.002% of the total ion mass). Nonetheless, the superior resolving power of FT ICR MS allows these isobaric species to be detected as distinct peaks (see boxed inset in Fig. 2B ▶).

HDX under mildly denaturing conditions not favoring EX1 mechanism: Semicorrelated exchange

One of the goals of the present work was to characterize HDX patterns under “intermediate exchange conditions,” when protein refolding and intrinsic exchange occur on a similar timescale (i.e., neither EX1 nor EX2 exchange mechanism is strictly applicable). In order to observe such an exchange pattern, extensive HDX measurements were carried out over a broad range of conditions, from pH 7, 60% methanol (where exchange clearly follows the EX2 mechanism) to pH 11, 60% methanol (where the correlated component of the exchange provides a clear indication of an EX1 mechanism). A very interesting exchange pattern was observed in the pH range 9–10, 60% methanol (Fig. 3A ▶). Some of the features of this exchange pattern are very similar to those of correlated exchange discussed earlier. Specifically, we note a bimodal shape of the isotopic distributions throughout a significant period of the exchange reaction. The relative abundance of the more protected (higher m/z) subcluster is progressively diminished, a process that apparently follows first-order kinetics (Fig. 3C ▶). Although the observed bimodal shape of the isotopic clusters of CI2 ions and their evolution strongly suggest the presence of two protein states (as revealed under correlated exchange conditions), no fully exchanged protein species are detected during the initial measurements. Instead, the lower m/z isotopic cluster initially retains a small but detectable amount of its ²H label and loses it gradually as the exchange reaction progresses. This is radically different from the exchange behavior observed under EX1 conditions, where the low-m/z isotopic cluster corresponds to a fully exchanged species as soon as it becomes visible in the mass spectrum (Fig. 2A ▶). The drift rate for the less protected (lower m/z) cluster under such intermediate conditions depends on temperature (Fig. 3D ▶). Such exchange behavior of a two-state protein (when the two states can be easily distinguished from one another based on the difference in ²H contents, although the fully unfolded state exhibits some apparent residual protection) will be termed “semicorrelated exchange” in the following discussion.

Figure 3.

HDX MS of CI2 under mildly denaturing conditions (pH 10, 70% methanol): evolution of isotopic distributions of CI2 ions (+5 charge state) at 8°C (A); kinetics of the N→U transition deduced from the semi-correlated component of the global exchange pattern at different temperatures (B); kinetics of uncorrelated exchange component caused by local fluctuations within the native state at different temperatures (C); and gradual loss of apparent residual protection within the protein species with low ²H content at different temperatures (D).

Discussion

Protein dynamics in a simplistic two-state model and observed HDX patterns

All HDX MS measurements presented in this work were carried out within pH range 7–11 and alcohol content of protein solution not exceeding 70%. We have previously demonstrated that under these conditions CI2 populates only two states (native, N, and unfolded, U) and the Boltzmann weight of the native state is significantly higher (Mohimen et al. 2003). Therefore, the exchange kinetics of individual amides can be adequately described using expression 3. We note, however, that the analysis of protein conformational dynamics based on monitoring charge state distributions is a low-resolution technique, which is insensitive to small-scale conformational changes that do not lead to significant alteration of the solvent-exposed protein surface.

In the following discussion, we will adopt a continuous Brownian-dynamic view of protein conformational kinetics (Qian 2002). In this case protein dynamics can be visualized as particle movement along the protein free energy surface, which comprises two potential wells (one for the native state of the protein, N, and another representing an unstructured state, U). If the system were noise-free, the particle would finally settle in one of the potential wells, depending on the initial conditions of the launch. However, coupling the particle to a thermal bath results in random excitation, leading to occasional hopping between the two basins of attraction. The frequency of traversing the boundary between the two potential wells in such a system will depend upon the ratio of the barrier height-to-noise level (or activation energy-to-temperature in thermally equilibrated systems). A simplistic two-dimensional representation of such energy surfaces is shown in Figure 4 ▶, where a narrow potential well corresponds to a native protein state, and a diffuse shallow well corresponds to the unfolded protein. We will initially assume that no exchange can occur within the N state, and there is no protection in the U state. While the energy difference between these two minima determines the relative occupancies of the two states, it is the height of the reverse activation energy barrier ΔG^‡_U→N that will determine the mechanism of the exchange. If the U basin of attraction is separated from the global minimum (exchange-incompetent N state) by a very low barrier ΔG^‡_U→N(Fig. 4A ▶), any excursion from N to U will be very short-lived. If this residence time is short on the timescale of the intrinsic exchange (i.e., 1/k_cl ≪ 1/k_int, which corresponds to U ≪ 1 defined in Materials and Methods), only a condition P_ex a small fraction of amides will undergo exchange during each opening event. If, on the other hand, the reverse activation energy barrier ΔG^‡_U→N is sufficiently high to ensure efficient trapping of the protein in the U state (Fig. 4B ▶), another extreme situation can be realized. The protein residence time in the U state would be very long on the time-scale of intrinsic exchange (P_ex^U ~ 1), so that almost any protein excursion from the N state to the U state would last long enough for all amides to be exchanged prior to protein refolding.

Figure 4.

A schematic representation of potential energy diagrams for a simplistic model of a two-state protein under conditions favoring EX2 (A) and EX1 (B) exchange regimes. Protein dynamics is visualized as Brownian motion on the energy surface. Projections of trajectories of Brownian motion are shown at the bottom of each diagram (there were two escapes from the global minimum during the time of each simulation).

Simulation of HDX patterns of a two-state protein using this simplistic model (see Materials and Methods for more detail) are presented in Figures 6A ▶ and 7A ▶ (see below) and provide idealized representations of canonical exchange patterns under EX2 and EX1 regimes (when P_ex^U≪ 1 and P_ex^U≅1, respectively). In one extreme (EX2 regime), the isotopic distribution shifts over time, following a simple mono-exponential decay kinetics (Fig. 6A ▶). The width of the isotopic cluster increases progressively and reaches its maximum when exchange is halfway to completion. The exchange rate is determined by the rate of mass change of the protein molecule. Another extreme (EX1) gives rise to “split” isotopic distributions, where one of the clusters represents full retention of labile deuterium atoms, and another shows full replacement of deuterons with protons (Fig. 7A ▶). The exchange rate is determined by the rate of change in relative abundance of either one of the two clusters within the isotopic distribution.

Figure 6.

Simulated HDX patterns for “simplistic” (A) and “realistic” (B) two-state systems carried out under the conditions mimicking EX2 exchange regime (P_U = 0.0005 and (P_ex^U = 0.05). Local structural fluctuations are totally ignored in A and accounted for in B using P_ex^N = 0.001. (48 out of 54 amides are assumed to be prone to local structural fluctuations.) Panel C shows time evolution of the model isotopic clusters during simulated HDX. Filled circles indicate the positions of the centroids of the simulated isotopic clusters in panel B plotted as a function of dimensionless time t* (see Materials and Methods). Error bars indicate uncertainty due to finite width of isotopic distribution caused by natural isotopic distribution of non-H elements expected for a typical protein of this size. A solid curve is obtained by substituting the numerical values used in the simulation to equation 7.

Figure 7.

Simulated HDX patterns for “simplistic” (A) and “realistic” (B) two-state systems carried out under the conditions mimicking EX1 exchange regime (P_U = 0.0005 and P_ex^U = 0.95). Local structural fluctuations are totally ignored in A and accounted for in B using P_ex^N = 0.001 (48 out of 54 amides are assumed to be prone to local structural fluctuations). Panel C shows time dependence of the relative abundance of the ²H-depleted species (○) and ²H-rich species (○). A solid gray curve is obtained by substituting the numerical values used in the simulation to equation 8. Panel D shows time dependence of the shift of the centroid of the simulated isotopic cluster in panel B (²H-rich species). A solid curve is obtained by substituting the numerical values used in the simulation to equation 9, assuming k* = k_intK_fluct.

Although the simulated HDX patterns shown Figures 6A ▶ and 7A ▶ bear certain qualitative resemblance to the experimentally measured HDX profiles of CI2 under near-native and mildly denaturing conditions (see Figs. 1A ▶, 2A ▶), they miss several key features. Specifically, they fail to account for the biexponential exchange kinetics and the lack of a significant broadening of the isotopic cluster under EX2 exchange conditions (Fig. 1A ▶), as well as the presence of an uncorrelated exchange component in the HDX pattern acquired under EX1 conditions (Fig. 2A,B ▶).

Protein dynamics in a modified two-state model: Local fluctuations and their influence on the observed HDX patterns under near-native conditions

The most serious deficiency of the simplistic two-state model discussed above is the assumption that the native state of the protein is static and thus that exchange can occur only from the denatured state. It is now commonly accepted that the native conformation of a protein in solution can hardly be viewed as a “fixed” structure, but rather as an ensemble of structurally similar microstates. Although the N ⇌ U transitions discussed above are important contributors to protein dynamics, they are presumably very rare (particularly under native conditions). Much more frequent dynamic events are the so-called “local structural fluctuations,” processes that result in transient and localized amide deprotection that appears to be uncooperative and denaturant independent (Milne et al. 1998). Amides exhibiting fast, denaturant-independent exchange usually reside at or near the protein surface, consistent with the notion of exchange proceeding via local fluctuation, as opposed to global unfolding, although a solvent-penetration model can also be invoked to explain this behavior (Miller and Dill 1995).

Our view of local fluctuations invokes the notion of an activated state N*, which is a collection of microstates, each having a structure or, more precisely, amide protection pattern identical to that of the native conformation with the exception of one (or few) amides at the protein surface. The reverse activation energy barrier separating this activated state from the ground state ΔG^‡_N*→N is very close to zero, so that any transition from N to N* would be very short-lived (Fig. 5A ▶). However, the energy of this activated stateΔ G_N* is significantly lower than that for the N→U transition, so that the fluctuations occur much more frequently than global unfolding events. Finally, local structural fluctuations in our model do not affect all backbone amides; however, all amides that are prone to exchange through local fluctuations can also exchange through global unfolding. This is perhaps the most significant difference between our model and that used by Robertson and coworkers to simulate dynamics of a small peptide OMTKY3 (Arrington and Robertson 2000). All backbone amides in that model had been divided into two “nonoverlapping” groups, namely, those exchanging through uncorrelated openings (in our interpretation, local structural fluctuations) and those undergoing exchange through correlated openings (global unfolding in our model). One of these groups is a subset of another in our model of hydrogen exchange, i.e., all amides that can exchange through local fluctuations also have a chance to be exchanged through much less frequent global unfolding events.

Figure 5.

Two alternative representations of microstates corresponding to local structural fluctuations within the native state, in which all structures are viewed as microstates comprising one activated state N* (A), and each such structure is viewed as a separate state, separated from others by significant energy barriers (B).

The presence of two different possible exchange processes gives rise to biexponential kinetics of the simulated HDX (Fig. 6B ▶), with the fast phase corresponding to exchange from the N* state (i.e., via local fluctuations) and the slow phase corresponding to exchange from the U state (i.e., through global unfolding). Because the exchange now proceeds essentially through two steps, broadening of the isotopic cluster becomes much less significant (Fig. 6 ▶, cf. A and B). The amplitude of the fast exchange phase gives the number of amides prone to structural fluctuations, while the two exponents immediately provide the rate constants of the two exchange processes. Since exchange follows EX2 kinetics, the measured rate constants can be used to calculate thermodynamic parameters. The assumption commonly made is that the two phases of exchange can be treated separately, as if they were affecting two independent sets of amides. In this approximation, the average number of retained ²H atoms as a function of the exchange time t is:

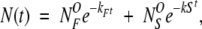(4)

where k_F and k_S are the rates of the fast and slow modes of exchange, while N_F^O and N_S^O represent the numbers of amides that can and cannot be exchanged through local fluctuations, respectively. Although this approximation is reasonable when the rate difference between the two processes is large (k_F ≫ k_S), a more rigorous treatment of the exchange kinetics should take into account the possibility of exchange of amides from the N_F^O group not only through local fluctuations, but also through global unfolding events. In this case, the total rate of depletion of ²H atoms would be determined as:

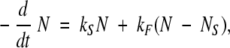(5)

assuming that all ²H atoms can be exchanged through rare global unfolding events (given enough time, of course), while more frequent local fluctuations can result in exchange of a smaller number of amides (N - N_S). The number of remaining ²H atoms that can be exchanged only through global unfolding N_S in equation 5 is not a fixed number, but changes according to

(6)

Combination of equation 6 with equation 5 allows the number of remaining ²H atoms to be expressed as a function of exchange time:

(7)

Although the difference between equations 4 and 7 is fairly insignificant under near-native conditions (since k_F ≫ k_S), this can be easily changed by shifting the N ⇌U equilibrium toward the unfolded state of the protein (e.g., using mild chaotropes). However, as long as the exchange follows the EX2 regime, thermodynamic parameters of both local fluctuations and global unfolding can be extracted from experimental data using equation 7, provided a reasonable estimate of k_int is available. Table 1 summarizes the structural and thermodynamic parameters of local fluctuations and global unfolding of CI2 under near-native conditions, which were calculated based on the experimental data presented in Figure 1 ▶ and estimations of k_int compiled by Dempsey (2001). One rather interesting conclusion from the analysis of the HDX kinetics of CI2 under near-native conditions is the gradual decrease of the number of amides inaccessible to solvent through local structural fluctuations in the temperature range 8°–55°C, followed by an apparent merging of the two exchange phases at 60°C (20°C below the midpoint of CI2 thermal denaturation [Jackson and Fersht 1991]). Such behavior may be interpreted as a result of increased accessibility of higher-energy activated states of the protein due to increased level of thermal activation.

Protein dynamics under nonnative conditions: Competition between efficient global unfolding and local fluctuations gives rise to convoluted HDX patterns with both correlated and uncorrelated components

Incorporating local fluctuations in HDX simulations under conditions favoring complete exchange during each unfolding event (i.e., P^U_ex ≅ 1) leads to generation of an exchange pattern that is remarkably similar to the one observed experimentally (cf. Figs. 2A,B ▶ and 7B ▶). Each global unfolding event still leads to full exchange within a protein molecule, as the reverse activation energy barrier ΔG^‡_U→N is high enough to insure efficient trapping of the protein in the unfolded state U. This leads to a gradual accumulation of protein species whose isotopic distribution reveals negligible ²H content (Fig. 7C ▶). As expected, this process clearly follows first-order kinetics:

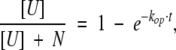(8)

suggesting that the absolute rates of global unfolding can be easily extracted from the experimental data. Furthermore, since the unfolding process is accompanied by a significant change of the solvent-accessible surface area, the two equilibrium states of CI2 can be easily distinguished in ESI MS based on the difference of the number of charges accommodated by each species upon transition from solution to the gas phase (Mohimen et al. 2003). Therefore, analysis of protein ion charge state distributions in ESI mass spectra can provide information on the relative occupancies of N and U states, thus yielding a value for the equilibrium constant of the unfolding process. As a result, the combination of HDX MS and analysis of charge state distributions can characterize global unfolding under these conditions both kinetically and thermodynamically.

In addition to the correlated exchange caused by global unfolding events, local structural fluctuations give rise to an uncorrelated exchange component within the overall HDX pattern. This is seen as a gradual shift of the isotopic cluster corresponding to a diminishing population of protein molecules that never visited the unfolded state. The kinetics of this process can be characterized by tracking the position of the centroid of this isotopic cluster (Fig. 7D ▶):

(9)

The actual meaning of the apparent rate constant for this uncorrelated exchange cannot be known a priori, because the uncorrelated character of this process does not necessarily mean the exchange proceeds via an EX2 mechanism. Indeed, if the local structural fluctuations leading to deprotection of each of the N_F^O amides are independent of each other (currently a commonly accepted view), then exchange will be uncorrelated even under EX1 conditions. In this case the measured rate constant k* will actually represent an average frequency of local fluctuations, i.e., k* = k_N→N*. If, however, exchange occurs in the EX2 regime, the measured rate constant k* would represent the thermodynamics, rather than kinetics, of local structural fluctuations. Unfortunately, in this case HDX MS measurements alone cannot provide a definitive conclusion as to what the exchange regime for local fluctuations is. Some circumstantial evidence suggests that the kinetics of the uncorrelated component of exchange does occur in the EX1 mode (when the experimental data presented in Figure 2 ▶ have been processed assuming that the exchange kinetics is EX2, the resulting ΔG^‡_N*→N values were found to be unrealistically high under these denaturing conditions). Alteration of the solvent-accessible surface area during each local fluctuation is too small to manifest itself through any detectable changes of the protein ion charge state distribution in ESI mass spectra. As a result, it is impossible to obtain an estimate of the relative abundance of native protein molecules affected by structural fluctuations.

HDX between the EX1 and EX2 extremes: Mixed exchange kinetics give rise to semi-correlated exchange pattern

One of the major motivations of this work was to characterize the HDX MS pattern of a two-state protein under intermediate conditions that favor neither EX1 nor EX2 exchange regime. Furthermore, our ultimate goal was to examine the possibility of extracting both kinetic and thermodynamic information under such conditions, which are usually avoided in HDX studies of protein dynamics.

To explore the HDX patterns in a two-state model system in this intermediate exchange regime (for the lack of a better term we will refer to it as EXX), we carried out a series of simulations in a wide range between the EX1 and EX2 extremes (P^U_ex ranging from 0.1 to 0.9). In addition to global unfolding, the simulations once again accounted for local structural fluctuations. The results of such simulations revealed an interesting exchange pattern (an example of which is shown on Fig. 8A ▶), which is remarkably similar to the HDX MS patterns acquired experimentally at pH 10, 70% methanol (Fig. 3A ▶). The isotopic distribution still has a bimodal appearance (just as under the EX1 conditions considered in the previous section), although now both clusters drift toward lower m/z. Therefore, three equations are now required in order to adequately describe the HDX kinetics in the EXX regime. Drift of the more protected cluster is still caused by local structural fluctuations within the native state and can be adequately described by equation 9 (the actual physical meaning of the apparent rate constant k* still cannot be deduced from these measurements alone). The rate of accumulation of protein species with low (but not negligible) ²H content can be adequately described by 8, allowing the absolute value of the rate of global unfolding k_op be extracted from the experimental data, even though exchange does not follow the canonical EX1 regime.

Figure 8.

Simulated HDX pattern for a “realistic” (A) two-state system carried out under the conditions corresponding to EXX exchange regime (P_U = 0.0005 and P_ex^U= 0.60). Local structural fluctuations are accounted for by using P_ex^N = 0.001 (48 out of 54 amides are assumed to be prone to local structural fluctuations). Panel B shows time dependence of the shift of the centroid of the simulated isotopic cluster in panel A (²H-rich species). A solid curve is obtained by substituting the numerical values used in the simulation to equation 9, assuming k* = k_intK_fluct. Panel C shows time dependence of the relative abundance of the ²H-depleted species (○) and ²H-rich species (○); a solid gray curve is obtained by substituting the numerical values used in the simulation to equation 8. Panel D shows time dependence of the shift of the centroid of the simulated isotopic cluster in panel B (for species with low ²H content); a solid curve is obtained by substituting the numerical values used in the simulation to equation 10, assuming k* = k_intK_fluct.

The gradual shift of the isotopic cluster with low ²H content is a new phenomenon and tracking this mass change requires a better understanding of what is causing it. It is intuitively clear that each global unfolding event in the EXX regime results in significant but incomplete reduction of the ²H content of a protein molecule. This results in the bimodal character of the isotopic distribution (Fig. 8A ▶). The initial separation of the two isotopic clusters depends on the length of time spent in the unfolded state compared with a characteristic time of amide exchange (k_int / (k_cl + k_int), which corresponds to a parameter P^U_ex in our simulations). Two processes will determine evolution of the isotopic cluster at lower m/z. First, protein molecules with low ²H content continue to undergo exchange through both local fluctuations and global unfolding. Second, the pool of the protein species in the low m/z cluster is continuously increased by protein species undergoing global unfolding. The isotopic content of such species will be determined by the ²H content of the natively folded proteins prior to exchange (which is gradually diminished due to local structural fluctuations) and the fraction of amides exchanged during a single unfolding event, k_int / (k_cl + k_int). This latter process is likely to be a major determinant of the shift of the lower m/z isotopic cluster during the initial stage of exchange (when relative abundance of the protein species that never visited the unfolded state is very high). Kinetics of this process (characterized by tracking the position of a centroid of the isotopic cluster at lower m/z) will actually depend on the kinetics of local fluctuations:

(10)

where k* is the apparent exchange rate due to structural fluctuations within the native state of the protein. As exchange progresses and the pool of protein molecules that never sampled an unfolded state is depleted, the shift rate of the isotopic cluster will begin to deviate from 10.

Generalized exchange model and interpretation of HDX MS data

The most important assumption of the proposed exchange model in a two-state protein is that there is a well-defined subgroup of backbone amides, each of which can be exchanged independently from the rest via frequent opening events. The rates of such processes are assumed to be identical for all amides within this subgroup. The rest of the backbone amides are assumed to be able to exchange only through global opening events, in which all labile hydrogen atoms lose protection simultaneously (i.e., there is no residual structure or structural preferences in the unfolded state of the protein). Despite the simplicity of this model, it has been able to account for all complex features observed in the HDX MS patterns acquired over a wide range of conditions. Furthermore, the analysis of simulated exchange profiles suggests that valuable kinetic and thermodynamic characteristics of protein dynamics can be extracted from the experimental data not only under those conditions that are employed most commonly in HDX experiments (i.e., EX1 and EX2 limits), but also under intermediate conditions (EXX). Despite their complex appearance, the semi-correlated HDX MS patterns of a small two-state protein (CI2) acquired in the EXX exchange regime can be interpreted in a rather straightforward manner and yield valuable information on both kinetic and thermodynamic aspects of large-scale protein dynamics. While the kinetics of global unfolding (k_op) can be deduced directly from the HDX MS data in the EXX regime, thermodynamic calculations require that the rates of intrinsic exchange be known beforehand, a task that can be carried out by measuring exchange rates of model unstructured peptides under the conditions of interest. Accomplishment of this task would, in theory, allow the unfolding equilibrium constants in the denaturing environment to be calculated based solely on HDX MS measurements and compared with the values deduced from the analysis of protein ion charge state distributions in ESI mass spectra. Such independent verification will be invaluable for further refining of HDX MS as a technique capable of probing the intimate details of protein dynamics under a variety of conditions.

The model presented in this paper highlights a fundamental problem of HDX MS measurements, namely, its inability to confidently assign a physical meaning to the apparent rate constant for the exchange component caused by small-scale uncorrelated events under mildly denaturing conditions. Finally, it must be mentioned that two-state proteins are relatively rare in nature, and the majority of proteins have at least one intermediate that can be sampled kinetically during refolding or else populated under mildly denaturing conditions. Presence of such intermediate state(s) whose degree of amide protection is different from both native and fully unfolded state of the protein certainly introduces further complications into interpretation of HDX MS data. We are now working toward extending the model presented in this paper to accommodate such intermediate states.

Materials and methods

Materials

Barley CI2 was a generous gift from Dr. Sophie E. Jackson (Cambridge University) and was used without further purification. Deuterium oxide (99% ²H) and d₄-acetic acid were purchased from Cambride Isotope Laboratories. All other chemicals were of analytical grade or higher.

HDX MS

HDX MS measurements were performed on an Apex III (Bruker Daltonics, Inc.) FT ICR mass spectrometer equipped with a standard ESI source and 4.7 T magnet. All proteins were fully deuterated prior to HDX MS experiments by repeated dissolution in ²H₂O/C²H₃CO₂ ²H followed by lyophilization. A stock solution of a deuterated protein was ~3 mg/mL in ²H₂O (the “completeness” of deuteration was verified with MS measurements). HDX was initiated by diluting an aliquot of the stock solution in 10 mM CH₃CO₂NH₄/H₂O (1:50, v:v). The pH of the exchange solution was adjusted to the desired level with CH₃CO₂H or NH₄OH and methanol was added when necessary. This solution was continuously infused into the ESI source at a 2 μL/min flow rate. Each spectrum was an average of four scans (acquisition time 20 sec). All spectra were acquired in broad-band mode (mass resolution 65,000–115,000).

HDX: Simulations

The simplest model of HDX within a two-state system extends the kinetic model of equation 1 to the entire protein. The native state N is treated as an exchange-incompetent state, while any transition to the denatured state U (treated as an exchange-competent state) leads to a total loss of protection. An exchange reaction for any amide hydrogen atom in this state is characterized by a finite rate constant k_int. All amide hydrogen atoms are assumed to be identical (as far as exchange behavior) in the open state and exchange independently of each other.

To define a timescale for HDX simulations, we will use dimensionless time t* = t/τ instead of physical time t. It is convenient to define a simulation step as time increment τ = 1 / (k_cl + k_op). The probability that a protein molecule will sample the exchange-competent state U during time interval τ in this model will be:

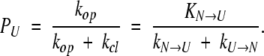(11)

Under near-native or mildly denaturing conditions k_U→N≫ k_N→U, and so P_U can be approximated with the equilibrium constant for the unfolding–refolding reaction.

We will assume that the protein is fully deuterated prior to exchange, i.e., all N backbone amide hydrogen atoms have been substituted with deuterium. This will result in a mass increase of the protein (over the unlabeled one) by N nominal mass units (or, more precisely, by 1.0063•N u). We will present the progress of exchange on a scale where the zero-point of the abscissa corresponds to the monoisotopic peak of the protein (i.e., ¹²C₃₃₀¹⁴N₈₇¹⁶O₉₄³²S₂¹H₅₄₉ for CI2). Point N on the same axis represents a fully deuterated species having the same isotope composition for C, N, O, and S. The ordinate will, of course, represent the relative abundance of each species, so that I(n, t*) will be an abundance of protein molecules retaining n deuterium atoms at time t*. Although the calculations will be carried out for a mono-isotopic peak, the output will be adjusted to account for the natural isotopic distribution of C, N, O, and S. Since the protein is initially fully deuterated, we can represent its isotope distribution at time t* = 0 as

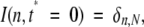(12)

where δ_n,N is a familiar Kronecker symbol (δ_n,N = 1 if n = N, and δ_n,N = 0 if n ≠ N). At time t* = 1 this peak will be transformed into a distribution

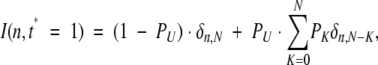(13)

the left-hand side of which represents the fraction of protein molecules that remained in the native (exchange-incompetent) conformation during this time interval. The right-hand side represents the fraction of protein molecules that did sample the unfolded (exchange-competent) state. P_K is the probability of exchanging K (and only K) of N possible amides during a single opening event. Once the protein is in the exchange-competent state U, the probability of exchange for each single amide will be determined by a rate competition between the intrinsic exchange and the closing (transition to an “exchange-incompetent” state N) rates:

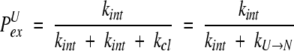(14)

The probability that J and only J amides (out of N absolutely identical ones) will exchange prior to the protein’s transition to an exchange-incompetent state will be given by a binomial distribution

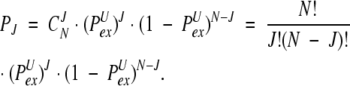(15)

Combining 13 and 15, one generates an “image” for the single initial “fully deuterated” peak 12:

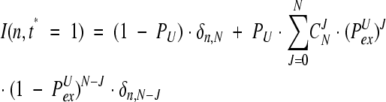(16)

HDX during the next time increment τ will produce images for each peak in distribution 16, summation of all these images to give I(n, t* = 2). This process is then cycled, so that an image of each peak I(M, t* = X) is calculated as

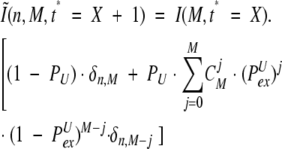(17)

Isotope distribution at time t* = X would then be calculated simply as

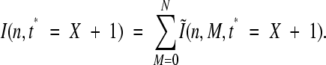(18)

The simplistic two-state model discussed above assigns zero conformational freedom for the native state N and unlimited uniform conformational freedom for the globally unfolded state U. To allow some conformational freedom within the native state N, we will consider an activated state N* whose structure and energetics are defined as follows. We will assume N* to be a heterogeneous state comprising a large number of equienergetic structures, with a total number of amides exchangeable from N* being L. Free energy of this state is significantly lower that that of the globally unfolded state (i.e., ΔG_U> ΔG_N* > ΔG_N), while the reverse activation energy barrier ΔG^‡_N*→N is zero or very close to zero. The former feature insures that N* is sampled by a protein molecule much more often than the globally unfolded state. The latter feature insures that such excursions are very short (e.g., these states are transient). Therefore, even though N* is allowed to have significant conformational freedom (L exchangeable amides), only very few exchange events will occur from N* during its lifetime. As a result, the N ⇌N* transitions will have all characteristics of local structural fluctuations, despite the fact that N* is formally introduced as a third state of the protein with limited exchange competence.

Strictly speaking, HDX occurring from the N* state can be explicitly described using two parameters, P_N* (the probability that a protein molecule samples the N* state during time interval τ) and P_ex^N*, probability of exchange of any single amide (from the pool of L identical ones) during the lifetime of N*:

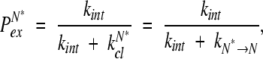(19)

where k_cl^N* is the rate constant for the N*→N transition. This system can be simplified by merging two states, N and N*. This can be done by assigning limited exchange competence to the native state N. The apparent loss of the “forward” activation energy barrier during structural fluctuation can be accounted for by using P_ex^N (probability of exchange of any single amide from the pool of L identical ones during time interval τ), which includes implicitly both P_N* and P_ex^N*:

(20)

Equation 8 can now be easily extended to include exchange of L amides via local fluctuations as well:

(21)

if M > N−L; and

(22)

if M ≤ N - L. The “1 - P_U” terms in 21, 22 describe exchange within the native state, while the “P_U” terms represent exchange from the “open” state. The extent of the former is limited (L < N), and once all L amides accessible from the N state have been exchanged, the HDX kinetics is determined by the global unfolding events.

Such presentation of local fluctuations differs from the traditional view, which assumes that every local fluctuation leads to a unique conformation (i.e., such local minima are separated from one another by significant barriers, so that these microstates cannot be grouped together). The reverse activation energy barriers separating each of these states from the exchange-incompetent state may also be significant (in which case the exchange will proceed through an EX1 mechanism). It is easy to show, however, that the HDX patterns produced by the two systems would be identical. Indeed, let us assume that protein states N_i^* (1 ≤ i ≤ L) represent conformations that are identical to the native (exchange-incompetent) state N with the exception of one amide at position i. Let us also assume that these states are iso-energetic and each of them is separated from “N proper” by an activation energy barrier of a uniform height, such that none of these states is sampled more than once during the time interval τ (in other words, k_U→N> k _Ni^*_→N). We can now introduce P_{N→ Ni}^*, the probability of sampling N_i^* during time interval τ. We will assume that P_Ni^*_{→ Nj}^* (the probability of transition from N_i^* and N_j^* during lifetime of N_i^*) is negligible compared with P_{N→ Ni}^*. In other words, all local fluctuations are independent and one fluctuation does not trigger another. The probability of exchange of the amide at position “j” in the N_i^* state of the protein would be

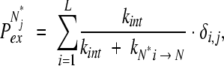(23)

where the “closing” rate will be determined by the height of the reverse activation energy barrier separating N_i^* from N. The probability that the j^th amide will exchange during time interval τ will be

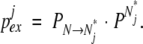(24)

Since all parameters of the N_i^* states are equivalent (except for the identity of the deprotected amide), all p_ex^j will be equal and we can use a single parameter P_ex^*. In this case, the probability that J and only J amides (out of pool of L) will exchange during time interval τ via local fluctuations will be

(25)

meaning that the mathematical expression for HDX kinetics will be the same as that defined in equations 20–22. An important practical implication is that even if the protein is trapped in the activated state for an extended period of time (i.e., exchange kinetics for each individual amide is governed by the EX1 mechanism), the overall appearance of the HDX MS pattern will be indistinguishable from that modeled for local fluctuations obeying the EX2 mechanism.

All calculations were carried out using FORTRAN90. Complete listings of the programs are available upon request.

Abbreviations

• CI2, chymotrypsin inhibitor 2

• ESI, electrospray ionization

• EX1, exchange regime 1

• EX2, exchange regime 2

• EXX, intermediate exchange regime

• HDX, hydrogen/deuterium exchange

• MS, mass spectrometry

• N, native state

• U, unfolded state

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.041001705.