Hippocampal mechanisms for the context-dependent retrieval of episodes

Abstract

Behaviors ranging from delivering newspapers to waiting tables depend on remembering previous episodes to avoid incorrect repetition. Physiologically, this requires mechanisms for long-term storage and selective retrieval of episodes based on time of occurrence, despite variable intervals and similarity of events in a familiar environment. Here, this process has been modeled based on physiological properties of the hippocampal formation, including mechanisms for sustained activity in entorhinal cortex and theta rhythm oscillations in hippocampal subregions. The model simulates the context-sensitive firing properties of hippocampal neurons including trial specific firing during spatial alternation and trial by trial changes in theta phase precession on a linear track. This activity is used to guide behavior, and lesions of the hippocampal network impair memory-guided behavior. The model links data at the cellular level to behavior at the systems level, describing a physiologically plausible mechanism for the brain to recall a given episode which occurred at a specific place and time.

A waiter only takes orders once from each customer at each mealtime in a restaurant. Similarly, a foraging rat should avoid immediate return to a food cache where it just ate all the food. The ability to avoid repeating a completed behavior in a highly familiar environment depends on the ability to selectively retrieve recent episodes based on temporal context (e.g. in order to remember which customers or garbage cans were visited in a given time period).

The context-sensitive properties of the spiking activity in the hippocampus may provide physiological mechanisms for this process. Some hippocampal neurons (“splitter cells” or “episodic cells”) fire selectively dependent on the context of a specific recent response or future goal (Wood et al., 2000; Frank et al., 2000; Ferbinteanu and Shapiro, 2003). For example, during performance of a spatial alternation task, many hippocampal pyramidal neurons fire selectively after right turn or left turn trials, even though the rat is running in the same direction through the same location on the stem of the maze on both types of trials, as shown in Figure 1 (Wood et al., 2000). The model presented here shows how this activity may depend upon selective retrieval of prior episodes of behavior.

Figure 1.

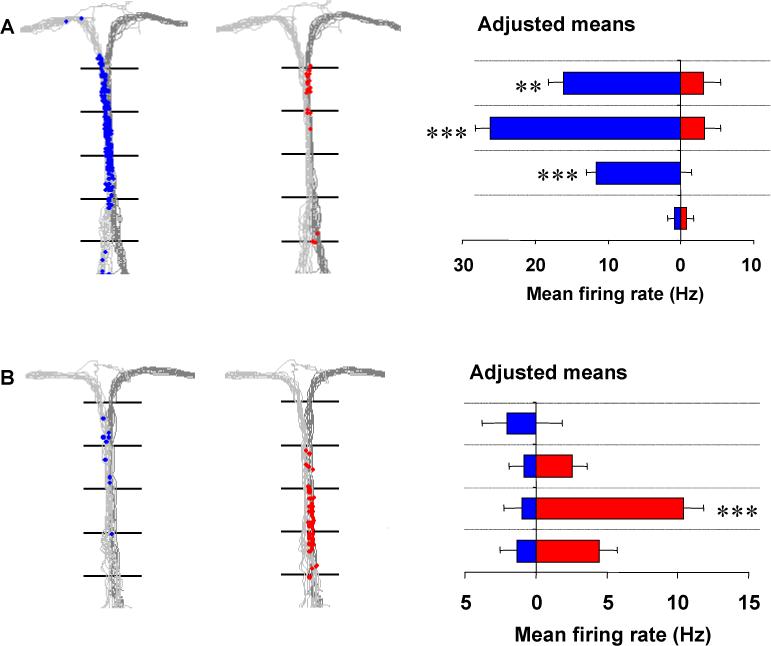
Examples of hippocampal “splitter” cells that fire when the rat is traversing the central stem of a T-maze while performing a spatial alternation task. On the left and middle panels of each example, the paths taken by the animals are plotted in light gray: (left-turn trials) and dark-gray (right-turn trials) and the location of the rat when individual spikes occurred is indicated separately for left-turn trials (blue dots), and right-turn trials (red dots). In the right panel, the mean firing rate of the cell for each of four sequential sectors of the central stem, adjusted for variations in the animal's speed, lateral position, and head direction, is shown separately for left-turn trials (blue) and right-turn trials (red). A. A cell that fired almost exclusively on left-turn trials as the rat traversed later sectors of the stem. B. A cell that fired almost exclusively on right-turn trials as the rat traversed early sectors of the stem. ** p<.01, *** p<.001.

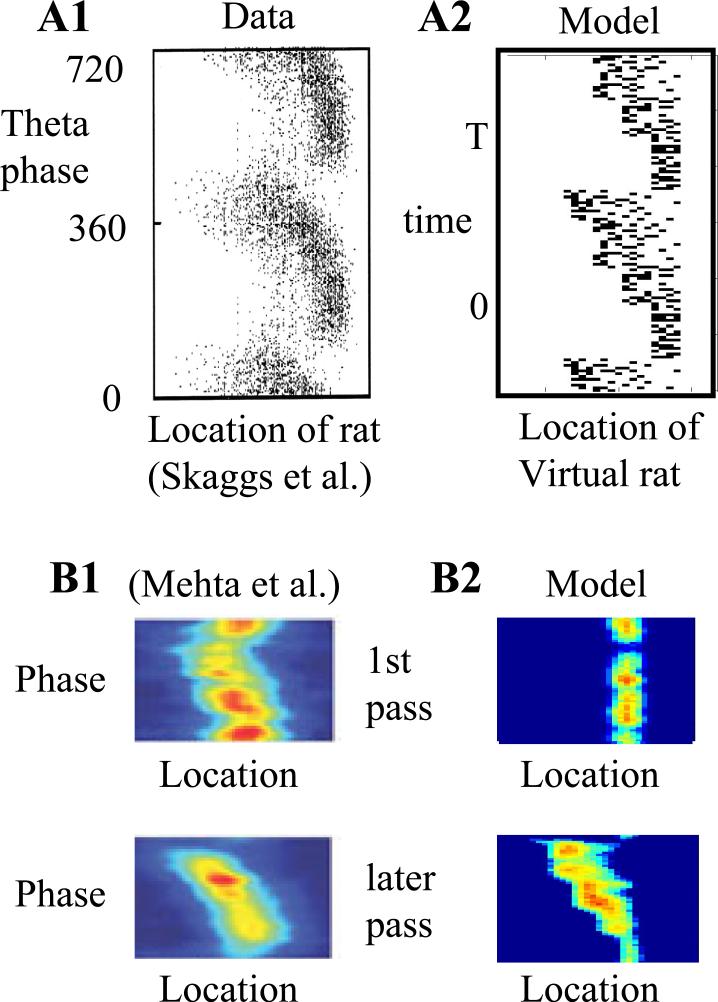
During recordings on a linear track, other neurons show systematic changes in phase relative to theta frequency (7 Hz) oscillations in the hippocampal EEG (O'Keefe and Recce, 1993; Skaggs et al., 1996; Huxter et al., 2003). However, this theta phase precession does not appear on the first trial of the day, but appears on later trials of each day (Mehta et al., 1997; Mehta et al., 2002). The model presented here shows how this change in the amount of precession on each day could reflect selective context-dependent retrieval of recent episodes on a given day.

The context sensitivity of theta phase precession suggests a role for hippocampal theta rhythm in memory for recent sequences of neuronal activity. Consistent with this, lesions which reduce theta rhythm cause behavioural impairments in tasks which require memory for specific prior episodes (Olton et al., 1979; Aggleton et al., 1995; Aggleton and Brown, 1999) such as delayed spatial alternation.

The amplitude of hippocampal theta oscillations correlates with memory-guided performance (Givens and Olton, 1990; Seager et al., 2002; Winson, 1978). The model presented here demonstrates how this functional role of hippocampal theta rhythm could result from the oscillations in synaptic input to region CA1 during theta rhythm (Brankack et al., 1993). In the model, these oscillations enhance the selective retrieval of episodes.

This work moves beyond previous hippocampal models of theta phase precession (Tsodyks et al., 1996; Jensen and Lisman, 1996a; Wallenstein and Hasselmo, 1997) and the role of theta rhythm in separation of encoding and retrieval (Hasselmo et al., 2002b; Hasselmo et al., 2002c), by simulating the selective retrieval of specific prior episodes despite variations in the intervening delay period, and despite potential interference from similar prior episodes. The same oscillations which are important for memory guided behavior in the spatial alternation task also serve to simulate 1.) the phase relationships of synaptic currents during theta rhythm (Brankack et al., 1993), 2.) the context-sensitivity of neuronal firing (“splitter cells”) during spatial alternation (Wood et al., 2000), 3.) the theta phase precession of place cells (O'Keefe and Recce, 1993; Skaggs et al., 1996; Huxter et al., 2003), and 4.) the change in magnitude of theta phase precession across different trials on a given day (Mehta et al., 1997; Mehta et al., 2002).

METHODS

The simulation presented here guides the movements of a virtual rat in a virtual spatial alternation task, as summarized in Figure 2. The model includes two main components. A simulation of hippocampal mechanisms for encoding and selective retrieval of prior episodes is the primary focus of this article, as data demonstrates that lesions of the hippocampus or the fornix specifically impair the ability to perform delayed spatial alternation, but not immediate alternations (Olton et al., 1979; Aggleton et al., 1995; Aggleton and Brown, 1999). In addition, a separate component representing prefrontal cortex uses simple reinforcement learning equations to perform selection of next action on the basis of the current behavioral state and the hippocampal retrieval of prior episodes.

Figure 2.

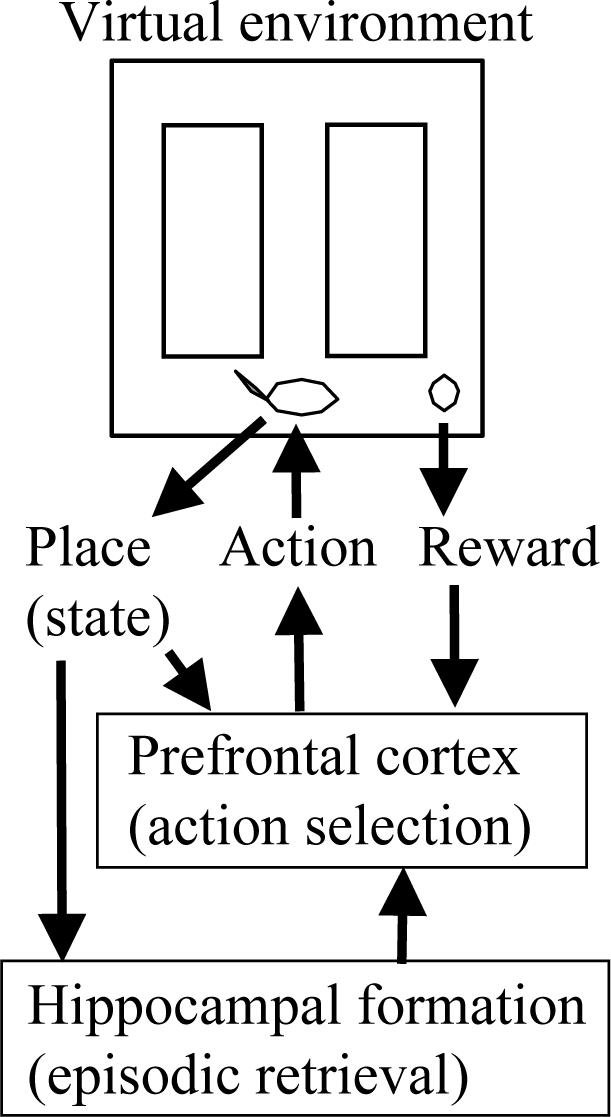
Top: The neural model guides movements of a virtual rat in a virtual spatial alternation task. The rat is shown at the choice point, with food reward in the right arm. Center: Sensory input from the virtual rat enters the neural model with information about its behavioral state (place/location) and food reward. Output from the simulated prefrontal cortex guides the selection of next action in the task. Sensory input comes into simulations of both prefrontal cortex and the hippocampal formation. Bottom: The hippocampal model mediates retrieval of prior episodes to guide behavior.

As the virtual rat moves through the environment, sensory input to the model identifies its current location (behavioral state) and indicates food reward when it is received. At each location, the hippocampal model retrieves the prior episode experienced at that location, and provides this information to prefrontal cortex. Output from the prefrontal cortex model guides selection of the next action (movement in one of four directions) in all components of the task. The structure of the model was constrained to fit the electrophysiological recordings of synaptic currents during theta rhythm, as well as the spiking activity of hippocampal neurons.

As shown in Figure 3, the model can guide the virtual rat to perform correct behavior in a continuous version of spatial alternation (Wood et al., 2000). In this task correct movement in a figure eight pattern depends upon accurate selective retrieval of specific prior episodes. In the model, locations encountered by the rat are encoded as state vectors b_s corresponding to sensory input about behavioral states s. In Fig 3A, these behavioral states are numbered sequentially in the order they are encountered. Moveable blocks guide the virtual rat from the start location at the top of the stem on every trial. During training, additional moveable blocks alternately guide left and right turn responses from the choice point during training, but these are not used during testing, allowing free selection of turns at the choice point. The neural model can guide correct behavior in the task, as shown here. The rat moves down the stem through multiple states (b_s=1 to b_s=2 to b_s=3), then into the right arm (b_s=4,5) where it receives reward (at b_s=5), and then follows the return path (b_s=6,7,8) to the top of the stem (b_s=9). The rat then encounters previously visited locations in the stem, which activate previously used vectors b_s with new indices s (e.g. the input vector b₉ is the same as b₁, b₁₀=b₂, and b₁₁=b₃). At the choice point (b_s=11), the virtual rat must choose the correct action (e.g. move into the left arm), by retrieving its memory of the previous response (e.g. the previous turn into right arm, b_s=4,5,6) and generating the opposite response (b_s=12, b_s=13).

Figure 3.

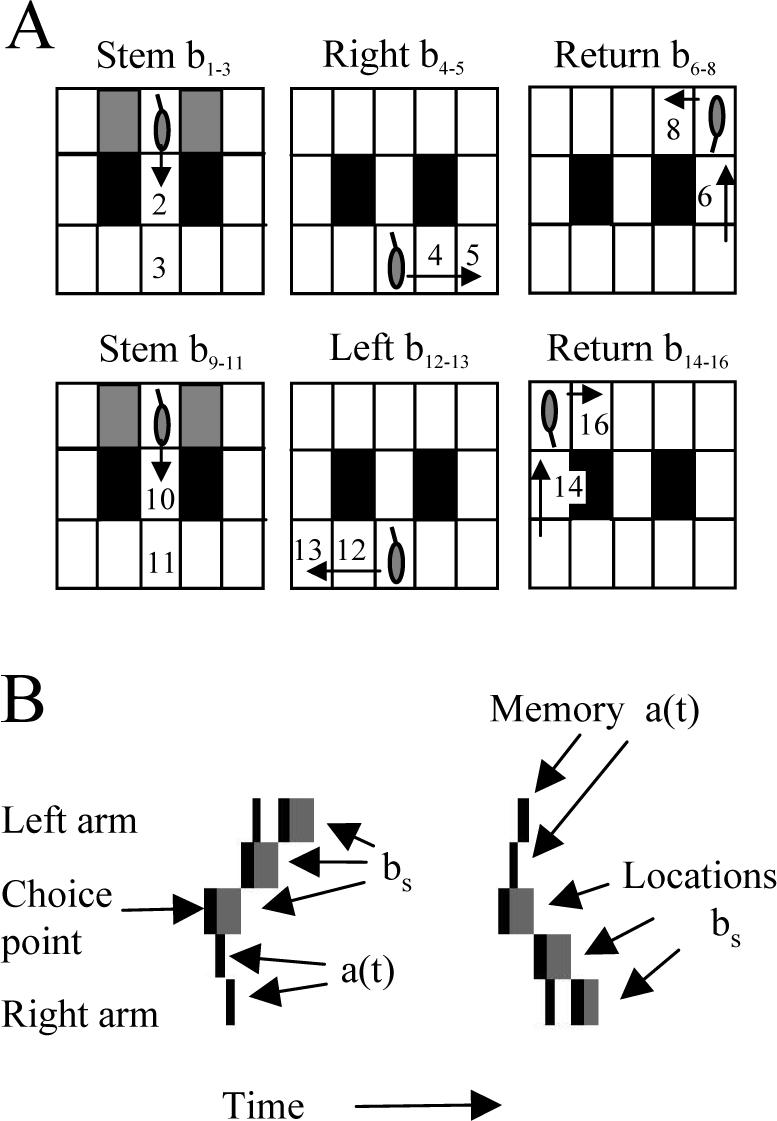
A. Movements of the virtual rat in the spatial alternation task. Rewards are presented alternately in left and right bottom corners. The virtual rat starts at top center and blocks (gray rectangles) guide it down central stem. At choice point (b₃), it goes right, obtains reward at b₅ and returns to start b₉, then goes down stem. At choice point b₁₁₌₃, retrieval of prior episode a(t)=b₄,b₅,b₆ allows correct choice of movement to left (b₁₂, b₁₃). B. . Memory retrieval guides movements at the choice point. The choice point location and two locations in each adjacent arm are plotted vertically, and time is plotted horizontally. At each new location state (gray rectangles), the hippocampal simulation retrieves the sequence of locations which previously followed this location (black rectangles). On the left, the virtual rat retrieves an earlier right arm response and moves to the left arm (gray rectangles going up). On the subsequent visit to the choice point, the simulation retrieves the left arm response (memory a(t) - black rectangles going up) and generates a correct right arm response (locations b_s - gray rectangles going down).

The correct performance of the task depends on the hippocampal simulation performing selective retrieval of prior episodes at each location, as shown in Figure 3B. The gray rectangles in Fig. 3B show the location (state) of the virtual rat in the maze at different times after training. (For simplicity, only a subset of locations near the choice point are shown). Black rectangles indicate activity of neurons in the hippocampal simulation, with activity plotted according to the location represented by each active neuron. At each location, the hippocampal simulation retrieves the sequence of subsequent states which previously followed that location (black rectangles which start at each gray rectangle representing current state). On the left, the rat makes a left arm response (gray rectangles moving upward). Then on the right, the rat retrieves the memory of this left arm response (black rectangles moving upward - “memory”), and uses this retrieval to guide selection of the correct right arm response (gray rectangles moving downward - “Locations”). The retrieval of episodes at each location is consistent with the proposal that theta phase precession represents compressed read-out of sequences of place cell firing at each location (Skaggs et al., 1996).

Hippocampal model

The hippocampal model encodes sequences of locations and retrieves specific episodes from the set of previously experienced sequences. The basic structure of the hippocampal model (Figure 4) was constrained by anatomical and physiological data (Amaral and Witter, 1989). As a simple overview, these subregions perform the following function (Figure 4A). At a given location, the current place input cues the forward retrieval of all previously experienced sequences from that location (forward association). At the same time, temporal context activates units according to the time since a sequence was experienced. The convergence of temporal context with forward associations allows episodic retrieval of just one of the sequences retrieved by forward association.

Figure 4.

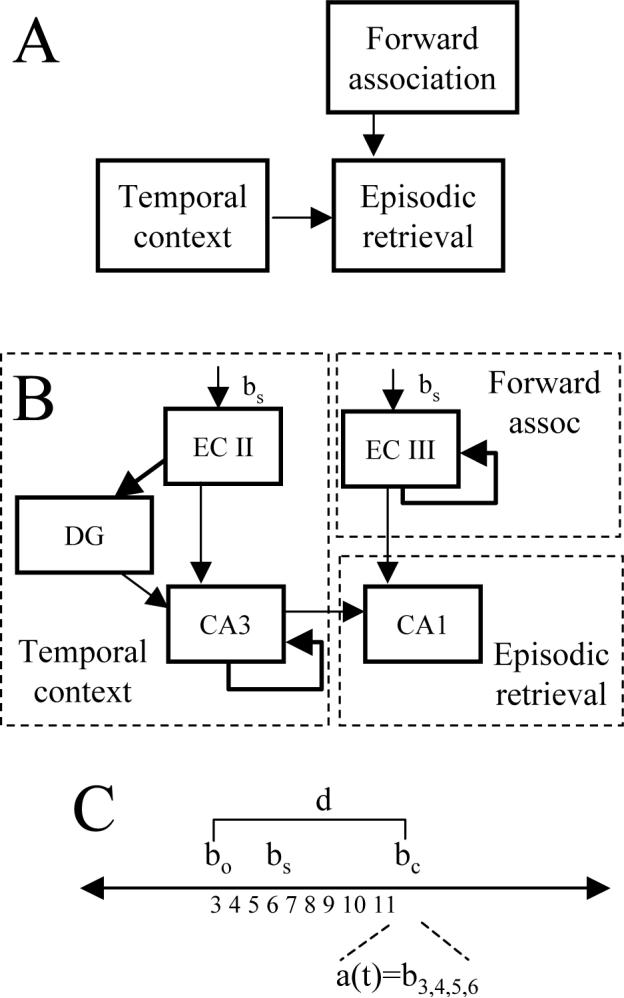
Hippocampal model. A. Retrieval of all previous episodes starting from a location is mediated by forward associations. This retrieval is gated by temporal context. The convergence of these two mechanisms allows selective retrieval of a single previous episode. B. Entorhinal cortex layer III (ECIII) encodes and retrieves all prior sequences from a given input. Sustained activity in pyramidal cells of entorhinal cortex layer II (ECII) (Lisman and Idiart, 1995; Klink and Alonso, 1997b; Fransen et al., 2002) allows formation of temporal context (Howard and Kahana, 2002) which then influences modification of connections with CA3. In region CA1, the interaction of temporal context from CA3 and forward spread from ECIII during each cycle of theta rhythm causes selective retrieval of episodes. C. Time line of behavioral states. The previous visit to choice point b_o=3 is followed by a sequence of states b_s up to current state b_c=11. At this point, the memory retrieval a(t) consists of the episode b_s=4.5.6 which followed the previous visit b_o=3.

As shown in Figure 4B, entorhinal cortex layer III (ECIII) performs encoding and retrieval of forward associations between adjacent spatial locations, allowing retrieval of all elements of previously experienced sequences at all locations. This means that at the choice point, once the virtual rat has made both types of responses, the forward associations retrieve all elements of the sequences corresponding to both left and right arm responses.

The retrieval of sequences based on current input resembles previous hippocampal models which use the current input to cue retrieval of a full sequence of states (Tsodyks et al., 1996; Levy, 1996; Jensen and Lisman, 1996a; Wallenstein and Hasselmo, 1997). However, these previous models perform the forward retrieval function in region CA3, whereas this model performs this function in ECIII. Note also that whereas region CA1 activity in this model sequentially retrieves one state at a time, the EC activity involves spreading activation starting with the current state and spreading to simultaneous activation of increasing numbers of states. This causes large scale activity in ECIII which could underlie the strong excitatory current sinks appearing rhythmically in stratum lacunosum-moleculare of region CA1 (Brankack et al., 1993).

This model also differs from previous models by using temporal context in entorhinal cortex to perform selective retrieval of sequences. The neurons representing entorhinal layer II (ECII) pyramidal cells in the model have persistent spiking activity representing gradually decaying temporal context for previously visited locations. This is based on data for intrinsic mechanisms of sustained spiking activity in ECII pyramidal cells (Klink and Alonso, 1997b; Fransen et al., 2002; Klink and Alonso, 1997a). In slice preparations perfused with cholinergic agonists, these neurons respond to input current injection by continuing to spike for extended periods after the input has ceased (Klink and Alonso, 1997b; Fransen et al., 2002; Klink and Alonso, 1997a). This corresponds to the temporal context representation used previously to model human verbal memory function and entorhinal function in rats (Howard and Kahana, 2002; Howard et al., 2004). This mechanism of sustained activity has also been proposed for short-term memory by Lisman (Lisman and Idiart, 1995; Jensen and Lisman, 1996b; Koene et al., 2003), because the persistent spiking in response to input allows memory of previous items or locations to be maintained after the input has ceased.

Synapses arising from region CA3 perform encoding and retrieval of associations with this temporal context from representations of distinct time points in dentate gyrus. This allows region CA3 activity to represent temporal context of events, consistent with the evidence for context-dependent firing of neurons in region CA3 (Leutgeb et al., 2004; Guzowski et al., 2004), and for impairment of context-dependent behavior with selective CA3 lesions (Lee et al., 2005).

The convergence of input from entorhinal cortex layer III and input from region CA3 on neurons in region CA1 allows context-dependent selection of a specific prior sequence. For example, it allows selective retrieval of the most recent prior response in the spatial alternation task. Thus, spiking activity in region CA1 of the simulation responds to a previously encountered state o resembling the current state c and recapitulates a linear sequence of each of the behavioral states b_o+_t which followed that state at a particular time. This function is shown here in simulations and in the mathematical analysis of the model in the appendix.

Simulation of behavioral states and activity timing in the model

As the virtual rat moves through the virtual spatial alternation task during all stages of performance, the virtual rat visits different behavioral states (locations) which are represented by the index s. These behavioral states activate internal vectors b_s representing the behavioral state. The notation b_s indicates binary nonoverlapping vectors (e.g. b_s=1=001000000000000).

The number of elements n in the internal state vector b_s depends upon the size of the environment and resolution of the representation. For example, in the spatial alternation example shown in Figure 3, the internal state vector has 15 different states (3 rows by 5 columns). In other simulations, the internal state vector had a higher resolution. In Figure 8, the resolution of the spatial alternation task was n=25 (5 rows by 5 columns). In Figure 9, the resolution of the linear track was n=18 (3 rows by 6 columns). The number of neurons in each subregion of the hippocampal simulation (ECII, ECIII, dentate gyrus, CA3 and CA1) was then set to be the same as the size n of the internal state vector. The same number n was used for the reinforcement learning value function representing action selection processes described below.

Figure 8.

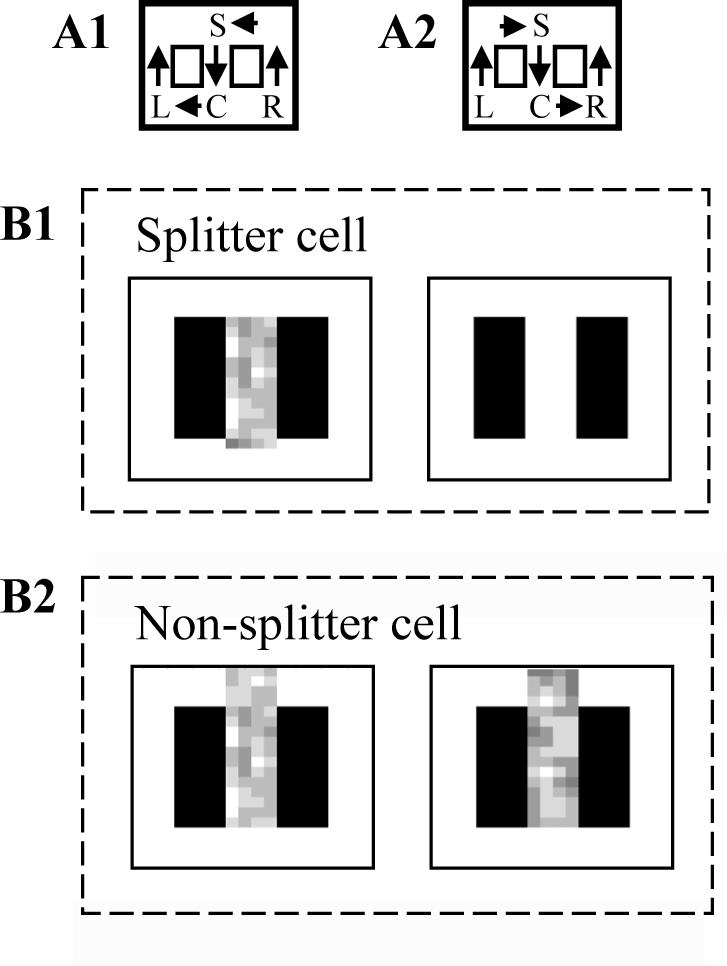
Simulation of “splitter cell” response. A. Behavioral context showing two trial types, including A1. Return from the right arm going to left, and A2: Return from left arm going to right. B1. A splitter cell representing the location just to the right of the choice point will fire as part of sequences retrieved in the stem after the virtual rat performs a right turn response (left side), but will not fire after a left turn response (right side). Gray scale represents number of spikes fired by simulations when virtual rat is in particular locations. B2. A non-splitter cell representing the choice point will fire after visiting either arm.

Figure 9.

Theta phase precession of cells in the simulation. A1. Experimental data (Skaggs et al., 1996), shows that the theta phase (y axis) of firing of a single neuron moves to earlier phases as the rat moves from left to right (x axis). A2: The simulation shows the same pattern for activation of a single place cell as the virtual rat moves in one direction around a retangular track. Early firing for a place field (corresponding to later portions of the retrieved sequence) are retrieved at late phases of theta (high values of t close to T). Late firing in the place field (corresponding to the afferent input driving spiking activity) occurs at early phases of theta (small values of t close to 0). B1: Experimental data (Mehta et al., 1997; Mehta et al., 2002), showing that theta phase precession is not strong on the first pass through a location on a given day (top), but is stronger on later passes through the same location (bottom). B2: Simulation showing that absence of temporal context on the first pass results in absence of phase precession (top). On later passes (bottom), temporal context results in increased theta phase precession.

In most simulations, the position of the virtual rat had a higher resolution than the internal state vector, consistent with the fact that a single place cell may fire over an extended region of the environment (Wood et al., 2000; Huxter et al., 2003; Skaggs et al., 1996; Muller et al., 1987; Muller and Kubie, 1989). In the simulations of splitter cells in Figure 8, the virtual rat could occupy a position anywhere in a 4 by 4 square array of locations for each element of the internal state vector, so that 16 external locations activated each internal state. Thus, 400 locations (represented with n_loc) were mapped to 25 internal states of the input vector. For the simulations of precession in Figure 9, the virtual rat could occupy a 1 by 4 array of locations for each element of the internal state vector, so that 72 locations were mapped to the 18 elements of the internal state vector. These location representations were only used for plotting the position of the virtual rat during activity of specific internal units.

In each discrete behavioral state, the network undergoes a single cycle of theta rhythm oscillations (see Figure 5) with phases of neural activity in different regions based on experimental data (Brankack et al., 1993; Buzsaki, 2002). Within each cycle, there are multiple steps of processing in memory time t, including separate phases of encoding and retrieval (Hasselmo et al., 2002b; Hasselmo et al., 2002c). The number of theta rhythm cycles for each state could easily be increased to multiple cycles. It was kept at one simply to speed computation. The matching of theta phase to the onset of new sensory input is consistent with data on phase locking of theta rhythm to the onset of sensory stimuli (Givens, 1996). Further simulations will address random timing of theta relative to movement. The time within a single cycle of theta oscillation is represented by t, which starts at 0 at each new state and increases to a consistent maximum T. Thus, the transition time between different behavioural states s runs slower than the progression of theta oscillation time t (for each new state s, theta time t progresses from 0 to T). Behavioral states are indicated by subscripts (s for general states, o for the old state which resembles the current state, and c for current state). Note that the reinforcement learning equations representing prefrontal cortex only perform one step of computation for each new location, so they use the last memory state on each cycle (at time T).

Figure 5.

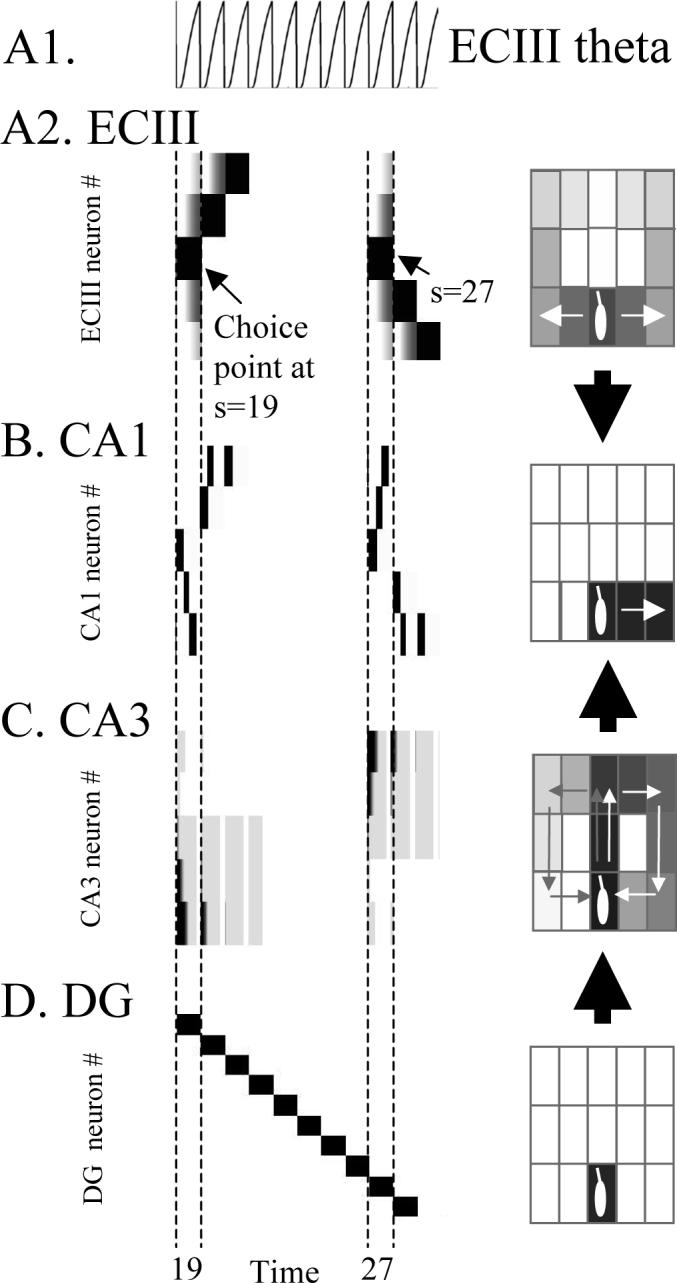
Activity in subregions of the hippocampal model during two trials of continuous spatial alternation. Multiple states s (and time t within each state) are plotted horizontally (starting when virtual rat is in choice point at state s=19), and activity of individual neurons is plotted vertically in different rows. For each region, the same neuronal activity is plotted on the right in terms of spatial locations coded by active neurons. A1. Time course of entorhinal cortex theta (EC theta). A2. Neural activity in region ECIII spreads to more neurons with each cycle of theta. At each time point, forward retrieval is cued by neurons coding the current behavioural state which matches the old state. Neurons responding to choice point are marked with arrows at s=19 and s=27. Activity spreads to neurons representing both left and right arms of the T-maze, resulting in less spatial selectivity on the right. The rat makes a left (upward) response after s=19 and a right (downward) response after s=27. B. Neural activity in region CA1 shows selective retrieval of the most recent episode. Black rectangles going upward at s=27 correspond to the previous behavioral output visible in EC activity for s=19. Spatial distribution is more localized than in ECIII. C. Neuronal activity in CA3 cued by dentate gyrus provides temporal context. Activity is strong (black) close to the current behavioral state and weaker for states from the more distant past (gray). The strength of temporal context decreases within each cycle. D. Neuronal activity in dentate gyrus provides a distinct representation of each time point that cues retrieval of temporal context in region CA3. The spatial distribution is highly localized.

Simulated neurons generated output (spikes) when they were above threshold on a time step t. The continuous values of activity in these equations model the membrane potential of units, and threshold functions are used to determine firing rate, but when activity spreads rapidly through the network, the onset of firing has properties corresponding to the spiking activity of individual units in more detailed biophysical simulations. The plots in Figures 8-9 effectively replicate spike times in experimental data (Skaggs et al., 1996; Wood et al., 2000; Mehta et al., 2000). Many of the mechanisms of forward association and context-dependent retrieval used here have been tested in previous models from this laboratory using integrate-and-fire neurons interacting via synapses with dual exponential time courses (Hasselmo et al., 2002a; Gorchetchnikov and Hasselmo, 2005; Koene et al., 2003). For example, those models demonstrate retrieval of sequences within a single theta cycle, though cycle time limits sequence length as in other models (Lisman and Idiart, 1995).

Summary of hippocampal model equations

The following sections present the equations and parameters used in the simulations for this paper shown in Figures 3 and 5-10, and in the mathematical analysis in the appendix. Equations 1-7 model the spread of activity and the mechanisms of synaptic modification at recurrent connections in subregions of the simulated hippocampal formation. The behavioral function of the neural model could be simulated with fewer equations, but these equations were selected to simultaneously address behavioral function and replicate physiological properties of hippocampal unit activity. The equations modeling prefrontal cortex (equations 8-10) guide movement of the rat based on current state and memory retrieval, using reinforcement learning equations representing action selection processes (in prefrontal cortex and other regions).

Figure 10.

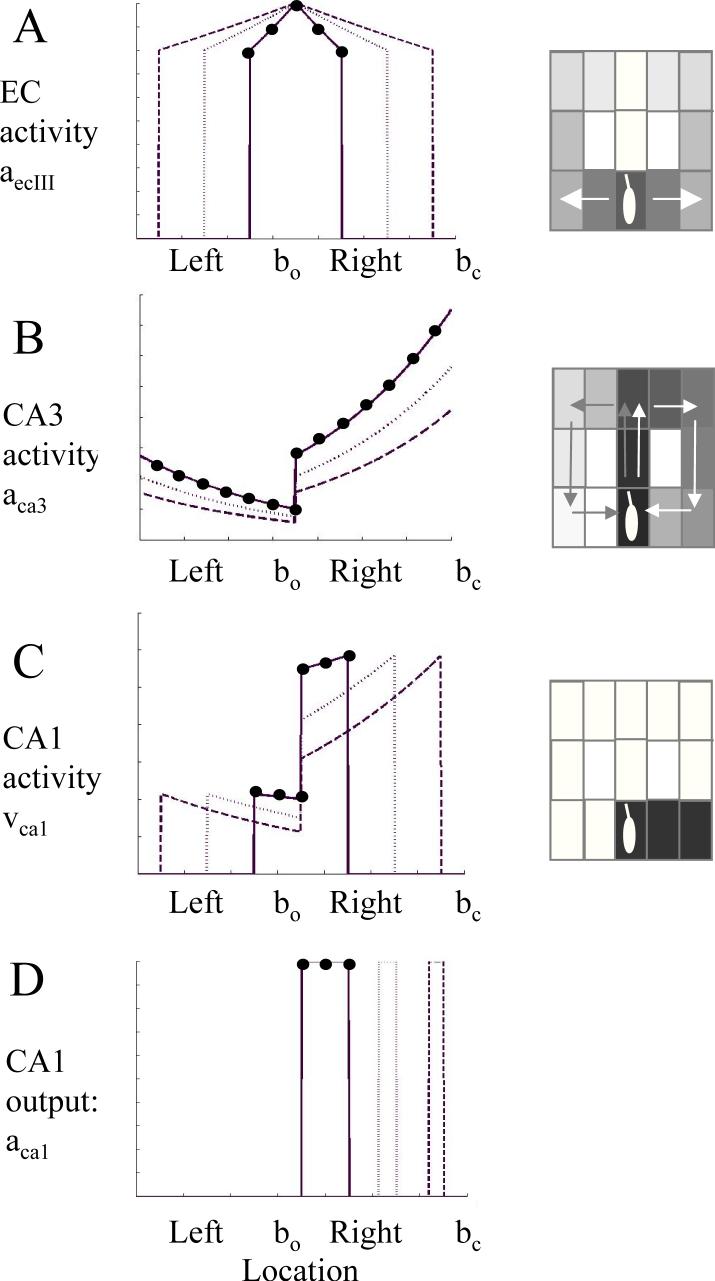
Simplified example of activity in different units in the hippocampal model during multiple time steps in a single state. The y axis shows magnitude of activity in different regions. The x axis indicates individual units representing the choice point (b_o) as well as the left and right arms (x axis). To make curves clearer, parameters differed from other simulations, using η=0.8, μ=0.75, , ε=0.000001, and ψ_ca1=0.1335. Different lines show magnitude of activity at different times during retrieval (ϕ=0) (solid: t=2, dotted: t=4, dashed: t=6. For t=2, unit activity is marked with black circles). Boxes on the right show gray scale depictions of the locations in the T-maze being represented by activity in the model (note that spread in this example is longer than in other simulations). A. Magnitude of input from entorhinal cortex (equation 2). EC activity spreads equally along previous stored forward associations, activating neurons representing both the left and right arm of the maze. The distance of suprathreshold spread increases as t increases. B. Magnitude input from region CA3 to region CA1 (equation 5). The magnitude of input is strongest for neurons representing current context b_c, and decreases exponentially for previously visited states, such that the locations visited recently in the right arm have stronger temporal context than the locations visited earlier in the left arm. Magnitude of temporal context decreases as t increases. C. Magnitude of multiplication of inputs in region CA1. Curves have same maximal amplitude for different events in the recent episode, and lower maximal amplitude for events in the more remote episode. D. Thresholded output of CA1. Thresholding with a constant threshold or on the basis of previous activity allows sequential read-out of spiking in CA1 representing just one of the retrieved sequences.

Most equations use vector notation. Lower case bold letters a and b are vectors representing neuronal activity in different regions (the vectors are all the same size n, scaled to the size of the environment being simulated as described above). Upper case letters W are matrices representing patterns of synaptic connectivity between different simulated subregions. Most regions have n neurons, so most matrices are n by n square matrices. To simplify the demonstration of network function, the only modifiable synapses in the simulation are the recurrent connections in ECIII (W_ecIII) and CA3 (W_CA3), as well as the connections from ECII to the dentate gyrus. Other synaptic connections in this model use an identity matrix I to transfer the same pattern of presynaptic activity to the postsynaptic region (Hasselmo et al., 2002c). For simplicity, identity matrices are used for connections from ECII to CA3, from ECIII to CA1, from DG to CA3 and from CA3 to CA1. This allows simpler viewing of the interaction of activity patterns in entorhinal cortex, CA3 and CA1. However, previous models have shown that it is possible to use modification in all of these connections while maintaining the mapping between elements of the neuronal representation in different regions of the model (Hasselmo and Wyble, 1997).

Entorhinal cortex layer III (ECIII)

Forward associations are provided by activity in ECIII and the modification of excitatory recurrent connections in this region. The synaptic modification for storage of forward associations in layer III depends on current and prior input to ECIII:

$$\Delta W_{ecIII}=a_{ecIII}{a}_{ecIII}^T=b_c{b}_{c-1}^T$$ (1)

This represents the change (Δ) in the matrix W_ecIII representing the strength of recurrent connections in ECIII (starting at zero, with maximum strength 1.0). The recurrent connections are strengthened on the basis of spiking activity a_ecIII(t) in neurons of EC layer III. Based on recent models of a buffer of sensory input in entorhinal cortex (Jensen and Lisman, 1996b; Koene et al., 2003), this activity uses sequential spiking with presynaptic spikes representing the preceding behavioral state (the location represented by variable b_c-1) followed by postsynaptic spikes representing the current behavioral state (location b_c). The activity representing preceding state is maintained by sustained afterdepolarization such as that observed in entorhinal slice preparations (Klink and Alonso, 1997b). No modification occurs at the start location c=1, but fast modification occurs between neurons representing each subsequent pair of sequential states (e.g. c=1 with c=2).

Note that these synapses alone can store memory of prior sequences. Recency could be represented by a decay in synaptic weight, but this would cause a permanent loss of the encoded memories. In contrast, the framework presented here allows maintenance of all stored sequence associations at full strength. Selective retrieval of individual sequences results from convergence of the forward associations from EC with temporal context from region CA3.

During each cycle of theta rhythm, the simulation of activity in the excitatory pyramidal cells of ECIII uses the equation:

$$a_{ecIII}\left(t\right)=b_c+{\eta }^{\tau ∕t}{W}_{ecIII}{[a_{ecIII}(t-1)-{\psi }_{ec}]}_{+}$$ (2)

Where a_ecIII(t) represents depolarization of neurons in EC layer III, b_c represents the current behavioral state, ψ_ec represents the spiking threshold of ECIII units, and [a_ecIII(t)−ψ_ec]₊ represents a threshold linear function, which takes the value a-ψ when a is above threshold, and zero when a is below threshold. This threshold function represents the total spiking of the population dependent upon membrane potential (Dickson et al., 1997). The theta rhythm function η^τ/t represents the rhythmic change in depolarization of neurons in ECIII (see Fig. 5A top), where t is the time from the start of retrieval within each theta cycle and the time constant τ determines the rate of change of this theta rhythm function. The theta function is based on data for differences in firing of entorhinal neurons at different phases of theta rhythm (Alonso and Garcia-Austt, 1987). Note that the parameter η is less than 1 ( 0<η<1). Therefore, as time t increases from 0 to T during each cycle of the theta rhythm, this function causes an increase in the amount of depolarization and synaptic spread in the model of entorhinal cortex layer III. This simulates the rhythmic change in spiking activity in entorhinal cortex (Alonso and Garcia-Austt, 1987), and the increase in synaptic current sinks during each cycle of theta in stratum lacunosum-moleculare of region CA1 (Brankack et al., 1993).

The equation for ECIII has the effect of storing all previous associations between sequential states, and retrieving all of these possible associations at once. Thus, retrieval in ECIII starts with the current state and progressively spreads to greater numbers of elements of the sequence, so that late in the theta cycle neurons representing many components of the sequence will be spiking together, causing a strong synaptic input to region CA1 at a specific phase (ECIII activity is shown in 5A and compared with data in Fig. 7A). Thus, at the choice point ECIII retrieves memories of entering both left and right arms. This general forward association function is consistent with data showing that selective lesions of the hippocampus which spare entorhinal cortex do not impair general associative memory, but impair discrimination of one recent episode from other similar episodes (Agster et al., 2002). This function is also consistent with data showing that cutting the input from CA3 to CA1 does not impair recognition, but does impair selective recall (Brun et al., 2002).

Figure 7.

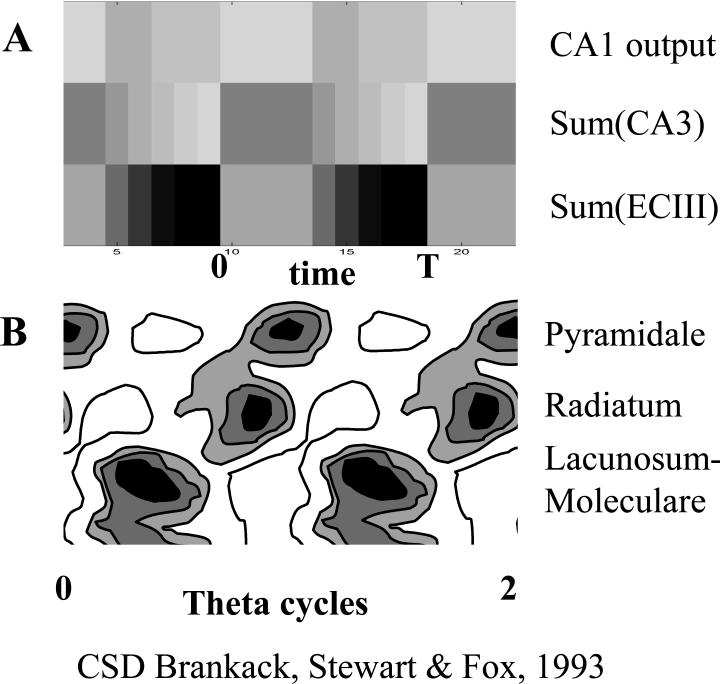
Rhythmic activity in different subregions of the model matches the theta phase of current sinks due to synaptic input in region CA1. A. Each band shows the sum of rhythmic activity in modeled subregions across two cycles (0 to T) of simulation time t plotted horizontally. Darker colors indicate stronger activity. The top band shows the sum of region CA1 output, the middle band shows the sum of region CA3 activity - Sum(CA3), and the bottom band shows sum of entorhinal cortex layer III activity - Sum(ECIII). B. Comparison with phase relationships of synaptic current sinks shown in different layers of region CA1 in experimental data (Brankack et al., 1993). Darker colors indicate stronger synaptic currents (indicating more activity in the region sending input). Current sinks at top indicate summed currents in region CA1 stratum pyramidale, middle sinks are caused by synaptic input from region CA3 to stratum radiatum and bottom sinks are caused by synaptic input from ECIII to stratum lacunosum-moleculare.

Entorhinal cortex layer II pyramidal cells (ECII)

Because layer III retrieves both possible sequences at the choice point, the episodic retrieval of a single prior sequence requires a context signal. Context provides disambiguation of overlapping sequences (Levy, 1996; Agster et al., 2002). In this model, a persistent but gradually decaying trace of previous activity provides temporal context which differs in magnitude for different trials in the task. The biological justification for this temporal context is the fact that ECII pyramidal cells in slice preparations show persistent but decaying spiking activity after depolarizing input (Klink and Alonso, 1997b; Klink and Alonso, 1997a). This feature was inspired by the model of temporal context developed for human verbal memory function by Howard and Kahana (Howard and Kahana, 2002; Howard et al., 2004).

The sustained activity of entorhinal neurons is represented by a vector which combines the current afferent input b_c and activity from the previous state:

$$a_{c,ecII}=b_c+\mu a_{c-1,ecII}$$ (3)

Where the vector a_c,ecII represents the activity of a population of ECII pyramidal neurons at the current behavioral state c. (Note that ECII activity does not change during the cycle of the theta rhythm, so it does not depend on the time t within a cycle). This activity combines afferent input about the current behavioral state b_c and the persistence of activity from activity a_c-1,ecII during the preceding behavioral state c-1. This persistence models the effect of an intrinsic afterdepolarization current present in ECII pyramidal cells but not stellate cells (Klink and Alonso, 1997b; Klink and Alonso, 1997a) which can maintain spiking activity in single neurons based on previous depolarization. The persistence is not complete. There is some decrease in membrane potential and firing over time. Therefore, this activity is modeled with a decay component μ which take a value less than 1 (0 < μ < 1). Computing equation 3 over many steps from s=1 to c gives the activity:

$$a_{c,ecII}=\sum _{s=1}^c{\mu }^{(c-s)}{b}_s$$ (3b)

Note that the activity in ECII reflects the decrease in persistent activity scaled to the difference between the current behavioral state c and each individual previous behavioral state s. Thus, each behavioral state vector b_s persisting in ECII decays in proportion to the factor μ raised to a power of the number of intervening states (c-s).

Dentate gyrus and region CA3

The activity from ECII enters region CA3 via the perforant path, where it causes postsynaptic dendritic depolarization scaled to temporal context. At the same time, the dentate gyrus forms a distinct representation g_c at each time step c during behavior which causes spiking in region CA3 via mossy fiber input. The distinct representation in dentate gyrus is similar to prior models of dentate gyrus function (O'Reilly and McClelland, 1994; Hasselmo and Wyble, 1997). This is also consistent with the very sparse representations formed in these regions, as indicated by the relatively small number of active place cells in the dentate gyrus for a given environment (Jung and McNaughton, 1993). Previous models have also used dentate gyrus to provide context for CA1 unit activity (Doboli et al., 2000).

Synaptic modification of region CA3 recurrent connections encodes associations between spiking induced by dentate gyrus input g_c and dendritic depolarization caused by input from ECII:

$$\Delta W_{ca3}=a_{ca3}{a}_{ca3}^T=a_{ecII}{g}_c^T=\sum _{s=1}^c{\mu }^{(c-s)}{b}_s{g}_c^T$$ (4)

Where the matrix W_ca3 represents strength of recurrent connections in region CA3 (starting from a small nonzero value) modified by activity in CA3 pyramidal cells. Presynaptic activity a_ca3 is assumed to be dominated by spiking induced by mossy fiber inputs from the dentate gyrus, so presynaptic activity can be replaced with the distinct episodic representation formed in the dentate gyrus at each time step g_c. The post-synaptic activity a_ca3 is assumed to involve dendritic spikes induced by direct entorhinal input from ECII activity a_ecII, consistent with evidence in CA1 for synaptic modification due to presynaptic spiking interacting with dendritic spikes (Golding et al., 2002).

Temporal context can then be retrieved by the spread of excitatory activity in region CA3, which is cued by dentate gyrus and modulated by theta rhythmic changes in depolarization within this region (with a phase that differs from theta in ECIII).

$$a_{ca3}\left(t\right)={\mu }^{t∕\tau }{W}_{ca3}{g}_{c-1}$$ (5)

Where the vector a_ca3(t) represents the activity of a population of CA3 pyramidal neurons at different times during the theta cycle, with presynaptic spiking activity driven by afferent input from the dentate gyrus g_c-1. Dentate activity for retrieval can be induced by current context or by input from ECII, but must be one step or more in the past to prevent retrieval of the current state only (déjà vu). The theta rhythm function μ^t/τ represents the rhythmic change in depolarization of neurons in CA3, where t is the time from the start of retrieval within each theta cycle and the time constant τ determines the rate of change of this theta rhythm function. This function is based on data for differences in rhythmic synaptic input to stratum radiatum in region CA1 from region CA3 (Brankack et al., 1993), as well as evidence for changes in depolarization in region CA1 neurons during each cycle of theta rhythm (Fox, 1989; Kamondi et al., 1998). Note that the parameter μ is less than 1 (0 < μ < 1). Therefore, as time t increases from 0 to T during each cycle of the theta rhythm, this function causes a decrease in the amount of depolarization in region CA3, and causes decreased output from region CA3 to region CA1. Region CA3 activity is shown in Figure 5C, and the sum of CA3 activity is shown in Figure 7A.

Region CA1

The convergent input to region CA1 allows the temporal context from region CA3 to selectively retrieve one of the sequences activated by forward associations in ECIII. The episode closest to a temporal context can be selectively retrieved via a multiplicative interaction of entorhinal cortex input and region CA3 input on the distal dendrites of region CA1 neurons (Otmakhova et al., 2002; Poirazi et al., 2003). This uses the following equation for excitatory activity in region CA1 (the thresholded activity of region CA1 is shown in Figure 5B).

$$a_{ca1}{\left(t\right)}_i={[a_{ecIII}{\left(t\right)}_i{}^{\ast }a_{ca3}{\left(t\right)}_i-{\psi }_{ca1}]}_H$$ (6)

Where the vector a_ca1(t)_i represents spiking activity of each neuron i in region CA1, ψ_ca1 represents the spiking threshold of CA1 units, and [...]_H represents a Heaviside function, which takes the value one when a is above threshold, and zero when a is below threshold. The threshold can be scaled to total activity. Note that because the input from both ECIII and CA3 to region CA1 involve identity matrix connections, the equation has been simplified to include only the presynaptic vectors from those regions.

These equations result in the retrieval of episodes shown in equation 7 below.

Primary function: Retrieval of episodes

Equations 1-7 provide encoding and sequential retrieval of each element of a prior episode which followed the previous visit to a specific location. This retrieval must avoid retrieval of other episodes, such as an earlier trial of spatial alternation. As shown in Figs. 3 and 5 and in the appendix, these equations allow activity in CA1 to show selective retrieval of a specific prior episode:

$$a_{ca1}\left(t\right)=b_{o+t}$$ (7)

In this equation, the activity in region CA1, a_ca1(t), changes rapidly over theta oscillation time t. This activity starts with the previously visited state o, which resembles the current state c. Retrieval of the memory then continues with time t, sequentially retrieving each of the states which followed the previously visited state o. This results in the index of retrieved states increasing with time (resulting in the retrieval index o+t).

Equation 7 constitutes a mathematical definition of a simple form of episodic memory, in which a particular sequence of prior behavioral states (from state o to state o+t) is retrieved over a brief time period within a theta cycle (as the oscillation time t increases within a theta cycle the index of the old memory states being retrieved increases). This sequence can be retrieved despite potential interference from multiple other sequences overlapping with the same states.

The selective retrieval of the most recent episode results from an interaction of ECIII forward retrieval input and CA3 temporal context input to region CA1 during each cycle of the theta rhythm. ECIII activity increases at the same time that CA3 activity decreases. This allows the CA1 activity underlying retrieval to show minimal variation in the size of individual elements b_s within an episodic memory. However, as shown in the appendix, every element of a memory is scaled to the distance d of the first state o from the retrieval context, thereby enhancing the selection of a single prior episode without interference from other episodes.

Because weight matrices do not decay, selection of an appropriate retrieval context can allow very old memories to read out with the same strength as new memories. Importantly, the selection of individual episodes depends on small and metabolically undemanding changes in the hippocampus which can retrieve a wide range of episodic representations based on strong associations in entorhinal cortex.

Note that precession could also be obtained in region CA3 if we included formation of forward associations on excitatory recurrent synapses between stellate neurons in entorhinal cortex layer II (ECIIstel), which then provide synaptic input to the dentate and region CA3. This would allow a similar retrieval process in both ECIIstel and ECIII. The ECIIstel activity could interact with the temporal context representation to allow sequential retrieval processes and phase precession in the dentate gyrus and region CA3 as well as region CA1. This context-dependent sequential retrieval could cause the phenomenon of splitter cells in CA3 as well as CA1, and could underlie the shift in center of mass of place fields in both region CA3 and CA1 (Mehta et al., 1997; Lee et al., 2004a).

Simulations

Simulation figures were all created from the same MATLAB script, using the same network parameters, with the values η=0.04, μ=0.01, ψ_ecIII=η−ε, ε=0.0001, ${\psi }_{ca1}=\gamma \sum {\nu }_{ca1}$, γ=0.25, maximum time steps T=48, and time constant τ = 12. Each theta cycle included an encoding period of 12 time steps during which the value of t was held constant at 1. Only a few specific differences were used in the different figures. Figure 6C used a small random variation (p=0.02) for selection of responses, which resulted in occasional imperfections of behavior that make the lines showing behavioural function more visible. For simulation of splitter cell responses in Figure 8B, the location of the virtual rat had a higher resolution so that multiple spatial locations were visited for the same behavioral state perceived by the virtual rat (4 positions in both x and y direction for each state). For simulation of theta phase precession in Figure 9, the same network variables were used during movement in one direction around a rectangular track but with higher spatial resolution only in the horizontal dimension, so that 4 positions in the direction of horizontal movement were included for each behavioral state. Also in Figure 9, random activation of afferent input with probability 0.6 resulted in more random retrieval of the sequence of behavioral states that followed each location.

Figure 6.

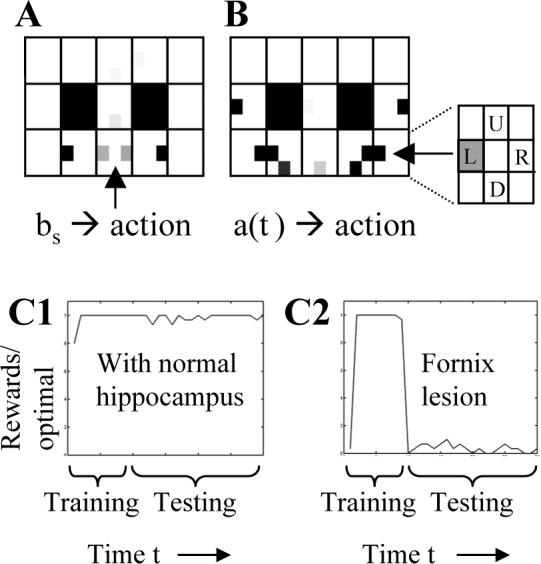
Action values guide behavior. A. The behavioral state action values can guide the movement once the rat enters an arm (e.g. for example in the right arm, the black rectangle indicates preference for right movement). However, at the choice point the state action values are ambiguous (gray rectangles on both left and right sides). B. The memory-state action values can guide the correct movement due to memory retrieval at the choice point. Retrieval activates memory states associated with the previous visit to right arm (arrow), which activates strong action values guiding movement to left (the inset shows that the action value for a left turn response at the choice point is strong when a right arm location is retrieved in memory). C. Average rewards received relative to maximum rate in 30 simulated rats. Training with blocks occurs during steps 1−60, and testing without blocks occurs in steps 61−240. C1. Performance during testing is excellent with hippocampal retrieval. C2. With a simulated fornix lesion, the network cannot perform the spatial alternation function after training ends (after step 60).

The prefrontal cortex model guides the virtual rat

The simulations in MATLAB guided movements of the virtual rat based on the retrieval of episodes in the hippocampus, along with reinforcement learning mechanisms representing action selection processes in prefrontal cortex. Similar to previous models of hippocampal mechanisms in navigation (Brown and Sharp, 1995; Burgess et al., 1997; Foster et al., 2000), the virtual rat generated actions A consisting of movements in four directions (Up, Down, Left, Right). It did not move into the space it just left. During behavioral training, direction of movement was regulated by alternately blocking the left and right arms (similar to behavioral training in experiments). After shaping, goal-directed movements were guided by the hippocampal simulation combined with standard reinforcement learning (Sutton and Barto, 1998; Foster et al., 2000). Reinforcement learning uses action value functions Q (equation 9), in which states are mapped to specific actions that result in reward. However, state action values generated for spatial alternation are ambiguous at the choice point, as shown in Figure 6A. Thus, simulation of alternation behavior requires that the behavioral states b_s be supplemented with memory states a_ca1(t). This allowed the retrieval of the prior episode to elicit the appropriate action at the choice point, based on action-value functions for memory states Q_hip (Equation 10 and Figure 6B). Memory states for locations in one direction (e.g. the Right arm) became associated with strong action values (arrow in Figure 6B) for generating the opposite response (e.g. go Left). The action-values labeled in the figure inset show that when memory of a right arm location is retrieved, a left turn response (L) is favored. Similarly, on the left it can be seen that retrieval of a left arm memory activates action values which favor a rightward movement. Reducing theta rhythm in the hippocampus prevents this accurate retrieval and thereby prevents effective performance of the task (Fig. 6C).

The model used standard actor-critic equations for the update of the value function V and the action value function Q (Sutton and Barto, 1998) with learning rate α. The model then added a separate action-value function Q_hip, which was gated by the memory state a(T, b_s) from the last time step (time T) of the theta cycle at behavioral state s.

$$\begin{array}{cc}\hfill & dV\left(s\right)=V(s+1)+R(s+1)-V\left(s\right)\hfill \\ \hfill & V\left(s\right)=V\left(s\right)+{\alpha }^{\ast }dV\left(s\right)\hfill \end{array}$$ (8)

$$Q(s,A)=Q(s,A)+{\alpha }^{\ast }dV\left(s\right)$$ (9)

$$Q_{hip}(s,A)=Q_{hip}(s,A)+a{(T,b_s)}^{\ast }{\alpha }^{\ast }dV\left(s\right)$$ (10)

These equations representing prefrontal cortex result in the action-value functions in Figure 6 illustrated for behavioral state (equation 9 - Figure 6A) and for memory state (equation 10 - Figure 6B). These equations use hippocampal memory retrieval to guide correct selection of responses in the spatial alternation task.

RESULTS

Behavioral function

As shown in Figures 3A and 3B, the simulation can guide correct performance of the virtual rat in the virtual spatial alternation task. At all locations in task, the hippocampal model retrieves the prior episode experienced at that location, and provides this information to prefrontal cortex. In most locations, the prefrontal cortex can guide correct action selection even without hippocampal input. However, at the choice point the location is associated with rewarded movements in either direction (Fig. 6A). In this location, memory of the prior episode provided by hippocampal output is essential to guide the correct selection of the opposite response (Fig. 6B). Thus, the correct performance shown in Fig. 3 depends upon an intact hippocampus. As shown in Fig. 6C1, the intact simulation allows the virtual rat to consistently obtain high levels of reward in the task.

The simulation can replicate the effects of fornix lesions on performance of this task, as shown in Figure 6C2. Fornix lesions consistently cause impairments in delayed spatial alternation tasks, and these lesions also cause reductions in amplitude of theta rhythm (Olton et al., 1979; Aggleton et al., 1995). The effect of a fornix lesion was simulated by setting the theta function in CA3 to zero (no oscillation), thereby removing the effect of temporal context on retrieval, and impairing the effective performance of delayed spatial alternation, as shown in Fig. 6C2. After training ends, performance by the lesioned network is very poor. The simulated fornix lesion did not impair performance of a task with a single stationary reward location (not shown).

Simulation of current source density data

The theta rhythmic properties of the simulation match data from EEG recordings of the hippocampal theta rhythm, as shown in Figure 7. In particular, the simulation matches the theta phase relationship of synaptic sinks in region CA1 of the hippocampus, as measured by current source density analysis of experimental data (Brankack et al., 1993). As shown in Figure 7A, the synaptic input to region CA1 can be approximated at each point in time by summing neural activity in ECIII to obtain synaptic input to stratum lacunosum-moleculare of region CA1, and summing neural activity in CA3 for the synaptic input to stratum radiatum. The time course of these rhythmic changes in the simulation match the time course of synaptic input in region CA1, as shown by current source density analysis (Brankack et al., 1993) in Figure 7B. The theta functions chosen for their role in sequence retrieval result in synaptic input from CA3 decreasing at the same time as the synaptic input from ECIII increases, consistent with the shape of experimental data using simultaneously recorded field potentials (Buzsaki, 2002) or current source density analysis (Brankack et al., 1993), and corresponding to the phase of theta during which theta phase precession occurs (Mehta et al., 2002). Consistent with current source density data showing very strong rhythmic current sinks in stratum lacunosum-moleculare of region CA1, the activity providing input from layer III becomes very strong on each theta cycle, due to the progressive broad spread of activity within recurrent connections of EC layer III.

Simulation of splitter cells (episodic cells)

As shown in Figure 8, the simulation also replicates the properties shown in recordings of action potentials generated by hippocampal neurons in rats during performance of spatial alternation tasks (Wood et al., 2000). In experimental recordings, some neurons show responses on the stem of the maze only after one type of response (e.g. a right turn), though the location, movements and sensory stimuli on the stem of the maze are equivalent after both types of response. These types of neurons are referred to as “splitter cells.” The two contexts are summarized in Figure 8A1 (after right turn) and Figure 8A2 (after left turn). As shown in Figure 8B1, some units in the simulation show properties of splitter cells. The unit shown in Fig. 8B1 fires only when the virtual rat moves down the stem of the maze after a right turn (average firing rate shown by gray scale squares), and does not fire when the virtual rat moves down the stem of the maze after a left turn, because this neuron encodes a location in the right arm and is only retrieved after a right turn response. This is an emergent property of the model due to retrieval activity being selected by temporal context only when the most recent episodic memory involves that location. Similar to experimental data, the model also contains neurons that show no splitting phenomenon. The neuron in Fig. 8B2 encodes the choice point and is therefore retrieved in the stem after both types of turning responses. The number of splitter cells is proportional to the length of the sequence being retrieved in the simulation. If the retrieved sequence is longer, then there are a larger number of units activated during retrieval in the stem that are not activated after the opposite response.

Simulation of theta phase precession

As shown in Figure 9A, the network also replicates the phenomenon of theta phase precession (O'Keefe and Recce, 1993; Skaggs et al., 1996; Huxter et al., 2003). This is demonstrated in a separate virtual task in which the virtual rat with the same simulation parameters runs one direction along a linear track shaped in a rectangle, replicating tasks used to study theta phase precession (O'Keefe and Recce, 1993; Mehta et al., 1997; Mehta et al., 2002; Skaggs et al., 1996). As in previous models of phase precession based on sequence retrieval (Tsodyks et al., 1996; Jensen and Lisman, 1996a; Wallenstein and Hasselmo, 1997), at each spatial location, b_s, the network generates a forward sequence of retrieval states which followed that location. This mechanism results in selective activation of units representing subsequent behavioral states. As shown in Figure 9A2, when the response of a single unit is plotted relative to the location of the virtual rat and the phase of simulated theta, the firing initially appears at late phases of theta, and gradually moves to early phases, matching experimental data (Fig. 9A1).

Simulation of context-dependent precession

As shown in Figure 9B, the model also specifically accounts for experimental data indicating that precession is not as strong on the first traversal of the track on a given day (Mehta et al., 2002; Mehta et al., 1997). This occurs because forward spread in entorhinal cortex only influences CA1 firing when linked with temporal context from CA3. The model activity is plotted with Gaussian smoothing to match the format of published experimental data (Mehta et al., 2002) shown in Figure 9B1. In the model (Fig. 9B2), the absence of a recent temporal context on the first pass does not allow precession, which then appears on later passes through the same location. The simulation of both precession and splitter cell responses allows the model to predict that the context-selective response of a splitter cell should appear in later phases of theta rhythm during the period of maximal precession (Yamaguchi et al., 2002; Mehta et al., 2002), and should not appear on the first trial of a testing day.

Note that in addition to accounting for the context-dependent change in theta phase precession over trials on a given day, this model also shows the change in center of mass of place fields demonstrated in experimental work (Mehta et al., 1997). The shift in ECIII results from the strengthening of excitatory connections between neurons representing sequentially activated place fields, as in the model which initially motivated the Mehta experiment (Blum and Abbott, 1996). However, because the appearance of this shift in CA1 depends on temporal context, the model presented here effectively addresses the problem of how the shift in place fields could appear anew over multiple trials on each day of testing. The model presented here allows for a shift in place fields on each day of testing without requiring any weakening of previously modified connections.

Activity in different subregions

As described in the methods and appendix, the context-dependent retrieval of sequences in region CA1 results from the multiplicative interaction of forward associations in ECIII with temporal context mediated by ECII, the dentate gyrus and region CA3. The different patterns of neuronal response in these regions of the model described in the methods and Figure 5 are consistent with differences in experimental data. The retrieval of multiple associations in ECIII results in large place fields which are similar between environments (Barnes et al., 1990; Quirk et al., 1992), whereas the gating of activity in region CA1 by context results in small place fields and firing differences between contexts, most striking in splitter cells (Wood et al., 2000). The formation of distinct representations in dentate gyrus is consistent with the low probability of finding dentate gyrus place cells and their small place fields (Barnes et al., 1990; Jung and McNaughton, 1993). The retrieval of temporal context in region CA3 is consistent with the dependence of unit firing in region CA3 on the room containing an experimental apparatus (Leutgeb et al., 2004). The model proposes a graded response of CA3 units to context similarity, but does not yet address the non-linear shift to enhanced similarity with shared context (Lee et al., 2004b).

DISCUSSION

This model demonstrates how physiological properties of the hippocampal formation, including intrinsic mechanisms for sustained activity in entorhinal cortex (Klink and Alonso, 1997b) and theta rhythm oscillations (Buzsaki, 2002; Brankack et al., 1993), could play an essential role in differentiating episodes experienced at different times. The hippocampal simulation based on electrophysiological data effectively encodes and selectively retrieves previously experienced episodes. This selective retrieval allows effective performance of the delayed spatial alternation task, as shown in Figures 3 and 6. As shown in Figure 6C2, damage to these mechanisms effectively simulates the effect of fornix lesions on delayed spatial alternation (Olton et al., 1979; Aggleton et al., 1995).

The function of this model depends upon context-dependent retrieval, and the model proposes specific mechanisms for the context-sensitive responses of place cells, including splitter (episodic) cells described in spatial alternation tasks (Wood et al., 2000), and the increase in theta phase precession over early trials in a linear track (Mehta et al., 2002; Mehta et al., 2000; Mehta et al., 1997). In the model, the context-sensitive properties resulted from a circuit including sustained activity in entorhinal cortex layer II neurons which interact with hippocampal synaptic modification to provide decaying temporal context, allowing selective retrieval of specific recent episodes despite variable delays and despite interference from other recent episodes. The model of temporal context presented here was directly inspired by the work of Howard and Kahana on the role of temporal context in human verbal memory function (Howard and Kahana, 2002), and Howard's work on place cell responses in entorhinal cortex (Howard et al., 2004). The role of hippocampus in temporal context is consistent with lesion data showing that lesions of the hippocampus proper do not impair general associative memory, but do impair memory guided behavior which requires discrimination of one recent episode from other similar episodes (Agster et al., 2002; Eichenbaum et al., 1999). The specific role of CA3 in temporal context is consistent with context-dependent properties of CA3 units (Leutgeb et al., 2004) and effects of selective lesions of region CA3 (Lee et al., 2005). These simulations focus on retrieval of sequences of place cell representations, but the same mechanisms can be utilized for encoding and retrieval of sequences of other non-spatial behavioral states, including odors or reward (Wiener et al., 1989; Eichenbaum et al., 1999).

The main driving force for retrieval of sequences was the spread of activity across modified synapses in entorhinal cortex. Each element of a stored sequence evoked subsequent elements of the sequence. This resembles the mechanism used for sequence storage and theta phase precession in previous models of region CA3 (Tsodyks et al., 1996; Blum and Abbott, 1996; Wallenstein and Hasselmo, 1997; Lisman, 1999; Jensen and Lisman, 1996a), but specifically moves this mechanism to entorhinal cortex, motivated by the following experimental data. Active motor behavior in rats is accompanied by a large amplitude theta frequency oscillation in the EEG (Buzsaki, 2002). The trough of fissure theta is associated with a large current sink in stratum lacunosum-moleculare of region CA1 (Brankack et al., 1993; Buzsaki, 2002), which receives excitatory afferent input from layer III of entorhinal cortex. Comparison of the timing of this sink relative to the peak of pyramidal cell firing in region CA1 (Fox et al., 1986; Skaggs et al., 1996) indicates that the initial falling phase of this current sink occurs during the period of theta phase precession of place cell firing (Mehta et al., 2002; Yamaguchi et al., 2002). This suggests that an increase in the magnitude of excitatory activity within entorhinal cortex drives the apparent forward sequence retrieval underlying the precession of place cells in region CA1, CA3 and the dentate gyrus.

The use of entorhinal cortex for associative memory function is consistent with lesion evidence that the entorhinal cortex appears important for retrieval of multiple non-competing associations (Eichenbaum et al., 1994), whereas the hippocampus itself becomes involved when individual relational or episodic associations must be retrieved without interference (Eichenbaum and Cohen, 2003; Agster et al., 2002; Olton et al., 1979; Aggleton and Brown, 1999; Eichenbaum et al., 1994). This is also consistent with data showing that cutting the input from CA3 to CA1 does not impair recognition, but does impair selective recall (Brun et al., 2002). Thus, in this model, the entorhinal cortex provides the primary driving force for associative retrieval of sequences, whereas the selective retrieval of specific recent episodes requires small scale, metabolically undemanding changes in hippocampal synapses which can selectively choose between a variety of episodes associated with a specific cue. This framework provides a mechanism for rapid context-dependent changes in neuronal responses, without requiring the weakening of previously strengthened synapses. The Mehta studies described above were initially motivated by the prediction from the Blum-Abbott model that strengthening of synapses between sequentially activated place cells should cause backward expansion of place fields (Blum and Abbott, 1996). However, the experimental data had the puzzling characteristic that this shift occurs anew on each day (Mehta et al., 1997). This change could be accounted for by weakening of the representation on each day, but this is inconsistent with behavioral evidence for sparing of spatial representations over multiple days. Instead, the model presented here provides an alternate framework in which the learned representations of the spatial environment remain strong, but the place field expansion depends on a new episodic temporal context which interacts with the forward associations on each day. Differences in timing of synaptic modification in different regions of the model could account for the differences in shift of center of mass in CA3 versus CA1 (Lee et al., 2004a).

Note that this system has the advantage that the synapses which drive spiking are not those encoding the temporal context of the episodic representation. Associations stored in entorhinal cortex can be of equal strength for all encounters with a pair of patterns, and the same strong set of connections can store the associations. The episodic representation depends only upon a difference in synaptic strength in the hippocampus which can be very small, allowing very small changes in weight in the hippocampus to select which stored sequences are retrieved. Thus, relatively subtle and metabolically undemanding changes can encode a wide range of episodic representations based on stronger redundant associations in entorhinal cortex.

APPENDIX

Mathematical analysis of network function

This appendix provides mathematical analysis demonstrating how this model of the interaction of different hippocampal subregions during theta rhythm allows retrieval of previously experienced episodes. This analysis uses the equations presented in the main text, but additional notation indicates the time course of retrieval from a specific starting time ϕ in each theta cycle (e.g. θ_ec(t)= η^{τ/[t−ϕ]₁}). The equations model: Synaptic modification of recurrent connections in ECIII.

$$\Delta W_{ecIII}=b_c{b}_{c-1}^T$$ (1)

Excitatory activity in ECIII, and theta rhythm modulation in this region.

$$a_{ecIII}\left(t\right)=b_c+{\theta }_{ec}\left(t\right)W_{ecIII}{[a_{ecIII}(t-1)-{\psi }_{ec}]}_{+}{\theta }_{ec}\left(t\right)={\eta }^{\tau ∕{[t-\varphi ]}_1}$$ (2)

Excitatory activity in ECII combining afferent input b_c and previous activity:

$$a_{c,ecII}=b_c+\mu a_{c-1,ecII}$$ (3)

Synaptic modification at region CA3 recurrent connections, between spiking induced by dentate gyrus activity g_c and dendritic depolarization caused by ECII:

$$\Delta W_{ca3}=a_{ecII}{g}_c^T=\sum _{s=1}^c{\mu }^{(c-s)}{b}_s{g}_c^T$$ (4)

Excitatory activity in region CA3, and theta rhythm changes in depolarization within this region.

$$a_{ca3}\left(t\right)={\theta }_{ca3}\left(t\right)W_{ca3}{g}_{c-1}{\theta }_{ca3}\left(t\right)={\mu }^{{[t-\varphi ]}_1∕\tau }$$ (5)

Excitatory activity in region CA1.

$$a_{ca1}{\left(t\right)}_i={[a_{ecIII}{\left(t\right)}_i{}^{\ast }a_{ca3}{\left(t\right)}_i-{\psi }_{ca1}]}_H$$ (6)

These result in the episodic retrieval of prior sequences shown in equation 7.

$$a_{ca1}\left(t\right)=b_{o+t}$$ (7)

In equation 7, activity in CA1 changes with time steps t within each theta cycle, sequentially reading out the episode of behavioral states (with index o+t) that followed the previous visit to the same behavioral state. This read-out can be seen in Figure 3B and Figure 5B. The following sections describe how activity in each region of the model interacts to obtain this function, presenting mathematical analysis to show how equations 1-6 result in the episodic retrieval summarized in equation 7.

Entorhinal cortex layer III – Forward associations

Entorhinal cortex layer III stores associations between sequentially encountered behavioral states and retrieves these associations as shown in Figure 5A. As noted in the main text, the learning rule for synaptic connections in layer III of entorhinal cortex is based on ECIII activity a_ecIII representing the prior behavioral state b_c-1 and current state b_c:

$$\Delta W_{ecIII}=a_{ecIII}{a}_{ecIII}^T=b_c{b}_{c-1}^T$$ (1)

This results in a weight matrix which stores associations between sequential behavioral states starting from the first time step of behavior s=1 to the association between current behavioral state c and the preceding state c-1.

$$W_{ecIII}=\sum _{s=1}^c{b}_s{b}_{s-1}^T=b_2{b}_1^T+\dots +b_{o+1}{b}_o^T+\dots +b_s{b}_{s-1}^T+\dots +b_c{b}_{c-1}^T$$ (1b)

The change in entorhinal cortex layer III activity a_ecIII at time t results from the spread across W_ecIII as follows, along with afferent input activating the current behavioral state b_c:

$$a_{ecIII}\left(t\right)=b_c+{\theta }_{ec}\left(t\right)W_{ecIII}{[a_{ecIII}(t-1)-{\psi }_{ec}]}_{+}$$ (2)

This equation models the activity caused by repeated stages of excitatory synaptic transmission across glutamatergic synapses within entorhinal cortex. The spread occurs rapidly across synapses with AMPA time courses. As shown in Figure 5A, this spread starts afresh at each discrete state b_s, as memory time t counts up through integer values from one to T. The distance of spread depends upon a scalar theta function θ_ec(t) (described in the following section) which represents oscillatory changes in the membrane depolarization of neurons in entorhinal cortex causing phasic changes in firing during theta (Alonso and Garcia-Austt, 1987). In simulations, the output firing rate of the population is represented by a threshold linear function [a_ecIII(t)−ψ_ec]₊ which takes the value a_ecIII(t)−ψ_ec for a_ecIII,i(t) > ψ_ec and 0 otherwise. Activity only spreads as far as the units are above the threshold ψ_ec = η−ε, ε << η.

When the virtual rat first enters a new behavioral state, the equation will start with a_ecIII(0) set to zero. The new input will set a_ecIII(1) = b_c, and this input remains present during the remainder of time in that state, during both the encoding phase and the subsequent retrieval phase. Retrieval occurs when the cue of current behavioral state b_c resembles previous encounters with that state. If the current state resembles multiple previous encounters, it retrieves sequences based on all encounters. Thus, equation 2 will simultaneously show retrieval for a_ecIII(1) = b_c ≅ b_o1, b_o2...b_on, where the indices of o represent different previous visits. For example, at the choice point in Figure 3A, the current context c=11 resembles the 1st visit to the choice point o₁=3, causing progressive activation of the sequence of right arm states s=4,5,6. On the next visit (c=19), the current context resembles both the 1^st visit (o₁=3) and the 2nd visit to the choice point (o₂=11), and causes activation of both the sequence of right arm states (s=4,5,6) and the sequence of left arm states s=12,13,14. This spread of activity in both directions is shown in Figure 5A. The previous states o₁, o₂...o_n occurred d₁, d₂...d_n steps previously (so that b_on+dn = b_c). The intermediate states s_n follow previous states such that (c_n − s_n) + (s_n − o_n) = c_n − o_n = d_n. Note that the index for different previous visits will be implicit, without explicit inclusion in many of the following equations.

Equation 2 can be evaluated by inserting equation 1b, then computing a_ecIII for time t when a_ecIII(1) = b_c = b_o. Because θ_ec(t) changes on each time step, and the effect of threshold builds up on each step, equation 2 is difficult to evaluate analytically. For the purpose of describing system function, the system becomes easier to understand with two simplifications: the use of a single value of t to approximate the value of θ_ec(t) during the forward spread at a particular phase of theta rhythm, and the use of output from the threshold function which does not subtract the threshold (applied after Equation 2c). Comparison of simulations with and without these approximations show that the overall behavioral function of the network is similar, but without simplifications the retrieval has some curvature rather than the linear form of equation 7. The simulations presented in Figure 3 and Figures 5-10 used equation 2 without these simplifications, but these simplifications were used in the mathematical analysis below. When using a single value of θ_ec(t), equation 2 becomes:

$$a_{ecIII}\left(t\right)={\theta }_{ec}\left(t\right){[b_s{b}_{s-1}^T...{\theta }_{ec}\left(t\right){[b_{o+1}{b}_o^T{\theta }_{ec}\left(t\right){[b_o-{\psi }_{ec}]}_{+}-{\psi }_{ec}]}_{+}...-{\psi }_{ec}]}_{+}$$ (2b)

Assume that the active elements of each state b_s are 1, and the dot product of each state with itself $b_s^T{b}_s=X$, then express in sum form:

$$a_{ecIII}\left(t\right)=\sum _{s-o=0}^c{[{\left(X{\theta }_{ec}\left(t\right)\right)}^{(s-o)}{b}_s-\sum _{k=1}^{s-o}{(X{\theta }_{ec}\left(t\right))}^{\left(k\right)}{\psi }_{ec}]}_{+}$$ (2c)

To make the mathematical analysis clearer, the function [a_ecIII(t)−ψ_ec]₊ will be modified to take the value a_ecIII(t) for a_i(t)>ψ_ec and 0 otherwise, thereby removing the threshold effects on the far right side of equation 2c.

Entorhinal cortex layer III theta function

The retrieval process depends strongly on the choice of theta functions in the model, which utilize the parameters η and μ. The theta function for entorhinal cortex layer III is shown at the top of Figure 5. This theta function represents the rhythmic depolarization of neurons in this region during theta rhythm, consistent with extensive evidence for differences in firing of entorhinal neurons at different phases of theta rhythm (Alonso and Garcia-Austt, 1987). Here this scalar function is modelled as: θ_ec(t)=η^{τ/[t−ϕ]₁}, with the parameter (0 < η < 1). This function was chosen to result in a spread of excitatory activity to new behavioral state representations which is linear with the increase in time t during retrieval (Figure 5A). During encoding, interference from forward spread (Hasselmo et al., 2002c; Hasselmo et al., 2002b) is prevented by setting the function [t < ϕ]₁ = 1, so only direct afferent input b_s is transmitted. During the retrieval phase of each cycle, the function has the form[t − ϕ]₁ = t − ϕ and therefore θ_ec(t) = η^τ/(t−ϕ). When t > ϕ, This function allows a linear relationship between the retrieval time t-ϕ and the distance in spread from the old state b_o to new states b_s (see Figure 5A). The function resembles the shape of field potentials recorded in stratum lacunosum-moleculare of CA1 (see Fig. 1 (Buzsaki, 2002))

The mathematical analysis will focus on retrieval, when the theta function has the form θ_ec(t) = η^τ/(t−ϕ), and ϕ will be set to zero for simplicity (simulations used ϕ of 12). The constant X will be set to 1. The analysis focuses only on states for which all previous activity was suprathreshold. Thus, equation 2c can be simplified to:

$$a_{ecIII}\left(t\right)=\sum _{s=o}^c{\eta }^{\tau (s-o)∕t}{b}_s$$ (2d)

In this equation, the excitatory activity in entorhinal cortex layer III will spread to new patterns b_s in linear proportion to the memory time t. The sum includes activity of each state s between the old state o and the current state c. This linear spread of excitatory activity in layer III is shown in Figure 5A.

The simplified version helps illustrate the effect of the chosen theta function θ_ec(t), and resembles what occurs in simulations with the unsimplified versions (note that Figure 3 and Figures 5-10 use the unsimplified version). In the simplified version, imagine that the threshold only has an effect on the last step, and has the value ψ = η − ε (where ε is very small). In this case, the extent of suprathreshold spread in entorhinal cortex would be at η^{τ(s_n−o_n)/t} ≥ η. Taking the natural log and dividing through by lnη yields s_n − o_n ≤ t/τ. Thus, the extent of spread from the old state to new states s increases in linear proportion to t/τ. (Note that the direction of the sign changes because η < 1 and lnη is negative. Note also that the spread is equivalent for all stored sequences). Thus, all sequences from b_c ≅ b_o1, b_o2...b_on read out with a linear relationship between pattern number and retrieval time. This can be seen in Figure 5A, where the activity in entorhinal cortex spreads to additional states in a manner which is linear in time. Thus, the approximation used here is effective in describing network function without the approximation. Note that the activity spreads in both directions from the choice point.

This allows an important change in the index of summation. Because activity is zero unless s_n − o_n ≤ t/τ, the maximum step in summation c in equation 2d can be set to s_n ≤ o_n + t/τ.

$$a_{ecIII}\left(t\right)=\sum _{s=o}^{s\le o+t∕\tau }{\eta }^{\tau (s-o)∕t}{b}_s$$ (2e)

Entorhinal cortex layer II – Temporal context

The above activity will retrieve all sequences which followed a previously experienced state (e.g. from the stem, it will retrieve memories of both the left and right turn). Selection of an individual correct recent sequence for retrieval depends upon a reverse spread using temporal context (Howard and Kahana, 2002). The temporal context depends upon activity in layer II of entorhinal cortex (not layer III) containing an element of sustained activity from the previous behavioral state. This is consistent with data from slice preparations showing sustained depolarization due to cholinergically activated cation currents in layer II (Klink and Alonso, 1997b). Thus, entorhinal cortex layer II activity is represented with a separate equation in which the change in activity is caused by current input b_c plus an element of the vector of previous activity a_ecII, scaled by the parameter μ between 0 and 1:

$$a_{c,ecII}=b_c+\mu a_{c-1,ecII}$$ (3)

When evaluated iteratively for states s leading up to current state c, this yields:

$$\begin{array}{cc}\hfill & a_{ecII}=b_{c=1}\hfill \\ \hfill & a_{ecII}=b_{c=2}+\mu b_{s=1}\hfill \\ \hfill & a_{ecII}=b_{c=3}+\mu b_{s=2}+{\mu }^2{b}_{s=1}\hfill \\ \hfill & ...\hfill \\ \hfill & a_{ecII}=\sum _{s=1}^c{\mu }^{(c-s)}{b}_s\hfill \end{array}$$ (3b)

This mechanism allows temporal context to be proportional to the interval between current time c and the past event s. This allows reverse search using dentate gyrus and region CA3.

Dentate gyrus – distinct representations

In the model, the dentate gyrus forms a distinct representation g_c of each current state. In the simulations, a separate vector g is formed for each index s, even if a similar behavioral state is encountered (e.g. b_s=3 = b_s=11 but g_c=3 ≠ g_c=11), though the network can also function with reuse of g_c representations through a winner take all mechanism (O'Reilly and McClelland, 1994; Hasselmo and Wyble, 1997) in response to temporally sustained activity from layer II of the entorhinal cortex. The representation g_c is associated with the current ECII activity $W_{DG}=g_c{\sum }_{s=1}^c{\mu }^{(c-s)}{b}_s^T$, to allow dentate gyrus to retrieve a separate context for past episodes based on buildup of input from ECII, or the network can use current context. The distinct representation formed in dentate gyrus causes spiking in region CA3 via the mossy fibers. Modification of the excitatory recurrent connections in W_ca3 associates this spiking in CA3 with dendritic depolarization caused by input from layer II. This allows a mapping between a distinct representation g_c in the dentate gyrus and the temporal context.

Region CA3 – Distinct representations linked to temporal context

The synaptic connections arising from region CA3 neurons mediate the temporal context effect illustrated in Figure 5C. The distinct representation in the dentate causes spiking of distinct representations in region CA3 via the strong synaptic input of the mossy fibers, setting presynaptic activity in CA3 to the pattern g_c. In region CA3, modification of the excitatory recurrent connections W_ca3 then associates presynaptic spiking activity a_ca3 caused by the distinct representations g_c with postsynaptic dendritic depolarization caused by synaptic input from the entorhinal cortex. For simplicity and ease of visualization of activity, both the mossy fiber input and the direct entorhinal input to region CA3 are modeled with identity matrices, so the presynaptic activity consists of the input vector g_c and the postsynaptic activity consists of the entorhinal input vector a_ecII. Thus, CA3 synaptic modification takes the form:

$$\Delta W_{ca3}=a_{ca3}{a}_{ca3}^T=a_{ecII}{g}_c^T$$ (4)

As noted above, this synaptic input from entorhinal cortex (equation 3b) corresponds to events at prior points proportional to the time difference between the current time c (when the temporal context association is formed) and the time s of each prior event. Combination of equation 3b with 4 and summation results in weights in CA3 as follows:

$$W_{ca3}=\sum _{c=1}^N\sum _{s_n=1}^c{\mu }^{(c-s_n)}{b}_{s_n}{g}_c^T$$ (4b)

This associates distinct representations from dentate gyrus with the temporal context present at each point. Note that this network has a distinct representation for each behavioral state, but could function effectively with associations formed for g_c consisting of only a subset of states c, thereby using fewer dentate gyrus neurons. This subset of representations could be retrieved by the entorhinal input to dentate gyrus, activating a context formed after the episode being retrieved.

Retrieval involves activation of a dentate gyrus representation by current input from entorhinal cortex layer II that is at least one state in the past (i.e. g_c-1). g_c-1 then activates the representation formed on the recurrent connections in Wca3 as follows:

$$a_{ca3}\left(t\right)={\theta }_{ca3}\left(t\right)W_{ca3}{g}_{c-1}$$ (5)

Because the weights contain an exponential decay of temporal context over prior patterns, this results in activity with an exponential decay over prior patterns, as shown in Figure 5C. Note that here we use a recent context g_c-1, but the model also functions with reactivation of prior context representations which allow modeling of context dependent activity in this and other tasks (Wiener et al., 1989; Ferbinteanu and Shapiro, 2003).

Theta function in region CA3

The theta function in region CA3 was chosen both for its match with current source density data (Brankack et al., 1993) (Figure 7) and for its functional interaction with the theta function chosen for entorhinal cortex layer III (Figure 5). During each cycle of the theta rhythm, the scalar theta function for region CA3 results in a decrease in strength of excitatory spread in this region. This results from the function θ_ca3(t) = μ^{[t−ϕ]₁/τ}, where 0 < μ < η < 1, causing a decrease in reverse temporal context over time as shown in Figures 5C and 10B. During encoding, the theta function uses [t < ϕ]₁ = 1, whereas during the retrieval phase of the cycle when t > ϕ, the function uses [t−ϕ]₁ = t − ϕ and takes the form θ_ca3(t) = η^(t−ϕ)/τ. Here, analysis focuses on retrieval, during which the function results in a decrease in spatial spread over time as shown in Figure 5C and 10B. For mathematical analysis, ϕ will be set here to zero (simulations used ϕ=12). This yields:

$$a_{ca3}\left(t\right)={\mu }^{t∕\tau }\sum _{c=1}^N\sum _{s_n=1}^c{\mu }^{(c-s_n)}{b}_{s_n}{g}_c^T{g}_{c-1}={\mu }^{t∕\tau }\sum _{s_n=1}^{c-1}{\mu }^{(c-1-s_n)}{b}_{s_n}$$ (5b)

The dentate gyrus representations are non-overlapping, and analysis focuses on retrieval cued by a single distinct representation of recent context c-1, so summation over c was removed. In addition, the analysis will focus on retrieval of just a single recent episode n, so when the subscript is omitted, the index refers to the most recent episode.

Region CA1 – context-dependent selection of a specific memory sequence

During retrieval, the specific episode closest to a temporal context can then be retrieved by bi-directional search, mediated by a multiplicative interaction of entorhinal cortex input and region CA3 input on the distal dendrites of region CA1 neurons (Otmakhova et al., 2002). As retrieval progresses, the increasingly broadly distributed entorhinal activity enters region CA1 and undergoes an element by element multiplicative interaction with CA3 input.

$$a_{ca1}{\left(t\right)}_i={[a_{ecIII}{\left(t\right)}_i{}^{\ast }a_{ca3}{\left(t\right)}_i-{\psi }_{ca1}]}_H$$ (6)

The function []_H is a step function, with output value zero below threshold and value one above threshold. The membrane depolarization ν in region CA1 can be considered as just this multiplicative interaction without the thresholding function:

$$v_{ca1}{\left(t\right)}_i=a_{ecIII}{\left(t\right)}_i{}^{\ast }a_{ca3}{\left(t\right)}_i$$ (6b)

Combination of this equation with equations 2d and 5b above, results in:

$$v_{ca1}\left(t\right)=\sum _{s=o}^{s\le o+t∕\tau }{\eta }^{\tau (s-o)∕t}{b_s}^{\ast }{\mu }^{t∕\tau }\sum _{s=1}^{c-1}{\mu }^{(c-1-s)}{b}_s$$ (6c)

As shown in Figures 5B and 10C, this equation can provide linear sequential retrieval of the episode closest to the temporal context c (i.e. the episode with d₁ < d₂...d_n), with a constant amplitude dependent on d₁. The linear sequential readout occurs as long as η > μ, and the threshold in CA1 is scaled to ψ_ca1 = μ^d₁. The following steps will analyze equation 6b to show the sequential read-out of the episode as described in equation 7.

Equation 6c can be simplified by using the relationship between the indices for current state c, the old state o, and intermediate states s. In particular, the current state differs from the old state by the delay d, so that c = o + d. Therefore the index c − s = o + d − s = d − (s − o), so the equation becomes:

$$v_{ca1}\left(t\right)=\sum _{s=o}^{s\le o+t∕\tau }{\eta }^{\tau (s-o)∕t}{b_s}^{\ast }{\mu }^{t∕\tau }\sum _{s=1}^{o+d-1}{\mu }^{d-1-(s-o)}{b}_s$$ (6d)

Previously, it was shown for equation 2e that the spread of activity in entorhinal cortex stays within the limit (s − o) ≤ t/τ. In equation 6d, the activity of state s is largest for the largest integer value satisfying (s − o) ≤ t/τ, or s ≤ o + t/τ, as long as μ < η. This can be proven by showing that the activity at state s is larger than s-x for all positive integers x between 1 and s-o. If one considers individual states s (e.g. setting i = s), then the summation over states and the equivalent threshold function can be removed from equation 6d. Recall that in the behavioral state active elements b_s = 1. So for a single state i = s, equation 6d becomes:

$$v_{ca1}{\left(t\right)}_{i=s}={\eta }^{\tau (s-o)t}{\mu }^{t∕\tau }{\mu }^{d-1-(s-o)}$$ (6e)

The following steps simplify equation 6e further.

If the activity is larger for state s than for s-x, this can be expressed as the inequality:

$${\eta }^{\tau (s-x-o)∕t}{\mu }^{t∕\tau }{\mu }^{d-1-(s-x-o)}<{\eta }^{\tau (s-o)∕t}{\mu }^{t∕\tau }{\mu }^{d-1-(s-o)}$$

The equivalent values for time can be inserted, to obtain:

$${\eta }^{\tau (t∕\tau -x)∕t}{\mu }^{t∕\tau }{\mu }^{d-1-(t∕\tau -x)}<{\eta }^{\tau (t∕\tau )∕t}{\mu }^{t∕\tau }{\mu }^{d-1-(t∕\tau )}$$

This can be algebraically reduced to: η^1−xτ/tμ^d+x < ημ^d, which is μ^x < η^xτ/t. This inequality can be further simplified by focusing on the interval where 1 ≤ t/τ. In which case, η^x < η^xτ/t, and the inequality can be simplified to μ^x < η^x or μ < η. Thus, as shown in Figure 10C, the magnitude of activity in CA1 is largest for the largest integer s ≤ o + t/τ, when t ≥ τ and μ < η.

The fact that the activity is consistently largest in CA1 for the furthest spread of entorhinal activity, means that a threshold can be selected which will result in activity of just this state representation in region CA1. The pattern of activity associated with a specific sequence can then be selected by choosing a threshold ψ_ca1 which picks out the closest sequence (d₁ < d₂...d_n) and also avoids preceding patterns t-1 by satisfying η^1−τ/tμ^d < ψ_ca1 < ημ^d−1. For t ≥ τ, the largest value of the preceding pattern is at t = τ. So, this gives the result that η^1−τ/τμ^d = η⁰μ^d = μ^d < ψ_ca1. To simplify discussion, consider the case where τ = 1, to focus on the specific integer values of t. In this case, when the threshold is set at ψ_ca1 = μ^d₁ then the only suprathreshold activity is at s_n-o_n=t.

With the planned use of this threshold, Equation 6d can now be simplified by selecting only the states which will be suprathreshold, where s₁ = o₁ + t, giving the result:

$$v_{ca1}{\left(t\right)}_{s=o+t}=\sum _{s=o+t}^{o+t}{\eta }^{(o+t-o)∕t}{b_{o+t}}^{\ast }{\mu }^t\sum _{s=o+t}^{o+t}{\mu }^{d-1-(o+t-o)}{b}_{o+t}$$ (6f)

Which is simply:

$$v_{ca1}{\left(t\right)}_{s=o+t}=\eta {\mu }^{d-1}{b}_{o+t}$$

As shown in Figure 3B and 5B, the activity in region CA1 during retrieval time steps t recapitulates a linear sequence of each of the behavioral states on the interval s = o to s = o + T, with no variation in the size of individual elements b_s within an episodic memory, but with every element of the memory scaled by ημ^d−1 to the magnitude of the distance d_n of the first state o_n from the retrieval context.

Output of region CA1 – sequential retrieval

As shown in Figure 5B, the output of region CA1 shows selective retrieval of the sequence of behavioral states which most recently followed the current state. The output function generates unit output for neurons which are above threshold. Thus, applying the ouput function as in equation 7a:

$$a_{ca1}\left(t\right)={[\eta {\mu }^{d-1}{b}_{o+t}-{\mu }^d]}_H$$ (7a)

Gives the simple retrieval summarized in equation 7:

$$a_{ca1}\left(t\right)=b_{o+t}$$ (7)

The output of the network specifically generates the states which previously followed state o resembling the current state c. For higher resolution time bases, when τ ≠ 1 the activity spreads progressively to states with the largest integer value satisfying s ≤ o + t/τ. Note that the theta function for CA3 was specifically chosen in order to prevent a growth of activity levels with t in the network. Thus, the retrieval amplitude in CA1 does not change when the theta function in entorhinal cortex (due to widespread depolarization of cells in entorhinal cortex) increases in the same manner as the decrease in widespread depolarization in region CA3. The difference in magnitude of two memories does not vary dependent on their distance in the past, but on their distance d from a selected temporal context. Because memories do not decay, selection of an appropriate retrieval context can allow very old memories to read out with the same strength as new memories.

The above system is sensitive to variation in delay, since it requires computation of μ^d as the threshold. A more robust system can be developed by assuming that feedforward inhibition can scale the threshold to the current activity in CA1 ν_ca1(t) using a parameter γ.

$${\psi }_{ca1}=\gamma \sum _{s=o}^{s\le o+t∕\tau }{\eta }^{\tau (s-o)∕t}{\mu }^{t∕\tau }{\mu }^{d-(s-o)}\approx \gamma {\int }_{x=0}^{x=t∕\tau }{\eta }^{\tau \left(x\right)∕t}{\mu }^{t∕\tau }{\mu }^{d-\left(x\right)}$$ (7b)

In the simulations shown in Figures 3 and 5-10, the network works well with γ as a multiplier of the sum of a_ca1 activity, with a fixed value of γ (simulations worked well with values anywhere between 0.25 to 0.75). The use of a variable threshold dependent on region CA1 activity provides a very robust means of selecting individual sequences, allowing the system to operate with other theta functions with different time courses. The theta functions in entorhinal cortex and region CA3 were here chosen to provide a linear retrieval for ease of analysis and simulation of spatial alternation. However, linear retrieval may not be the optimal retrieval function for guiding behavior. An exponential relationship between behavioral state retrieval and t may be more appropriate, in which case the theta functions could be linear in t. Alternately, the network also performs well with oscillating functions shifted to be all positive, such as θ_ec(t) = cos(ωt + ϕ)².

This system has the advantage that the synapses which drive spiking are not those encoding the temporal context of the episodic representation. Associations stored in entorhinal cortex can be of equal strength for all encounters with a pair of patterns, and the same strong set of connections can store the associations. The episodic representation depends only upon a difference in synaptic strength in the hippocampus which can be very small, allowing very small changes in weight in the hippocampus to select which stored sequences are retrieved. Thus, relatively subtle and metabolically undemanding changes can encode a wide range of episodic representations based on stronger redundant associations in entorhinal cortex.