Shifting Paradigm of Association Studies: Value of Rare Single-Nucleotide Polymorphisms

Summary

Currently, single-nucleotide polymorphisms (SNPs) with minor allele frequency (MAF) of >5% are preferentially used in case-control association studies of common human diseases. Recent technological developments enable inexpensive and accurate genotyping of a large number of SNPs in thousands of cases and controls, which can provide adequate statistical power to analyze SNPs with MAF <5%. Our purpose was to determine whether evaluating rare SNPs in case-control association studies could help identify causal SNPs for common diseases. We suggest that slightly deleterious SNPs (sdSNPs) subjected to weak purifying selection are major players in genetic control of susceptibility to common diseases. We compared the distribution of MAFs of synonymous SNPs with that of nonsynonymous SNPs (1) predicted to be benign, (2) predicted to be possibly damaging, and (3) predicted to be probably damaging by PolyPhen. Our sources of data were the International HapMap Project, ENCODE, and the SeattleSNPs project. We found that the MAF distribution of possibly and probably damaging SNPs was shifted toward rare SNPs compared with the MAF distribution of benign and synonymous SNPs that are not likely to be functional. We also found an inverse relationship between MAF and the proportion of nsSNPs predicted to be protein disturbing. On the basis of this relationship, we estimated the joint probability that a SNP is functional and would be detected as significant in a case-control study. Our analysis suggests that including rare SNPs in genotyping platforms will advance identification of causal SNPs in case-control association studies, particularly as sample sizes increase.

Introduction

The common-disease common-variant (CDCV) hypothesis^1–4 has been the prevailing paradigm for case-control association studies for the past decade. Although the CDCV hypothesis¹ originally defined common polymorphisms as those with a population frequency of ≥1%, in practice researchers often exclude single-nucleotide polymorphisms (SNPs) that have frequencies <5% from case-control association studies. The International HapMap Project was designed to improve the efficiency of case-control association studies and intentionally targeted SNPs with minor allele frequencies (MAFs) of ≥5%.^5,6 Common SNPs (SNPs with MAF ≥5%) are preferentially queried in most case-control association studies for two major reasons: (1) the statistical power is not sufficient for rare SNPs when sample sizes are limited, and (2) common SNPs can significantly contribute to disease prevalence even if their effect on disease risk is modest.

Case-control association studies have led to the identification of several polymorphisms that affect a person's risk for common diseases, including Alzheimer's disease (APOE),⁷ type 2 diabetes (PPARG and KCNJ11),^8–10 and several others.^11–14 Furthermore, several common SNPs affecting cancer susceptibility have been identified.^15–18 However, many of these currently identified SNPs have modest effects on cancer risk and have low reproducibility.^19–23

It is also noteworthy that most of the cited studies were conducted with relatively small study samples (400–1000 study subjects). Recent technological advances enable genotyping of hundreds of thousands of SNPs in thousands of cases and controls (e.g., ²⁴ and ²⁵). A large sample size allows SNPs with MAF <5% to be analyzed. The dominance of the CDCV hypothesis has dissuaded genotyping companies from including rare SNPs in coding and promoter regions in their SNP genotyping panels. In this analysis, we evaluated the hypothesis that in large case-control association studies, targeting SNPs with MAF <5% is likely to be more effective than targeting common SNPs in detecting genetic susceptibility to common diseases, including cancer.

Material and Methods

Data Retrieval

We used the International HapMap database (rel22_Build36)²⁶ to retrieve data on the distribution of MAFs for SNPs annotated as intronic, synonymous, or nonsynonymous by the dbSNP database.^27,28 The HapMap data are subdivided into three groups or samples by race: whites of North European origin, Asians (Chinese and Japanese), and Yoruba in Ibadan, Nigeria. In this study, we separately analyzed CEPH and Yoruba samples because there is considerable variation in allele frequencies between them.^29–31 We did not include Chinese and Japanese samples because different sample sizes were queried: If analyzed separately, the sample size is lower than those for CEPH and Yoruba; if combined, the sample size is bigger. A separate analysis was run with SNPs data from the ENCODE project.³² We obtained the ENCODE data by sequencing ten 500 kb regions in 48 individuals (16 from each group). The novel SNPs detected by sequencing were then genotyped in all 269 HapMap DNA samples.³²

Data from the dbSNP database were used for the analysis of the relationship between MAF and the proportions of nsSNPs predicted to be protein disturbing. Not all SNPs reported in the dbSNP are true polymorphisms; according to some studies, the false-discovery rate might be as high as 10%.^33,34 To decrease the proportion of false discoveries in our sample, we used only frequency-validated SNPs. Thus, 6158 frequency-validated nsSNPs from 3912 genes were used in the analysis.

SeattleSNPs Database

The SeattleSNPs project generated SNP data for samples from both European and African populations. At the time of our access (August 2007), the database contained sequencing data from 307 genes ranging in length from 3 Kb (ICAM4 gene) to 653 Kb (SEC15L2 gene). The SNP data were available for 24 African descent (AD) and 23 European descent (ED) subjects. The total number of SNPs detected in the analysis included 31505 intronic, 764 synonymous, and 720 nonsynonymous SNPs. We did not include deletions, insertions, and sites with more than two alleles in the analysis. The SNPs were identified by sequencing of genomic DNA and, therefore, provide unbiased representation of different types of SNPs in gene regions. Because the number of nonsynonymous SNPs was low in this sample, we subdivided SNPs in ten MAF categories with increments of 5%. Nonsynonymous SNPs were subdivided into two groups: (1) benign (B) and (2) possibly or probably damaging SNPs (Pos.D./Prob.D.). We combined the possibly and probably damaging SNPs together because overall there were only 214 damaging SNPs.

Intronic Ratio

We used the ratio of absolute numbers of nsSNPs to the absolute number of intronic SNPs in a given MAF bin (intronic ratio) to visualize the effect of purifying selection.³⁵ A constant intronic ratio suggests that there are no differences in the intensity of purifying selection among MAF bins. Counts of the SNPs of different MAF categories for HapMap and SeattleSNPs samples are shown in Tables 1 and 2.

Table 1.

Counts of SNPs in Different MAF Categories in the HapMap Data Set

Population	MAFa	Type of SNP
		Intronic	S	B	Pos.D.	Prob.D.
CEPH	0–0.025	38755	5626	4675	1584	987
CEPH	0.025–0.05	5778	571	370	109	51
CEPH	0.05–0.075	5580	462	403	82	40
CEPH	0.075–0.1	5262	458	317	74	38
CEPH	0.1–0.125	5402	414	300	52	34
CEPH	0.125–1.15	5217	355	280	57	27
CEPH	0.15–0.175	5182	332	272	48	32
CEPH	0.175–0.2	5320	341	214	43	33
CEPH	0.2–0.225	5293	286	235	55	34
CEPH	0.225–0.25	5082	296	206	37	26
CEPH	0.25–0.275	5181	297	225	54	22
CEPH	0.275–0.3	5097	268	237	45	24
CEPH	0.3–0.325	5213	299	210	35	16
CEPH	0.325–0.35	4981	304	236	36	19
CEPH	0.35–0.375	5124	243	197	34	20
CEPH	0.375–0.4	5054	277	199	36	19
CEPH	0.4–0.425	5038	251	164	38	25
CEPH	0.425–0.45	5181	240	171	46	26
CEPH	0.45–0.475	5190	271	200	26	26
CEPH	0.475–0.5	5155	223	212	31	13
	Total	138085	11814	9323	2522	1512
		Type of SNP
Population	MAFa	Intronic	S	B	Pos.D.	Prob.D.
Yoruba	0–0.025	33463	4650	4230	1475	930
Yoruba	0.025–0.05	7351	745	512	135	72
Yoruba	0.05–0.075	6903	618	447	92	57
Yoruba	0.075–0.1	6521	542	369	84	54
Yoruba	0.1–0.125	6404	554	309	67	31
Yoruba	0.125–1.15	5950	498	368	70	34
Yoruba	0.15–0.175	5952	400	312	74	44
Yoruba	0.175–0.2	5804	417	263	42	20
Yoruba	0.2–0.225	5397	356	212	42	26
Yoruba	0.225–0.25	5311	389	232	35	28
Yoruba	0.25–0.275	5174	338	221	55	20
Yoruba	0.275–0.3	4996	317	211	33	30
Yoruba	0.3–0.325	4928	282	218	32	21
Yoruba	0.325–0.35	4757	247	196	28	13
Yoruba	0.35–0.375	4527	244	178	33	24
Yoruba	0.375–0.4	4614	236	187	36	22
Yoruba	0.4–0.425	4560	266	175	29	19
Yoruba	0.425–0.45	4532	262	177	36	23
Yoruba	0.45–0.475	4352	263	166	40	16
Yoruba	0.475–0.5	4548	226	169	27	15
	Total	136044	11850	9152	2465	1499

S, synonymous; B, benign; Pos.D., possibly damaging; and Prob.D., probably damaging SNPs.

^aIn each MAF category, the upper limit was included and the lower limit was excluded, e.g., 0.45–0.475 includes all SNPs with 0.45 < MAF ≤ 0.475.

Table 2.

Counts of SNPs of Different MAF Categories in the SeattleSNPs Data Set

Population	MAFa	Type of SNP
		Intronic	S	B	Pos.D.	Prob.D.
ED	0–0.05	20239	513	346	95	73
ED	0.05–0.1	2126	53	32	9	4
ED	0.1–0.15	1664	44	25	5	5
ED	0.15–0.2	1277	18	17	4	1
ED	0.2–0.25	1236	31	18	1	6
ED	0.25–0.3	1275	32	17	5	0
ED	0.3–0.35	952	17	19	0	0
ED	0.35–0.4	818	18	17	0	2
ED	0.4–0.45	981	22	9	1	0
ED	0.45–0.5	937	16	6	1	2
	Total	31505	764	506	121	93
		Type of SNP
Population	MAFa	Intronic	S	B	Pos.D.	Prob.D.
AD	0–0.05	15722	370	292	81	59
AD	0.05–0.1	4732	122	56	16	13
AD	0.1–0.15	2488	68	35	6	5
AD	0.15–0.2	1747	40	33	7	3
AD	0.2–0.25	1717	49	17	2	5
AD	0.25–0.3	1243	24	20	3	2
AD	0.3–0.35	1106	26	16	3	1
AD	0.35–0.4	812	13	9	0	3
AD	0.4–0.45	943	28	13	1	1
AD	0.45–0.5	995	24	15	2	1
	Total	31505	764	506	121	93

ED, European descent; AD, African descent; S, synonymous; B, benign; Pos.D., possibly damaging; and Prob.D., probably damaging SNPs.

^aIn each MAF category the upper limit was included and the lower limit was excluded, e.g., 0.45–0.5 includes all SNPs with 0.45 < MAF ≤ 0.5.

Prediction of Functional SNPs

NsSNPs that are likely to disturb protein structure or function can be predicted with bioinformatics approaches. Several bioinformatics tools for predicting the functionality of nsSNPs have been developed.^36–38 In this study, we used SIFT and PolyPhen to evaluate the functional significance of SNPs because those methods are the most frequently used.³⁶ SNPs predicted to be intolerant by SIFT were considered functional, and SNPs predicted to be tolerant were considered nonfunctional. For the PolyPhen-based prediction, possibly or probably protein-damaging SNPs were considered functional, and SNPs predicted to be benign were considered nonfunctional.

For estimating the relationship between MAF and the proportion of predicted protein-disturbing SNPs among nsSNPs, the nsSNPs were binned into 20 categories defined by MAF increments of 2.5%. For each MAF category, we computed the proportion of SNPs predicted to be protein disturbing. To compare MAF distributions for different types of SNPs, these were also were binned into 20 groups defined by MAF increments of 2.5%.

Radical and Conservative Missense Mutations

To stratify amino acid substitutions into radical and conservative, we adopted the classification system used by Dagan et al.³⁹ In brief, all amino acids were subdivided into three groups according to their charge: positive (R, H, and K), negative (D and E), and uncharged (A, N, C, Q, G, I, L, M, F, P, S, T, W, Y, and V). The amino acids were further subdivided by volume and polarity: special (C), neutral and small (A, G, P, S, and T), polar and relatively small (N, D, Q, and E), polar and relatively large (R, H, and K), nonpolar and relatively small (I, L, M, and V), and nonpolar and relatively large (F, W, and Y). Any substitutions that moved an amino acid from one category to another were considered radical, whereas substitutions that did not change amino acid category were classified as conservative. We performed separate analyses for radical (totaling 3695) and conservative (totaling 2463) substitutions.

Statistical Analysis

Spearman's nonparametric correlation was used for estimation of the association between MAF and the proportion of nsSNPs predicted to be protein disturbing, P(F). We used logarithmic regression, $P\left(F\right)=a\cdot \ln \left(MAF\right)+b$, and linear regression, $P\left(F\right)=a\cdot MAF+b$, to fit the binned data by the least-squares method.

Statistical power was computed by assuming a case-control design with independent cases and controls, and the data were analyzed by an uncorrected chi-square test.⁴⁰ The sample size was varied from 100 to 10,000 in increments of 100. The MAF was assumed to vary from 0 to 0.5 in increments of 0.025. Dominant and recessive models with genotypic risk ratios of 1.3 and 1.5 were considered. Critical p values of 0.05 were used.

Adjusting the Proportion of Functional nsSNPs by Sensitivity and Specificity of PolyPhen

The observed proportion of functional nsSNPs depends on the true proportion and on the sensitivity and specificity of the predicting method. Let P_tf be the true proportion of functional nsSNPs in a given MAF category (bin) and P_obs be the observed proportion of functional SNPs. For PolyPhen, the probability of identifying a SNP as functional when it is functional (sensitivity) is ∼0.82, and the probability of identifying a SNP as functional when it is nonfunctional (1 specificity) is ∼0.08.³⁸ The observed proportion of functional SNPs, given that the true proportion is P_tf, can be computed as follows: P_obs = P_tf·0.82 + (1 − P_tf) 0.08; therefore, P_tf = (P_obs − 0.08)/0.74. We used the latter equation to adjust the estimated proportion of protein-disturbing nsSNPs for the sensitivity and specificity of PolyPhen. We were not able to find estimates of specificity and sensitivity for SIFT and, therefore, were not able to provide a similar correction for the proportion of SNPs predicted to be functional by SIFT.

Results

Distribution of SNPs by MAF

The International HapMap Project²⁶ and the dbSNP database^27,28 were used as sources of data. We retrieved data from the International HapMap Project on the distribution of MAFs in coding regions (rel22_Build36). A separate analysis was run with SNPs data from the Encyclopedia of DNA Elements (ENCODE) project.³² The ENCODE data were obtained by sequencing ten 500 kb regions in 48 individuals (16 from each group). The novel SNPs detected by sequencing were then genotyped in all HapMap DNA samples.³²

We compared the proportion of SNPs in different MAF categories by using the ENCODE SNPs and all the HapMap SNPs (Figure 1). The total number of SNPs in the ENCODE data set was 93,149, and the total number of SNPs in the phase II HapMap database (rel22_NCBI_Build36) was 3,839,363 for the Centre d'Etude du Polymorphisme Humain (CEPH) population and 3,782,818 for the Yoruba population. Only parents were included in the analysis. SNPs were included in the analysis regardless of their MAF and binned into 20 MAF groups. We found that the proportion of SNPs with MAF <5% in the ENCODE data set (0.50 ± 0.01) was significantly greater than the proportion of rare SNPs in the entire HAPMAP data set (0.38 ± 0.01). Because ENCODE SNPs were identified by direct sequencing of a constant sample size, they are expected to be less biased than phase II HapMap SNPs for which the initial SNP discovery phase reflects a combination of pooled sequencing and direct sequencing conducted on varying number of subjects; this result strongly suggests that the majority of SNPs in the human genome have MAF <5%. The limited number of 45 individuals sequenced by ENCODE further suggests that the actual proportion of rare SNPs could be greater than 50%.

Figure 1.

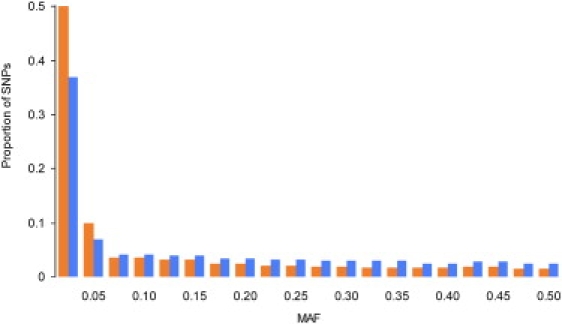
Distribution of SNPs from the Encyclopedia of DNA Elements and of All SNPs Reported in the International HapMap Database by Minor Allele Frequency

The distribution of encyclopedia of DNA elements (orange) and all single-nucleotide polymorphisms (SNPs) reported in the International HapMap database (blue) by minor allele frequency (MAF) are shown. All SNPs regardless of their functional category were included in the analysis.

MAF and the Intronic Ratio Based on HapMap Data

The ratio of absolute numbers of SNPs of specific categories reported in the database (e.g., nsSNPs) to the absolute number of intronic SNPs (here referred to as the intronic ratio) can be used as a relative measure of selection.³⁵ A constant intronic ratio across different MAF categories suggests that there are no differences in intensity of selection among MAF categories. An increased intronic ratio at low MAFs suggests purifying selection against nsSNPs. We computed intronic ratios for 20 MAF categories from the HapMap data for (1) nonsynonymous SNPs predicted to be probably damaging protein structure and function damaging (Prob.D.), (2) nonsynonymous SNPs predicted to be possibly damaging protein structure and function damaging (Pos.D.), (3) nonsynonymous SNPs predicted to be benign (B), and (4) synonymous SNPs (S). We used PolyPhen for prediction of functionality.³⁸ The list of nsSNPs with prediction of functionality can be found in Table S1 available online.

Figures 2A and 2D show the intronic ratios for nsSNPs for CEPH (Europeans) and YRI (Africans) samples correspondingly. We found that the intronic ratio was nearly constant for nsSNPs with MAF >20%. However, for nsSNPs with MAF <10%, and especially for SNPs with MAF <5%, the intronic ratio increased sharply, suggesting a strong effect of purifying selection. We further found that the relationship between MAF and intronic ratio for benign SNPs was similar to that for synonymous SNPs. We also found an increased intronic ratio at lower MAFs for Prob.D. and Pos.D. SNPs, suggesting stronger purifying selection against these categories. The intronic ratio was increased for rare synonymous and benign SNPs for HapMap data set, but this effect could reflect a bias against genotyping of rare intronic SNPs.

Figure 2.

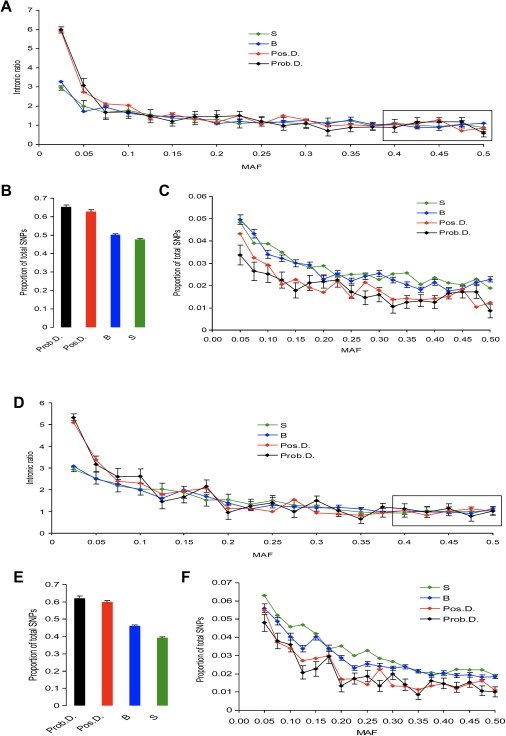
Distribution of Intronic Ratios and MAFs for Various Types of the HapMap SNPs in Coding Regions of the Human Genome: S, B, Pos.D., and Prob.D. SNPs

(A)–(C) show the CEPH (Europeans) sample; (D)–(F) show the YRI (Africans) sample. (A) and (D) show intronic ratios for synonymous SNPs (S), nonsynonymous SNPs predicted to be benign (B), nsSNPs predicted to be possibly damaging (Pos.D.), and nsSNPs predicted to be probably damaging (Prob.D.). Absolute numbers of S, B, Pos.D., and Prob.D. SNPs varied drastically, thereby making direct comparisons of intronic ratios difficult. For visual clarity, we scaled the average ratios to 1 by anchoring the distributions by their rightmost parts (i.e., 0.4–0.5). Standard errors (SEs) are shown for S and Prob.D. SNPs. (B) and (E) show the distribution of SNPs with 0–0.025 MAFs. The proportion of SNPs in the 0–0.025 MAF category is shown separately because it was much greater than proportions in the other categories. MAF was portioned into 20 bins by a 2.5% step. (C) and (F) show the proportion of SNPs in MAF >0.025 categories.

Comparison of MAF Distributions of SNPs of Different Functional Types in the Coding Region Based on HapMap Data

Not all SNPs reported in the database are true polymorphisms; according to some studies, the false-discovery rate might be as high as 10%.^33,34 To decrease the proportion of false discoveries in our sample, we used only frequency-validated SNPs. Thus, 6158 frequency-validated nsSNPs from 3912 genes were used in the analysis.

We found that the MAF distribution of the probably damaging SNPs (SNPs that are most likely to disturb protein structure and function) was left-shifted in CEPH and YRI samples (Figures 2B, 2C, 2E, and 2F). There was also a trend for SNPs that were likely to be functional to have lower MAF. The difference between SNP categories suggests that purifying selection shapes MAF distributions of SNPs in the coding region. We excluded intronic SNPs from this analysis of MAF distributions because of a bias against genotyping intronic SNPs; intronic SNPs are less likely to be chosen for genotyping by HapMap compared with the SNPs in the coding regions.

Intronic Ratios and MAF Distributions Based on SeattleSNPs Data

Figures 3A and 3D show the intronic ratios for SNPs identified by sequencing of genomic DNA (SeattleSNPs database) for the subjects of European and African descent correspondingly. We found that in European subjects in the group of rare SNPs (MAF ≤0.05) the intronic ratio for Pos.D./Prob.D. SNPs was 3.74 ± 0.18, which was significantly higher compared to the intronic ratio for both synonymous (1.23 ± 0.14) and benign (1.41 ± 0.17) SNPs (t test for S versus Pos.D./Prob.D. SNPs was 9.6, N = 32,269, p << 0.001). No significant differences were detected between benign and synonymous SNPs. Intronic ratios for these two types of SNPs were constant across MAF categories. Similar results were obtained for the subjects of African descent (Figure 3D).

Figure 3.

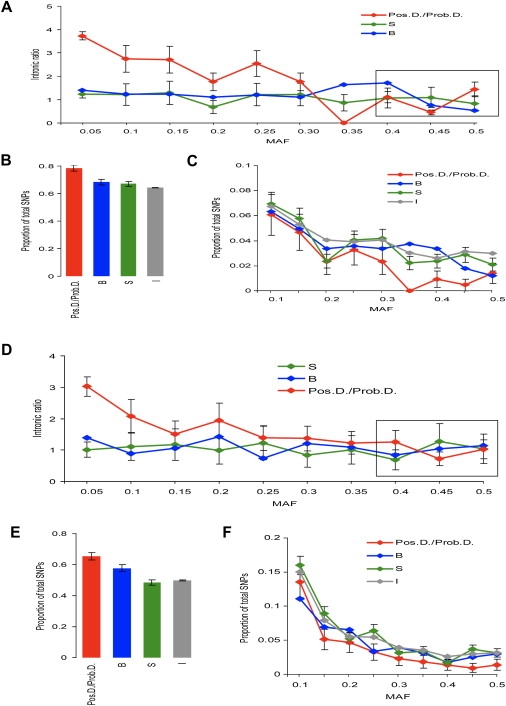
Distribution of Intronic Ratios and SNPs by MAF Categories, SeattleSNPs Database

(A)–(C) show European descent; (D)–(F) show African descent. (A) and (D) show intronic ratios for synonymous SNPs (S), nonsynonymous SNPs predicted to be benign (B), nsSNPs predicted to be possibly or probably damaging (Pos.D./Prob.D.). The distributions were anchored by their rightmost parts similarly as in Figure 2. SEs are shown for S and Pos.D./Prob.D. SNPs. (B) and (E) show the distribution of SNPs with 0–0.05 MAFs. Proportions of SNPs in 0–0.05 MAF category are shown separately because they were much greater than proportions in the other categories. (C) and (F) show proportions of SNPs in MAF >0.05 categories.

Figures 3B, 3C, 3E, and 3F show the distribution of MAF for intronic, synonymous, benign, and damaging SNPs among Europeans and Africans correspondingly. For Europeans, we found that the proportion of Pos.D./Prob.D. SNPs was highest in MAF 0–0.05 (0.78 ± 0.02); the proportion of benign SNPs was not significantly different from the proportion of synonymous SNPs, with 0.68 ± 0.02 and 0.67 ± 0.02, correspondingly. The proportion of intronic SNPs in the MAF category 0–0.05 (0.64 ± 0.01) tended to be lower compared to that of benign and synonymous SNPs. Similar results were obtained for the subjects of African descent (Figures 3E and 3F).

Relationship between MAF and the Proportion of Protein-Damaging SNPs

We analyzed the relationship between the MAF and the proportion of nsSNPs predicted to be protein damaging by PolyPhen (Figure 4A) (Spearman's correlation coefficient was −0.75, n = 25, and p < 0.001). The logarithmic regression of the observed proportion of functional nsSNPs on the MAF was $\stackrel{⌢}{P}\left(F\right)=-0.04\cdot \ln \left(MAF\right)+0.17$. In this case, logarithmic regression explained 79% of the variation and also fitted the data better than did linear regression, which explained 56% of the observed variation. For the PolyPhen method, we also adjusted the prediction curve by PolyPhen sensitivity and specificity as described in the Material and Methods.

Figure 4.

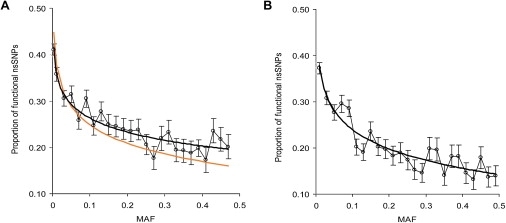
Proportion of Nonsynonymous Single-Nucleotide Polymorphisms Predicted to be Protein Damaging Plotted against Minor Allele Frequency

Each point represents the proportion of functional nsSNPs in a given MAF category. (A) shows the proportion predicted by the PolyPhen method. Dark solid lines are the logarithmic-regression curves. The orange line is the regression curve adjusted for PolyPhen's sensitivity and specificity (see Material and Methods for details). Vertical bars represent SEs computed on the basis of the multinomial distribution. (B) shows the proportion predicted by the sorting intolerant from tolerant (SIFT) method.

A similar result was obtained for the proportion of the nsSNPs predicted to be protein damaging by sorting intolerant from tolerant (SIFT).⁴¹ MAF was negatively correlated with the proportion of SIFT-predicted protein-damaging nsSNPs (Spearman's nonparametric correlation coefficient was −0.73, n = 25, and p < 0.001) (Figure 4B). Logarithmic regression explained 74% of the observed variation and fitted the data better than did linear regression, which explained only 54% of the variation.

Obviously MAF is not the only indicator of the probability that a SNP is functional. The category of SNP is also associated with its functionality. For example, synonymous SNPs are less likely to be functional compared with nsSNPs. If we consider SNPs from a specific functional category (e.g., synonymous SNPs), the overall probability for SNPs from that category to be functional will vary from that for SNPs in other categories. Within a category, however, one can expect to see the same inverse relationship between MAF and the proportion of functional SNPs because purifying selection will drive down MAFs of functional SNPs. We compared the proportion of SNPs predicted to be functional separately for nsSNPs producing radical mutations and for nsSNPs producing conservative missense mutations (Figure 5). A radical missense mutation replaces wild-type amino acid with an amino acid that is chemically different, whereas conservative mutations replace wild-type amino acids with chemically similar ones. Therefore, the overall proportion of functional substitutions is expected to be greater among radical missense mutations than among conservative ones. We found that the overall probability that a SNP is functional is almost two times greater for nsSNPs producing radical missense mutations than for nsSNPs producing conservative missense mutations. We also found that the logarithmic-regression curves of the proportion of functional SNPs on MAF were very similar for these two types of SNPs, suggesting that the same factors influence MAF-functionality relationships for SNPs having different prior probabilities to be functional.

Figure 5.

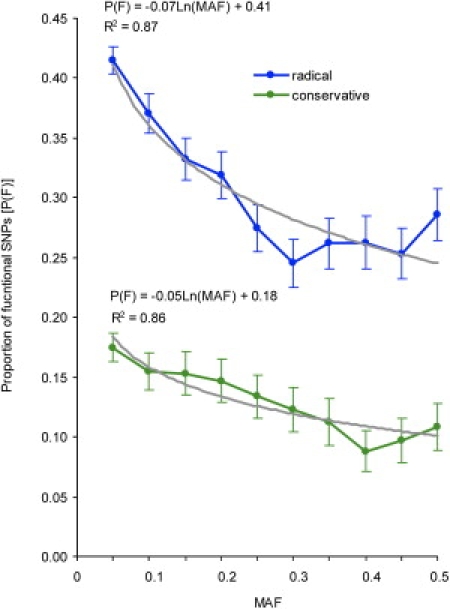
Conservative versus Radical Amino Acid Substitutions

Proportions of functional SNPs among radical (blue line) and conservative (green line) amino acid substitutions are shown. Vertical bars represent SEs. Predictive curves (gray) and equations are shown separately for radical and conservative substitutions.

Statistical Power to Detect Effects of Rare SNPs

Statistical power depends on many factors including effect size (usually expressed as the odds ratio [OR]), sample size, mode of inheritance (e.g., dominant or recessive), and MAF. The statistical power is generally lower for rare SNPs than for common SNPs of a similar effect size. Figure 6 illustrates the relationship between statistical power and the needed sample size for a series of SNPs with MAF ≤5%, assuming a dominant model. For a SNP with OR = 1.5 and MAF = 5%, a sample size of 1862 (931 cases and 931 controls) would be needed to achieve 80% statistical power to detect the effect at a p level of 0.05. For a SNP with OR = 1.5 and MAF = 2.5%, the required sample size would be 3420, and for MAF = 1%, the required sample size would exceed 8120. The power is very sensitive to the OR. With OR = 2 and MAF = 5%, the required sample size is 580 (290 cases and 290 controls). For the same OR and MAF = 2.5%, the required sample size is 1050, and for MAF = 1%, the required sample size is 2450. This shows that when the effect of rare SNPs is relatively high (OR ≥2), there is sufficient power to detect the effect of a rare SNP, even for a modest sample size of 1000.

Figure 6.

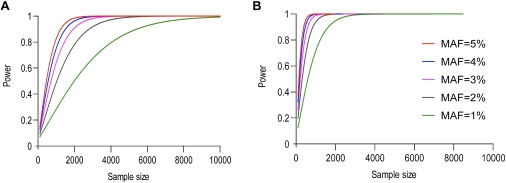
Relationship between Statistical Power and Needed Sample Size

The model shows a dominant causal single-nucleotide polymorphism with a minor allele frequency (MAF) ≤5%. (A) shows OR = 1.5, and (B) shows OR = 2.0. We used a 5% significance level. The power calculations were performed on the basis of the assumption that only one SNP is being typed (no corrections for multiple testing).

Power to Detect a True Association

Not all nsSNPs are functional and impart a potential to be disease associated. Statistical power predicts the probability that a SNP will be detected as significant conditional on its being functional, which we denote as P(S,F). Thus the joint probability that a SNP is significant and functional is expressed as P(S,F) = P(S|F)P(F), for which P(S,F) is the joint probability that a SNP is significant and functional, P(S|F) is the power, and P(F) is the probability that a SNP is functional. If we assume P(F) = 1, we will obtain the statistical power that is usually used to design case-control association studies. Our analysis demonstrated, however, that the probability that a SNP was functional was negatively correlated with MAF, whereas the probability that a SNP will be detected as significant was positively correlated with MAF. In other words, there is a trade-off between gain in probability of detection and loss in the proportion of functional SNPs when MAF increases. To account for this inverse relationship, we used the P(S,F) = P(S|F)P(F) formula to compute the joint probability that a SNP is functional and will be detected as significant. We defined this joint probability as the power to detect a true association (PDTA), which predicts statistical power when P(F) ≠ 1 but depends on MAF.

Figure 7 gives a quantitative example of computing PDTA and shows that PDTA first increases, reaches a maximum, and subsequently decreases. The MAF at which PDTA is maximal is an important parameter for the design of a case-control study because it maximizes the chance that a functional SNP will be detected as significant. The MAF at which PDTA is maximal was denoted as the most powerful MAF (mpMAF).

Figure 7.

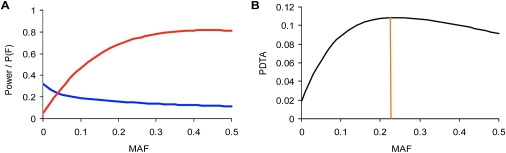
Example of Computing Probability to Detect True Association and Most Powerful Minor Allele Frequency

Study of single-nucleotide polymorphisms in a dominant model of inheritance with 300 cases and 300 controls. An OR = 1.5 was assumed. In (A), the red line shows the dependence of the statistical power on minor allele frequency (MAF), and the blue line shows the predicted proportion of functional SNPs P(F), predicted by formula 1. (B) shows the dependence of PDTA on MAF. The mpMAF is marked by the vertical line, which indicates ∼0.22 in this case.

For this and other computations of PDTA, we used a conservative assumption that the OR did not depend on MAF and that only the proportion of functional SNPs did. However, rare SNPs might disturb gene function to a greater extent than common SNPs and therefore have higher ORs. If this is true, statistical power should increase with the increasing rarity of SNPs compared with a model with a constant OR.

Like statistical power, PDTA depends on sample size, effect size, inheritance model, and MAF. PDTA's dependence on the sample size is important because sample size is one of the key parameters in case-control-study design. We computed PDTAs for a set of sample sizes and MAFs. Recessive and dominant models were analyzed (Figure 8). Ridges on the PDTA surfaces mark MAFs at the mpMAF, where the PDTA is maximal. The mpMAF ridge was much sharper for the dominant model than the recessive model, suggesting that a given deviation in MAF from the mpMAF leads to a much stronger decrease in the PDTA in the dominant model than in the recessive model.

Figure 8.

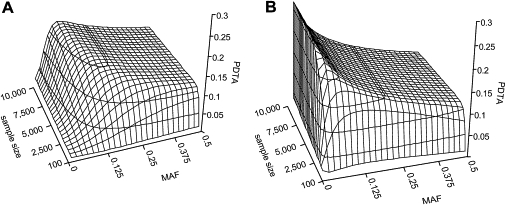
Dependence of the Probability to Detect a True Association on Minor Allele Frequency and Sample Size

Equal sample sizes for cases and controls were assumed, and the total sample size is shown. OR = 1.5 in both the (A) recessive and (B) dominant models.

The results presented in Figure 8 suggest an inverse relationship between mpMAF and sample size. We further investigated the relationship between mpMAF and sample size by computing PDTAs and mpMAFs for dominant and recessive models with ORs of 1.3 and 1.5. We found that for all scenarios, mpMAF decreased as the sample size increased (Figure 9). For the dominant model, with a modest OR of 1.5, mpMAF was <5% when the sample size was ≥1500. For the recessive model, with an OR of 1.5, mpMAF was <5% when the sample size was ≥6000. We also found that, given the same sample size, mpMAF was higher for lower ORs (for a given sample size, mpMAF increased as OR decreased). mpMAFs were higher for the recessive model than for the dominant one.

Figure 9.

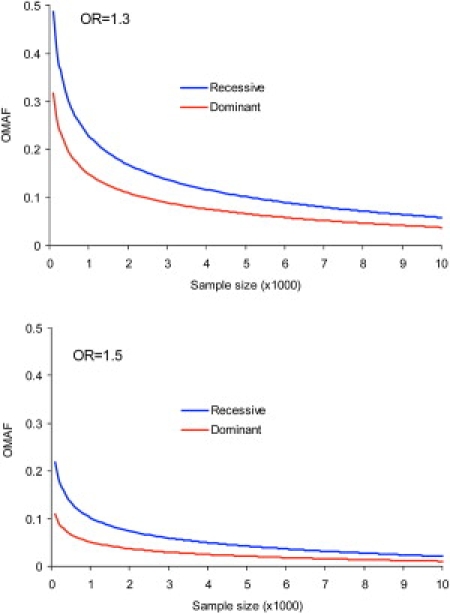
Predicted Dependence of Most Powerful Minor Allele Frequency on the Sample Size

Recessive (blue lines) and dominant (red lines) models were assumed. The sample comprises equal numbers of cases and controls, and the total size is shown. (A) shows OR = 1.3. (B) shows OR = 1.5.

Discussion

Genetic Architecture of Common Disease

The number and penetrance of alleles affecting disease risk, i.e., the genetic architecture of a disease, directly affect the strategy for identifying polymorphisms that modulate disease susceptibility. Few theoretical analyses of the genetic architecture of common human diseases have been published.^42–44 The expected number and distribution of disease alleles in the population depend on mutation rate, selection, and population demography. Mutation rate in this case means mutation rate for disease alleles. This rate depends on the number of the potential sites for deleterious disease-causing mutations in the disease-related gene and also on the number of disease genes in the genome. The disease mutation rate is higher than the nucleotide-substitution rate, which is estimated as ∼10⁻⁸ mutations per nucleotide per generation.^45,46 By assuming that (1) the disease mutation rate is ∼10⁻⁶ disease-associated mutations per disease locus, that (2) a single dramatic expansion of the human population occurred approximately 70,000 years ago, and (3) that no genetic drift has occurred, Reich and Lander⁴⁴ concluded that one or two common polymorphisms can explain genetic susceptibility to common human diseases. However, the analysis probably oversimplifies the real situation because it assumes no bottlenecks or effects of genetic drift for susceptibility mutations. Pritchard,⁴² who used stochastic modeling to estimate the level of genetic diversity for common diseases, concluded that “it is unlikely that any single mutation will constitute a large fraction of the susceptible class.” Simulation analysis of the genetic architecture of common human diseases by Peng and Kimmel⁴⁷ demonstrated that mutation spectra are expected to be simple for a single-locus model. If, however, a common disease is caused by multiple loci, then a diverse allelic spectrum with rare causal alleles is predicted.

Recently, Kryukov et al.⁴⁸ combined analysis of mutations causing human Mendelian diseases, of human-chimpanzee divergence data and the data on human genetic variation, and found that ∼53% of new missense mutations have mildly deleterious effects. The authors also found that up to 70% of low-frequency missense alleles are mildly deleterious. Kotowski et al.⁴⁹ used sequencing to identify rare polymorphisms in the PCSK9 gene controlling plasma levels of low-density lipoprotein cholesterol. The authors identified several rare nsSNPs with strong phenotypic effects on cholesterol level, providing support for the importance of including rare sequence variants in association studies.

As noted above, the major parameter that defines the diversity of disease alleles in a population is mutation rate per gene per generation. Unfortunately, there are no reliable estimates of this parameter. Reich and Lander⁴⁴ estimated a mutation rate for disease-associated mutations as 3.2 × 10⁻⁶. Pritchard's⁴² estimate ranged from 2.5 × 10⁻⁶ to 1.3 × 10⁻⁴. Estimates based on the analysis of mutations reported in the human gene mutation database^50,51 suggest that the mutation rate for slightly deleterious mutations is ∼10⁻⁵. If the mutation rate for susceptibility alleles is ∼10⁻⁵ or higher, it is likely that the genetic architecture of common diseases is diverse and that there are many susceptibility alleles in the population. Another factor that affects the genetic architecture of common disease is the number of genes contributing to genetic control of disease susceptibility. If several genes affect disease susceptibility, it is likely that many polymorphic susceptibility variants underlie disease risk. For many common human diseases, there are probably many susceptibility loci.

Cancer is a good example of a common disease with many loci affecting disease susceptibility. The development of cancer is a multistage process that involves genes important for cell-cycle control, cell proliferation, apoptosis, angiogenesis, and other cellular-pathway functions. Therefore, it is plausible to suggest that many causal SNPs modulate cancer susceptibility. We suggest that sdSNPs, which are subjected to weak purifying selection, are the major players in genetic control of susceptibility to many common diseases. However, cancer is predominantly a disease of late age when reproduction is mostly completed. Therefore, natural selection could not have affected the frequencies of alleles in cancer genes purely on the basis of their effect on cancer risk. On the other hand, genes that affect the risk of cancer did not evolve merely as cancer-risk genes; this function emerged relatively recently with the recent increase in life expectancy. Cancer suppressors and oncogenes play an important role in the control of the cell cycle, apoptosis, angiogenesis, and development processes that are under pressure of purifying selection. Therefore, protein-damaging mutations in cancer-related genes would be expected to be under the pressure of purifying selection and thus to have a lower population frequency.

SdSNPs and MAF

SdSNPs are not eliminated from the population because the reduction in fitness they cause is too small. If we assume that the observed population frequency of sdSNPs is a result of equilibrium between purifying selection and mutations, then the intensity of purifying selection against sdSNPs can be estimated on the basis of the classical formula q = μ/hs, where q is the equilibrium frequency of a mutant allele, μ is the mutation rate per generation, h is the dominance coefficient, and s is selection coefficients.⁵² Accepting that μ is ∼10⁻⁸ (see ⁴⁵ and ⁴⁶) and h is ∼0.1 (see ⁵³) and assuming q = 0.05, the selection coefficient will be ∼10⁻⁶ − 10⁻⁵. Genetic drift is expected to affect the population frequency of deleterious alleles when s << 1/N_e, where N_e is the effective population size. There is general agreement that for the human population, N_e is ∼10⁴.⁵⁴ Therefore, it follows that selection and drift play a role in the distribution of MAFs for sdSNPs. This might also explain the existence of causal SNPs with high MAF for some common human diseases.^11–14

The high prevalence of SNPs with low MAF among nsSNPs, higher intronic ratios for rare SNPs, and the inverse relationship between the proportion of protein-damaging SNPs and MAF strongly suggest that functional SNPs are under weak purifying selection and therefore tend to have lower MAFs. With respect to intronic ratio, we acknowledge that the increase of intronic ratio for low MAF can be a result of genotyping bias against intronic SNPs, especially those with low MAF when HapMap data are analyzed. It is also possible that some synonymous SNPs can be functional because of their effect on splicing or codon usage.^55–58 Recent studies demonstrated that synonymous SNPs undergo a slight purifying selection.^59,60

Results of our study are in agreement with other reports on the negative correlation between MAF and the proportion of functional SNPs.^35,61 Cargill et al.³⁵ analyzed 392 SNPs located in the coding regions of 106 genes and found that the proportion of nsSNPs was highest among SNPs with a low MAF. Wong et al.⁶¹ observed a similar relationship between MAF and the proportion of nsSNPs predicted to be protein damaging. The results of our analysis of the relationship between MAF and the proportion of functional SNPs are based on a much larger number of SNPs than that previously studied, and they are in agreement with previous studies and provide a more comprehensive picture of the relationship between MAF and the proportion of protein-damaging SNPs.

In this study, we used two data sets to retrieve MAF data: the HapMap and SeattleSNPs. The HapMap sample size is much larger compared to the SeattleSNPs sample size. However, the HapMap database is likely to underreport intronic SNPs, especially those with low MAF. This bias is probably the major source of the increased intronic ratio for benign and synonymous SNPs at low MAF category (Figures 2A and 2D). The intronic ratio was constant for benign and synonymous SNPs when the SeattleSNPs data were analyzed (Figures 3A and 3D). We cannot exclude also that a weak purifying selection against benign and synonymous SNPs might as well have contributed to the increased intronic ratio for benign and synonymous SNPs as suggested from the analysis of MAF distributions (Figures 3B, 3C, 3E, and 3F).

Our analysis was based on the assumption of the independence of SNPs. This is violated to some extent due to linkage disequilibrium (LD) between SNPs. If SNPs that are in strong LD tend to have similar MAFs, then the number of independent observations will be lower than the number of SNPs in the analysis. It is difficult, however, to imagine a biological phenomenon that can link MAFs of the SNPs on the basis of their position. We are not aware of any studies that address this phenomenon on a genome-wide level. Nevertheless, we have addressed this concern by analysis of singletons—single SNP per gene. In our data set, ∼47% of nsSNPs are singletons. Those SNPs are unlikely to be in strong LD unless the genes are located very close to one another. The analysis conducted with singleton SNPs yielded very similar results in terms of MAF distribution between benign and possibly and probably damaging SNPs (data not shown).

Most SNPs in the Human Genome Are SNPs with MAF <5%

The MAF distribution of SNPs from the International HapMap Project shows that more than 40% of SNPs have MAF <5%. Because the International HapMap Project preferentially targeted common SNPs, the real proportion of rare SNPs is definitely higher than 40%. We estimate, on the basis of ENCODE data, that ∼60% of SNPs have MAF <5%. This estimate is supported by Wong et al.,⁶¹ who sequenced 114 genes from the Environmental Genome Project.^62,63 A total of 64, 38, and 12 genes were sequenced in 44, 90, and 450 individuals, respectively. Across this gene set, each base was evaluated on an average sample size of 84 individuals. The authors found that SNPs with MAF <5% constituted >60% of the total number of SNPs. If we include SNPs with MAF < < 1% in our analysis, the proportion of rare SNPs will be even higher. On the basis of practical considerations, we suggest that rare SNPs be considered those with MAF ≥0.5% and ≤5%. Indeed, current sample sizes do not allow effective detection and comparison of frequencies of SNPs with MAF <0.5%. Another reason for setting the lower limit at 0.5% for rare SNPs is that very rare SNPs would need extremely high penetrance (similar to that for dominant Mendelian mutations) to greatly affect the prevalence of disease.

Conclusions

We hypothesized that interindividual variation in susceptibility to common diseases is mainly caused by sdSNPs in genes implicated in disease pathways. Our hypothesis suggests that causal SNPs have low MAF; however, the low population frequency of the causal SNPs is compensated for by the large number of such SNPs in the genome. The deleterious effect of sdSNPs is deleterious enough to impair gene function and increase disease risk. It is, however, not strong enough for selection to totally eradicate them from the population (genetic drift, founder effects, and population bottlenecks are factors that help retain sdSNPs).

The principal difficulty in explaining common diseases by sdSNPs is that sdSNP might be too rare to explain the observed disease's prevalence. The high proportion of rare SNPs in the genome, however, can counter the low MAF of the causal SNPs. According to the Build 126 of the dbSNP database, there are >56,000 nsSNPs in the human genome. The real number of nsSNPs is probably higher because rare SNPs are underreported. If we assume that there are twice as many nsSNPs as there have been reported today⁶⁴ and half of these nsSNPs are slightly deleterious with MAF <5%, and that there are ∼24,000 genes in the human genome, there should be two to three rare sdSNPs per gene. The real number might be higher still because we did not consider promoter SNPs or SNPs located in sites important for splicing. This suggests that the effect of rare sdSNPs on disease prevalence can be substantial.

Our many rare SNPs hypothesis suggests that targeting rare SNPs in large case-control association studies has more power to detect causal SNPs than does targeting common SNPs. We found that there is a negative correlation between sample size and mpMAF, and this explains why most of the causal SNPs identified to date are common. Indeed, studies that have identified (and confirmed) causal SNPs used sample sizes of between 500 and 1000 subjects; for such sample sizes, the mpMAF ranges from 8% to 30%, depending on the OR and type of model. For case-control studies with sample sizes of ≥2000, the mpMAF is expected to be <5% (at least for the dominant model), suggesting that targeting rare SNPs in large studies might be a better strategy for identifying causal SNPs than targeting common SNPs, which are less likely to be functional. We conclude that targeting SNPs with MAF <5% in large case-control studies is a sound strategy to identify causal SNPs. Direct sequencing of candidate regions in a subset of cases and controls (e.g., 100 cases and 100 controls) can be used to identify rare SNPs. Those rare SNPs should be then genotyped in the whole sample with custom-designed chips.

We believe that targeting rare potentially functional SNPs (nsSNPs and SNPs located in promoter regions) can be a more appropriate strategy to understand the genetic architecture of many complex diseases compared with the strategy that targets common SNPs. Therefore, a practical recommendation from our analysis is the need for genotyping rare SNPs, especially those from the coding and promoter regions, into genotyping platforms. Another application of our analysis relates to assigning priors in Bayesian association analysis framework—SNPs can be assigned different prior weights depending on their MAFs, with higher weights being given to those with lower MAF.

In conclusion, we hypothesized that numerous rare functional SNPs are major contributors to susceptibility to common diseases, including cancer. The analysis of joint probability that a SNP is functional and that it will be detected as significant in a case-control study demonstrated that, for a given sample size, there is a MAF for which this joint probability is maximal—the most powerful MAF. We found that the larger the sample size, the lower the mpMAF, suggesting that for studies with large sample sizes (5000 and higher) targeting rare SNPs will be a better strategy for identifying causal SNPs than targeting common SNPs.

Supplemental Data

One table is available at http://www.ajhg.org/cgi/content/full/82/1/100/DC1/.

Web Resources

The URLs for data presented herein are as follows:

• HapMap, http://www.hapmap.org/

• NCBI dbSNP, http://www.ncbi.nlm.nih.gov/sites/entrez?db=snp&cmd=search&term=

• SeattleSNPs Database, http://pga.mbt.washington.edu/