Analysis of Pattern Precision Shows That Drosophila Segmentation Develops Substantial Independence From Gradients of Maternal Gene Products

Abstract

We analyze the relation between maternal gradients and segmentation in Drosophila, by quantifying spatial precision in protein patterns. Segmentation is first seen in the striped expression patterns of the pair-rule genes, such as even-skipped (eve). We compare positional precision between Eve and the maternal gradients of Bicoid (Bcd) and Caudal (Cad) proteins, showing that Eve position could be initially specified by the maternal protein concentrations but that these do not have the precision to specify the mature striped pattern of Eve. By using spatial trends, we avoid possible complications in measuring single boundary precision (e.g., gap gene patterns) and can follow how precision changes in time. During nuclear cleavage cycles 13 and 14, we find that Eve becomes increasingly correlated with egg length, whereas Bcd does not. This finding suggests that the change in precision is part of a separation of segmentation from an absolute spatial measure, established by the maternal gradients, to one precise in relative (percent egg length) units.

INTRODUCTION

Segmentation is an essential feature of many animal body plans. How general, or how multitudinously specific, are the ways in which it originates, in arthropods, annelids, and chordates? Davis and Patel (1999) stated: “within phyla … the homology of segments is generally accepted” but “it is perhaps too soon to conclude that segmentation is homologous between the various phyla … convergence at the level of developmental mechanism is perhaps more intriguing.” This topic is strongly related to the even more general matter of how positions are specified in the developing embryo. The concept of “positional information” was stated for plants by Vöchting (1877) and for animals by Driesch (1893) and elaborated by Wolpert (1969, 1996, 2002). That gradients specify position was proposed by Boveri (1904, 1910, reviewed by Sander, 1994). Wolpert (and also Crick, 1970) postulated that these gradients are of concentrations of chemical substances. In Drosophila melanogaster, bicoid (bcd) mRNA, transcribed in the mother, is deposited at the anterior end of the fertilized egg, and the Bcd protein is translated and diffuses to form an anteroposterior (AP) concentration gradient (Fig. 1A), monotonic and quantitatively exponential (Fig. 1E) for most of the embryo’s length by interphase 13 of the nuclear division sequence (Driever and Nüsslein-Volhard, 1988a). Bcd is cited as a prime example of positional specification by gradients (Wolpert, 1996, 2002; Ephrussi and St. Johnston, 2004), acting in a concentration-dependent manner on its downstream targets (Driever and Nüsslein-Volhard, 1988b; Struhl et al., 1989).

Fig. 1.

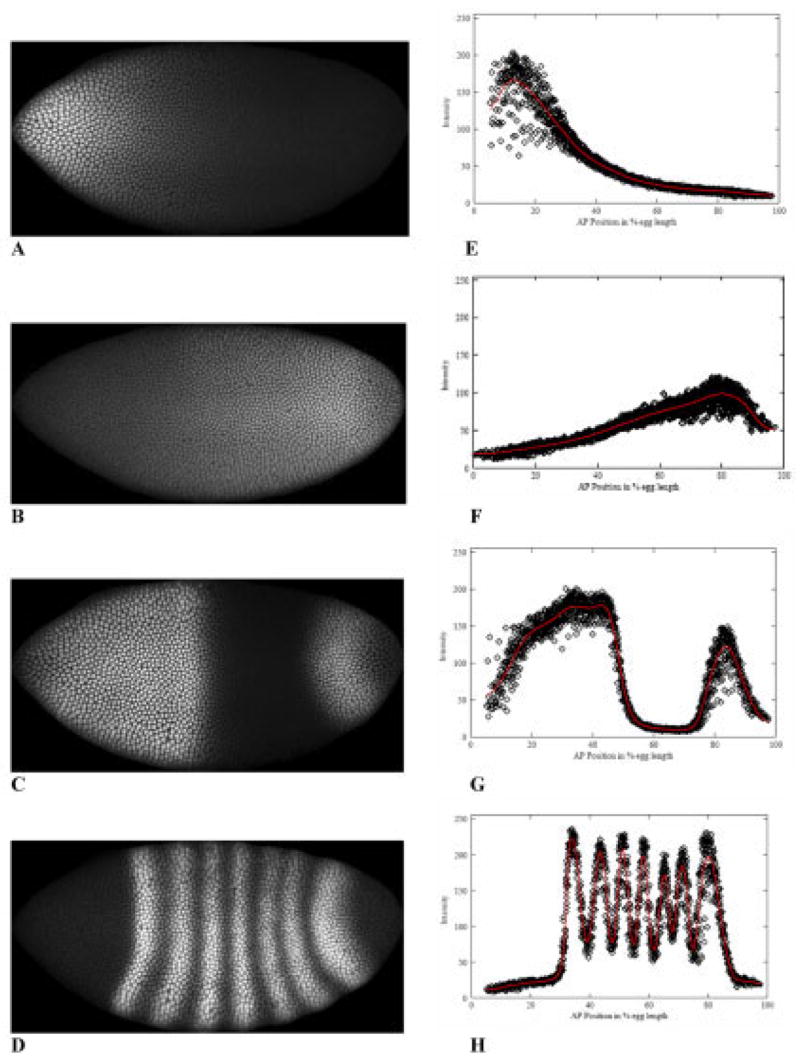
The segmentation hierarchy in Drosophila. A: An anterior-high gradient of the maternally derived protein Bicoid (Bcd) is established before zygotic gene expression. Posterior gradients also form: a major regulator of downstream expression is B) Caudal (Cad), graded by translational repression by Bcd. C: Gap genes, such as hunchback (hb) are expressed in response to maternal regulators and cross-interactions. D: The first periodic segmentation patterns are observed in the expression of the pair-rule genes, such as even-skipped (eve). Although Eve expression depends in a complicated way on upstream regulators and cross-interactions, direct comparison of the precision in positioning Eve stripes to Bcd spatial precision shows that passive reading of the maternal gradient is sufficient to initiate Eve, but not for the mature segmentation pattern. A–D are confocal microscope images from embryos stained with fluorescently tagged antibodies to the above proteins (anterior left, posterior right, dorsal up, ventral down). A, B, and D are from the same, triply stained, embryo. Most of the pattern formation occurs in nuclear cleavage cycle 14A, before cellularization (each dot is a nucleus). The embryos shown are from later cycle 14A (T6, see the Experimental Procedures section for temporal classes). E–H: For Bcd, Cad, Hb, and Eve, respectively, fluorescence intensity (on an 8-bit [0–255] scale), at each nucleus, vs. anteroposterior (AP) position (relative, in percent egg length [%EL]; 0% anterior, 100% posterior), with the extracted profile (see the Experimental Procedures section for details) in red.

In Drosophila, segmentation is first seen in the periodic seven-stripe expression patterns of the pair-rule gene products, such as the Even-skipped (Eve) protein (Fig. 1D,H), formed downstream of maternal and gap gene (e.g., Hunchback, Hb, Fig. 1C,G) products. What is the relation between maternal gradient specification and the periodic pattern? We approach this problem by quantifying between-embryo variability in the positions at which proteins in the segmentation hierarchy are seen, and comparing these variabilities between proteins. Our question for relating maternal signal to segmentation is, does the maternal gradient have enough positional information to specify the seven stripe positions, or is something else necessary? Problems with positional specification by monotonic gradients have long been known: Lacalli and Harrison (1991) showed that positional specification should worsen (linearly) from anterior to posterior for a gradient like Bcd. Here, we quantify Bcd precision and confirm that it does follow such a trend (which remains very constant in time). If segmentation followed passively from the Bcd gradient, it should show a similar trend in positional precision. We quantify Eve precision and show that it does follow the maternal trend as it is first expressed, in nuclear cleavage cycle 13 and early cycle 14, but that variability becomes low and uniform (stripe 7 is as precise as stripe 1) as the seven-stripe pattern matures during cycle 14, indicating an important role for additional regulation in positioning the stripes precisely.

Complicating understanding of what this regulation may be is the fact that Eve has numerous regulators that affect the final periodic pattern: maternal, gap, and pair-rule (Levine and Harding, 1989; Pankratz et al., 1990; Ŝtanojević et al., 1991; Small and Levine, 1991; Small et al., 1992; Rivera-Pomar and Jäckle, 1996; Arnosti et al., 1996; Fujioka et al., 1999; Clyde et al., 2003). If Eve passively responds to its regulators, then variability in Eve expression should be a sum of the variabilities of its regulators (no matter whether Eve depends on sums, ratios, products, or differences of its regulators). (To the degree that regulators are correlated with each other, this sum would be reduced, but perfect correlation cannot be reached for molecular species that differ in any of their regulatory pathways.) This sum will reflect regulators’ precision trends, as in the correspondence between early Eve and Bcd. To achieve the uniform precision of late Eve, such spatially dependent trends must be overcome. (And any decrease in positional variability indicates error-suppression in gradient-reading kinetics, which is not necessarily the same as pattern sharpening or refinement of early, broad patterns: patterns can be sharpened in the wrong positions.)

At what level might the Bcd trend be overcome? Maternally, posterior gradients have been postulated to compensate for the imprecision in the Bcd gradient (Houchmandzadeh et al., 2005; Howard and Rein ten Wolde, 2005), but the potential compensation does not appear to be enough to match data (Aegerter-Wilmsen et al., 2005), and no such gradients have been found. For the known posterior regulator Caudal (Cad, Fig. 1B,F), we show that precision trends do not compensate Bcd’s; rather, the precision also worsens anterior to posterior (not unexpected, because Bcd inhibits Cad translation). There has been much recent evidence that gap expression overcomes Bcd variability: Hb is expressed far more precisely at mid-embryo than Bcd (Houchmandzadeh et al., 2002; Spirov and Holloway, 2003a; Holloway et al., 2003), even under strong temperature perturbations (Lucchetta et al., 2005). For understanding specification of the periodic segmentation pattern (14 border positions), though, this is an intermediate step. Our observations of diverging precision between maternal gradient and segmentation pattern depend on looking at spatial trends in precision, along the length of the AP axis. Such trends cannot be as reliably made by comparing different gap genes, which have different intensity measurement errors (Myasnikova et al., 2005). Gap boundaries may be quite precise, but it will require much inference to comment on pair-rule precision from gap precision (because gaps regulate pair-rule transcription in different ways). Also, our analysis of precision trends is not as susceptible to intensity measurement errors as analyzing single gap boundaries (a critique of the Hb results raised by Crauk and Dostatni, 2005). Finally, it is well documented that other pair-rules play an important role in sharpening Eve stripes during cycle 14 (e.g., Fujioka et al., 1995; Yu and Pick, 1995). Such interactions may be involved in increasing precision, but proper position does not necessarily follow from sharper stripes.

We find that, as precision trends diverge, Bcd positions remain quite uncorrelated with egg length (see also Houchmandzadeh et al., 2002), whereas Eve becomes increasingly correlated with egg length. This finding suggests that Eve’s increase in precision is partly a transition away from specification by a maternal gradient set up in absolute (μm) units (dependent on transport and decay parameters), to positioning robust to egg length variability (which is approximately 30%), precise in relative (percent egg length) units. Our work reinforces earlier conclusions, that zygotic positioning does not follow passively from maternal gradients. (In addition to the above Hb statistical studies, there is evidence from Bcd dosage experiments, in which downstream positions do not move in absolute proportion to Bcd concentration (Driever and Nüsslein-Volhard, 1988b), and from anterior shifting of gap patterns during nuclear cleavage cycle 14, which depend on gap–gap interactions (Jaeger et al., 2004a,b). By following Eve’s development, however, we also show that both maternal specification and zygotic independence appear to be part of the patterning process: early expression follows maternal precision; mature segmentation pattern does not. Our study characterizes the establishment of spatial precision in Drosophila segmentation, an aspect of development that must be considered in the regulatory interactions underlying any pattern forming process.

RESULTS

Spatial and Temporal Trends in Positional Variability

Our study involves a quantification of protein pattern precision in space (along the AP axis) and time (nuclear cleavage cycles 12 to 14). These spatial and temporal trends in precision give insight into regulatory interactions during segmentation. We characterize the precision in anterior (Bcd) and posterior (Cad) maternal gradients, then compare these with the development of precision in the pair-rule product Eve.

Maternal Gradients

Bicoid

Figure 2A overlays 61 Bcd gradients from early cycle 14A (T1–2). (See the Experimental Procedures section for T [time] classes and data processing and statistical procedures.) A great deal of between-embryo variability is immediately apparent, striking for a gradient of positional information. (Similar variability was shown in Houchmandzadeh et al. 2002; their fig. 2A.) Their data were normalized, which distorts positional trends in the variability but does indicate that the variability is intrinsic, and not experimentally derived. We quantify this variability as positional error in Figure 2B,C. Figure 2B shows the mean position, with one-standard-deviation error bars, for equally spaced intensity values along the Bcd gradient (i.e., what is the scatter in positions at which a particular concentration is seen?). Figure 2C plots these standard deviations against AP position, clearly demonstrating a posteriorly rising trend in Bcd’s positional error. Linear regression (R² = 0.97) gives a statistically significant rise (99% confidence), with a slope of 0.124. Note we are not discussing Bcd precision in the far posterior of the embryo: errors are quantified between 30 and 60 percent egg length (%EL), and the trend is evident even in the anterior half of the embryo alone—precision is significantly worse at 50 %EL than at 30 %EL.

Fig. 2.

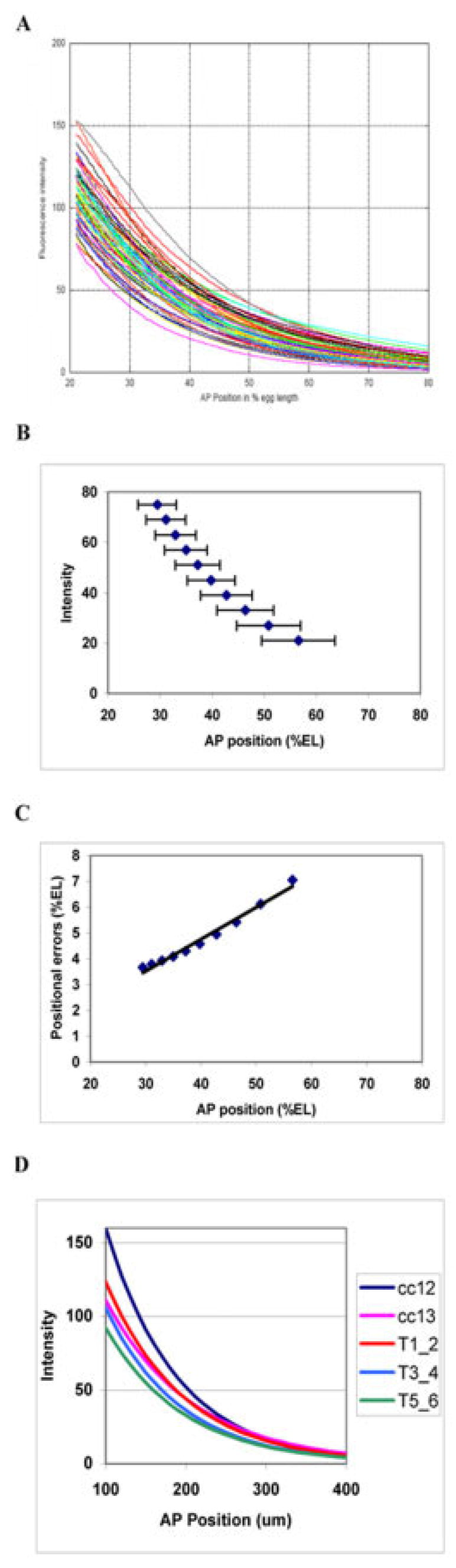
Multiple-embryo overlays for Bcd, with summary statistics and precision trends. A: Overlay of Bcd gradients from 61 embryos, early cleavage cycle 14 (T1–2). Fluorescence intensity (proportional to concentration) is on the vertical, anteroposterior (AP) position (percent egg length [%EL]; 0% anterior, 100% posterior) on the horizontal. Each line is the profile extracted (see the Experimental Procedures section) from a single embryo (e.g., red line in Fig. 1E). The broad scatter of positions at which any particular concentration of Bcd is encountered suggests low precision for positional specification. B: Mean positions, for selected intensities, with one standard deviation error bars, for the same embryos. C: Positional error (standard deviation) against AP position. There is a posteriorly rising trend in the positional errors. D: Bcd gradients in time. Each curve is generated from the average exponential parameters of each developmental stage; this is a pictorial representation of the profiles for mean k and C₀ values in Table 1. There appears to be some deterministic drop in Bcd over these stages. However, Bcd’s exponential decay constant (k) does not change over cycle 14A (see text), so spatial dependence of positional errors also remains unchanged.

These precision trends for the Bcd gradient are very stable in time. Table 1 summarizes Bcd characteristics over time, for cycles 12 through 14A. Columns 3 and 4 are the averages of the exponential parameters obtained from curvefitting individual embryos (see the Experimental Procedures section, exponentials give very good fits to most Bcd gradients and allow us to go further in analyzing the sources of positional error trends, see below), whereas columns 5 and 6 are obtained from positional errors for multiembryo overlays (e.g., Fig. 2A–C). Results are reported for absolute spatial units (μm), as the best measure of intrinsic variability in the gradients (units discussed further below). In Figure 2D, a curve is computed for each time class from its exponential parameters, visually summarizing columns 3 and 4.

TABLE 1.

Parameters for Exponential Curves and Positional Errors for Bcd, in Developmental Time^a

		Exponential parameters for Bcd profiles		Positional errors vs. AP position
Cleavage cycle (time classes in 14)	n	k × 10−3/μm (SD)	C0 fluor. units (SD)	Slope (by linear regression)	Smallest value (μm)
12	14	11.2 (12%)	489 (34%)	0.034	19.4
13	72	9.2 (19%)	278 (27%)	0.112	17.7
14 (T1-2)	61	10.3 (18%)	345 (28%)	0.130	15.2
14 (T3-4)	45	10.7 (16%)	308 (27%)	0.112	18.2
14 (T5-6)	33	10.3(15%)	258 (21%)	0.106	15.2

^aAP, anteroposterior.

The fractional slope of the gradient (exponential decay constant, k) does not change over cycle 14A (analysis of variance test on means). Cycle 12 has larger k and cycle 13 smaller k than cycle 14A. The standard deviations of the k values (Table 1, column 3) demonstrate a large intrinsic (nonexperimental) variability in the Bcd gradients, which does not change over the period measured (pairwise F-tests). These standard deviations are reflected in the linearly rising trend in Bcd variability (Lacalli and Harrison, 1991). For any stage, the slope of this trend (e.g., in Fig. 2C; Table 1, column 5) should be given by the standard deviation of the k (Holloway et al., 2003), and we see fair agreement with this in Table 1 (column 3 vs. column 5). (Cycle 14A differences in column 5 are probably due to small deviations from linearity in the trends [although all R² > 0.97].)

We see a greater variability in the initial (anterior-most) values of Bcd (C₀ parameter; Table 1, column 4) than in the k values. C₀ variability has no spatially dependent effect on positional errors (Lacalli and Harrison, 1991). The smallest positional errors in multiembryo overlays (Table 1, column 6) can be taken as an estimate of this uniform variability. As with the k-variability, estimates from the overlays are close to, but somewhat lower than, predictions from the exponential parameters (found by dividing column 4 variability by the k values from column 3; Holloway et al., 2003). C₀ values (a measure of protein produced from the maternal mRNA) do appear to decrease in time, with a slight upsurge going from cycle 13 to cycle 14. Cycle 12 has especially high C₀ variability and low k variability (reflected in the low column 5 slope). Cycle 12 also had by far the largest proportion (half) of nonexponential profiles, perhaps reflecting that Bcd is not yet at steady-state for many embryos at this stage (Bcd takes roughly 30 min, starting in cycle 9, to achieve a steady-state profile (unpublished data).

To summarize, Bcd establishes a characteristic precision pattern in cycle 12, with variability in k giving a significant (99% confidence) linear increase in gradient variability from anterior to posterior. Yucel and Small (2006) recently speculated on the time course of the Bcd variability: we find the variability and its spatial pattern remain stable through the segmentation process (especially so during cycle 14A).

Caudal

In relation to the worsening precision in the Bcd gradient toward the posterior, the question arises whether posterior maternal gradients may have opposite trends, such that downstream expression would show larger, additive errors, but precision would be more uniform. Bcd’s anterior functions are shared by several posterior maternal factors. Nanos translationally inhibits Hb, as Bcd inhibits Cad, but it is Cad that has a downstream transcriptional activation role, like Bcd’s in the anterior (Schultz and Tautz, 1995; Rivera-Pomar et al., 1995). Figure 3 shows overlays of Cad patterns for cleavage cycle 13 and early cycle 14 (T1–2). In cycle 13 (Fig. 3A), a gradient of Cad has formed (by anterior translational repression from a uniform mRNA distribution). Cad variability is very high, in gradient shape (unlike Bcd), as well as magnitude and slope. The variability does not increase with decreasing Cad but, rather, appears to directly follow Bcd’s trend: it is most precise in the anterior, at low Cad, but precise Bcd (Fig. 3B,C); a not unexpected result if Bcd repression is a dominant effect in creating the Cad gradient. This trend is slightly more pronounced in early cycle 14 (Fig. 3D–F, compare Bcd in Fig. 2A–C), perhaps reflecting the sustained effect of Bcd repression. To summarize, by early cycle 14 the precision in maternal spatial information, from Bcd and Cad, gets steadily worse from anterior to posterior (again, we are quantifying these trends chiefly in the anterior half of the embryo).

Fig. 3.

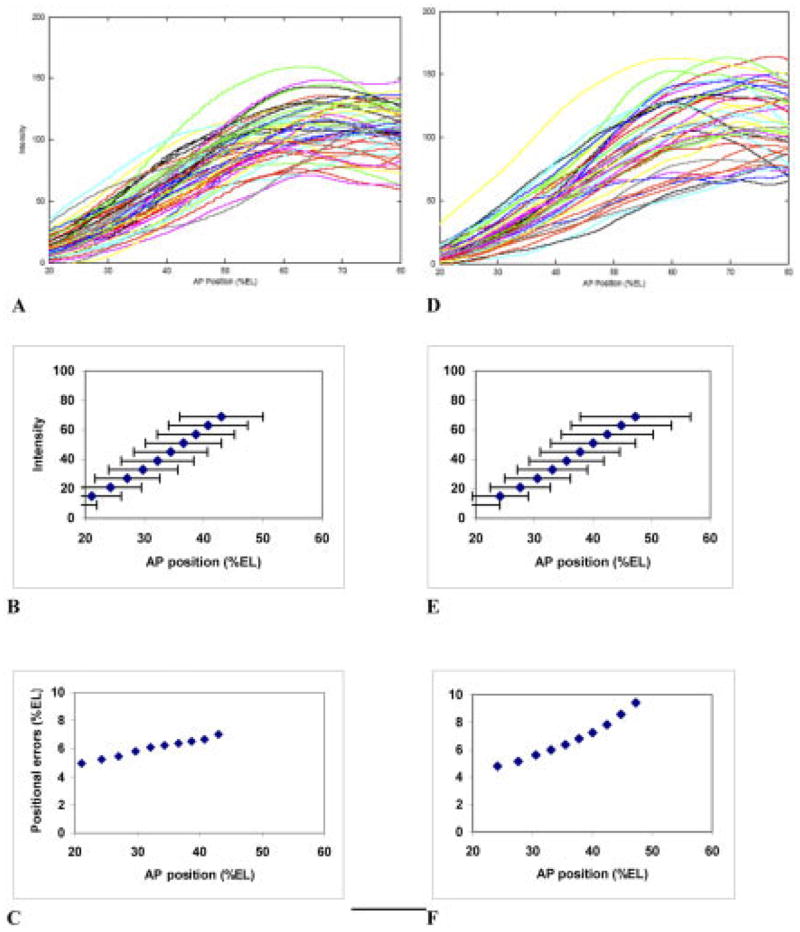
Overlay of Cad patterns, with summary statistics and trends. A–C: Cleavage cycle 13 pattern. A: Overlay of anteroposterior (AP) profiles, for 47 embryos. B: Mean positions, at select intensities, with one standard deviation error bars. C: Plot of these standard deviations against AP position. Like Bcd, Cad shows a rise in positional errors toward the posterior. D–F: Early cleavage cycle 14 (T1–2). D: Overlay of AP profiles, for 43 embryos. E: Mean positions, at select intensities, with one standard deviation error bars. F: Plot of these standard deviations against AP position. The posteriorly rising trend in positional errors increases from cycle 13. Bcd is a translational repressor of Cad: the change between C and F may reflect the sustained effects of Bcd’s greater variability toward the posterior.

Segmentation Pattern (Even-skipped)

Our interest is chiefly in investigating the degree to which maternal positional information can account for segmentation positioning. We address this question by directly quantifying positional information (precision) in Eve pattern and comparing with the results above. For comparing hierarchical signals, there is likely to be a time lag due to production delay (transcription, translation, splicing, nuclear export, etc.), which we estimate at 5 to 7 min (not more than one cycle-14 time class, unpublished observations). Because Bcd variability is so stable over cycles 13 and 14, the magnitude of this lag is not likely to be crucial to interpreting our results: Eve can be reasonably compared with any earlier Bcd. Cad only serves to exacerbate the Bcd trend.

In contrast to Bcd’s stability, Eve’s pattern develops dramatically, changing from a single peak in cycle 13 (Fig. 4A) and early cycle 14 (T1, Fig. 4D), to the mature periodic pattern of late cycle 14 (T7, Fig. 4G). Eve’s positional error trends are not unlike those of Bcd in cycle 13 (Fig. 4B,C), with a posterior rise in errors. Variability is too great, at this stage, for resolution of the segmentation pattern into seven stripes (peak to peak distance is approximately 8 %EL for mature stripes, comparable to the positional errors in Fig. 4C). In early cycle 14, the rise in errors is still evident in the posterior (Fig. 4E,F, still excessive to resolve stripes), but there has been a sharp decrease in variability at the anterior edge of Eve expression, with the lowest error around 24–28 %EL (approaching 2 %EL positional error, sufficiently low to resolve pair-rule stripes). By late cycle 14, the variability has become equally low, and uniform, along the whole Eve pattern (Fig. 4H,I; precision is sufficient to resolve stripes, i.e., seven distinct stripes can be seen in the simple overlay of Fig. 4G). As a comparison, Eve variability stays quite constant between anterior Eve stripe 1 and posterior Eve stripe 4 (Fig. 4I, 30–60 %EL), while the Bcd variability doubles over this distance (Fig. 2C). Eve’s dynamic increase in precision does not correspond to the stable-in-time, posterior-high-variability supplied by the maternal gradients, but points to active error suppression in zygotic regulatory pathways during cycle 14A. Eve may well be following Bcd in a one-on-one concentration-specific manner (directly, or through gap gene mediation), therefore, displaying all the Bcd variability, as it is first being expressed. But, as the periodic segmentation pattern develops, Eve variability becomes increasingly independent of Bcd variability, pointing to increasing independence of pattern formation, and a departure from one-to-one reading of the maternal signal. Our data for expression of the pair-rule genes hairy and fushi-tarazu show similar independence of positional error trends from those of Bcd (data not shown).

Fig. 4.

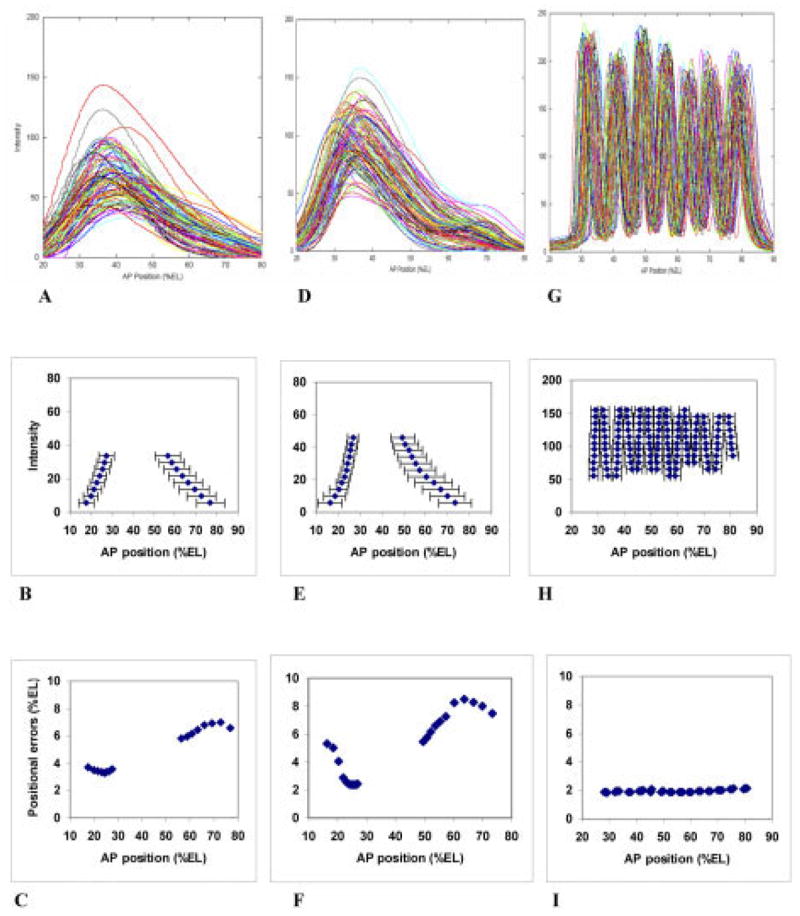
Eve patterns, over time, with summary statistics and trends. A–C: cleavage cycle 13. A: Overlay of anteroposterior (AP) profiles for 93 embryos. B: Mean positions, at select intensities, with one standard deviation error bars. C: Plot of these standard deviations against AP position. At this stage, both anterior and posterior error trends are comparable to Bcd (cf. Fig. 2C; Table 1, 2nd row). D–F: Early cycle 14 (T1) Eve pattern. D: Overlay of AP profiles for 101 embryos. E: Mean positions, at select intensities, with one standard deviation error bars. F: Plot of these standard deviations against AP position. The posterior error trend is still comparable to Bcd’s (Fig. 2A–C), but the anterior (20–30 percent egg length [%EL]) of the early Eve peak is becoming much more precise. G–I: Mature (late cycle 14A, T7) Eve segmentation pattern. G: Overlay of AP profiles for 96 embryos. H: Mean positions, for selected intensities, with one standard deviation error bars. I: Plot of these standard deviations against AP position. These errors are much lower than Bcd’s, and no longer have a posteriorly rising trend, pointing toward a divergence of maternal positional specification and zygotic segmentation patterning over cycle 14A. Note: H and I show positional errors calculated with 94, 95, or 96 of the embryos, to show positional errors along all stripe borders. See Supplementary Figure S4 for the same plots with all 96 embryos: not as many positional errors can be calculated, but the trends are the same.

Spatial Scaling: What Are Bcd and Eve Measuring?

It is hypothesized (Lacalli and Harrison, 1991; Houchmandzadeh et al., 2002) that the exponential Bcd gradient is set up by diffusion and first-order degradation. The ratio of the diffusivity and degradation constants for these processes would measure out the gradient in absolute spatial units (μm; Harrison, 1993, Fig. 2.2). From this standpoint, the k variability we have measured from the embryos would be the result of variability in the diffusion and degradation constants. Hence, we have presented Table 1 in μm, as the best measure of the posterior rise in errors inherent in the Bcd gradient (and lowest measure, conversion to %EL could be expected to increase Bcd variability, see Fig. 5, below).

Fig. 5.

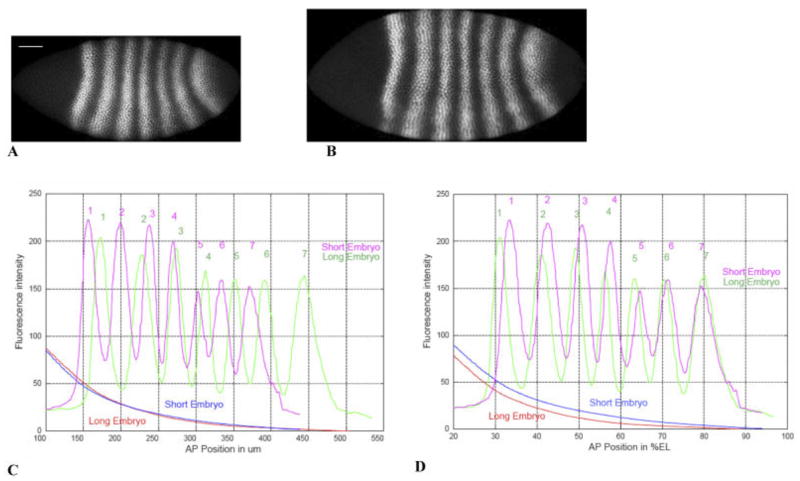
Spatial scaling. A,B: Eve staining on two embryos in later cycle 14A (T6), on the same spatial scale. A is 468 μm long (white bar, 50 μm), B is 555 μm long. C: The Eve and Bcd patterns in these embryos are shown, in absolute units (μm). D: The same patterns, in relative units (percent egg length [%EL]). Long embryo: Bcd, red; Eve, green. Short embryo: Bcd, blue; Eve, magenta. Bcd patterns are similar (precise) in absolute units, whereas Eve patterns are similar (precise) in relative units. The absolute scale for Bcd likely reflects its establishment by diffusion and degradation, while the relative scale for Eve suggests that zygotic patterning involves feedback with egg size. This is an example for one pair of embryos: see text for statistics on 17 embryos of the same time class.

If we look at Eve in absolute units, rather than the more usual %EL units, the between-embryo differences are striking. Figure 5 illustrates this for two T6 embryos, a short one (468 μm; Eve staining, Fig. 5A) and a long one (555 μm; Eve staining, Fig. 5B). Bcd and Eve profiles for these embryos are shown in Figure 5C (absolute units, μm) and 5D (relative units, %EL). Eve stripes show noticeably different spacing in μm (Fig. 5C), between the two embryos, with both stripes 6 and 7 of the long embryo posterior to stripe 7 of the short embryo. At the same time, the Bcd’s for these two embryos look very similar to each other. Eve differences can largely be accounted for by egg length, however; using relative units (Fig. 5D), the stripes become nearly coincident (especially in the posterior). Eve does a precise job of marking relative positions in the embryo (Fig. 4G–I). By contrast, Bcd becomes more variable with conversion from μm to %EL: the similar Bcd’s in Figure 5C are spread apart in Figure 5D. Gradients set up by diffusion, in μm, mark different relative positions in embryos of different length. Figure 5C,D argues that Bcd measures in absolute units, whereas Eve measures in relative units.

Figure 5C suggests that quite different Eve patterns can occur in embryos with quite similar Bcd gradients. We can look at the factor by which Bcd decreases from the Eve stripe 1 (peak) position to the Eve stripe 7 (peak) position for each embryo (this relative factor is unaffected by multiplicative experimental errors, such as between-embryo variability in Bcd-antibody binding, which could strongly affect comparison of absolute concentrations between embryos). In the short embryo in Figure 5, Bcd goes down by a factor of 8.7 between Eve stripes 1 and 7; for the long embryo Bcd goes down by a factor of 22.6. Although the stripe 1–stripe 7 distance is longer in the longer embryo for this pair, this is not always the case: several T6 embryos have nearly identical stripe 1–stripe 7 distance, but quite different factors by which Bcd drops over that distance. In total, we have 17 T6 embryos (displaying both Eve stripes and Bcd gradients). For these embryos, the standard deviation in stripe 1–stripe 7 distance is 5.6% (4.1% for %EL), whereas the standard deviation in the Bcd factor is 30%. The correlation between the Eve distance and the Bcd factor is 0.41 (0.29 for %EL), insignificant for this sample size. Another illustration of Bcd’s lack of scaling to egg length is that there is no (P < 0.01) correlation between the Bcd gradient parameters (k, C₀) and egg length. The conclusion must be that Eve stripes are not positioned relative to stripe 1 by some particular drop in Bcd concentration.

Finally, we can look at how Eve’s scaling proceeds in developmental time. Houchmandzadeh et al. (2002) showed that the position of the Hb mid-embryo boundary correlates well with egg length (i.e., measures well in relative units), whereas Bcd thresholds show no significant correlation with egg length. Using the position of the first Eve peak, we see correlation with egg length (linear correlation coefficient significantly different than zero, P < 0.01) in cleavage cycles 13 and 14. However, there is a significant (P < 0.01, Fisher z-test) difference in this correlation between cycle 13 (R = 0.55) and cycle 14, T1 (R = 0.81). Figure 6 shows the scatterplots for these stages, as well as for T2 (later cycle 14 timeclasses are comparable to T2). Complementing the sharpening of pattern and decrease in positional errors for anterior Eve shown in Figure 4A,D, the correlation increase indicates that Eve is also becoming better defined in relative units from cycle 13 to cycle 14.

Fig. 6.

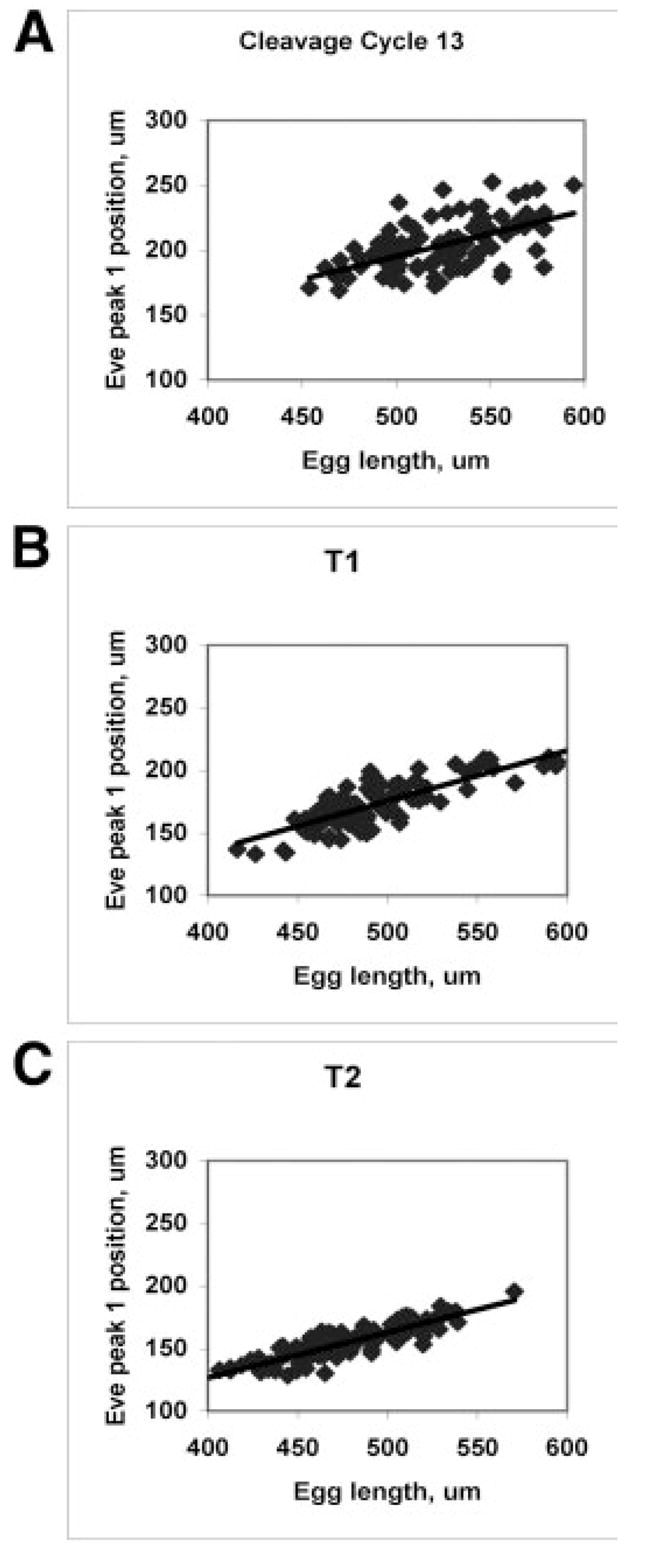
Eve position increasingly correlates with egg length (becomes more precise in relative units). A: Cycle 13, Eve peak 1 position vs. egg length (both in μm), R = 0.55. B: Cycle 14, T1, R = 0.81. C: Cycle 14, T2, R = 0.87. Scatterplots later in cycle 14 are comparable to T2.

DISCUSSION

By comparing positional information (precision) between maternal gradients and the pair-rule product Eve, we have shown that initial activation of Eve could be passively reading the maternal signal (directly, and through gap intermediates). As the striped segmentation pattern develops in cycle 14, however, it is evident that Eve patterning undergoes strong error suppression, such that the first visible periodic segmentation pattern is uniformly precise and free from the error trends in the maternal signals.

Mature Eve and Bcd are most precise in different spatial units: Bcd in absolute units (μm) and Eve in relative units (%EL). Two aspects of this finding should be highlighted. First, Eve has parametric stability: it can respond reliably to highly variable input parameters (i.e., Bcd gradients). Second, Eve’s observed error reduction is part of a larger transition from absolute maternal positioning to relative zygotic positioning, robust to egg length variability. This finding suggests that the kinetics of the zygotic mechanism depends in some way on length, area, or volume (e.g., a volume-dependent rate constant, see Harrison, 1993, sec. 10.4). In contrast to the evidence that Bcd does not compensate for egg length variability in D. melanogaster (this study; and Houchmandzadeh et al., 2002), there is very intriguing evidence that Bcd does do this between species, perhaps through evolutionary alteration of Bcd’s degradation rate (Wieschaus et al., 2005; Gregor et al., 2005).

It has been proposed that double maternal gradients (anterior and posterior) could compensate for each others’ errors (Houchmandzadeh et al., 2005; Howard and Rein ten Wolde, 2005). These proposals have been applied to the Hb mid-embryo boundary and are most precise at that position (although not precise enough to match known Hb precision, Aegerter-Wilmsen et al., 2005; and uncorrelated source fluctuations [i.e., gradients differing in regulatory pathways] on the order of those we report in Table 1 are likely to give much higher than observed Hb variability [Howard and Rein ten Wolde, 2005; their fig. 3]). Achievement of uniform precision along the whole AP axis is likely to require another mechanism. And, such an equal, yet opposite, posterior gradient has not been found. We have shown in this study that the known posterior maternal activator Cad is noisy and follows, rather than compensates for, Bcd errors.

The timing of Eve’s error suppression is important for determining the regulatory interactions responsible: this mechanism must manifest during cycle 14. Although some time lag is likely between upstream regulators and effects on Eve, it is unlikely that maternal regulation changes, such that Eve would display Bcd errors early, but not later, in cycle 14. We find it much more promising that zygotic regulatory interactions in cycle 14 are responsible for the Eve error reduction. There are indications that Hb precision is established much earlier than Eve’s: Houchmandzadeh et al. (2002) report a cycle 13 standard deviation for the mid-embryo boundary of 1.5 %EL, just slightly larger than the cycle 14 value of 1.0 %EL; and Lucchetta et al. (2005) found that, although Hb precision is remarkably robust to experiments in which anterior and posterior halves of embryos were held at different temperatures, Hb precision could be destroyed by reversing temperatures (to anterior–cold, posterior–hot) during an early window in development (before zygotic expression, during the time of maternal gradient formation). The slight cycle 13 to cycle 14 reduction in variability for Hb may compare with what we see in anterior Eve (Fig. 4A,D) at this time, but it is rather earlier than the major change we see in Eve precision during cycle 14. It may be that Eve error suppression is chiefly under gap control, and we are seeing the end result of a chain of events in which gap patterns “tighten up,” perhaps starting with Hb in early cycle 14. Pair-rule cross regulation may also be important for this increase in precision. Given likely time lags for protein production on the order of from 5 to 7 min (for Eve, unpublished observations) to 19 min (Fushi-tarazu target expression; Nasiadka et al., 2002), it seems probable that the establishment of pair-rule precision is chiefly a function of the rapid cycle 14A dynamics, rather than reflecting a long-delayed response to error-suppressing events in cycle 13 and earlier.

By studying between-embryo variability, we are able to establish that the Eve patterning mechanism is robust to varying input parameters and robust to egg length variability (by some spatial dependence in its kinetics). Chemical mechanisms are also subject to intrinsic concentration fluctuations (noise), likely to be relatively large at the low concentrations encountered in development (and fluctuations may be ultimately responsible for a significant proportion of parametric variability). For example, if there are roughly 500 Bcd molecules per nucleus at mid-embryo (estimated from Driever and Nüsslein-Volhard, 1988a), a conservative estimate of fluctuation size would be $1\sqrt{500}\approx 4.5\%$. Study of fluctuations in patterning will require quantification of within-embryo (between-nuclei) noise, but we comment here on a few of the ideas for noise attenuation which may bear on the current work.

Simple time-averaging could potentially suppress upstream concentration fluctuations, as long as downstream time-scales are slower than upstream time-scales: uncertainty in reading mean values is typically inversely proportional to the square root of the sample size, disappearing only with infinite sample size, or sampling time. In segmentation, the downstream processes are likely to be initiations of transcription, irreversible when started and on a faster time-scale than the time-scales of chemical kinetics and diffusion establishing and maintaining the Bcd gradient. For example, Bcd pattern establishes over cycles 9 to 11, a period of roughly 30 min, compared with the segmentation gene expression timescales of 5–19 min referred to above. This may give some time-averaging ability (beyond instantaneous reading), but the relative time-scales are likely to largely transmit Bcd’s fluctuations. We previously demonstrated, computationally, that multi-step reading of concentration gradients is likely to amplify upstream fluctuations, and exponential gradients are likely to give fluctuations stronger positional effect toward the posterior (Holloway and Harrison, 1999).

There is much new work on the kinetics of temporal error reduction (e.g., Savageau, 1974; Barkai and Leibler, 1997; Paulsson et al., 2000; Becksei and Serrano, 2000; Thattai and van Oudenaarden, 2002; Blake et al., 2003; Paulsson, 2004; Fraser et al., 2004; Colman-Lerner et al., 2005; Brandman et al., 2005) which may give insight into the kinetics of spatial precision. And, there are beginning to be several quantitative models for how pattern-forming kinetics can suppress spatial errors (Eldar et al., 2002, 2003; Mizutani et al., 2005); especially intriguing are mechanisms which selectively amplify the correct patterns, while suppressing high-frequency patterns, i.e., noise (Gierer and Meinhardt, 1972; Holloway and Harrison, 1999; Howard and Rutenberg, 2003). For Drosophila, modelling will have to proceed in concert with experimental and statistical work to focus in on the type of kinetics used during segmentation.

The study of variation in biological developmental outcomes is more than a century old (e.g., Bateson, 1894), in the forms in which it has been intimately associated with concepts of evolution. It started and continues today to lead very largely to the enormously extensive study of mutant forms as a principal driving-force of mainstream biology. Studies of variation within a wild-type population or of minor irregularities within a wild-type individual’s phenotypes during the most active stages of development have been much less frequent. The advanced molecular techniques available in Drosophila segmentation, and the wealth of data they have generated, make this system quite conducive to such investigations. Our work is one of several in recent years to study pattern variability in early Drosophila development. Such a statistical outlook is necessary to, in turn, pursue computational, genetic, and physicochemical approaches to elucidate the kinetics underlying spatial precision in developmental pattern formation.

EXPERIMENTAL PROCEDURES

Images of Drosophila Gene Expression

Gene expression (at the protein level) in wild-type Oregon-R embryos was measured using fluorescently-tagged antibodies as described in Kosman et al. (1997, 1998) and Janssens et al. (2005). For each embryo a 1,024- × 1,024-pixel image with 8 bits of fluorescence data in each of 3 channels (one per protein) was obtained (Fig. 1A–D). Image processing transforms each image into an ASCII table containing a series of data records, one for each nucleus. Approximately 2,500–3,000 nuclei are obtained from each image. Each nucleus is characterized by a unique identification number, the AP and DV (dorsoventral) coordinates of its centroid, and the average fluorescence levels of three gene products. Every embryo is stained for Eve, for temporal classification (see below), as well as two other gene products. The overall result is the conversion of an image to a set of numerical data which is then suitable for further processing. There are currently images of roughly 1,000 embryos, with data on 14 segmentation genes (Poustelnikova et al., 2004; http://flyex.ams.sunysb.edu/FlyEx/, or http://urchin.sbpcas.ru/FlyEx/). In this study, we present data from the segmentation genes bcd, cad, and eve.

Temporal Classification

We include data from nuclear cleavage cycles 12, 13, and 14 (Foe and Alberts, 1983). While cycles 12 and 13 are 12 min or less in duration, cycle 14A (syncytial blastoderm) is approximately 50 min. Nuclear count is sufficient to distinguish cycles from one another, but segmentation patterns are highly dynamic in cycle 14. To enable statistical analysis of the patterns, cycle 14A is divided into 8 equal time classes (T1 to T8), each approximately 6.5 min long, based on observation of the Eve pattern and the advance of blastoderm cellularization (Myasnikova et al., 2001). Maternal pattern does not change so quickly; in these cases we pool two time classes (e.g., T1–2) to match the cycle 12 and 13 lengths.

AP Expression Profiles

Because the expression of segmentation genes is largely a function of position along the AP axis, it is natural to use the AP profiles of gene expression as a first step toward characterization of between-embryo variability. For sound statistics, we want to use as many nuclei as possible in an image, but due to the discrete and irregular location of nuclei, and DV dependence of AP expression (stripe bending, e.g., Fig. 1D), extraction of AP profiles is a nontrivial problem in image processing. We use an optimization procedure to find the coefficients for a polynomial deformation of the original AP, DV nuclear coordinates to new ones in which pair-rule stripes have been straightened, i.e. all DV dependence (e.g., for AP position along a stripe edge) removed. For details of the method, see Spirov et al. (2002) and Spirov and Holloway (2003b).

We use straightened data from a rectangle 50% of the DV height of the embryo, centered on the AP axis. This captures approximately 1,400–1,700 nuclei (cleavage cycle 14). Plotting nuclear intensity vs. AP position gives a scatterplot (Fig. 1E–H). For between-embryo comparisons, we used singular spectrum analysis (SSA; Elsner and Tsonis, 1996), a nonparametric technique with an adaptive filter, to extract a profile from these plots (red lines in Fig. 1E–H). For this, we used the methods of Golyandina et al. (2001), software developed by Theodore Alexandrov (St. Petersburg State University). In Figures 2A, 3AD, 4ADG, and 5CD, each line is the profile extracted from a single embryo.

Quantification of Positional Error

Between-embryo variability is calculated from the differences between the single-embryo profiles. The intensity scale (0–255) is divided into a number of intervals. For the monotonic Bcd and Cad gradients, if all embryo profiles in a temporal class cross a given intensity value, a mean and standard deviation is calculated for the position at which the value is crossed (Figs. 2B,C, 3B,C,E,F). For Eve, this procedure is done for each peak to trough region (Fig. 4B,C,E,F,H,I). For early Eve (Fig. 4B,C,E,F), standard deviations were calculated using all available embryos; for later Eve (Fig. 4H,I), where we have 96 embryos, we calculate standard deviations with 94, 95, or 96 embryos, to show variability at all Eve borders. (Supplementary Figure S4, which can be viewed at http://www.interscience.wiley.com/jpages/1058-8388/suppmat, shows standard deviations strictly using all 96 embryos.) The standard deviations measure the positional variability for protein concentrations: low standard deviation is high precision, high standard deviation is low precision. We refer to these standard deviations as positional errors (Figs. 2B,C, 3B,C,E,F, 4B,C,E,F,H,I).

AP Trends in Positional Errors

Finding the AP-trends in Bcd’s positional errors is central to this study, yet care must be taken in quantifying positions along such graded patterns: variability can have much greater effect on a gradient than on a sharp on-off expression pattern (due to the relative values of their slopes). To separate intrinsic from experimental contributions to these trends, we take advantage of the exponential form of the Bcd gradient (present results; plus Driever and Nüsslein-Volhard, 1988a; Houchmandzadeh et al., 2002). Representing this as C = C₀e ^−kx + B (where C is the Bcd intensity (proportional to concentration), C₀ is the maximum intensity, k is the exponential decay constant (in terms of distance, not time), x is the spatial dimension along the AP axis, and B is background intensity), variation in two of these parameters (k and B) has a position-dependent effect on Bcd precision (variation in C₀, which includes variability in Bcd-antibody binding, has uniform effect on Bcd precision, Lacalli and Harrison, 1991; therefore Crauk and Dostatni’s (2005; their Fig. 7) critique that such variability compromises measurement of boundary precision does not apply to our investigation of positional dependence of errors). Variability in B is experimental, expected from variation in nonspecific antibody binding between embryos. B-variability gives exponentially increasing positional errors toward the posterior (because the slope of the gradient decreases exponentially). k-variability is intrinsic, likely stemming from embryo-to-embryo variability in Bcd degradation and transport, and gives linearly increasing positional errors toward the posterior (Lacalli and Harrison, 1991). It is therefore important that we closely estimate these parameters, to remove the effects of B-variability and determine the magnitude of k-variability. We did this by means of nonlinear regression (Levenberg-Marquardt algorithm), weighted in inverse proportion to intensity noise (to give better estimates of B), on the interval of 20–80 %EL in relative spatial units, and 100–400 μm in absolute units. Most embryos (80% in cycles 13 and 14) yielded excellent fits to exponentials (straight-line log-plots, very high R²). For examining AP-trends, we did not use embryos with poor exponential fits: these are likely due to experimental problems with particular images, yield poor parameter estimates, and Houchmandzadeh et al. (2002) found strong exponentiality in their data using a different imaging technique. We removed nonspecific background variability in our data by subtracting the B’s from each embryo’s intensity profile.

For the other two species studied, Cad and Eve, we do not have the advantage of a simple function which fits the data so well. Yet, we still need to remove background to get the best representation of intrinsic variability. For Cad and Eve, we remove the polynomial intensity pattern seen in null mutants (see Surkova et al., in preparation, for details of the method; and Myasnikova et al., 2005, for a related technique). For comparison, we show all of our results, with background, in the Supplementary Figures S1–3: background-removal does not affect our conclusions.

Supplementary Material

Fig. 1 Suppl

The Supplementary Material referred to in this article can be found at http://www.interscience.wiley.com/jpages/1058-8388/suppmat