The role of race in cesarean rate case mix adjustment

Introduction

It has been well established that perinatal outcomes vary by the race and ethnicity of the mother. Prematurity, cesarean delivery, infant death, and maternal death are higher in the black population than in the white population. ^1,2 The causes of these differences have been of great interest to the obstetric community. ^3,4 There are many possible causes of racial disparities in obstetrics, including economics, biology, and discrimination. ⁵ There is likely overlap in these categories and it is unclear whether a lucid answer will ever be delineated.

Despite this uncertainty regarding the mechanism by which race and ethnicity influence perinatal outcomes, perinatal outcomes are used as a measure of the quality of obstetric care. Outcomes are often measured at the hospital level. Case mix adjustment is a technique used to account for differences in baseline patient characteristics that influence outcomes. This is done so that hospitals caring for sicker patients who are more likely to have poor outcomes are not penalized in the evaluation of quality. ⁶

Risk-adjusted primary cesarean rates are a promising new measure of obstetrical quality that can be used to effectively identify hospitals with poorer outcomes.⁷,⁸,⁹ A risk-adjustment model is first developed to predict the probability of a cesarean delivery for each patient associated with the institution, using a series of well-accepted risk factors for cesarean delivery that were developed by practicing obstetricians ^{10, 11}. The estimated probabilities of cesarean delivery for each patient are then summed across the institution in order to create an institutional predicted primary cesarean rate. These rates are then directly compared to actual observed rates of primary cesarean delivery. Risk-adjusted primary cesarean rates are particularly appealing because they are associated with both maternal and neonatal outcomes. ¹² Hospitals that have risk-adjusted primary cesarean rates that are below expected have higher rates of poor maternal and neonatal outcomes. ¹³,¹²,¹⁴,¹⁵ Risk-adjusted cesarean rates do not provide a “target” cesarean rate. They do not pass judgment as to whether any particular cesarean was appropriate, and they do not attempt to assess the quality of surgical technique. The model simply predicts each patient’s chance of a cesarean delivery given their personal risk factors in the hands of a typical provider. An institution’s predicted rate is based solely on its case mix.

In assessing the quality of a risk-adjustment model, it is important to address predictive accuracy in terms of both discrimination and calibration. Discrimination may be thought of as the ability of the model to accurately separate patients into those who will undergo a primary cesarean delivery and those who will not. The C statistic (also called the area under the receiver operating characteristic curve) is the standard approach to quantifying discrimination, The C statistic falls between 0.5 (worst case) and 1.0 (ideal scenario), with larger values indicating better discrimination ¹⁶.

In addition to discrimination, any risk-adjustment model should be assessed in terms of its calibration. This may be thought of as the model’s ability to predict accurately throughout the range of possible probabilities (i.e., for patients at all levels of risk). Calibration of a risk-adjustment model is most commonly assessed using a statistical test of goodness of fit due to Hosmer and Lemeshow, where small p-values indicate poor model calibration.

Because race impacts perinatal outcomes and because the race/ethnicities of patients are not equally distributed among hospitals, race is a potential variable for risk-adjustment models. The inclusion of race in risk-adjustment models is controversial. If racial differences are based in economics or biology, this is a legitimate addition to a risk adjustment model. On the other hand, if racial differences are due to discrimination, race/ethnicity should not be included in risk-adjustment models because such an approach would mask an important social issue. To better understand the role that race and ethnicity play in risk-adjustment models for primary cesarean delivery, our study sought to compare models with and without race and ethnicity to assess their impact on the discrimination and calibration of risk-adjustment models.

Methods

After obtaining IRB approval from the MetroHealth Medical Center and the State of California Committee for the Protection of Human Subjects, we obtained 2003 California birth certificate data that has been linked to a hospital discharge data set for mothers and infants. All linkages are done by the State of California prior to release. ¹⁷

We limited the data set to women at risk for a primary cesarean delivery who delivered at a hospital having more than 50 deliveries per year. Additionally, we considered only viable deliveries – those births >24 weeks and >500 grams with no major anomalies. Lastly, we considered data only from patients that had complete data on the variables in our risk adjustment model, and excluded patients with clearly mistaken entries (such as a vaginal delivery of a 15 lb infant).

A risk-adjustment model (Model A) for primary cesarean delivery was created using multivariate logistic regression on the following predictor variables: maternal age, race, ethnicity, and medical conditions, gestational age, multiple births, insurance, nulliparity, complications of pregnancy, and the trimester in which prenatal care began. These variables have been previously identified as being important in a risk-adjustment model. ¹¹ Clinically relevant categories of variables were created for most variables, including gestational age. Maternal age was expressed in years.

We then created model A1 excluding race and ethnicity. We summarize the predictive validity and accuracy of the resulting models in several ways. We calculated positive predictive value and negative predictive value for each model in predicting cesarean delivery across the entire sample. We compared C statistics (area under the receiving operating curve) to assess the discrimination of each model and Hosmer-Lemeshow tests to gauge model calibration.

To determine if the addition of interaction terms and splines would improve model performance, we built a series of more complex models to predict primary cesarean delivery. Model B adds product terms to Model A, to capture interaction effects between race/ethnicity, maternal age, and maternal medical conditions with the other risk factors. Model C adds cubic splines of gestational and maternal age to Model B in order to account for non-linear relationships between the risk factors and cesarean delivery.

In building these models, we made heavy use of methodologies for checking model fit and model assumptions. ¹⁸ These included detailed consideration of appropriate residuals, as well as standard tests of goodness of fit, and direct model comparisons. ¹⁹ To avoid overfitting, we performed extensive checks of model validation, using both split-sample and bootstrap approaches.

We adapted a bootstrap resampling approach to the assessment of validation for each model we built. ^{18, 20} Our goal was to verify that our model’s predicted values accurately predict responses on subjects not included in building the model. Bootstrapping provides a method to estimate measures of statistical precision when no formula is otherwise available. The crucial advantage of bootstrap approaches for model validation is that the bootstrap yields efficient and unbiased estimates of predictive accuracy. For each model, we made appropriate bootstrap point and interval estimates of the C statistic (area under the receiver operating characteristic curve) by sampling with replacement to generate 200 replications of the entire dataset. ^{18 21}

In a final validation step, we randomly split the data into a model development sample and an evaluation sample of 100,000 births at risk for primary cesarean delivery. We then developed the models described above on the development sample and checked C statistics and calibration measures on the validation sample. In light of our very large sample size, we anticipated (and observed) largely comparable results between the bootstrap and split-sample validation procedures.

Results

Our final analytic sample includes 371,468 deliveries, after the exclusion of 279 otherwise eligible deliveries due to missing information on the outcome (cesarean delivery status), and 45,144 additional deliveries with missing values in any of our set of predictor variables (Table I). Distributions of non-missing independent variables as well as cesarean delivery rates were similar across the analyzed and excluded samples. Models with and without race/ethnicity show similar performance (Table I). The positive and negative predictive values are very close and the overall percent correct are similar. The C statistics for models with and without race and ethnicity are very close (0.7628 for Model A with race and 0.7617 for model A1, without race and ethnicity) suggesting nearly identical levels of discrimination. As for calibration, full sample Hosmer-Lemeshow test results are very similar and generally acceptable across the two models.

Table I.

Assessing the fit of models with and without race and ethnicity

Model	Description	Positive Predicted Value	Negative Predicted Value	% Classified Correctly	Split Sample C Statistic	Bootstrap Bias-Corrected C statistic (95% CI)
A	INCLUDES race and ethnicity	80.58%	85.18%	84.99 %	0.763	0.766 (0.764, 0.767)
A1	EXCLUDES race and ethnicity	80.58%	85.16%	84.97%	0.762	0.764 (0.763, 0.765).

Odds ratios for all variables in models A and A1 are shown in Table II. The very modest differences in estimated odds ratios are nonetheless associated with a highly statistically significant difference according to a likelihood-ratio test (chi-square = 517 on 5 df, p < 0.0001). The very small p-value in this comparison is mostly due to the enormous sample size, as the models are nearly indistinguishable using metrics of predictive validity. Because the effect estimates are very similar between models A and A1, there is no evidence of confounding by race/ethnicity.

Table II.

Odds ratios (95% CI) for primary cesarean risk adjustment models with and without race and ethnicity, using the entire data set

Variable	Model A With race and ethnicity	Model A1 Without race and ethnicity
Maternal age	1.071 (1.069, 1.073)	1.067 (1.066, 1.069)
Gestational age
24-30 wks vs. 37-40 wks	2.151 (1.923, 2.405)	2.195 (1.963, 2.454)
31-36 wks vs. 37-40 wks	1.234 (1.192, 1.278)	1.247 (1.205, 1.291)
41+ wks vs. 37-40 wks	1.264 (1.235, 1.295)	1.265 (1.235, 1.295)
Multiple births	14.023 (13.268, 14.820)	13.822 (13.080, 14.606)
Insurance	0.824 (0.805, 0.843)	0.776 (0.759, 0.792)
Nulliparity	5.048 (4.939, 5.159)	4.887 (4.783, 4.992)
Start of prenatal care
First Trimester vs. No Care	1.435 (1.151, 1.790)	1.429 (1.146, 1.782)
Second Trimester vs. No Care	1.306 (1.045, 1.632)	1.302 (1.042, 1.626)
Third Trimester vs. No Care	1.279 (1.014, 1.614)	1.272 (1.009, 1.604)
Complications of pregnancy	45.097 (42.250, 48.137)	44.662 (41.846, 47.669)
Medical Conditions	1.058 (1.043, 1.074)	1.050 (1.034, 1.066)
Race
(Black vs. White)	1.465 (1.404, 1.529)
(Native Amer vs. White)	1.032 (0.898, 1.186)
(Asian vs. White)	0.904 (0.876, 0.933)
(Other vs. White)	1.067 (1.038, 1.097)
Hispanic ethnicity	1.143 (1.116, 1.172)

For more extensive validation, we completed additional comparisons using split-sample and bootstrap techniques. In Figure 1, we present split-sample calibration plots based on the Hosmer-Lemeshow test for the two models. These plots provide evidence regarding how well the predicted probabilities of cesarean delivery match the observed risks of such a delivery across the distribution of all deliveries. A perfectly calibrated model would thus follow the straight line describing observed = predicted shown in each Figure. Points honing closely to the line indicate regions in the distribution of predicted risk levels that are well calibrated, while points far from the line indicate regions with relatively poor calibration. Models A and A1 appear to be similarly well-calibrated, except for a bump between predicted risks of approximately 0.5 to 0.8, where the sample sizes are relatively small.

Figure 1.

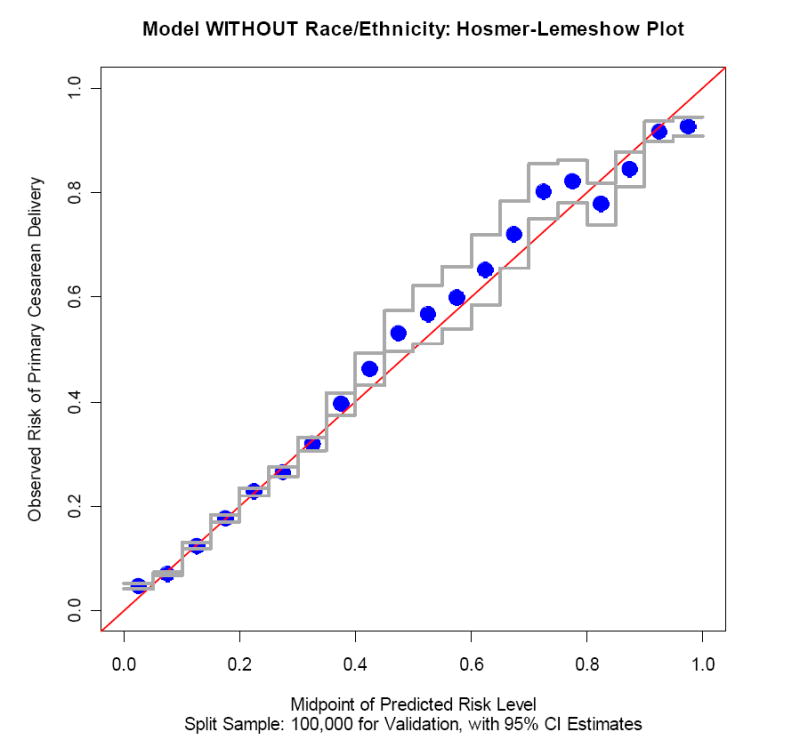
a. Hosmer-Lemeshow Calibration Plot for model including race and ethnicity

b. Hosmer-Lemeshow Calibration Plot for model not including race and ethnicity

The results of adding product terms and restricted cubic splines to Model A (including race and ethnicity) are shown in table III. Model A is the main effects model, Model B adds product terms to study the interaction of the other factors in combination with maternal age, race, ethnicity and medical conditions to Model A, and Model C adds restricted cubic splines for maternal and gestational age to Model B. Model B shows a slightly higher C statistic than the other two approaches, though differences are small. Validation through bootstrapping or splitting the sample shows minimal differences in C statistics (discrimination) between the methods. Similarly, split-sample assessments by the Hosmer-Lemeshow statistic as well as calibration plots (not shown) suggest that all three models (A, B and C) are well calibrated, with p values exceeding 0.2.

Table III.

Assessing the Fit of Risk-Adjustment Models including race and ethnicity.

Model	Description	Positive Predicted Value	Negative Predicted Value	% Classified Correctly	Split Sample C Statistic	Boot Strap Bias-Corrected C statistic (95% CI)
A	Main Effects (includes race and ethnicity)	80.58%	85.18%	84.99%	.7628	.766 (.764, .767)
B	Adds product terms to A	79.36%	85.26%	85.00%	.7636	.767 (.765, .768)
C	Adds age splines to B (maternal & gestational)	78.65%	85.31%	85.01%	.7627	.765 (.764, .767)

^*Model A contains the following predictors: maternal age and race, gestational age, indicators of Hispanic ethnicity, multiple birth, insurance, mother’s marital status, nulliparity, complications of pregnancy, maternal medical conditions, and the trimester in which prenatal care began

^**Model B contains product terms for maternal age, race, and indicators of Hispanic ethnicity and maternal medical conditions with the other predictors.

Discussion

Our study suggests that removing race and ethnicity from risk-adjustment models has no substantial impact on predictive ability. Given the controversy that surrounds the inclusion of race and ethnicity in risk-adjustment models, it is important to understand the implications of leaving race and ethnicity in or out of the models. Regardless of any other concerns, these analyses suggest that race and ethnicity can safely be left out of primary cesarean rate risk-adjustment models. The impact of race and ethnicity on the predictive quality of the models is small enough that leaving them in cannot “explain away” substantial outcome differences due to discrimination. Nor does exclusion of race/ethnicity show any substantial evidence of important reductions in our ability to effectively adjust for differences in risk related to case mix. Finally, the impact of race and ethnicity does not appear to confound the other associations described by our model.

Although this study design does not allow us to directly investigate the possibility, the fact that the models do not change substantially with and without race and ethnicity suggests that race’s independent impact, if real, may in fact be thought of primarily as a marker for other model variables. Other authors have shown that medical conditions that impact pregnancy and hospitalizations for them vary by race.^22,23 Our model includes markers of both medical conditions and socioeconomics, and it appears that the incremental value of including race and ethnicity to such a model is still quite small.

Risk-adjustment models are difficult to understand for many practicing obstetricians. Our data show that model discrimination and calibration changes were minimal when product terms, polynomials, and splines were added. Keeping the models as simple as possible increases both the efficiency and clarity of the model. On the basis of these results, we believe that a main effects logistic regression model can safely be used to risk-adjust primary cesarean rates.

The strengths of our study are that it is based on the entire population in California and that the population is quite diverse. Furthermore, race is self-identified on birth certificates suggesting that the data should be accurate. While our results are consistent with the notion that race and ethnicity are markers for other processes that place a patient at risk for cesarean delivery, the study has limited ability to determine which other processes are responsible. California is racially and ethnically more diverse than other parts of the country. There are higher percentages of Asians and Hispanics, and fewer African Americans than much of the country. This is helpful in that California has higher numbers of underrepresented minorities to be studied. However, California has a higher market penetration of HMOs than elsewhere in the country. Our odds ratios are similar to odds ratios in primary cesarean risk-adjustment studies in other populations suggesting that our conclusions are not limited to California.¹⁰,²⁴ While we do not have direct evidence that the racial make up and HMO market penetration would effect our results, the possibility that our results are unique to California cannot be completely discounted. Future work in this area may help to elucidate the mechanism through which race affects perinatal outcomes. Lastly, the value of statistical tests of significance is limited here, as the large data set renders these tests more or less useless in assessing the effectiveness of the two models. In this setting, even clinically unimportant) differences between models appear to be statistically significant.

Conclusions

The mechanisms for how race and ethnicity affect perinatal outcomes may never be fully delineated. Despite this uncertainty, race and ethnicity show no substantial impact on the quality of risk-adjustment models for primary cesarean delivery.