Microvascular and tissue oxygen gradients in the rat mesentery

Abstract

One of the most important functions of the blood circulation is O₂ delivery to the tissue. This process occurs primarily in microvessels that also regulate blood flow and are the site of many metabolic processes that require O₂. We measured the intraluminal and perivascular pO₂ in rat mesenteric arterioles in vivo by using noninvasive phosphorescence quenching microscopy. From these measurements, we calculated the rate at which O₂ diffuses out of microvessels from the blood. The rate of O₂ efflux and the O₂ gradients found in the immediate vicinity of arterioles indicate the presence of a large O₂ sink at the interface between blood and tissue, a region that includes smooth muscle and endothelium. Mass balance analyses show that the loss of O₂ from the arterioles in this vascular bed primarily is caused by O₂ consumption in the microvascular wall. The high metabolic rate of the vessel wall relative to parenchymal tissue in the rat mesentery suggests that in addition to serving as a conduit for the delivery of O₂ the microvasculature has other functions that require a significant amount of O₂.

Blood entering capillaries is only 50% saturated (1), thus one-half of the O₂ gathered by the lung exits the circulation before arrival in the capillaries. This rate of O₂ loss from the arteriolar network has been found and documented in different species and tissues at rest (2–7). It was noted in one study that this loss is an order of magnitude greater than expected from simple diffusion (8). Possible sinks for the O₂ exiting before the capillaries include O₂ shunting from arterioles to parallel venules (9), periarteriolar tissue consumption (10), and arteriolar-capillary O₂ diffusional shunting (11). The contribution of arterio-venous shunting appears to be negligible during normal conditions (9), and although arterio-capillary diffusional shunting has been demonstrated (11), the conditions under which it might occur, i.e., an arteriole crossing a capillary network, are not common in the mesentery. It therefore is important to examine in detail the loss of O₂ from arterioles to surrounding tissue. The outward flux of O₂ from blood is governed by the law of diffusion and defined by O₂ gradients between blood and the surrounding tissue. O₂ delivery to the tissue surrounding the microvessels has not been extensively studied because of the lack of methods that can measure pO₂ in both blood and tissue. Recently, an optical method has been developed that makes such a study feasible (12).

The objective of our study was to use noninvasive phosphorescence quenching microscopy to determine the radial pO₂ profiles in vivo for the periarteriolar tissue of the rat mesentery. With this method it was possible to determine the contribution of microvascular wall metabolism to the precapillary O₂ exit. Intravascular and extravascular measurements were carried out by using the same pO₂ measuring technique, and validation of tissue fluxes was obtained by O₂ mass balance between O₂ entering and exiting vascular segments, and the O₂ diffusional fluxes were determined by the measured O₂ gradients.

MATERIALS AND METHODS

Phosphorescence Quenching Microscopy.

Pd-phosphorescence quenching microscopy, based on the relationship between the decay rate of excited Palladium-mesotetra-(4-carboxyphenyl)porphyrin (Porphyrin Products, Logan, UT) bound to albumin and the pO₂ according to the Stern-Volmer equation, was used to measure pO₂ in the microcirculation (13). The method was used previously in microcirculatory studies to determine blood pO₂ levels in different tissue under different conditions (14–18). In our system, a xenon strobe (EG & G, Salem, MA; decay constant of 10 μsec, frequency of 30 Hz; peak wave length of 420 nm) excites the phosphorescence by epi-illumination of a tissue area for 3 sec. Phosphorescence emission from the target tissue area passes through an adjustable rectangular optical slit and light filter (630-nm cutoff) and is captured by a photomultiplier (EMI, 9855B; Knott Elecktronick, Munich, Germany). A digital oscilloscope (Tektronix, 2434) averages 90 photomultiplier decay signals, and the resulting smoothed curve is stored to a computer. Decay curves are analyzed off-line, by using a standard single exponential least-squares numerical fitting technique, and the resultant time constants are applied to the Stern-Volmer equation to calculate pO₂, where k_Q, the quenching constant and τ₀, the phosphorescence lifetime in the absence of O₂ measured at pH = 7.4 and T = 37°C are 325 mmHg⁻¹ sec⁻¹ and 600 μs, respectively. The phosphorescence decay caused by quenching at a specific pO₂ yields a single decay constant (12), and in vitro calibration has been demonstrated to be valid for in vivo measurements.

As a consequence of the two-dimensional, single-layer planar characteristic of the vasculature in the exteriorized mesentery preparation, our phosphorescence exponential decay signal is not contaminated by signals from vessels above and below the focus plane and usually is fitted with a high level of correlation (r > 0.92) by a single exponential. Modeling of the decay curves obtained from our measurements as multiple exponentials does not alter the results obtained with a single exponential fit. Our measurements, based on minimal and uniform light exposure, do not show evidence of changes in phosphorescence intensity within the tissue near the vessel wall. Furthermore, we found no change in the measured pO₂ distribution when using windows slits of widths varying from 7.5 to 20 μm for characterizing the gradient when the center line of the window was assumed to be the location of the measurement, indicating that the window provides a consistent average of the decay curves within the window.

Interstitial pO₂ Measurement.

The albumin-bound probe passes into the interstitium according to the exchange of albumin from blood to tissue (19). The resulting accumulation of albumin-bound dye within the tissue, which may contain up to 10% of the total albumin in the organism, allows measurement of tissue and intravascular pO₂ at high resolution with the same technique. The reflection coefficient of albumin in different vascular networks varies, changing the equilibration time between intravascular and extravascular dye/albumin. Because measurement of pO₂ is possible anywhere Palladium-porphyrin albumin-bound complex is located given an adequate signal-to-noise ratio (15–17), in our model tissue pO₂ measurements could be made within 20 min after injection. Interstitial pO₂ profiles were determined by measuring pO₂ in the tissue at specific distances from the vessel lumen.

Phosphorescence generated by the light excitation of the porphyrin probe consumes O₂. This photoactivation could be a factor affecting tissue O₂ measurements made in a slow-moving or stationary fluid. To determine the extent of this photoactivation on our interstitial measurements, we performed in vitro measurements in sealed tubes. We estimated O₂ consumption by the technique in sealed 75-mm long hematocrit tubes filled with Pd-meso-tetra(4-carboxyphenyl)porphyrin bound to albumin solution (0.1 mg/ml) saturated to pO₂ of 37 mmHg with the same system used for animal experiments. The concentration of probe used is approximately that which would be found in interstitial fluid. Albumin concentration in tissue at steady state is approximately one-third lower than in blood, therefore the probe concentration of 0.26 mg/ml plasma within the blood (= 10 mg/ml probe × 0.1 ml probe/100 g animal × 100 g animal/7.0 ml blood × 1 ml blood/0.55 ml plasma) corresponds to an interstitial fluid probe level of 0.09 mg/ml. The initial pO₂ within the tube was measured at three locations 1.5 mm apart with a 3-sec, 30 flashes/sec pulsed light. The center of the tube was masked and exposed to 45 min of pulsed illumination at a rate of 30 flashes/sec, in such a fashion that 0.5 mm of tube length was exposed to flash illumination. Immediately after the pulsed exposure, the tube content was mixed by a nylon bar sealed in the tube, which was made to move by gravity along the length of the tube for 5 sec in each direction during a 5-min period. PO₂ measured in the tube at the three locations decreased from 37 to 31 mmHg. Therefore 81,000 light flashes lowered pO₂ within the exposed tube segment by (6 mmHg × 75 mm/0.5 mm × 8.1 × 10⁴) = 0.01 mmHg/flash. The decrease in O₂ at the excitation spot was initially a factor of 2 higher than the rate determined for the entire flashing period. O₂ initially is consumed solely at the excitation spot, establishing a concentration gradient whereby consumption is lowered by diffusion of O₂ from surrounding areas into the excitation spot.

We used 90 flashes (3 sec) for each measurement. We estimate that the free fluid in the mesentery in which albumin-bound probe is present is at most 20% of the total tissue volume; the rest of the tissue is not occupied by the probe and constitutes a reservoir of O₂. Therefore the maximal reduction in pO₂ during each determination, assuming the highest rate found for O₂ consumption by the flash, is about 0.02 mmHg/flash × 90 flashes × 0.2 = 0.4 mmHg.

We also examined the accuracy of the tissue pO₂ measurements with the phosphorescence method in vivo by simultaneous continuous measurements with approximately 5-μm diameter recessed tip gold cathode microelectrodes (20). Measurements were made in avascular tissue areas of the hamster skin fold preparation (15–17). In these studies, the tissue was isolated from extraneous sources of O₂ by superfusing with a Krebs Henseleit solution (1.3 × 10⁻¹ M NaCl, 1.2 × 10⁻³ M Mg SO₄, 2.0 × 10⁻³ M CaCl₂, 4.7 × 10⁻³ M KCl, 2.2 × 10⁻² M NaHCO₃) bubbled with 100% N₂. A maximum divergence of 2% was found between the methods over the tissue pO₂ range of 5–40 mmHg. Extended flashing over a period of up to 1 min did not produce a detectable change in the microelectrode measurement. The congruence between microelectrode and phosphorescence quenching microscopy measurements demonstrates that excitation of the porphyrin probe in the tissue is minimal and does not affect tissue pO₂ in our model. It should be noted that those investigators (15–17) using the same technique reported that capillary pO₂ in the hamster skin fold preparation was 29 mmHg, tissue pO₂ was 23 mmHg, and the gradient at the capillary wall was 4 mmHg (21). This finding is incompatible with the assumption that the pO₂ decrease on the order of 20 mmHg found near arterioles is caused by O₂ consumption by the dye in the tissue, because capillaries have 100-fold lower O₂ delivery capacity than the arterioles in this study, which would result in a near-zero pericapillary tissue pO₂ measurement.

Mesentery Preparation.

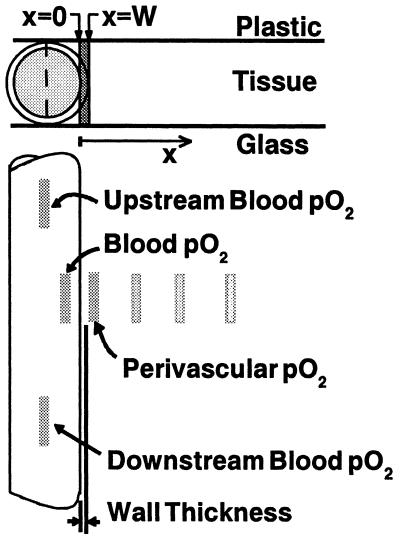
The mesentery of male Wistar rats (250–350 g) was exteriorized, and the upper and lower surfaces of the tissue were sandwiched between two essentially gas-impermeable and transparent barriers, allowing O₂ to exit from the vasculature only in the plane of the tissue as shown diagrammatically in Fig. 1. After anesthetizing the animal (Nembutal, 40 mg/kg i.m. into left hind limb), the right femoral vein and artery are cannulated for: (i) injection of Pd-phosphorescence probe and supplemental anesthesia (5–10 mg/kg), and (ii) monitoring blood pressure. The animal is placed on a microscope stage with a circulating water heater (37°C). The mesentery is exteriorized through an epigastric incision, partially extracted, and kept moist with dripped buffered Krebs Henseleit solution, pH corrected by bubbling a gas mixture of 5% CO₂ and 95% N₂. It is viewed by draping it over a thin circular glass platform. Before the experiment the tissue is covered with a thin strip of transparent plastic film (Saran, Dow Corning) to prevent gas exchange [diffusion coefficient of 6.2 × 10⁻¹³ cm³ O₂/(cm × mmHg × sec)] and desiccation. The heated drip without the gas is continued onto the plastic to maintain tissue at 37°C during the study. A temperature probe (Physitemp, Clifton, NJ) was placed on the plastic and positioned above the mesenteric window under study to monitor tissue temperature during the experiment.

Figure 1.

(Upper) The geometry of the exteriorized mesentery preparation. Mesentery is sandwiched between O₂ impermeable upper and lower barrier of plastic and glass. Circle represents blood vessel with vessel wall. O₂ diffuses in the planar, x, direction, x = 0 is the blood side of the blood/tissue interface. W is the thickness of the vessel wall. (Lower) The positions of the optical window (shaded rectangles) are shown schematically. Upstream and downstream pO₂ along with vessel diameter, blood velocity with a given separation distance is used to calculate the convective O₂ losses. O₂ mass balance is studied by comparing O₂ loss along and diffusional loss out of the vessel. pO₂ levels detected in blood and at increments in tissue, illustrated by the staggered window in x-direction are used to construct pO₂ profiles. Window size was a 5 μm × 20 μm rectangle.

Experimental Protocol.

The animal was positioned on an inverted microscope (IMT-2, Olympus, New Hyde Park, NY) equipped with a 40× objective (WPlan FL40x, 0.7 water). Measurements began 20 min after injection of phosphorescence probe (10 mg/ml, 0.1 ml/100 g). Transillumination (halogen lamp, 12 V, 100 W) was used to measure vessel diameter (22) and blood flow velocity (23), followed by intravascular and perivascular pO₂ determinations using phosphorescence quenching microscopy. Transillumination measurements were made with a maximum of 2–3 V power to the lamp to reduce possible light toxicity and photoactivation of the phosphorescence probe. All pO₂ measurements were performed after extraneous light from the transillumination lamp and the room were eliminated. Each intravascular pO₂ measurement was repeated after perivascular pO₂ determinations to assure constant delivery conditions were maintained. Vessels whose intravascular pO₂ readings differed by more than 5 mmHg were not included in the study. Measurements were obtained in vessels with sharp focus and not in close proximity to other vessels (>250 μm separation). The optical measuring windows (5 μm × 20 μm) were placed as shown in Fig. 1 relative to the vasculature under study. Extravascular pO₂ profiles were obtained by progressively displacing the optical measuring window away from the blood/tissue interface. All measurements were performed within a 30-min period. The resolution of the optical window does not allow for pO₂ measurements within the vascular wall.

Vessel Wall Gradient.

In this model, an O₂ gradient between blood and perivascular tissue greater than that dictated by simple diffusion is indicative of O₂ consumption by the vessel wall when the calculated diffusion flux shows mass balance with the decrease of O₂ content in the flowing blood. Thus the vessel wall gradient, the difference between intra- and perivascular pO₂, was used to determine the rate of vessel wall oxidative metabolism and later used in determining the mass balance in vessel segments. The perivascular pO₂ profile was used to calculate tissue oxidative metabolism. The pO₂ measured in tissue adjacent to the O₂ source (about 4 μm from the blood-tissue interface) could, in principle, be contaminated by the higher intensity phosphorescence decay signal from blood. The net effect of this contamination, if it exists, would result in a higher perivascular pO₂ reading and thus underestimate the measured vessel wall gradient.

Theoretical Simulation and Analysis.

Our system consisting of a thin tissue whose thickness is much less than the distance between adjacent vessels, can be modeled in terms of diffusion from a linear source (the blood vessels) with thickness equal to that of the tissue (assumed to be identical to the separation between the impermeable barriers). This process is described by Fick’s law of diffusion for O₂ into a semi-infinite region extending away from the source in the x direction, where the consumption rate is g and the diffusivity is D. The governing equation at steady state is:

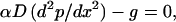1

where p = oxygen tension and α = solubility constant for O₂. We assume that there is no O₂ gradient perpendicular to the tissue plane and that the mesentery is a homogenous tissue with a constant rate of O₂ consumption.

Tissue and Vessel Wall Metabolic Rate.

With boundary conditions of a constant O₂ source p_W at the vessel wall/tissue interface x = W and a no flux of O₂ at a penetration distance δ from vessel wall/tissue interface, the solution of Eq. 1 is:

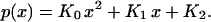2

The coefficients are K_O = g/(2Dα), K₁ = −(gδ)/(Dα), and K₂ = p_W − [(gW)/(Dα)][(W/2)−δ]; W, is the location of the vessel/tissue interface. Curve fitting of the perivascular pO₂ profiles to the second-order polynomial solution was used to determine the tissue consumption rate from the coefficient K_o. The distance of O₂ penetration from the vessel wall/tissue interface, δ, is determined from K₁.

A finite difference numerical approximation of Eq. 1 is used to calculate the steady-state profile for the perivascular tissue, consisting of two metabolically active regions representing the vascular wall and the tissue proper. By using the consumption rate of tissue obtained with curve fitting and the distance of O₂ penetration, the rate of vessel wall metabolism is iterated until the measured intra- and perivascular difference is attained. The boundary and regional conditions are: (i) At blood side of blood/tissue interface, x = 0, O₂ tension is equal to intravascular pO₂, p = p_i; (ii) At interface between vessel wall p_w and tissue p_T, x = W, O₂ flux is continuous Dα (dp_w/dx) = Dα (dp_T/dx); (iii) At penetration distance, x = δ, O₂ level is constant, dp/dx = 0; (iv) g_W, O₂ consumption rate in region comprising the vessel wall (0 < x ≤ W); and (v) g_T, O₂ consumption rate in region beyond the vessel wall (x > W) to the penetration depth (x = δ).

Mass Conservation Analysis of O₂ Transport.

The law of mass conservation stipulates that the amount of O₂ lost from a vascular segment must be equal to the diffusional O₂ flux, determined by the perivascular pO₂ gradient. We studied longitudinal and radial O₂ losses from nonbranching vessel segments to determine the extent of O₂ loss in our animal model. The equation for the rate of longitudinal O₂ loss along the length of a microvessel is:

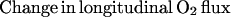3

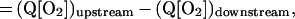where Q = vπr² and [O₂] = C_b [fHCT] SO₂. The parameters are: Q, blood flow; v, blood flow velocity, corrected for velocity profile shape (24); r, vessel radius; [O₂], O₂ content; C_b, O₂ binding capacity of blood; [fHCT], ratio of microvascular to systemic hematocrit, a function of vessel diameter (25) (physically dissolved O₂ is neglected because of low solubility of O₂ in plasma); SO₂, hemoglobin O₂ saturation, intravascular pO₂ measurements are converted to SO₂ (26).

Longitudinal O₂ exit must be matched by the rate of O₂ exit by diffusion and O₂ consumption by the vessel wall. The area through which O₂ diffuses out of the blood vessel into the tissue is assumed to be the plane perpendicular to the impermeable barriers. The remaining portion of the blood vessel, V_W, in contact with the impermeable barriers is assumed to consume O₂ at the experimentally determined rate g_w. However this portion of the vessel wall does not contribute to the diffusive flux into the tissue. This rate of O₂ exit by diffusion and O₂ consumption by the vessel wall is expressed as

4

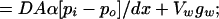where D, diffusivity (1.70 × 10⁻⁵ cm²/sec) (27); A, surface area; α, O₂ solubility constant (2.14 × 10⁻⁵ ml O₂/cm³ mmHg) (27); p_i, intravascular pO₂; p_o, perivascular pO₂; dx, vessel wall thickness, approximated as 10% of vessel diameter (2.3 μm); V_W, volume of vessel wall; g_w, O₂ consumption rate of vessel wall determined by the theoretical analysis of measured tissue pO₂ profiles.

Curve fitting to the data was performed by first transforming the data to allow for linear least-squares regression. Gauss-Jordan method for matrix inversion then was used to determine the coefficients from the transformed data (Table Curve 2-D, Jandel, San Rafael, CA). Results are presented mean ± standard error unless otherwise stated.

RESULTS

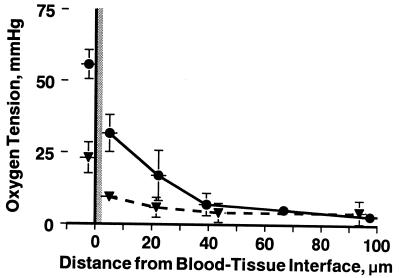
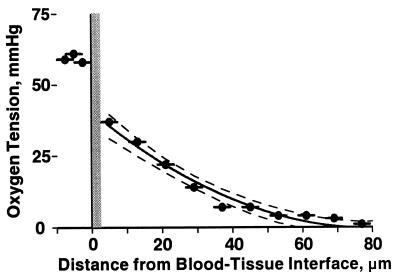
PO₂ profiles were obtained in 12 animals from 31 arterioles with sharp focus and not in close proximity to other vessels (>250-μm separation). Results were grouped according to intravascular pO₂ levels (p_i > 50; 40 < p_i ≤ 50; 30 < p_i ≤ 40; and, 20 < p_i ≤ 30 mmHg). Profiles for two groups are shown in Fig. 2 to demonstrate the pronounced fall between intravascular (x = 0) and perivascular (x = 5 μm) pO₂, a distance spanning the vessel wall, which includes endothelium and smooth muscle. The finding of a steep fall in pO₂ near the vessel wall was common to all groups. Fig. 3 shows a more closely sampled pO₂ profile, which exhibits the same characteristics as those more sparsely sampled profiles used in the analysis.

Figure 2.

Large drop in pO₂ across the blood/tissue interface. PO₂ profiles from blood into tissue for high (•) and low (▴) intravascular pO₂. Results were grouped according to intravascular pO₂ levels. Intravascular pO₂ measurements were made flush to the intraluminal vessel wall with the center of the window slit 2.5 μm from the vessel wall. Perivascular pO₂ begins with the window flush with the abluminal vessel wall. The solid horizontal bars at each data point represent the width of the rectangular slit. The vascular wall is depicted as the shaded area. Individual measurements from different profiles are grouped as function of distance from intraluminal wall (mean ± SD).

Figure 3.

Example of pO₂ profile found in the rat mesentery. Closely sampled pO₂ measurements allow for a detailed view of tissue pO₂ profile. Solid line is the curve fitting of the pO₂ profile within the tissue, dotted lines are the 95% confidence intervals of the data. Intravascular pO₂ averaged 59.3 ± 1.5 mmHg (horizontal bar), shown left of the blood tissue-interface. The wall was taken to be 2.5 μm thick, and each data point represents the pO₂ within the sampling window whose width is represented by the horizontal bars.

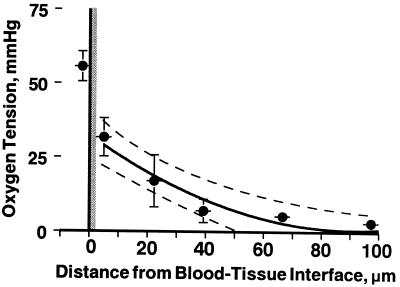
The theoretical profile for diffusion from a constant source into a consuming medium was constructed to determine whether measured pO₂ profiles corresponded to a region with a single metabolic rate, implying that vessel wall O₂ consumption is equal to that in the tissue proper, or whether the vessel wall and tissue have different metabolic rates (Eq. 2). The measured tissue pO₂ profiles were fitted to the theoretical solution for the tissue region beyond 2.5 μm of the blood/tissue interface to determine the tissue O₂ consumption rate and penetration. Average g_T and δ for all groups were 2.4 × 10⁻⁴ ± 0.5 ml O₂/(cm³ tissue sec) and 93.6 ± 11.1 μm, respectively. Least-squares regression correlation coefficients of the curve fit to the profiles ranged from r = 0.87 to 0.99, being all statistically significant P < 0.01. Fig. 4 shows the mean pO₂ profile from the pO₂ > 50 mmHg group and the curve fit used to determine the tissue O₂ consumption rate.

Figure 4.

Graph shows curve fitting to the tissue profile with tissue having one consumption rate. An average g_T of 2.4 × 10⁻⁴ ± 0.5 ml O₂/(cm³ tissue sec) and δ of 93.6 ± 11.1 μm were determined from the coefficients. Least-squares regression correlation coefficient of the curve fit to the perivascular portion of the pO₂ profiles is r = 0.98, and the dotted line represents the 95% confidence intervals. When the two-compartment model is used to fit the tissue pO₂ profile with the intravascular pO₂ of 55.6 mmHg, the vessel wall consumption rate was found to be 141 times the tissue rate. Data is grouped axially and presented as mean ± SD (n = 6 profiles).

The two-compartment model was used to determine the vessel wall O₂ consumption rate relative to the tissue. We found the average vessel wall metabolic rate needed to achieve the intravascular pO₂ levels given the tissue pO₂ profiles was 277.8 ± 45.0 (range 141–323) times that of the tissue metabolic rate or 3.9 ml O₂/(cm³ tissue min).

If the O₂ consumption of the vessel wall is as great as the calculation above suggests there should be a corresponding loss of O₂ longitudinally. Therefore we measured the rate of O₂ exit both longitudinally and radially in 12 vessel segments of five animals. Longitudinal saturation drop was 2.4 ± 0.3%/100 μm in vessels with average diameter of 23.2 ± 2.9 μm and blood flow velocity of 1.5 ± 0.3 mm/sec. Intravascular pO₂ was 43.3 ± 3.7 mmHg and the intraperivascular difference was 18.1 ± 1.7 mmHg.

Loss of O₂ along each individual vessel segment (Eq. 3) was found to be within 3.3 ± 19.6% of their diffusional losses (Eq. 4), confirming that the rate of O₂ exit is caused by the extremely large O₂ gradient in the tissue compartment that includes the vessel wall. The average convective loss of 2.4 ± 0.5 × 10⁻⁵ ml O₂/cm² sec and diffusive loss of 2.2 ± 0.2 × 10⁻⁵ ml O₂/cm² sec in all of the vessels studied agreed within 8.6%. Calculation of O₂ loss from averaged parameters does not yield mass balance because the parameters that determine O₂ fluxes are not related in an additive form.

DISCUSSION

This study shows that there is a substantial O₂ loss from the blood as it passes through the arteriolar network in the rat mesentery. This was first reported by Duling and Berne (1) using recessed microelectrodes in the hamster cheek pouch and subsequently in other laboratories (2–7) using microelectrode and spectrophotometric measurement techniques.

In addition to the large O₂ loss, we found a large pO₂ gradient across a tissue region that includes the arteriolar vessel wall. The presence of this gradient can account for the large rate of O₂ loss from microvessels because, in accordance with the law of mass balance, our results require that the large rate of O₂ exit from arterioles be driven by a large O₂ gradient. The steep O₂ gradient across the wall could be caused by a large amount of O₂ consumption or an increased diffusional resistance within the vessel wall (lower diffusion constant and/or permeability). However, in the latter case the resulting steep gradient would lead to significantly lower O₂ exit, and therefore a large difference between longitudinal O₂ loss and tissue O₂ flux and a large disparity in mass balance.

The low levels of pO₂ in the tissue (and therefore large gradients) could be caused by O₂ consumption by the technique because the fluid containing the probe in the tissue is virtually stationary during the period of measurement. Intravascular measurements would not be affected by O₂ consumption because the blood flow would replace the consumed O₂. Simultaneous measurements of tissue pO₂ levels using our phosphorescence decay system and recessed microelectrodes found no statistical change in pO₂ during our 3-sec measurement period or during prolonged flashing. Moreover when using the phosphorescence technique to measure tissue pO₂ in the hamster skin fold chamber we found values between 23 and 25 mmHg (7, 15–17), similar to the value of 26 mmHg reported by Endrich et al. (28), who used surface platinum multiwire electrodes in the same tissue. Our values obtained using the phosphorescence technique are higher than those reported with microelectrode measurements in the hamster cremaster muscle, which ranged from 11 to 17 mmHg (29, 30). Therefore our tissue pO₂ measurements are within the range of previous measurements made by other investigators using different techniques and are not unduly lowered by photoactivation of the phosphorescence probe.

Our in vitro measurements of the amount of O₂ consumption per flash described in Materials and Methods also corroborated the electrode findings that O₂ quenching by photoactivation of the probe is not a factor affecting our measurements. The equivalent lowering of tissue pO₂ was found to be about 0.4 mmHg. This number is indicative of the maximum possible error in the measurement; however, the actual error is much smaller because as O₂ is consumed it also is replenished by diffusion from the arteriole. Tissue O₂ depletion by flash illumination in the area of measurement (about 140 μm in diameter, 50 μm thick) is calculated to be 1.4 × 10⁻¹² ml O₂/sec, whereas the arterioles supply O₂ at a rate of 4.1 × 10⁻⁹ ml O₂/sec, or a rate that is about 3,000 times greater than that at which O₂ is consumed by the probe during the measurement, indicating that pO₂ measurements are not affected by probe O₂ consumption near the vessel wall.

The spatial resolution of our technique is not sufficient to measure the pO₂ profile within the vessel wall; however, we can accurately measure the pO₂ difference across the vessel wall. To measure pO₂ as close as possible to the blood-tissue interface, the optical windows were as narrow as possible, compatible with the need for adequate signals. The tissue pO₂ profile also was determined with a window that was 10 μm by 20 μm, double the width used in this study, and there was no difference in the pO₂ measurements even in regions of steep gradients, indicating that in these experiments pO₂ is averaged within the window.

In our mass balance calculations, we approximated vessel wall thickness to be 10% of the average vessel diameter. We found that vessel wall thickness of the vessels studied ranged from 1.3 to 7.5 μm, the magnitude greatly depending on the position of the nucleus of endothelial cells and smooth muscle cells. Wall thickness tends not to be uniform in these vessels, and we used an average wall thickness based on the lumen size. Varying the vessel wall thickness from 2 to 3 μm in our mass balance calculations shifted the balance between O₂ loss along each vessel segment and the diffusional flux to deviate by −5.6% and 17.0%, respectively.

Our measurements of the pO₂ gradient in the mesentery itself provides an estimate of O₂ consumption rate of mesenteric tissue of 2.4 ± 0.5 × 10⁻⁴ ml O₂/cm³ tissue sec, which is about four times higher than the value for loose connective tissue of 5.6 × 10⁻⁵ ml O₂/cm³ tissue sec determined from the renal capsule of the goat (31), a comparison between the same tissue type but from different size animals. O₂ consumption relative to the body size is much higher in smaller than in the larger mammals. By using the empirical relationship of mammals size and O₂ consumption, assuming that connective tissue also can be similarly scaled, we estimate that the O₂ consumption rate of the rat to be on the order of 3–4 times higher than the goat (32), and therefore similar to the one found in this study.

Investigations in other tissues and models that used different measurement techniques also found evidence of a high rate of vessel wall metabolism. When endothelium is removed from the dog hind limb O₂ consumption decreases by 34% (33). Measurements in larger arterial vessels using microelectrodes show that the ratio between the O₂ consumption rate and the diffusivity increases nearly 10-fold as the electrode is advanced from the abluminal side toward the blood/vessel interface (34). Therefore given a constant diffusivity the rate of O₂ consumption increases significantly near the blood/vessel interface. However, the O₂ consumption rate suggested by that study was significantly lower than the one we measured, a discrepancy that may be, in part, because of the resolution limitation of 10–15 μm microelectrode tips. Investigations of O₂ consumption by endothelial cells cultured from vascular tissue found a metabolic rate “as much as 5,000-fold” over the rate in organized tissues (35).

The endothelial lining of blood vessels has, until recently, been regarded as simply a barrier between the blood and the parenchyma, greatly restricting passage of macromolecules while allowing rapid exchange of gases and crystalloids. Mitochondria density is not particularly pronounced within endothelium (36) and cannot solely account for the high respiratory rate of the vessel wall suggested by our findings. However, endothelial cells are the site of chemical synthesis and metabolic processes that require O₂ (renin, prostaglandins, collagen, conversion of angiotensin I to II, degradation of bradykinin and prostaglandins, and the clearance of lipids and lipoprotein) (37). The endothelium is a principal mediator in many homeostatic (38) and disease processes (39, 40) and has been considered a widely influential “organ” (41). Moreover, endothelial cells have an active actin/myosin-based contractile system that also may consume O₂ (42, 43). In the blood/tissue interface, endothelium overlays and interacts with smooth muscle throughout the vasculature with the exception of the capillaries, giving origin to the regulatory mechanism that modulates the vessel diameter and controls tissue perfusion. The metabolic cost of this array of endothelial function has not been addressed previously. It is worth noting that because of its location, the endothelium has the highest O₂ availability of all tissues.

Previous studies on microvascular O₂ distribution relied on a spectrophotometric method for intravascular O₂ determination and electrode measurements to characterize tissue pO₂ gradients. Those studies were carried out either longitudinally or radially, but only rarely in both directions with the same technique. Lack of direct evidence for steep gradients at the vessel wall led to the concept that the O₂ diffusion constant for the arteriolar wall may be an order of magnitude larger than that of water to account for the large rate of O₂ loss (8).

Microelectrode studies by Duling et al. (2) in pial vessels of the cat revealed both a longitudinal gradient along the vessel and transmural gradient across the vessel wall. They found a difference between blood pO₂ and vessel surface pO₂, which ranged from 27 mmHg in the largest (234 μm diameter) to 6 mmHg in the smallest (22 μm diameter) arterioles. O₂ consumption by the wall was estimated to be 2.8 × 10⁻² ml O₂/sec g tissue, which is similar to our finding. Yaegashi et al. (44) in their study of pO₂ distribution in mesenteric microcirculation, which used O₂-sensitive fluorescence-coated 3-μm silica gel beads embedded in a silicone rubber membrane 5 μm thick suspended an average 38 μm above the mesenteric surface, found a longitudinal pO₂ gradient three times smaller than the value reported by ourselves and others. Their study did not find the wall pO₂ gradient seen in our study. Because of the separation of the O₂-sensitive membrane and the tissue surface, this method may have limited resolution. From their measurements, they estimated O₂ consumption rate in the rat mesentery to be 8.2 × 10⁻⁶ ml O₂/cm³ tissue sec, which is 30 times lower than our finding.

The metabolic rate of endothelium may vary among organs and vessels within the same organs as they all are subjected to different local conditions and influences. Our finding of a high metabolic rate in the wall of mesenteric arterioles may help to explain in part the large O₂ loss observed in other arteriolar networks in other tissues but this requires further study.

In summary, this report documents the existence of steep O₂ gradients at the wall of arterioles in the rat mesentery. The steepness of the O₂ gradient is compatible with the hypothesis that the arteriolar vessel wall is a region of high O₂ consumption. This finding in the rat mesentery suggests that O₂ delivery to parenchymal tissue is, in part, determined by the vessel wall metabolism in the microcirculation.