Differential Evanescence Nanometry: Live-Cell Fluorescence Measurements with 10-nm Axial Resolution on the Plasma Membrane

Abstract

We present a method to resolve components within a diffraction-limited object by tracking simultaneously the average axial positions of two different sets of fluorescent molecules within it. The axial positions are then subtracted from each other to determine the separation of the two sets of fluorophores. This method follows the dynamic changes in the separation of the two sets of fluorophores with freely rotating dipoles using sequential acquisitions with total internal reflection and wide-field illumination, and it can be used to measure the formation of small structures on living cells. We have verified that we can achieve a resolution of 10 nm, and we have used the method to follow the location of clathrin and its adaptor AP-2 as they are recruited to a diffraction-limited coated pit during its assembly at the plasma membrane. We find a gradually increasing axial separation between the centroids of clathrin and AP-2 distribution, up to a final value of 30 nm just before coated-pit pinching and formation of the coated vesicle.

INTRODUCTION

The finite size of the diffraction-limited observation volume in far-field light microscopy sets a resolution limit of ∼200 nm in the focal plane and 500 nm in the axial direction (1,2). Ways to break this resolution limit include reducing the observation volume or, correspondingly, increasing the available Fourier space of the image, as elegantly demonstrated by 4Pi (3,4), patterned illumination (5,6), reversible saturable optical fluorescent transition (RESOLFT) (7), and stimulated emission depletion microscopy (STED) (8–10). These methods illuminate ensembles of fluorescent molecules and can achieve resolutions as low as 20 nm in the focal plane and 100 nm in the axial direction. To date, only 4Pi and STED have been successfully used to image living cells with 100- to 150-nm resolution (9,11), whereas use of all of the other methods has been restricted to fixed samples due, in part, to high excitation intensities that result in photobleaching and phototoxicity (12).

Diffraction-limited multiprotein structures, such as clathrin coated pits (13–16), focal adhesion sites (17–19), and budding viruses (20–22), form on the plasma membrane of cells. Current applications of live-cell imaging methods, such as confocal, wide-field (WF), and total internal reflection fluorescence (TIRF) microscopies, can be used to follow the assembly dynamics of such structures, including the independent recruitment of differentially labeled components. Because the centroid of a fluorophore can be located with far more accuracy than the nominal resolution, it is theoretically possible to “resolve” two components to an accuracy of <10 nm, provided that ∼10,000 photons/fluorophore can be recorded (23,24). This principle is the basis for photoactivated localization microscopy (25), fluorescence photoactivation localization microscopy (26), and stochastic optical reconstruction microscopy (27). Use of these methods has been largely restricted to fixed samples, however, because of limits set by photobleaching of currently available fluorophores (28). For accurate determination of axial position within ∼200 nm of the specimen surface, TIRF is particularly efficient, because of the penetration fall-off of the evanescent field (29,30). This property has been used to demonstrate the inward movement of clathrin-containing structures at the plasma membrane by means of alternating TIRF and WF illumination (15,16). It is possible to determine experimentally the distance dependence of the evanescent field and to track the axial position (determined as emitted intensity) of a single fluorophore with nanometer precision using just 1000 photons—a method referred to as evanescence nanometry (31).

In the approach described here, of general application to freely rotating fluorescent dipoles, we have taken advantage of evanescence nanometry and independent detection of two fluorophores to track simultaneously the axial positions of the fluorophore centroids within a diffraction-limited object on the surface of a living cell. We use WF images to correct for the varying number of molecules within the object as it assembles or disassembles, and the ratio of TIRF to WF intensity to determine position. With this method, which we call differential evanescence nanometry (DiNa), we can determine the difference in axial positions of the two fluorophore centroids to an accuracy of ∼10 nm. The position of one fluorophore serves as a reference for the other, thus correcting for overall axial motions of the cell surface.

Clathrin-coated pits and coated vesicles form at the plasma membrane of eukaryotic cells. The assembly dynamics of these diffraction-limited objects has been followed in cells expressing fluorescent chimeras of clathrin (13–16) and its AP-2 adaptor complex (13). BSC1 monkey cells are particularly advantageous for such studies, since >95% of the clathrin-coated pits on the plasma membrane are diffraction-limited and barely move in the focal plane during their assembly (13). The growth period of the coated pit has an average lifetime of 50 s and results in a fully formed coated vesicle upon scission from the plasma membrane. We describe here the use of DiNa to monitor the axial separation between clathrin and AP-2 as the coat forms in the cell. Our observations clearly indicate an increasing separation of these components of up to ∼30 nm, reached by the end of the assembly process. This separation in the average distributions of clathrin and AP-2 agrees with the relative asymmetric positions of clathrin and AP-2 within coated vesicles isolated from calf brains, as determined by cryoelectron microscopy tomographic reconstruction from single coated vesicles (32).

THEORY

When a laser beam is reflected at an interface between two media, the total internal reflection creates an evanescent field, which decays exponentially from the interface:

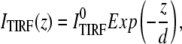(1)

where I_TIRF(z) is the excitation intensity in the evanescence wave and 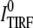is the excitation intensity directly adjacent to the interface surface. The total TIRF from N molecules positioned at z can be written as

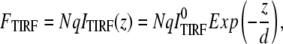(2)

in which q is a product of the quantum yield, the absorption coefficient, and the detection efficiency. The total fluorescence under wide-field illumination, F_WF, can be written as

(3)

where I_WF is independent of z. The axial position of the group of molecules can be calculated as

(4)

If the number of molecules is a function of time, the above relationship will still work, as long as the TIRF and the WF measurements are made relatively fast in comparison to the rate of change in the number of fluorescent molecules:

(5)

In DiNa we calculate the separation in the axial position of proteins tagged with two different colors. Thus,

(6)

in which the superscripts r and g stand for the red and green channel quantities, respectively.

Normalization of the excitation intensity and establishment of origin

Absolute position measurements with respect to the glass require the knowledge of the exact WF and TIR excitation intensities at each point in the image, as shown in Eq. 5. TIR calibration measurements as outlined in this article measure the penetration depth of the TIR but do not measure the absolute laser intensities. Thus, a change in the position of molecules can be measured, but their absolute position will not be known. By normalizing the fluorescence intensities to intensities at a particular location, a reference point can be established. At this position, which has z = 0, the fluorescence of the TIRF and WF signals are equal (by the normalization step). If the number of contributing molecules in the object is fixed, then the WF intensity is constant; under these conditions, a point of origin can be found anywhere by normalizing the TIRF signal to its WF signal. This normalization should be carried out in both channels at the same time, so that in that particular point, the separation of colors would be zero by default.

When the object grows by addition of molecules until it reaches a final size, there may not be sufficient molecules at the beginning of the structure formation to perform a normalization. Normalizing the intensities at the beginning of such a trace has advantages, however, because the overall size of the structure is very small at the beginning, and therefore it can be assumed that the two colors truly overlap at this point. To normalize the intensities in such experiments, the fluorescence intensities are added during an initial segment of structure formation (<30% of the structure), and their ratio is used for normalization as shown below:

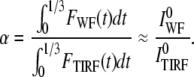(7)

The integration of signal allows for a reasonable signal/noise ratio while normalizing the fluorescence values. There are two assumptions made in Eq. 7. We assume that the structure does not have a significant size when <30% of the structure is completed; in addition, we assume that the building process proceeds relatively quickly, and that in the initial phase, the structure does not move appreciably in the vertical direction. Both of these assumptions are valid for clathrin coat formation.

Equation 7 can be rewritten using this normalization technique as

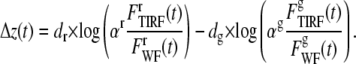(8)

The effects of the error of normalization

The addition of noise in the normalization component may lead to a constant increase in separation distance as shown below:

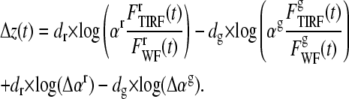(9)

The last terms in Eq. 9 would present a time-independent increase in the calculated separation of the two colors, but because its value is constant, it does not significantly affect interpretation.

Center of fluorescence (COF)

When the molecules under observation are not all present in a single plane and are distributed within an object of diameter comparable to the penetration depth, then the distribution of the fluorophores in the object has to be considered for derivation of the TIRF intensity. Under these conditions the equation for z(t) would represent the COF distributed in the object, defined as

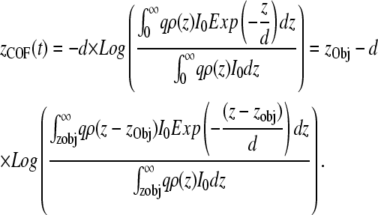(10)

The COF can be written as the sum of the position of the object and the position-independent term alone, which depends only on the shape of the object. Typically, the difference between the COF as defined above and the geometrical center of mass of the object is very small. For example, for a uniform sphere with a diameter of 90 nm the difference between the COF and its geometrical center is only 4 nm in a TIRF field with 90-nm penetration depth (see also Supplementary Material for the derivation showing minimal dependence of COF with penetration depth).

METHODS

For a schematic representation of the instrumentation used in this study, see Supplementary Material (Fig. S1).

Two solid-state lasers (473 and 561 nm; Crystal Laser, Reno, NV) are used as sources of excitation light for TIRF illumination. These lasers are coupled through an acousto-optical tunable filter unit, and the light is carried by a single-mode polarization-maintaining fiber optic (Point Source, Hamble, UK) to the TIRF slider of a Zeiss 200 M inverted microscope equipped with a 100× TIRF α-Plan Fluor NA 1.45 lens (Zeiss, Oberkochen, Germany). A Lambda DG4 unit (Sutter Instruments, Novato, CA) is used for supplying the wide-field excitation light delivered through a liquid light guide. A custom-made dual-pass excitation filter (Chroma, Rockingham, VT) optimized for EGFP (470/30 nm) and Tomato (560/30 nm) excitation is placed within the DG-4 unit. The excitation illumination is reflected toward the objective using a z470/562 two-color dichroic (Chroma). The combination of filters and dichroics allows for simultaneous excitation of both EGFP and Tomato fluorophores in either TIRF or wide-field illumination, without the use of any mechanical shutters or filter-cube rotations.

Emission path

The fluorescence emission, collected through the TIRF objective, passes the dichroic mirror but no emission filters are placed inside the microscope. The focused image of the sample is collected at the side port of the microscope through the lenses of a spherical aberration correction unit (SAC; Intelligent Innovations Imaging, Denver, CO). The image is then passed on through a dual-view optical unit (Roper Scientific, Tucson, AZ), which splits the emissions of EGFP and Tomato into two separate parts of the CCD chip using a 565DCXR dichroic mirror and the HQ525/40 and HQ620/50 emission filters. A back-illuminated Cascade 512B (Roper Scientific) is used for image acquisition under no-gain magnification mode.

Software and controls

Slidebook (Intelligent Imaging Innovations) is used for controlling the imaging apparatus and acquisitions. Lambda DG4 and the AOTF are synchronized with TTL pulses from the output of the camera, to turn off the illumination during the readout time of the CCD camera.

Calibration of the TIRF field

We used a method similar to that of evanescence nanometry (31) to calibrate the evanescent field. An aqueous solution (8 μl) of 100-nm Tetra Speck beads (Molecular Probes/Invitrogen, Carlsbad, CA) was placed onto the surface of a clean (methanol-wiped) No. 1.5 coverslip (Electron Microscopy Sciences, Hatfield, PA); a 15 μl drop of methanol was then added and the mixture spread before letting it dry for 15 min. The coverslip was then washed three times with phosphate-buffered saline (PBS) buffer (137 mM NaCl, 10 mM phosphate, and 2.7 mM KCl, pH 7.4), placed onto the imaging chamber, and overlaid with 1–2 ml PBS. A sharpened 4B graphite pencil fastened onto a P721 nanopositioner (Physik Instrumente, Karlsruhe, Germany) is then lowered toward the surface of the coverslip. Upon contact, some of the beads adsorbed to the glass surface transfer to the graphite; we observe little or no release of beads adsorbed to the glass or the pencil tip for the duration of the experiments. It is important to note that the fluorescence from the beads under TIRF conditions is different from the fluorescence in vivo, since the dye composition of the beads is not EGFP and Tomato, and also the laser intensities in the in vitro and in vivo experiments are not identical.

With beads attached, the pencil is moved 300 nm away from the coverslip, and the camera is focused onto the beads on the surface of the coverslip. The focus of the camera is then moved 200 nm into the solution using the lenses in the SAC unit without any adjustments to the position of the TIRF lens and the microscope nosepiece. Under these conditions, the TIRF beam is focused on the coverslip, whereas the camera is focused 200 nm deeper into the solution; the acquisition time is increased by a factor of 5, so the beads can be detected at this distance from the surface. The pencil is then lowered to the glass surface in 10-nm steps, and in each step three TIRF acquisitions are made in each channel separately. The two colors are imaged separately rather than simultaneously to ensure absence of cross-excitation of the beads. Since the camera is focused 200 nm into the solution, the beads can be imaged approaching the glass surface well before the pencil actually makes contact with the glass (Fig. S8).

These experiments correspond to a penetration depth of 80 nm and 90 nm for TIRF illuminations in the blue (473 nm) and green (561 nm) channels (Fig. S2); as expected, the evanescent field behaves as a single-exponential decay (31).

Spherical aberration correction (SAC)

The SAC unit is designed to correct spherical aberrations resulting from index of refraction mismatches. We observed that acquisitions using the SAC unit resulted in a 20% increase in signal compared with those done without it, regardless of the illumination source (Fig. S3). This calibration was done with WF illumination by imaging the same set of 100-nm Tetra Speck beads, dried onto the surface of a coverslip as outlined for the TIRF calibration, using two CCD Cameras (Cascade 512B, Roper Scientific) operating with no gain. One camera was mounted on the left port of the microscope, after the SAC device, whereas the other was mounted on the right port, after a 2× beam expander (to match the 2× magnification introduced by the SAC device (Fig. S3)). The transmission efficiency was the same for both ports.

Chromatic aberration correction

The chromatic aberration was revealed by imaging 100-nm Tetra Speck beads dried to the surface of a coverslip as described under the TIRF calibration section. After focusing on the beads, the nosepiece was moved in 100-nm steps and the beads were imaged onto the camera. Under conditions of no chromatic aberration correction, the red and green fluorescence from the point-spread images of the same beads appears to be ∼600 nm out of focus from each other (Fig. S4). This problem is solved through addition of a convex lens (f = 250 mm) placed immediately after the HQ 620/50 emission filter (red channel) in the dual-view unit and before the camera (Fig. S1). A software scale modification was introduced to correct for the slight difference in magnification (∼1.25×) between the two channels.

Data collection

Any point in the object space will emit its fluorescence as a point spread function on the CCD camera. The fluorescence signal generated by diffraction-limited objects was determined using a mask of 21 pixels (5 × 5-pixel area except for the four pixels at the corners). The average background fluorescence was determined from the fluorescence values measured in the immediately surrounding 28 pixels within one pixel of the mask. The sum of pixel values within the 21-pixel mask minus the background calculated times the number of pixels is the net fluorescence from a single spot. The standard deviation of the background was used for the noise analysis, as outlined below. The intensity profiles are filtered with a (0.2,0.6,0.2) wavelet filter for the purposes of normalization. This wavelet filter (equivalent to a convolution with a “smoothing” function) is defined as

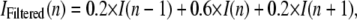(11)

where I(n) is the intensity at time point n.

Our temporal resolution is mainly limited by the 300-ms delay between sequential WF and TIRF measurements. Because the TIRF and WF measurements are consecutive rather than simultaneous, the wavelet filter does not truly decrease the time resolution, but the division and logarithm operators involved in calculation of z amplify the noise in the fluorescence intensities. The wavelet filter is placed so that the effect of noise magnification is minimized.

Noise analysis of the fluorescence intensity

In each fluorescence measurement, we sum over all the pixels that represent the point-spread function to yield the total number of photons detected. The noise associated with collecting p photons from an object whose immediate background intensity on each pixel is defined as b can be written as

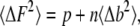(12)

where n is the number of pixels used in calculating the sum of the intensity. In our measurements, n = 21 and b is determined experimentally from the immediate 28 surrounding pixels. This equation is similar to that defined by Thompson et al. (24). In this equation, the first term is the detector noise and the second term is the noise contributed by the background to the final fluorescence signal. It is assumed that the two sources of noise are uncorrelated and that their contributions are simply additive. The standard deviation of the background is the standard deviation of the residuals from the fit of a plane to the intensity values within the 7 × 7-pixel area (excluding the mask of 21 pixels).

Monte Carlo simulations

The possible effect of noise on the calculations of DiNa was evaluated with the aid of Monte Carlo simulations. We set up a virtual DiNa experiment in which a diffraction limited structure growing linearly with time creates intensity profiles in both TIRF and WF illumination. A structure was simulated in which the COF of both channels was moved away from the coverslip in 15 steps from 0 to 30 nm (to approximate the distance of the center of a fully formed, small-barrel coated pit from the plasma membrane), whereas the WF fluorescence intensity was increased from 0 to 1000 in both fluorescence channels. The intensity of the TIR fields was set at 1.5 times that of the WF illumination to mimic the experimental conditions. The fluorescence intensity profiles for such a structure were created from Eqs. 2 and 3 using Mathlab (version 2006a, MathWorks, Natick, MA). Noise was then added to the fluorescence intensities according to Eq. 12; part of the assumed noise was shot noise, with a magnitude as defined by the fluorescence intensity, whereas the rest was background noise. The latter was created through a random number generator; the shot noise was calculated using a Poissonian random number generator based on the amount of signal. The amount of background noise applied to the TIRF channels was identical to the corresponding WF channels. For each condition of background noise, 50 virtual experiments were done to obtain the residual of the calculated position from the true position. Resolution was defined as the standard deviation of these residuals. The background noise was then raised and experiments repeated, to cover the range of signal/noise ratio from 5 to 40.

Selection criteria for clathrin-coated pits

Clathrin-coated pits were selected according to the following criteria, in a manner similar to that used before (13,33–35): 1), the fluorescent objects appeared and disappeared within the time series; 2), the objects displayed the limited movement expected for coated pits in the horizontal plane during their growth phase (<500 nm/lifetime); and 3), the objects did not collide with each other.

Cell culture

BSC1 cells stably expressing LCa-EGFP or σ2-EGFP (13) were used in conjunction with transient expression of LCa-Tomato and imaged ∼48 h posttransfection. Roughly 20,000–40,000 cells were plated on glass coverslips (22.5 and 25 mm in diameter) 6 h before the actual experiment. Up to this point, the cells were maintained at 37°C and 5% CO₂ in Dulbecco's modified Eagle medium (DMEM) with 10% fetal bovine serum. Cells were imaged in PBS supplemented with 20 mM Hepes, pH 7.4, 0.1 mM CaCl₂, 1 mM MgCl₂, and 2.5% fetal bovine serum at 37°C with constant humidification and 5% CO₂. The temperature of the sample holder (20-20 Technologies, Québec, Canada) was kept at 37°C using a Peltier-controlled holding device. The holding device and the stage were surrounded by a custom-designed air-controlled environmental chamber kept at 33–35°C.

RESULTS

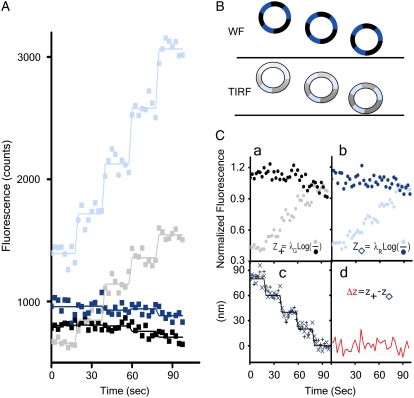
We first confirmed that DiNa is insensitive to fluctuations of the objects along the vertical axis by using two sets of experiments, one based on imaging beads and the other on visualization of clathrin-coated pits. The first experiment uses diffraction-limited beads homogeneously labeled with two fluorophores. The difference in the COF of the fluorophores should remain zero as the bead is moved along the z axis, because the positions of the fluorophores are locked with respect to each other. The beads were adsorbed to the tip of a pencil, which was then moved in steps of 20 nm toward the evanescent wave. A series of eight consecutive alternate TIRF and WF images were acquired for each step during a period of 20 s (Fig. 1 A) using exposure times that produced 1000–3000 photons in each channel. As schematically shown in Fig. 1 B, the WF signal is constant, whereas the TIRF signal increases as the bead moves toward the coverslip. The TIRF and WF signals of each fluorophore were normalized to their corresponding values obtained when the monitored bead was closest to but not touching the coverslip (Fig. 1 C, a and b). This step corrects for the difference in illumination intensities in TIRF and WF excitation; it also defines as zero the position of the COF closest to the coverslip (Fig. 1 C c), obtained using the experimentally determined distance dependence of the evanescent field (Fig. S2). As expected, the average difference between the COF of the fluorophores within each bead is zero (Fig. 1 C d). The standard deviation of these measurements corresponds to an experimental resolution of 8 nm between both determinations.

FIGURE 1.

Calibration of the evanescent field. 100 nm Tetra Speck beads (Molecular Probes) were adsorbed onto the tip of a graphite pencil as described in Methods; the pencil, mounted on a piezo device was then moved toward the glass coverslip in 20-nm steps. At the end of each step, eight consecutive TIRF and WF images were acquired, each collected simultaneously at 525/40 and 620/50 nm. (A) The fluorescence intensities of the TIRF and WF acquisitions, shown as gray and black for 525-nm and light blue and dark blue for 620-nm emission. (B) Schematic representation of the axial position of a representative bead during the experiment. (C) Analysis of bead position derived from analysis of the fluorescence data. (a and b) The normalized fluorescence intensity of the bead, with its intensities normalized to the value acquired closest to the coverslip. (c) The calculated axial position of the bead derived by Eq. 6 using the data shown in a and b. (d) Difference in bead-position fluorescence acquired for each fluorophore obtained in c as a function of the bead position along the z axis.

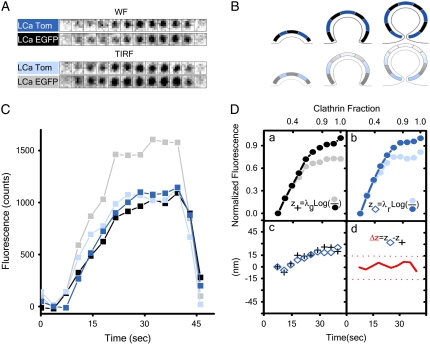
The second experiment was performed in vivo and takes advantage of previously acquired knowledge based on electron microscopy, which indicates that clathrin triskelions are equally distributed throughout the coat (36,37). It is also based on the knowledge that triskelions bind its light chain LCa in vivo regardless of whether it is fused to EGFP or Tomato (34,35); these triskelions incorporate equally into coating pits, as shown by the unbiased recruitment of both fluorophores to clathrin-coated pits in BSC1 cells simultaneously expressing clathrin light-chain LCa-EGFP and LCa-Tomato (Fig. S5). Using DiNa on assembling pits, we found a complete overlap in the axial location of the ensemble of clathrin molecules labeled with EGFP or with Tomato. This experiment was done by simultaneous illumination in two wavelengths during the acquisition of the time-lapse series, alternating TIRF (100-ms exposure) and WF (500-ms exposure) images at a frequency of 3.5 s (Supplementary Material, Movie 1). We present, as an example, a time series showing the complete dynamics during the formation of a single coated pit and the corresponding fluorescence intensities (Fig. 2, A–C). The next step corrects for the differences in excitation intensity by normalizing the TIRF and the WF signals with respect to each other at early time points, when <30% of the coat has formed. At this point, the increase in fluorescence intensity is mainly due to the accumulation of components, because the pits are still relatively shallow (Methods and Fig. 2 D, a and b). The centers of fluorescence for LCa-EGFP and LCa-Tomato calculated from these traces continuously move away from the coverslip (Fig. 2 D c); each trace represents the spatial contribution to the COF by the ensemble of triskelions within the pit and the movement of the underlying membrane from which the pit is growing. The membrane contribution, eliminated by simple subtraction of these values, shows that the average difference in the vertical position of the two classes of fluorescent light chains is zero (Fig. 2 D d), as expected for a lattice with homogenous distribution of triskelions, regardless of composition.

FIGURE 2.

Formation of clathrin-coated pits on the plasma membrane of cells expressing Clathrin LCa EGFP and LCa Tomato. (A) Representative fluorescence snapshots selected from Supplementary Material (Movie 1) corresponding to an individual coated pit as it assembled on the surface of the cell in direct contact with the coverslip. The panels correspond to alternating TIRF and WF images simultaneously acquired for LCa-EGFP and LCa-Tomato. (B) Model representing sequential stages during the formation of a coated pit. (C) Fluorescence-intensity plots corresponding to the coated pit shown in A. (D, a and b) Fluorescence-intensity plots for the coated pit after normalization of the TIRF and WF signals to correct for differences in the WF and TIRF illumination intensities as outlined in Methods. The traces were filtered with a (0.2,0.6,0.2) wavelet filter (Methods, Data collection). (c) The axial position measurement as a function of time corresponding to the ensemble of clathrin labeled with LCa-EGFP and LCa-Tomato derived using Eq. 5. (d) Relative axial position corresponding to the COF of LCa-EGFP with respect to that of LCa-Tomato.

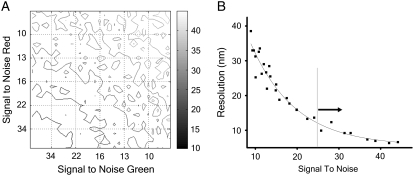
Coated pits mature into coated structures of different sizes (13) and therefore display varying final fluorescence intensities at the end of the assembly process. The initial structure also has a lower signal/noise ratio, which may affect the analysis. We therefore studied the relationship between the signal/noise ratio of the fluorescence signal and the expected resolution of DiNa, as follows (Methods, Monte Carlo simulations). First, we generated a model in which the WF fluorescence intensity of the object increased in 15 steps from 0 to 1000, whereas the COF varied linearly from 0 to 30 nm and the corresponding TIR fluorescence changed accordingly (Eq. 2). Second, we added random noise to each of the WF and TIR channels independently. The added noise had two components: The background noise was added with equal intensity throughout the trace, whereas the shot noise was scaled to the fluorescence signal. By changing the background noise, in effect we changed the signal/noise ratio as defined by the maximum fluorescence signal divided by the average standard deviation of the noise (Methods). Third, we subjected the fluorescence profiles to the same analysis, to track the axial position of the fluorescent molecules during the assembly of coated pits, and we used the standard deviation of the difference between the two channels as an estimate of resolution. The results of such a simulation are shown in Fig. 3 A, which depicts a resolution isoplot as a function of the signal/noise ratio for both channels determined with 50 independent calculations for each point. The relationship between DiNa resolution and equivalent variations for both channels in signal/noise ratio (Fig. 3 B) shows an expected resolution of 12 nm for a signal/noise ratio of ∼25, which was therefore chosen as part of the selection criteria for the remaining in vivo experiments. Most of the experimental data points had a signal/noise ratio >30, with an expected resolution of 10 nm or lower.

FIGURE 3.

Resolution analysis. (A) Isoresolution contours showing the expected resolution of DiNa plotted as a function of signal to noise in the fluorescence signal of two fluorophores recorded independently of each other. Each point represents the average resolution from 50 independent simulations, as outlined in Methods. (B) Relationship between resolution and changes in the signal/noise ratio along the gray line in A; this condition corresponds to equal signal/noise ratios for the two fluorophores. We used a signal/noise ratio of 25 as the criterion for analysis for DiNa.

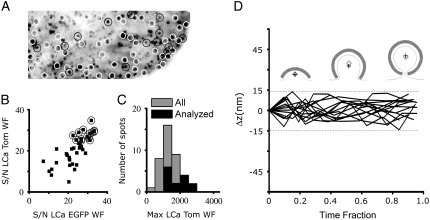
Different stages of the analysis corresponding to a complete data set acquired from ∼200 μm² of one cell are illustrated in Fig. 4. Fig. 4 A shows a time projection of all the TIRF signals of LCa-Tomato detected during the time series (60 frames, 3.5 s apart). We removed the fluorescent objects present at the start or end of the time series (white circles) and identified 40 objects that follow the selection criteria outlined in Methods; this set shows the expected appearance rate of 2.5 objects/10⁸ nm²/s (13). The pits displaying a signal/noise ratio of 25 or greater in their final maximal WF fluorescence (both channels) were selected for DiNa analysis (Fig. 4, A and B, red circles) and represent the whole range of sizes (as defined by their maximal fluorescence intensity) and lifetimes (40–140 s) (13) (Fig. 4 C, red lines). Pits excluded from this set correspond to those with signal/noise ratios of <25, because they are too dim (∼15%) or have a high background (∼60%). The average difference in the vertical position of the two types of fluorescent light chains bound to triskelions is zero (Fig. 4 D), as expected for coats displaying an even distribution of triskelions, and with a standard deviation of 10 nm, which represents the resolution of the measurements.

FIGURE 4.

Axial colocalization of clathrin labeled with two different fluorophores. (A) Time projection obtained from the fluorescence intensities of the coated pits as they form on the plasma membrane of BSC1 cells. The image represents the location of every pit that forms during Movie 1 of Supplementary Material. The white circles surround pits that were present at the beginning or end of the time series and were therefore eliminated from further analysis; note the absence of pits with lifetimes longer than the duration of acquisition (210 s). Red circles surround pits selected according to the criteria outlined in the text for final analysis using DiNa. (B) Plot of the signal/noise ratio (see Methods for definition) for all the pits with start and end times included in Movie 1. Pits with signal/noise values >25 in the fluorescence signal for LCa-Tomato (red circles) were selected for DiNa analysis. (C) Histogram corresponding to the maximum value in the fluorescence intensity of the LCa-Tomato signal for all the pits in B (black) and for those selected for DiNa analysis (red). The maximum fluorescence intensity reflects the size of the pit as it becomes a fully formed coated vesicle (13) (D) Difference in axial position of LCa-EGFP with respect to that of LCa-Tomato (Δz) determined for the individual pits selected for DiNa analysis. The difference of axial position within each pit is plotted as a function of time; to facilitate the comparison between pits of different lifetimes, the time component is normalized as a fraction of each lifetime.

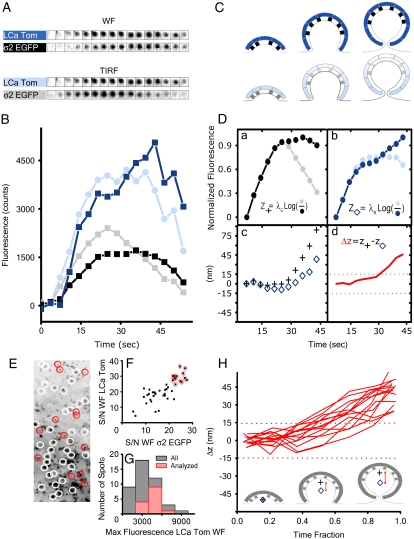
DiNa can be used to detect the separation of components in coated pits because of the large ratio of their sizes (70 nm or larger) to the resolution of DiNa (∼10 nm). Thus, as a final test of DiNa we asked if it is possible to detect in assembling pits the asymmetric distribution of AP-2 complexes observed in single coated vesicles using cryoelectron microscopic tomographic reconstruction (32). This experiment was carried out in cells simultaneously expressing clathrin labeled with LCa-Tomato and AP-2 labeled with σ2-EGFP (Fig. 5). As previously shown (13), AP-2 containing objects only form at the plasma membrane and they all colocalize with clathrin; these structures correspond to forming coated pits and vesicles. Fig. 5, A and B, shows a representative time-lapse series during the formation of a single pit (from Supplementary Material, Movie 2) acquired exactly as for the clathrin experiments; they illustrate the simultaneous capture of fluorescent signals from AP-2 and clathrin. The corresponding fluorescence intensity plots for the TIRF and WF are shown before (Fig. 5 B) and after (Fig. 5 D, a and b) intensity normalization. As with clathrin only, the COFs of both clathrin and AP-2 shift away from their starting position close to the coverslip toward the cell interior (Fig. 5 D c). At first, the COFs of AP-2 and clathrin coincide, but then, as the pit continues to grow, the COF of AP-2 diverges in its position from that of clathrin (Fig. 5 D d). This divergence corresponds to the faster loss of AP-2 with respect to the clathrin TIRF signal observed midway before completion of the coat, as shown in Fig. 5 D a.

FIGURE 5.

Formation of clathrin-coated pits on the plasma membrane of BSC1 cells expressing clathrin LCa Tomato and AP-2 σ2-EGFP. (A) Representative fluorescence snapshots selected from Movie 2 corresponding to an individual coated pit. The panels correspond to alternating TIRF and WF images simultaneously acquired for σ2-EGFP and LCa-Tomato. (B) Fluorescence-intensity plots corresponding to the coated pit shown in A. (C) Model representing sequential stages during the formation of the coated pit. (D, a and b) Fluorescence-intensity plots for the coated pit after normalization of the TIR and WF signals to correct for differences in the WF and TIRF intensities, as outlined in Methods. The traces were filtered with a (0.2,0.6,0.2) wavelet filter. (c) The axial position measurement corresponding to the ensemble of clathrin labeled with LCa-Tomato and AP-2 labeled with σ2-EGFP within the forming pit, as derived using Eq. 5. (d) Relative axial position corresponding to the COF of LCa-Tomato. (E) The projected image of the coated pits forming on the plasma membrane. The image is the time projection of all the pits observed in Supplementary Material (Movie 2). The white circles surround pits that were eliminated from the analysis because they were present at the beginning or end of the time series. None of the pits remained for the whole duration of the movie (210 s). Red circles indicate pits whose traces were analyzed using DiNa. (F) The signal/noise ratio (defined in Methods) for all the pits in the movie whose whole cycle was captured. Red circles mark the pits selected for DiNa analysis because their LCa-Tomato fluorescence signal/noise ratio was >25, measured as the maximum signal divided by the average noise from the whole profile. (G) Distribution of maximum intensities determined for the clathrin LCa-Tomato signal for all the pits (gray) and for those selected for DiNa analysis (red). (H) Δz calculated for the difference in the average axial position between clathrin LCa-Tomato and AP-2 σ2-EGFP from the individual pits selected for DiNa analysis plotted as a function of the fraction of their respective lifetimes. Values outside of the red dotted lines represent meaningful data in excess of 1.5 times the expected calculated resolution of Δz.

We have extended the analysis (Fig. 5, E–H) to include all of the objects present in the time-lapse series (Supplementary Material, Movie 2) adhering to the selection criteria used above for coated pits labeled only with clathrin (Fig. 4) and found a comparable surface density of assembling pits (2.5 objects/10⁸ nm²/s). Similarly, ∼30% of the pits had the signal/noise ratio required for detailed analysis (>25; see Methods); their maximum fluorescence intensity distribution of clathrin (proportional to pit size) represents most of the population in the time lapse with the exception of the dimmer ones (Methods). The divergence of COFs between clathrin and AP-2 is a characteristic feature observed in every one of the analyzed pits, with the separation becoming statistically significant during the last 30% of the life on the coated pit (Fig. 5 H). Similar data were obtained from two additional cells, from which 20 more objects were analyzed using DiNa.

DISCUSSION

We provide here an experimental approach that permits determination of the average axial positions of an ensemble of proteins within a diffraction-limited object labeled with two different fluorophores. The method is applicable to imaging conditions for living cells, with a practical resolution of ∼10 nm. This approach relies on the use of TIRF illumination to track changes in axial position and therefore is unsuited for immobile or fixed samples. The high resolution is attained because the method relies on the simultaneous differential tracking of COFs along the axial direction, in effect an extension of the concept of independent localization. An advantage of the differential measurement is its intrinsic correction for the position of the object. DiNa can also be used to follow the relative position of single molecules if sufficient signal/noise is achieved.

We note that DiNa is currently restricted to the study of objects embedded in the evanescent field. In contrast, some three-dimensional methods, such as 4pi microscopy, allow imaging throughout the volume of the sample, whether live or fixed (11). The current resolution of 4pi is ∼100 nm, as shown by imaging of the Golgi apparatus in a living cell, but this resolution is not sufficient to resolve the location of components within objects whose size is ∼100 nm, such as coated pits (38). Fluorescence resonance energy transfer (FRET) can be used to resolve distances of <10 nm, an approach that is also based on the measurement of relative distances; in this case, however, the measured distances need to be within 10 nm to ensure efficient energy transfer (39,40). A second limitation on the current use of DiNa concerns the effect of polarized excitation under TIRF conditions. The polarization of the laser beam can be either parallel to the surface (S) or perpendicular to it (P). The resulting evanescent field always has a polarization component that is parallel to the coverslip (in both S and P modes); in addition it has a perpendicular component under the P mode of illumination (41). DiNa can be applied regardless of polarization when the orientation of the fluorophore dipole is not restricted by its linkage to the object under observation; this is typically the condition attained with fluorophores attached to proteins by standard, flexible linkers. If the dipole orientation is fixed, then significant errors in the DiNa calculation are introduced under the P mode of illumination, when the evanescent field has a polarization component perpendicular to the coverslip.

An alternative way to resolve distances in the focal plane is based on localizing spectrally separated molecules. Using this method, it was possible to track the relative position of two myosin heads to within 10 nm resolution as the molecule walked along actin fibers adsorbed to a glass surface (42). Although similar in concept, DiNa resolves distances along the axial direction. In its current realization, however, it is not a single-molecule technique.

We developed DiNa to establish whether the asymmetric distribution of adaptors detected in cryoelectron microscopic tomographic reconstructions of single coated vesicles (32) is generated during the formation of their precursor, the clathrin-coated pits. It is possible that the asymmetric distribution observed in the frozen coated vesicles could simply be accounted for by a partial loss of AP-2 adaptors during the freezing step used for the electron microscopic imaging. Our results rule out this possibility, however. We show that when coated pits form at the plasma membrane, they do so in such a way that the average distribution of AP-2 clearly follows the axial distribution of clathrin during early stages of coat assembly, but the two then diverge from each other at later stages. Thus, the axial polarity of AP-2 within the clathrin-coated pit determined dynamically in a living cell using DiNa confirms the asymmetric distribution deduced previously by static observations from electron microscopy of frozen coated vesicles (32). The result validates DiNa as a feasible approach and confirms that it is possible to obtain a resolution of at least 10 nm. Our results also explain why, as the coated vesicle buds off from the plasma membrane, the TIRF signal of the axially polarized AP-2 is lost before the corresponding decrease of the TIRF signal generated by the evenly distributed clathrin (43).

Finally, we envisage using DiNa to follow other biological processes, such us vesicle fusion to the plasma membrane during exocytosis, viral budding from the cell surface, and the formation of focal adhesions during cell locomotion. In addition, DiNa could be extended to analyze the axial distribution of molecules in immobile samples by simply recording TIRF signals using illumination conditions of different penetration depths.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.