The Dynamics of Phosphodiesterase Activation in Rods and Cones

Abstract

Phototransduction starts with the activation of a rhodopsin (respectively, coneopsin) molecule, located in the outer segment of rod (respectively, cone) photoreceptors. The subsequent amplification pathway proceeds via the G-protein transducin to the activation of phosphodiesterase (PDE), a G-protein coupled effector enzyme. In this article, we study the dynamics of PDE activation by constructing a Markov model that is based on the underlying chemical reactions including multiple rhodopsin phosphorylations. We derive explicit equations for the mean and the variance of activated PDE. Our analysis reveals that a low rhodopsin lifetime variance is neither necessary nor sufficient to achieve reliable PDE activation. The numerical simulations show that during the rising phase the variability of PDE activation is much lower compared to the recovery phase, and this property depends crucially on the transducin activation rates. Furthermore, we find that the dynamics of the activation process greatly differs depending on whether rhodopsin or PDE deactivation limits the recovery of the photoresponse. Finally, our simulations for cones show that only very few PDEs are activated by an excited photopigment, which might explain why in S-cones no single photon response can be observed.

INTRODUCTION

Phototransduction is a multistep process which starts when a photon activates a rhodopsin (respectively, coneopsin) molecule in the outer segment of a rod (respectively, cone) photoreceptor. Upon diffusional encounter on internal disks in rods and on the surface membrane in cones, the activated opsin binds successively to many copies of transducin, a G-protein coupled receptor. Finally, each of the activated transducin binds to a single phosphodiesterase (PDE) effector protein (1–6). The set of activated PDE molecules hydrolyze cGMP, a cytosolic diffusible second messenger, which leads to the closure of cGMP-gated ion channels and thus to the photoreceptor hyperpolarization. In rods, physiological studies have revealed that even the absorption of a single photon can be detected (2,7–9), while for cones, many quasisynchronous absorbed photons (approximately seven) are needed to generate a signal that overcomes the noisy background (10–12). Remarkably, in rods also the single photon response time course is very reproducible (see, e.g., (2)). Despite of major progresses, it is still a challenging problem to unravel the precise mechanisms responsible for the accuracy and reproducibility of the single photon response in rods.

A high reliability of the rod single photon response implies a low variability of the number of activated PDE. This condition can be achieved by controlling accurately the amplification process. Several factors are involved in this amplification, such as the lifetime of activated rhodopsin and the rates of transducin activation. The chemical reactions that control the deactivation of rhodopsin depend on rhodopsin kinase, recoverin, and arrestin (4–6). Recent studies (13–17) have suggested that the reproducibility of the single photon response might be due to a low variability in the lifetime of activated rhodopsin, achieved through rhodopsin deactivation via multiple phosphorylation steps. However, it is still unclear how many deactivation steps are necessary to reproduce the experimental data. In Field and Rieke (14) it was suggested that at least 12–14 steps are needed; however, numerical studies based on Monte Carlo simulations have shown that already seven phosphorylation sites are sufficient to reproduce experimental data (18,19).

To extract the main principles underlying the variability of the photoresponse, we present here a stochastic analysis of PDE activation for both rod and cone photoreceptors. Our model is based on the well-accepted molecular cascade leading to the activation of the G-protein. To analyze the PDE dynamics and the associated fluctuation, we derive equations for the mean and the variance of activated PDE. Since our approach allows us to compute the time course of the mean and the variance of excited PDE, it complements previous stochastic simulations (18,20,21). We derive analytic expressions for the mean and the variance of rhodopsin lifetime and the number of activated PDE, and provide numerical simulations. Furthermore, we study the influence of various parameters such as the number of rhodopsin phosphorylation sites and phosphorylation and transducin activation rates. We explore the impact of the rhodopsin lifetime on the accuracy of PDE activation. We study PDE response for scenarios representing rods and cones in mice and toads. We show that during the rising phase, the PDE variability is much lower compared to the recovery phase. We also analyze the role of whether rhodopsin or PDE lifetimes limit the recovery of the photoresponse. Our results show that the variability of the PDE response depends most significantly on the transducin activation rates. Finally, we present simulations suitable for cones. We find that in cones only very few PDE molecules are activated, which confirms an earlier suggestion (22).

THEORY

Model for PDE activation

The transduction process following the absorption of a photon has been well documented both experimentally and theoretically (for reviews see (1–6)). The Pugh-Lamb model (1,20,23) was based on the properties of two-dimensional random collisions and it predicts accurately the rising phase of the photoresponse. Based on a Markovian approach and using stochastic simulations of diffusion and chemical reactions, in Felber et al. (21), the mean and the variance of the simulated photoresponse were obtained for different lifetimes of activated rhodopsin. We approximate here the different steps leading to PDE activation by first-order chemical reactions and we neglect the molecular dynamics due to diffusion. This approximation is justified by the large number of molecules and the fast diffusion constant. Thus, the number of activated molecules resulting from diffusional collisions has the same temporal law compared to reaction equations.

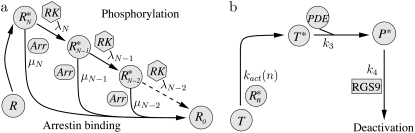
The well-accepted scenario for PDE activation embodied in our model is the following (see Table 1 for a guide to the parameters used): After a photon absorption, a rhodopsin molecule, denoted by R, undergoes a conformational modification and changes from an inactive into an active form R*. R* deactivation occurs through multiple phosphorylation steps, catalyzed by rhodopsin kinase (RK), and finally through arrestin binding (15,24–27). We take into account that the affinity of R* for transducin, RK, and arrestin are altered by sequential phosphorylations (18,28). The number of rhodopsin phosphorylation sites is denoted by N_p. After photon absorption, rhodopsin changes into the activated state n = N. The parameter N equals the total number of R* deactivation steps, and we assume that it is given by N = N_p + 1 (13) (number of phosphorylation sites + arrestin binding). When R* encounters RK, with a certain probability a phosphorylation occurs and R* undergoes a transition from the state n to n − 1, modeled by a state-dependent phosphorylation rate λ_n. When R* binds to arrestin, there is a certain probability that R* becomes deactivated, modeled by a transition rate μ_n from the state n to the deactivated state n = 0. In each state n > 0, R* activates G-proteins transducin (T) with a rate k_act(n). While T* can bind to a PDE with a rate k₃ to form a complex denoted by PDE*, the same complex can be deactivated with a rate k₄. The reciprocal of the rate k₄ is the lifetime of PDE* and depends crucially on the concentration of RGS9 (29–32). We neglect depletion of transducin and PDE because the amount of activated molecules is negligibly small compared to the total pool of available transducin and PDE molecules. The kinetic reactions underlying the model (illustrated in Fig. 1) are summarized as

(1)

The model presented in Eq. 1 is a stripped-down version of a more detailed model, such as the one presented in Hamer et al. (18). To keep the model simple and clear, we did not include backward reaction rates. We decided to focus on conditions that can lead to a minimal PDE* variance and therefore omitted backward reaction rates, which would certainly increase the variability of the activation process, as was already noticed in Field and Rieke (14). However, our analysis can be extended without much effort to include backward reaction rates and intermediate bound states between R* and RK. For example, the reactions used to model R* phosphorylation in Eqs. 1a–c in Hamer et al. (18) can be incorporated by using appropriate backward rates 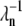(n now labels also intermediate states),

In contrast, there is no straightforward method to extend our analysis to incorporate also intermediate bound states between R* and transducin (for example, as modeled by the reactions Eqs. 3a–d in (18)). Indeed, as will be seen later on, our mathematical derivations rely on the assumption that R* deactivation occurs independently from transducin and PDE activation. In this case, the analysis of R* deactivation can be decoupled from the analysis of transducin and PDE activation, which greatly reduces the complexity of the computations. Such a decoupling is justified when the lifetime of possible bound states between R* and transducin is short compared to the lifetime of the phosphorylation states. Since transducin activation occurs much faster compared to R* phosphorylation, we assume that under normal conditions R* deactivation occurs almost independently from transducin and PDE activation.

TABLE 1.

Parameters used in the model

Symbol	Description
R*n	Activated rhodopsin in state n
R0	Deactivated rhodopsin
T	Transducin
T*	Activated transducin
PDE	Phosphodiesterase
PDE*	Activated PDE
Np	Number of rhodopsin phosphorylation sites
λn	Phosphorylation rate in state n
μn	Arrestin binding rate in state n
kact(n)	Transducin activation rate in state n
k3	PDE activation rate
k4	PDE* deactivation rate
Rτ	Mean/SD ratio of rhodopsin lifetime
RPs	Steady-state mean/SD ratio of PDE*
RP(t)	Time-dependent mean/SD ratio of PDE*
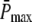	Maximum number of PDE*

FIGURE 1.

Model for PDE activation. (a) Activated rhodopsin (R*) can be phosphorylated by rhodopsin kinase (RK) or deactivated by arrestin binding. The phosphorylation rates λ_n and arrestin binding rates μ_n depend on the state n of rhodopsin phosphorylation. Through phosphorylation, R* undergoes a transition from a state n to n − 1. (b) R* in state n activates transducin with a phosphorylation-dependent activation rate k_act(n). Activated transducin (T*) binds to PDE with a rate k₃ and forms a complex denoted by PDE*. PDE* is deactivated through RGS9 with a deactivation rate k₄.

We now proceed with the analysis of the chemical reactions given in Eq. 1. To describe the state of our model, we introduce three stochastic variables (𝒩, ℒ, 𝒦) that can adopt the values (n, l, k): the phosphorylation state n of R*, the number l of T*, and k of PDE*. The dynamics of the joint probability P(n, l, k, t), that at time t we find R* in the state n and l T* and k PDE* molecules, satisfies a Master equation (33,34). To derive this equation, we first determine from the system of chemical reactions displayed in Eq. 1 the transition matrix W(n, l, k|n′, l′, k′, t) between two states (n, l, k) and (n′, l′, k′),

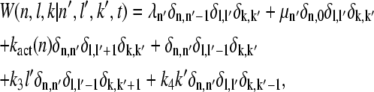(2)

where δ_x,y is the Krönecker delta. From the general shape of the Master equation (33,34)

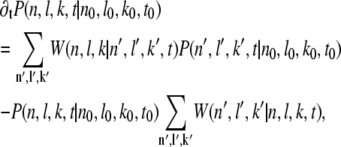(3)

we obtain, by inserting Eq. 2 into Eq. 3 (we suppress the initial indices (n₀, l₀, k₀, t₀)),

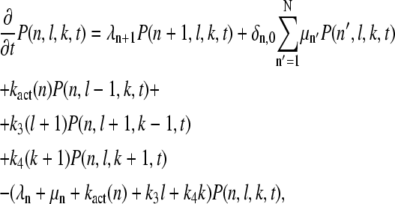(4)

where N = N_p + 1. The boundary conditions are

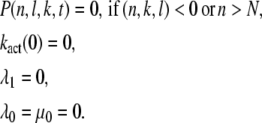The conditions λ₀ = μ₀ = 0 express that the deactivated state is stable. The condition λ₁ = 0 accounts for the fact that in the state n = 1 all sites are phosphorylated. Immediately after photon absorption, R* is in state n = N and the number of T* and PDE* are zero. Thus, the initial condition for P(n, l, k, t) is given by

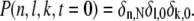(5)

Dynamics of activated rhodopsin

We now analyze the dynamics of R*. In particular, we estimate the mean and the variance of the duration until R* becomes deactivated by arrestin binding. We start by computing the probability P(n, t) that a R* molecule is in the state n at time t. Our analysis ends with an estimation of the mean to the standard deviation (SD) ratio of R* lifetime.

State probability P(n, t)

To describe the dynamics of R*, we sum Eq. 4 over the indices l and k. We obtain an equation for the probability P(n, t) to find R* in the state n at time t,

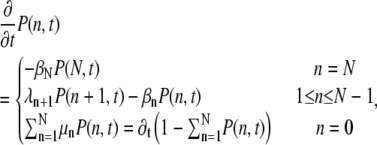(6)

where β_n = λ_n + μ_n. The initial condition is given by P(n, t = 0) = δ_n,N. Using the vector notation with 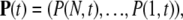we rewrite this system as

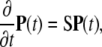(7)

where the matrix S is given by

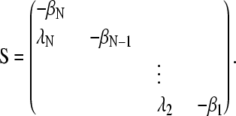(8)

For pairwise different eigenvalues β_n we can diagonalize S and using the eigenvectors of S we derive explicit expressions for P(n, t). With the notation p_i = λ_i/β_i, P(n, t) is given by

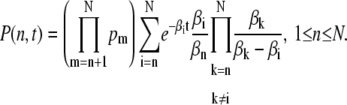(9)

Mean and variance of rhodopsin lifetime

To compute the mean and the variance of the random R* lifetime T, we use the probability P_R(t) that R* is still active at time t, given by

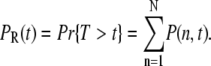(10)

A direct computation using P(n, t) from Eq. 9 (and the identities in Eq. 71 and Eq. 72) yields for the mean and the variance of the R* lifetime

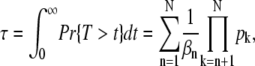(11)

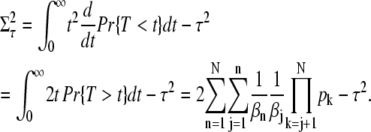(12)

Equation 11 for the mean R* lifetime has an intuitive interpretation: it is the sum of the mean lifetimes in each state n multiplied by the probability to reach this state before being deactivated by arrestin binding.

Reliability of rhodopsin lifetime

We characterize the reliability of R* lifetime by the ratio of the mean to the standard deviation, denoted by R_τ, which is simply the reciprocal of the coefficient of variation (CV). If R_τ is high (respectively, low), the reliability is high (respectively, low). By using Eqs. 11 and 12, and following the analysis in the Appendix, we obtain the following estimate:

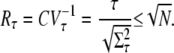(13)

The upper limit for R_τ depends only on number of R* deactivation steps N. Based on very general considerations, this result has already been anticipated (16,17). However, by using the explicit formulas we can now study the behavior of R_τ as a function of the underlying rates. Indeed, the maximum value 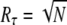is achieved if β_n = const and p_n = 1 for all n. The condition β_n = const conveys that all deactivation states need to have the same lifetime, while p_n = 1 is fulfilled if the arrestin binding rates μ_n vanish for all n > 1. Thus, the latter condition states that arrestin only binds when R* is in the state n = 1 and is therefore fully phosphorylated. This assumption is reasonable, since nonvanishing arrestin binding rates for n > 1 effectively reduce the number of deactivation steps and therefore increase the variance.

Mean and variance of the transducin activation rate

The mean and variance of the transducin activation rate are defined as

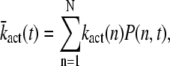(14)

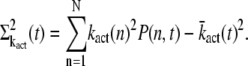(15)

In principle, the mean and the variance of the activation rate (and any other quantity that depends only on the phosphorylation state of R*) can be computed by using the probabilities P(n, t) given in Eq. 9. However, we will use an alternative method of calculation that relies on differential equations and the decomposition of the activation rate (see below). This method does not require us to explicitly compute P(n, t) and facilitates the derivation of differential equations for the cross-correlation terms (see Eq. 34). We now derive a differential equation for 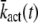by differentiating Eq. 14 with respect to time and by using Eq. 7,

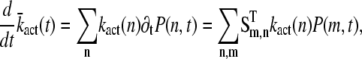(16)

where S^T is the transposed matrix of S. To solve this equation, we decompose the vector 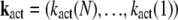into the sum of eigenvectors 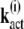of the matrix S^T,

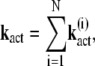(17)

with

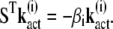(18)

By induction, we obtain for the components of the vectors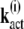

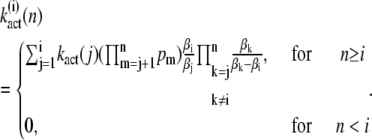(19)

The differential equation for the mean of 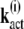is given by

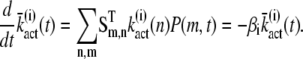(20)

Using the initial condition that at time t = 0 R* is in the state n = N yields

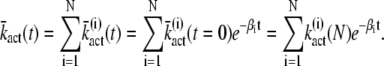(21)

Note that the expression for 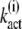(N) provided in Eq. 19 can be verified by comparing Eq. 21 with the result for 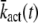obtained by inserting Eq. 9 into Eq. 14.

The variance 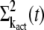is calculated analogously to 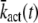by decomposing the vector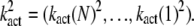

Mean and variance of activated transducin and PDE

The mean and variance of T* and PDE* are defined as

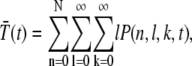(22)

(23)

Differentiating Eqs. 22 and 23 with respect to time and using the Master equation Eq. 4 yields

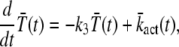(24)

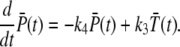(25)

The definitions for the variance and the correlations read

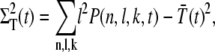(26)

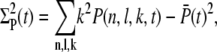(27)

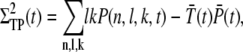(28)

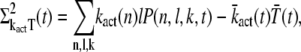(29)

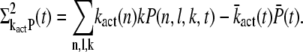(30)

The equations for the time derivatives of 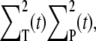and are given by

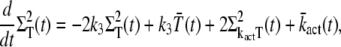(31)

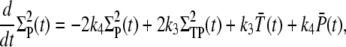(32)

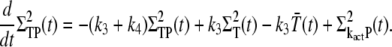(33)

To close this system of equations we additionally have to derive differential equations for 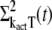and 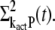This is done by using the decomposition of k_act given in Eq. 17. We first write

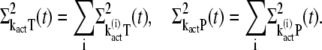(34)

The time derivatives of 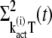and 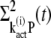are derived as

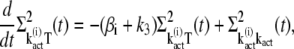(35)

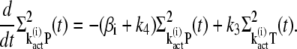(36)

The correlations between k_act and 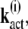defined by

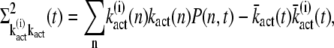(37)

are computed by decomposing the vectors 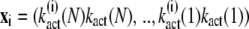into the sum of eigenvectors of the matrix S^T,

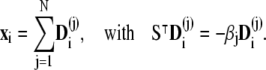(38)

This yields

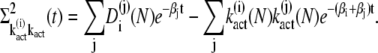(39)

In practice, the coefficients 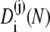are computed numerically by diagonalizing the matrix S^⊺. However, by using Eq. 19, also analytic expressions can be derived.

Finally, we define the time-dependent PDE reliability ratio R_P(t) as

(40)

SUMMARY

The explicit expressions for 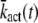and allow us to close the system of differential equations for the variance of PDE*. This system consists of Eq. 21 and Eqs. 24 and 25 for the mean and Eqs. 31–33, Eqs. 35 and 36, and Eq. 39 for the variances. The simulation results will be obtained by using this close system of equations.

Mean and variance of the total number of activated PDE

It is usually assumed that reliable R* deactivation entails reliable PDE activation (13–16); however, it is worthwhile to have a closer look at the connection between R* lifetime and PDE activation. For this we compute the mean and the variance of the total number of PDE* molecules produced during an single photon response (SPR), obtained by setting k₄ = 0, and compare it to the variance of R* lifetime. For vanishing PDE* deactivation rate k₄, after R* shutoff, a steady state will be reached that contains all the PDE* molecules activated during the SPR. In the Appendix we derive expressions for the steady-state mean and variance of PDE*,

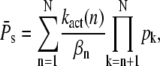(41)

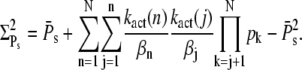(42)

These expressions share similarities with the ones obtained for R* lifetime (Eqs. 11 and 12), since merely 1/β_n is replaced by k_act(n)/β_n. We define the steady-state reliability ratio R_Ps, which corresponds to the reliability of the total number of PDE*, as the ratio of the steady-state mean to the SD. The reliability ratio R_Ps is the inverse of the coefficient of variation (CV). In the Appendix we obtain a sharp upper bound for R_Ps,

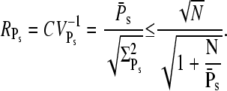(43)

In the case when R* activates many PDE* (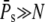), the upper limits for 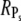and R_τ are both equal to 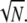However, it is interesting to examine whether maximal values for and R_τ can be attained simultaneously. The conditions k_act(n)/β_n = const and p_n = 1 are required such that 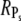achieves its maximum, whereas β_n = const and p_n = 1 are needed to maximize R_τ. The condition k_act(n)/β_n = const expresses that, in each state, the same amounts of PDE* have to be activated, whereas 1/β_n = const requires that each state has the same lifetime. By adjusting the activation rates k_act(n), the condition k_act(n)/β_n = const can be achieved even when the rates β_n are very different. In that case, R_Ps can be maximal while R_τ is far from being maximal. In general, because of the transducin activation rates, maximal values for R_Ps and R_τ are not achieved simultaneously, which shows that reliable R* lifetime is neither necessary nor sufficient to achieve reliable PDE activation. Only for constant transducin activation rates, k_act(n) = k_act, the steady-state results for PDE* are determined by the mean and variance of R* lifetime,

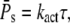(44)

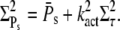(45)

We shall now discuss some aspects of the reliability ratio R_Ps, which contains the variability of all the molecular events contributing to PDE activation. R_Ps is closely related to the coefficient of variation of the area below the PDE* time response, denoted by CV_areaP. In Hamer et al. (18) it was shown that

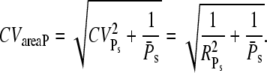(46)

It is remarkable that CV_areaP depends only on the molecular details involved in PDE activation and not on the PDE* deactivation rate k₄. Consequently, CV_areaP does not depend on whether PDE* or R* deactivation limits the recovery of the SPR. For large numbers of activated PDE, it follows that

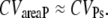(47)

The coefficient of variation CV_area of the area below the SPR current was introduced in Field and Rieke (14). It measures the integrated variability of the SPR: when PDE* dynamics and the SPR current are related by a scaling relationship, we have that CV_area ≈ CV_areaP (18), which finally leads to 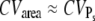(for sufficiently large 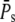). Consequently, the measured value of CV_area can be used to obtain a lower bound of the number of R* deactivation steps (by using Eq. 43). Indeed, experimental results for mutated mouse rods (13) show that CV_area behaves approximately like 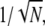the limiting behavior of 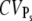(this is the case under the assumption that the number of deactivation steps N correlates with the number of phosphorylation sites N_p through N = N_p + 1). We conclude that CV_area is a close measure of 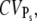but in general, it is not for the coefficient of variation of R* lifetime CV_τ.

RESULTS

Numerical simulations of PDE dynamics

To study the PDE dynamics (mean and variance), we run numerical simulations of Eq. 21, Eqs. 24 and 25, Eqs. 31–33, Eqs. 35 and 36, and Eq. 39. Our aim is to examine the influence of the various parameters on the dynamics of PDE activation.

Choice of parameters

It has been well documented that the time course of the single photon response (SPR) differs substantially between amphibian and mammalian rod photoreceptors (13,14,16,17,35). In mouse rods, the maximum of the SPR amplitude occurs at ∼0.1 s (13,35,36), whereas in toad rods, the maximum of the amplitude occurs at ∼1.9 s (16,17). Hence, we decided to run simulations for two different scenarios called Mouse Rod and Toad Rod (see Table 2). Following recent results (35), the mouse rod scenario is characterized by a R* lifetime of 0.080 s and a PDE* deactivation rate of 5 s⁻¹. Unfortunately, as far as we know, similar experimental data is not available for toad rods. To match the time course of the toad rod photoresponse, we chose for the toad rod scenario a R* lifetime of 3 s and a PDE* deactivation rate of 1 s⁻¹. Most important, we chose the toad rod parameters such that, contrary to the mouse rod scenario, recovery is limited by R* lifetime and not by PDE* deactivation. This will allow us to explore the impact of whether rhodopsin R* or PDE* lifetime limits the recovery. To compare simulations, we decided to fix the maximum of the mean number of PDE* 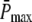at a value of 150, as suggested in Leskov et al. (37). It is important to note that for our purpose this value is not critical, because other values will result in a simple scaling. Finally, we chose k₃ = 50 s⁻¹ for the T*-PDE* binding rate (in (18,19) the authors use k₃ = 200 s⁻¹). However, the exact value for k₃ is not very important, as long it is not rate-limiting. Our choice of the parameters is summarized in Table 2.

TABLE 2.

Toad rod and mouse rod parameters

	Mouse rod scenario	Toad rod scenario
PDE activation rate (k3)	50 s−1	50 s−1
PDE deactivation rate (k4)	5 s−1	1 s−1
Mean rhodopsin lifetime (τ)	0.080 s	3 s
Max. value of 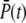(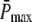)	150	150

The PDE deactivation rate and rhodopsin lifetime for the mouse rod scenario are taken from Krispel et al. (35).

Motivated by previous studies (18,28), we consider that transducin activation rates k_act(n) decay exponentially with the number of rhodopsin phosphorylations, that is

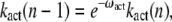(48)

where ω_act is an adjustable parameter. We also assume that the affinity of rhodopsin kinase for R* decays exponentially with the number of phosphorylations,

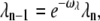(49)

where ω_λ is also a free parameter.

Since we are interested in conditions leading to the smallest PDE* variance, we will mostly present simulations for a simplified scenario, where the arrestin binding rates μ_n vanish unless R* is fully phosphorylated (which is the case when R* is in the state n = 1). Such a scenario is optimal to achieve a high R* deactivation reliability. Furthermore, we choose the arrestin binding rate for n = 1 equal to 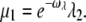When ω_λ = ω_act, this choice ensures that k_act(n)/β_n = const and therefore maximizes the reliability ratio R_Ps. Moreover, the choice 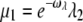adapts the arrestin binding rate to the phosphorylation rates. In summary, the arrestin binding rates will be chosen as

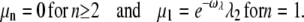(50)

Although we made an effort to decrease the number of free parameters, we still have to specify N, λ_N, k_act(N), ω_λ, and ω_act. However, the rates λ_N and k_act(N) are fixed by adjusting rhodopsin's lifetime and 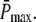For given values N and ω_λ, λ_N is determined by rhodopsin lifetime according to Eq. 11. For given values N, ω_λ, and ω_act we determine numerically the value of k_act(N) by fixing 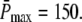Thus, the remaining parameters that have to be specified are N, ω_λ, and ω_act.

Impact of the number of phosphorylation sites

Using the theory developed in the previous section, we now study the impact of the number of R* phosphorylation states on the PDE* response. Such an analysis is particularly relevant, since there are transgenic experiments with reduced number of rhodopsin phosphorylation sites (13,15). We run some simulations for the mean and the variance of PDE* for toad rod parameters and ω_λ = ω_act = 0.1. The condition ω_λ = ω_act ensures that the ratio k_act(n)/β_n values are constant and thus leads to a maximal steady-state reliability R_Ps (see Eq. 43). This condition has also been used previously for simulating the photoresponse (18,19).

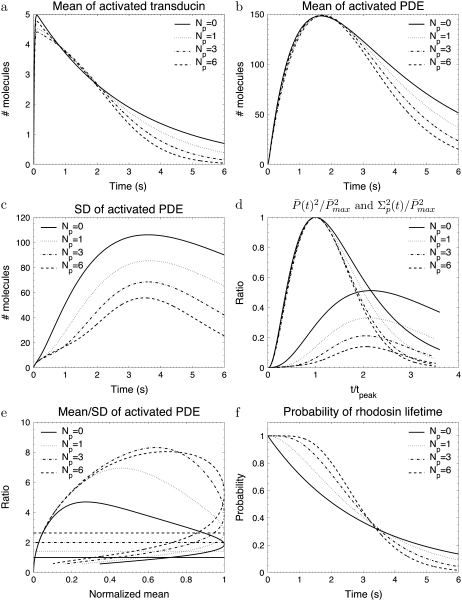
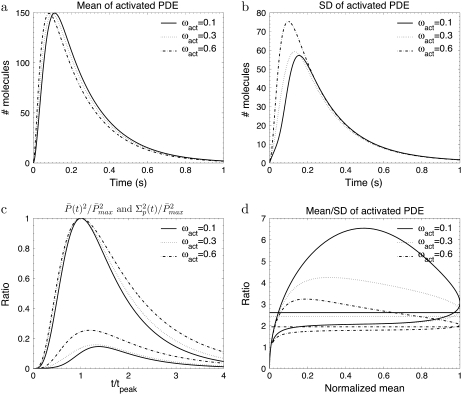
Fig. 2 a shows that during the photoresponse the mean number of T* is very small. Since each T* binds to only one PDE, the number of transducin and PDE molecules that become activated are equal. However, unlike PDE*, T* does not accumulate due to the large rate k₃ = 50 s⁻¹. Contrary to the assumption that during the rising phase the ratio of the number of PDE* to T* is constant (1,3,23), we found by comparing Fig. 2 a with Fig. 2 b that the time course of PDE* is not proportional to the time course of T*.

FIGURE 2.

The simulations show the impact of the number of rhodopsin phosphorylation sites for the toad rod scenario defined in Table 2. The phosphorylation dependency of the phosphorylation, arrestin binding, and transducin activation rates are given by Eqs. 48–50 with ω_λ = ω_act = 0.1. The rates λ_N and k_act(N) are adapted to ensure that the rhodopsin lifetime and the maximum number of activated PDE are according to Table 2. For N_p = (0, 1, 3, 6), λ_N and k_act(N) are (0.33, 0.70, 1.6, 3.2) s⁻¹ and (257, 228, 224, 245) s⁻¹.

We explore in Fig. 2 c how the PDE variance decreases with growing number of phosphorylation sites N_p (Fig. 2 c). The maximum and the temporal width of the variance both decrease by increasing the number of phosphorylation sites. Additionally, the variance does peak approximately two-times later than the mean and this feature depends only slightly on the number of phosphorylation sites, as it can be observed in Fig. 2 d. For six phosphorylation sites, the simulations in Fig. 2 d are very similar to experimental recordings for the photocurrent presented in Field and Rieke (14).

Fig. 2 e shows the PDE reliability R_P(t) as a function of the normalized mean of PDE*, defined as 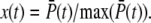The value x = 1 corresponds to the time to peak of the mean. We decided to plot the reliability ratio R_P(t) as a function of the normalized mean, since this provides a better resolution of the rising phase and additionally shows how R_P(t) changes as a function of the number of PDE* molecules. The horizontal lines in Fig. 2 e represent the steady-state values R_Ps. Our choice of the parameters implies that R_Ps is maximal and approximately equal to 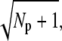see Eq. 43. It is interesting to note in Fig. 2 e that during the rising phase, R_P(t) reaches values that are much beyond the steady-state value R_Ps. This apparent paradox is a consequence of the activation dynamics and cannot be anticipated from steady-state considerations.

Finally, in Fig. 2 f we plot the probability P_R(t) (given by Eq. 10) that R* is activated up to time t. With increasing deactivation steps, R* lifetime becomes less variable and more concentrated around the mean value τ. Moreover, since the decay rate ω_λ is small, the lifetimes of the states n are very similar and therefore R_τ is very close to the optimal value 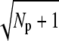(data not shown).

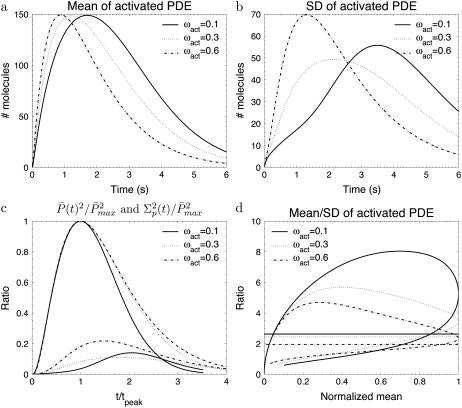
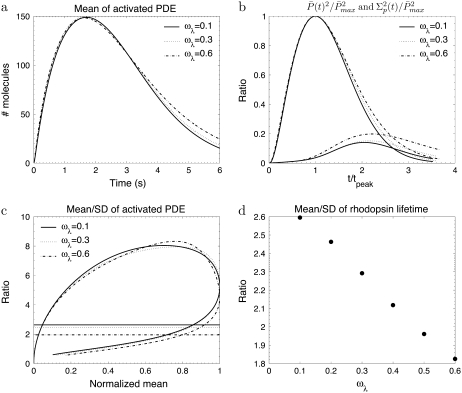
Transducin activation rates strongly influence the dynamics of PDE activation

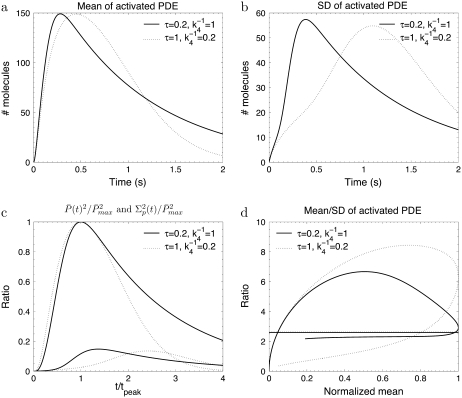
To study the impact of the transducin activation and phosphorylation rates, we present in Fig. 3 and Fig. 4 simulations for toad rods, obtained for various decay rates ω_act and ω_λ. The number of R* phosphorylation sites is fixed to N_p = 6, which is the value found in mouse rods and many other species (13,15,28). If R* activity decays only slightly with subsequent phosphorylations (e.g., ω_act ∼ 0.1), the PDE* variance peaks nearly twice later than the mean (Fig. 3 c) and the ratio R_P(t) at time to peak is much higher than the steady-state ratio R_Ps (Fig. 3 d). In contrast, Fig. 4, a–c, illustrates that the parameter ω_λ, which controls the decay of the phosphorylation rates, does not affect much the dynamics of PDE activation, although ω_λ strongly influences the reliability of R* lifetime (Fig. 4 d). We conclude that the behavior of the transducin activation rates is more decisive for the PDE* variance than the variability of R* lifetime.

FIGURE 3.

The simulations show the impact of the phosphorylation dependency of the transducin activation rates for the toad rod scenario defined in Table 2. The behavior of the phosphorylation, arrestin binding, and transducin activation rates are given by Eqs. 48–50 with ω_λ = 0.1 and N_p = 6. For ω_act = (0.1, 0.3, 0.6) the rates λ_N and the k_act(N) are given by (3.2, 3.2, 3.2) s⁻¹ and (245, 356, 482) s⁻¹.

FIGURE 4.

The simulations show the impact of the phosphorylation dependency of the rhodopsin phosphorylation rates for the toad rod scenario defined in Table 2. The behavior of the phosphorylation, arrestin binding, and transducin activation rates are given by Eqs. 48–50 with ω_act = 0.1 and N_p = 6. For ω_λ = (0.1, 0.3, 0.6), the rates λ_N and k_act(N) are given by (3.2, 6.8, 26.6) s⁻¹ and (245, 273, 312) s⁻¹.

High activation reliability during the rising phase

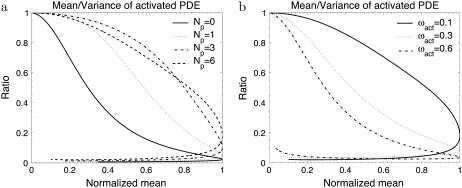
We now investigate more closely the time course of the reliability ratio R_P(t) during the rising phase. The simulations depicted in Fig. 2 e and Fig. 3 d reveal that during the rising phase R_P(t) reaches a maximum that can be much higher than the steady-state value R_Ps. Indeed, this behavior follows from the fact that initially the variance and the mean are almost equal (see Eq. 68). As a consequence, as long as the variance and the mean are close, R_P(t) approximately increases like the square root of the mean and, depending on the number of PDE*, can reach values that are much beyond the steady-state limit. At a later time, the variance becomes much larger than the mean and R_P(t) decreases. To show this initial behavior of the variance, we plot in Fig. 5 a (respectively, Fig. 5 b) the mean to the variance ratio of PDE* corresponding to the set of parameters used in Fig. 2 e (respectively, Fig. 3 d).

FIGURE 5.

Mean/variance ratio of activated PDE. The simulations are obtained for the scenarios described in Fig. 2 and Fig. 3.

To achieve a high reliability ratio R_P(t) during the rising phase, it is both necessary that the number of phosphorylation sites N_p is large (Fig. 2 e) and the transducin activation rates are almost constant (Fig. 3 d). Indeed, the main contributions to the PDE* variance during the rising phase are due to the variability of R* lifetime and the variability of the transducin activation rates. The latter can be reduced by choosing ω_act close to zero. Increasing the number of phosphorylation sites reduces the variability of R* lifetime, especially for small times. Fig. 2 f shows that by increasing the number of phosphorylation sites, a growing initial time-window emerges, during which it is very unlikely that R* becomes deactivated. During this period, the variability of R* lifetime is very low, and in particular much lower than the variability of the whole R* lifetime.

Impact of whether rhodopsin or PDE deactivation limits recovery

In Fig. 6 we present simulations for the mouse rod scenario, where the overall PDE* dynamics is much faster compared to toad rods. In the mouse rod scenario, PDE* deactivation limits the recovery, whereas it is R* shutoff in the toad rod case. By comparing the mouse rod simulations in Fig. 6 with the corresponding toad rod simulations in Fig. 3, we conclude that the dynamics of PDE* activation strongly depends on whether R* or PDE* lifetime limits recovery. Consequently, interchanging PDE* and R* lifetime should affect the overall dynamics, as shown by the simulations in Fig. 7. We now examine more closely these two opposing scenarios (see discussion corresponding to Fig. 6 in (18)) where R* deactivation is much faster than PDE* deactivation and then when it is the opposite.

FIGURE 6.

The simulations show the impact of the phosphorylation dependency of the transducin activation rates for the mouse rod scenario defined in Table 2. The behavior of the phosphorylation, arrestin binding, and transducin activation rates are given by Eqs. 48–50 with ω_λ = 0.1 s and N_p = 6. For ω_act = (0.1, 0.3, 0.6), the rates λ_N and k_act(N) are given by (120, 120, 120) s⁻¹ and (3821, 6300, 10,242) s⁻¹.

FIGURE 7.

The simulations show the impact of interchanging the lifetimes of activated rhodopsin and PDE. The phosphorylation, arrestin binding, and transducin activation rates are given by Eqs. 48–50 with ω_λ = ω_act = 0.1, N_p = 6, k₃ = 50 s⁻¹. For τ = (0.2, 1) s, the rates λ_N and k_act(N) are (48.2, 9.6) s⁻¹ and (1274, 1067) s⁻¹.

When R* lifetime is much shorter than PDE* lifetime, we can ignore PDE* deactivation during the activation period, and PDE activation and decay occur as two consecutive events. It follows that the peak of the mean number of PDE* occurs at a time when R* becomes deactivated (Fig. 6 a and Fig. 7 a) and is given by the steady-state value 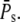The PDE* reliability ratio R_P(t) at the time to peak is given by the steady-state value R_Ps (see Fig. 6 d and Fig. 7 d). Moreover, during the recovery phase, R_P(t) is largely constant and close to R_Ps, which can be understood as follows: Since PDE is first activated and then deactivates, during the recovery phase, the mean and the variance of PDE* are given by a decay process with initial values 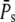and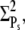

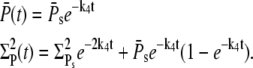For a timescale smaller than 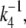we approximate 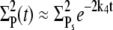and thus

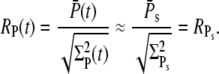The times to peak of the PDE* mean and variance are close (Fig. 6 c and Fig. 7 c). If we define the duration of the PDE* response as the time until all the PDE* molecules become deactivated, then, for large 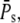the mean duration increases logarithmically with the number of PDE* as 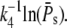Using some computations, it can be shown that the CV of the duration decreases logarithmically with 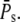We conclude that the duration of the response becomes more and more reliable with increasing number of PDE*, but the CV of the duration is not zero (see also (18)).

When R* lifetime is much larger compared to PDE* lifetime, because PDE activation and deactivation occur simultaneously, unexpected effects are generated. In that case, the PDE* reliability at time to peak can be much higher than the steady-state ratio R_Ps (Fig. 7 d). However, since the ratio R_P(t) cannot grow faster than 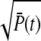(see Eq. 70), the reliability at time to peak remains bounded by 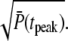Consequently, the CV of the amplitude cannot become zero (see (18)). Even for constant R* activity k_act, a steady state is reached with 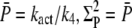and thus the CV is given by 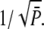If R* deactivation is rate-limiting, the duration of the PDE* response is determined by R* lifetime and the CV of the duration is given by CV_τ in Eq. 13, which can be very different from CV_areaP. Most of the variability is generated during the recovery phase, which causes the variance to peak much later than the mean (Fig. 7 c).

Finally, Fig. 7 d reveals that there is a tradeoff between the reliability during the rising and recovery phase: the higher the reliability during the rising phase, the lower the reliability will be during the recovery phase. To analyze this behavior, we remark that CV_areaP is independent of what rate limits recovery (see Eq. 46) and depends only on the number of phosphorylation sites. Thus, CV_areaP is identical in both scenarios presented in Fig. 7 d. Now, if R* lifetime limits the recovery, the PDE* reliability during the rising phase is high, which implies a low area variability in this phase. Consequently, the reliability of PDE* during the recovery phase has to decrease (which implies a higher area variability in this phase) to ensure the overall value for CV_areaP.

Influence of arrestin binding rates

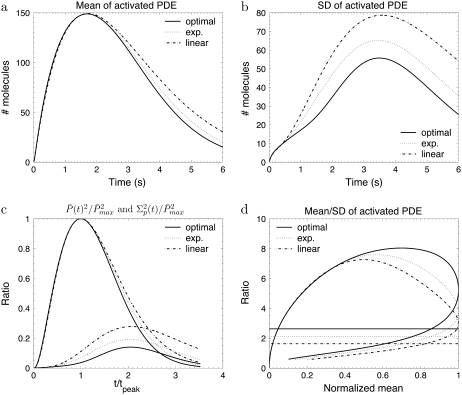
We now examine the impact of linearly and exponentially increasing arrestin binding rates. In the previous simulations, we allowed arrestin to bind only when R* was fully phosphorylated. For a given number of phosphorylation sites, this condition is optimal to minimize the variance. However, experimental results indicate that arrestin already weakly binds before R* is fully phosphorylated. Biochemical data (28) suggested that arrestin binds only to phosphorylated rhodopsin and the affinity increases linearly with the number of phosphorylations. Such a linear behavior was used for photoresponse simulations (18,19). However, experiments (15) have indicated that R* phosphorylation at three sites is needed to trigger arrestin binding with high affinity, which does not imply a gradual increase of the binding affinity. In addition, data obtained from transgenic mice lacking arrestin do not favor a gradual increase of the arrestin binding rates. Finally, there are no specific reasons to favor a linear decay of the arrestin binding affinity, while rhodopsin kinase and transducin affinities show an exponential profile.

To investigate the impact of arrestin binding on PDE* dynamics, we compare in Fig. 8 three arrestin binding scenarios called optimal, exp., and linear, obtained for toad rods with N_P = 6 and ω_act = ω_λ = 0.1: in the optimal scenario, arrestin binds only when R* is fully phosphorylated. In the linear scenario, the arrestin binding rates μ_n increase linearly with each phosphorylation step. Finally, in the scenario labeled by exp., the arrestin binding rates increase twofold with every phosphorylation step. To better compare these three scenarios, we chose the arrestin binding rates such that they reach the same maximal rate μ_N = 1.8 s⁻¹ when R* is fully phosphorylated. The simulations in Fig. 8 show that a linear increase leads to the highest PDE* variance and the lowest reliability ratio R_P(t). This behavior is reasonable, since a linear increase also strongly affects the states before R* is fully phosphorylated. With an exponential increase, arrestin binding rates become predominant when R* is almost fully phosphorylated, while they are relatively weak before. By comparing the simulations in Fig. 8 with the ones in Fig. 2, we deduce that large arrestin binding rates that come up already before R* has been fully phosphorylated have a similar impact to reducing the number of R* deactivation steps. For example, the curves in Fig. 8 for the linear scenario are similar to corresponding ones in Fig. 2 for N_p = 1. We conclude that for a given number of deactivation steps, linearly increasing arrestin binding rates are not efficient to achieve a high PDE activation reliability.

FIGURE 8.

The simulations show the impact of different arrestin binding scenarios for the toad rod scenario defined in Table 2. The behavior of the phosphorylation and transducin activation rates are given by Eqs. 48 and 49 with ω_λ = ω_act = 0.1 and N_p = 6. In the optimal scenario, arrestin binds only when rhodopsin is fully phosphorylated and the rate is given by Eq. 50. In the exp. scenario, the arrestin binding rates increase twofold with each phosphorylation step according to μ_n = 1.8 s⁻¹ e^{−0.7(n–1)} for n < N and μ_N = 0. In the linear scenario, the arrestin biding rates increase linearly according to μ_n = (N − n) 0.3 s⁻¹. The arrestin binding rates are chosen such that in each scenario they reach the final value μ₁ = 1.8 s⁻¹. For the (optimal, exp., linear) scenarios, the rates λ_N and k_act(N) are given by (3.2, 2.05, 0.9) s⁻¹ and (245, 237, 227) s⁻¹.

Only a few activated PDE molecules in cones

In cone photoreceptors, several synchronous photons have to be absorbed (10–12) to detect a signal out of the noise. For that reason, it is not possible to estimate experimentally the number of PDE* following a single photopigment excitation. Furthermore, due to experimental difficulties, many fundamental chemical constants are still missing for cones. A modeling approach is thus an unavoidable tool to investigate PDE activation in cones.

The origin of the background noise differs between L- and S-cones (12): in L-cones, a large spontaneous photopigment activation rate (12) constitutes the main source of the noise and this is a direct obstruction of a single photon detection. In contrast, the photopigment of S-cones is very stable and the background noise originates from spontaneous PDE activation (12,22).

Since spontaneous PDE activation is the main source of dark noise in rods and S-cones, we would like to investigate the question of why a single photon response can be observed in rods, but not in S-cones. A possible answer comes from biochemical data (38,39), which suggest that an excited photopigment presumably activates only very few PDE molecules. Biochemical results for carp cones (39) suggest that R* phosphorylation is much faster in cones compared to rods (∼50 times faster), which seems to be caused by a higher rhodopsin kinase concentration and activity. Moreover, experimental data (39) also imply that the transducin activation rates are much smaller in cones compared to rods (∼25 times smaller) and PDE deactivation is several times faster in cones compared to rods. This fast rate can be attributed to the higher RGS9 concentration (40,41).

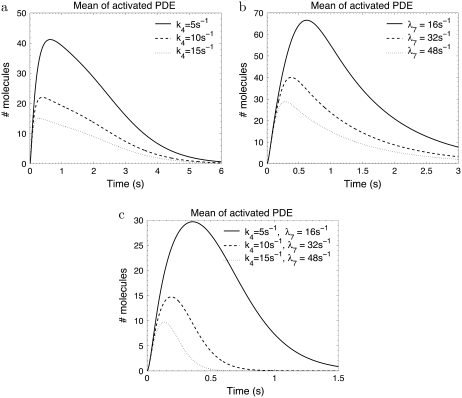
To estimate the amount of PDE* molecules following a photopigment excitation, we have run various simulations. As expected, we found with no surprise that this amount is a decreasing function of PDE and R* deactivation (Fig. 9). The simulations presented in Fig. 9 are obtained by increasing the PDE* deactivation and R* phosphorylation rates of a toad rod by factors of 5, 10, and 15 (the parameters and simulations corresponding to the toad rod can be found in Fig. 2 for N_p = 6). We do not alter the transducin activation rates, but smaller transducin activation rates (as suggested in (39)) would additionally diminish the amount of PDE* in cones. Fig. 9 a shows that increasing the PDE* deactivation rate k₄ from 1 s⁻¹ to 15 s⁻¹ decreases the amount of PDE* from 150 (amount for rod) to ∼15. Since R* lifetime is not changed by increasing k₄, the recovery of the photoresponse is not affected. In Fig. 9 b, R* deactivation is enhanced. Compared to Fig. 9 a, this shows that a faster R* deactivation is less effective in diminishing the number of PDE* molecules. In Fig. 9 b PDE* deactivation becomes rate limiting (k₄ = 1 s⁻¹) since R* lifetime is reduced from 3 s to 0.6 s, 0.3 s, and 0.2 s. Finally, in Fig. 9 c, PDE* and R* deactivation are increased simultaneously, which additionally reduces the amount of PDE*.

FIGURE 9.

How to make a cone from a rod. The simulations show the mean PDE response for faster PDE and rhodopsin deactivation. The initial values for the rates are given in Fig. 2 for N_p = 6. In panel a, the PDE deactivation rate k₄ is increased from the initial value 1 s⁻¹ by factors of 5, 10, and 15. In panel b, only the phosphorylation rate λ₇ is increased from the starting value 3.2 s⁻¹ by factors of 5, 10, and 15. As a consequence, rhodopsin lifetime decreases from 3 s to 0.6 s, 0. 3 s, and 0.2 s. In panel c, k₄ and λ₇ are increased simultaneously.

From our simulations we conclude that in cones, consistent with biochemical data (39), only very few PDE molecules are activated by an excited photopigment. This result can explain that for S-cones, contrary to rods, many synchronous photon absorptions are needed to produce a signal that overcomes the noise amplitude generated by spontaneous PDE activation.

DISCUSSION

We have studied here PDE activation by a single excited photopigment molecule using a Markov model and obtained explicit equations for the mean and the variance. This approach allowed us to investigate in detail the dynamics of PDE activation, which is indispensable and fundamental for the understanding of the photoresponse in rods and cones. Most experimental recordings are about the photocurrent, and today, unfortunately, there are no direct measurements of PDE activity, which is the main subject here. A full quantitative analysis of the photocurrent will imply to extend the model by including diffusible cGMP. Nevertheless, it is reasonable to assume that the photocurrent time course is largely determined by the one of activated PDE. In that case, our results can be connected to the photocurrent in two ways: first, to predict the photocurrent characteristics; and second, to infer from the observed photocurrent properties some of the unknown molecular details governing PDE activation.

Accurate rhodopsin deactivation does not necessarily lead to a reliable PDE activation

In rods the low variability of the photoresponse has been attributed mainly to the reliability of the lifetime of activated rhodopsin (13–16). In contrast, we have found that reliable PDE activation can be achieved even when rhodopsin lifetime is unreliable. To show this result, we estimated the reliability ratio R_τ (mean to standard deviation (SD)) of rhodopsin lifetime, and the reliability ratio R_Ps of the number of activated PDE during a SPR. We have found that the upper bound for both R_Ps and R_τ is 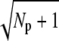(N_p is the number of rhodopsin phosphorylation sites); however, maximal values for the ratios R_Ps and R_τ are in general not achieved simultaneously. R_Ps is maximal when all rhodopsin deactivation states have the same lifetime, whereas R_Ps becomes maximal when in each state the same amount of PDE molecules are activated. Our results suggest that, in general, reliable rhodopsin deactivation and reliable PDE activation are not achieved simultaneously. In the literature, the focus is mainly on the reliability of rhodopsin deactivation, but one has to remember that the goal is not to reliably deactivate rhodopsin, but to reliably activate PDE.

In this work we assumed that each rhodopsin phosphorylation occurs through a single step and we did not investigate the effect of possible intermediate states, which implies that the number of rhodopsin deactivation states is given by N = N_p + 1. However, rhodopsin phosphorylation could proceed through additional intermediate steps (as was assumed in (18)). In such a case, the number of rhodopsin deactivation states N will become much larger than N_p + 1, which could significantly alter the variability of rhodopsin lifetime and activated PDE. In this context it is important to clarify whether rhodopsin activity in the intermediate states is zero or not. In Hamer et al. (18), the activity in intermediate states was assumed to be zero and so PDE activation occurred only in a much smaller subset of the deactivation states. However, it is also possible that rhodopsin activity persists in intermediate states, which can lead to a higher PDE activation reliability. In any case, with intermediate states the connection between the reliability of rhodopsin lifetime and PDE activation is less obvious, and it is possible to decouple the reliability of rhodopsin deactivation from the one of PDE activation.

High activation reliability during the rising phase

Our analysis revealed that the PDE variability is much smaller during the rising compared to the recovery phase (see, for example, Fig. 3). This finding agrees with similar observations for the photoresponse current (13,14,16). In particular, we have shown that during the rising phase the reliability ratio R_P(t) reaches a maximum that can be much higher than the upper limit 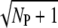valid for R_τ or R_Ps. The rational behind this result is as follows: at the beginning, PDE variance closely equals the mean and therefore R_P(t) rises like the square-root of the mean. For a large R_P(t) maximum it is equally important that rhodopsin deactivates through many steps and the transducin activation rates decrease only slightly (not more than 10–20%) with subsequent phosphorylations (see Fig. 2 e and Fig. 3 d).

Biochemical data (28) indicate that the rhodopsin-transducin affinity decreases nearly twofold with each phosphorylation step, suggesting a similar decrease for the transducin activation rates. For the numerical simulations presented in Hamer et al. (18), the rhodopsin-transducin affinity was chosen to decrease nearly twofold with each phosphorylation step, in agreement with Gibson et al. (28). Nonetheless, since a reaction cascade with high backward reactions rates was used to model transducin activation, the effective transducin activation rates decreased much less than twofold. Taking into account the statement that phosphorylation was responsible for ∼66% of the total rhodopsin activity reduction (18), we estimated an effective decrease at ∼14% with each phosphorylation step. Moreover, experimental results (27) indicate that rhodopsin's activity decreases in mouse rods through phosphorylation (at six phosphorylation sites) by ∼50%, suggesting also subsequent decrease at ∼10%. Finally, it is difficult to imagine that the transducin activation rates decrease by twofold with every phosphorylation step, since the activation rate would diminish to a very low value until rhodopsin is fully phosphorylated. In this case, the final rhodopsin shutoff through arrestin would be somehow obsolete and would barely change rhodopsin's activity, contrary to what is found (27).

A high activation reliability at peak time requires that rhodopsin deactivation limits recovery

The reliability ratio R_P(t) at the time to peak depends crucially on whether rhodopsin or PDE deactivation is rate limiting (as illustrated in Fig. 7). If rhodopsin lifetime is much shorter than PDE lifetime, PDE deactivation can be neglected during the rising phase. In this case, the ratio R_P(t) at time to peak and during the recovery phase is determined by the steady-state value R_Ps. Furthermore, since most of the PDE variance is generated by the activation process, the peak of the PDE mean and variance occur temporally close. In contrast, when rhodopsin lifetime is much larger than PDE lifetime, interesting dynamic effects show up. First, the ratio R_P(t) at time to peak is no longer determined by R_Ps and can reach values that are much larger than 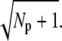Second, much of the PDE variance is now generated during the recovery phase which causes the variance to peak much later than the mean.

If the PDE variance determines the variance of the single photon response current and rhodopsin lifetime limits the photoresponse recovery, our results explain several experimental findings about the variance of the single photon response (14,16,17). Indeed, the measured coefficient of variation at the peak of the single photon response current, denoted by CV_amp, is found to be at ∼0.2 and much less than the expected value 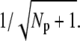Such a low value is predicted by the simulations in Fig. 2 e, where we found a value R_P(t) at ∼5 at peak time (since we expect that 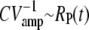at peak time). Furthermore, experiments show that the variance of the single photon response peaks approximately twice later than the mean (14,16,17), which is similar to what we have found for the PDE variance in Fig. 2 d.

In mouse rods, PDE deactivation limits the recovery of the photoresponse (35). In that case, our analysis and the simulations in Fig. 6 d predict a value for CV_amp at ∼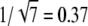 (N_p = 6). In contrast, CV_amp in mouse rods is found to be ∼0.2 (F. Rieke, 2007, personal communication), which is much too low to be explained by R_P(t) at peak time. At this stage, it is not clear how CV_amp can become so small even when PDE lifetime limits the recovery. One possible explanation can be that the PDE variance is not representative for the current variance, and including the cGMP-pathway might reveal more.

Number of activated PDE molecules during a single photon response

The maximum number of PDE molecules that are activated during the single photon response in rods seems to be an unresolved issue and indeed, a large discrepancy is found in the literature. For example, in Makino et al. (42) it was argued that >100 PDE molecules become activated. The numerical simulations presented in Hamer et al. (18) lead in average to 220 activated PDEs, and the rates provided in the literature (3,43,44) suggest a maximum value of <50. In contrast, based on noise analysis, it was suggested (45) that at least 2000 PDE molecules have to be active at peak time. Because of these large uncertainties, we decided to fix the maximum number of activated PDE at a value of 150. At this stage of our model, this choice has no important consequences, but it will become a serious issue for further investigations that include cGMP dynamics. Since the magnitude of cGMP hydrolysis depends on the number of activated PDE molecules, this quantitative question will have to be resolved to predict from molecular details the current of a photoresponse.

A related problem concerns the transducin activation rates. For amphibian rods, a value at ∼150 s⁻¹ was reported (37), while for mammalian rods a rate at ∼1300 s⁻¹ was provided (46). Because the rod photoresponse time course in mammalians is much faster compared to amphibians, this suggests that the transducin activation rates are regulated to ensure the activation of a reasonable amount of PDE molecules. For example, a transducin activation rate at ∼150 s⁻¹ would lead in mouse rods (where the rhodopsin lifetime seems to be <0.1 s (35)) to the activation of <10 PDE.

Only a few PDE molecules are activated by a excited photopigment in cones

Studying PDE activation in cones faces certain difficulties due to the limited amount of biochemical information available. However, by using the biochemical results for carp cones (39) as a guideline, our simulations (Fig. 9) suggest that only very few (<10) PDE molecules are activated by a single excited photopigment. This behavior would explain why in cones many quasisynchronous photon absorptions are needed to generate a signal that overcomes the background noise (10–12). In L-cones, the small amount of activated PDE is not an important issue, since already the large spontaneous photopigment activation rate (12) impedes the observation of a single photon absorption. However, in S-cones the photopigment is very stable (12) and, contrary to rods, the absorption of many photons seems to be necessary to activate sufficient PDE molecules that overcome the background noise set by spontaneous PDE activation.

APPENDIX

Mean and variance of the total number of PDE*

For k₄ = 0 and after R* shutoff, the number of PDE* reaches a steady-state value that accounts for all the PDE* activated during the response. Since every T* converts into a PDE*, the steady-state mean and variance of PDE* can be obtained by calculating the steady-state values of T* (for k₃ = 0). By setting k₃ = 0, integrating Eq. 24 from zero to infinity and using Eq. 21, we obtain the steady-state mean of T* and PDE* as

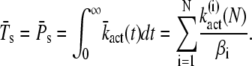(51)

Inserting the expressions for 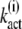(N) in Eq. 19 yields the explicit solution

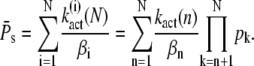(52)

The steady-state variance of PDE* is obtained similarly from Eq. 31,

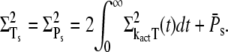(53)

Using Eq. 34 and Eq. 39, the integral can be evaluated to give

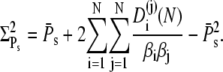(54)

By using the formula (which can be derived by induction on N)

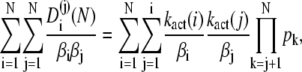(55)

we finally get

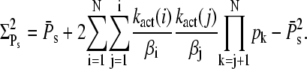(56)

Steady-state reliability ratio R_Ps

We now derive an upper limit for the steady-state ratio of the mean to the variance of PDE*, given by

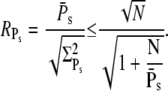(57)

To prove Eq. 57, we start from the Eq. 52 and Eq. 56 and introduce x_i = k_act(i)/β_i and 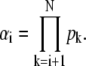In terms of x_i and α_i, we get

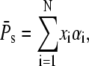(58)

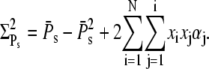(59)

Because Eq. 57 is equivalent to 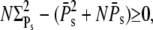using Eq. 59 we have to show that

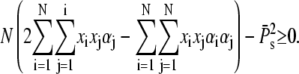(60)

For α_i ≤ 1, we have

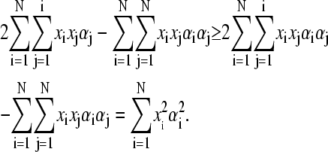Finally, using the Cauchy-Schwarz inequality yields

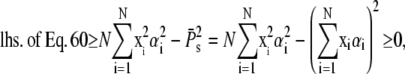(61)

which completes the proof.

The upper estimate for the ratio R_τ of R* lifetime is derived analogously to R_Ps by replacing k_act(i) with 1. The result is

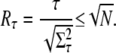(62)

Explicit expressions for the mean of T* and PDE*

Expressions for the mean of T* and PDE* are derived by integrating Eq. 24 and Eq. 25,

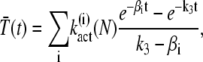(63)

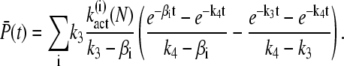(64)

Small time asymptotic

To derive the small time asymptotic of the mean and the variance of PDE*, we use a Taylor expansion in Eq. 24 and Eq. 25 that leads to

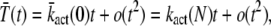(65)

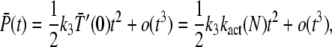(66)

where 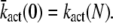We conclude that for small time, the mean of PDE* rises like t², in contrast with the linear asymptotic result proposed in the literature (1,23), where PDE activation by T* was considered to occur instantaneously. Using again a Taylor expansion in Eqs. 31–33 and in Eqs. 35 and 36, we find the small time asymptotic for the variance of T* and PDE* as

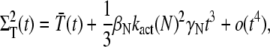(67)

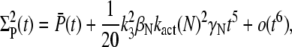(68)

where β_N = λ_N + μ_N and

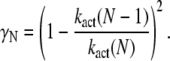(69)

For small time asymptotic, the variance of T* and PDE* equal the mean. Since all parameters in Eq. 68 and Eq. 67 are positive, the variance cannot be smaller than the mean and becomes minimal for γ_N = 0 (k_act(N) = k_act(N − 1)). In that case, when R* undergoes a transition from the state N to N − 1, the activation rate does not change and therefore does not generate any additional source of variability. The variance becomes also minimal for β_N = 0, that is when activated rhodopsin is stable. In this case, transducin activation proceeds as a Poisson process.

We now estimate the small time asymptotic of the reliability ratio R_P(t), defined in Eq. 40. Using Eq. 66 and Eq. 68, we obtain

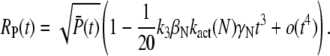(70)

For small time, R_P(t) rises proportional to 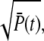while for larger times, the second term in Eq. 70 becomes predominant and thus attenuates the rising of R_P(t). Moreover, for γ_N = 0, the ratio R_P(t) in Eq. 70 becomes maximal and the duration of the rising phase is prolonged.

Mathematical identities

The following identities are true for all N real numbers β_k:

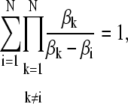(71)

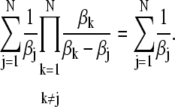(72)

These formulas can be derived by induction on the number N.