Abstract
Solutions of intact cardiac thin filaments were examined with transmission electron microscopy, dynamic light scattering (DLS), and particle-tracking microrheology. The filaments self-assembled in solution with a bell-shaped distribution of contour lengths that contained a population of filaments of much greater length than the in vivo sarcomere size (∼1 μm) due to a one-dimensional annealing process. Dynamic semiflexible modes were found in DLS measurements at fast timescales (12.5 ns–0.0001 s). The bending modulus of the fibers is found to be in the range 4.5–16 × 10−27 Jm and is weakly dependent on calcium concentration (with Ca2+ ≥ without Ca2+). Good quantitative agreement was found for the values of the fiber diameter calculated from transmission electron microscopy and from the initial decay of DLS correlation functions: 9.9 nm and 9.7 nm with and without Ca2+, respectively. In contrast, at slower timescales and high polymer concentrations, microrheology indicates that the cardiac filaments act as short rods in solution according to the predictions of the Doi-Edwards chopsticks model (viscosity, η ∼ c3, where c is the polymer concentration). This differs from the semiflexible behavior of long synthetic actin filaments at comparable polymer concentrations and timescales (elastic shear modulus, G′ ∼ c1.4, tightly entangled) and is due to the relative ratio of the contour lengths (∼30). The scaling dependence of the elastic shear modulus on the frequency (ω) for cardiac thin filaments is G′ ∼ ω3/4 ± 0.03, which is thought to arise from flexural modes of the filaments.
INTRODUCTION
Cardiac disease continues to be the predominant cause of death in the western world. The specialized variety of striated muscle found in heart tissue therefore requires detailed research. In the sarcomere, thick (myosin) and thin (actin with regulatory proteins) filaments are arranged in an interdigitated hexagonal array. Myosin II motors walk along the thin filaments in a nonprocessive manner (a substantial population of attached molecules is required for the continuous motion of a filament (1)) that provides the muscle with motility, and large parallelized arrays of the filaments allow substantial forces to be created with a similar time response to that of the individual molecular motors.
In both skeletal and cardiac muscle, contraction is regulated by the intracellular Ca2+ concentration. The molecular basis for Ca2+ regulation was first established by Ebashi and co-workers in the 1960s (2,3), when troponin and tropomyosin were identified as the principal proteins for Ca2+ regulation. Troponin and tropomyosin are located along the polymerized actin backbone in thin filaments, and striated muscle contains a troponin/tropomyosin/actin molar ratio of 1:1:7. It is believed that by binding to troponin, Ca2+ induces an azimuthal shift of tropomyosin around the filament axis. The mechanism and the consequences of this process are still not fully understood, but motion of the tropomyosin can provide a steric barrier for the binding of the myosin heads (4). Thin filaments have been shown to self-assemble in situ in striated muscle, allowing passive tension to be reestablished in disrupted networks (5). Thus, self-assembly processes are of direct significance to the repair of damaged heart muscle.
Over the last 10 years, strong experimental evidence has accumulated for the unique dynamic modes that occur in semiflexible polymers, of which F-actin is a prime example (6). A wide range of experimental techniques, including dynamic light scattering (DLS) (7,8), optical tweezers (9,10), particle tracking (11), magnetic tweezers (12), and diffusing wave spectroscopy (13), point to the existence of unique t3/4 modes (t is time) in semiflexible polymers. It is now clear that much of the older DLS literature on biopolymers needs to be reinterpreted taking into consideration the possibility of semiflexible behavior in addition to the well established Zimm and Rouse models for flexible polymeric dynamics, and liquid-crystalline models for rigid polymers. Many of the apparent momentum-transfer-dependent diffusion coefficients previously measured for semiflexible biopolymers with DLS may have been due to stretched exponential semiflexible internal modes (14,15).
In addition to our aim of establishing the semiflexible nature of cardiac thin filaments (CTF), the main motivations for our work on CTF were the identification of changes in their structure induced by the presence or absence of Ca2+, their self-assembly, and their mechanical behavior. Negative-stain transmission electron microscopy (TEM) image analysis results are reported that provide information concerning the geometry of the cardiac thin filament. The filaments self-assemble with intact subunits containing both the tropomyosin and troponin that are vital for in vivo functioning. Particle-tracking microrheology (PTM) (10,16–19) allowed the linear viscoelasticity of minute volumes of cardiac thin filament solutions to be measured. Dynamic light scattering measurements are presented that enable the bending rigidity of the cardiac thin filaments to be accurately calculated in terms of their semiflexible dynamics (6). Comparison is also made between the behavior of short intact cardiac thin filament specimens and that of long synthetic actin filaments, and large differences are observed between their viscoelasticities at long times (20).
MATERIALS AND METHODS
Cardiac thin filaments
Native cardiac thin myofilaments were extracted from glycerinated porcine myocardial tissue in the presence of protease inhibitors (21). The salt buffer consisted of 100 mM KCl, 3 mM MgCl2, 10 mM imidazole, and 5 mM DTT, pH 7.3. The manipulations during this purification method were all at near-physiological salt concentrations and pH. Experiments with and without calcium were carried out in the presence of 0.1 mM CaCl2 and in 1 mM EGTA with no added calcium, respectively. In the solution with EGTA, the free calcium concentration would have been <1 nM and the troponin would not have had bound calcium. In the presence of 0.1 mM calcium, the troponin would have been saturated with calcium.
Microscopy
Images were recorded using a Jeol 1200 transmission electron microscope (Tokyo, Japan). Samples were stained with uranyl acetate for improved contrast in the resultant images. Micrographs were obtained in the bright-field mode at a magnification of 50,000×.
Dynamic light scattering
An ALV (Langen, Germany) dynamic light scattering apparatus was used with a 100-mW argon ion laser (Spectra Physics, Mountain View, CA) with a fast correlator (12.5 ns to 1000 s). All the measurements were performed at 25.0 ± 0.1°C. Correlation functions (g(q,t)) were collected at a series of angles in the range 30–140° (momentum transfers, 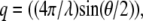 were in the range 8.86–32.18 μm−1, where the wavelength (λ) was 488 nm and θ is the scattering angle) with a step size of 10° using an ALV compact goniometer.
were in the range 8.86–32.18 μm−1, where the wavelength (λ) was 488 nm and θ is the scattering angle) with a step size of 10° using an ALV compact goniometer.
Particle tracking microrheology
Experiments were performed on an upright BH2 microscope (Olympus, Melville, NY) with a Hitachi video camera and a 100× oil immersion objective, as described previously (22,23). The apparatus was placed on a vibration-isolated optical table. Carboxylic-acid-modified polystyrene spheres (0.489 μm) were used as probes over a range of CTF solution concentrations. Many particles (20–30/frame) were tracked simultaneously for movies of 5-min length. IDL image analysis routines (Research Systems, Boulder, CO) developed from the software of Weeks et al. (24) were used. Complex shear moduli (G*(ω)) were extracted from the mean-squared displacements (MSDs) of the tracked probes using the generalized Stokes-Einstein equation (22,25). Dynamic (finite camera shutter time) and static (bead displacement noise) errors on the averaged MSD of the particle trajectories were negligible for the range of frequencies (0.003–25 Hz) and viscoelastic moduli were measured (22,26). The apparatus was calibrated using a range of Newtonian (glycerol/water mixtures (22)) and viscoelastic standards (flexible polyelectrolytes such as polyacrylamide and polymaleic anhydride copolymers).
RESULTS AND DISCUSSION
Electron microscopy image analysis
The thin-filament length in amphibian and mammalian cardiac muscle can vary by up to 45% within a single species (rat, 0.6–1.1 μm; frog, 0.8–1.3 μm) (27); in human striated muscles, the length is ∼1.1 μm, with variations of only a few percent (28). It is thought that skeletal filaments are exactly assembled (correct to one actin subunit), specified by the giant protein nebulin spanning the entire filament as a template. The CTF used in this work was obtained from pig heart following the procedure of Speiss et al. (21). The CTF length for pigs is comparable to that for humans, rats, and frogs (∼1 μm). Fig. 1 shows two contour length distributions obtained by digital analysis of TEM images (Jeol 1200) of uranyl-stained CTF originating from two sets of solutions prepared with the same buffer with and without 0.1 mM of Ca2+. The first unexpected result was that both distributions are extended up to 3.2–3.6 μm (far beyond the ∼1 μm expected for a single intact sacromere filament), providing strong evidence that the CTFs undergo an annealed self-assembly process in solution, probably as a result of fragmentation by homogenization during preparation. The contour length distribution of the CTF is not exponentially distributed as expected for a simple one-dimensional self-assembly process (1,29). Indeed, simple models of self-assembly predict an exponential decrease in the probability as a function of filament length
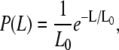 |
(1) |
where P(L) is the probability that a particular fiber is of length L, and L0 is a characteristic length (L0 = −d/lna1 where d is the monomer size and a1 is the monomer concentration).
FIGURE 1.
(a) Contour length distributions of CTF with/without Ca2+ (open symbols/closed symbols), obtained by TEM image analysis. The one parameter fit of the Hill model (30) to the bell shaped distribution is shown (Eq. 2) as a continuous line. The contour length distribution was insensitive to the presence of Ca2+. (b) Representative TEM image used in the digital analysis of CTF lengths, showing the characteristic length scales of the CTF and of a 0.5 μm polystyrene particle tracking microrheology probe bead.
However, bell-shaped curves such as those shown in the figure are observed experimentally. Such a behavior has been predicted in a more sophisticated self-assembly theory due to Hill (30), which incorporates the entropic (rotational and translational) effects of the conformations of rodlike filaments, which favors the creation of a large proportion of fibers of intermediate length. The dissociation constant for self-assembly in this model thus depends on the length of the filament, and the probability distribution is given by
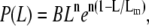 |
(2) |
where B is a normalization constant and n is expected to be in the range 4–6, dependent on steric constraints (n = 6 in our case, indicating no steric constraints, and Lm is 2591 nm). A fit of the model is shown in the figure and the agreement is very good, considering that only one fitting parameter (Lm) was used. In contrast to CTFs, synthetic F-actin filaments are typically much longer, with contour lengths >10 μm, but again bell-shaped distributions are observed (31).
During calcium regulation of cardiac muscle, the troponin (Tn) complex is known to change its position and conformation with respect to the actin backbone (28). These modifications induce structural reorganization of the ternary actin-tropomyosin (Tm)-Tn system and increase the diameter of the filament due to the extension of the TnIreg subdomain that is distributed along the CTF every ∼38.5 nm. The CTF diameters measured from TEM images with and without Ca2+ are clearly consistent with this schematic model (Supplementary Material). F-actin (in the absence of Tm and Tn) is found to have an average diameter of 9.2 ± 0.1 nm, whereas CTFs have a diameter of 9.72 ± 0.08 nm without Ca2+, and 9.9 ± 0.2 nm with Ca2+. The detailed molecular model (27) indicates that at low Ca2+ concentration, TnIreg must form an extra attachment to actin-tropomyosin so that the troponin-tropomyosin strand is tied down onto the actin filament. At high Ca2+ concentrations, TnIreg is thought to be detached from actin-tropomyosin, and is associated with the N lobe of TnC in an extended form. Studying the distribution of the measured diameter in TEM images, the model is supported by the presence of the tail in the distribution of filament diameters above the mean diameter value in the CTF with Ca2+ (Supplementary Material).
From further image analysis, the distance distributions between two neighboring troponin molecules along the CTF backbone are found to be 38.5 ± 0.3 nm, independent of the presence of Ca2+, as expected (2–4) (Supplementary Material). The low polydispersity in troponin positioning indicates a very small population (if any) of gaps between consecutively bound tropomyosin molecules, as expected for a highly cooperative self-assembly process (32). Plotting histograms of the contour length (L) distributions as L/38.5 nm integer(L/38.5 nm) indicates no statistically significant tendency of the filaments to self-assemble into integral or half-integral lengths of the tropomyosin repeat distance (similarly Fourier analysis indicates no characteristic lengths other than Lm). We also find that the contour length distribution does not change appreciably with Ca2+ concentration.
Particle-tracking microrheology
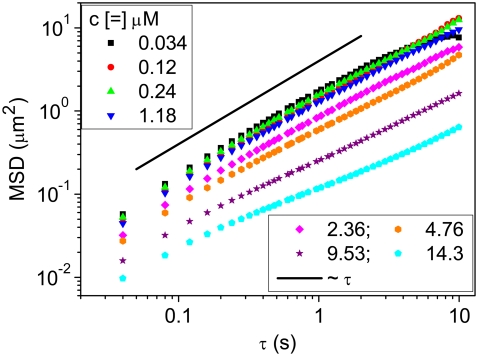
PTM was used to investigate the two sets of cardiac thin filament solutions at slow and intermediate timescales. PTM is well suited to the current cardiac protein application due to the minute amounts of sample required (∼20 μL) (16,32,33). Furthermore, short actin filaments are known to function well, with particle-tracking microrheology (11) giving confidence in the agreement with conventional bulk rheology measurements. The two solutions were investigated over a range of concentrations from 0.026 to 26 μM. With the PTM technique, 0.5-μm carboxylic-acid-coated polystyrene spheres were used as probe particles, and their Brownian motion was tracked, allowing the viscoelastic properties of the solution to be calculated. The viscoelastic responses of the CTF solutions were compared with theoretical scaling predictions for semiflexible and rodlike polymer solutions. The CTF solutions, prepared without Ca2+, were also investigated over eight concentrations ranging from 0.034 to 14.3 μM. Fig. 2 shows the MSDs of the probes versus lag time (τ) for solutions at different CTF concentrations.
FIGURE 2.
MSDs of probe spheres from particle-tracking microrheology measurements on CTF solutions without Ca2+ at different concentrations. The solid line is the predicted MSD for beads 0.489 μm in diameter in water at 25°C using the Stokes-Einstein equation (D = kT/6πηrh, where kT is the thermal energy, rh is the hydrodynamic radius, and η is the solvent viscosity).
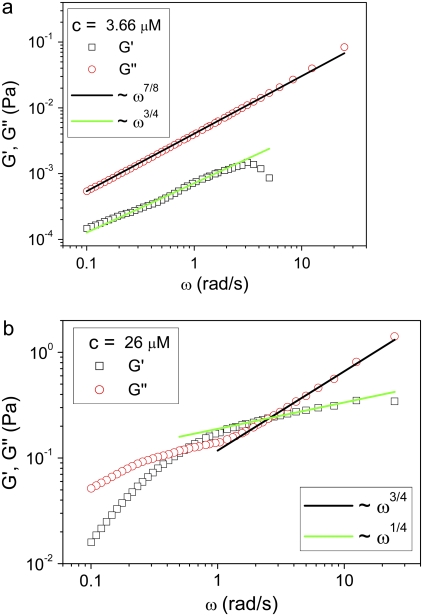
Fig. 3, a and b, shows the corresponding values of both the storage and loss moduli versus frequency calculated from the MSDs using the generalized Stokes-Einstein equation (25). The shear moduli are predominantly viscous and a range of power laws is observed for the frequency dependence of the viscoelastic spectrum. It is unusual that, in addition to the G′ ∼ ω3/4±0.03 dependence often observed for semiflexible polymers, an unmistakable G″ ∼ ω7/8±0.04 regime is found in many of the spectra (where G″ is the loss shear modulus and ω is the frequency (Supplementary Material (34)). Such ω7/8 functional forms have been previously predicted at much higher frequencies for longitudinal fluctuations of the fibers parallel to their lengths (34–36). Their origin in the current experiments requires further research, and they could just be a crossover scaling behavior. Similar results were found for the second set of CTF solutions with Ca2+, investigated over nine concentrations ranging from 0.026 to 26 μM.
FIGURE 3.
Loss (circles) and storage (squares) shear moduli versus frequency for CTF solutions with Ca2+ at two different concentrations: (a) 3.66 μM and (b) 26 μM. The solid lines are a guide for the gradients. Both ω3/4 (semiflexible flexural modes) and ω7/8 modes are observed.
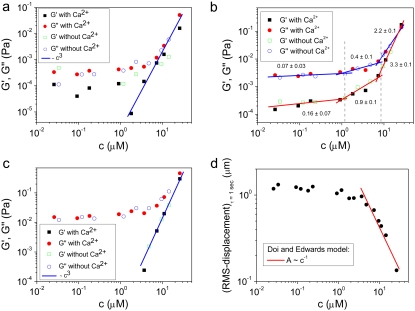
To identify the different stress contributions to the complex modulus (G*(ω)), we examined the behaviors of both the loss and storage moduli as a function of CTF concentration (Fig. 4, a–c), extracted from the viscoelastic spectra (Fig. 3, and Supplementary Material) at specific frequency (ω) values of 0.1, 1, and 6.25 rad/s. In Fig. 4, a–c, the results obtained from solutions with and without Ca2+ have been plotted together to identify different behaviors induced by the presence or absence of Ca2+. It is clear that, within the experimental accuracy, there are no significant differences in the viscoelasticity between the two CTF solutions. This implies that the addition of Ca2+ does not significantly perturb the self-assembly process, since the viscosity is normally a sensitive function of the contour length distribution. For this reason, the data analysis has been performed as if the CTF concentration (c) were the only parameter differentiating the solutions. In all three plots (Fig. 4, a–c), it is possible to identify two extreme scaling behaviors of both moduli as functions of CTF concentration: 1), at low concentrations, a concentration-independent region occurs up to a value of ∼1 μM, above which 2), the two moduli smoothly tend to a scaling law of ∼c3. Such behavior is characteristic of concentrated rodlike polymer solutions (persistence length 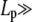 contour length L). Doi and Edwards (37) provide the following expression for the specific viscosity:
contour length L). Doi and Edwards (37) provide the following expression for the specific viscosity: 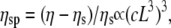 where ηs is the solvent viscosity.
where ηs is the solvent viscosity.
FIGURE 4.
(a) Loss and storage shear moduli, measured at a frequency (ω) of 0.1 rad/s, versus the CTF concentration (with and without Ca2+). (b) The loss and storage shear moduli, measured at a frequency value of 1 rad/s, versus the CTF concentration (with and without Ca2+). (c) The loss and storage shear moduli, measured at 6.25 rads/s, versus the CTF concentration (with and without Ca2+). (d) RMS displacement of a bead in a PTM experiment at a lag time of 1 s versus CTF concentration and the Doi-Edwards prediction for the tube diameter (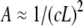 ) is shown. The solid lines are guides for the gradients.
) is shown. The solid lines are guides for the gradients.
The intermediate scaling laws between the two concentration extremes are clearly identified in Fig. 4 b. The two moduli scale as G′ ∼ c0.9±0.1 and G″ ∼ c2/5±0.1 for concentrations between ∼1 and ∼7 μM (where G′ is the elastic shear modulus and G″ the dissipative shear modulus). This scaling sharply contrasts with the behavior observed for long synthetic actin filaments that follow the predictions of semiflexible models for long filaments (20). At high concentrations, using an identical PTM apparatus, we found that the elastic modulus scales as G′ ∼ c1.4±0.05 (consistent with the predictions for the tightly entangled regime) with synthetic actin filaments (13,20,38,39).
In Fig. 4 c, the two scaling behaviors at low and high concentrations are very well defined. G″ is concentration-independent up to ∼1 μM, and then smoothly approaches the scaling ∼c3. G′ is measurable only at high concentrations for such a frequency, and it also scales with the cube of the concentration.
Specific viscosities (ηsp) were evaluated using the complex viscosities (η* = G*/ω) extracted from data such as that shown in Fig. 3, where 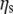 is the viscosity of water at 25°C. The results are again in good agreement with the Doi and Edwards predictions for concentrated solutions of rodlike polymers
is the viscosity of water at 25°C. The results are again in good agreement with the Doi and Edwards predictions for concentrated solutions of rodlike polymers 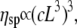 especially at high concentration values; but they are in disagreement with Bird and Yamakawa (40,41) predictions for dilute solutions of rodlike polymers
especially at high concentration values; but they are in disagreement with Bird and Yamakawa (40,41) predictions for dilute solutions of rodlike polymers 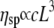 (Supplementary Material). It appears that no large increases in the self-assembled length of the CTF fibers occur over the range of concentrations probed (rheology is fairly sensitive to contour length of rigid rods due to the ∼L9 dependence of the viscosity), since this would lead to an exponential dependence of viscosity on concentration (1).
(Supplementary Material). It appears that no large increases in the self-assembled length of the CTF fibers occur over the range of concentrations probed (rheology is fairly sensitive to contour length of rigid rods due to the ∼L9 dependence of the viscosity), since this would lead to an exponential dependence of viscosity on concentration (1).
A qualitative explanation of the different scaling behaviors of the shear moduli at different frequencies may be provided by considering the relative magnitudes of the two characteristic lengths for particle-tracking microrheology: the bead diameter (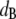 ) and the polymer solution mesh size (ξ). For
) and the polymer solution mesh size (ξ). For 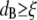 and for relatively short times, a probe bead should reveal the bulk properties of the polymer solution, since it is almost caged by the polymer chains. However, for
and for relatively short times, a probe bead should reveal the bulk properties of the polymer solution, since it is almost caged by the polymer chains. However, for 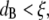 only for times long enough that the root mean-squared (RMS) displacement of the bead is comparable to the polymer mesh size should the microrheology measurements reveal the viscoelastic response of the polymer solution. For short times, the beads only explore a small distance compared to the mesh size, experiencing only the hydrodynamic effects due to the presence of the polymer chains, without interacting directly with them. This picture is consistent with the above results; indeed, at high frequency (i.e., short time (Fig. 4 b)) and low concentrations (
only for times long enough that the root mean-squared (RMS) displacement of the bead is comparable to the polymer mesh size should the microrheology measurements reveal the viscoelastic response of the polymer solution. For short times, the beads only explore a small distance compared to the mesh size, experiencing only the hydrodynamic effects due to the presence of the polymer chains, without interacting directly with them. This picture is consistent with the above results; indeed, at high frequency (i.e., short time (Fig. 4 b)) and low concentrations (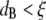 ), the beads reveal only the viscous component of the system up to a concentration of ∼1 μM; above that concentration (
), the beads reveal only the viscous component of the system up to a concentration of ∼1 μM; above that concentration (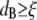 ), both viscoelastic components are measured. The square root of the bead MSD (i.e., the RMS displacement) extracted from Fig. 2 at a lag time of 1 s can be plotted versus CTF concentration (for both types of solution, i.e., with and without Ca2+). The Doi and Edwards (37) scaling prediction for the transverse distance (A) between two rods in a concentrated solution of rigid rods is A ∼ 1/(cL2). In this case, as for synthetic F-actin, the agreement with the model prediction is very good, especially at high filament concentrations (Fig. 4 d). This result provides further support for the novel technique of measuring the tube diameter in entangled solutions of semiflexible polymers. Moreover, in the case of synthetic F-actin the results are in agreement with fluorescence microscopy experiments (31).
), both viscoelastic components are measured. The square root of the bead MSD (i.e., the RMS displacement) extracted from Fig. 2 at a lag time of 1 s can be plotted versus CTF concentration (for both types of solution, i.e., with and without Ca2+). The Doi and Edwards (37) scaling prediction for the transverse distance (A) between two rods in a concentrated solution of rigid rods is A ∼ 1/(cL2). In this case, as for synthetic F-actin, the agreement with the model prediction is very good, especially at high filament concentrations (Fig. 4 d). This result provides further support for the novel technique of measuring the tube diameter in entangled solutions of semiflexible polymers. Moreover, in the case of synthetic F-actin the results are in agreement with fluorescence microscopy experiments (31).
Dynamic light scattering
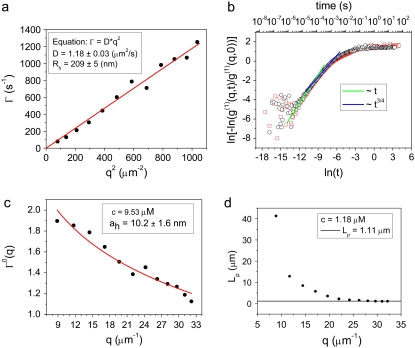
To measure both the persistence length and the diameter of the cardiac thin filaments in the presence and absence of Ca2+, DLS measurements were performed on both sets of solutions. DLS can measure a wide range of timescales (12.5 ns to 1000 s), including those that are much faster than those accessible to particle tracking microrheology. Two sets of five concentrations were investigated: 1), 0.91, 1.82, 3.66, 7.33, and 11 μM; and 2), 1.18, 2.36, 4.76, 9.53, and 14.3 μM, the first with and the second without Ca2+. All the measurements were performed at 25°C and at different angles in the range 30°–140° (i.e., q = 8.86–32.18 μm−1) with a step size of 10°. Correlation functions from DLS were initially examined with CONTIN to detect the presence of simple dominant relaxation modes such as the diffusive motion of the scattering centers. Only for the lowest CTF concentration in the presence of Ca2+ was it possible to identify a diffusionlike mode (Fig. 5 a). It cannot be definitively identified as a purely diffusive mode, since the polydispersity of the samples (Fig. 1 a) could affect the linear relationship (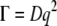 ) between the relaxation rate (Γ) and the momentum transfer (q) (D is the diffusion coefficient for monodisperse spheres), as described elsewhere (see 48,49). However, the linear behavior of Γ(q2) shown in Fig. 5 a suggests that there is not substantial variation of the form factor of the wormlike CTF fibers over the range of lengthscales examined (i.e., the cross-sectional radius is too small, and both the length and the persistence length too long, to have a significant signature in the q-dependent diffusion coefficient with light scattering).
) between the relaxation rate (Γ) and the momentum transfer (q) (D is the diffusion coefficient for monodisperse spheres), as described elsewhere (see 48,49). However, the linear behavior of Γ(q2) shown in Fig. 5 a suggests that there is not substantial variation of the form factor of the wormlike CTF fibers over the range of lengthscales examined (i.e., the cross-sectional radius is too small, and both the length and the persistence length too long, to have a significant signature in the q-dependent diffusion coefficient with light scattering).
FIGURE 5.
(a) Diffusive linear dependence of the decay rate (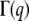 ) versus q2 at low concentrations from dynamic light scattering. The line is the best linear fit. The CTF concentration is 0.91 μM with a 0.1-mM Ca2+ concentration. (b) The double logarithm of the normalized dynamic structure factor (g(1)(q,t)) plotted versus the logarithm of time at a scattering angle of 90°, for CTF concentrations of 2.36 μM (gray circles) and 1.82 μM plus 0.1 mM of Ca2+ (red squares). The solid lines are a guide for the gradients. (c) The normalized initial decay rate (Γ0) versus momentum transfer (q) for CTF solutions without Ca2+ at 9.53 μM. The line is the best fit of Eq. 3 using the hydrodynamic diameter (ah) as a single free parameter. (d) The persistence lengths extracted from 1.18-μM CTF solutions from stretched exponential fits to Eq. 4. The plateau at high q indicates that internal dynamic modes have been measured.
) versus q2 at low concentrations from dynamic light scattering. The line is the best linear fit. The CTF concentration is 0.91 μM with a 0.1-mM Ca2+ concentration. (b) The double logarithm of the normalized dynamic structure factor (g(1)(q,t)) plotted versus the logarithm of time at a scattering angle of 90°, for CTF concentrations of 2.36 μM (gray circles) and 1.82 μM plus 0.1 mM of Ca2+ (red squares). The solid lines are a guide for the gradients. (c) The normalized initial decay rate (Γ0) versus momentum transfer (q) for CTF solutions without Ca2+ at 9.53 μM. The line is the best fit of Eq. 3 using the hydrodynamic diameter (ah) as a single free parameter. (d) The persistence lengths extracted from 1.18-μM CTF solutions from stretched exponential fits to Eq. 4. The plateau at high q indicates that internal dynamic modes have been measured.
Thus, the linear fit in Fig. 5 a represents the diffusive behavior of the scattering centers for a low concentration of filaments (42,43) and, by using the Stokes-Einstein relationship, it is possible to obtain the hydrodynamic radius (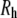 ) of the filament:
) of the filament: 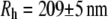 (from the Doi-Edwards model (37),
(from the Doi-Edwards model (37), 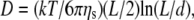 where kT is the thermal energy, ηs is the solvent viscosity, L is the contour length, and d is the chain diameter, which implies that L = 2.2 μm when d = 10 nm from TEM/DLS). This result provides additional evidence for the assumptions made in the previous section, since they confirm that 0.91 μM is the upper limit of the dilute regime. Only above this concentration is it possible to consider the presence of a polymer network characterized by a mesh size (ξ(c)). For the higher filament concentrations, diffusive modes were not detected. The Kroy and Frey model (44) was used for semiflexible filaments, as shown in Fig. 5, b and c. This model predicts a t3/4 dependence (where t is time) in the correlation functions due to transverse fluctuations (similar in origin to the ω3/4 flexural fluctuations observed in the microrheology data (6,13); Fig. 3 b) and the dependence of the initial decay of the momentum transfer due to the hydrodynamics of the chains (Fig. 5 c). No t7/8 mode was observed in DLS (in contrast to the ω7/8 seen in PTM), but this technique is sensitive to different modes of motion in the sample, e.g., longitudinal fluctuations cannot be easily detected since there is little optical contrast for this mode of vibration.
where kT is the thermal energy, ηs is the solvent viscosity, L is the contour length, and d is the chain diameter, which implies that L = 2.2 μm when d = 10 nm from TEM/DLS). This result provides additional evidence for the assumptions made in the previous section, since they confirm that 0.91 μM is the upper limit of the dilute regime. Only above this concentration is it possible to consider the presence of a polymer network characterized by a mesh size (ξ(c)). For the higher filament concentrations, diffusive modes were not detected. The Kroy and Frey model (44) was used for semiflexible filaments, as shown in Fig. 5, b and c. This model predicts a t3/4 dependence (where t is time) in the correlation functions due to transverse fluctuations (similar in origin to the ω3/4 flexural fluctuations observed in the microrheology data (6,13); Fig. 3 b) and the dependence of the initial decay of the momentum transfer due to the hydrodynamics of the chains (Fig. 5 c). No t7/8 mode was observed in DLS (in contrast to the ω7/8 seen in PTM), but this technique is sensitive to different modes of motion in the sample, e.g., longitudinal fluctuations cannot be easily detected since there is little optical contrast for this mode of vibration.
To evaluate the hydrodynamic diameter (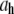 ) of the filaments, the initial decay rates (
) of the filaments, the initial decay rates (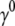 ) of the dynamic structure factors (g(1)(q,t)) were extracted from the measurements in a time window ranging from 10−7 to 4 × 10−5 s, a procedure that performed well in previous experiments with long synthetic actin filaments and peptides (7,45). For each filament concentration and scattering angle (characterized by a scattering vector q), the normalized initial decay rate (
) of the dynamic structure factors (g(1)(q,t)) were extracted from the measurements in a time window ranging from 10−7 to 4 × 10−5 s, a procedure that performed well in previous experiments with long synthetic actin filaments and peptides (7,45). For each filament concentration and scattering angle (characterized by a scattering vector q), the normalized initial decay rate (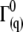 ) was measured and fitted to the expression calculated by Kroy and Frey:
) was measured and fitted to the expression calculated by Kroy and Frey:
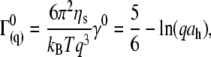 |
(3) |
where ηs is the solvent viscosity, 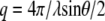 (λ is the wavelength of 488 nm and θ is the scattering angle), and kT is the thermal energy. The dynamic structure factors (g(1)(q,t)) behaved at short times as single exponentials (Fig. 5 b) for all the solutions investigated. To evaluate the hydrodynamic diameter (
(λ is the wavelength of 488 nm and θ is the scattering angle), and kT is the thermal energy. The dynamic structure factors (g(1)(q,t)) behaved at short times as single exponentials (Fig. 5 b) for all the solutions investigated. To evaluate the hydrodynamic diameter (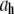 ) of the CTF filaments, Eq. 3 was used to fit the data shown in Fig. 5 c. The results for all the concentrations investigated are reported in Table 1.
) of the CTF filaments, Eq. 3 was used to fit the data shown in Fig. 5 c. The results for all the concentrations investigated are reported in Table 1.
TABLE 1.
Hydrodynamic diameter (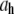 ) of CTFs without Ca2+ from DLS measurements as a function of CTF concentration
) of CTFs without Ca2+ from DLS measurements as a function of CTF concentration
| CTF concentration (μM) |
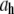 (nm) (nm)
|
|---|---|
| 2.36 | 8.9 ± 3.5 |
| 4.76 | 9.5 ± 1.7 |
| 9.53 | 10.2 ± 1.6 |
| 14.3 | 10.4 ± 1.8 |
The diameter values of Table 1 are in good agreement with those of the cardiac thin filaments reported in the literature (46) (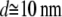 ). Their mean value,
). Their mean value, 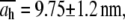 is also in very good agreement with the TEM image analysis result,
is also in very good agreement with the TEM image analysis result, 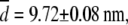 obtained for the same system, but slightly larger than small-angle neutron measurements (7–9 nm) (47). At longer times, the intermediate scaling function from DLS has a characteristic stretched exponential dependence on time (t) (8,44), in agreement with the prediction for semiflexible polymers:
obtained for the same system, but slightly larger than small-angle neutron measurements (7–9 nm) (47). At longer times, the intermediate scaling function from DLS has a characteristic stretched exponential dependence on time (t) (8,44), in agreement with the prediction for semiflexible polymers:
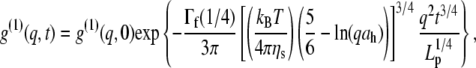 |
(4) |
where Lp is the persistence length and Γf is the gamma function. Having established the very good agreement between DLS and TEM measurements, a diameter of 9.72 nm was used in Eq. 4 to evaluate the best fit value of 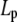 for the CTF solutions in the absence of Ca2+, whereas a diameter of 9.9 nm was used for the CTF solutions with Ca2+. The resultant persistence lengths (
for the CTF solutions in the absence of Ca2+, whereas a diameter of 9.9 nm was used for the CTF solutions with Ca2+. The resultant persistence lengths (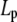 ) are reported in Table 2, together with the corresponding bending moduli (
) are reported in Table 2, together with the corresponding bending moduli (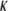 ). As noted by Kroy and Frey (44), Eq. 4 only applies to momentum transfers (q) small enough to resolve single filaments. For momentum transfers larger than that corresponding to the mesh size (2π/ξ), the intermediate structure factor includes contributions from the mutual fluctuations of neighboring fibers, and Eq. 4 no longer holds. It is therefore the large q asymptote that marks the true persistence length in Fig. 5 d. We thus only report averaged values of Lp for q values >22 μm−1 in Table 2.
). As noted by Kroy and Frey (44), Eq. 4 only applies to momentum transfers (q) small enough to resolve single filaments. For momentum transfers larger than that corresponding to the mesh size (2π/ξ), the intermediate structure factor includes contributions from the mutual fluctuations of neighboring fibers, and Eq. 4 no longer holds. It is therefore the large q asymptote that marks the true persistence length in Fig. 5 d. We thus only report averaged values of Lp for q values >22 μm−1 in Table 2.
TABLE 2.
Persistence length (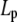 ) and bending modulus (
) and bending modulus (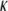 ) of CTF with and without Ca2+ as a function of CTF concentration
) of CTF with and without Ca2+ as a function of CTF concentration
|
CTF without Ca2+
|
CTF with 0.1 mM of Ca2+
|
||||
|---|---|---|---|---|---|
| Concentration (μM) |
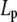 (μm) (μm)
|
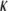 (10−27 Jm) (10−27 Jm)
|
Concentration (μM) |
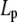 (μm) (μm)
|
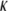 (10−27 Jm) (10−27 Jm)
|
| 1.18 | 1.11 ± 0.04 | 4.6 ± 0.2 | 0.91 | - | - |
| 2.36 | 1.6 ± 0.1 | 6.6 ± 0.4 | 1.82 | 2.4 ± 0.2 | 9.9 ± 0.8 |
| 4.76 | 1.98 ± 0.07 | 8.2 ± 0.3 | 3.66 | 2.6 ± 0.2 | 10.7 ± 0.8 |
| 9.53 | 3.1 ± 0.2 | 12.8 ± 0.8 | 7.33 | 2.9 ± 0.2 | 11.9 ± 0.8 |
| 14.3 | 3.8 ± 0.2 | 15.6 ± 0.8 | 11 | 4.5 ± 0.1 | 18.5 ± 0.4 |
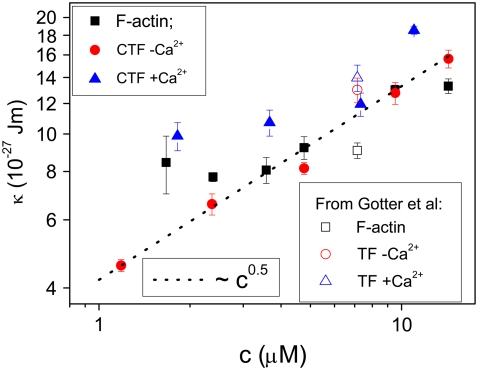
We compared the above results with those presented by Götter et al. (7) on reconstituted thin filaments. They investigated the effects of the tropomyosin/troponin complex on the stiffness of synthetic actin filaments (with and without Ca2+) using dynamic light scattering. They reconstructed the thin filaments by mixing the three separate components (all extracted from rabbit muscles) at a molar ratio of actin/tropomyosin/troponin equal to 7:1:1. On the basis of their DLS results, Gotter et al. (7) concluded that in the presence of Ca2+, Tm/Tn causes an increase of the bending modulus of F-actin by ∼50%. For comparison, Fig. 6 shows the bending moduli versus concentration of the CTF and actin systems we investigated combined with the averages over the scattering vector (q) of the Gotter et al. data obtained for a single concentration.
FIGURE 6.
Bending modulus (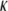 ) versus concentration for synthetic F-actin and CTF solutions with and without Ca2+ (solid symbols), and for F-actin and reconstituted thin-filament solutions with and without Ca2+ (open symbols), with values adapted from the literature (7). The dotted line is a guide for the gradient.
) versus concentration for synthetic F-actin and CTF solutions with and without Ca2+ (solid symbols), and for F-actin and reconstituted thin-filament solutions with and without Ca2+ (open symbols), with values adapted from the literature (7). The dotted line is a guide for the gradient.
Good agreement between our measurements and those obtained by Gotter et al. (7) is seen in Fig. 6 for the magnitude of the bending modulus (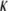 ), but it is equally clear that measurements performed at just one concentration may not discriminate between slightly different values of the bending modulus. Over the range of concentrations explored, the stiffness of the CTF in the presence of Ca2+ is slightly greater than that in the absence of Ca2+, especially at low concentrations. The CTF stiffness values in the absence of Ca2+ are almost equal to those of pure F-actin in the same buffer conditions. The small differences between the CTF bending modulus values in the presence and absence of Ca2+, and the invariance of the contour length distribution, are consistent with the inability of the microrheology measurements to detect any differences between the two solutions. In Fig. 6, the dotted line represents a proposed power law scaling to characterize the concentration functionality of the bending modulus (κ ∼ c0.5), which as yet does not have a theoretical prediction (it is, however, inversely proportional to the hydrodynamic screening length (ξh), since ξh ∼ c−0.5).
), but it is equally clear that measurements performed at just one concentration may not discriminate between slightly different values of the bending modulus. Over the range of concentrations explored, the stiffness of the CTF in the presence of Ca2+ is slightly greater than that in the absence of Ca2+, especially at low concentrations. The CTF stiffness values in the absence of Ca2+ are almost equal to those of pure F-actin in the same buffer conditions. The small differences between the CTF bending modulus values in the presence and absence of Ca2+, and the invariance of the contour length distribution, are consistent with the inability of the microrheology measurements to detect any differences between the two solutions. In Fig. 6, the dotted line represents a proposed power law scaling to characterize the concentration functionality of the bending modulus (κ ∼ c0.5), which as yet does not have a theoretical prediction (it is, however, inversely proportional to the hydrodynamic screening length (ξh), since ξh ∼ c−0.5).
CONCLUSIONS
Intact cardiac thin filaments are found to self-assemble in vitro with a bell-shaped distribution of their contour lengths, which is due to an annealing process. Changes in the cardiac thin filament induced by the presence or absence of Ca2+ have been investigated and identified using three different techniques: TEM, PTM, and DLS. TEM revealed that the troponin (Tn) complex changes conformation in the presence or absence of Ca2+, consistent with the structural model proposed by Takeda et al. (28). PTM measurements were made over a wide range of cardiac thin filament concentrations from 0.026 to 26 μM. The dynamics of the filaments were examined within the framework of modern theories for semiflexible/rodlike dynamics, and intermediate behavior was found to depend on the timescale probed. At high concentrations and slow timescales, the viscoelasticity is in good agreement with the Doi and Edwards predictions for concentrated solutions of rodlike polymers (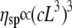 ). However, at fast times with DLS measurements, the Kroy and Frey model (44) for semiflexible polymer dynamics was required, and it allowed us to determine both the diameter (d ≈ 9.9 nm and d ≅ 9.72 nm with and without Ca2+, respectively) and the bending modulus (
). However, at fast times with DLS measurements, the Kroy and Frey model (44) for semiflexible polymer dynamics was required, and it allowed us to determine both the diameter (d ≈ 9.9 nm and d ≅ 9.72 nm with and without Ca2+, respectively) and the bending modulus (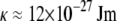 at
at 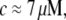 with or without Ca2+) of the cardiac thin filaments from their transverse fluctuations. Both the parameters are in good agreement with the literature values for synthetic filaments (d ≈ 10 nm (46) and
with or without Ca2+) of the cardiac thin filaments from their transverse fluctuations. Both the parameters are in good agreement with the literature values for synthetic filaments (d ≈ 10 nm (46) and 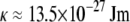 at
at 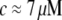 (6)) and TEM measurements, but significant changes in the bending modulus are detected as a function of concentration and the presence of Ca2+. A ω3/4 dependence observed in the linear shear viscoelasticity of the CTF solutions is thought to be due to flexural fluctuations of the semiflexible filaments (6).
(6)) and TEM measurements, but significant changes in the bending modulus are detected as a function of concentration and the presence of Ca2+. A ω3/4 dependence observed in the linear shear viscoelasticity of the CTF solutions is thought to be due to flexural fluctuations of the semiflexible filaments (6).
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Acknowledgments
We thank Dr. Tanniemola Liverpool for useful discussions. The cardiac thin filaments were a kind gift from Dr. Howard White (Eastern Virginia Medical School, Norfolk, VA).
Editor: Shin'ichi Ishiwata.
References
- 1.Howard, J. 2001. Mechanics of Motor Proteins and the Cytoskeleton. Sinauer, Sunderland, MA.
- 2.Ebashi, S., and M. Endo. 1968. Calcium ion and muscle contraction. Prog. Biophys. Mol. Biol. 18:123–183. [DOI] [PubMed] [Google Scholar]
- 3.Ebashi, S., M. Endo, and I. Otsuki. 1969. Control of muscle contraction. Q. Rev. Biophys. 2:351–384. [DOI] [PubMed] [Google Scholar]
- 4.Vibert, P., R. Craig, and W. Lehman. 1997. Steric model for activation of muscle thin filaments. J. Mol. Biol. 266:8–14. [DOI] [PubMed] [Google Scholar]
- 5.Fujita, H., K. Yasuda, S. Niitsu, T. Funatsu, and S. Ishiwata. 1996. Structural and functional reconstitution of thin filaments in the contractile apparatus of cardiac muscle. Biophys. J. 71:2307–2318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.MacKintosh, F. C. 2006. Polymer-based models of cytoskeletal networks. In Cytoskeletal Mechanics: Models and Measurements. M. R. K. Mofrad and R. D. Kamm, editors. Cambridge University Press, New York. 152–170.
- 7.Gotter, R., K. Kroy, E. Frey, M. Barmann, and E. Sackmann. 1996. Dynamic light scattering from semidilute actin solutions: a study of hydrodynamic screening, filament bending stiffness, and the effect of tropomyosin/troponin-binding. Macromolecules. 29:30–36. [Google Scholar]
- 8.Hohenadl, M., T. Storz, H. Kirpal, K. Kroy, and R. Merkel. 1999. Desmin filaments studied by quasi-elastic light scattering. Biophys. J. 77:2199–2209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Allersma, M. W., F. Gittes, M. J. deCastro, R. J. Stewart, and C. F. Schmidt. 1998. Two-dimensional tracking of ncd motility by back focal plane interferometry. Biophys. J. 74:1074–1085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schnurr, B., F. Gittes, F. C. MacKintosh, and C. F. Schmidt. 1997. Determining microscopic viscoelasticity in flexible and semiflexible polymer networks from thermal fluctuations. Macromolecules. 30:7781–7792. [Google Scholar]
- 11.Liu, J., M. L. Gardel, K. Kroy, E. Frey, B. D. Hoffman, J. C. Crocker, A. R. Bausch, and D. A. Weitz. 2006. Microrheology probes length scale dependent rheology. Phys. Rev. Lett. 96:118104. [DOI] [PubMed] [Google Scholar]
- 12.Uhde, J., N. Ter-Oganessian, D. A. Pink, E. Sackmann, and A. Boulbitch. 2005. Viscoelasticity of entangled actin networks studied by long-pulse magnetic bead microrheometry. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 72:061916. [DOI] [PubMed] [Google Scholar]
- 13.Palmer, A., T. G. Mason, J. Y. Xu, S. C. Kuo, and D. Wirtz. 1999. Diffusing wave spectroscopy microrheology of actin filament networks. Biophys. J. 76:1063–1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schmidt, K. 1990. An Introduction to Dynamic Light Scattering. Academic Press, New York.
- 15.Cummins, H. Z., F. D. Carlson, T. J. Herbert, and G. Woods. 1969. Translational and rotational diffusion constants of tobacco mosaic virus from Rayleigh linewidths. Biophys. J. 9:518–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mason, T. G., K. Ganesan, J. H. vanZanten, D. Wirtz, and S. C. Kuo. 1997. Particle tracking microrheology of complex fluids. Phys. Rev. Lett. 79:3282–3285. [Google Scholar]
- 17.Xu, J., V. Viasnoff, and D. Wirtz. 1998. Compliance of actin filament networks measured by particle-tracking microrheology and diffusing wave spectroscopy. Rheol. Acta. 37:387–398. [Google Scholar]
- 18.Tseng, Y., and D. Wirtz. 2001. Mechanics and multiple-particle tracking microheterogeneity of α-actinin-cross-linked actin filament networks. Biophys. J. 81:1643–1656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Apgar, J., Y. Tseng, E. Fedorov, M. B. Herwig, S. C. Almo, and D. Wirtz. 2000. Multiple-particle tracking measurements of heterogeneities in solutions of actin filaments and actin bundles. Biophys. J. 79:1095–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Morse, D. C. 1998. Viscoelasticity of concentrated isotropic solutions of semiflexible polymers. 2. Linear response. Macromolecules. 31:7044–7067. [Google Scholar]
- 21.Spiess, M., M. O. Steinmetz, A. Mandinova, B. Wolpensinger, U. Aebi, and D. Atar. 1999. Isolation, electron microscopic imaging, and 3-D visualization of native cardiac thin myofilaments. J. Struct. Biol. 126:98–104. [DOI] [PubMed] [Google Scholar]
- 22.Waigh, T. A. 2005. Microrheology of complex fluids. Rep. Prog. Phys. 68:685–742. [DOI] [PubMed] [Google Scholar]
- 23.Papagiannopoulos, A., T. A. Waigh, T. Hardingham, and M. Heinrich. 2006. Solution structure and dynamics of aggrecan cartilage. Biomacromolecules. 7:2162–2172. [DOI] [PubMed] [Google Scholar]
- 24.Crocker, J. C., and E. Dufresne. 2000. Particle tracking using IDL. http://www.physics.emory.edu/∼weeks/idl/.
- 25.Mason, T. G., and D. A. Weitz. 1995. Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids. Phys. Rev. Lett. 74:1250–1253. [DOI] [PubMed] [Google Scholar]
- 26.Savin, T., and P. S. Doyle. 2005. Static and dynamic errors in particle tracking microrheology. Biophys. J. 88:623–638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Robinson, T. F., and S. Winegrad. 1979. The measurement and dynamic implications of thin filament lengths in heart muscle. J. Physiol. 286:607–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Takeda, S., A. Yamashita, K. Maeda, and Y. Maeda. 2003. Structure of the core domain of human cardiac troponin in the Ca2+ saturated form. Nature. 424:35–41. [DOI] [PubMed] [Google Scholar]
- 29.Oosawa, F., and S. Asakura. 1975. Thermodynamics of the Polymerization of Protein. Academic Press, New York.
- 30.Hill, T. L. 1980. Directed elongation model for microtubule GTP hydrolysis. Proc. Natl. Acad. Sci. USA. 77:4803–4807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kas, J., H. Strey, J. X. Tang, D. Finger, R. Ezzell, E. Sackmann, and P. A. Janmey. 1996. F-actin, a model polymer for semiflexible chains in dilute, semidilute, and liquid crystalline solutions. Biophys. J. 70:609–625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vilfan, A. 2001. The binding dynamics of tropomyosin on actin. Biophys. J. 81:3146–3155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.MacKintosh, F. C., and C. F. Schmidt. 1999. Microrheology. Curr. Opin. Colloid Interface Sci. 4:300–307. [Google Scholar]
- 34.Everaers, R., F. Julicher, A. Ajdari, and A. C. Maggs. 1999. Dynamic fluctuations of semi-flexible filaments. Phys. Rev. Lett. 82:3717–3720. [Google Scholar]
- 35.Le Goff, L., F. Amblard, and E. M. Furst. 2002. Motor-driven dynamics in actin-myosin networks. Phys. Rev. Lett. 88:0181011–0181014. [DOI] [PubMed] [Google Scholar]
- 36.Liverpool, T. B., and A. C. Maggs. 2001. Dynamic scattering from semiflexible polymers. Macromolecules. 34:6064–6073. [Google Scholar]
- 37.Edwards, S.F., and M. Doi. 1986. The Theory of Polymer Dynamics. Oxford University Press, Oxford, UK.
- 38.Xu, J., A. Palmer, and D. Wirtz. 1998. Rheology and microrheology of semiflexible polymer solutions: actin filament networks. Macromolecules. 31:6486–6492. [Google Scholar]
- 39.Hinner, B., M. Tempel, E. Sackmann, K. Kroy, and E. Frey. 1998. Entanglement, elasticity, and viscous relaxation of actin solutions. Phys. Rev. Lett. 81:2614–2617. [Google Scholar]
- 40.Bird, R. B. 1977. Dynamics of Polymeric Liquids, Vols. 1 and 2. John Wiley, Hoboken, NJ.
- 41.Yamakawa, H. 1971. Modern Theory of Polymer Solutions. Harper and Row, New York.
- 42.Cao, X. X., R. Bansil, K. R. Bhaskar, B. S. Turner, J. T. LaMont, N. Niu, and N. H. Afdhal. 1999. pH-dependent conformational change of gastric mucin leads to sol-gel transition. Biophys. J. 76:1250–1258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Berne, B. J., and R. Pecora. 2000. Dynamic Light Scattering. Dover, Mineola, NY.
- 44.Kroy, K., and E. Frey. 1996. Dynamic scattering from solutions of semiflexible polymers. Phys. Rev. E. 55:3092–3101. [Google Scholar]
- 45.Carrick, L., M. Tassieri, T. A. Waigh, A. Aggeli, N. Boden, C. Bell, J. Fisher, E. Ingham, and R. M. L. Evans. 2005. Internal dynamic modes of charged self-assembled peptide fibrils. Langmuir. 21:3733–3737. [DOI] [PubMed] [Google Scholar]
- 46.Engel, A. G. 1993. Myology, Vol. 1. McGraw-Hill, New York.
- 47.Norman, A. I., R. Ivkov, J. G. Forbes, and S. C. Greer. 2005. The polymerization of actin: structural changes from small-angle neutron scattering. J. Chem. Phys. 123:154904. [DOI] [PubMed] [Google Scholar]
- 48.Pusey, P.N. W.van Megen. 1984. Detection of small polydispersities by photon correlation spectroscopy. J. Chem. Phys. 80:3513–3520. [Google Scholar]
- 49.Schmidt, M., W. Burchard, and N. C. Ford. 1978. Quasi-elastic light scattering: an experimental study of polydispersity. Macromolecules. 11:452–454. [Google Scholar]