Stochastic Severing of Actin Filaments by Actin Depolymerizing Factor/Cofilin Controls the Emergence of a Steady Dynamical Regime

Abstract

Actin dynamics (i.e., polymerization/depolymerization) powers a large number of cellular processes. However, a great deal remains to be learned to explain the rapid actin filament turnover observed in vivo. Here, we developed a minimal kinetic model that describes key details of actin filament dynamics in the presence of actin depolymerizing factor (ADF)/cofilin. We limited the molecular mechanism to 1), the spontaneous growth of filaments by polymerization of actin monomers, 2), the ageing of actin subunits in filaments, 3), the cooperative binding of ADF/cofilin to actin filament subunits, and 4), filament severing by ADF/cofilin. First, from numerical simulations and mathematical analysis, we found that the average filament length, 〈L〉, is controlled by the concentration of actin monomers (power law: 5/6) and ADF/cofilin (power law: −2/3). We also showed that the average subunit residence time inside the filament, 〈T〉, depends on the actin monomer (power law: −1/6) and ADF/cofilin (power law: −2/3) concentrations. In addition, filament length fluctuations are ∼20% of the average filament length. Moreover, ADF/cofilin fragmentation while modulating filament length keeps filaments in a high molar ratio of ATP- or ADP-P_i versus ADP-bound subunits. This latter property has a protective effect against a too high severing activity of ADF/cofilin. We propose that the activity of ADF/cofilin in vivo is under the control of an affinity gradient that builds up dynamically along growing actin filaments. Our analysis shows that ADF/cofilin regulation maintains actin filaments in a highly dynamical state compatible with the cytoskeleton dynamics observed in vivo.

INTRODUCTION

Actin filaments, a major component of the cytoskeleton, grow by polymerization of actin monomers and organize into dendritic networks or bundles in cell compartments (lamellipodia or filipodia) (1). A long-standing challenge in cell biophysics is to understand the molecular mechanisms controlling the assembly and disassembly of actin cytoskeleton, a dynamical process that generates forces and ultimately cell movement (2–4). Indeed, depending on how actin filaments are initiated by a nucleation-promoting factor (i.e., Arp2/3 complex, spire, formins), actin filaments will elongate between 11.6 μM⁻¹ s⁻¹ and 38 μM⁻¹ s⁻¹ (5–7). In the meantime, to avoid a depletion of the cellular concentration of actin monomers, actin filaments need to be rapidly recycled (8). Biomimetic systems helped to identify the minimal set of actin binding proteins that are essential to maintain this high turnover rate and induce actin-based motility (9,10). Among these proteins, actin depolymerizing factor (ADF)/cofilin stimulates actin cytoskeleton dynamics by severing actin filaments (11–13) and increasing filament turnover in vitro (14) or in biomimetic systems (9,10). Recently ADF/cofilin has been shown to control the filament length in parallel with a reduction of the subunit residence time in filaments (6). Because these new facts change our understanding of actin dynamics, we present a model for the polymerization of actin filaments in the presence of ADF/cofilin. We base our approach on accepted mechanisms for the polymerization of actin monomers and the interactions between ADF/cofilin and actin subunits in a filament.

First, we assumed that each polymerized ATP-actin subunit hydrolyzes its ATP independently in a first-order reaction that is not influenced by surrounding subunits (15). Second, ADF/cofilin accelerates phosphate dissociation (16). Third, ADF/cofilin exclusively binds to actin subunits loaded with ADP (16). Fourth, ADF/cofilin binds cooperatively to subunits in the filament (17). In addition, we assumed that ADF/cofilin severs filaments between two adjacent decorated subunits only. A recent study questioned the acceleration of depolymerization at the pointed end, showing that it is almost independent of the presence of ADF/cofilin (12). Therefore, we assumed that the pointed- and barbed-end depolymerization rates are unaffected by ADF/cofilin. Finally, we simulated the set of chemical reactions in the presence of a large excess of actin monomers, an assumption relevant to the conditions in cells and to the experimental data used to validate our approach.

We combined a stochastic molecule-based model, in which single actin monomers or subunits inside the filament and ADF/cofilin are the modeling units, and a continuous approach to analyze the statistical properties of the control exerted by ADF/cofilin on filament dynamics. The Monte Carlo simulation of the stochastic model illustrates how ADF/cofilin controls the emergence of a stable dynamical regime for actin dynamics and stimulates actin subunit turnover in filaments. Then, from the statistical distribution of filament population, we analytically determined the average filament length and the residence time of subunits in filaments, with respect to the rate constants for the reactions and the concentrations of actin monomers and ADF/cofilin. Our study offers a satisfactory and coherent understanding of the experiments in biomimetic assays (6) and presents a useful tool to analyze in vivo mechanisms for cytoskeleton dynamics, in particular its fast actin turnover.

METHODS

Model and simulation methods

Kinetic model for filament polymerization and severing

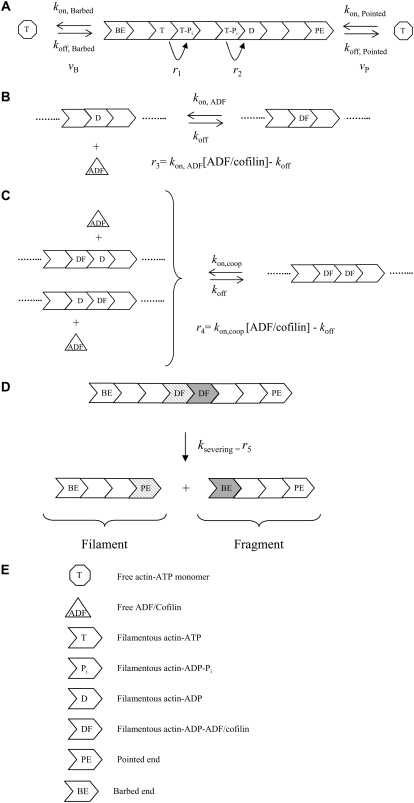
We developed a kinetic model to simulate the dynamics of polymerization of ATP-actin monomers in the presence of ADF/cofilin. Since free actin monomers and free ADF/cofilin are small molecules (respectively, 42 kD and 15 kD) that diffuse rapidly, we assumed their spatial distribution is homogeneous. In addition, we hypothesized that the compartment where reactions take place exchanges molecules with a large reservoir so that concentrations of actin monomers and free ADF/cofilin are constant. We considered polymerization of actin at both filament ends (reaction rates v_B and v_P, Fig. 1 A, Tables 1 and 2), ATP hydrolysis and inorganic phosphate release (respectively, reaction rates r₁ and r₂, Fig. 1 A, Tables 1 and 2). ATP hydrolysis and phosphate release are assumed to be independent and affect actin subunits randomly. ADF/cofilin binding to ADP-bound subunits induces the acceleration of phosphate release from surrounding ADP-P_i subunits and the cooperative binding of new ADF/cofilin molecules (16). Recently, Prochniewicz et al. (18) established that the binding of a single ADF/cofilin facilitates two distinct structural changes on actin filament that may explain ADF/cofilin effects. First, we assumed that the binding of a single ADF/cofilin to one ADP subunit accelerates the release of inorganic phosphate and enhances the production of F-ADP for the whole filament (modification of r₂, Fig. 1 A). To justify this drastic hypothesis, we investigated different models in which phosphate release acceleration is limited to the R (R is an integer) subunits on both sides of a bound ADF/cofilin. Numerical simulations proved that infinite cooperativity (i.e., a bound ADF/cofilin affects the phosphate release of the whole filament) is an excellent approximation of the filament dynamics. Second, we modeled ADF/cofilin binding to actin subunits in filaments as a two-step process. Initially, a single ADF/cofilin binds to a subunit bound to the nucleotide ADP (F-ADP) whose two neighbors are free from ADF/cofilin (reaction rate r₃, Fig. 1 B, Tables 1 and 2). Subsequently, the binding of a second ADF/cofilin to an F-ADP subunit is facilitated by the neighboring decorated subunits (reaction rate r₄, Fig. 1 C, Tables 1 and 2).

FIGURE 1.

Molecule-based stochastic model for actin filament elongation and severing. (A) Actin filament elongation by addition of actin monomers bound to ATP at filament ends. v_B and v_P are, respectively, the barbed- and pointed-end polymerization rates. We assumed that random ATP hydrolysis (rate r₁) is followed by the release of the inorganic phosphate P_i (rate r₂). (B) ADF/cofilin binds reversibly to an isolated ADP-actin subunit in the filament. (C) Cooperative binding of ADF/cofilin molecules facilitates the formation of decorated subunit pairs along one of the two actin filament strands. (D) Severing occurs between two consecutive F-ADP-ADF subunits, creating a piece containing the “old” pointed end and “new” barbed end (fragment) and a piece containing the “old” barbed end and a new pointed end (filament). (E) Code for the different symbols in A–D. The elongation and reactions rates (v_B, v_P, and r_1-5) represent molecule fluxes and are basically obtained as the product of an intrinsic reaction rate by a concentration (Tables 1 and 2).

TABLE 1.

Chemical rates constant

Chemical rate	Numerical value	Reference
kon,B	11.6 μM−1 s−1 (GATP)	(5)
koff,B	1.4 s−1 (GATP)	(5)
kon,P	1.3 μM−1 s−1 (GATP)	(5)
koff,P	0.8 s−1 (GATP) 0.27 s−1 (GADP)	(5)
kATP-hydrolysis	0.35 s−1	(15)
kPi-release	0.0019 s−1	(32)
kPi-release (in the presence of ADF/cofilin)	0.035 s−1	(16)
kon,ADF	0.0085 μM−1 s−1	(16)
koff,ADF	0.005 s−1	(16)
kcoop,ADF	0.075 μM−1 s−1	(16)
ksevering	0.012 s−1	(5,16)

GATP, ATP-loaded monomer.

GADP, ADP-loaded monomer.

TABLE 2.

Reaction rates

Variable	Reaction	Expression
vB	Elongation rate at the barbed end	kon,B[Actin]-koff,B
vP	Elongation at the pointed end	kon,P[Actin]-koff,P
v	Total elongation	v = vB + vP
r1	ATP hydrolysis	kATP-hydrolysis
r2	Phosphate release	kPi-release
r3	Binding/unbinding of ADF/cofilin to F-ADP subunits	kon,ADF[ADF/cofilin]-koff,ADF
r4	Cooperative binding/unbinding of ADF/cofilin to F-ADP subunits	kcoop,ADF[ADF/cofilin]-koff,ADF
r5	Severing	ksevering

We also assumed that filament severing occurs between two adjacent F-ADP-ADF subunits (reaction rate r₅, Fig. 1 D, Tables 1 and 2). The two new pieces generated by severing have different fates (Fig. 1 D). Because of the large amount of capping proteins in vivo (8), we assumed that the piece associated with the new barbed end (i.e., fragment, Fig. 1 D) is immediately capped and cannot elongate. Therefore, to simplify simulations and the mathematical analysis in the Appendix, the piece associated with the old barbed end, referred to as the “filament” (Fig. 1 D), remains under investigation. The other piece, associated with the old pointed end, referred to as the “fragment” (Fig. 1 D), is discarded from simulations, except in Fig. 5 B.

FIGURE 5.

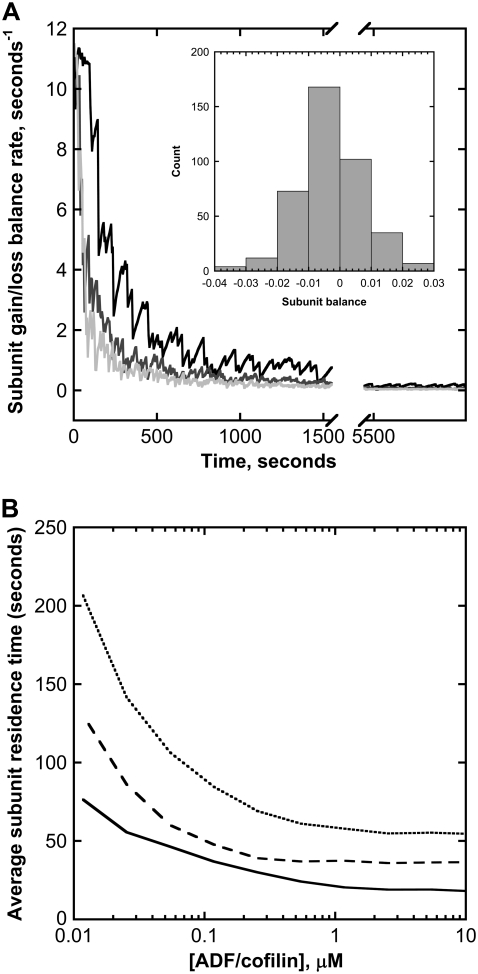
Subunit dynamics in a single filament. (A) Variation of the subunit gain/loss balance rate. After an initial transient decrease, the net balance between gain and loss of actin subunits rapidly converges to zero, regardless of the ADF/cofilin concentration used in simulations (black curve corresponds to 0.1 μM; dark and light gray are obtained with 1 and 10 μM, respectively). (Inset) Net balance fluctuation histogram determined over the last 2000 s of simulations. (B) ADF/cofilin-severing activity controls the average time spent by a subunit in actin filaments (solid black curve) and in the different fragments generated by the same filament (dashed black curve). The average duration of a life cycle (monomer to filament to monomer) is given by the dotted black curve. Parameters for simulations are listed in the legend of Fig. 2 B.

Models for actin filament dynamics predicted the existence of a diffusive length (∼30–34 monomers² s⁻¹) at the barbed end in conditions close to chemical equilibrium (19,20). This result agrees with experimental work (21,22) but represents only minor fluctuations of the filament length. Here, although we used the same set of chemical reactions, we addressed the specific role of ADF/cofilin in stimulating large filament fluctuations and fast monomer turnover.

Simulation methods

We used the Gillespie algorithm to determine the evolution of the filament and the chemical transformation of subunits (23,24). This molecule-based approach provides precise information on the dynamics of actin filaments. In particular, we could determine the spatial and temporal distribution of actin subunits along the filament, the nature (i.e., ATP, ADP-P_i, or ADP) of the nucleotide bound to the subunit, and the subunit residence time. All averaged variables (e.g., filament length or subunit residence time) were determined from the sampling of time-dependent simulations (typically, simulations during 10,000 s were sampled every 20 s). The analytical distribution of filament length and subunit residence time in filaments is presented and analyzed in the Appendix section.

RESULTS

ADF/cofilin induces large amplitude fluctuations in growing actin filaments

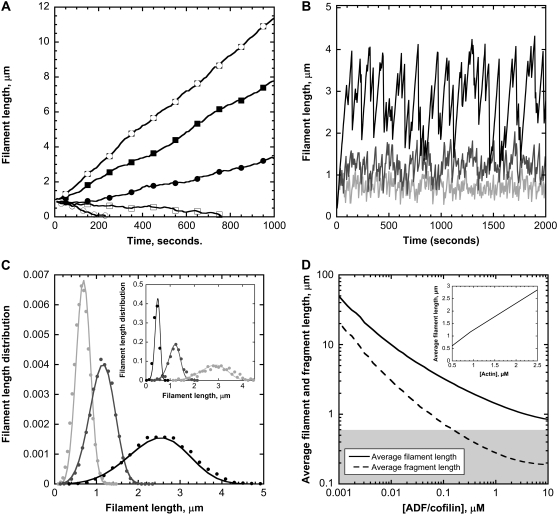
Initially, we addressed the question of how actin filament length reaches a steady dynamical regime by balancing assembly and disassembly of subunits at both ends, independent of the biochemical conditions in cells or in biomimetic assays. We investigated the key issue of actin filament length control by the severing activity of ADF/cofilin. First, we assumed a control of the length of actin filaments based only on an increase in the rate of depolymerization and in the absence of ADF/cofilin-severing activity (k_severing = 0) (Fig. 2 A). Simulations show that a steady dynamical regime is achieved for only a single value of the actin monomer concentration, somewhere between 0.8 and 0.9 μM (Fig. 2 A). For different concentrations of actin monomer, actin filaments will grow (above 0.9 μM) or shrink to zero length (below 0.8 μM). Addition of the severing activity of ADF/cofilin to this model substantially modified the behavior of actin filaments (Fig. 2 B). After an initial period of continuous growth for ∼150–300 s, actin filaments follow periods of sustained polymerization and sudden shrinkage mediated by ADF/cofilin severing (Fig. 2 B). Although the rate of polymerization of actin subunits is constant, severing prevents unrestricted filament growth and induces large-amplitude fluctuations that follow a well-defined distribution (Fig. 2 C).

FIGURE 2.

Steady-state dynamics of actin filaments. (A) Filament length time course for different actin monomer concentrations. We assumed that depolymerization at the pointed end is multiplied by a factor of up to 25 and that ADF/cofilin has no severing activity (14). The actin monomer concentrations used in the simulations are (from bottom to top) 0.63 (○), 0.71 (□), 0.81 (•), 0.92 (▪), and 1.05 () μM. (B) ADF/cofilin-mediated large amplitude fluctuations. Increasing concentrations of ADF/cofilin reduce the average filament length and the amplitude of the fluctuations. We used a single actin monomer concentration of 1 μM; no qualitative changes have been observed for different actin monomer concentrations. Black curves 0.1 μM ADF/cofilin, dark gray 1 μM ADF/cofilin, and light gray 10 μM ADF/cofilin. (C) Increasing severing activity decreases both the average and the variance of the distribution of filament length for different values of ADF/cofilin (light gray 10 μM; gray 1 μM, and black 0.1 μM) and [Actin] = 1 μM. The model prediction from the balance equation (Eq. A5, solid curve) matches the empirical distribution based on the molecule-based model (points). (Inset) Model prediction (solid curve) and empirical (points) distributions for the filament length with different concentrations of actin monomers (light gray curve 0.5 μM, gray curve 1 μM, and black curve 2 μM). The ADF/cofilin is fixed at 1 μM. (D) ADF/cofilin controls the average filament length (solid curve) and the average fragment size (dashed curve); [Actin] = 1 μM. Note that for ADF/cofilin above 0.2 μM, the fragment size is <0.5 μM, the resolution limit in light microscopy, as indicated by the shaded area. (Inset) The average filament length increases with the concentration of actin monomers. ADF/cofilin is held constant at 1 μM. Parameters for A are v_B = 11.6[Actin] s⁻¹, v_P = 1.3[Actin]-6.75 s⁻¹, r₁ = 0.3 s⁻¹, r₂ = 0.0019s⁻¹, r₃ = 0 s⁻¹, r₄ = 0 s⁻¹, and r₅ = 0 s⁻¹. Parameters for B–D are v_B = 11.6[Actin] s⁻¹, v_P = 1.3[Actin]-0.27 s⁻¹, r₁ = 0.3 s⁻¹, r₂ = 0.035 s⁻¹, r₃ = (0.0085[ADF/cofilin]-0.005) s⁻¹, r₄ = (0.075[ADF/cofilin]-0.005) s⁻¹, and r₅ = 0.012 s⁻¹.

The succession of elongation and shortening periods for actin filaments depends on the efficiency of the severing activity of ADF/cofilin (Fig. 2 B). Despite the highly irregular behavior (see Fig. 2 B), the length distribution is bell-shaped, with a marked peak sharper than in a Gaussian distribution (Fig. 2 C and Eq. A9). Conversely, the average and standard deviation of the filament length increase with the concentration of actin monomers (Fig. 2 C, inset). We derived a very simple relation between the average (respectively the standard deviation) of the filament length and the rates of reactions for the polymerization and ADF/cofilin-dependent severing (Eqs. A10, A12, and A13). Basically, the average filament length, 〈L〉 (respectively standard deviation, ), depends almost linearly on the actin monomer concentration (power law: 5/6) and is inversely proportional to the ADF/cofilin concentration (power law: −1/3):

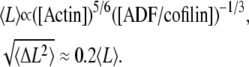This analytical result shows that the average filament length and the size of the fluctuations, determined by the standard deviation of the distribution, are reduced in the presence of a high ADF/cofilin concentration, in agreement with the numerical simulations presented in Fig. 2 C (and inset). This reduction of fluctuations is also visible in Fig. 2 B, with a marked correlation between the severing activity of ADF/cofilin and the fluctuation amplitude. The actin fragment average length (Fig. 2 D) decreases to a value below 0.5 μm for ADF/cofilin concentration above 0.2 μM. This emphasizes that high ADF/cofilin concentrations will generate actin filaments too small to be detected in light microscopy. Inversely, for a constant concentration of ADF/cofilin (1 μM) an increase in actin monomer concentration induces an almost linear increase in actin filament mean lengths (Fig. 2 D, inset, and Eq. A14).

We also analyzed models where R actin subunits (R is an integer) on both sides of a bound ADF/cofilin have their rate of phosphate release increased. In the case of finite cooperativity, the average phosphate release rate for a filament slows the transformation of F-ADP-P_i into F-ADP and the subsequent binding to ADF/cofilin. Therefore, the average filament length is increased in reference to the model with infinite cooperativity (compare black and red curves in Supplementary Material Fig. S1, inset). However, the deviation from this last model, which is maximal for R in the range 10–90 actin subunits, becomes practically undetectable for R larger than 125 subunits. Prochniewicz et al. (18) measured that the increased torsional flexibility after the binding of a single ADF/cofilin affects 427 ± 355 subunits, to which a parameter R in the range 40–390 corresponds in our modeling approach. Hence, because these numbers are highly variable and because model outputs are practically indistinguishable for R ≥ 125 subunits, the infinite cooperativity hypothesis is excellent; we used it throughout this study.

Chemical composition of the actin filament

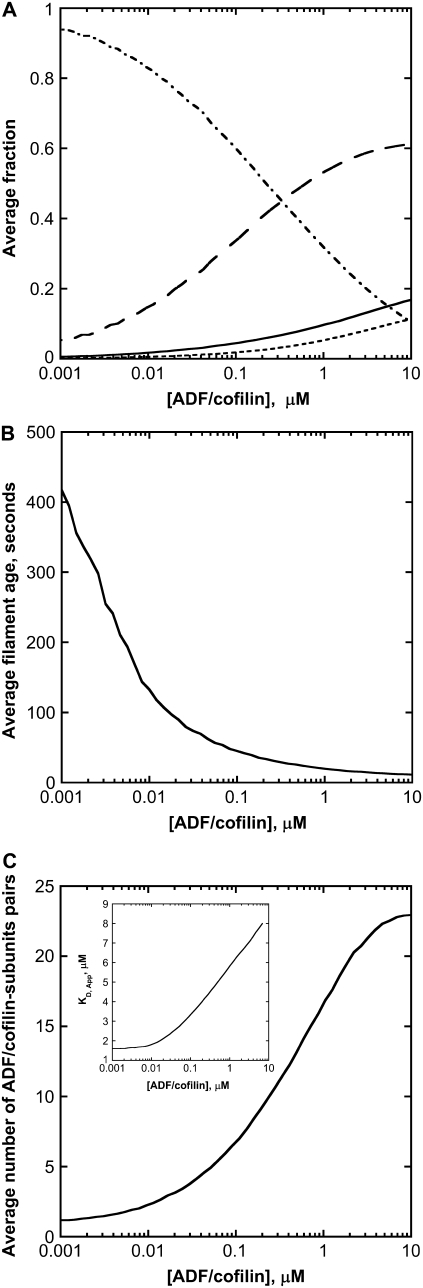
ADF/cofilin controls the emergence of a steady dynamical regime, with a well-defined average length and fluctuation amplitude (Fig. 2 C). Since ADF/cofilin preferentially binds to ADP-actin subunits, the severed fragments are principally made of subunits bound to ADP, whereas the remaining actin filament is composed of younger subunits bound to ATP or ADP-P_i. Consequently, in the steady regime, the molar fraction of the different nucleotide on a filament is highly dependent on the severing activity, as shown in Fig. 3 A. Although ATP or ADP-P_i represent only transient chemical states for the nucleotide bound to subunits (half-time lives are, respectively, 2 s and 6 min), their molar fraction in the actin filament increases regularly with ADF/cofilin concentrations (Fig. 3 A). At ADF/cofilin concentrations above 0.1 μM, ATP/ADP-P_i-bound subunits represent >50% of the total subunits in a filament (Fig. 3 A). Conversely, most of ADP-bound subunits are removed from the filament by severing, and their molar fraction drops to only 20% for ADF/cofilin above 1 μM (Fig. 3 A). Therefore, ADF/cofilin directly controls the age of the filament by removing subunits bound to ADP (Fig. 3 B).

FIGURE 3.

Chemical composition of actin filaments at steady state. (A) ADF/cofilin concentration controls the molar fraction of the nucleotide bound to subunits in filament: F-ATP (solid thick curve), F-ADP-P_i (long dashed curve), F-ADP (dot-dashed curve), and F-ADP-ADF/cofilin (dotted curve). The removal of a large piece made of F-ADP subunits favors the molar ratio ATP or ADP-P_i versus ADP and ADP-ADF/cofilin-bound subunits. (B) The age of the filament decreases with ADF/cofilin activity. The age of a particular subunit in an actin filament at time t is the time spent by this subunit since its polymerization in the filament before time t. The filament age is determined by averaging the subunit ages in a filament. (C) The number of ADF/cofilin decorated subunit pairs depends on the ADF/cofilin concentration. The number of ADF/cofilin-decorated subunit pairs is a sigmoidal function of the ADF/cofilin concentration, which plateaus at high ADF/cofilin level. (Inset) Variation of the apparent dissociation equilibrium constant, K_D,App for the binding of ADF/cofilin to actin filaments. For concentrations of ADF/cofilin below 0.01 μM, the K_D,App is low and almost constant. Because high ADF/cofilin levels favor low F-ADP molar ratio in filaments, K_D,App increases linearly with ADF/cofilin concentration. At concentrations of ADF/cofilin higher than 50 μM, K_D,App plateaus at a value of 20 μM (data not shown). Parameters for simulations are listed in the legend of Fig. 2 B.

Although the ADF/cofilin concentration used in the simulations lies in the range 0.001–10 μM, the number of decorated pairs remains globally low and plateaus at ∼25 pairs per filament (Fig. 3 C), which represents only a small percentage of the total number of actin subunits. To measure the apparent drop of binding efficacy of ADF/cofilin, we defined an apparent “dissociation equilibrium constant” of cofilin bound to actin filament by

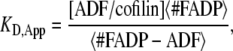where 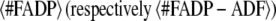is the average number of actin subunits bound to ADP in the filament (respectively the average number of ADF/cofilin molecules bound to the actin filament). Simulations demonstrated that K_D,App increases with the concentration of free ADF/cofilin (Fig. 3 C, inset). This apparent dissociation equilibrium constant remained low at ADF/cofilin concentrations below 0.1 μM. For ADF/cofilin concentration in the range 0.1–10 μM, the K_D,App increased, implying a drop in the available binding sites for ADF/cofilin on the filament.

To test the role of subunit ageing, we determined the average spatial distribution of actin subunits, given the state of the associated nucleotide (ATP, ADP-P_i, or ADP, Figs. S2 and S3). It turns out that a long simulation (10,000 s) is sufficient for the spatial distribution of actin subunit to stabilize, except large fluctuations at the pointed end (Fig. S2). Using the time-dependent solution of the system of Eq. A2, which expresses the time course of the chemical transformation of the nucleotide, and from the conversion between time and space 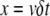where x is the position of an actin subunit incorporated into the filament t ago (δ and ν are, respectively, the size of an actin subunit and the polymerization rate), we can match the time-dependent curves (Fig. S3) with the spatial distribution obtained from a long run of the stochastic model (Fig. S2). This result suggests that chemical transformation of ATP into ADP-P_i and ADP, and the subsequent binding of ADF/cofilin to F-ADP subunits, provides the timer necessary to control the elongation/severing cycle.

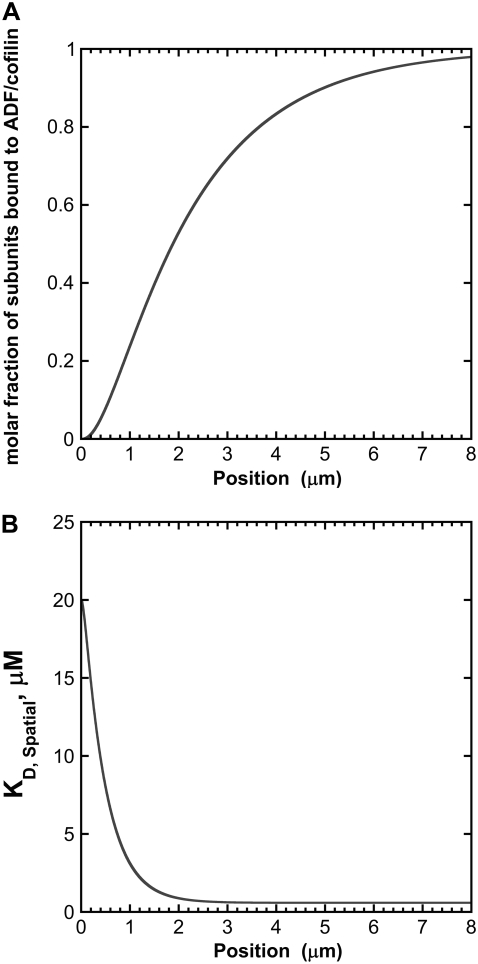
To further investigate the effect of subunit ageing on the binding of ADF/cofilin along growing actin filaments, we analyzed the fraction of subunits bound to ADF/cofilin and the spatial variation of the local dissociation constant of the actin subunit-ADF/cofilin complex formation, denoted K_D,Spatial as a function of the position along the actin filament (Fig. 4). (Note that K_D,App is the average of the dissociation constant determined from the whole filament, discarding the information coming from the spatial position of actin subunits with respect to the barbed end.) The 0 intercept with the x and y axes corresponds to the position of the growing barbed end where actin subunits are always in the ATP-bound state (Fig. 4 A). At this position, K_D,Spatial is ∼20 μM (Fig. 4 B) and the molar fraction of bound ADF/cofilin is nearly 0 (Fig. 4 A). K_D,Spatial decreases sharply to reach the value of the actual dissociation constant of ADF/cofilin for ADP-bound actin filaments (Fig. 4 B) at 2 μm from the growing barbed end, corresponding to a molar fraction of bound ADF/cofilin of ∼1 (Fig. 4 A).

FIGURE 4.

Effect of the ageing of actin filament on the binding of ADF/cofilin. (A) The binding of ADF/cofilin to ADP-bound actin subunits increases with the distance to the growing barbed end, symbolized by the x, y axis 0 position. We assumed a constant level (time and space) for the actin monomer concentration ([Actin] = 1 μM) and ADF/cofilin ([ADF/cofilin] = 1 μM). We simulated Eq. A2 with r₁ = 0.3 s⁻¹, r₂ = 0.035 s⁻¹, r₃ = 0.0085[ADF/cofilin]-0.005 s⁻¹, r₄ = 0.075[ADF/cofilin]-0.005 s⁻¹, and r₅ = 0.012 s⁻¹. Note that the spatial distribution was obtained by converting time into space (Eq. A4). The growing barbed end is assumed to be at position 0. (B) ADF/cofilin-actin subunit dissociation constant at steady state. From the spatial distribution of the different nucleotide states bound to actin subunit (ATP, ADP-P_i, or ADP) found by solving Eq. A2 (the simulation parameters are given in A), we determined the local apparent dissociation constant of the complex ADF/cofilin-actin subunit given by 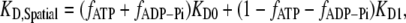where K_D0 (respectively K_D1) is the dissociation constant of the complex ADF/cofilin with F-ATP and F-ADP-P_i (respectively with actin ADP). K_D0 = 20 μM and K_D1 = 0.58μM (16); f_ATP, f_ADP-Pi are, respectively, the average fraction of actin subunits bound to ATP, with ADP-P_i at position x from the barbed end.

Residence time of actin subunits in the actin filament

We next examined the role of ADF/cofilin on the time spent by subunits in the filament and on the global turnover of actin monomers. The restricted filament length variation, as shown in Fig. 2 B, suggests that gain and loss of actin subunits should be balanced over long periods. To further test this assumption, we plotted the net balance of actin subunits in the filament (i.e., the difference between the rates of addition and loss of actin monomers) for three ADF/cofilin concentrations (Fig. 5 A).

After the first initial transient phase, due to the lag between actin filament elongation and ATP hydrolysis of subunits (Fig. 5 A), the balance between subunit gains and losses presents zero-centered fluctuations (Fig. 5 A and inset) indicating that, on average, the number of subunits in the filament will practically remain constant. Note that the actin subunit loss includes contributions from actin monomer depolymerization at both ends and the sudden removal of a large amount of subunits in the case of filament severing. In the simulations, this latter phenomenon represented ∼80% of the total subunit loss (Fig. S4).

The dynamics of actin filament length regulation directly affects the residence time of actin subunits in the filament. We analyzed the average time spent by a particular subunit in the filament, between its incorporation and its release, either by depolymerization or by severing (Fig. 5 B). ADF/cofilin drastically reduces this average time at concentrations below 1 μM. However, further reductions are hardly seen for concentrations above 1 μM, and the minimal average time remains ∼25 s. Both ADF/cofilin and actin monomer control the average residence time negatively (Supplementary Material Figs. S5 and S6), in agreement with the analytical distribution (Eqs. A6 and A7; compare also Figs. 2 C and S5). In addition, note that actin concentration increases the average length (Fig. 2 C, inset) whereas it has an opposite effect on the subunit residence time (Fig. S6).

To address the question of the global turnover of a monomer, we also determined the residence time of one subunit in the fragments obtained after filament severing. Assuming that fragments are immediately capped, as in vivo, the time spent by a particular subunit in the successive fragments is about twice the time spent in the filament (Fig. 5 B, dashed curve). Finally, we also determined the average actin monomer life cycle duration (i.e., from monomer to filament to monomer). As shown by the dotted curve in Fig. 5 B, the total time spent is substantially reduced (down to ∼50 s) in the presence of high ADF/cofilin concentrations, above 1 μM, and the global monomer turnover is accelerated by a factor of >100, when compared to the situation without cofilin (data not shown).

Fragments generated by ADF/cofilin severing

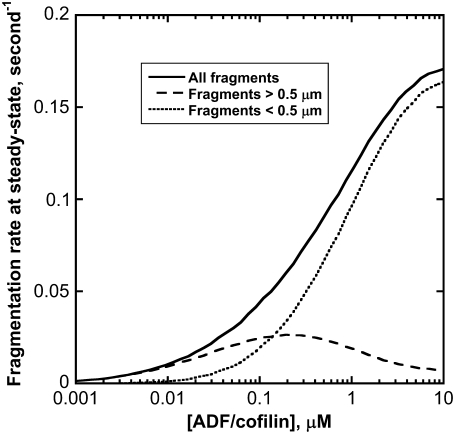
The severing of filaments produces fragments of different sizes. To analyze the fragmentation process, we determined the distribution of the fragment lengths generated from a single filament (Fig. S7). Although ADF/cofilin favors filament severing, the proportion of large filaments, above 0.5 μm, diminishes abruptly with the severing activity (compare red, blue, and black curves in Fig. S7). This observation suggests that most of the severing activity above 1 μM ADF/cofilin will be undetectable by light microscopy. This conclusion is valid over four orders of magnitude for the ADF/cofilin concentration and is consistent with the statistical distribution of filaments (Fig. 2 C). At steady state, the fragmentation rate increased with the severing activity before plateauing at high ADF/cofilin concentration (Fig. 6, solid curve). If we considered fragments larger than 0.5 μm only (that are observable experimentally by light microscopy), the apparent fragmentation rate is optimal for [ADF/cofilin] of ∼0.2 μM (Fig. 6, dashed curve). However, fragments <0.5 μm are preferentially produced at higher concentrations of ADF/cofilin (Fig. 6, dotted curve; see also Fig. S7).

FIGURE 6.

ADF/cofilin severing at steady state. The production of new actin filament increases with ADF/cofilin activity (solid black curve). Large filaments, above 0.5 μm, are optimally produced for low severing activity (dashed black curve); conversely, pieces below 0.5 μm are predominant at large ADF/cofilin concentration (dotted black curve). Parameters for simulations are listed in the legend of Fig. 2 B.

DISCUSSION

Dynamic organization of actin filaments into highly ordered arrays (actin cables or a dendritic network) that produce the forces necessary to deform or move cells requires a coordination of actin-binding protein activity together with the transduction of chemical energy into force (1). Recently a biomimetic system, comprising a minimal set of actin-interacting proteins (including formin, ADF/cofilin, and profilin), was able to reproduce actin filament dynamics at a rate compatible with in vivo actin filament turnover (6). This study demonstrated that ADF/cofilin was the only actin-binding protein necessary to rapidly disassemble growing actin filaments generated by an actin-promoting factor from the formin family. Here, we developed a kinetic model for the control of ADF/cofilin on single actin filament dynamics. We showed that ADF/cofilin regulates the actin filament length (Fig. 2), resembling the fast elongation periods followed by abrupt shrinkage events observed in biomimetic assays (6). Model simulations (Fig. 2) and mathematical analysis (Appendix) suggest that the conjunction of the ageing of subunits in the actin filament and the binding of ADF/cofilin to actin subunits loaded with ADP followed by severing are essential for actin filament dynamics. Under these conditions, actin filament length distribution reaches a stable stationary regime. This is an emergent property of the actin system that constitutes a building block for future investigations of the ADF/cofilin-driven control over actin dynamics in more complex systems, both experimentally and in modeling approaches.

Filaments are in a stable dynamical regime that is independent from the chemical conditions

The presence of actin-interacting proteins produces different biochemical conditions that can affect actin filament polymerization quite dramatically. Therefore, we addressed whether a stable regime for actin dynamics (i.e., a balance between assembly and disassembly) is possible, whatever the biochemical conditions in cells or in biomimetic assays. In the presence of ADF/cofilin, simulations suggest that filament length and chemical composition, though highly variable, have a perfectly defined average and standard deviation (Eqs. A10–A12). Additionally, both the average and the amplitude of actin filament length fluctuations depend on the actin monomer or ADF/cofilin concentrations only, with a constant fluctuation/average ratio (∼20%, Eq. A13). The existence of a stable dynamical regime, as shown in Fig. 2, implies that the contribution of actin filament elongation is balanced by subunit loss (combining depolymerization and severing). The match between gain and loss of actin subunits emerges from the combination of constant ageing of actin subunits in the filament and from the specific higher affinity for binding of ADF/cofilin to F-ADP subunits (16). Since only a few ADF/cofilin-actin subunit pairs are necessary to fragment an actin filament, the balance between gain and loss of subunits becomes almost independent of the actual ADF/cofilin concentration, except at very low ADF/cofilin (∼0.1 nM). This resolves the apparent contradiction between the drop of the apparent binding affinity of ADF/cofilin at large concentration (Fig. 3 C, inset) and the severing efficacy illustrated in Figs. 2 B and 5 B.

This result has important consequences for in vivo or in vitro conditions, where nonequilibrium conditions often prevail. A previous report (6) and this study highlight that a stable dynamical regime is achieved for a whole set of ADF/cofilin and actin monomers (Fig. 2, C and D). This is possible because ADF/cofilin cannot bind to F-ATP or F-ADP-P_i actin subunits (16) and, consequently, the filament region close to the elongated barbed end is never severed. This has the further consequence of preventing total disassembly of a filament at its growing end due to ADF/cofilin activity that is too high.

Subunit residence time in filaments and global turnover of actin monomers

By severing the oldest part of the filament, ADF/cofilin largely contributes to the active turnover of subunits (Fig. 5 B), simultaneously enriching the molar ratio of the remaining actin filament with subunits bound to ATP or ADP-P_i (Fig. 3 A). Experiments (6) and simulations prove that the maximal efficiency of ADF/cofilin is obtained at concentrations below 1 μM, in agreement with the evolution of K_D,App.

We also investigated the dynamics of fragments, assuming that they were immediately capped by capping proteins before further severing by ADF/cofilin. We found that the average subunit residence time in such daughter fragments, originating from the same mother filament, happens to be twice the average time spent in the mother filament (Fig. 5 B). Similarly, we examined the global monomer turnover by looking at the time spent by a particular monomer throughout its complete life cycle. All residence times decrease rapidly at low ADF/cofilin level (below 1 μM, Fig. 5 B), whereas further time reduction is hardly seen at concentrations above 1 μM, in agreement with experimental data (see Fig. 3 E in Michelot et al. (6)). This is a consequence of the protection provided by the F-ATP and F-ADP-P_i population of subunits against severing. The residual turnover observed at large ADF/cofilin concentrations represents the time delay necessary for ATP hydrolysis and phosphate release (Figs. S2 and S3). More interestingly, Fig. 5 B gives the correct order of magnitude for actin filament turnover (∼50 s) in vivo (3) or in biomimetic assays (9). As suggested by the model and in conjunction with experimental data, ADF/cofilin-driven filament fragmentation is likely the most important factor that determines actin turnover through the acceleration of the monomer life cycle in filaments and/or fragments.

Nucleation of new filaments and inhibition of severing

Each fragment generated by severing is a potential seed for the generation of a new actin filament (Fig. 6), unless rapidly capped with capping protein. To reconcile this model-driven analysis with recent results showing that ADF/cofilin severs filaments, with optimal activity ∼0.01 μM (whereas higher levels, above 0.1 μM, stabilize the filaments (12,25,26)), one has to consider the initial composition of the actin filament. All previous studies use F-ADP actin filaments, which become decorated on each subunit very rapidly in the presence of excess ADF/cofilin. This rapid and huge change of the composition stabilizes the filament and prevents its severing. In our model, we started from short filaments made of ATP-bound subunits which become decorated by ADF/cofilin after the hydrolysis and the release of the γ-phosphate bound to the nucleotide. However, since ADF/cofilin-decorated subunits are scattered, severing occurs before the complete stabilization of the structure, giving rise to a new filament made of ATP or ADP-P_i-bound subunits. Therefore, the initial composition keeps the severing of growing actin filaments on, avoiding the stabilization of growing actin filaments at high ADF/cofilin concentration.

Apparent non-mass-action kinetics

Most of the parameters analyzed so far (average filament length, subunit residence time, fraction of bound ADF/cofilin to filaments, or apparent equilibrium dissociation constant of ADF/cofilin for growing actin filaments) show a marked drop at high ADF/cofilin concentration (Figs. 2 D, 3 B, 4, and 5 B). Although the binding of ADF/cofilin to actin subunits has a constant affinity (Table 1), the apparent equilibrium dissociation constant, K_D,App, increases from 1.66 μM at very low ADF/cofilin concentrations to 8 μM at 10 μM of ADF/cofilin (Fig. 3 C, inset). At low ADF/cofilin activity, long and aged filaments (most of the subunits are bound to ADP, Fig. 3 A) offer a large number of binding sites, hence the low value for K_D,App. Conversely, if severing activity is high, actin filaments are short and subunits are predominantly bound to ATP or ADP-P_i (Fig. 3 A). As a consequence, the number of potential binding sites for ADF/cofilin is low, resulting in a low apparent affinity of ADF/cofilin for actin filaments.

Extension of the model to in vivo situations

This numerical study documents quantitatively the role of ADF/cofilin severing on actin filament turnover and predicts that growing filaments reach a stable dynamical regime, independent from the concentration of the different factors modulating the reaction rates (formin, profilin, ADF/cofilin) or the concentration of available actin monomers ready to polymerize. This may explain how different cell types or organisms use the same battery of proteins (i.e., formin, profilin, ADF/cofilin) with similar but fluctuating activities and concentrations to control actin filaments length, chemical composition, and turnover.

In addition, we proposed that the activity of ADF/cofilin in vivo is modulated by a gradient of spatial affinity. At the growing barbed end of actin filaments, which is likely located near a membrane structure, the high apparent dissociation equilibrium constant K_D,Spatial limits ADF/cofilin activity. As we moved along the growing actin filament from the barbed end to the pointed end, the K_D,Spatial decreased progressively to reach a low value ∼2 μm away from the growing barbed end (Fig. 4, A and B). Therefore, the molar ratio of ADF/cofilin along growing actin filaments derived from our analysis (Fig. 4 A) is an effective way to predict the number of available sites for the fixation of ADF/cofilin. This predicted gradient of ADF/cofilin binding sites based on the variation of K_D,Spatial agrees with the observed localization of ADF/cofilin activity in vivo (27,28).

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

APPENDIX

Distribution of filament length and subunit residence time

Model variables and parameters

Parameter or variable	Dimension	Definition
x	L	Monomer position along the filament (origin at the barbed end)
t	T	Time
L	L	Filament length
T	T	Subunit residence time in a filament
[Actin]	μM	Concentration of actin monomers (assumed constant and homogeneous)
[ADF/cofilin]	μM	Concentration of ADF/cofilin (assumed constant and homogeneous)
F(L)	L−1	Distribution of filaments of length L
G(T)	T−1	Distribution of subunits of age T in the filament
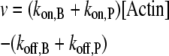	T−1	Global (de)polymerization rate
δ	L	Step change in filament length associated with polymerization of one monomer
r1	T−1	Pi dissociation rate (F-ATP to F-ADP-Pi)
r2	T−1	Pi release rate (F-ADP-Pi to F-ADP)
r3	T−1	Fixation rate of the first ADF/cofilin molecule on F-ADP
r4	T−1	Cooperative-fixation rate of the second ADF/cofilin molecule on F-ADP-ADF
r5	T−1	Severing rate of F-ADP-(ADF)2
P(L)	L−1	Filament-severing probability at a distance L from position x = 0 (position of the filament barbed end)

Modeling hypothesis and equation

We combined the contribution of both barbed and pointed ends to filament dynamics into a unique term, denoted v:

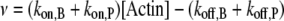Note that v can be modulated by actin-binding proteins or the concentration of available actin monomers. For example, in the presence of profilin, the polymerization at the pointed end vanishes (i.e., 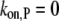); another simplification occurs if we consider formin-driven polymerization, for which one has 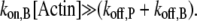Here, we assume that a), free actin monomers are continuously supplied to the reaction system, and b), the polymerization rate at the pointed end is negligible.

Let x be the position of a subunit along the filament. By convention, the barbed end is at x = 0 so that the position of a subunit in the filament also indicates the distance it traveled since its addition to the filament at the barbed end. The number of filaments of length L at time t, denoted F(L,t), is the solution of an integrodifferential equation (29):

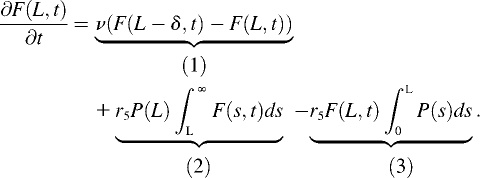The first term (1) represents filament elongation (or shortening, if v < 0) by monomer addition at the filament barbed end (x = 0). The second term (2) represents the fragmentation by severing the filament at position L. The last term (3) gives the removal of a filament of length L by cutting anywhere between x = 0 and L. Because of the modification of the nucleotide bound to actin subunits (due to ATP hydrolysis and phosphate release), the function P changes in time. However, Monte Carlo simulations showed that the spatial distribution of subunit types along the filament is rapidly achieved at steady state (see Supplementary Material Fig. S2); hence, we are justified in using a time-independent expression for P.

Since a typical filament length, L, is much larger than δ, one uses the Taylor expansion of the first term to obtain

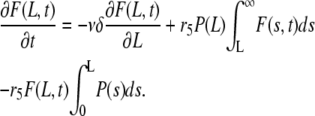At steady state, we have

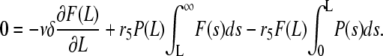Introducing an auxiliary variable 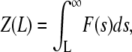the final equation reads

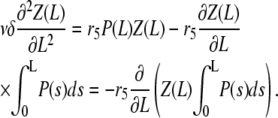By direct integration, and using the conditions 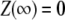and 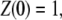one gets

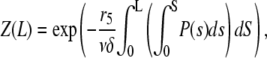from which we obtain the number of filaments of length L at steady state

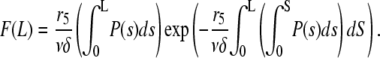(A1)

This result is analogous to Eq. 8 in Edelstein-Keshet and Ermentrout (29).

Model for the severing probability function P

Let

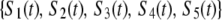be the probability distribution that a given subunit is in one of the states listed below

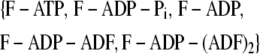at time t, given that it entered the filament, as F-ATP, at time t = 0. Note that the cooperative binding of a second ADF/cofilin molecule is coded into the state F-ADP-(ADF)₂, which actually represents pairs of actin subunits decorated by ADF/cofilin. Because of probability conservation

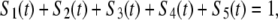we are left with a system of four linear differential equations

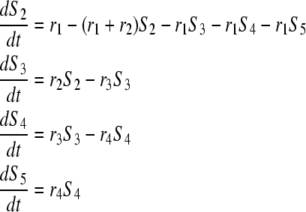(A2)

with initial conditions

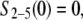and 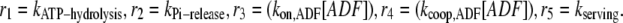Note that in Eq. A2, we neglect ADF/cofilin dissociation from actin filaments. The probability that a subunit is in the state F-ADP-ADF₂ at time t is obtained as the solution of Eq. A2:

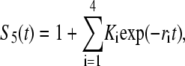(A3)

with

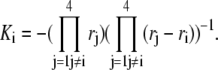To determine the severing probability, P, we need a connection between the actin subunit age, t, and its position in the filament, x. If we neglect stochastic fluctuations of the actual (de)polymerization rate, the distance travelled by an actin subunit during time t is

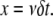(A4)

In consequence, the probability that a filament is severed in the interval [x,x+δ] is

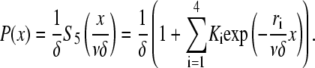The prefactor δ⁻¹ ensures normalization so that P is the probability density for severing. Using this expression for P and Eq. A1, the steady-state distribution for filament length reads

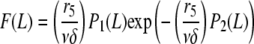(A5)

with

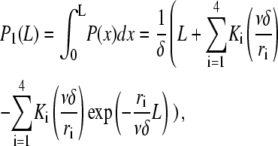and

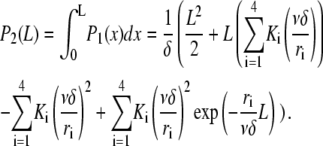Distribution of monomer lifetime in filaments

To gain further insight into the distribution of filament age or subunit residence time in filament, we look at the subunit loss after severing. We changed the previous analysis slightly and used a different set of differential equations, including 1), the polymerization step, v (first equation), and 2), the outflow after severing (last equation, variable S₆(t))

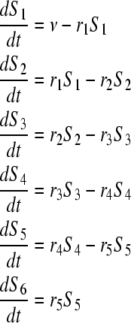(A6)

The other variables or parameters are those of Eq. A2. The probability that a monomer incorporated at time t = 0 (as F-ATP) leaves the filament at time T > 0

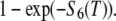where S₆(T) represents the probability that a subunit is severed from the filament at time T. The distribution of the residence time of a single subunit in the filament is obtained by differentiating the above expression with respect to T

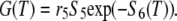(A7)

Average and variance of the filament length at low reaction rates

From Eqs. A5 or A7, one can obtain the average and variance of the filament length or subunit residence time. Unfortunately, no closed expression for these parameters is possible in the general case. However, in the limit of large polymerization rate, i.e., if

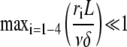(A8)

holds, the Taylor expansion of P (Eq. A5) reads

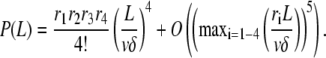Therefore, we get the filament length distribution

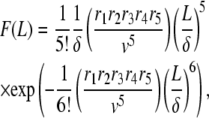(A9)

to which corresponds an average filament length

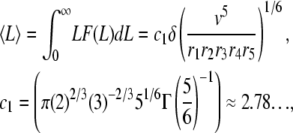(A10)

and variance

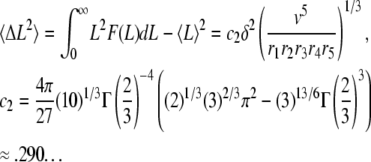(A11)

Using Eq. A7, and the condition (Eq. A8) to simplify the expression of S₆(t) in Eq. A6, we get the average and variance of the subunit residence time:

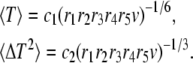(A12)

where c₁ and c₂ are given by Eqs. A10 and A11.

Equations A9–A12 have important consequences that characterize the dynamics of actin filaments subjected to ADF/cofilin severing. First, the ratio standard deviation to average length (respectively subunit residence time) is independent of the kinetic parameters r_1-5, v, or δ:

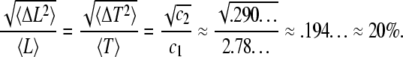(A13)

Second, the control of the average filament length by actin scales as

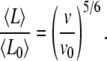where v and v₀ correspond to two different polymerization rates (e.g., two different actin monomer concentrations). In the presence of a large excess of actin monomers or rapid polymerization (e.g., with formins (30,31)), v is approximately proportional to the concentration of actin monomers. Therefore, the average filament length can be expressed directly as

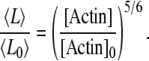(A14)

The control exerted by ADF/cofilin through rates r_3,4 gives a different scaling:

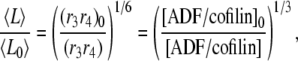(A15)

where 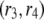and 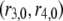are associated to two different ADF/cofilin concentrations. From Eq. A12, we see that the average residence time for a single subunit in the filament scales as

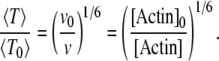(A16)

Conversely, two different levels of ADF/cofilin (at constant actin monomer concentration) give an equation similar to Eq. A15:

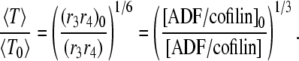(A17)