Image Correlation Spectroscopy of Multiphoton Images Correlates with Collagen Mechanical Properties

Abstract

Multiphoton microscopy (MPM) holds promise as a noninvasive imaging technique for characterizing collagen structure, and thus mechanical properties, through imaging second harmonic generation (SHG) and two-photon fluorescence in engineered and real connective tissues. Controlling polymerization pH to manipulate collagen gel microstructure, we quantified pore and fiber dimensions using both standard methods and image correlation spectroscopy (ICS) on MPM, scanning electron, and darkfield microscopy images. The latter two techniques are used to confirm microstructural measurements made from MPM images. As polymerization pH increased from 5.5 to 8.5, mean fiber diameter decreased from 3.7 ± 0.7 μm to 1.6 ± 0.3 μm, the average pore size decreased from 81.7 ± 3.7 μm² to 7.8 ± 0.4 μm², and the pore area fraction decreased from 56.8% ± 0.8% to 18.0% ± 1.3% (measured from SHG images), whereas the storage modulus G′ and loss modulus G″, components of the shear modulus, increased ∼33-fold and ∼16-fold, respectively. A characteristic length scale measured using ICS, W_ICS, correlates well with the mean fiber diameter from SHG images (R² = 0.95). Semiflexible network theory predicts a scaling relationship of the collagen gel storage modulus (G′) depending upon mesh size and fiber diameter, which are estimated from SHG images using ICS. We conclude that MPM and ICS are an effective combination to assess bulk mechanical properties of collagen hydrogels in a noninvasive, objective, and systematic fashion and may be useful for specific in vivo applications.

INTRODUCTION

Collagen plays an important role in determining gross tissue mechanical properties, imparting tensile strength and rigidity to tissues such as skin, tendon, and lung. These mechanical properties have roots in fibrillar collagen's microstructure, network organization, and orientation (1,2). For example, a tendon is more rigid axially than laterally due to collagen fiber orientation parallel to the tendon axis (3), and the volume fraction of collagen fibers in myocardium correlates with increased myocardial stiffness (4,5). Consequently, collagen fiber hyperplasia, hypertrophy, and excessive cross-linking often impair tissue function and perpetuate disease phenotypes in diabetes (6,7), keloid scarring (8,9), chronic obstructive pulmonary disease, asthma (10,11), and other diseases involving collagen dysregulation. Moreover, microstructure-dictated mechanical properties influence cell phenotype (12,13) and tumor cell migration (14,15).

Multiple researchers have exploited collagen's strong second harmonic generation (SHG)—produced when collagen's noncentrosymmetric structure interacts with a highly focused infrared laser beam to generate photons at half the laser wavelength—to assess the collagen network microstructure in engineered (16–19) and natural (20–25) tissues. A detailed and predictive understanding of the relationship between quantifiable multiphoton microscopy (MPM) image parameters and tissue mechanical properties has yet to emerge, in part because of the many microstructural parameters which affect both MPM signals and tissue mechanics, such as fiber diameter, length, cross-linking, orientation, composition, pore number density, and pore dimensions.

Collagen I hydrogels are a useful model to study the interplay between tissue microstructure and mechanical properties. In addition, tissue engineers widely use collagen hydrogels as a scaffolding biomaterial. Our lab and others have shown that collagen SHG and two-photon fluorescence (TPF) signals noninvasively yield structural and fluorescent cross-link information (18,26,27). Polymerization conditions and cell behavior can modify collagen gel microstructure and mechanical properties, and these changes may be tracked with MPM and various mechanical testing techniques. Furthermore, scaling relationships between mechanical properties such as the shear modulus with microstructural parameters such as pore size, extensively developed for actin gels (28–30), may be applied to collagen, another network-forming semiflexible biopolymer.

This study manipulates the collagen microstructure using polymerization pH then correlates mechanical properties of the collagen gels with microstructural parameters determined from MPM and image correlation spectroscopy (ICS) (31–33). Our results demonstrate that MPM and ICS are an effective means of noninvasively, objectively, and systematically assessing the mechanical properties of an in vitro extracellular matrix and may be useful for in vivo applications.

MATERIALS AND METHODS

Collagen hydrogel preparation

Collagen hydrogels were polymerized by mixing the following components in order on ice: 100 μl 10× phosphate-buffered saline (PBS; Sigma, St. Louis, MO; consisting of 0.1 M phosphate buffer, 1.38 M NaCl, and 0.027 M KCl, pH 7.4); 0.5 ml ddH₂O with sodium hydroxide added at concentrations of 0.00125 M, 0.005 M, 0.023 M, or 0.03 M, and sodium chloride added at concentrations of 0.02875 M, 0.025 M, or 0.007 M, respectively (to equalize ionic strength); and 0.4 ml 10.00 mg/ml acid-soluble rat tail tendon collagen (BD Biosciences, San Jose, CA). Final gel ionic strength was I ∼ 0.2. After vortexing the samples with three or four 1-s pulses, the collagen concentration was 4 mg/ml at pH 5.5, 6.5, 7.5, or 8.5. For MPM imaging, the collagen mixture was immediately pipetted into eight-chambered coverglasses (Fisher, Hampton, NH) at 0.1 ml/chamber and incubated for 48 h at room temperature. For rheology, the gels were polymerized directly between the rheometer's (RFSII, Rheometrics, New Castle, DE) testing plates.

Acid-soluble rat tail tendon collagen forms D-banded fibrils that are morphologically similar to fibrils in vivo (34). Acid-soluble collagen monomers are ∼1.5 nm × 300 nm and contain a central triple helical region and short (11–26 residues) nonhelical telopeptides important for fibril cross-linking and ordered assembly (34). Despite producing fibrils of similar morphology, self-assembly and in vivo assembly partially differ mechanistically: cells, enzymes such as lysyl oxidase, and other extracellular matrix components can all affect in vivo assembly. Self-assembled fibril diameter is limited to the range 10–120 nm, whereas enzyme-treated collagen and collagen in the presence of glycosaminoglycans such as dermatan sulfate in vivo can form fibrils more than 500 nm in diameter (34,35).

Scanning electron microscopy

Scanning electron microscopy (SEM) was performed on processed collagen hydrogels using a Phillips XL-30 SEM (Eindhoven, The Netherlands) with a secondary electron detector. The processing method was published previously (26). Briefly, the hydrogels were fixed with 4% formaldehyde in PBS, stained with 1% osmium tetroxide, and then dehydrated with serial water/ethanol and ethanol/hexamethyldisilazane (HMDS) soaks. The gels were cut in three pieces and allowed to dry overnight on aluminum foil so that the bottom, top, and cross section of the gel were facing up. Before imaging, the gels were sputter coated with Pd/Au to a thickness of 6 nm using a Polaron SC7620 sputter coater (Watford, UK). The specimens were imaged at 10 kV and magnifications of 2000×, 20,000×, and 100,000×. SEM images were analyzed using NIH ImageJ software (Dr. Wayne Rasband, National Institutes of Health, Bethesda, MD). Fiber diameters were hand measured from the 20,000× images using ImageJ's line-drawing feature as previously reported (26).

Multiphoton microscopy

SHG and TPF signals from collagen hydrogels were collected in the epiconfiguration using a Zeiss LSM 510 meta multiphoton microscope (Jena, Germany). A circularly polarized Mai Tai laser was tuned to 780 nm and focused on the sample with an EC Plan-Neofluar 40×/1.3 numerical aperture (NA) oil differential interference contrast objective (Zeiss). Power before the objective was ∼250 mW and ∼225 mW at the focal point. Each 12-bit image contained 512 × 512 pixels representing a 230 × 230 μm field of view. Pixel sampling rate was 625 kHz (pixel dwell time = 1.6 μs); 16 scans were averaged per image. SHG was collected with the meta detector set for wavelengths between 388 and 398 nm; TPF was collected with an infrared-blocking, 480–520 nm band-pass filter. Collagen hydrogels were imaged in eight-chambered coverglass (170 μm thick; Fisher).

Darkfield microscopy

For darkfield imaging, collagen hydrogels were homogenized with a Polytron PT 1200C homogenizer (Kinematica, Littau, Switzerland) at 15,000 rpm for 5 s, which disrupted the fiber network without destroying individual fibers. Rotor-stator gap was 360 μm. The resulting homogenate was diluted 1:10 in PBS, pipetted onto microscope slides, and covered with no. 1 borosilicate coverslips (Fisher). The homogenates were viewed on a Nikon Eclipse E800 upright microscope (Nikon, Tokyo, Japan) using a 40×, 0.75 NA PlanFluor air objective and a darkfield substage stop and imaged with a 2-megapixel Microfire digital camera (Olympus America, Center Valley, PA).

Rheology

Two rheological parameters were measured: the storage modulus, G′, and the loss modulus, G″. These two parameters reflect the amount of energy stored elastically in the collagen network and the amount of energy dissipated through viscous effects, respectively. The ratio G″/G′ = tan(δ) describes the relative elasticity of the gel.

Collagen gels were tested in a RFSII rheometer (Rheometrics) using dynamic shear mode, parallel plate geometry, and a hydrated chamber as previously described (26,36). Plate diameter was 25 mm, and the gap between plates was 0.2 mm. Initial frequency sweeps and amplitude sweeps were conducted for each polymerization condition, with dynamic strain frequency varying from 0.1 to 100 s⁻¹ and strain varying 0–20%. At 5% strain, collagen hydrogel mechanical spectra were relatively frequency independent over the frequency range tested. During frequency sweeps, G″ tended to exceed G′, whereas during single frequency measurements G′ tended to exceed G″, although the relative magnitude of G′ and the trend of the complex modulus with collagen gel polymerization condition remained the same. Subsequently, all shear modulus measurements were taken at 5% strain, which falls within the linear viscoelastic region of these hydrogels and at a frequency of 10 rad/s.

Collagen hydrogel components were mixed together on ice, and the resulting solution was immediately pipetted onto the rheometer's lower parallel plate, which was maintained at 24°C. The upper plate was then lowered until the gap between the two plates was 0.2 mm, and the gels were allowed to polymerize between the rheometer plates for 45 min, during which time the hydrogel storage modulus increased and then reached a plateau. Polymerization times were necessarily shorter for rheology than for MPM imaging samples, since evaporation could not be completely prevented while the gels were between the rheometer plates and MPM imaging chambers were sealed. Collagen gels polymerized for 45 min displayed similar microstructural trends to those polymerized for 48 h, as assessed by MPM.

Image correlation spectroscopy and image processing

To measure fiber diameters in SEM, MPM, and darkfield images and fiber lengths in darkfield images, the line-drawing feature of ImageJ was used (and referred to in this study as “hand measurements”). Diameters were measured in the middle of the fiber or in the middle of the discernable portion of the fiber. Lengths were measured as the sum of one to six straight line segments along straight or slightly curved collagen fibers. Line measurements were converted from pixels to microns using the appropriate pixel length scale.

For some ICS and pore measurements, MPM images were thresholded to separate void and collagen-containing pixels. The average and standard deviation of pixel intensity were determined in four MPM images from three regions of interest per image containing void and noise but no clearly discernable collagen fibers. The average and standard deviation of pixel intensity from these 12 regions were averaged, and the threshold value was set just above the average plus twice the standard deviation at 530 and 940 on a 12-bit scale for the SHG and TPF images, respectively. Similarly, for some ICS and pore measurements, SEM images were thresholded at 90 on an 8-bit scale, a value that was found to separate clearly distinguishable fibers from deeper fibers with a poor signal/noise ratio.

To measure average pore size, pore area fraction, and pore density, SHG and SEM images were thresholded as described above, inverted, and analyzed with the particle analysis (subscript PA) feature of ImageJ, including particles on edges but excluding particles with fewer than four pixels.

For ICS analysis of pores, SHG and SEM images were thresholded. For ICS analysis of fibers, SHG and SEM images were analyzed raw, and SHG images were also thresholded, noise subtracted, and high- and low-frequency filtered. For noise subtraction, pixels with values ≤530 were set to zero, whereas pixels with greater intensity were decreased by 530. For frequency filtering, SHG images were converted to frequency domain images using ImageJ's fast Fourier transform (FFT) function, and the central 1085 pixels were either set to zero (low spatial frequency mask) or preserved, whereas all other pixels were set to zero (high spatial frequency mask). These masked frequency domain images were then converted back to spatial domain images with ImageJ's inverse fast Fourier transform (IFFT) function before computing the autocorrelation function (ACF). An ImageJ plug-in was written to calculate the two-dimensional (2-D) spatial ACF (32):

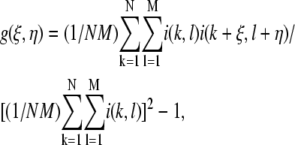(1)

where 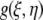is the ACF, ξ and η are the separation distance between pixels in the x and y directions, respectively, and i is the intensity function over the spatial coordinates k and l for an N × M image. In practice, this function is calculated via the 2-D spatial FFT function as the inverse FFT of the power spectrum (32).

Another plug-in was written to fit the central 32 × 32 pixels of the ACF to a 2-D Gaussian function:

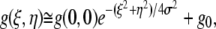(2)

where 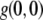is the extrapolated ACF peak value, 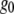is a direct current (dc) offset to account for nonzero ACF at long scales, and σ is the standard deviation of the Gaussian fit. The ICS characteristic fiber length scale, 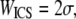and pore size scale, 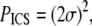provide quantitative indices of the fiber and pore structure. The peak of the ACF (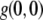) was not included in the fit or the displayed figures as it contains the shot noise for the image, which is not of interest for this analysis.

To ensure random fiber orientation for ICS, the 512 × 512 pixel MPM images and the SEM images were each separated into four 256 × 256 subregions, each rotated 0°, 90°, 180°, and 270° and stacked or montaged before calculating the ACF, which was averaged over the four stacked subregions or simply calculated for the montaged image.

To quantify the ratio of SHG and TPF from fibers more parallel to the image plane versus SHG and TPF from fibers more transverse to the image plane, particle analysis was performed on noise thresholded TPF images using ImageJ. Particles with circularity (i.e., 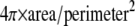) 0–0.1 were designated as fibers more parallel to the image plane, whereas particles with circularity 0.5–1 were designated as fibers more perpendicular to the image plane. Masks were created containing these two particle sets, and the masks were multiplied with the original TPF image and its SHG counterpart to isolate signal-containing pixels colocalizing with one or the other particle set. All other pixel values were set to zero as a result of the mask multiplication, whereas the colocalizing pixel values remained unchanged. A noise floor was then subtracted from these pixels—226 for SHG and 493 for TPF images. Particle analysis performed on these mask-multiplied images revealed the average SHG or TPF intensity values of these particles. The ratios TPF_e/TPF_c and SHG_e/SHG_c represent the noise-subtracted signal from elliptical (subscript “e”) cross section (parallel to image plane) particles divided by the noise-subtracted signal from circular (subscript “c”) cross section (perpendicular to image plane) particles.

Calculation of SHG intensity orientation dependence

The theoretical orientation dependence of SHG signal was determined by utilizing the previously described expression for SHG intensity, I_2ω (37):

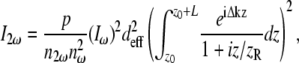(3)

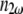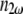where p is a lumped term of fundamental constants and beam parameters, and are the index of refraction at the SHG and fundamental wavelengths, 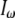is the laser intensity at the focal point, is collagen's orientation-dependent effective second-order nonlinear susceptibility, z_R is the Rayleigh distance, and Δk is the phase mismatch. Assuming that p, n_ω, n_2ω, z_R, and Δk remain constant over any fiber orientation, the ratio of SHG intensities from fibers nearly perpendicular (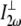) versus fibers nearly parallel (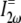) to the laser propagation direction is then

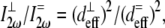(4)

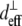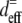where and are the effective second-order nonlinear susceptibilities of collagen fibers perpendicular and parallel to the laser propagation direction, respectively. For parallel polarized laser light, the nonlinear susceptibility 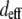is (37)

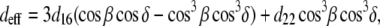(5)

where β is the angle of the (assumed randomly oriented) fiber axis with respect to the fundamental electric field, and δ is the angle between the fiber axis and the imaging plane. The case of circularly polarized laser light corresponds to allowing β to vary between 0° and 360° and averaging 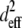over all values of β for a specific value of δ between 0° (fiber perpendicular to laser propagation) and 90° (fiber parallel to laser propagation). The ratio 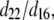necessary to calculate d_eff, was estimated to be ∼2, based upon previous studies in collagen (37,38). Finally, experimentally determined ratios of 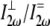were compared to these calculations to determine their reasonableness.

Statistics

Parameters from SHG, TPF, and SEM images were compared across image conditions using either parametric single-factor analysis of variance (ANOVA) or nonparametric Kruskal-Wallis ANOVA for the four polymerization conditions. Student's t-test was used to compare best-fit slopes of the shear moduli data. All statistical tests were performed using Instat 2.01 (GraphPad Software, San Diego, CA) or manually in Excel (Microsoft, Redmond, WA) using standard methods (39). Unless reported otherwise, error bars in graphs represent standard error for data sets in which averaged measurements within images were averaged across multiple images.

RESULTS

Polymerization pH affects collagen fiber dimensions

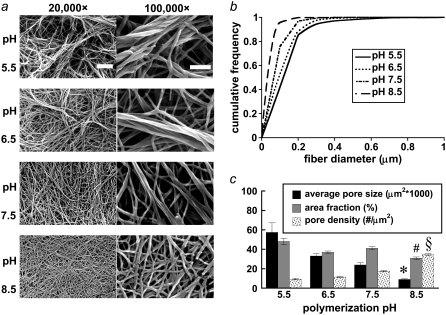
To determine how polymerization pH affects collagen fiber and network formation, collagen hydrogels were imaged with SEM, MPM, and darkfield microscopy. Sample processing for SEM shrinks the gels and the fibers but preserves relative microstructural trends (26). Medium- and high-magnification SEM images show that fiber diameter decreases with increasing polymerization pH and that fewer fibrils per fiber, rather than thinner fibrils, explain this trend (see Fig. 2 a). MPM (see Fig. 1 a) and darkfield microscopy (see Fig. 3 a) confirm the fiber diameter trend in hydrated fibers. From SEM images, the geometric means of hand-measured fiber diameters, d_SEM (1σ lower bound through 1σ upper bound) are 117 (62–221 nm), 105 (60–182 nm), 77 (50–121 nm), and 59 (43–82 nm) for the pH 5.5, 6.5, 7.5, and 8.5 conditions, respectively (statistically significant difference between medians; Kruskal-Wallis test, p < 0.0001). Note that the left-skewed fiber diameter distributions measured from SEM images justify the use of the geometric mean of the hand-measured fiber diameters from these images, called here d_SEM. From SHG images, mean fiber diameter ± SE was 3.7 ± 0.7 μm, 2.9 ± 0.6 μm, 2.1 ± 0.4 μm, and 1.6 ± 0.3 μm for the pH 5.5, 6.5, 7.5, and 8.5 conditions, respectively (statistically significant difference between medians; Kruskal-Wallis test, p < 0.0001). From darkfield images, mean fiber diameters ± SE were similar to those measured from SHG images: 4.1 ± 1.3 μm, 2.8 ± 1.0 μm, 2.5 ± 0.9 μm, and 1.3 ± 0.5 μm for the pH 5.5, 6.5, 7.5, and 8.5 conditions, respectively (statistically significant difference between means; ANOVA on log-transformed data, p < 0.0001).

FIGURE 2.

(a) Representative SEM images reveal collagen network and fiber characteristics at 20,000× magnification (left column; bar represents 2 μm) and 100,000× magnification (right column; bar represents 500 nm) for the polymerization pH conditions. n = 9, 9, 9, and 6 20,000× images were used for microstructure quantification and statistics. (b) pH-dependent fiber diameter frequency distributions were constructed from n = 477, 513, 629, and 905 fiber diameter measurements for the pH 5.5, 6.5, 7.5, and 8.5 conditions, respectively. (c) Mean pore size, pore area fraction, and pore density were quantified for each polymerization condition from noise-thresholded, inverted SEM images. Symbols (*, #, and §) indicate statistical significance among polymerization pH groups.

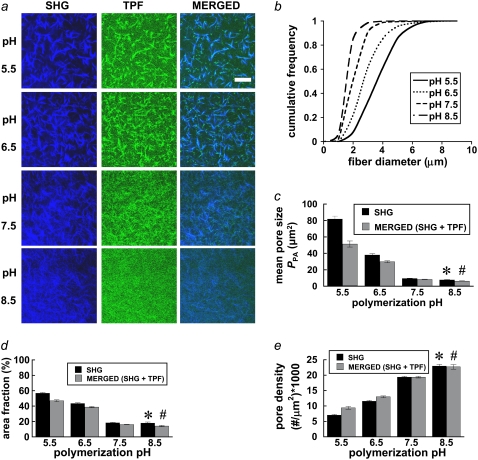
FIGURE 1.

(a) Representative SHG (left column, blue) and TPF (middle column, green) images from collagen hydrogels polymerized at pH 5.5, 6.5, 7.5, and 8.5. Images are 512 × 512 pixels and 230 × 230 μm. n = 12 images per condition were used for microstructure quantification and statistics. Bar represents 50 μm. (b) pH-dependent fiber diameter frequency distributions were constructed from n = 358, 605, 564, and 492 fiber diameter measurements for the pH 5.5, 6.5, 7.5, and 8.5 conditions, respectively. (c) Mean pore size, (d) pore area fraction, and (e) pore density were quantified for each polymerization condition from noise thresholded, inverted SHG, or merged (SHG + TPF) images. Symbols (* and #) indicate statistical significance among polymerization pH groups.

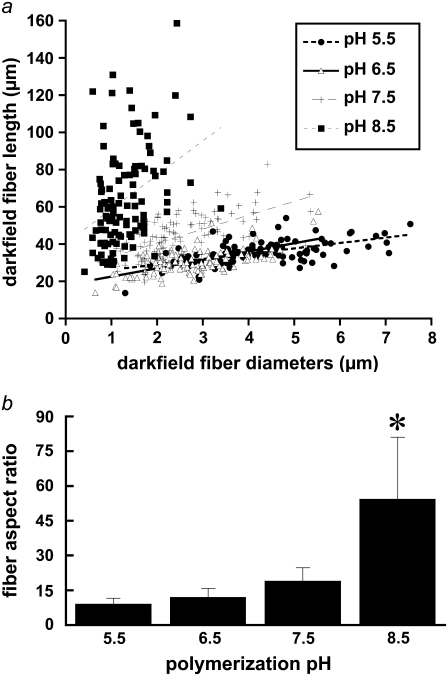
FIGURE 3.

(a) Lengths and diameters of isolated collagen fibers were quantified using ImageJ's line-drawing feature from darkfield images of homogenized collagen hydrogels polymerized at pH 5.5 (•), 6.5 (▵), 7.5 (+), and 8.5 (▪). Each point on the graph represents the length and diameter of one fiber. n = 108 fibers were measured from each polymerization condition. Lines represent linear best fits to the data from each polymerization condition. (b) Mean fiber aspect ratio measured from darkfield images for each pH condition. Error bars represent standard deviation. Symbol (*) indicates statistical significance among pH conditions.

The cumulative frequency histograms plot hand-measured fiber diameter distributions from SHG (Fig. 1 b) and SEM (Fig. 2 b) images; whereas Fig. 3 a shows fiber length and diameter distributions hand-measured from isolated fibers in darkfield images. Fiber diameters measured from SEM images were closer to log-normal distributions, whereas fiber diameters measured from SHG and darkfield images were closer to Gaussian distributions. Polymerization pH alters both fiber diameter and length distributions (Fig. 3 a) and increases fiber aspect ratio with polymerization pH (Fig. 3 b). Fiber length is difficult to quantify in SHG images from the intact entangled fiber network, whereas darkfield microscopy of isolated fibers from homogenized gels provides an independent assessment of collagen fiber length and diameter. Mean fiber aspect ratio (length/diameter) ± SD calculated from darkfield images was 9.1 ± 2.3, 12.0 ± 3.8, 19.0 ± 5.7, and 54.3 ± 26.7 for the pH 5.5, 6.5, 7.5, and 8.5 conditions, respectively (statistically significant difference among medians, Kruskal-Wallis test, p < 0.0001).

Polymerization pH affects collagen gel pore characteristics

Pore characteristics affect the mechanical properties of polymer networks, and these characteristics were quantified from SHG and merged (SHG + TPF) images (Fig. 1, c–e) and SEM images (Fig. 2 c) of the collagen gels. Average pore size and pore area fraction tended to decrease, whereas pore number density increased with increasing polymerization pH, as the available collagen tended to form more numerous, thinner fibers at higher pH values. Particle analysis of thresholded SHG images calculated a mean pore size ± SE of 81.7 ± 3.7 μm² for the pH 5.5 condition, decreasing ∼90% to 7.8 ± 0.4 μm² for the pH 8.5 condition (Fig. 1 c; statistically significant difference among means, ANOVA on log-transformed data, p < 0.0001), with a concurrent drop in the pore area fraction from 56.8% ± 0.8% to 18.0% ± 1.3% (Fig. 1 d; statistically significant difference among medians, Kruskal-Wallis test, p < 0.0001). The number density of pores increased ∼3.2-fold from 7.1 ± 0.2 to 23.0 ± 0.6 per 1000 μm² (Fig. 1 e; statistically significant difference among medians, Kruskal-Wallis test, p < 0.0001). Similarly, particle analysis of thresholded SEM images calculated an average pore size ± SE of 0.057 ± 0.010 μm² for the pH 5.5 condition, decreasing ∼84% to 0.0090 ± 0.0007 μm² for the pH 8.5 condition (Fig. 2 c; statistically significant difference among medians, Kruskal-Wallis test, p < 0.0001), with a concurrent drop in the pore area fraction from 48.1% ± 3.4% to 30.8% ± 1.3% (Fig. 2 c; statistically significant difference among means, ANOVA on inverse-transformed data, p < 0.0001). The number density of pores increased ∼3.7-fold from 9.3 ± 0.7 to 34.5 ± 0.9 pores per μm² (Fig. 2 c; statistically significant difference among means, ANOVA, p < 0.0001).

After performing particle analysis on noise-thresholded SHG and merged (SHG + TPF) images, we compared the subsequent pore measurements from the two image types (Fig. 1, c–e). The pore measurements were rather similar, especially with increasing polymerization pH, although average pore size and area fraction tended to be smaller for the merged images. The merged image pore measurements were statistically significant across polymerization conditions (statistically significant difference among medians, Kruskal-Wallis test, p < 0.0001 for each of the three pore parameters).

SHG signal is orientation dependent; TPF signal is orientation independent

In Fig. 1 a, particularly for collagen polymerized at pH 5.5 and 6.5, the SHG and TPF signals from collagen fibers that are generally in the image plane clearly colocalize, whereas fiber cross sections cut more or less perpendicular to the image plane generate a punctate TPF signal with little or no SHG. Nevertheless the colocalized fraction of noise-subtracted TPF signal was measured to be greater than the colocalized fraction of noise-subtracted SHG signal (Fig. 4 a), a result which follows from the SHG signal's greater signal/noise ratio, especially at fiber edges which the TPF signal fails to resolve (Fig. 1 a, merged images).

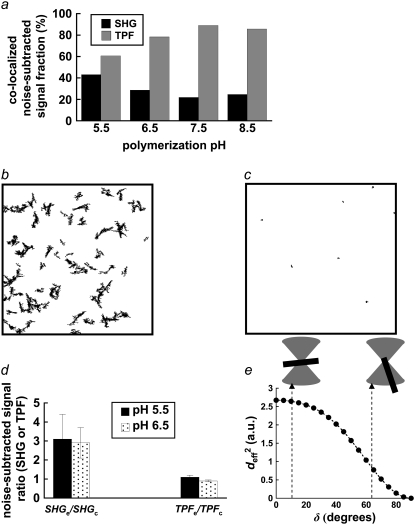
FIGURE 4.

(a) Percentage of colocalizing SHG and TPF pixels, summed from n = 12 paired, noise-subtracted SHG and TPF images per polymerization condition with respect to total SHG and TPF signal-containing pixels. (b) Mask of a representative thresholded TPF images, showing outlines of particles with circularity 0–0.1. (c) Mask of representative thresholded TPF images, showing outlines of particles with circularity 0.5–1. (d) After applying the previous two masks separately to the noise-subtracted TPF image or its SHG counterpart, the mean signal within elliptical particles of circularity 0–0.1 (SHG_e, TPF_e) was divided by the mean signal within particles of circularity 0.5–1 (SHG_c, TPF_c). Error bars represent standard deviation. (e) 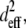in arbitrary units, was estimated for various angles of tilt of the collagen fiber axis with respect to the laser propagation direction, δ: fibers at 10° and 63° of tilt are diagrammed.

Fibers parallel and perpendicular to the image plane are visible in TPF images and can be segmented after thresholding based upon particle circularity (Fig. 4, b and c), whereas only fibers with scattering interfaces more or less parallel to the image plane (and perpendicular to the laser propagation direction) produce a strong backward-detected SHG signal. For the microscope settings defined above, SHG average noise ± SE was 226 ± 17 whereas TPF average noise ± SE was 493 ± 24 for 12-bit images. TPF_e/TPF_c ± SE was 1.1 ± 0.1 for the pH 5.5 condition and 0.90 ± 0.05 for the pH 6.5 condition; SHG_e/SHG_c ± SE was 3.1 ± 1.3 for the pH 5.5 condition and 2.9 ± 0.8 for the pH 6.5 condition (Fig. 4 d). Only in these two polymerization conditions were the fibers large enough to easily quantify signal intensity from elliptical (i.e., in-plane) and circular (i.e., transverse) fiber cross sections.

The squared effective nonlinear susceptibility of collagen was calculated using Eqs. 3–5 and plotted as a function of δ, the angle of the fiber axis with respect to the image plane (Fig. 4 e). A ratio of 3 for SHG_e/SHG_c, for example, corresponds to 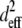values of 2.64 and 0.88 for fibers oriented at δ = 10° and 63°, respectively (Fig. 4 e). These example values were chosen to show that the theoretical estimation of the ratio of 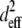based upon fibers tilted at shallow versus at steep angles tends to predict a SHG intensity ratio similar to experimentally determined values.

Microstructure determines G′, G″

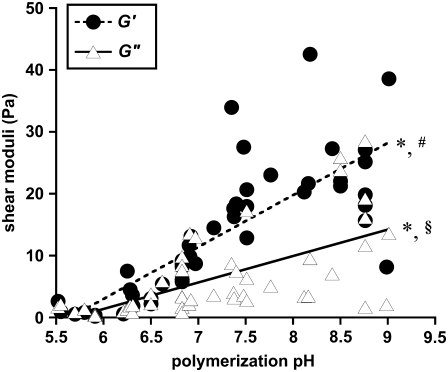
To characterize the mechanical property-microstructure relationship in these hydrogels, collagen polymerized between pH 5.5 and 9 were shear tested by rheometry to quantify the storage (G′) and loss (G″) moduli. The collagen solution pH was measured before polymerization and rheometry, revealing some variability in gels designed to be at pH 5.5, 6.5, 7.5, and 8.5. As polymerization pH increased, both G′ and G″ increased, whereas tan(δ) (=G″/G′) tended to decrease (Fig. 5). Comparing gels polymerized between pH 5.5 and 6 to gels polymerized between pH 8.2 and 8.8, G′ increased ∼33-fold from 0.72 ± 0.77 Pa to 24.1 ± 7.5 Pa; G″ increased ∼16-fold from 0.90 ± 0.68 Pa to 14.7 ± 9.5 Pa; and tan(δ) decreased ∼2-fold, from 1.48 ± 0.55 to 0.66 ± 0.47. The best fit slopes of 8.41 and 4.27 Pa/pH unit were statistically significantly different from a zero slope (Student's t-test, p < 0.001 for each case), and the two slopes were statistically significantly different from each other (Student's t-test, p < 0.001).

FIGURE 5.

G′ and G″ of collagen hydrogels, measured by parallel-plate rheometry, vary with polymerization pH. G′ (•) and G″ (▵ ) were collected at 5% strain and 10 s⁻¹ oscillating shear frequency for n = 48 hydrogels polymerized at pH 5.5–9.0. Lines represent linear best fits to the data for G′ and for G″. The symbol * indicates that the best fit slopes are significantly different from each other; the symbols # and § indicate that each slope is significantly different from a slope of zero.

ICS parameters from MPM, SEM images correlate with microstructure

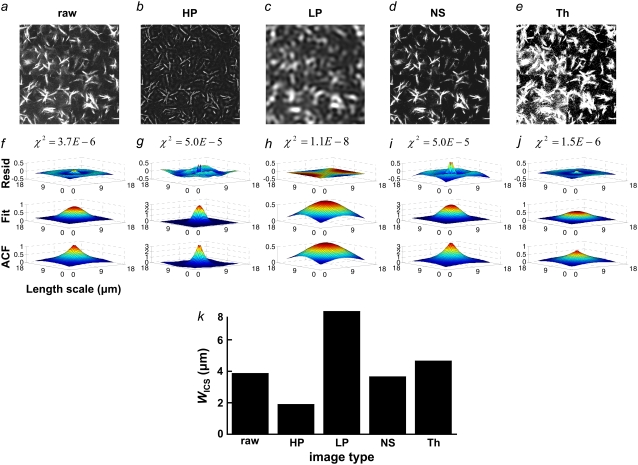
We hypothesized that ICS analysis of collagen microstructural images would capture the characteristic length scale of microstructural features in these images. To determine how image features affect the ACF, we performed ICS on one 512 × 512 SHG image that was preserved as raw data (Fig. 6 a), high-pass filtered (Fig. 6 b), low-pass filtered (Fig. 6 c), noise-subtracted (Fig. 6 d), or thresholded (Fig. 6 e). The resulting ACFs, Gaussian fits, and residuals are plotted in Fig. 6, f–j. The residuals were generally <10% of the ACF height. The standard deviations of the Gaussian fits are compared in Fig. 6 k. Note that most ACFs have sharper and taller peaks and more concave slopes than the corresponding two-dimensional Gaussian fits but that the ACF of the low-pass filtered image is very closely fit by a Gaussian. The low-pass filter clearly blurs the fiber intensity profile, emphasizing larger fibers and attenuating smaller fibers and fiber features. As a result, the standard deviation of the Gaussian fit was largest for the low-pass filtered image. Thresholding transforms the fiber intensity profile into a step function, weighting dim and bright fiber regions equally. As a result, the standard deviation of the Gaussian fit was next largest for the thresholded image. In contrast, noise-subtraction and high-pass filtering produce narrower ACFs than that of the raw image. Noise-subtraction dims fibers, whereas the high-pass filter emphasizes small fiber features and erases large fibers.

FIGURE 6.

One 512 × 512 SHG image (a, raw) unprocessed, (b, HP) high-pass filtered, (c, LP) low-pass filtered, (d, NS) noise-subtracted, and (e, Th) thresholded was analyzed with ICS, and (f–j) the ACF, Gaussian fit, and residuals plotted, with the χ² value of the fit reported above the residuals. (k) W_ICS from each of the Gaussian fits.

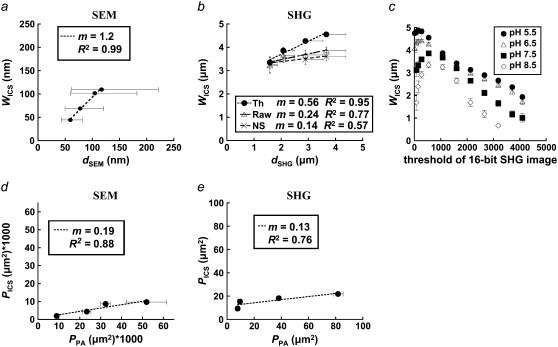
The ICS characteristic fiber size, W_ICS, from SEM and thresholded SHG images correlates well with the corresponding mean hand-measured fiber diameter, d_SEM or d_SHG, for each polymerization condition (SEM R² = 0.99, Fig. 7 a; SHG R² = 0.95, Fig. 7 b). In comparison, W_ICS measured from raw and noise-subtracted SHG images correlate less strongly with d_SHG. Mean W_ICS calculated from SHG but not SEM images tended to be larger than the corresponding mean hand-measured fiber diameter. The best fit slope was near 1 for SEM (m = 1.2) and <1 for thresholded SHG images (m = 0.56). The correlations and linear fit slopes were smaller when comparing W_ICS and d_SHG from noise-subtracted and raw SHG images (Fig. 7 c). The values of W_ICS ± SE in Fig. 7 a are, in order of decreasing polymerization pH, 44 ± 1 nm, 69 ± 2 nm, 102 ± 2 nm, and 110 ± 3 nm. The corresponding values of the geometric mean d_SEM (1σ lower bound through 1σ upper bound) are 59 (43–82 nm), 77 (50–121 nm), 105 (60–182 nm), and 117 (62–221 nm). Similarly, the values of W_ICS ± SE in Fig. 7 b for thresholded SHG images are, in order of decreasing polymerization pH, 3.4 ± 0.3 μm, 3.9 ± 0.2 μm, 4.3 ± 0.1 μm, and 4.6 ± 0.1 μm. The corresponding values of the arithmetic mean d_SHG ± SE are 1.6 ± 0.5 μm, 2.1 ± 0.7 μm, 2.9 ± 1.1 μm, and 3.7 ± 1.3 μm.

FIGURE 7.

(a) SEM images were analyzed with ICS, and W_ICS compared to the geometric mean of hand-measured fiber diameters, d_SEM. x axis error bars represent the 1σ lower and upper bounds around the geometric mean. (b) Thresholded (Th), noise-subtracted (NS), and unprocessed (RAW) SHG images were analyzed with ICS and by hand measurements; d_SHG represents the arithmetic mean of hand-measured fiber diameters from SHG images. (c) W_ICS was calculated as a function of threshold value for SHG images of collagen polymerized at the four pH values. (d) Thresholded, inverted SEM and (e) SHG images were analyzed with ICS, and P_ICS compared to mean pore size from particle analysis, P_PA.

ICS analysis performed on SHG images thresholded at multiple values reveals that W_ICS was maximized or near maximum at the chosen noise threshold (of 530), decreasing sharply if the threshold was either increased, eroding collagen SHG-containing structures, or decreased, obscuring and merging collagen SHG structures (Fig. 7 c).

Finally, the characteristic pore size estimated from ICS, P_ICS, has a similar trend to the mean pore size determined by particle analysis, P_PA, for SEM (Fig. 7 d) and SHG images (Fig. 7 e). The correlations are modest (R² = 0.88 and R² = 0.76, respectively), and the best-fit slopes are <1 (m = 0.19 and m = 0.13, respectively).

For SHG images, 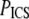drops ∼57% from 21.8 ± 1.4 μm² at pH 5.5 to 9.3 ± 1.8 μm² at pH 8.5; for SEM images, 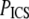drops ∼80% from 0.0097 ± 0.003 μm² at pH 5.5 to 0.0020 ± 0.0002 μm² at pH 8.5. For both sets of image measurements, there is a statistically significant difference among means (ANOVA on all four pH conditions, p < 0.0001 for both SHG and SEM images).

G′ scales with microstructural parameters estimated with ICS

Acid-soluble collagen hydrogels consist of an uncross-linked, tightly entangled network of semiflexible (but rather rod-like) polymer chains (i.e., fibers), and as such their viscoelastic properties may be modeled, employing only a handful of microstructural input parameters (29,30). Specifically, the storage modulus G′ scales as

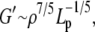(6)

where ρ is the density of polymer contour length per unit volume and 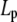is the chain's persistence length. A network mesh size, 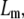which we propose may be estimated by 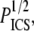relates to ρ as 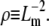A fiber's persistence length is proportional to its bending modulus, which for collagen scales with the fourth power of fiber diameter, d (40,41). Recasting the scaling relationship of Eq. 6 in terms of mesh size and fiber diameter we get

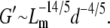(7)

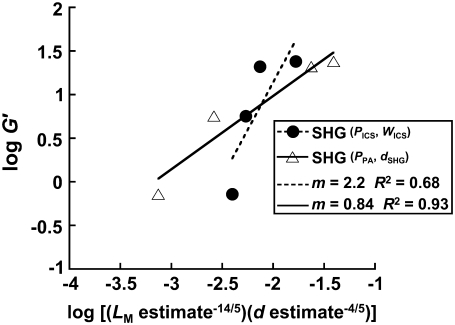
Fig. 8 compares our data from SHG images to the scaling relationship in Fig. 7 by plotting log G′ versus log (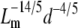). The mesh size and fiber diameter are estimated either using 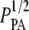and the mean hand-measured fiber diameter d_SHG or with the ICS parameters 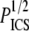and W_ICS. The correlation using the ICS parameters is modest (R² = 0.68); the correlation using the particle analysis and hand-measured parameters is good (R² = 0.93). The best-fit slopes are of order one, much closer to the input parameters 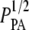and d_SHG (m = 0.84) than to 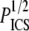and W_ICS (m = 2.2).

FIGURE 8.

Scaling relationship for the storage modulus, G′, was calculated using rheometric data and ICS, particle analysis, or hand-measured estimates of mesh size and fiber diameter from SHG images. Best-fit slopes and R² values are given in the figure.

DISCUSSION

Temperature (26,42), pH (43), ionic strength (43), ion stoichiometry (42), and monomer concentration all affect the acid-soluble collagen polymerization reaction and the resulting microstructure. How the microstructure influences the bulk mechanical properties and how to assess the microstructure in a systematic and noninvasive fashion remain important unanswered questions. Our study is the first, to our knowledge, to use polymerization pH, MPM, and ICS to manipulate and characterize the collagen microstructure and predict bulk mechanical properties. Our study determined that increasing pH decreased fiber diameter and network pore size, as assessed by MPM and ICS and confirmed by darkfield and SEM, but increased fiber length, as measured from darkfield images. Furthermore, increasing pH results in stiffer collagen gels, as indicated by increasing G′ and G″. These observations are consistent with network theory of semiflexible fibers (29,30). We conclude that MPM and ICS may be used to noninvasively, objectively, and systematically predict bulk mechanical properties of collagen gels and thus may also be useful in assessing the mechanical properties of tissues in situ.

Our fiber diameter and length measurements are in concordance with previous studies (44,45). A recent transmission electron microscopy study of acetic acid-solubilized rat tail tendon collagen showed fibers with misaligned D-banded fibrils at pH 5–6, transversely aligned fibrils at pH 6.5–9, and a fibril association at pH 9 that is looser than that at lower pH values (43). Increasing polymerization pH decreases the net positive charge on each collagen monomer (by deprotonating amino acid side chains), increasing hydrogen bonding between triple helices (46) and increasing triple helix melting temperature (47). Thus, it is likely that the decreased monomer stability and attraction at lower pH, which correlates with increased lateral monomer association in fibrils and increased fibril diameter (45,48), allows increased lateral association of fibrils into larger-diameter fibers, possibly through increased attractive forces between fibrils.

The trends of decreasing pore size, area fraction, and increasing pore density with increasing pH leading to stiffer gels are consistent with our previous report using different gelation temperatures to perturb microstructure and alter gel stiffness (26). In addition, Roeder et al. used confocal reflectance/uniaxial tensile testing to quantify pH-varied collagen gel microstructure and elastic modulus. These researchers found that for 2 mg/ml acid-soluble calf skin collagen, mean fibril diameter and elastic modulus were 490 ± 96 nm and 1.8 ± 0.7 kPa for pH 6.0-polymerized gels and 392 ± 65 nm and 33.0 ± 7.0 kPa for pH 9.0-polymerized gels. Though the methods differed from the study presented here and pore characteristics were not quantified, it is clear that the same microstructural and mechanical property trends exist.

The 1:1 ratio of TPF signal from fibers predominantly parallel to versus transverse to the image plane confirm the isotropic angular distribution of TPF generation in collagen. In contrast, one would expect greater backward-detected SHG from fibers parallel to the image plane, both because of the scattering of forward-generated SHG at the fiber bottom interface (17) and because of the collagen dipoles' optimal orientations to the laser propagation direction (37,49–51). Indeed, we measured a 3:1 ratio of SHG intensity from fibers roughly parallel versus roughly transverse to the image plane, which is consistent with theoretical considerations using a lower NA (37). The higher NA (1.3) used in this study introduces a component of the electric field transverse to the image plane, which would change the SHG angular power distribution (52) from fibers aligned with the z axis. Specifically, these fibers should emit forward-generated SHG at a steeper angle (∼40–47°) from the z axis than does the lower NA case but should emit no backward-generated SHG (49,52). Fibers aligned parallel to the laser propagation should exhibit lower 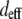(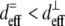) as well as reduced single and multiple scattering of SHG photons from the highly forward-directed SHG emission compared to fibers oriented perpendicular to the laser propagation direction. These two properties could explain the observed threefold difference in SHG signal.

Using Eq. 4, we calculated a ratio of SHG signal intensities based on estimated values of 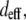which depend on the orientation of collagen's dipoles with respect to the incident electric field. This calculation is valid if the phase mismatch Δk and the index of refraction remain constant regardless of fiber orientation. In fact, collagen's birefringence of Δn ∼ 0.003 (where n along the collagen monomer's long axis is greater than n along the short axes) (53,54) is assumed to be negligible for our calculations. This seems a valid assumption since we are not specifying fiber orientations but rather comparing our calculation to an experimental SHG signal averaged over an ensemble of collagen fibers only roughly aligned. Furthermore, Δk may be assumed constant since the SHG interaction volume (roughly the focal volume dimensions, ∼200 nm lateral × 600 nm axial) is smaller than the mean fiber diameter and length in these cases and can be assumed to be completely filled when centered on a collagen fiber regardless of fiber orientation (49). For an incident wavelength of 780 nm, Δk ∼ 0.48 μm⁻¹, with a corresponding coherence length of 6.5 μm, allowing efficient SHG from the ∼3-μm thick bundles of collagen fibrils (37).

Despite SHG orientation dependence, SHG images of collagen capture more collagen microstructure than TPF images alone, evidenced by the high proportion of SHG not colocalized with TPF (Fig. 4 a). In acellular gels, a merged SHG + TPF image best describes collagen's microstructure (Fig. 1, c–e), but since collagen's TPF signal overlaps with cell and elastin autofluorescence in vivo, SHG signal alone may be a more appropriate method to accurately assess collagen fiber and pore characteristics, especially for thin fibers (Fig. 1, c–e).

2-D spatial ICS was first applied to confocal images of fluorescently labeled beads and PDFG-β2 cell surface receptors (32). These were roughly the same size as or smaller than the laser beam waist (and pixel size), and particle numbers were estimated by fitting the 2-D spatial ACF with a 2-D Gaussian using three fitting parameters: a dc image noise component, g_o; a laser beam width, w; and an extrapolated ACF peak, g(0,0), where w, g(0,0), and the image area were used to calculate the number of fluorescent particles (32). Also, the spatial ACF has been used to estimate the size of fluorescently labeled HLA-1 transmembrane protein clusters: ∼300–600 nm on fixed, hydrated cells imaged with near-field scanning optical microscopy with a pixel resolution of ∼40 nm (31).

As Hwang et al. did in their study (31), we used ICS to estimate a characteristic spatial dimension of collagen fibers spanning multiple pixels. Collagen fibers are much larger than the electron beam interaction volume or infrared laser beam waist. Therefore, fiber length and width both contribute to the characteristic length 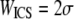; however, as Fig. 7 a suggests, W_ICS is weighted toward fiber diameter rather than length, as would be expected if the ACF is calculated by stepwise correlations across elongated fibers with random orientation. Correlations along the fibers' long axes would rarely occur; correlations oblique to the long axis would occur more commonly and would be closer, on average, to the mean fiber diameter than to its length. W_ICS is comparable to d_SHG and d_SEM: the correlations are very good (R² = 0.99 and R² = 0.97 for the SEM and thresholded SHG images, respectively). The linear fit slope of W_ICS versus d_SEM, the geometric mean of the hand-measured log-normal fiber diameter distributions from SEM images, is close to 1 (m = 1.2). In contrast, the scaling of W_ICS with d_SHG, the arithmetic mean of the hand-measured normal fiber diameter distributions from SHG images, is much less than 1:1 (m = 0.14–0.56). W_ICS becomes increasingly greater than d_SHG as d_SHG decreases for the higher polymerization pH conditions. As polymerization pH increases, not only do fiber diameters decrease, but also pore size and pore area fraction decreases whereas fiber number density increases, leading to an increased overlapping of fibers in SHG images. We suggest that the ACF is sensitive to fiber overlap, which systematically increases W_ICS.

Importantly, the ACFs of SHG and SEM images of collagen tended to be taller, with a narrower peak but broader foot than corresponding Gaussian fits. This holds true after performing thresholding, noise-subtraction, and high-pass filtering on SHG images (Fig. 6); but the ACF of the low-pass filtered SHG image is nearly perfectly Gaussian. Since the low-pass filter attenuates small fiber features and broadens and smoothes SHG intensity profiles, the ACF departure from the Gaussian shape must be due to either steeply graded SHG intensity profiles or the size distribution of fibers and fiber features, including fiber persistence length and diameter. W_ICS from the Gaussian fit of the ACF is largest after low-pass filtering, which emphasizes large fibers; in comparison thresholding only increases W_ICS slightly compared to the raw image's W_ICS, due to the increased weighting of dim fiber edges mentioned above upon applying the threshold. In contrast, noise subtraction, which dims fibers, and high-pass filtering, which emphasizes small fibers, decrease W_ICS compared with that of the raw image.

Presumably, with an appropriate analytical model, fiber diameter and persistence length distributions may be extracted from the ACF. Nonetheless, the standard deviation of the Gaussian fit correlates well with fiber diameter in thresholded SHG images, though increasing fiber overlap appears to increase W_ICS; in fact, the correlation with mean hand-measured fiber diameter is better after thresholding than with the raw or noise-subtracted images (Fig. 7 b). This could be due to the fact that thresholding destroys signal gradients, turning the SHG intensity profile of a fiber into a step function, weighting dim and bright regions equally in the ACF. Note that W_ICS is maximized or near maximal at the appropriate noise threshold (530 for SHG; Fig. 7 c). Larger threshold values remove SHG signal, eroding fibers; smaller threshold values merge fibers together and combine strong SHG signal with poorly resolved signal, confounding estimation of fiber diameter.

Finally, ICS can also be used to determine a characteristic pore size from an image, once the image is thresholded to separate fibers from pores and inverted to create an artificial “pore signal”. We suggest that the characteristic pore size determined from ICS, P_ICS, corresponds to the average pore cross-sectional area and maps to our estimates of this area using particle analysis, P_PA. The correlations are modest for SHG images but good for SEM images (Fig. 7, c and d); P_PA tends to be larger, possibly because the particle analysis excluded pores of four pixels or less and because particle analysis measures rather tortuous pores which would appear as several smaller autocorrelations with ICS analysis. Since 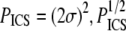has units of length and thus may estimate network mesh size, L_m.

These results suggest that ICS is a robust method to characterize SEM and MPM images of fibrillar extracellular matrix and that the characteristic length scale derived by fitting the ACF is related to the population of apparent fiber diameters and lengths within the image or to the pore dimensions. Microstructural parameters characterizing fiber and pore dimensions, quantifiable from SHG images, can explain bulk shear moduli of pure, tightly entangled, uncross-linked acid-soluble type I collagen hydrogels using a semiflexible network theory (Fig. 8). The correlation between experiment and theory was best with particle analysis and hand measurements from SHG images (R² = 0.93) with slope m = 0.84, fairly close to the predicted slope of m = 1. In contrast, the ICS analysis of the SHG images had a somewhat worse correlation with slope of 2.2. Sources of systematic error potentially arise from the data or the scaling relationships. Potential errors from the ICS method are discussed above. The theoretical scaling relationship assumes collagen fibers are monodisperse, cylindrical, tightly entangled, and semiflexible. In reality, the fibers are polydisperse and, especially for the pH 5.5 condition, tapered and somewhat sparse. Future work must improve our understanding of how ICS parameters deviate from true microstructural parameters and whether network theory of semiflexible uncross-linked fibers is the most appropriate model.

For in vivo applications, impurities, i.e., cells or other extracellular matrix components, and collagen cross-linking complicate the relationship among SHG, microstructure, and tissue mechanics. Information about these contributors to network mechanics may be gleaned from TPF images—at least for highly autofluorescent cells, elastin, and cross-links (17,25,26)—or from confocal reflectance or optical coherence microscopy (55). We anticipate that SHG and TPF images of normal and fibrotic mammalian tissue will reveal microstructural changes correlating with and predicting the component of bulk tissue mechanical properties due to collagen and elastin fibers. Notably, a recent study correlated an increased volume fraction of SHG-containing pixels from 3-D image stacks of bleomycin-treated mouse lungs compared to control lungs (20).

In summary, altering the polymerization pH of collagen hydrogels significantly influences the resulting microstructure and mechanical properties. An increasing pH results in longer, thinner collagen fibers, a reduced pore area fraction and size, and an increased pore density. These features result in stiffer gels as measured by increasing storage and loss moduli. MPM of the collagen gels followed by ICS analysis of the images can noninvasively, objectively, and systematically assess the microstructure and predict the mechanical properties. We conclude that MPM may be a useful noninvasive technique to assess bulk mechanical properties of the extracellular matrix.