Abstract
Micromechanical bending experiments using atomic force microscopy were performed to study the mechanical properties of native and carbodiimide-cross-linked single collagen fibrils. Fibrils obtained from a suspension of insoluble collagen type I isolated from bovine Achilles tendon were deposited on a glass substrate containing microchannels. Force-displacement curves recorded at multiple positions along the collagen fibril were used to assess the bending modulus. By fitting the slope of the force-displacement curves recorded at ambient conditions to a model describing the bending of a rod, bending moduli ranging from 1.0 GPa to 3.9 GPa were determined. From a model for anisotropic materials, the shear modulus of the fibril is calculated to be 33 ± 2 MPa at ambient conditions. When fibrils are immersed in phosphate-buffered saline, their bending and shear modulus decrease to 0.07–0.17 GPa and 2.9 ± 0.3 MPa, respectively. The two orders of magnitude lower shear modulus compared with the Young's modulus confirms the mechanical anisotropy of the collagen single fibrils. Cross-linking the collagen fibrils with a water-soluble carbodiimide did not significantly affect the bending modulus. The shear modulus of these fibrils, however, changed to 74 ± 7 MPa at ambient conditions and to 3.4 ± 0.2 MPa in phosphate-buffered saline.
INTRODUCTION
Collagen, the most abundant protein in the human body, provides structural stability and strength to various tissues. About 25 types of collagen have been identified, of which collagen type I is the major component of the fibrous structure of skin, tendon, and bone in the human body (1).
Studies on the collagen type I structure have shown a complex hierarchical arrangement of collagen subunits. In this hierarchical arrangement, it is widely accepted that five tropocollagen molecules assemble into microfibrils (2–4). Of the various hypothesized models, the compressed microfibril model (2) and the supertwisted right-handed microfibril model (3) most closely fit the x-ray diffraction data. Recently, the structure of microfibrils has been visualized using atomic force microscopy (AFM) imaging (5). These microfibrils aggregate in lateral and longitudinal direction to form fibrils. The collagen fibrils with diameters between 10 and 500 nm further assemble into fibers that become part of the structural skeleton of tissues. Because of the highly organized mode of self-assembly, a single collagen fibril is regarded as homogeneous, which means it has the same composition throughout the fibril. However, the alignment of collagen molecules and microfibrils in the longitudinal fibril direction may induce mechanical anisotropy of the single collagen fibrils. The packing of these structural components and the organization of the collagen fibrous structure are crucial to the mechanical function of tissues. Mechanical anisotropy of tissues such as tendon, bone, and cartilage has been studied with different techniques (6–9) and using theoretical modeling (10–12). It is suggested that the mechanical anisotropy at the fibril level and the highly ordered parallel packing of fibrils result in mechanical anisotropy of most tissues (13,14). However, current mechanical approaches cannot easily separate the contribution of mechanical anisotropy as a result of the hierarchical arrangement of collagen molecules in the fibril and/or parallel packing of the fibrils.
Efforts have been made to determine the mechanical properties of collagen single fibrils using different micromechanical techniques. Graham et al. (15) stretched in vitro-assembled type I collagen fibrils obtained from human fibroblasts using AFM and obtained a Young's modulus of 32 MPa. Eppell et al. (16) studied the stress-strain relation of single type I collagen fibrils isolated from the sea cucumber and found a Young's modulus of 550 MPa in the hydrated state. Also, in our lab, we used a home-built AFM system to perform tensile tests on single collagen type I fibrils isolated from bovine Achilles tendon (17). A Young's modulus of 5 ± 2 GPa for dry collagen type I fibrils was found, and when these fibrils were immersed in phosphate-buffered saline (PBS), the Young's moduli ranged from 0.2 to 0.5 GPa. Very recently, the reduced modulus of collagen single fibrils isolated from rat tail tendons was determined by nanoindentation using AFM (18) in air at room temperature and ranged from 5 to 11 GPa. These results support the hypothesis that the anisotropy of collagen results from the alignment of subfibrils along the fibril axis. However, current methods to investigate the mechanical properties of single collagen fibrils are limited as no shear related mechanical properties are measured.
Recently an AFM-based three-point bending technique has been developed by different groups to measure the mechanical properties of nanoscale beams and wires (19–22). This method has been applied to silicon beams (19), ZnS nanowires (21), SiO2 nanowires (23), and most recently to electrospun polymer-ceramic composites (24) and individual amyloid fibrils (25). By use of the same principle, bending of single-walled carbon nanotubes (26) and microtubules (27) has been performed with contact-mode AFM. In their measurements (26,27), the bending moduli (Ebending) related to the bending stiffness (EbendingI) representing the resistance of the material on bending were determined (I is the second moment of area of the beam or tube). From the unit-load equation, the shear moduli of tested materials were determined by bending the materials with different length/diameter ratios. The determined shear moduli of single-wall carbon nanotubes and microtubules are two or three orders of magnitude lower than the Young's modulus, which confirms the mechanical anisotropy of the materials. Adapting the same technique, mechanical anisotropy in single vimentin intermediate filaments (IFs) was determined (28). This experimental approach offers new insights in separating the contribution of the actin filaments, microtubules, and vimentin IF networks to the stiffness of the cytoskeleton (28).
To gain more insight into the mechanical behavior of tissues, an AFM-based bending technique was developed to study the mechanical behavior of single collagen type I fibrils isolated from bovine Achilles tendon. Using a home-built AFM system and a glass substrate with microchannels, fibril bending by cantilever movement in the z-direction was combined with a continuous scanning motion along the fibril. In this way, the slope of the force-displacement curve (dF/dz) at different positions of the fibril spanning a channel can be obtained. The bending moduli of tested single collagen fibrils were determined by fitting the slope (dF/dz) of multiple individual bending experiments to well-established mechanical models. This method allows a more accurate determination of the bending modulus and allowed the calculation of the shear modulus of a collagen fibril for the first time, to our knowledge. Chemical cross-linking is often necessary to improve the stability of collagen-based biomaterials. Therefore, the change of the mechanical properties on cross-linking the fibrils was investigated.
MATERIALS AND METHODS
Quartz glass substrates with parallel microchannels were prepared by reactive ion etching using a RIE Elektrotech system (Elektrotech Twin PF 340, London, UK). The width and depth of the channels were determined by AFM (home-built instrument) and SEM (LEO Gemini 1550 FEG-SEM, LEO Elektronenmikroskopie GmbH, Oberkochen, Germany) measurements.
Isolation and deposition of single collagen fibrils
Insoluble bovine Achilles tendon collagen type I from Sigma-Aldrich (Steinheim, Germany) was swollen in hydrochloric acid (0.01 M) overnight at 0°C. The resulting slurry was homogenized for 10 min at 9500 rpm using a Braun MR 500 HC blender (Braun, Kronberg, Germany). The temperature was kept <5°C. The resulting mixture was filtered using a 74-μm filter (collector screen 200 mesh, Bellco Glass, Vineland, NJ). The helical content of the collagen suspension after filtration was determined by FTIR (FTS-60, Biorad, Hercules, CA) according to a method described by Friess and Lee (29). After filtration, 1 ml of the collagen dispersion was diluted with 150 ml of PBS (pH = 7.4). Deposition of the collagen fibrils on the quartz glass substrates was done by incubating the substrates for 10 min in the diluted collagen dispersion. Subsequently, the substrates were washed with PBS for 10 min and three times with demineralized water for 10 min each and finally dried at ambient conditions for at least 24 h. The bending tests of collagen fibrils in PBS buffer were carried out after equilibration of the fibrils for 15 min in PBS at room temperature. Longer equilibration times did not lead to changes in the results of the bending tests.
Cross-linked collagen fibrils were prepared by mixing 2 ml of the nondiluted collagen dispersion with a solution of 1.73 g 1-ethyl-3-(3-dimethyl aminopropyl)carbodiimide hydrochloride (EDC) and 0.45 g N-hydroxysuccinimide (NHS) in 215 ml 2-morpholinoethane sulfonic acid (MES) (0.05 M, pH = 5.4) for 2 h. The resulting cross-linked fibrils were deposited on the quartz glass substrates and washed as described above.
Collagen denaturation temperature and free amino group content
The diluted native collagen fibril dispersion was centrifuged for 15 min at 4500 rpm (Hettich Mikco Rapid/k, Depex, De Bilt, the Netherlands). The solution was removed, and the collagen was washed twice with MilliQ water for 30 min each. Similarly, a diluted cross-linked collagen fibril dispersion was centrifuged as described above and then washed twice with PBS buffer for 30 min each and four times with MilliQ water for 30 min each. After the washing steps, both native and cross-linked collagen samples were frozen in liquid nitrogen and subsequently freeze-dried for 24 h.
The degree of cross-linking of the collagen samples is related to the increase of the denaturation (shrinkage) temperature (Td) after cross-linking. The Td values were determined by DSC (DSC 7, Perkin Elmer, Norwalk, CT). Freeze-dried native and cross-linked collagen samples of 3–5 mg were swollen in 50 μl of PBS (pH = 7.4) in high-pressure pans overnight. Samples were heated from 20°C to 90°C at a heating rate of 5°C/min. A sample containing 50 μl of PBS (pH = 7.4) was used as a reference. The onset of the endothermic peak was taken as the Td.
The free amino group content of native and cross-linked samples was determined using the 2,4,6-trinitrobenzenesulfonic acid (TNBS) assay. Collagen samples of 3–5 mg were incubated for 30 min in 1 ml of a 4 wt % solution of NaHCO3. To this mixture 1 ml of a freshly prepared solution of TNBS (0.5 wt %) in 4 wt % NaHCO3 was added. The resulting mixture was left for 2 h at 40°C. After the addition of HCl (3 ml, 6 M), the temperature was raised to 60°C. Degradation of collagen was achieved within 90 min. The resulting solution was diluted with 5.0 ml MilliQ water and cooled to room temperature. The absorbance at 420 nm was measured using a Varian Cary 300 Bio spectrophotometer (Middelburg, the Netherlands). A blank was prepared by applying the same procedure, except that HCl was added before the addition of TNBS. The absorbance was correlated to the concentration of free amino groups using a calibration curve obtained with glycine. The free amino group content was expressed as the number of free amino groups per 1000 amino acids (n/1000).
Micromechanical bending in scanning mode using AFM
Modified triangular silicon nitride cantilevers (coated sharp microlevers MSCT-AUHW, type F, spring constant k = 0.5 N/m, Veeco, Cambridge, UK) were used in the bending test. The tip on the AFM cantilever was removed using a focused ion beam (FIB) (FEI, NOVALAB 600 dual-beam machine). After the cutting, the modified cantilevers were inspected using the built-in SEM (30). The spring constant of each tipless cantilever was calibrated by pushing on a precalibrated cantilever as described elsewhere (31). The sensitivity (S) of the AFM system with the cantilever, i.e., the ratio between the bending of the cantilever and the deflection, as measured by the quadrant detector, was derived from a force-indentation curve measured on a glass surface with an identical scan rate and amplitude as used in the bending experiments.
RESULTS AND DISCUSSION
Sample preparation and characterization
AFM images of the quartz glass substrates (Fig. 1 A) show that ion etching allows the preparation of a substrate with well-defined microchannels with a width of ∼3 μm. The depth of the channels is ∼600 nm, which is sufficient for the intended bending experiments of collagen fibrils spanning these channels and supported by the glass rims.
FIGURE 1.
(A) Tapping mode AFM height image of a glass surface patterned with channels; the full z-range of the image is 1 μm. (B) Tapping mode AFM height image of single collagen fibrils on a glass surface at ambient conditions; the full z-range of the image is 250 nm. (C) Tapping mode AFM height image of single collagen fibrils on a glass surface in PBS buffer; the full z-range of the image is 225 nm. (D) SEM image of a single collagen fibril spanning multiple channels. The width of the channel is 3.0 ± 0.2 μm.
The glass substrates were incubated in a freshly prepared and highly diluted suspension of collagen fibrils. After washing and drying of the samples, single fibrils perpendicularly spanning the microchannels were selected and used in the scanning-mode mechanical bending tests (vide supra). The characteristic 67-nm D-period of the collagen fibrils deposited on the glass surface was visualized by AFM images both for fibrils at ambient conditions (Fig. 1 B) and in PBS buffer (Fig. 1 C). Collagen fibrils at least 50 μm in length crossed more than 3 channels on the glass substrate (Fig. 1 D). The diameters of all tested fibrils were determined by high magnification SEM images.
The helical content of the collagen in the fibrillar suspension was determined with FTIR and revealed a maximum percentage of helicity (29). The single collagen fibrils used were also characterized by determining their characteristic denaturation temperature (Td) and number of free amino groups (n/1000). The Td of the native fibrils was 55.0°C and increased to 74.5°C after cross-linking with the water-soluble carbodiimide EDC in the presence of N-hydroxysuccinimide (NHS). The free amino group content decreased from 28 per 1000 amino acids to a value of 8, which is in line with previously reported data (32). These results reveal a high degree of cross-linking.
Micromechanical bending of native and cross-linked collagen type I fibrils
Under an optical microscope, collagen fibrils that freely and perpendicularly span multiple channels of the glass substrate were selected for the bending tests. The actual scanning bending procedure was started after a successful approach of the AFM tipless cantilever above the fibril. In scanning mode, fibril bending by cantilever movement in the z-direction was combined with a continuous scanning motion along the fibril. To achieve this, the output signal for the fast scanning direction as used in AFM scanning was used to drive the piezo movement in the z-direction while the one for the slow scanning direction was used to move the cantilever along the fibril (Fig. 2). During the bending tests, the total scanning distance was chosen to be 4–5 μm, which is slightly larger than the channel width. A typical piezo movement of 1.5–3.0 μm with a frequency of 1.3 Hz in the z-direction was applied. In each step, one cycle (approach and retraction) of the cantilever deflection and piezo movement was recorded. After every step, the tip was moved one step further along the fibril. A complete scan consisted of 256 steps with a total measuring time of 200 s.
FIGURE 2.
Schematic representation of the cantilever movement over a single collagen type I fibril during the scanning-mode bending experiments. Each cycle (approach and retraction) of the cantilever movement in the z-direction gives a piezo movement-deflection curve. After each cycle, the cantilever moves one step further along the fibril. In total, 256 steps along the fibril gave 256 piezo movement-deflection curves.
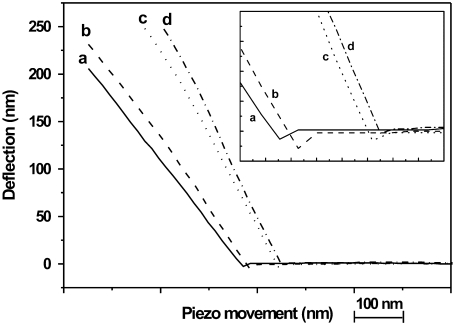
Four of the individual piezo movement-deflection curves obtained from bending the fibril at the middle point of the channel (a), between the middle and edge of the channel (b), and at the edge of the channel (c), and indenting the fibril on the glass surface (d) are presented in Fig. 3. During the first part of the approach, there is no deflection, indicating that the cantilever is not interacting with the collagen fibril. As the cantilever moves closer, a snap-in point can be observed (negative deflection). After this point a linear relation between the piezo movement and deflection of the fibril is found for all individual bending measurements. The slope of the piezo movement-deflection curve differs from one position to the next.
FIGURE 3.
Four individual piezo movement-versus-deflection curves obtained at different positions along the fibril (diameter 240 nm) (a) at the middle of the channel, (b) between the middle and edge of the channel, (c) at the edge of the channel, (d) on the glass surface. (Inset) Enlargement of the snap-in points in the same piezo movement-versus-deflection curves. The scale units are 10 nm and 5 nm for horizontal axis and vertical axis, respectively.
A custom computer program, written in Labview (version 6.1, National Instruments, Austin, TX) was used to analyze the data. A force-displacement curve of every 256 bending measurements was obtained using the following equations:
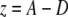 |
(1) |
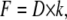 |
(2) |
in which z is the displacement of the fibril in the z-direction during bending, A is the piezo movement in the z-direction, and D is the calibrated deflection signal of the cantilever (nm). F is the force applied to the fibril, and k is the calibrated spring constant of the cantilever.
The slope of each force-displacement curve of the tested fibril was determined by linear fit, and the obtained data are presented in Fig. 4. A decrease in the slope (dF/dz) was found during scanning from the edge up to the middle of the channel, which clearly proves that the fibril is freely suspending the microchannel. In all experiments, no difference was found in the force-displacement curves on bending the same collagen fibril multiple times, which ensures the reproducibility of the test and confirms that no permanent deformation of the collagen fibrils occurred. It must be noted that, in the measurements near the edges of the channel, the cantilever can touch the glass surface when the fibril is bent, and those data were omitted from analysis.
FIGURE 4.
Slope of the force-versus-displacement curve of a collagen type I fibril (diameter 240 nm) as a function of the scanning position along the channel. The dashed line in the image indicates the middle point of the channel (channel width is ∼3.2 μm). The dF/dz data at the left half and right half of the channel are fitted to Eq. 3 separately.
When a force is applied to the suspended part of the fibril, a possible displacement in the z-direction at both rims of the channel has to be taken into account. Because of the strong surface adhesion properties of collagen to glass (15) and the fact that each collagen fibril crosses at least three channels (the length of the fibril is more than 50 μm), it is assumed that the fibril is firmly attached to the surface at the supporting rims and that the rim behaves as a stiff material, and thus, the displacement can be neglected. Also, it has been reported that slippage of a collagen fibril on the supporting points or loading points during the bending tests will result in a nonlinear force-displacement curve (33). This nonlinearity was not observed in our experiments.
Determining the mechanical properties of native and cross-linked single collagen fibrils
Deflections of a rod induce both bending and shear deformation. A bending modulus Ebending as previously defined by Kis et al. (27) equals the Young's modulus (E) if the rod is isotropic or the length/diameter ratio fulfills the following requirement: 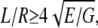 where G is the shear modulus. The Ebending of the suspended fibril can be obtained by fitting the measured slope of the force-displacement curves at all positions to Eq. 3 (34),
where G is the shear modulus. The Ebending of the suspended fibril can be obtained by fitting the measured slope of the force-displacement curves at all positions to Eq. 3 (34),
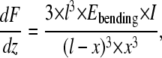 |
(3) |
in which x is the relative position along the fibril (0 ≤ x ≤ l/2), l is the width of the channel, I is the moment of inertia 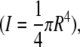 and dF/dz is the slope deduced from the force-displacement curve obtained during bending of the collagen fibril. The fibril is considered a rod with a circular cross-section with radius R.
and dF/dz is the slope deduced from the force-displacement curve obtained during bending of the collagen fibril. The fibril is considered a rod with a circular cross-section with radius R.
As shown in Fig. 4, the dF/dz data do fit to Eq. 3. The standard error in the least-squares fit parameter is 2–6%, and values obtained from the left and right halves of the fibril are similar (average difference 3–4%).
Recently we reported on the determination of the Young's modulus of dry collagen fibrils by single-point bending tests (30). The Young's modulus of a fibril crossing a channel in a poly(dimethylsiloxane) substrate was determined close to its middle point using Eq. 4, which is derived from Eq. 3 by substituting x = l/2
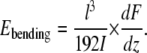 |
(4) |
Compared with a single-point bending procedure, the scanning-mode bending allows a more precise determination of the bending modulus (Young's modulus for isotropic materials or high length/diameter ratio) because it results from fitting multiple individual bending experiments. Furthermore, data generated from multiple bending experiments of the suspended fibril and fitted to the model of bending a rod reveal that no permanent deformation of the collagen fibril occurred during the bending tests. The relative error (∼23%) in the bending modulus using the applied scanning-mode bending method is derived from the error (SE) of the diameter (∼3%), the width of the channel (∼3%), the spring constant of the cantilever (∼5%), and the fitting (∼3%). The largest contribution to the error of the bending modulus results from the error in the diameter of the fibril (∼3%). This leads to a 12% error in the bending modulus. Improvement of the accuracy in the fibril diameter determination is critical for reducing the error further.
The ranges of the bending modulus values that were obtained from the scanning-mode bending tests are presented in Table 1. Typically, the bending modulus of a collagen fibril with a diameter of 240 nm is ∼2.4 GPa (Fig. 4) at ambient conditions. The bending modulus of such a fibril decreased with a factor of ∼20 to 120 MPa when immersed in PBS buffer. Introducing cross-links between collagen molecules by activation of carboxylic acid groups of glutamic or aspartic acid residues with a carbodiimide, which subsequently react with amine groups with the formation of amide bonds (32) and with hydroxyl groups with the formation of ester bonds (35), did not significantly affect the bending modulus of the fibril.
TABLE 1.
Bending and shear moduli of collagen type I fibrils obtained from scanning bending measurements
| Collagen type I fibril | Conditions | Number of samples | Range of diameters‡ (nm) | Bending moduli¶ (GPa) | Shear modulus§ (MPa) |
|---|---|---|---|---|---|
| Native | Dry | 18 | 187–305 | 3.9–1.0 | 33 ± 2 |
| Cross-linked* | Dry | 11 | 205–303 | 3.1–1.7 | 74 ± 7 |
| Native | PBS buffer† | 12 | 280–426 | 0.17–0.07 | 2.9 ± 0.3 |
| Cross-linked* | PBS buffer† | 13 | 287–424 | 0.14–0.06 | 3.4 ± 0.2 |
Cross-linking was performed with EDC and NHS in MES buffer.
PBS: phosphate-buffered saline, pH = 7.4.
Ranges of diameters of different fibrils used in the mechanical tests. The error in the diameter of individual fibrils is ∼3% (SE) calculated from multiple measurements on the same fibril.
Ranges of bending moduli determined from fibrils with different diameters. A 23% relative error is estimated for the value of the bending modulus determined for individual fibrils.
The error in the shear modulus is the standard error of the weighted least-squares fit parameter.
For isotropic rods or rods with high length/diameter ratio, the bending modulus is equal to the Young's modulus and is independent of the rod diameter. Otherwise, the contribution of shear in the deflection of the rod can not be ignored. The deflection from bending and shear deformation when a force is applied at the middle of the channel can be written as (34):
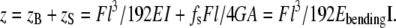 |
(5) |
In Eq. 5, z is the total displacement of the fibril in the z-direction, zB is the deflection resulting from bending, zS is the deflection resulting from shearing, E is the Young's modulus, G is the shear modulus, fs is the form factor of shear, and A is the cross-sectional area of the rod. For a rod with a circular cross-sectional area, the form factor of shear fs equals 10/9 (34).
Equation 5 can be converted into Eq. 6 using A = πR2, fs = 10/9 and I = πR4/4.
 |
(6) |
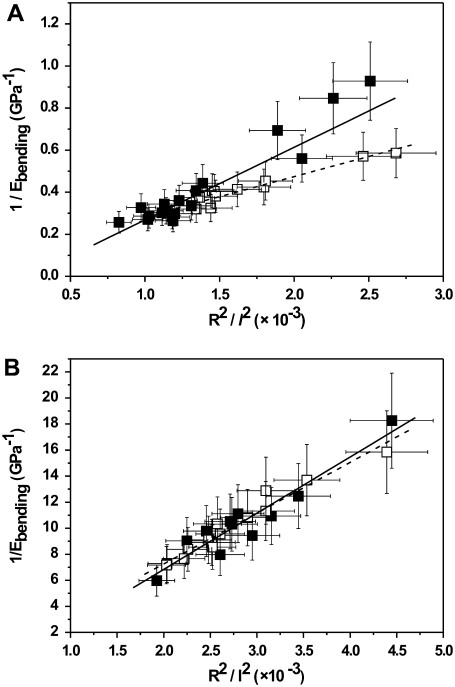
From Eq. 6, a diameter-dependent bending modulus is expected. Such a diameter-dependent bending modulus was observed before in microtubules (27) and single-wall nanotube ropes (26) with relatively weak bonds between the subunits in the lateral direction. Here, a large number of fibrils were tested, and we found that the bending modulus increased with decreasing fibril diameter at both ambient conditions and in PBS buffer (Fig. 5, A and B).
FIGURE 5.
Bending moduli of collagen type I fibrils as a function of diameter at ambient conditions (A) and in PBS buffer (B). Data points are of native collagen fibrils (filled squares) and collagen fibrils cross-linked by EDC/NHS (open squares). N = 18 for native collagen (at ambient conditions); N = 11 for cross-linked collagen (at ambient conditions); N = 12 for native collagen (in PBS buffer); and N = 13 for cross-linked collagen (in PBS buffer). The relative error in the bending modulus of every individual fibril is derived from the errors in fibril diameter (SEM measurements), the length of the channel, and the spring constant of the cantilever.
By use of Eq. 6, the shear modulus of the tested collagen fibrils can be determined from the slope of the linear relation between 1/Ebending and (R2/l2). A similar equation has been used by Kis et al. (27) for studying the bending and shear modulus of microtubules. With the linear fit as shown in Fig. 6 A, the shear modulus of native single collagen fibrils at ambient conditions is 33 ± 2 MPa. After cross-linking with EDC/NHS, the shear modulus increases to 74 ± 7 MPa. Also, as shown in Fig. 6 B, the shear modulus of the collagen fibrils placed in PBS buffer can be estimated from the linear plot. The values of the shear moduli are 2.9 ± 0.3 MPa and 3.4 ± 0.2 MPa for native and EDC/NHS cross-linked fibrils, respectively, which are not statistically different. The differences in the increase of the shear modulus for fibrils at ambient conditions and when placed in PBS buffer before and after cross-linking may relate to the different hydration states of the fibrils. Intermolecular cross-links in collagen fibrils are mainly present in the telopeptide regions. Cross-linking using a carbodiimide such as EDC involves the formation of additional amide bonds by reaction of free amine groups (lysine residues) and activated carboxylic acid groups (glutamic and aspartic acid) and ester bonds by reaction of hydroxyl groups (serine, hydroxyproline, and hydroxylysine residues) and activated carboxylic acid groups as well, which results in additional inter- and intramolecular cross-links in the collagen fibrils. It is not expected that cross-links can be formed between microfibrils because the distance is too long. However, displacement of microfibrils with respect to each other at ambient conditions may be hampered by the friction resulting from the surface decoration with activated carboxylic acid groups. In PBS buffer, the surface decoration does not hamper the displacement of microfibrils with respect to each other. It is expected that after cross-linking, the displacement of collagen molecules with respect to each other becomes more difficult. However, the similar shear moduli for native and cross-linked collagen fibrils placed in buffer indicate that the displacement of microfibrils with respect to each other is probably the main factor influencing the shear modulus of single collagen fibrils. The values of shear moduli for different collagen fibrils at different conditions are listed in Table 1. In a previous study (30), the diameter-dependent bending modulus was not observed because we used channels with a larger width, resulting in a higher length/diameter ratio ( ); therefore, the Ebending corresponds more closely with the Young's modulus.
); therefore, the Ebending corresponds more closely with the Young's modulus.
FIGURE 6.
Reciprocal bending modulus (Ebending) as a function of R2/l2 of collagen type I fibrils at ambient conditions (A) and in PBS buffer (B). R is the collagen fibril radius, and l is the suspended length of the fibril over the channel. Data points and linear fit are of native collagen type I fibrils (solid squares; fit, solid line) and collagen type I fibrils cross-linked by EDC/NHS (open squares; fit, dashed line). N = 18 for native collagen (at ambient conditions); N = 11 for cross-linked collagen (at ambient conditions); N = 12 for native collagen (in PBS buffer); and N = 13 for cross-linked collagen (in PBS buffer).
According to current models described in literature (2,3,36,37), collagen molecules and microfibrils are arranged parallel to the fibril axis. Intermolecular cross-linking for native collagen is believed to occur only via lysine and hydroxylysine groups within the telopeptide regions (3). The interaction between the collagen subunits in the parallel direction will be different from that in the lateral direction, leading to mechanical anisotropy. Previously, microtensile tests of single collagen fibrils have been performed in our group. The Young's modulus of single collagen fibrils was determined to be 5 ± 2 GPa and 0.2–0.5 GPa at ambient conditions and in PBS buffer, respectively (17). The shear modulus of the single collagen fibrils determined from the bending experiments is two orders of magnitude lower than the Young's modulus, which confirms anisotropy at the single-collagen-fibril level.
To summarize, in this study, the mechanical properties of insoluble collagen type I fibrils isolated from tendon were investigated using scanning-mode bending tests with a home-built AFM. Single fibrils perpendicularly spanning multiple channels in a glass substrate were subjected to bending tests using an AFM cantilever without a tip.
Subjecting a single collagen fibril to the scanning-mode bending test afforded multiple force-displacement curves at different positions across the channel. From the slope of these curves (dF/dz), the bending modulus of the fibrils could be determined using an elastic rod model. For single collagen type I fibrils immersed in buffer, the bending modulus decreased by a factor of 20 compared with fibrils at ambient conditions. Cross-links introduced on reaction with a carbodiimide did not change the bending modulus of the fibril.
The dependence of the bending modulus on the collagen fibril diameter allowed for the first time, to our knowledge, an estimation of the shear modulus. The calculated shear modulus indicates that the collagen fibrils are mechanically anisotropic. For collagen fibrils in PBS buffer, it is shown that cross-linking through amide bond formation between amine and carboxylic acid groups and ester bond formation between hydroxyl and carboxylic acid groups does not affect the shear modulus of the fibril. These results provide new insight into the mechanical behavior of collagen-based tissues.
Acknowledgments
This research was financially supported by the Softlink program of ZonMw. Project number: 01SL056.
Editor: Thomas Schmidt.
References
- 1.Veis, A. 1997. Collagen fibrillar structure in mineralized and nonmineralized tissues. Curr. Opin. Solid St. Mater. Sci. 2:370–378. [Google Scholar]
- 2.Piez, K. A., and B. L. Trus. 1981. A new model for packing of type-I collagen molecules in the native fibril. Biosci. Rep. 1:801–810. [DOI] [PubMed] [Google Scholar]
- 3.Orgel, J. P. R. O., T. C. Irving, A. Miller, and T. J. Wess. 2006. Microfibrillar structure of type I collagen in situ. Proc. Natl. Acad. Sci. USA. 103:9001–9005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wess, T. J., A. P. Hammersley, L. Wess, and A. Miller. 1998. Molecular packing of type I collagen in tendon. J. Mol. Biol. 275:255–267. [DOI] [PubMed] [Google Scholar]
- 5.Habelitz, S., M. Balooch, S. J. Marshall, G. Balooch, and G. W. Marshall. 2002. In situ atomic force microscopy of partially demineralized human dentin collagen fibrils. J. Struct. Biol. 138:227–236. [DOI] [PubMed] [Google Scholar]
- 6.Hoffmeister, B. K., S. M. Handley, S. A. Wickline, and J. G. Miller. 1996. Ultrasonic determination of the anisotropy of Young's modulus of fixed tendon and fixed myocardium. J. Acoust. Soc. Am. 100:3933–3940. [DOI] [PubMed] [Google Scholar]
- 7.Kostyuk, O., H. L. Birch, V. Mudera, and R. A. Brown. 2003. Structural changes in loaded equine tendons can be monitored by a novel spectroscopic technique. J. Physiol. 554:791–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fan, Z., P. A. Smith, E. C. Eckstein, and G. F. Harris. 2006. Mechanical properties of OI type III bone tissue measured by nanoindentation. J. Biomed. Mater. Res. A. 79:71–77. [DOI] [PubMed] [Google Scholar]
- 9.Elliott, D. M., D. A. Narmoneva, and L. A. Setton. 2002. Direct measurement of the Poisson's ratio of human patella cartilage in tension. J. Biomech. Eng. 124:223–228. [DOI] [PubMed] [Google Scholar]
- 10.Akkus, O. 2005. Elastic deformation of mineralized collagen fibrils: an equivalent inclusion based composite model. J. Biomech. Eng. 127:383–390. [DOI] [PubMed] [Google Scholar]
- 11.Natali, A. N., P. G. Pavan, E. L. Carniel, M. E. Lucisano, and G. Taglialavoro. 2005. Anisotropic elasto-damage constitutive model for the biomechanical analysis of tendons. Med. Eng. Phys. 27:209–214. [DOI] [PubMed] [Google Scholar]
- 12.Bischoff, J. E. 2006. Reduced parameter formulation for incorporating fiber level viscoelasticity into tissue level biomechanical models. Ann. Biomed. Eng. 34:1164–1172. [DOI] [PubMed] [Google Scholar]
- 13.Wu, J. Z., and W. Herzog. 2002. Elastic anisotropy of articular cartilage is associated with the microstructures of collagen fibers and chondrocytes. J. Biomech. 35:931–942. [DOI] [PubMed] [Google Scholar]
- 14.Hellmich, C., J. F. Barthélémy, and L. Dormieux. 2004. Mineral-collagen interactions in elasticity of bone ultrastructure-a continuum micromechanics approach. Eur. J. Mech. A/Solid. 23:783–810. [Google Scholar]
- 15.Graham, J. S., A. N. Vomund, C. L. Phillips, and M. Grandbois. 2004. Structural changes in human type I collagen fibrils investigated by force spectroscopy. Exp. Cell Res. 299:335–342. [DOI] [PubMed] [Google Scholar]
- 16.Eppell, S. J., B. N. Smith, H. Kahn, and R. Ballarini. 2006. Nano measurements with micro-devices: mechanical properties of hydrated collagen fibrils. J. R. Soc. Interface. 3:117–121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.van der Rijt, J. A. J., K. O. van der Werf, M. L. Bennink, P. J. Dijkstra, and J. Feijen. 2006. Micromechanical testing of individual collagen fibrils. Macromol. Biosci. 6:697–702. [DOI] [PubMed] [Google Scholar]
- 18.Wenger, M. P. E., L. Bozec, M. A. Horton, and P. Mesquida. 2007. Mechanical properties of collagen fibrils. Biophys. J. 93:1255–1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Namazu, T., Y. Isono, and T. Tanaka. 2000. Evaluation of size effect on mechanical properties of single crystal silicon by nanoscale bending test using AFM. J. Microelectromech. Syst. 9:450–459. [Google Scholar]
- 20.Ni, H., and X. Li. 2006. Young's modulus of ZnO nanobelts measured using atomic force microscopy and nanoindentation techniques. Nanotechnology. 17:3591–3597. [DOI] [PubMed] [Google Scholar]
- 21.Xiong, Q., N. Duarte, S. Tadigadapa, and P. C. Eklund. 2006. Force-deflection spectroscopy: a new method to determine the Young's modulus of nanofilaments. Nano Lett. 6:1904–1909. [DOI] [PubMed] [Google Scholar]
- 22.Jeng, Y. R., and P. C. Tsai. 2005. Molecular-dynamics studies of bending mechanical properties of empty and C60-filled carbon nanotubes under nanoindentation. J. Chem. Phys. 122:224713. [DOI] [PubMed] [Google Scholar]
- 23.Ni, H., X. Li, and H. Gao. 2006. Elastic modulus of amorphous SiO2 nanowires. Appl. Phys. Lett. 88:043108. [Google Scholar]
- 24.Lee, S. H., C. Tekmen, and W. M. Sigmund. 2005. Three-point bending of electrospun TiO2 nanofibers. Mater. Sci. Eng. A/Struct. 398:77–81. [Google Scholar]
- 25.Smith, J. F., T. P. J. Knowles, C. M. Dobson, C. E. MacPhee, and M. E. Welland. 2006. Characterization of the nanoscale properties of individual amyloid fibrils. Proc. Natl. Acad. Sci. USA. 103:15806–15811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Salvetat, J. P., G. A. D. Briggs, J. M. Bonard, R. R. Bacsa, A. J. Kulik, T. Stöckli, N. A. Burnham, and L. Forró. 1999. Elastic and shear moduli of single-walled carbon nanotube ropes. Phys. Rev. Lett. 82:944–947. [Google Scholar]
- 27.Kis, A., S. Kasas, B. Babić, A. J. Kulik, W. Benoît, G. A. D. Briggs, C. Schönenberger, S. Catsicas, and L. Forró. 2002. Nanomechanics of microtubules. Phys. Rev. Lett. 89:248101-1–248101-4. [DOI] [PubMed] [Google Scholar]
- 28.Guzmán, C., S. Jeney, L. Kreplak, S. Kasas, A. J. Kulik, U. Aebi, and L. Forró. 2006. Exploring the mechanical properties of single vimentin intermediate filaments by atomic force microscopy. J. Mol. Biol. 360:623–630. [DOI] [PubMed] [Google Scholar]
- 29.Friess, W., and G. Lee. 1996. Basic thermoanalytical studies of insoluble collagen matrices. Biomaterials. 17:2289–2294. [DOI] [PubMed] [Google Scholar]
- 30.Yang, L., K. O. van der Werf, H. F. J. M. Koopman, V. Subramaniam, M. L. Bennink, P. J. Dijkstra, and J. Feijen. 2007. Micromechanical bending of single collagen fibrils using atomic force microscopy. J. Biomed. Mater. Res. A. 82:160–168. [DOI] [PubMed] [Google Scholar]
- 31.Torii, A., M. Sasaki, K. Hane, and S. Okuma. 1996. A method for determining the spring constant of cantilevers for atomic force microscopy. Meas. Sci. Technol. 7:179–184. [Google Scholar]
- 32.Olde Damink, L. H. H., P. J. Dijkstra, M. J. A. van Luyn, P. B. van Wachem, P. Nieuwenhuis, and J. Feijen. 1996. Cross-linking of dermal sheep collagen using a water-soluble carbodiimide. Biomaterials. 17:765–773. [DOI] [PubMed] [Google Scholar]
- 33.Ljungcrantz, H., L. Hultman, J. Sundgren, S. Johansson, N. Kristensen, and J. Schweitz. 1993. Residual stresses and fracture properties of magnetron sputtered Ti films on Si. microelements. J. Vac. Sci. Technol. A. 11:543–553. [Google Scholar]
- 34.Gere, J. M., and S. P. Timoshenko. 1991. Mechanics of materials, 3rd edition. Chapman & Hall, London.
- 35.Everaerts, F., M. Torrianni, M. Hendriks, and J. Feijen. 2007. Quantification of carboxyl groups in carbodiimide cross-linked collagen sponges. J. Biomed. Mater. Res. A. 83:1176–1183. [DOI] [PubMed] [Google Scholar]
- 36.Buehler, M. J. 2006. Nature designs tough collagen: Explaining the nanostructure of collagen fibrils. Proc. Natl. Acad. Sci. USA. 103:12285–12290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Prockop, D. J., and A. Fertala. 1998. The collagen fibril: the almost crystalline structure. J. Struct. Biol. 122:111–118. [DOI] [PubMed] [Google Scholar]