Mechanism-Based Pharmacokinetic-Pharmacodynamic Models of In Vitro Fungistatic and Fungicidal Effects against Candida albicans

Abstract

Mechanism-based pharmacokinetic-pharmacodynamic (PK-PD) models describing the fungistatic activity of fluconazole and the fungicidal activity of caspofungin were developed using dynamic in vitro models. Antifungal-drug pharmacokinetics was simulated in vitro, assuming a one-compartment model with an elimination half-life of 3 h and using a wide (1 to 10,000) range of initial concentrations. The number of CFUs over time was determined for up to 31 h and used for PK-PD modeling. A model incorporating first-order natural growth and natural death, plus a maximum number of viable Candida cells, was used to characterize Candida growth in the absence of a drug. Fluconazole was considered to inhibit Candida growth and caspofungin to stimulate Candida death according to an E_max pharmacodynamic model. The data were analyzed with Nonmem, using a population approach. A good fit of the data was obtained with satisfactory estimates of PK-PD parameters, especially with drug concentrations producing 50% of the maximal effect: 50% inhibitory concentrations for fluconazole growth inhibition and 50% effective concentrations for caspofungin death stimulation. In conclusion, mechanistic PK-PD models were successfully developed to describe, respectively, the fungistatic and fungicidal activities of fluconazole and caspofungin in vitro. These models provide much better information on the drug effects over time than the traditional PK-PD index based on MICs. However, they need to be further characterized.

The MIC is the in vitro reference value that describes the activity of antimicrobial agents against microorganisms (25, 27). The MIC is the lowest concentration that completely inhibits visible growth of the organism as detected by the unaided eye, usually after 16 to 24 h for antibiotics and 48 h for antifungal agents, using a standard inoculum of approximately 10⁵ CFU·ml⁻¹ with antibiotics and between 0.5 and 2.5 × 10³ CFU·ml⁻¹ with antifungal agents (31). The MIC corresponds to the net result of microorganism growth and kill over the selected period of time, and many different combinations of growth and kill rates can result in the same MIC (27), even for drugs presenting different mechanisms of action (e.g., growth inhibition versus death stimulation). Therefore, the MIC is not an intrinsic characteristic of antimicrobial activity. Furthermore, it is usually determined at a fixed concentration of the antimicrobial agent, which does not reflect the in vivo situation, in which drug concentrations vary with time. The pharmacokinetic-pharmacodynamic (PK-PD) index based on the MIC has been derived in order to accommodate for that difference and has led to the distinction between antimicrobial agents that exhibit time-dependent killing and those that exhibit concentration-dependent killing (8, 27). For time-dependent antimicrobial agents, efficacy is usually assessed from the time above the MIC (t > MIC), expressed as the percentage of the dosing interval, and for concentration-dependent agents, it is most often characterized by the peak concentration-to-MIC ratio or by the ratio of the 24-h area under the curve to the MIC (8). PK-PD indices are also currently used with antifungal drugs (1-4, 13). The 24-h area under the concentration-time curve-to-MIC index was found to correlate with the efficacy of fluconazole (5, 23). This index also correlated with caspofungin efficacy in a murine model of systemic candidiasis (22), whereas the peak concentration-to-MIC index correlated with caspofungin efficacy in a murine model of invasive pulmonary aspergillosis (32). Therefore, uncertainty exists about the best index or exact breakpoints to use (33). Furthermore, although these PK-PD indices are useful predictors of the potency of the drug-microorganism interaction, they present both PK and PD disadvantages that have recently been reviewed (27). For pharmacokinetics, the MIC is most often compared to plasma concentrations, regardless of protein binding and tissue distribution, with only a few exceptions (1). For pharmacodynamics, the MIC does not provide information on the rate of antimicrobial activity and whether changing drug concentrations may change the rate. Furthermore, these indices provide only all-or-nothing concentration-effect relationships.

Therefore, a different and probably more powerful approach to assess the efficacy of antimicrobial agents in vitro is the use of PK-PD modeling based on time-kill curves, where microbial killing and growth can be followed as functions of both time and antimicrobial-agent concentrations (27). The advantage of PK-PD modeling is that it allows direct comparisons of the effects of various concentration profiles and, therefore, characterization of the full time course of antimicrobial effects (27). However, only a few groups have used this approach to characterize antibiotic efficacy both in vitro (7, 15, 26, 28, 29) and in vivo (16, 34), and even less has been done with antifungal agents (14), at least to our knowledge. Furthermore, these previously published studies using PK-PD analysis based on an E_max pharmacodynamic model or Hill equation did not try to make a distinction between net effects resulting from growth inhibition and those resulting from death stimulation.

Therefore, the objective of the present study was to develop and compare mechanistic PK-PD models characterizing the effects of drugs acting by fungal growth inhibition with those acting by fungal death stimulation in a dynamic in vitro model of infection with Candida albicans.

Azole antifungal agents are known to exhibit fungistatic activity (1, 30). They act primarily on ergosterol biosynthesis by inhibiting cytochrome P450-dependent conversion of lanosterol to ergosterol. The resulting ergosterol depletion interferes with the bulk functions of ergosterol as a membrane component, but more importantly, severe ergosterol depletion may also interfere with the “sparking” functions of ergosterol, affecting cell growth and proliferation (11). For this experiment, fluconazole was selected as a representative fungistatic drug that acts by inhibiting the growth of Candida albicans.

Echinocandin derivatives have a fungicidal activity on Candida spp. (19), inhibiting the synthesis of β-(1,3)-d glucan, an essential component of cell wall growth, and therefore affecting membrane integrity. The cell wall loses its mechanical strength and becomes unable to resist intracellular osmotic pressure, leading ultimately to destruction of the fungal cell. Caspofungin was selected as a representative fungicidal drug that acts by stimulating the death of Candida albicans.

The PK-PD parameters estimated from these models could be proposed to characterize the efficacy of antifungals instead of the MIC. This possibility is interesting not only from an academic point of view but also because invasive, opportunistic fungal infections, particularly those due to Candida albicans, have become an increasing and important cause of nosocomial infections associated with substantial morbidity and mortality in immunocompromised patients, and the development of modern PK-PD modeling approaches should be of benefit to these patients (12).

However, our initial objective was to use a simple, well-controlled, dynamic in vitro system to assess the ability of PK-PD models to characterize the effect-versus-time profiles of antifungal agents with parameters that would discriminate between compounds acting by growth inhibition and those acting by death stimulation as an alternative to MICs.

MATERIALS AND METHODS

Isolate of Candida albicans.

An American Type Culture Collection (ATCC) reference strain of Candida albicans (ATCC 3153) was used throughout the study. For each study, two fungal colonies were subcultured onto Sabouraud-chloramphenicol agar (Bio-Rad, Marnes-La-Coquette, France), and the plates were incubated at 37°C for 48 h. The cultures were grown at 37°C for 18 h in Difco yeast nitrogen base broth (Becton Dickinson, MD) under gentle agitation, washed three times, suspended in sterile saline, and quantified in a Malassez hemocytometer (VWR, France). The suspension was diluted with sterile saline in order to obtain a starting concentration of 5 × 10³ organisms per ml.

The MICs of fluconazole and caspofungin were determined by using RPMI 1640 media (with l-glutamine and without bicarbonate) buffered with 0.165 M 3-(N-morpholino)propanesulfonic acid (MOPS) at a pH of 7. A Candida inoculum was prepared by suspending the yeast in RPMI-MOPS to a final concentration of 10³ CFU per ml, and the MIC was determined after a 48-h incubation at 37°C, without shaking. The MIC was defined as the lowest drug concentration allowing no visible fungal growth (31). The tests were performed in duplicate.

Antifungal agents.

A 2-mg·ml⁻¹ intravenous commercial solution of fluconazole (Triflucan I.V.; Pfizer, Paris, France) and a 50-mg·ml⁻¹ intravenous commercial solution of caspofungin (Cancidas; Merck Sharp Dohme-Chibret, Paris, France) were used throughout the study.

Antifungal-drug carryover.

The carryover of the antifungal drugs was studied at concentrations equal to 100 μg·ml⁻¹ of fluconazole and 10 μg·ml⁻¹ of caspofungin, which corresponds to the highest concentrations of antifungal drugs studied in the in vitro models. A fungal suspension was prepared with isolate 3153 to yield an inoculum of approximately 5 × 10³ cells per ml and spiked with 100 μl of fluconazole or caspofungin solution to give a final concentration equal to 100 μg·ml⁻¹ or 10 μg·ml⁻¹, respectively. The resulting suspension was diluted 1:10 and 1:100 in sterile saline, and 100-μl aliquots were plated onto Sabouraud-chloramphenicol agar for the determination of viable colony counts. Following 48 h of incubation at 37°C, the number of CFUs was determined. Tests were conducted in triplicate. The mean colony count data were compared with the results obtained with the control. Significant fluconazole or caspofungin carryover was defined as a reduction of >25% in the mean number of CFUs per milliliter compared with the colony count for the control (17). If significant carryover was detected, the same procedure was repeated with samples washed twice with sterile saline in order to eliminate the antifungal drug (22).

In vitro infection model.

A one-compartment in vitro infection model was developed to simulate exponentially changing drug concentrations of fluconazole or caspofungin in the presence of viable Candida albicans cells. The glass compartment was filled with 400 ml of RPMI 1640 (Invitrogen, Cergy-Pontoise, France) supplemented with 2% sorbitol (6) containing only a fungal culture (for the control growth experiment) or a fungal culture and either fluconazole or caspofungin at various initial concentrations (C₀s). The compartment contained a magnetic stir bar for continuous mixing and sample ports. A peristaltic pump (Masterflex L/S; Fischer Scientific Labosi, Elancourt, France) continuously supplied and removed the culture broth from the central compartment at a flow rate adjusted to simulate a half-life equal to 3 h. Attainment of this value was checked experimentally for both fluconazole and caspofungin (data not shown). The whole system was maintained at 37°C throughout the experiment. The starting inoculum of Candida albicans in the central compartment was 5 × 10³ cells per ml. Four hours after introduction of the inoculum, fluconazole- or caspofungin-diluted solutions were introduced into the central compartment to yield various predefined C₀s. Samples were taken from the central compartment 4 h after the introduction of the inoculum—immediately before the introduction of fluconazole—and at approximately 4, 6, 8, 15, 18, 22, and 27 h after the introduction of fluconazole. Similarly, samples were taken 4 h after the introduction of the inoculum—immediately before the introduction of caspofungin— and at approximately 1, 2, 3, 4, 8, 19, 22, and 27 h after the introduction of the caspofungin. Since carryover was detected with caspofungin, the samples were washed twice with sterile saline before being processed. The samples were then serially diluted 1:10 in sterile saline, and 100-μl aliquots were plated onto Sabouraud-chloramphenicol agar. After 48 h of incubation at 37°C, the colonies were counted, and the results were expressed in CFUs per ml. Two series of three experiments were conducted with each agent. For each experiment, a control and three different initial drug concentrations were studied according to the experimental plan reported in Table 1. Note that a total of six controls was used.

TABLE 1.

Experimental plan with initial concentrations of fluconazole and caspofungin tested

Drug	C0 (μg·ml−1) for indicated experiment:a
	Experiment 1	Experiment 2	Experiment 3
Fluconazole	0b	0b	0b
	100	100	10
	1	10	1
	0.1	0.1	0.01
Caspofungin	0b	0b	0b
	10	1	0.1
	1	0.1	0.001
	0.01	0.01	0.001

^aC₀, initial concentration.

^bControl.

PK-PD modeling. (i) Natural growth and death of Candida.

The initial growth of Candida cells in the absence of a drug can be described by the following equation (34):

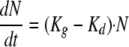(1)

where K_g is the growth rate constant and K_d is the natural-death constant of Candida albicans. However, this equation could not describe the observed growth saturation over time. The model described by Mouton et al. (26) was implemented to account for it. It incorporates a parameter that corresponds to the maximum number of Candida cells (CFU·ml⁻¹; N_max) obtained in the in vitro system according to the following equation:

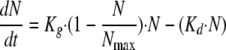(2)

Because the in vitro model operates by dilution, a correction for fungal loss due to broth renewal was introduced in the PK-PD model as follows:

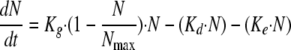(3)

where K_e corresponds to the elimination rate constant due to broth renewal. K_e was set equal to 0.23 h⁻¹, corresponding to the 3-h drug elimination half-life.

(ii) Effects of antifungal drugs.

Fungistatic agents should inhibit cell division (11), whereas fungicidal agents are supposed to stimulate cell death (19). Because fluconazole exhibits fungistatic activity both in vitro (30) and in vivo (1), a growth inhibition model was developed for this drug:

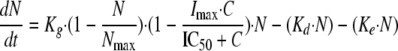(4)

where I_max, the parameter reflecting the maximum fractional extent of inhibition, may vary between 0 and 1, C is the drug concentration, and IC₅₀ is the inhibitory concentration producing 50% of maximal inhibition.

Caspofungin exhibits fungicidal activity both in vitro (30) and in vivo (1), so a death stimulation model was developed for this compound. The fungicidal effect was added to the natural death rate:

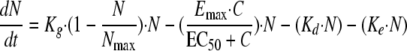(5)

where E_max is the maximum killing rate and EC₅₀ is the drug concentration producing 50% of the maximum effect.

(iii) PK-PD analysis.

Data were analyzed using the population analysis software Nonmem (version 1.1; Globomax, MD). All data from the six experiments were fitted simultaneously in a single analysis. PK parameters were fixed in the PK-PD model and set equal to their selected values (V = 0.4 liters, where V is the volume corresponding to the bulk volume in the glass compartment, and CL = 1.54 ml·min⁻¹, where CL is clearance, accounting for an elimination half-life of 3 h with the 0.4-liter volume). A single estimated value of Candida-related parameters (K_g, K_d, N_max) was obtained by fitting the data from the six experiments with the PK-PD model. The drug-related PK-PD parameters, IC₅₀ and I_max for fluconazole and EC₅₀ and E_max for caspofungin, were obtained by fitting the data from the corresponding experiments. The algorithm used for the analysis was the first-order method. An exponential error model was used to describe interindividual variability. An exponential residual error model was used in the analysis.

(iv) Model validity.

Model performance was assessed by analyzing the weighted residuals, the relationship between the observed data and the corresponding predictions, residual variability, and the precision of the parameter estimates. Discrimination between tested models was assessed by the difference in the objective function value (−2 log likelihood). The criterion for inclusion of a single parameter was a decrease in the objective function value of 3.84 (P < 0.05).

RESULTS

MICs.

The median MICs for Candida albicans ATCC 3153 were assessed as equal to 1.56 μg·ml⁻¹ and 0.015 μg·ml⁻¹ for fluconazole and caspofungin, respectively. This strain could therefore be considered susceptible to fluconazole on the basis of National Committee for Clinical Laboratory Standards interpretative guidelines (31). The MIC of caspofungin is in the range of values typically observed with Candida albicans, which could also be considered susceptible to caspofungin (10).

Carryover of antifungal drugs.

No antifungal carryover was observed with fluconazole, since all samples were within 25% of the mean count of the control colony. A significant carryover was observed with caspofungin, but it disappeared after the samples were washed twice with sterile saline.

PK-PD modeling.

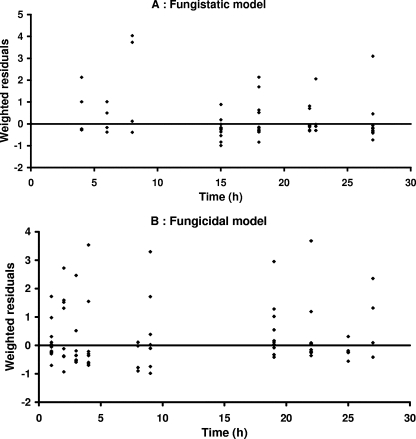
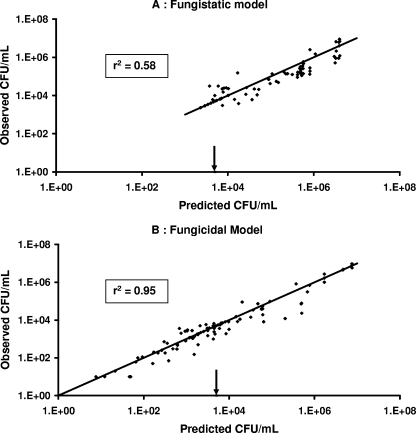
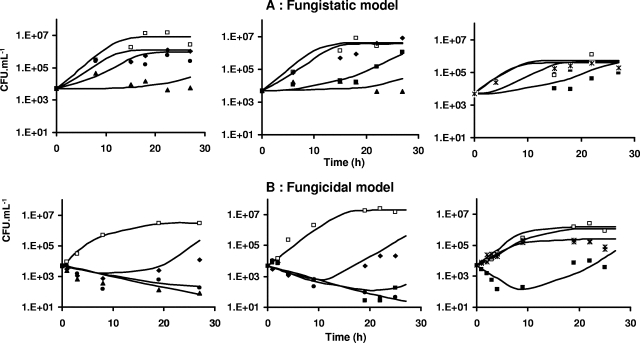
In the presence of fluconazole, Candida growth was delayed but no decay was observed, even at the highest concentrations, whereas in the presence of sufficiently high concentrations of caspofungin, decay of Candida spp. over time, followed by a regrowth phase, was observed. Accordingly, the growth inhibition or fungistatic model best describes the fluconazole data, whereas the death stimulation or fungicidal model adequately describes the caspofungin data. Weighted residuals were randomly scattered around 0 except for a small bias observed at early times with the fungistatic model (Fig. 1). Corresponding Bayesian estimates obtained with the post hoc option of Nonmem showed a good correlation between individual predicted and observed experimental data (Fig. 2). A relatively large variability was associated only with the N_max parameter (Table 2). According to the standard error, the parameters of the PK-PD models were properly estimated (Table 2). Residual and interindividual variabilities were also well estimated (Table 2). The growth inhibition model adequately described the fungistatic effect of fluconazole (Fig. 3A), whereas the fungicidal effect of caspofungin was best described using the death stimulation model (Fig. 3B). The estimated value of the natural growth rate constant K_g was about 20-fold and 4-fold higher, respectively, than the values of the natural death rate constant K_d and the rate of broth renewal (Table 2).

FIG. 1.

Weighted residuals versus time for the fungistatic (A) and fungicidal (B) models. Included are horizontal lines at 0.

FIG. 2.

Goodness-of-fit plots of individual observed CFU·ml⁻¹ versus model-predicted CFU·ml⁻¹ for the fungistatic (A) and fungicidal (B) models. Included are lines of identity. Arrows indicate beginning inoculum values.

TABLE 2.

Parameter estimates of PK-PD models with typical values

Parametera	Typical value	SEb
Candida specific
Kg (h−1)	8.64 × 10−1	3.21 × 10−2
Kd (h−1)	4.14 × 10−2	2.45 × 10−2
Nmax (CFU·ml−1)	1.48 × 106	5.54 × 105
Fluconazole PK-PD
IC50 (μg·ml−1)	9.29 × 10−2	5.67 × 10−2
Imax	6.75 × 10−1	3.42 × 10−2
Caspofungin PK-PD
EC50 (μg·ml−1)	2.51 × 10−4	4.62 × 10−5
Emax (h−1)	8.04 × 10−1	5.11 × 10−2
Interindividual variability (% CV)
η (Nmax)	225	218
η (Emax)	65	56
Residual variability (% CV)
ɛ1 Fluconazole	197	199
ɛ1 Caspofungin	96	63

^aCV, coefficient of variation; η, parameter for interindividual variability; ɛ₁, parameter for residual variability.

^bSE, standard error.

FIG. 3.

Plots showing CFU·ml⁻¹ of fungi over time for the fungistatic (A) and fungicidal (B) models. Each graph represents one experiment. Symbols for fungistatic experiments shown in panel A: control, □; C₀ = 100 μg·ml⁻¹, ▴; C₀ = 10 μg·ml⁻¹, ▪; C₀ = 1 μg·ml⁻¹, •; C₀ = 0.1 μg·ml⁻¹, ⧫; C₀ = 0.01 μg·ml⁻¹, *. Symbols for fungicidal experiments shown in panel B: control, □; C₀ = 10 μg·ml⁻¹, ▴; C₀ = 1 μg·ml⁻¹, •; C₀ = 0.1 μg·ml⁻¹, ▪; C₀ = 0.01 μg·ml⁻¹, ⧫; C₀ = 0.001 μg·ml⁻¹, *. Lines represent individual predictions based on the developed PK-PD models.

DISCUSSION

In vitro PK-PD models based on time-kill curves have been used to assess the antimicrobial efficacy of antibiotics (6, 7, 21, 24, 26, 28). However, no such experiments had previously been conducted with antifungal agents, at least to our knowledge. Furthermore, mechanistic PK-PD models were developed here for the first time to differentiate between growth inhibition and death stimulation of microorganisms. The basic idea was that the changing number of CFUs over time is governed by the difference between the rate of growth and the rate of death, with antimicrobial agents either inhibiting microbial growth (i.e., static effect) or stimulating microbial death (i.e., killing effect). Mechanistic PK-PD models derived from those published by Zhi et al. (34) and others (21, 26) could then be developed to account for these distinct mechanisms of action.

In in vitro models, drug concentrations may be kept constant or left to vary with time (26, 27). The main advantage of the latter is that in vivo concentration-time profiles can be simulated under various dosing regimens, using both central and even peripheral compartments if necessary, to investigate antimicrobial effects. However, the main concern with these models is that the volume of the broth in the flask may be difficult to control over time. A filter was tentatively used to prevent the outflow of Candida cells, but this led to blockage of the membrane and could not be used. Therefore, equations were adjusted to account for loss of Candida inoculum due to broth renewal. The initial inoculum concentrations usually ranged between 0.5 × 10³ and 2.5 × 10³ CFU·ml⁻¹. Our initial inoculum concentration (5 × 10³ CFU·ml⁻¹) was slightly higher than the usual values, although it was previously used in similar experiments (20), in particular to properly characterize the decay followed by the regrowth phase in the presence of caspofungin.

At this stage, a one-compartment PK model was considered. Experimental data were analyzed using a population approach, allowing descriptions of the mean tendencies in the population as well as between experiments and between experimental-day variabilities. The natural growth and death rate constants were estimated from the experiments conducted with both fluconazole and caspofungin during the same Nonmem run, since they were considered specific to the Candida strain used and independent of the drug. Following preliminary experiments, the drug elimination half-life was arbitrarily set to 3 h (corresponding to K_e = 0.231 h⁻¹) for both fluconazole and caspofungin. The advantage of using such a relatively short half-life was that the drug concentrations varied quickly from active values (much higher than MICs) to inactive values (much lower than MICs), allowing completion of the study in a relatively limited period of time. In these conditions, parameters characteristic of the selected Candida strain as well as those characteristic of drug efficacies were adequately estimated (Table 2). A relatively large interindividual variability was associated with the estimated value only for N_max (Table 2). A potential explanation was that the experiment was stopped after 31 h, which may have been too early for adequate description of the plateau and, therefore, optimal estimation of N_max. However, the saturable growth exponential model (7, 26) is a convenient but probably crude representation of a much more complex reality, which should also contribute to the relatively poor estimate of N_max. A more sophisticated model describing the stationary phase as a switch occurring from normally growing cells to resting cells was recently proposed by Nielsen et al. (28) to account for the stationary phase. However, using our data, this model was not superior to the initial N_max model. Furthermore, it requires mechanistic assumptions of phenotypic switching that are not documented for Candida albicans and was therefore not selected.

The mechanistic PK-PD models used in this study were inspired by indirect response models, proposed by Jusko and colleagues (9), that account for the pharmacodynamics of drugs acting by inhibition or stimulation of the factors controlling either the production or dissipation of the drug response. The major difference was that Jusko and colleagues considered a constant-rate process for production of the response, whereas Candida development required introduction of an initial saturable exponential growth function in the model. PK-PD models similar to ours have recently been successfully tested to describe the changes in bacterial population dynamics during in vitro experiments where Staphylococcus aureus was exposed to different concentration-time profiles of ciprofloxacin (7). In this study, a growth inhibition and a death stimulation model were both fitted to experimental data but without any a priori assumption on the mechanism of action of ciprofloxacin. Under certain circumstances, the growth inhibition and death stimulation models can predict virtually similar net effects, and discrimination between the two is made possible only by letting concentrations vary within a wide range. In the previous study (7), a growth inhibition model was preferred because it best described the data. As a consequence, when fluoroquinolone concentrations are high enough to completely inhibit bacterial growth, the resulting maximal bacteria-killing rate should represent the natural death rate of Staphylococcus aureus.

Our study provides data corresponding to these two different mechanisms of action, allowing direct comparisons between the two types of models. The developed fungistatic model (equation 4) supposes that the drug inhibits Candida growth with no effect on its death. This hypothesis is consistent not only with the mechanism of action of fluconazole (11) but also with previously published in vitro data showing that even doses producing fluconazole concentrations exceeding the MIC by more than a factor of 200 did not result in killing of the organism (1). However, it was expected that at high concentrations of fluconazole, Candida growth would be totally inhibited, leading to a decay of CFUs over time corresponding to natural death, as observed with ciprofloxacin and Staphylococcus aureus (4). But no CFU decay could be observed experimentally, even when the initial fluconazole concentrations were much higher than the estimated IC₅₀. Instead, Candida growth slowed but was still observed at the highest initial fluconazole concentrations. The elimination half-life (16.7 h) corresponding to the natural death constant (4.14 × 10⁻² h⁻¹) is quite long, but due to broth renewal and the resulting Candida albicans dilution in the absence of filters, CFUs should decay with an elimination half-life of close to 3.0 h after growth is totally inhibited, which should be readily observable. Therefore, our results suggest that growth inhibition due to fluconazole cannot be complete even at very high drug concentrations. Consistent with those results, the I_max parameter in equation 4, initially set equal to 1, was estimated at only 0.675 (Table 2). A complementary set of experiments was conducted in vitro without broth renewal and using a concentration of fluconazole as high as 100 μg·ml⁻¹, kept constant with time. Even with these drastic conditions, Candida growth was observed, confirming the absence of total inhibition. Although there is no explanation for these observations, a rapid decrease in the susceptibility of Candida albicans to fluconazole occurring during the experiment and resulting from rapid development of resistant mutants could be hypothesized, although it is unlikely in such a short period of time. This hypothesis was tested and ruled out, since no difference could be observed between the MIC values determined at the beginning and at the end of the experiment. The death stimulation model corresponding to a fungicidal effect adequately described the concentration-dependent initial decay of CFUs, followed by regrowth, in the presence of caspofungin.

The two mechanistic PK-PD models predict different types of effect-versus-time profiles (Fig. 3). As already mentioned, a decay of CFUs over time was observed with the death stimulation model, providing initial drug concentrations were sufficiently high, since the two models predict virtually similar profiles of effects over time at the lowest concentrations tested.

Since the IC₅₀ and EC₅₀ correspond to different mechanisms of action, they should not be compared, but IC₅₀ values of various fungistatic compounds or EC₅₀ values of fungicidal compounds would be interesting to compare and could eventually be used to predict the time courses of drug effects that cannot be done with MICs.

The basic idea underlying this PK-PD modeling experiment was that the IC₅₀ or EC₅₀, but not the MIC, which is a static parameter, could allow prediction of the effect of drugs in vivo when concentrations change over time. In fact, these mechanistic models provide much better information on the intensity of drug effects over time than the traditional PK-PD index based on MICs. However, a mathematical relationship exists between the IC₅₀ and the MIC as well as between the EC₅₀ and the MIC (25). Therefore, it should theoretically be possible to compare MIC values determined experimentally with those predicted by the PK-PD models. Yet, because the IC₅₀ and EC₅₀ were not estimated in conditions similar to those of the MICs, direct comparisons were not possible. The experimentally determined MIC corresponds to the lowest concentration preventing opalescence that was observed when the CFU reached a value close to 5 × 10⁷. However, this value is more than 10-fold higher than the maximal number of CFUs (N_max = 1.48 × 10⁶ CFU·ml⁻¹) obtainable using the in vitro dynamic model, due essentially to rapid broth renewal. Accordingly, complementary experiments conducted in the same conditions (400 ml of medium in a glass vial) but without bulk renewal to prevent Candida outflow showed that the maximal obtainable number of CFUs in the absence of the drug (N_max) was close to 10⁸ CFU·ml⁻¹. Experimental conditions allowing direct comparisons between the IC₅₀ or EC₅₀ and the MIC are being developed.

Another major issue to consider in the future is the comparison between in vitro and in vivo data. In vivo experiments lead to important interanimal variability because the initial inoculum and the dose of the drug administered cannot be exactly the same between animals and because not all animals handle drugs and Candida species in exactly the same manner. This variability can be controlled in vitro. Furthermore, the range of concentrations in vitro is not limited by toxicity issues and may be selected to provide optimal estimation of PK-PD parameters for fungicidal drugs in particular, as previously discussed. Drug elimination half-lives may also be adjusted in vitro to any desirable value. Yet differences between in vivo and in vitro environments (changes in microbial growth patterns, effects of protein binding, immune defense system differences) exist (21). Therefore, the key issue remains that of not only knowing whether the in vitro estimates of parameters characteristic of the PK-PD model, in particular the IC₅₀ or EC₅₀, are predictive of their in vivo value, but also of knowing whether the general structure of the model itself applies in vivo. These questions are presently under investigation.

In conclusion, the two developed mechanistic PK-PD models allow the description of Candida growth inhibition by fluconazole and Candida death stimulation by caspofungin according to the documented mechanisms of action of these drugs. The IC₅₀ or EC₅₀ parameter could be used in vitro to compare drug potencies and to study drug combinations during preclinical and clinical development. The developed, integrated PK-PD models allow much better characterization of drug efficacy over time than the MIC-based PK-PD index and could therefore represent an interesting alternative to optimize drug therapy during fungal infections by improving efficacy as well as controlling the emergence of drug-resistant Candida spp. (18). However, the usefulness of these models in the clinical setting requires further evaluation, particularly in vivo.