Variability in Stepping Direction Explains the Veering Behavior of Blind Walkers

Abstract

Walking without vision results in veering, an inability to maintain a straight path that has important consequences for blind pedestrians. We addressed whether the source of veering in the absence of visual and auditory feedback is better attributed to errors in perceptual encoding or undetected motor error. Three experiments had the following results: no significant differences in the shapes of veering trajectories were found between blind and blindfolded participants; accuracy in detecting curved walking paths was not correlated with simple measures of veering behavior; and explicit perceptual cues to initial walking direction did not reduce veering. We present a model that accounts for the major characteristics of our participants' veering behavior by postulating three independent sources of undetected motor error: initial orientation, consistent biases in step direction, and most importantly variable error in individual steps.

In the context of human locomotion, veering is any deviation from an intended path. When walking an intended straight line, veering is the lateral deviation from that line. Veering by human pedestrians becomes evident when visual targeting cues are absent as in cases of blindness or severely reduced visibility (e.g., walking in the dark or in a blizzard). For blind people, veering can be an everyday problem, potentially threatening safety when crossing a street at a busy intersection. Non-visual environmental cues such as wind direction, slope of the ground plane, or directional acoustic cues, can help blind pedestrians accurately navigate across spaces. Unfortunately, reliable non-visual cues are not always available. In the absence of such cues, our research and the findings of others (to be reviewed below) show that blind people veer away from intended straight pathways. The purpose of the present study was to answer the question: What causes this veering behavior? Our research suggests that a simple explanation – unperceived motor noise at the level of individual steps – may explain the veering behavior of both blind pedestrians and sighted pedestrians who are blindfolded.

Some early proposals for explaining veering behavior, reviewed by Guth and LaDuke (1994) and by Cratty (1965, 1971), included dominance or difference in leg strength or leg length, biomechanical asymmetries, and evolutionary hypotheses. Cratty (1965) and later studies reviewed by Guth and LaDuke (1994) focused on blind pedestrians, and were motivated by interests in enhancing mobility skills of blind people. Cratty noted that early studies showed the presence of veering in blind walkers, but magnitudes were not accurately measured or reported. Cratty also recognized that prior empirical studies of human veering were flawed either because of inaccurate or nonobjective measures. Later, Guth and LaDuke (1994) explained that the majority of prior empirical studies used group mean measures of walking performance that were insufficient to accurately characterize individual veering behavior. As emphasized by Guth and LaDuke (1994), these group measures did not describe the distinct characteristics of individuals. They argued that both directional bias and trial to trial variability should be considered in order to capture the veering patterns of individuals. Earlier studies were problematic because they collapsed individual data across trials and days. Furthermore, these hypotheses predicted consistent rather than variable patterns of walking.

Guth and LaDuke (1995) focused their analysis on the lateral offsets from a nominal straight line (veer) at the end of a non-visual walking trial. We took their analysis further by recognizing that different walking trajectories can result in the same lateral offset. For instance, one person might walk a perfectly straight line, but end up with an offset from the intended straight line because of an initial orientation error. Another person might begin straight and curve away from the intended pathway, possibly due to a directional stepping bias, but end up in the same final location as the first person. Because these trajectory differences may arise from distinct causes, it is informative to measure and analyze individual trajectories and their patterns, rather than just their end points.

A pedestrian's ability to walk a straight line depends both upon the availability and quality of sensory information about walking direction (Loomis & Beale, 1998; Philbeck, Loomis, & Beall, 1997; Rieser, Ashmead, Talor, & Youngquist, 1990), and the capacity to execute movements in an intended direction. In addition to vision, sources of sensory information used during navigation include acoustic, tactile, vestibular, proprioceptive and kinesthetic cues. Vision and audition can be used to maintain a constant heading toward a distant target. Tactile cues may be useful for following a prescribed route (e.g., a gravel path). Vestibular, proprioceptive or kinesthetic cues may be useful in detecting rotation away from a straight path (Chance, Gaunet, Beall, & Loomis, 1998). Evidence from a study of patients with vestibular pathologies (Cohen, 2000) suggested that normal veering could be related to sensitivity in the vestibular system. Finally, interfering sensory cues may influence veering. For instance, Millar (1999) showed that extraneous auditory noise and influences on postural signals (such as a handbag in one hand) can result in greater veering.

Even in the absence of any sensory input, it is possible that a human (or robot) could proceed along a fairly straight path. This notion forces us to consider the precision of the motor system in executing movements in a constant linear direction. Imagine, for example, a robotic vehicle with no sensors of any kind. If it is placed on a flat surface, with isotropic frictional characteristics, and if there are no deflecting forces such as wind, the ability of the vehicle to travel in a straight line would depend on the mechanical design and characteristics of the motor. Imprecision could manifest as a predisposition for the vehicle to take the wrong heading, curve toward the left or right, or zigzag erratically. Similarly, it is possible that when people are deprived of adequate perceptual input for maintaining an intended path, motor or biomechanical limitations may limit accuracy and account for veering behavior. More generally, the ability of a human or robot to travel a straight line would depend on motor precision, the quality of sensory feedback, and the information loop connecting these two.

Although blind walkers often make use of acoustic or tactile cues during walking, those cues are often uninformative and sometimes misleading. For that reason, we asked what factors limit straight-line walking in the absence of visual, acoustic or tactile cues.

In Experiment 1, we assessed the veering behavior of blind walkers and sighted walkers who were blindfolded. They repeatedly attempted to walk a straight line after being physically aligned to the desired walking direction. Two-dimensional walking trajectories were sampled every 1.52 meters, for a total of 9.14 meters. These measurements and methods were similar to those employed by Guth and LaDuke (1995), providing a replication of their work and a baseline for comparison and modeling in subsequent parts of our study.

In Experiment 2, we asked whether sensory limitations (vestibular, proprioceptive or kinesthetic) account for the magnitude of veering errors. We did this by measuring participants' thresholds for detecting the curvature of walking paths (similar to Cratty, 1965). We reasoned that if the ability to walk a straight line is limited by the sensory capacity to detect deviations from straightness (i.e., the ability to detect curved paths) then people with poor curvature detection should exhibit greater veering behavior.

In Experiment 3, we asked how veering is affected by three different initial orientation conditions, including physical alignment used in Experiment 1, and two conditions with explicit perceptual pointers. This experiment tested whether veering behavior is due to inadequate perceptual information of initial orientation. The results address the merits of providing explicit perceptual cues, such as physical pointers that indicate walking direction, which may be of practical value in blind mobility.

Finally, in the modeling section, a simple random-walk model replicated the types of trajectories and statistical properties of human performance when walking without vision. We found that this model can simulate qualitative and quantitative characteristics of human veering behavior. The agreement found between model and human behavior suggests that motor noise may explain human veering in the absence of vision. We believe that motor noise occurs at the level of individual human steps. In other words, errors in individual steps can accumulate over time, causing the pattern of veering exhibited by blind walkers.

Experiment 1

Objective

How accurately do blind and blindfolded sighted people walk a straight line without vision, and are there differences between these groups? Studies of blind versus sighted individuals suggest that people with different visual experience may have only slight differences in performance under a variety of different motor tasks, such as walking a maintained heading and replicating distance (Klatzky, Golledge, Loomis, Cicinelli, & Pellegrino, 1995) and wayfinding tasks (Giudice, 2004). In walking a straight line, blind people might perform better because they are experienced in non-visual locomotion and make better use of vestibular, proprioceptive or kinesthetic feedback. On the other hand, sighted people may perform better because they constantly make use of visual feedback, including optical flow, to calibrate their motor responses (cf., Rieser, Hill, Talor, Bradfield, & Rosen, 1992). Finally, sighted and blind pedestrians may perform equally well if performance is limited by non-perceptual factors such as intrinsic noisiness of the motor system.

Method

Participants

Five blind and five sighted individuals participated (see Table 1). Three of the blind participants had slight residual vision, but all participants relied primarily on non-visual cues for mobility. All blind participants used dog guides for day-to-day travel, but dogs were not used during the experiments.

Table 1.

Experiment 1 Participants

Participant	Age	Gender	Pathology	Onset	Vision level
Blind
P1	48	F	Glaucoma	Birth	No Light Perception
P2	27	M	Leber's Congenital Amaurosis	Birth	OU: Light Perception, 20/1500
P3	36	M	Diabetic Retinopathy	15 yrs	No Light Perception
P4	48	F	Retrolental Fibroplasia	Birth	OD: Reads Large Print; OU: Light Perception, < 20/400
P5	29	F	Micro Thalmus, Clouded Cornea	Birth	OD: Light Perception, Prosthetic; OS: Color/Light Perception
Sighted
P6	24	M
P7	21	M
P8	50	F
P9	41	M
P10	31	F

Testing Arrangements and Procedure

Experiments were conducted in a 5.5 by 20.1 meter room in the basement of Elliott Hall at the University of Minnesota. We used 1.9 cm tape to mark a 4.88 meter wide by 9.14 meter long area on the floor. Along the 9.14 meter pathway, a perpendicular line was taped at every 1.52 meter interval, and marked with 0.30 meter hash marks (seen in Figure 1C). These markings were not detectable by the participants. The long edge of a 0.91 by 1.83 meter rectangular table was placed at the beginning of the walking pathway, and was oriented perpendicular to the desired line of travel.

Figure 1.

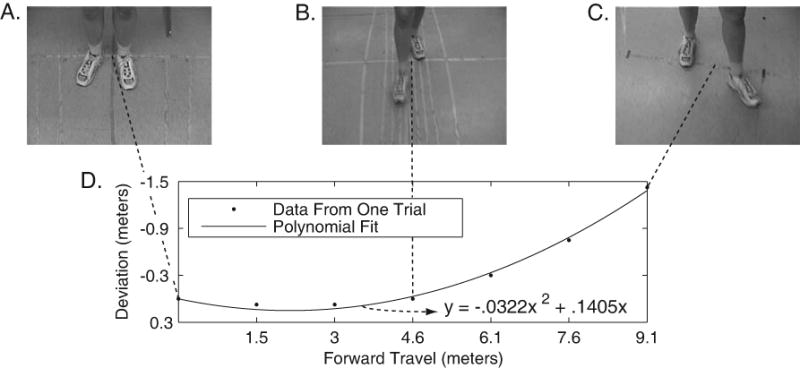
Example of One Trial and Polynomial Fit. A unique second-order polynomial was fitted for each trial.

Blind participants with residual vision (participants P2, P4 and P5) and sighted participants wore blindfolds. Blind participants P1 and P3 did not require blindfolding because they had no residual vision. All participants wore ear muffs to minimize sound cues. The experimenter could communicate with participants via FM radio headphones placed inside the ear muffs. With earmuffs and blindfolds in place, there were no acoustic, tactile or visual cues for direction. Trials were conducted in the center of the room, away from the walls, and participants were assured that they would be prevented from colliding with obstacles or walls.

Participants began each trial by physically aligning their backs against the edge of the table, using their hands to feel the table's straight edge. The experimenter made sure that participants straddled the beginning of the intended trajectory line (seen in Figure 1A). They were instructed to walk a straight line directly away from (perpendicular to) the table, at a comfortable speed, until the experimenter asked them to stop. Trials were terminated either when they crossed a goal line 9.14 meters from the table, or veered more than 2.44 meters from the intended pathway. Trials for each participant were recorded over 3 to 4 days, with a minimum of 9 trials per day, and 39-45 trials per person (see Table 5).

Table 5.

Walking Parameter Estimates (Experiment 1)

Participant	Day	Initial orientation*		Bias*		N trials
		Mean	S.D.	Mean	S.D.
1	1	-1.06	1.03	-0.67	1.84	10
	2	1.69	2.07	0.29	1.70	11
	3	2.56	2.19	0.27	0.93	12
	4	3.00	2.63	0.17	2.44	11
2	1	-4.91	1.93	-0.12	1.50	10
	2	-1.95	4.54	-0.015	0.74	10
	3	-7.66	2.73	-0.003	0.77	10
	4	-1.24	3.97	-0.058	1.43	11
3	1	-1.09	2.23	0.44	1.26	10
	2	-0.85	2.41	0.86	1.03	10
	3	-2.15	2.56	0.55	1.43	10
	4	-3.00	1.52	0.22	0.58	10
4	1	0.11	3.08	0.98	1.59	10
	2	-1.62	2.38	0.014	1.73	10
	3	3.86	2.68	0.69	1.61	11
	4	-1.36	2.82	-0.21	1.37	10
5	1	-4.19	1.96	-0.62	1.34	11
	2	-0.80	2.45	0.24	1.57	10
	3	1.59	2.17	-0.28	1.07	11
	4	1.97	1.67	-0.40	0.95	10
6	1	5.33	1.77	1.63	1.12	12
	2	5.87	1.58	1.17	1.55	12
	3	1.83	1.25	0.25	1.06	10
	4	3.37	1.77	0.46	0.88	11
7	1	0.52	2.66	0.64	1.65	11
	2	0.28	2.32	0.33	1.99	9
	3	-0.22	2.00	0.52	1.34	10
	4	0.80	1.53	0.66	0.72	10
8	1	-2.57	1.70	0.51	1.60	12
	2	-4.32	3.25	0.20	1.15	12
	3	-4.42	3.27	-0.54	1.05	11
	4	-2.12	2.05	-0.002	1.01	10
9	1	1.32	1.67	0.39	1.69	14
	2	3.57	2.14	0.13	1.28	13
	3	2.23	2.75	-0.05	1.36	14
10	1	0.82	1.90	0.15	2.03	10
	2	-2.10	2.07	0.82	0.94	10
	3	2.41	2.96	0.65	1.96	11
	4	-3.44	2.21	0.11	1.21	10

^*Unit = Degrees

Trials were videotaped and reviewed for scoring. The data were based on measurements taken from video frames at the points where participants passed over each 1.52-meter line. Locations were visually estimated in the video frames, and deviations were recorded to the nearest 8 to 10 cm (Figure 1).

Across the ten participants, there were 420 trials. Four hundred trials were sampled at 1.52-meter intervals out to the 9.14 meter goal line. The remaining twenty trials were sampled in the same manner, but not out to the goal line, due to veering more than 2.44 meters from the intended pathway. Although fewer samples were recorded in these 20 trials they were still included in the analysis.

Since individual trajectories were fairly smooth (i.e., not much zigzagging), a least-squares polynomial with linear and quadratic terms was fitted to each sampled trajectory. Second-order polynomials were chosen because neither straight lines nor parabolas alone satisfactorily fit the data. We examined the properties of the linear and quadratic coefficients of these fits, and the correlations between them.

Results

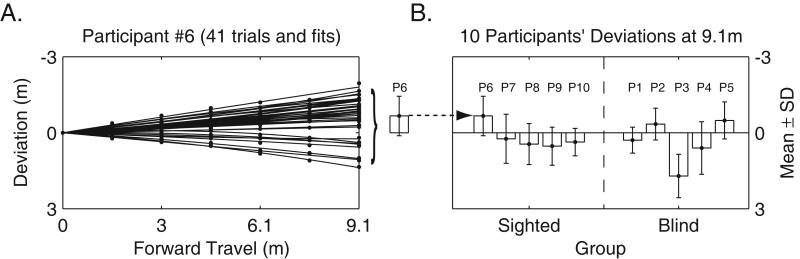
Mean signed (constant) veering errors at 9.14 meters across all trials for individual participants ranged from -0.67 meters (left) to +1.74 meters (right) (Table 2 and Figure 2B). Mean unsigned (absolute) veering errors (mean of the absolute value of the errors) at 9.14 meters ranged from 0.45 meters to 1.74 meters (Table 2).

Table 2.

Mean Veering Error at 9.14 Meters

	Mean Error in Meters
Participant	Signed	Unsigned
Blind
P1	0.30	0.77
P2	-0.35	0.63
P3	1.74	1.74
P4	0.61	0.71
P5	-0.49	0.70
Sighted
P6	-0.67	0.95
P7	0.24	0.45
P8	0.45	0.84
P9	0.54	0.73
P10	0.37	0.69

Figure 2.

Walking Performance without Vision. Figure 2A shows sighted participant P6's performance on 41 trials. The fan shape created over many trials is typical of this and earlier studies of veering associated with walking without vision. Figure 2B shows the average deviation for each participant, 9.14 meters from the origin (See Table 2 for values). In this study, leftward veering is associated with a negative sign, and rightward veering is positive.

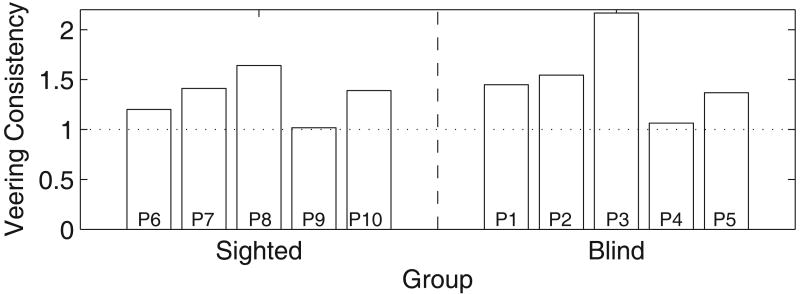
Individual differences (between participants) and variability over days (within participants) were evident. Veering consistency was calculated as the ratio of signed endpoint variance ${\delta }_{\text{total}}^2$ (across days) to the average of the within day variances ${\delta }_i^2$ for each participant: $\frac{{\delta }_{\text{total}}^2}{\frac{1}{n_{\text{days}}}\left({\delta }_1^2+{\delta }_2^2+\Lambda +{\delta }_{n_{\text{days}}}^2\right)}$ (see Figure 3). There were no clear differences between the blind and sighted groups. A 2-factorial, group by day, nested ANOVA on deviations at 9.14 meters, indicated no effect of group (blind versus sighted): F(1,8) = 0.15, p = .71, but indicated a within participants effect of day: F(29,381) = 13.93, p < .001. A second 2-factorial ANOVA showed significant within and between participant differences. This ANOVA was performed in addition to the first, since a balanced design was required to observe the effect of participants, days, and the interaction (which did not test for a group effect). Our analysis in this ANOVA excluded participant P9 because he was tested over 3 days, whereas all other participants in this experiment were tested over 4 days: between participants effect: F(8,240) = 52.23, p < .001; within participants effect over days: F(3,240) = 5.96, p = .017. A significant interaction between participants and days was also found: F(24,240) = 25.10, p < .001. These findings are consistent with the findings of Guth and LaDuke (1995) that showed individual and day to day variations in performance.

Figure 3.

Veering Consistency Across Days. Figure 3 shows the ratio of signed endpoint variance ${\delta }_{\text{total}}^2$ across days to the average of the within day variances ${\delta }_i^2$.

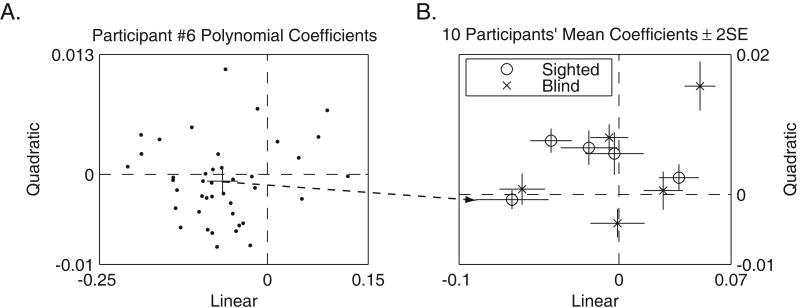
Analysis of trajectories showed that in many trials, there were statistically significant linear and quadratic contributions to the veer (Figure 4). The linear and quadratic coefficients were not strongly correlated (Table 3). Figure 4A shows a scatter plot of the linear and quadratic coefficients for participant P6, over 41 trials. The crosshair in the center of the scatter plot shows the mean (± 2 standard errors). The crosshairs in Figure 4B show corresponding mean values (± 2 standard errors) for all 10 participants in Experiment 1. Trajectories were analyzed in terms of the quadratic and linear coefficients from the polynomial fits. For example, a trajectory with a nonzero linear term and a zero quadratic term would correspond to a straight-line trajectory at a fixed heading away from the target path, but a trajectory with a zero linear term and a nonzero quadratic term would correspond to a portion of a circular path, with the tangent line pointing straight ahead at the starting point. An example of a typical trajectory is shown in Figure 1. It was fit by a curve with a positive linear coefficient (coefficient = 0.1405), and a negative quadratic coefficient (coefficient = -0.0322).

Figure 4.

Quadratic and Linear Contributions to Walking Trials. Figure 4A shows the distribution of linear and quadratic coefficients over 41 trials for participant P6. Each data point represents a polynomial fit for a single trajectory. The crosshair in the middle of Figure 4A shows the mean ± 2 standard errors. Figure 4B shows the mean polynomial coefficients for all 10 participants.

Table 3.

Correlations between linear and quadratic polynomial coefficients

Participant	r2	p-value
Blind
P1	.014	.44
P2	.003	.74
P3	.023	.32
P4	.025	.33
P5	.001	.83
Sighted
P6	.009	.55
P7	.042	.20
P8	.003	.72
P9	.002	.79
P10	.0001	.96

Discussion

The findings in Experiment 1 tell us that people without vision veer significantly when trying to walk a straight line. Furthermore, the results reveal that groups (blind versus blindfolded) do not differ in their veering behavior. Apparently, the large differences in visual experience between the two groups do not have an important influence on the ability to walk a straight line non-visually. This lack of a difference is consistent with the possibility that limitations in the motor system can account for veering behavior. Additionally, we found the lack of correlation between linear and quadratic terms to be somewhat surprising. Due to the lack of correlation, we explored the possibility that components of the polynomial fits were related to different phenomena in walking. In the Model section, we will revisit these data and provide an explanation for them in terms of intrinsic motor noise.

The experiment described here was similar to the experiment conducted by Guth and LaDuke (1995), with the caveat that our experiment was conducted indoors, and therefore used trials of shorter distance. Since Guth and LaDuke tested veering at distances of 25 meters, whereas we tested veering at 9.14 meters, a direct numerical comparison can not be made. However, the model to be presented below will permit us to extrapolate our findings at 9.14 meters to a prediction for veering at 25 meters, and to make an informative comparison with the findings of Guth and LaDuke (1995). We will return to this comparison in the discussion section of the model.

Next, we consider the possibility that veering behavior could be related to sensitivity in sensory feedback. We will address this issue in Experiment 2.

Experiment 2

Objective

The lack of difference in veering behavior between the sighted and blind participants suggests that a history of visual experience is not critical to performance on this task. It remains possible, however, that both sighted and blind people are able to regulate non-visual walking using feedback from vestibular, proprioceptive or kinesthetic signals. For instance, the semicircular canals in the inner ear might detect subtle angular accelerations, a cue to detecting curvature of the walking path. Additionally, feedback signals from muscles or joints in the knees or ankles might provide cues to deviation from a straight line. In either case, compensatory motor commands based on these feedback signals will contain random errors (and possibly systematic errors) that could produce deviation from a straight line. If the ability to walk a straight line is limited by errors in perceptual cues about curvature, we would predict that participants who are good at detecting path curvature (i.e., those with a low perceptual error rate) would also be good at walking straight lines. Conversely, those who are poor at detecting curved walking paths should exhibit more severe veering. Given these possibilities, we asked how the extent of veering relates to sensitivity in detecting curved pathways. We tested the hypothesized relationship between path curvature detection and veering.

Method

Participants

The same 10 participants from Experiment 1 were tested in Experiment 2.

Testing Arrangements and Procedure

The two sets of measurements (straight line walking in Experiment 1 and curvature detection in Experiment 2) were conducted in the same sessions over 3 to 4 days within a several week period. Curvature detection trials were evenly spread over all sessions.

We considered several methods for guiding blind participants along curved pathways to minimize rotational cues from the apparatus itself. It was decided that a smooth operating and non-rigid guiding apparatus would perform best at minimizing confounding feedback. The participants were guided along circular curved paths by a handheld tethered ball, which was attached to a 3-wheeled, ballasted cart (Figure 5). This method was chosen over several other designs because it provided the least amount of rotational torque (a cue for curvature), while still providing an acceptable level of adherence to the intended pathway.

Figure 5.

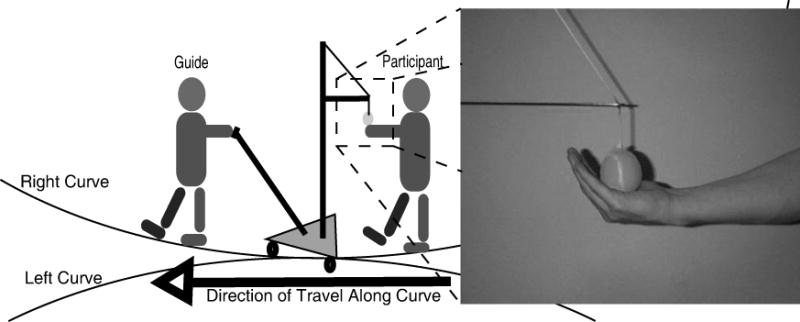
Curvature Detection Guiding Apparatus.

The 10 curves were 4.57 meters long, and had radii of 9.14, 12.19, 18.29, 27.43 and 36.58 meters, left and right. Quantifying curvature by “radius” is equivalent to saying that the curved path is an arc of a circle of the given radius. For instance, a 4.57-meter curve with a radius of 12.19 meters is equivalent to a 4.57-meter portion of the circumference of a circle with a radius of 12.19 meters. Participants were also tested on 9.14 meter-long curves but these data will not be reported here.

Each participant performed a total of 194 to 200 trials, over the 3 to 4 day testing period. Some participants were exceptionally good or poor at the curvature detection experiment on day one. For these people, the best two curves (near perfect) or worse two curves (near chance) were eliminated from subsequent trials, leaving time for more trials in the relevant range of sensitivity.

After walking along each path, participants were asked to give a two alternative forced choice (AFC) response for the direction of curvature. A block of trials consisted of 10 or more trials on all 10 different arcs in random order.

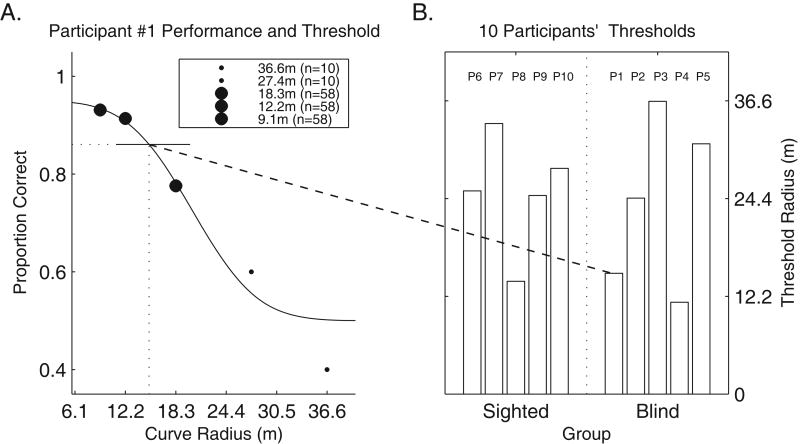
We constructed psychometric functions of percent correct versus radius of curvature. Cumulative Gaussian curves were fit to the data using a constrained maximum-likelihood method (Figure 6A), and threshold was defined as the curvature yielding 90% correct. The psychometric function took all trials into account during the fitting process.

Figure 6.

Curvature Detection Performance and Threshold Calculations. Figure 6A shows curve detection performance of one participant. Figure 6B shows 90% correct threshold radii for all participants.

Results

The mean threshold in the curvature discrimination task across the 10 participants was a radius of 24.47 meters, and did not differ significantly between blind participants and blindfolded sighted participants: t(8) = 0.26, p = .60. Figure 6B shows that the thresholds ranged from radii of 11.46 to 36.48 meters.

We tested the hypothesis that curvature detection is related to veering behavior by computing the correlations across participants between the curvature thresholds and four measures of veering behavior: mean signed error (offset at 9.14 meters), mean unsigned error (offset at 9.14 meters), mean linear coefficient, and mean quadratic coefficient (see Experiment 1 for details of these measures). We found no significant correlation between curvature thresholds and any of these four measures of veer: curvature threshold versus signed error: r(8) = .10, p = .78; threshold versus unsigned error: r(8) = .30, p = .39; threshold versus linear coefficient: r(8) = -.15, p = .68; threshold versus quadratic coefficient r(8) = .27, p = .46.

Discussion

The results of the present experiment do not support the hypothesis that people who veer the least by the above measures are most sensitive to path curvature. To emphasize this point, the participant (P3) who was best at curvature detection (threshold radius = 36.48 meters) was also the one that veered the most in the straight line walking task (mean unsigned deviation = 1.73 meters). However, we will show in the Model section that a more adequate measure of veering behavior (i.e., variability in stepping) is in fact correlated with curvature detection performance.

Cratty (1965) also measured curvature detection of blind walkers. It is difficult to make a quantitative comparison with Cratty's findings because he used a different method for guiding participants along curved paths (by means of curved guide rails) and a different psychophysical paradigm (i.e., Cratty used a 3 AFC design, versus our 2 AFC design). Nevertheless, it appears that our participants were better at curvature detection. Cratty stated that people averaged 55.45% correct (chance = 33.3%) on 12.8-meter radius curves. From his table (Table II, p. 53), Cratty's participants reached 90% accuracy when the curved paths had radii of only 5.49 meters. Our findings, as noted above, show mean thresholds to be about 24.47 meters at 90% correct (chance = 50%). This discrepancy may be due to the difference in psychophysical paradigm, or the difference in the guiding apparatus (or both). The guiding apparatus used by Cratty consisted of pairs of curved rails, with hand-held batons used to touch the rails.

In the curvature detection trials, we tried to approximate the walking speeds that were observed in the veering trials of Experiment 1. Although the guiding apparatus did not generate precisely constant speed, we argue that small speed fluctuations would not influence performance in curvature detection or its relationship with veering performance. We don't believe the speed fluctuations would be any greater than in Experiment 1, because the ballast in the cart provided smooth velocities and accelerations throughout each trial. In other words, the inertia of the apparatus should have reduced the fluctuations in speed somewhat over normal walking.

The results of this experiment do not show a direct relationship between sensitivity for detecting curved paths and the ability to walk a straight line. It remains possible, however, that subtler measures of vestibular, kinesthetic or proprioceptive function might yet reveal such a linkage. Our results prompted us to consider the possibility that undetected noise in the motor system might account for veering behavior. We will return to the matter of curvature detection in detail in Appendix B, after introducing and discussing the Model.

Before turning to explanations for veering based on the motor system, we considered the possibility that our method for conveying heading to participants (Experiment 1) might have resulted in initial directional uncertainty. Based on this, we asked whether providing a perceptual pointer would improve performance in straight line walking (Experiment 3).

Experiment 3

Objective

In Experiment 1, participants were instructed to walk a straight line perpendicular to the edge of a table behind them (physical alignment starting condition). Uncertainty in identifying the perpendicular to the table edge or in translating this direction into a vector for walking might have contributed to orientation uncertainty. In other words, it is possible that we provided our participants with insufficient perceptual input regarding the intended direction for straight-line walking. We asked if we could reduce veering behavior by providing explicit indicators of the intended direction, termed perceptual pointers.

There is practical value in determining what starting conditions minimize veer. Optimal cues could be implemented in the design of crossing guides at intersections to assist visually impaired pedestrians. More generally, improved strategies for designating a walking direction could be incorporated into orientation and mobility training techniques.

Methods

Participants

Five blindfolded normally sighted undergraduate female college students, ranging in age from late teens to early twenties, participated. None had participated in Experiments 1 or 2.

Testing Arrangements and Procedure

Three counterbalanced starting conditions were tested, including “physical alignment”, “static perceptual pointer”, and “dynamic perceptual pointer”. In each condition, participants performed a total of 39-41 trials over two separate days. In the “physical alignment” condition (a replication of Experiment 1), participants were initially positioned with their backs aligned to a rigid boundary (the edge of a table) perpendicular to the desired walking direction. By squaring their bodies against this boundary, they naturally assumed the appropriate initial orientation. In this task, there was no explicit pointer for the intended walking direction.

In the two “perceptual pointer” conditions, the desired walking direction was indicated explicitly by aligning the rigid boundary (the edge of the table) parallel to the desired direction of travel. Participants felt the parallel edge and used this cue to determine the appropriate walking direction. The “static perceptual pointer” condition relied on a perceptual estimate of the correct starting direction while the participant was stationary at the beginning of the trial. In the “dynamic perceptual pointer” condition, participants again used the edge of the table, aligned parallel to the desired direction. However, they were able to walk for 1.83 meters at the beginning of the trial while continuously feeling the edge of the table, before “launching” in the desired direction of travel. In both of the perceptual pointer conditions, the table was offset by 0.30 meters, in order to position the participant's center of gravity over the desired walking pathway. We reasoned that the perceptual alignment methods should provide enhanced perceptual cues (either static or dynamic) for the desired walking direction. To the extent that these perceptual cues provide improved information about orientation, we would expect better performance (less veering). If perceptual factors do not limit performance in the veering task, the physical alignment condition might yield equivalent, or perhaps even better, performance than the conditions with the additional perceptual cues.

Results

Veering patterns in the “physical alignment” condition were similar to the data collected with the same procedures in Experiment 1.

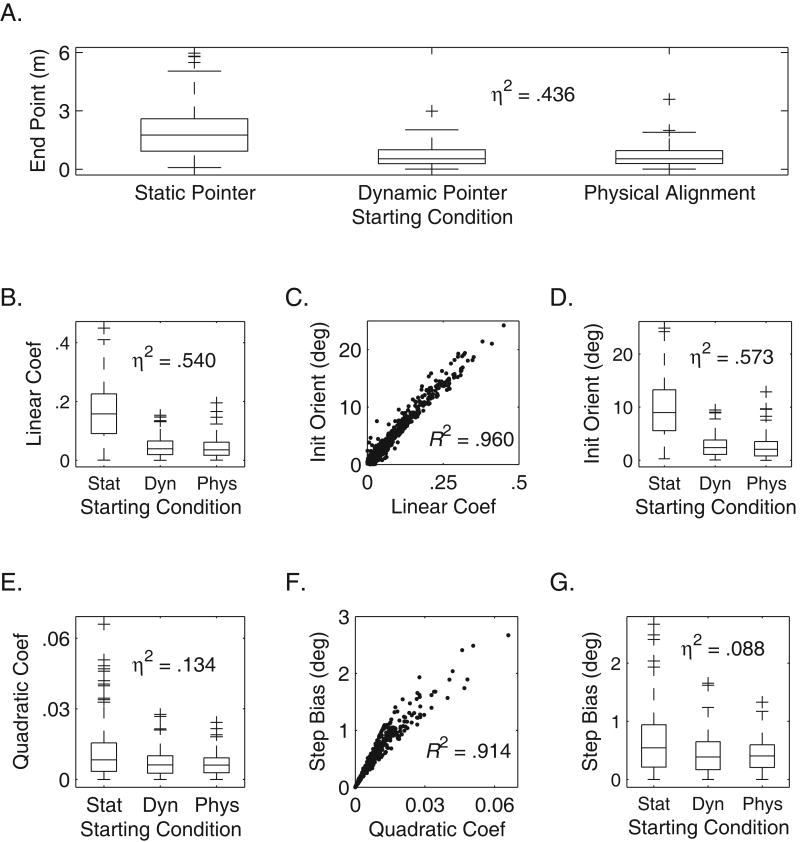
Figure 7 and Table 4 show an analysis of three dependent variables (endpoint, linear coefficient and quadratic coefficient) on three different starting conditions. Additionally, the effects on initial orientation and stepping biases (which are related to the linear and quadratic components, respectively) are shown. We will discuss initial orientation and stepping bias in detail as model parameters in the Model section. These measures are highly correlated with the linear and quadratic coefficients, respectively. Initial orientation can be thought of as the initial direction that the walker assumed at the beginning of each trial. Stepping bias can be thought of as the mean tendency to change heading at each step.

Figure 7.

Effects of 3 Starting Conditions on 5 Measures of Veering Trajectories. These graphs show effects of starting condition on measures of veering. All data were analyzed in absolute values. Figure 7A shows box plots of the distributions of end point offsets at 9.14 meters (repeated measures ANOVA effect size of starting condition: η² = .436). Figure 7B and 7E show the effect of starting condition on linear and quadratic coefficients of the trajectories. Figure 7D and 7G show the effect of starting condition on initial orientation and step direction bias. Figure 7C and 7F show the linear relationships between these measures and the polynomial coefficients. See Table 4 for statistics.

Table 4.

Effects of 3 Starting Conditions on 5 Measures of Veering Trajectories

Effects	df	F	η2	p-value
End Point	2	150.52	.436	< .001
Linear Coefficient	2	228.65	.540	< .001
Initial Orientation	2	261.46	.573	< .001
Quadratic Coefficient	2	30.06	.134	< .001
Stepping Bias	2	18.75	.088	< .001
Correlations			R2	p-value
Initial Orientation vs. Linear Coefficient			.960	< .001
Stepping Bias vs. Quadratic Coefficient			.914	< .001

In Figure 7, it can be seen that the addition of the perceptual cues did not reduce veering compared to the physical alignment condition. Furthermore, it can be seen that the linear coefficient is what was driving the effect of endpoint. This suggests that initial orientation was being affected by the initial cues (or position), rather than stepping bias (as shown in the relatively small effect on the quadratic component).

It is important to note the possibility of an effect of the lead foot – that is the foot that took the first step in each trial. We tested whether the lead foot had an effect on endpoint, or linear and quadratic components of trials. In the physical alignment condition, an ANOVA revealed an effect of lead foot on the linear component. Leading with the right foot resulted in an average linear slope of -0.0383, while leading with the left foot resulted in an average linear slope of 0.0160: F(1,193) = 6.90, p = .033. There was no effect found on either endpoint: F(1,193) = 1.05, p = .357, or the quadratic component: F(1,193) = .111, p = .755. The absence of an effect on the quadratic component suggests that there is no lead-foot effect on the stepping bias estimation. There may be practical implications on the effect of lead foot for orientation and mobility training. In other words, the lead foot probably influences the initial orientation of the walker.

Figure 7A shows that the endpoint offsets were similar for the physical alignment condition and the dynamic perceptual pointer condition, but the offsets were greater (i.e., more veer) for the static perceptual pointer condition. Detailed analysis of the polynomial fits to the trajectories in the three conditions revealed that both the linear and quadratic coefficients were significantly larger in the static perceptual pointer condition than in the other two conditions, but the effects on linear coefficients were substantially more pronounced than the effects on quadratic coefficients. A repeated measures ANOVA showed that 54% of the variation in linear coefficients can be accounted for by the variation in the three starting conditions (see Figure 7B), while a repeated measures ANOVA on the quadratic coefficients showed an effect size of only 13.4% (see Figure 7E). See Table 4 for statistics.

Discussion

An explicit indicator of intended walking direction did not reduce veering behavior. In fact, in the case of the static pointer condition, veering actually increased compared with the physical alignment condition in which there was no explicit pointer. The increased veer is mainly due to a larger linear component in the participants' trajectories. This increase is likely to be accounted for by larger errors in initial orientation at the start of the trajectories. In the modeling section to follow, we will make use of the variable representing initial orientation (shown in Figure 6D). The lack of improvement in straight line walking when an explicit cue for walking direction is present implies that veering is not due to insufficient information about the intended walking direction.

Performance was better in the dynamic pointer condition than in the static pointer condition, and equivalent to the physical alignment condition. The dynamic condition allowed the participant to get a moving start by following the edge of the table. We speculate that the benefit occurred because the moving start and associated inertia provided alignment at the start of the trajectory, equivalent in accuracy to the physical alignment condition.

These findings imply that physical pointers may not be effective in designating walking direction for visually impaired people, e.g., in crossing a street. A better strategy may be to provide a guide bar perpendicular to the crossing direction and encourage the pedestrian to back against it to establish the starting orientation. Alternatively, if a guide rail is aligned parallel with the crossing direction, the visually impaired pedestrian could follow the rail to get a moving start before crossing the street.

The linkage between linear coefficients and orientation at the beginning of trials is evident from this experiment. In the modeling section to follow, we will discuss initial orientation and an additional measure of veering: stepping-direction bias. These measures are closely linked conceptually to the linear and quadratic coefficients of the polynomial fits, and closely correlated with them (see Figure 7C, Figure 7F and Table 4).

Model

Objective

The results of our curvature detection experiment (Experiment 2) imply that something other than sensory feedback may limit performance on straight-line walking. Moreover, perceptual pointers provide a less reliable cue to initial orientation than physical alignment (Experiment 3), and hence greater initial orientation errors. These observations raise the possibility that veering may be due to noise in the motor system that is not detectable by vestibular or kinesthetic feedback. We hypothesized that small amounts of independent motor noise (occurring in each individual step) can explain veering behavior when people attempt to walk a straight line without vision. To explore this idea, a random walk model was developed to simulate noisy steps in simulated walking trials.

Methods

The model presented here simulates the effects of noisy steps (variability in the length and direction of individual steps) on the immediate position and orientation of a walker. The model is intended to be a radical simplification of actual walking in order to focus on the causes of veering. In particular, the model considers only the 2D position and direction of steps, intentionally ignoring biomechanical aspects of walking (including the distinction between left and right feet, and deviations in step height).

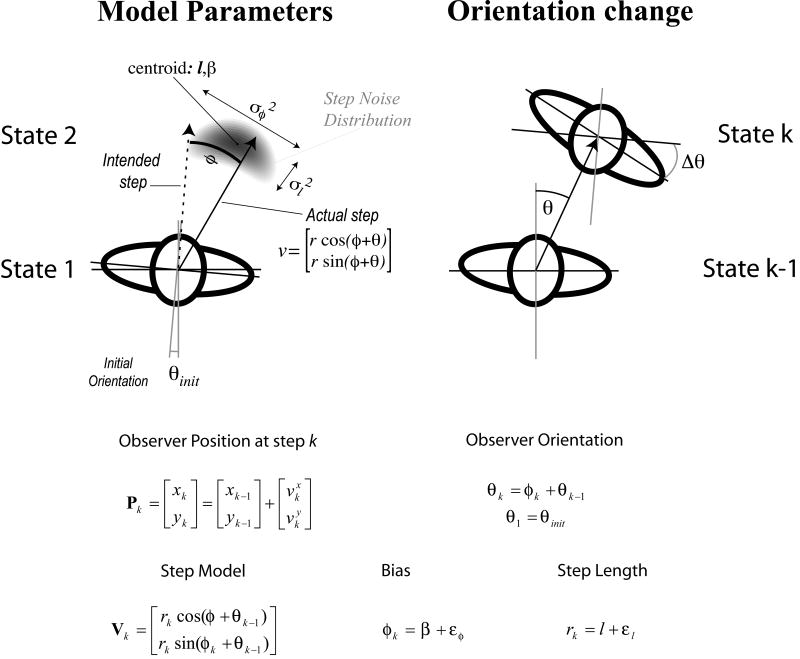
The walking model, summarized in Figure 8, contains six parameters: mean initial orientation prior to the first step θ_init, initial orientation variability (occurring over numerous trials) ${\sigma }_{\theta }^2$, mean step length l, step length variability ${\sigma }_l^2$, mean step direction bias β, and step direction variability ${\sigma }_{\phi }^2$. The initial orientation variable simulates the initial direction of travel, and has a value of 0 if the walker is initially aligned with the desired heading. Mean step length refers to the average distance traveled in a single step (in this paper, step size is equal to 0.5 stride length). Step direction bias β represents a bias in the step direction away from orientation in the previous state. A bias of +1 degree, for example, refers to a walker whose average step rotates 1 degree clockwise from the local straight-ahead orientation. Accumulated step direction bias across a path results in consistent deviations from a straight line. Step length and bias variability are the step length variance and step direction variance, respectively.

Figure 8.

Stepping Model for Walking. The walker's state is specified by her global 2D position p_k and orientation θ_k. Each step of average length l is in the direction of the walker's current orientation, but the executed step v_k differs by the addition of noise in both the length (mean = l, variance = ${\sigma }_l^2$) and direction of the step (mean = β, variance = ${\sigma }_{\phi }^2$). By the end of each step, the walker's orientation has changed to point in the direction of the executed step. Initial orientation is a random variable across walks.

Each of the parameters in our model can be estimated from the human trajectory data, as follows:

Average step length l

Average step length was estimated by dividing the distance traveled d_k on each trial k by the number of steps N_k recorded from the video data in Experiment 3: $l=\frac{1}{K}\text{∑}_{k=1}^K\frac{d_k}{N_k}=\frac{1}{K}\text{∑}_{k=1}^K{l}_k$

Step-length variance ${\sigma }_l^2$

An indirect measure of variability was computed from the variance of l_k across trials scaled up by the average number of steps per trial. This estimate is justified by observing that (assuming independent steps) the standard deviation of l_k will be reduced over the variance of individual steps by a factor of $\sqrt{N}=\sqrt{\frac{1}{K}{\sum }_{k=1}^K{N}_k}$ on average. Essentially, we convert an estimate of the standard error of the mean into a standard deviation.

The remaining four parameters are estimated from the polynomial fits to the human data by re-sampling individual steps along the fitted trajectories. In particular, for each polynomial fit, the cumulative arc length s(x) is computed from the polynomial y(x): $s(x)={\int }_0^x\sqrt{{\left(\frac{\text{dy}}{\text{dx}}\right)}^2+1\hspace{0.17em}\text{dx}}$

Because s(x) is monotonic in x, and represents the cumulative distance along the path, the x-values corresponding to equally spaced steps of length l along the path can be computed from s(x)^-1. The y-values corresponding to these x-values are then computed from the fitted polynomial. The result is a series of step vectors {u₁, …, u_M} that divide the trajectory into M pieces of length l. The orientation of each step vector u_j with respect to the y-axis was simply computed as $\psi ={\text{tan}}^{-1}(u_x/u_y)$.

Given the step vectors, the remaining parameter estimates are easy to describe. In order to preserve information about individual variation, all estimates are computed within participants and days.

Initial Orientation

The initial orientation θ_init was estimated by averaging the orientation of the first step vector across trajectories for each participant: ${\theta }_{\text{init}}=\frac{1}{K}\text{∑}_{k=1}^K{\psi }_1^k$, where k indexes the trajectory number. For simulation purposes, the variance of ψ₁ was computed as well.

Step Direction Bias β

The step direction bias β was estimated by averaging the orientation difference between steps both within and across trajectories: $\beta =\frac{1}{K(N-1)}\text{∑}_{k=1}^K\text{∑}_{j=2}^{N_k}({\psi }_j^k-{\psi }_{j-1}^k)\approx \frac{1}{K}\text{∑}_{k=1}^K{\beta }_k$, where k indexes the trajectory number, N represents the average number of steps per trial and j indexes the step number within a trajectory.

Step Direction Variance ${\sigma }_{\phi }^2$

An accurate measure of the step direction variance ${\sigma }_{\phi }^2$ is subtler. Because the steps are derived from polynomial fits that smooth step variability within a trajectory, the variability of ${\psi }_j^k$ across steps j is smaller than the underlying step variability. To get around this difficulty, we used an argument like that for step length variability, appropriately scaling the variance of the average step direction across trials: ${\sigma }_{\phi }^2=\frac{N-1}{K}\text{∑}_{k=1}^K{\{{\beta }_k-\beta \}}^2$, where k indexes the trajectory number. Our human data suggest that angular stepping variability does not change much across individuals or days.

These parameters are used to compute a noisy step v_k, which modifies the walker's position and orientation as follows: The first step of the simulated walk is in the direction of the initial orientation value. At the end of each subsequent step k, the new heading θ_k is perturbed away from its previous value θ_k-1 by the current step. Accordingly, heading varies from step to step in a kind of “random wobble”. However, for small values of the step direction variance the trajectories remain smooth.

Parameter estimates for individual performance on each day (Experiments 1 and 3 – Veering) were used in the model (Tables 5 and 6). From the Experiment 3 physical alignment condition, we were able to obtain estimates for initial orientation, bias and step size parameters; while in Experiment 1, we were able to obtain estimates for initial orientation and bias, assuming an average step length of about 0.62 meters (estimate from Experiment 3 data). From these data, models for each person/day combination were evaluated on Experiment 3 participants. The parameterized models have three free parameters: mean orientation, mean step length and mean bias, and three fixed variance parameters based on population estimates.

Table 6.

Walking Parameter Estimates (Experiment 3)

Participant	Day	Initial orientation*		Step length†		Bias*		N trials	Mean n steps
		Mean	S.D.	Mean	S.D.	Mean	S.D.
11	1	0.47	1.79	0.59	0.085	0.39	1.16	20	15.7
	2	-1.54	1.98	0.58	0.081	-0.19	1.38	21	15.8
12	1	2.11	3.70	0.61	0.14	-0.10	1.49	21	15.0
	2	0.85	2.20	0.63	0.083	-0.43	1.12	20	14.5
13	1	0.37	1.97	0.57	0.055	-0.17	0.81	20	16.2
	2	-3.47	1.79	0.58	0.034	-0.58	0.83	20	16.1
14	1	-2.68	2.62	0.51	0.27	-0.48	1.58	19	18.5
	2	-0.63	1.68	0.62	0.073	-0.38	1.56	20	14.8
15	1	-2.63	1.62	0.71	0.087	0.36	1.45	20	13.0
	2	-4.36	2.48	0.78	0.088	0.35	1.94	20	11.9
Marginal Means		-1.15	2.18	0.62	0.100	-0.12	1.33
Other Studies
Bauby & Kuo (2000)			1 to 3	0.76	0.119		1 to 3
Donelan, Shipman, Kram & Kuo (2004)				0.72	0.091		1 to 2

^*Unit = Degrees

^†Unit = Meters

Given the parameter estimates from the last section, it is straightforward to simulate walking paths by means of the model. Each model trajectory was generated using the following steps: 1) An initial orientation was generated by sampling from a Gaussian distribution whose mean and variance were derived above; 2) At each step, the step length and bias were generated by sampling from the corresponding Gaussian distributions; 3) The position and orientation state variables are updated according to the equations given in Figure 8.

In order to make the comparison with human data fair, the simulated trajectories were treated exactly the same way as the human data. In particular, each simulated trajectory was sampled every 1.52 meters, after which it was analyzed exactly like the human data. Using the same techniques implemented in human experiments, individual modeled trajectories were fit with second-order polynomials by least-squares.

Matlab code for implementing the model is given in Appendix A.

Results

We first parameterized the model using pooled data from our human experiments (see Table 6 for mean estimates). This yielded a simulated walker whose trajectories and ensemble statistics are similar to average walkers (Figure 9). The fan-shaped distribution of modeled trajectories is similar to the corresponding cluster of human trajectories, and is due to the stochastic variables, particularly the noise in stepping direction ${\sigma }_{\phi }^2$.

Figure 9.

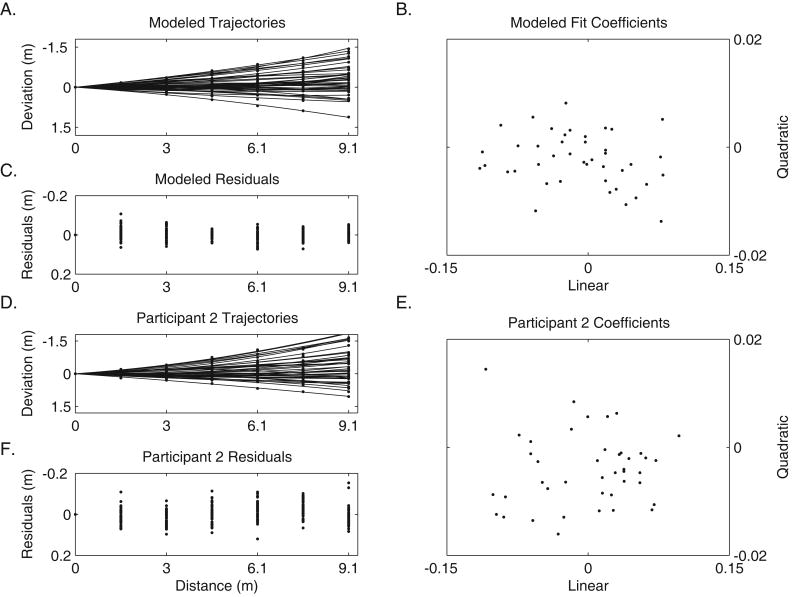
Human and Model Comparison. Figure 9A shows modeled data with fitted curves, resulting polynomial coefficients (Figure 9B), and their corresponding residuals (Figure 9C) – for modeled trajectories based on parameters from an “average” walker (see marginal means in Table 6). Empirical data from Participant 2 are shown in 9D, 9E and 9F.

The simulation shown in Figure 9A-C used the following fixed parameters (based on Experiment 3 results, (Table 6): θ_init = -1.15 deg., ${\sigma }_{\theta }^2$ = 2.18 deg., l = 0.62 meters., ${\sigma }_l^2$ = 0.10 meters, β = -0.12, and ${\sigma }_{\phi }^2$ = 1.33 degrees. Incidentally, we have conducted simulations showing that step length variability ${\sigma }_l^2$ (at any reasonable magnitude) does not have a significant effect on the veering behavior of our model. Mean step length l has a scaling effect in the model. For example, larger steps produce fewer steps for a given distance – and hence less overall veering, while smaller steps have the opposite effect. The simulated trajectories were analyzed in the same way as human trajectories – sampling was done at the same 1.52-meter intervals, and polynomials were fit to the data (see Figure 1). Figure 9A shows sampling and polynomial fits (Figure 9D shows participant 2). Figure 9B shows the corresponding coefficient scatter plot for the averaged model (Figure 9E shows participant 2).

If individual model trajectories behave like human trajectories, then we would predict that the distribution of model polynomial coefficients would match the distribution of coefficients found in human data. In Figure 9 we can compare human (Figure 9E) and modeled (Figure 9B) coefficients. Recall the simulated trials shown in Figure 9A. The trajectories of the model produce coefficients which are uncorrelated, similar to coefficients of blind and blindfolded human walkers.

A further comparison of the modeled trajectories is a plot of the residuals between data and least-squares polynomial fits (Figure 9C and 9F). This similarity shows that the polynomial fits are equally good for the model and human trajectories.

While the average model is an idealization of actual walking, we believe it captures the aspects of walking most important for an explanation of veering. As illustrated in Figure 9, individual trajectories and their accompanying polynomial coefficients are indistinguishable from the performance of a typical human participant.

Our findings in Experiments 1 and 3, confirming earlier findings by Guth and LaDuke (1995), show that individuals behave slightly differently from day to day and from one another. These individual differences are not accounted for by the average walker model. In order to account for these differences, we derived parameter estimates from individuals (see Tables 5-6), and ran simulated trials based on those parameters. Next, we will show that the model can replicate individual and day-to-day variations in human performance through day-to-day variations in the means of initial orientation, step length and bias.

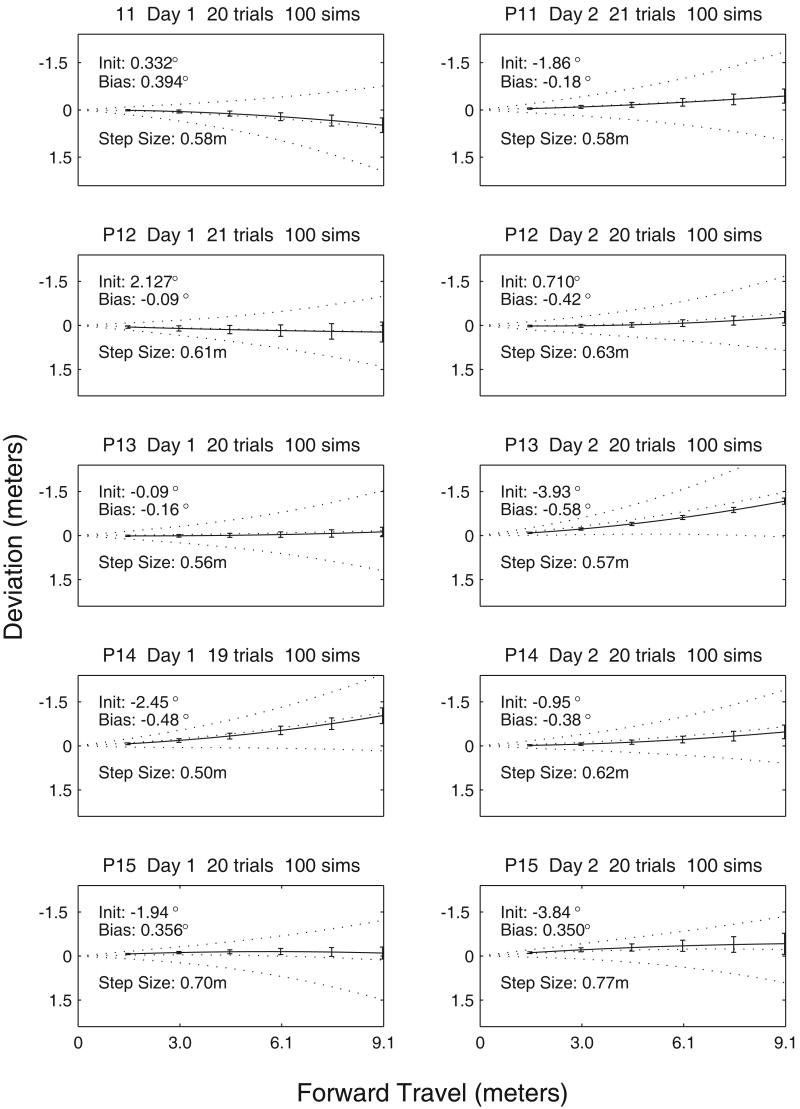
Data collection in Experiment 3 included counts of the number of steps in each human trajectory. The number of steps for each trajectory was translated into average step size, and is listed in Table 6. Using parameter estimates for individuals from Experiment 3 (Table 6), 100 modeled trajectories were simulated for each of the 10 individual/day combinations. Linear and quadratic coefficients of simulated trials were compared to corresponding values from each set of human trajectories. Bonferroni adjusted Hotelling t² tests were used to compare the linear-quadratic component combinations between human estimates and modeled estimates. The Hotelling t² test is essentially an n-dimensional t-test, and can be used to take both components of polynomial coefficients into account at once. None of the simulated data were significantly different than corresponding human data, with these parameter estimates. Each simulation has three free (individually estimated) parameters, including initial orientation (labeled ‘Init’ in Figure 10), Bias and Step Size. Patterns of the model and corresponding human performance are also visually similar, as noted in Figure 10.

Figure 10.

Real and Simulated Trajectories. Each panel shows a summary for trials based on the estimated parameters from Experiment 3. Solid curves show the means (± 1 SE) of Experiment 3 trajectories. Simulated trajectories are shown with 3 dotted curves, representing the mean (± 1 SD).

We have constructed a model to investigate how well model trajectories match human veering trajectories. For the model to be compelling: 1) it should produce individual trajectories that look like human trajectories, and 2) the statistical properties of an ensemble of model trajectories should match those of human trajectories. Assessment of the similarities of simulated trials showed that polynomial fits to modeled trajectories matched those of humans in both the value of coefficients and the residuals to the fits.

Discussion

While the model captures salient aspects of veering behavior, it involves a number of abstractions away from actual walking behavior. For example, the walker's position in the model represents the projection of some distinguished point (like the center of mass) onto the ground plane (similarly with orientation). A more complete characterization would involve the position of several points (e.g., head location, center of mass, center of hips) in 3D. Nevertheless, we believe our model parameters can be identified with biomechanical properties of real walkers. Initial orientation is simply the initial walking direction (where walking direction is defined by the direction of motion of the participant's center of mass) and initial orientation variability is the variation in initial walking direction between trials. The model steps, however, involve more abstraction.

Model steps do not directly represent where the feet are placed. Instead they represent the consequences of foot placement and postural instability during a step on the walker's position and direction, rather than the foot placement per se. Actual steps are quite complicated, and foot placement controls are chosen to simultaneously satisfy two distinct goals: transporting the walker and maintaining postural stability (Bauby & Kuo, 2000; Donelan, Shipman, Kram, & Kuo, 2004). In our model, step direction represents the walking direction at each step and step length represents the distance traveled in that direction. Because steps are in the forward direction on average, the step length parameter should represent actual forward step length (distance between steps in the walking direction). To relate step direction to actual steps requires a discussion of how postural stability is maintained by step placement.

The simplest model of 3D walking dynamics (McGeer, 1990; Garcia, Chatterjee, Ruina, & Coleman, 1998) consists of two cylindrical legs connected by a pelvis, with ball joints at the hips, and curved feet connected by pin joints to the end of the legs. Surprisingly, when this model walker is placed on a tilted platform, it is passively stable in the walking direction, which means it requires no energy expenditure or control signals to maintain both walking gait and postural stability in the walking direction (McGeer, 1990; Garcia, et al., 1998; Kuo, 1999; Kuo, 2001). However, this passive stability does not extend to the direction lateral to the walking direction (Garcia, et al., 1998; Bauby & Kuo, 2000; Donelan et al., 2004). In order to maintain balance, walkers must actively control lateral postural stability, which is accomplished in large part by varying the lateral placement of foot position (Bauby & Kuo, 2000; Donelan et al., 2004). Because the center of mass must be brought sufficiently over the foot during the next step, lateral foot placement will result in both positional noise in the lateral direction, and (more importantly) changes in the orientation of the walker. Changes in direction should occur both from torques generated by foot impact and to reduce twist at the ankle. Foot impact events are the most important part of the walking cycle because nearly all force control is applied at impact (Donelan, et al., 2004). At impact, contact forces generated by a foot placement forward and to the side will produce a force component in the desired lateral direction, but will also produce a torque component around the walker's main axis (the gravity axis) in the direction of the step that will modify the walker's direction unless accurately sensed and corrected. Thus lateral foot placements should produce perturbations in the direction of the walker that we have modeled with our step direction parameter. In particular, systematic direction perturbations from lateral foot placement can be associated with mean step direction bias, while random perturbations would be associated with step direction variance.

Given the previous discussion, we can try to relate the values for the parameters in our model to results from previous studies. In particular, we will focus our attention on two recent studies (Bauby & Kuo, 2000; Donelan et al., 2004) that measure both step length and step variability in both the forward and lateral directions. The values reported in these two studies are converted into the units used in this paper and are summarized in the bottom of Table 6. Step length and variability comparisons were straightforward unit conversions. In general, step length is about 0.8 of the walker's leg length, but step length is difficult to directly compare across studies because the walking speed used in our study was probably slower than that in the comparison studies (due to the nature of non-visual walking versus sighted walking). We will further discuss the effects of step length and speed on veering below. We converted lateral foot placement variability into step direction variability by making the simplistic assumption that a lateral foot placement of x degrees to the side of the current walking direction would result in a corresponding change in direction at the next step. Finally, because initial orientation variability represents the variability in the first step direction, we would expect its value to be nearly the same as step direction variance. Given the simplifying assumptions, we believe the close agreement between our values and those measured in carefully controlled studies using state-of-the-art tracking methods bolster the case for the viability of our model.

Relative Role of Model Parameters on Veering

The results of our modeling effort suggest that there are three important and distinct causes of veering from a designated straight line: 1) error in initial direction, captured by the initial orientation and variance parameters; 2) systematic errors in stepping direction, modeled by step direction bias; and 3) undetected random errors in step direction, modeled by step direction variance. The difference between these causes and the role of the other parameters will be discussed below.

The initial orientation parameters are included in the model to account for the impact of initial misalignment on veer trajectories. Even if no other bias or source of noise were present, a misalignment by angle θ at the beginning of a trial will result in an offset by a distance l · tanθ at the end of a trial from the straight-ahead length l. For small angles, l · tanθ ≈ l · θ, with θ measured in radians. From our estimates in Table 6, the mean absolute initial orientation misalignment of our participants was 1.15 degrees (0.02 radians), producing an average offset for l = 9.14 meters of 0.18 meters. While smaller than the mean absolute offset we observed of 0.82 meters in Experiment 1 (Table 2), it is clear that the initial orientation error is a contributor to the veering effect. Although errors of initial orientation may be important in real-world situations, such as crossing a street at an intersection non-visually, this parameter represents only a starting direction in the model, and is not relevant to the stochastic properties of veering.

Many earlier proposals for explaining veering behavior (reviewed by Guth & LaDuke, 1994; Cratty, 1965, 1971) like biomechanical asymmetries and dominance or difference in leg strength or leg length, can be reinterpreted as proposals for sources of systematic errors in step direction. Based on the average mean step direction bias of -0.12 degrees, a step length of 0.62 meters, and an average of 15 steps, we can estimate the effect of the stepping bias as follows: Each step introduces a deviation like the initial orientation, but affects only the remaining trajectory (i.e., there is a diminishing effect on overall deviation as each step approaches the end). Thus the effect of bias is a cumulative sum of the last 14 steps, ${\sum }_{j=1}^{14}j\cdot s\cdot tan\theta$, which results in an average effect of 0.13 meters, which is small compared to 0.82 meters. Thus, while some of our participants show strong systematic veering tendencies, the modeling results suggest the impact of step direction variance is the dominant factor influencing veering. This dovetails with our findings and others (Cratty, 1971; Guth & LaDuke, 1995) that show the direction of veer is not one-sided.

The dominant cause of veering in an established walk appears to be undetected errors in step direction. The unexplained mean offset is 0.50 meters, which agrees exactly with the effect of step direction variability observed in our simulations. The idea that veering is caused by undetected motor error constitutes a novel explanation for the veering phenomenon. It is important to point out that the term motor error does not distinguish between errors in step planning and execution. Because blind walking must rely heavily on a dead-reckoning type movement accumulation to assess relative position and orientation, the idea that motor error is a problem is no surprise. However, motor error is only a problem to the extent that it is not perceived. For motor error to go unnoticed, the typical amount of motor error should be below perceptual threshold. If the typical amount of motor error is below perceptual threshold, then the walker simply does not know that errors are being introduced at each step. In order to test this idea, we converted thresholds from the curvature detection experiment (Experiment 2) into an equivalent perceptual error, measured as a variance on orientation change per step using a simple formula derived in Appendix B: ${\sigma }_{\text{perceived}}\ge \frac{89.5}{R}$. A threshold radius of 24.48 meters translates into a perceptual error variance of 1.12 degrees, which is within measurement error of the step direction variance of 1.33 degrees. However, because participants actually took 6-8 steps before making a decision (along the 4.57-meter curves), the perceptual variance is almost surely higher (for reasons explained in Appendix B). This result is also much larger than the estimated step direction bias values, suggesting participants are unaware of their systematic walking errors. The similarity between perceptual variance and step direction variance is unlikely to be an accident – if a motor error is detected, it should be corrected. This idea suggests that participants with the highest curvature detection thresholds (i.e., those most sensitive to curve detection) should have the smallest step direction variances. To test this idea, we first counted the mean number of steps measured from Experiment 3, and used this value to estimate stepping variability in participants from Experiment 1. After the variances were estimated for each participant, the values were correlated with the inverse of each participant's curvature detection threshold measurement (see Appendix B for details). In fact, we found a significant correlation (r =.64, p = .045) between perceptual variance (a curvature detection measure) and step direction variance (r = .72 Blind, r = .60 Sighted). This correlation would likely increase if the exact number of steps in the trajectories from Experiments 1 and 2 were known.

Not surprisingly, no significant relationship was found between perceptual variance and step direction bias or initial orientation. Thus, curvature detection is related to one of the causes of veering, in that it acts as an upper bound on step direction variability. There is a simple explanation for the discrepancy between these results and the results of Experiment 2 (i.e., there is no direct correlation between curvature detection thresholds and measures of veering), namely that the correlation between the perceptual and step direction variances does not survive the conversions to curvature detection thresholds and veering measures, due to the presence of non-linear transformations and the fact that step direction variance is only one of several factors that potentially causes veering. In other words, an inability to detect the curvature of the path we are on is not a direct cause of veering.

Intuitively, we would expect the mean step length and step-length noise parameters of our model to be less critical to the veering phenomenon than the other variables. This is what we found through exploration of the model's behavior. Recall that changes in mean step length have a scaling effect, while variability in step length has a negligible effect on veering. But if the model were used to estimate distance traveled, rather than offsets in direction, the step-length variables would be more important. In a recent empirical study in our lab (Mason, Legge, & Kallie, 2005) we estimated mean step length and step-length variability for normally sighted and visually impaired walkers. Our interest was motivated by the possibility of using step counts (recorded by a computer-readable pedometer) to estimate distances traveled and to use these estimates to update the pedestrian's position in a computer-readable map. In the study, participants repeatedly walked a fixed distance. The number of steps taken was used to estimate mean step length and variability across trials. We found no significant differences in mean step length or step-length variability between sighted and visually impaired walkers (some of whom used a white cane or dog guide). For this group of 18 participants, mean step length at their preferred pace ranged from 0.55 to 0.88 meters, with an overall mean of 0.74 meters. Across the group of 18 participants, the variability was very small, near 2%, meaning that the number of steps to walk 24.38 meters varied by only about 2% across trials for a given participant. It is likely that the model presented in the present paper, with particular attention to mean step length and variability, could be used to account for variations in distances walked by human pedestrians.

In addition, our model does not take into account walking velocity, which Cicinelli (1989) found was inversely related to veering. We do know however, that preferred step length increases with walking velocity both empirically (Grieve, 1968; Mason, et al., 2005) and theoretically (Kuo, 2001). Within our model, an increase in mean step length has the effect of reducing veer because longer steps mean that a given distance is covered in fewer steps, contributing fewer noisy samples to the trajectory. For example, for our 9.14 meter distance, we compared 10,000 simulated trials with step lengths of 0.61 meters and 0.91 meters, keeping all other parameters equal to zero except for stepping noise ( ${\sigma }_{\phi }^2=1.33\hspace{0.17em}\text{degrees}$), the corresponding standard deviations of the endpoints were 0.50 meters and 0.42 meters, respectively. This translates to 20% greater end point variability with the shorter steps, after 9.14 meters of walking. The effect of velocity might therefore be related to its effect on mean step length.

Experiments 1 and 3 gave us the opportunity to make parameter estimates of human walking performance – to be used in the modeling effort. Using average parameter estimations from Experiment 3, we are able to simulate walking over longer distances. In 1995, Guth and LaDuke measured 3 participants' veering behaviors at 25 meters on three separate days. They reported 3 error measurements describing performance – constant error, variable error and absolute error. Constant error was the mean offset at 25 meters, while variable error was the standard deviation, and absolute error was the mean of the absolute values. From their Table 1 (Guth & LaDuke, 1995, p. 31), the constant errors ranged from -4.94 meters (left) to 5.75 meters (right); variable errors ranged from 1.97 to 3.70 meters; and absolute errors ranged from 1.84 to 5.75 meters.

Using average parameters in our model, as discussed in connection with Figure 9 above, we ran 10,000 simulated trajectories out to a distance of 25 meters, and calculated the same three measures of error used by Guth and LaDuke. The simulation produced a constant error of -1.64 meters (left), variable error of 2.43 meters, and an absolute error of 2.30 meters. These values are all well within the range of Guth and LaDuke's human participants. The congruence of our model-based extrapolations with the data of Guth and LaDuke enhance our confidence in the viability of our model, and also provide an indirect verification that the veering behavior of our participants was similar to the veering behavior measured by these authors.

In this paper, we have used the model to account for veering behavior over a small distance of 9.14 meters. Over larger distances, the step-by-step accumulation of small errors in direction can result in quite severe misorientation. The model may explain why people sometimes get lost when attempting to walk moderate distances non-visually.

General Discussion

Why do people veer away from their intended paths when attempting to walk a straight line in the absence of vision? Veering is an everyday problem for blind mobility, and has been the downfall of many normally sighted people who have become lost in blizzards, severe fog or in the dark. Our theoretical answer is that directional errors resulting from noisy steps is a major cause for the veering behavior observed in blind walking. We estimate that individual steps in blind walking have directional variability with a standard deviation of about 1.3 degrees. Accumulation of the effects of errors of this size across steps leads to curved walking trajectories, and deviations away from intended pathways. Deviation is modest for short distances such as 9.14 meters, but increasingly more severe at greater distances. If, as our results suggest, these small errors in directional stepping are not perceptually detectable in the absence of visual or auditory targets for reference, the walker will have no reliable sensory signal for correcting the deviations away from the intended path.

In the Model section, we presented a simple stochastic model of veering behavior. In addition to step direction bias and noise, the model includes variability in step length and initial heading direction. Three noise parameters, along with the corresponding mean values of the three random Gaussian variables comprise the model. We have used this model to account for the veering behavior of our human participants (Experiments 1 and 3), including day-to-day and individual variations, and to compare our data with prior findings of Guth and LaDuke (1995).

In Experiment 1, we measured veering by asking participants to repeatedly walk a 9.14-meter straight path. Participants exhibited curved trajectories that were well fit by polynomials with linear and quadratic components. Across the ten participants, the mean unsigned deviation away from the intended path at the 9.14 meter distance ranged from 0.45 meters to 1.74 meters (Table 2). In agreement with the findings of Guth and LaDuke (1995), we found significant individual differences and day-to-day differences in veering. In this experiment, we compared the veering behavior of two groups of participants, a group of five blind participants and a group of five blindfolded sighted participants. We made this comparison to determine whether experience with visual perception would affect veering behavior. There were no significant differences between the two groups.

In Experiment 2, we asked whether ability to detect curved walking paths was related to veering behavior. If people monitor perceptual signals from their vestibular organs or from joints or muscles to tell them about deviations away from a straight path, we would predict that people who are better at detecting path curvature should veer less. In the experiment we measured thresholds for path curvature detection by having participants walk along 4.57-meter-long arcs of circles curving left or right, with radii ranging from 9.14 meters to 36.58 meters. On each trial, a forced-choice decision on whether the path curved left or right was made. Across the ten participants, threshold radii (90% correct criterion) ranged from 11.46 meters to 36.48 meters with a mean of 24.48 meters. There was no significant correlation between these thresholds and any of several measures of veering deviation. From this result, we conclude that veering is not limited by a perceptual capacity to detect curvature away from a straight line.

In Experiment 1, the intended direction for walking was defined implicitly by aligning the participant with his or her back to a boundary perpendicular to the desired direction. In Experiment 3, we asked whether performance could be improved (i.e., reduce veering) by providing an explicit perceptual cue for the intended direction. The cue was an elongated pointer (edge of a table) aligned with the intended walking direction. We found that veering actually increased when participants relied on the static perceptual cue and did not use physical alignment. In a third condition in this experiment, participants began the trial with a moving start along the pointer in the intended direction, which yielded performance equivalent to the physical alignment condition. The results of this experiment imply that physical/mechanical factors are more effective in providing cues to initial orientation than are static explicit perceptual cues.

The totality of our findings point to non-perceptual factors, especially motor or biomechanical factors associated with movement, as the primary determinants of veering behavior. The four key findings contributing to this argument are: 1) history of visual experience does not influence veering behavior; 2) psychophysical thresholds for path-curvature detection are not correlated with veering behavior – although perceptual limitations of the motor system reveal a connection between curvature detection and veering behavior; 3) explicit perceptual cues for intended walking direction are less effective than physical alignment without an explicit perceptual cue; and 4) a simple stochastic model of walking behavior, assuming only stepping noise and no perceptual feedback, can account for the major features of our veering data.

Previous proposals for the origins of veering have focused exclusively on causes that would create systematic deviations in walkers' trajectories away from a straight line. The most comprehensive review of these proposals is in Guth and LaDuke (1994), where they describe a variety of physical and biomechanical asymmetries, and spiraling behavior, and conclude that none of the historical proposals are plausible due to the fact that the veering tendency is not always systematic. Our proposal is the first viable explanation of veering phenomena, and the only one that can handle both systematic and unsystematic aspects of veering.

Appendix A: A random walk model for walking without vision

The following Matlab code will execute simulated walking trials. The parameters are fully adjustable, including the six mentioned walking parameters, and the number of trials and number of steps per simulated trial.

% Matlab code simulation for walking without vision
nsims = 20;	% n simulations
nsteps = 20;	% n steps
in = [−1.152 2.182].*pi/180;		% orientation (mu, sd) (degrees to radians)
ro = [2.024 0.328].*0.3048;		% step length (mu, sd) (feet to meters)
th = [−0.122 1.332].*pi/180;		% bias (mu, sd) (degrees to radians)
cumth = cumsum([normrnd(in(1),in(2),nsims,1)…
normrnd(th(1),th(2),nsims,nsteps)],2);
steps = normrnd(ro(1),ro(2),nsims,nsteps);
cumx = cumsum([ones(nsims,1).*0 cos(cumth(:,2:end)).*steps],2);
cumy = cumsum([ones(nsims,1).*0 sin(cumth(:,2:end)).*steps],2);
plot(cumx',cumy','.:');

Appendix B: Relating Curvature Detection to Perceptual Error in Orientation Change Processing

We can estimate a perceptual orientation change threshold from the curvature detection data as follows: First we will convert the threshold curvature radius into a threshold orientation change per step. Then we will convert this threshold into an equivalent orientation change noise – a variance that characterizes the amount of error contained in the perceptual estimate of orientation change per step.

The orientation change γ that occurs at each step of length s when walking a circle of radius R can be found approximately by dividing the circumference of the circle into N = 2πR/s steps of length s. Then $\gamma =\frac{360}{N}=\frac{360\cdot s}{2\pi R}=57.3\frac{s}{R}\text{degrees}$.

This result holds when the step length is much smaller than the circumference, and is valid up to 3 decimal places for the radii and step lengths used in this paper.

If we assume that the walker's perceived orientation change at a given step is represented by an internal variable α corrupted by Gaussian noise with zero mean and variance ${\sigma }_{\text{perceived}}^2$, then we can use a simple signal detection theory argument to relate the threshold γ to the variance of this noise. The 2 alternative forced choice error rate for detecting an orientation change from one step based on α is given by (Green and Swets, 1974): $\frac{{\alpha }^2}{{\sigma }_{\text{perceived}}^2}=Z{(P_c)}^2$, where Z(P_c) is the Z-score of the probability correct P_c which is .9 for our curvature experiment. At threshold, α = γ, so that ${\sigma }_{\text{perceived}}=\frac{\gamma }{Z(P_c)}=\frac{57.3s}{R\hspace{0.17em}Z(0.9)}=\frac{57.3\cdot 2}{R\cdot 1.28}=\frac{89.5}{R}$.

For a threshold of 24.48 meters, this gives σ_perceived equal to 1.12 degrees. However, in our task walkers make 6-8 steps before they have to make a decision. If the decision is made on the basis of measurements at more than one step, then the estimate above is a lower bound. For instance, if the decision is made on the basis of an average of α over T steps and the corrupting noise is independent at each step, then: $\frac{{\sigma }_{\text{perceived}}}{\sqrt{T}}=\frac{89.5}{R}$.

For example, if participants pool over the equivalent of 2 steps, then ${\sigma }_{\text{perceived}}=\sqrt{2}\cdot \frac{89.5}{R}$, which is 1.58 degrees for R = 24.48 meters.