Origin and dynamics of extraclassical suppression in the lateral geniculate nucleus of the macaque monkey

Abstract

In addition to the classical, center/surround receptive field of neurons in the lateral geniculate nucleus (LGN), there is an extraclassical, non-linear surround that can strongly suppress LGN responses. This form of suppression likely plays an important role in adjusting the gain of LGN responses to visual stimuli. We performed experiments in alert and anesthetized macaque monkey to quantify extraclassical suppression in the LGN and determine the roles of feedforward and feedback pathways in the generation of LGN suppression. Results show that suppression is significantly stronger among magnocellular neurons than parvocellular neurons and that suppression arises too quickly for involvement from cortical feedback. Furthermore, the amount of suppression supplied by the retina is not significantly different from that in the LGN. These results indicate that surround suppression in the macaque LGN relies on feedforward mechanisms and suggest that suppression in the cortex likely includes a component established in the retina.

Introduction

Throughout the visual system, the visual responses of neurons are often modulated by stimuli that extend beyond the classical receptive field (reviewed in Fitzpatrick, 2000; Sillito and Jones, 2002; Angelucci and Bressloff, 2006). In the lateral geniculate nucleus (LGN) of the thalamus, the classical receptive field has a concentric center/surround organization (Kuffler, 1952). Overlapping the classical receptive field and extending beyond it, LGN neurons also have an extraclassical surround that is frequently referred to as the non-linear surround or suppressive surround, as stimuli of either sign (on or off) reduce the responsiveness of neurons (Levick et al., 1972; Murphy and Sillito, 1987; Felisberti and Derrington, 1999; Przybyszewski et al., 2000; Girardin et al., 2002; Sillito and Jones, 2002; Solomon et al., 2002; Webb et al., 2002, 2005). Accordingly, this form of suppression has been suggested to contribute to a variety of phenomena, including gain control and perceptual “pop-out” (Sillito and Jones, 2002; Bonin et al., 2005).

Surround suppression is also robust in primary visual cortex where it has been measured in all six cortical layers (Kapadia et al., 1999; Sceniak et al., 1999, 2001; Jones et al., 2000; Walker et al., 2000; Cavanaugh et al., 2002a; Levitt and Lund, 2002; Webb et al., 2005; Angelucci and Sainsbury, 2006; Smith et al., 2006). Indeed, neurons in layer 6 have been proposed to play a critical role in the emergence of surround suppression in the LGN, as past studies describe a pronounced reduction in LGN suppression in animals with cortical inactivation (Murphy and Sillito, 1987; Sillito and Jones, 2002; Webb et al., 2002; Nolt et al., 2007). Given the anatomical strength and spatial extent of the corticogeniculate pathway, this role for feedback is attractive (Guillery, 1969; Erisir et al., 1997). Other studies, however, suggest less involvement, if any, from corticogeniculate neurons in the emergence of extraclassical suppression in the LGN, as suppression (1) is present among LGN afferents in a pharmacologically silenced cortex (Sceniak et al., 2006), (2) occurs with stimuli drifting at spatial and temporal frequencies not preferred by cortical neurons (Bonin et al., 2005), and (3) is present in the retina (Solomon et al., 2006; Nolt et al., 2007; see also Ruksenas et al., 2000; Nolt et al., 2004).

Given past results implicating involvement by both the feedback and feedforward pathways to suppression in the LGN, along with the possibility of species-specific differences in experimental results and differences between early and more recent methods for evoking and measuring suppression, we wished to determine the extent to which feedback vs. feedforward mechanisms contribute to surround suppression in the LGN of the macaque monkey. To do so, we first quantified and compared the strength of suppression among magnocellular and parvocellular neurons in anesthetized and alert monkeys. We then studied the temporal evolution of LGN surround suppression, as any suppression supplied by the cortex should show a delay relative to the initial excitatory response. Finally, we compared the amount of suppression among retinal ganglion cells and LGN neurons using the same stimulus conditions and same analytical tools. Our results demonstrate that (1) surround suppression is significantly greater among magnocellular LGN neurons than parvocellular neurons, (2) surround suppression emerges too quickly in the LGN for involvement from cortical feedback, and (3) the strength of surround suppression in the retina is not significantly different from that in the LGN. From these results we conclude that extraclassical suppression in the early visual system of the macaque monkey follows feedforward projections. These results further suggest that a component of cortical suppression likely relies on suppression supplied by retinal mechanisms.

Results

This study was motivated by two objectives: (1) to determine the influence of extraclassical surround suppression on visual responses in the macaque LGN, and (2) to determine the role of feedforward and feedback mechanisms in the generation of extraclassical suppression.

Surround suppression in the LGN

To examine the influence of surround suppression on visual processing in the LGN, we recorded single-unit responses from 84 LGN neurons in the anesthetized macaque monkey. Seventy-one neurons were held for sufficient time to classify as magnocellular (n=47) or parvocellular (n=24) on the basis of their contrast response functions and the contrast required to evoke a half-maximum response (C50). Although we cannot rule out the inclusion of koniocellular neurons from our sample, efforts were made not to record from neurons in the intercalated layers where koniocellular neurons reside. For each neuron, we measured responses to drifting sinusoidal gratings (4 Hz, optimal spatial frequency) that varied in aperture size.

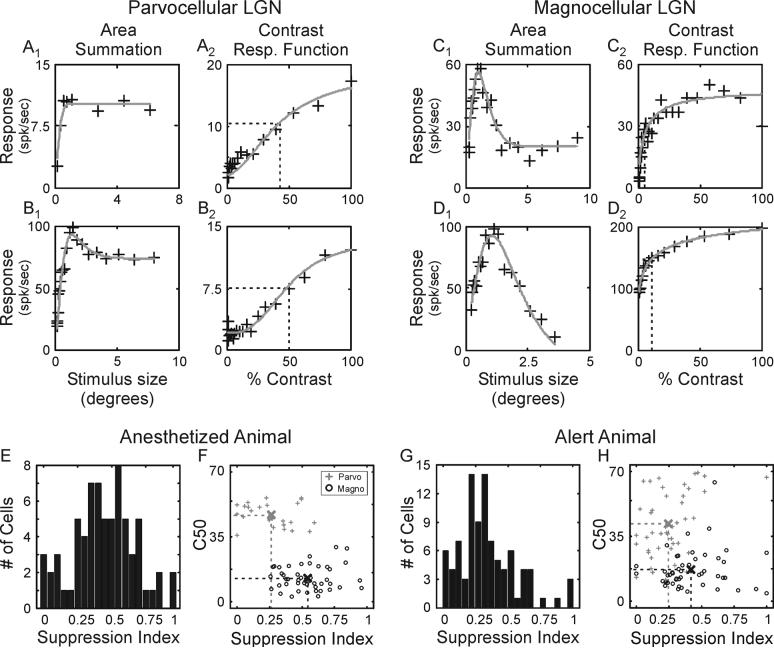
Surround suppression was more prominent in magnocellular neurons than in parvocellular neurons. Area summation tuning curves from 4 representative neurons—2 parvocellular neurons and 2 magnocellular neurons—are shown in Figure 1(A-D) along with their contrast response functions. For each neuron, response rate initially increases as stimulus size increases. This rate increase is taken as reflecting an increase in the amount of excitatory drive provided to the classical receptive field. For the two parvocellular neurons in Figures 1, response rates peak and then either plateau or show modest suppression as stimulus size increases. In contrast, both of the magnocellular neurons show pronounced suppression in their firing rate as stimulus size increases beyond the preferred.

Figure 1.

Area summation tuning properties of LGN neurons in the macaque monkey. A-D. Area summation tuning curves and contrast response functions for 2 representative parvocellular neurons and 2 representative magnocellular neurons. Area summation tuning curves (A₁, B₁, C₁, D₁) were fitted to a spatial domain difference of Gaussians (DOG_S) equation (gray line); contrast response functions (A₂, B₂, C₂, D₂) were fitted to a hyperbolic ratio (gray line). Dashed lines in the contrast response functions show the contrast to evoke a half-maximum response (C50). E and G. Distribution of suppression index values across LGN neurons in anesthetized and alert animals. F and H. Scatter plots showing the relationship between suppression index and C50 across cells in anesthetized and alert animals. Sample means are indicated by crosses located at the intersections of the two dashed lines.

To quantify the strength of suppression for each neuron in our sample, we employed a suppression index (SI = 1 – (Response_{(large diameter stimulus)} / Response_{(preferred diameter stimulus)}), where values near one would represent neurons with strong suppression and values near zero would represent neurons with weak suppression. Although there was considerable range in suppression index values (Figure 1E), magnocellular neurons displayed significantly greater suppression than parvocellular neurons (Figure 1F; 0.54+/−0.26 vs. 0.26+/−0.38, respectively; p<< 0.001).

Results from experiments in the cat and marmoset indicate that suppression in the LGN relies on feedback projections from primary visual cortex (Murphy and Sillito, 1987; Sillito and Jones, 2002; Webb et al., 2002). Given the possibility that anesthesia might reduce activity among corticogeniculate neurons and thereby reduce the strength of suppression in our experiments, we recorded LGN responses from two alert macaque monkeys while neurons were excited with drifting gratings that varied in aperture size. Similar to results from anesthetized animals, there was a wide range of suppression index values for LGN neurons in the alert animals with magnocellular neurons showing significantly greater suppression than parvocellular neurons (Figure 1G and H; 0.43 +/−0.03 vs. 0.27 +/−0.03, respectively; p<0.05). Importantly, there was not an increase in suppression strength in the alert animals. Accordingly, this finding indicates that anesthesia does not adversely affect the mechanisms, whether they be feedforward or feedback, that establish suppression in the LGN.

Linear vs. non-linear contributions to surround suppression

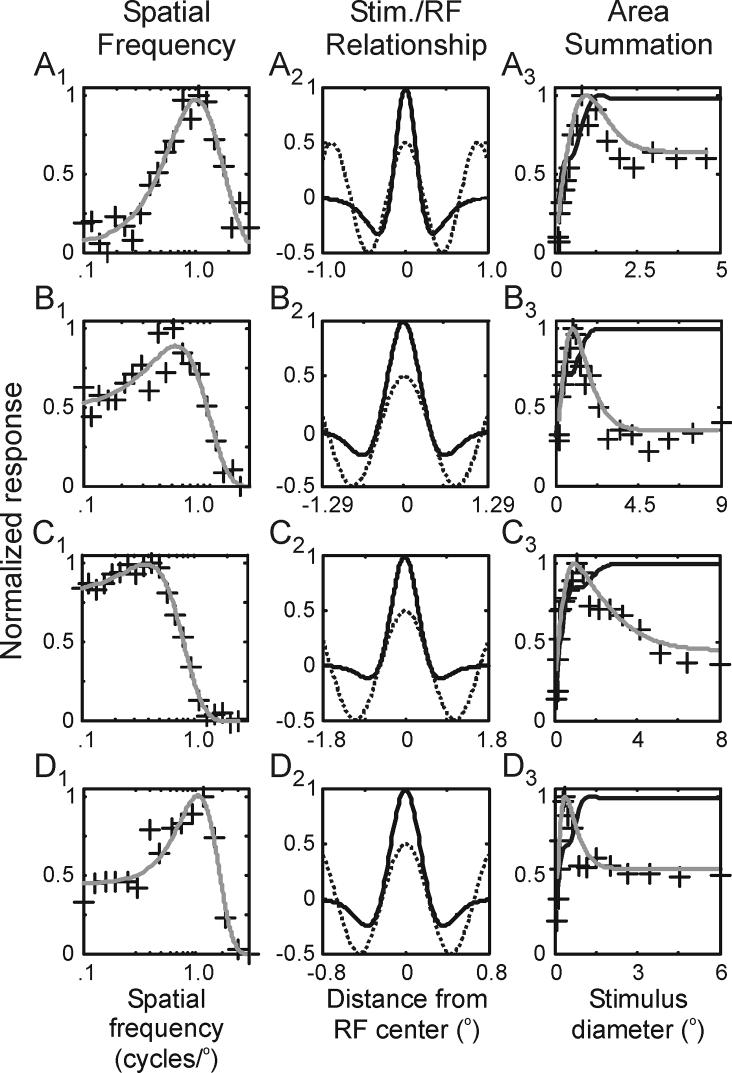
Although the suppression measured in an area summation tuning curve is generally viewed as reflecting nonlinear mechanisms operating within the extraclassical receptive field, linear mechanisms operating within the classical receptive field can influence the shape of tuning curves depending on the spatial correspondence between the classical receptive field and the spatial frequency of the sine-wave grating used to measure neuronal responses. To determine the extent to which linear mechanisms influenced our measures of suppression, we first determined the spatial parameters of the classical receptive field based on each neuron's spatial frequency tuning curve. As illustrated with 4 representative neurons in Figure 2 (A₁, B₁, C₁, D₁), responses were fit to a frequency domain difference of Gaussians equation (DOG_f). By convolving the stimulus used for the area summation experiments with the estimated spatial profiles of the classical receptive field (Figure 2, A₂, B₂, C₂, D₂), we were able to estimate the extent to which linear mechanisms contribute to surround suppression. For the four neurons shown in Figure 2 (A₃, B₃, C₃, D₃), predicted area summation tuning curves based solely on spatial estimates of the classical receptive field displayed little or no suppression as stimulus size increased beyond the preferred. In contrast, the actual tuning curves for each neuron showed significant suppression as stimulus size increased beyond the preferred.

Figure 2.

Estimating the contribution of linear suppression to area summation tuning curves. A₁, B₁, C₁, D₁. Spatial frequency tuning curves from 4 representative neurons fitted to a frequency-domain difference of Gaussians (DOG_f) equation (lines). A₂, B₂, C₂, D₂. DOG receptive field profiles of the 4 representative neurons (dark lines) along with the luminance profiles of the sine-wave gratings used in the area summation experiments (dashed gray lines). A₃, B₃, C₃, D₃. Estimated area summation tuning curves based on the classical receptive fields of the 4 representative neurons (dark lines) along with their measured tuning curves (gray lines).

Across our sample of LGN neurons, the amount of suppression in each neuron's area summation tuning curve was significantly greater than that predicted from purely linear mechanisms (Figure 3A; suppression index = 0.49 vs. 0.05, respectively; p<<0.001). Along these lines, ∼90% of the suppression present in the sample's tuning curves can be attributed to non-linear mechanisms.

Figure 3.

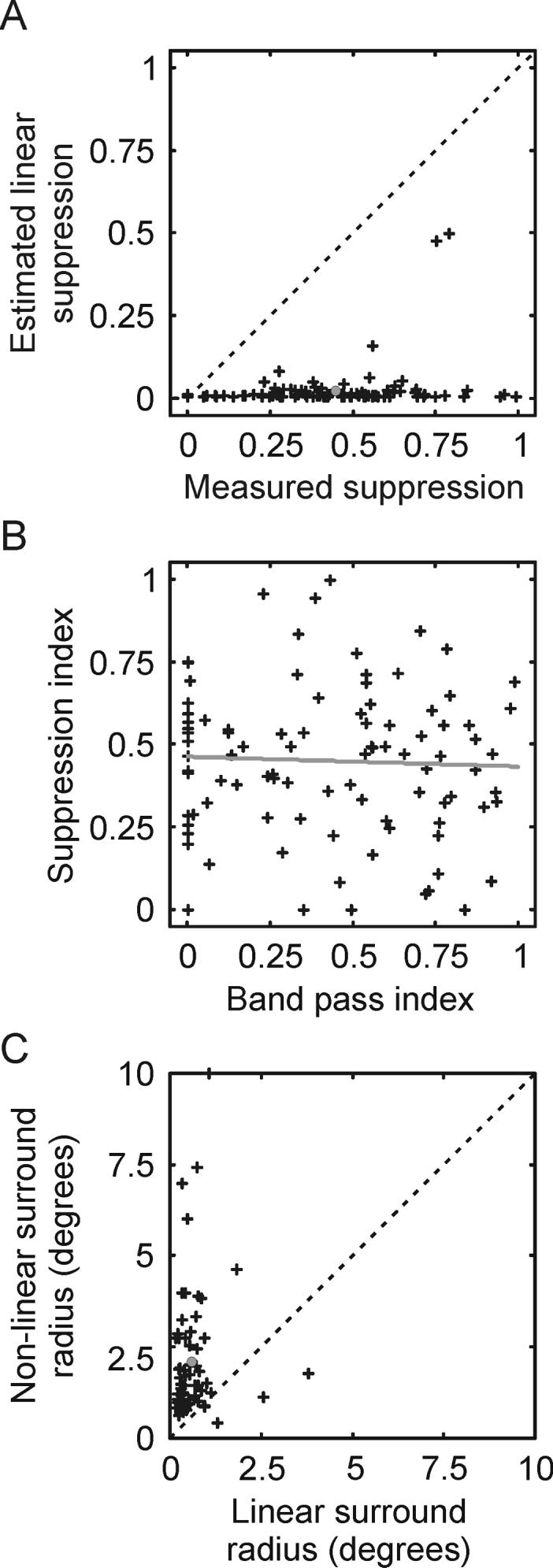
Relationship between the classical surround and extraclassical surround of LGN neurons. A. Scatter plot comparing suppression index values calculated from estimates of the linear contribution to suppression coming from the classical receptive field to actual suppression index values measured from area summation tuning curves. B. Scatter plot comparing extraclassical surround strength to classical surround strength. Extraclassical surround strength is quantified using a suppression index calculated from area summation tuning curves; classical surround strength is quantified using a band-pass index calculated from spatial frequency tuning curves. The dashed line shows the linear regression of the two values across cells. C. Comparison of the spatial size of the extraclassical receptive field with the size of the classical receptive field.

Because LGN neurons have both a classical surround (with linear responses) and an extraclassical surround (with non-linear responses), we wished to determine whether the strength of the linear surround was predictive of the strength of the non-linear surround. To quantify the strength of the linear surround, we calculated a band-pass index (BPI = 1 − (Response_{(low SF)} / Response_{(preferred SF)}) for each neuron using its spatial frequency tuning curve. With this index, values near one represent neurons with linear surrounds that are nearly as strong as their centers, while values near zero represent neurons with weak surrounds relative to their centers. Although there was considerable range in both the band-pass index values and suppression index values across our sample of neurons, there was not a correlation between the two values (Figure 3B, r² =−0.05). These results demonstrate independence between the linear and non-linear surrounds of LGN neuron as well as provide support for the view that the linear surround has little influence on the amount of suppression measured in our area summation experiments.

Traditionally, the spatial extent of the non-linear surround has been viewed as extending beyond that of the linear surround (Murphy and Sillito, 1987; Girardin et al., 2002; Sillito and Jones, 2002; Webb et al., 2002; but see Bonin et al., 2005; Nolt et al., 2007). Having determined the spatial parameters of each neuron's linear and non-linear surround (i.e. radius of the respective surround subunit (r_s), taken from the frequency domain and spatial domain DOG equations; see Experimental Procedures), we compared these values across our sample of neurons. As shown in Figure 3C, the size of the nonlinear surround was significantly greater than that of the linear surround (p<<0.001), as the non-linear receptive field was 1.79 times larger, on average, than the linear surround.

The time course of surround suppression in the LGN

Past studies in cats indicate that the corticogeniculate pathway contributes significantly to extraclassical suppression in the LGN (Murphy and Sillito, 1987; Sillito and Jones, 2002; Webb et al., 2002). Given the time required to activate feedback pathways (Briggs and Usrey, 2007), it would seem reasonable to predict that suppression in the LGN should be delayed relative to the initial excitatory response.

To determine the time course of surround suppression in the LGN, we measured the responses of LGN neurons in anesthetized monkeys to brief presentations of stationary sine-wave gratings of various aperture sizes. We then calculated area summation tunings curves based on responses at different times relative to stimulus onset. Representative area summation tuning curves from three LGN neurons are shown in Figure 4 (A₁, B₁, C₁). For each neuron, the purple curve shows responses to different size stimuli two milliseconds before 25% of maximum firing rate was achieved, while progressively warmer color curves show responses at times later in the cell's activity profile. For each neuron, there is evidence of surround suppression at the earliest times following stimulus onset, indicating that excitation and surround suppression develop with very similar latencies in the LGN. Along these lines, large-aperture stimuli never evoked activity as robust as the maximal activity evoked by optimal-size stimuli, indicating that suppression takes effect before excitatory activity peaks.

Figure 4.

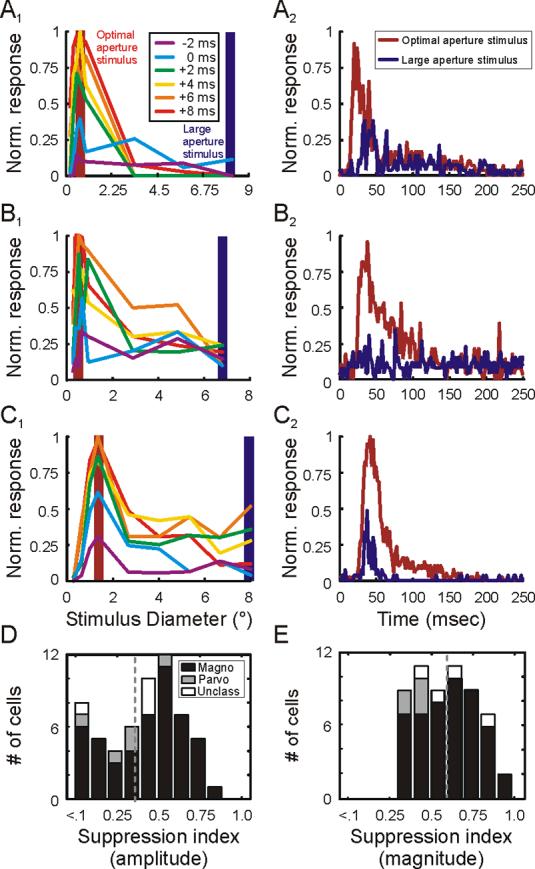
Temporal dynamics of area summation in the LGN. A₁, B₁, C₁. Area summation tuning curves for 3 representative neurons at 6 different relative times. The time when cells reached 25% of maximum response is defined as 0 msec. Each of the colored curves represents responses at times relative to 0 msec. Shaded red and blue bars highlight responses to optimal-size stimuli and large stimuli, respectively. A₂, B₂, C₂. Time course of responses to optimal-size stimuli (red traces) and large stimuli (blue traces) for the 3 representative neurons. D and E. Distribution of suppression index values using amplitude (D) and magnitude (E) measures from each cell's area summation tuning curve. Magnocellular neurons represented in black, parvocellular neurons represented in gray, unclassified neurons represented in white.

To compare suppression resulting from stationary and drifting gratings, we calculated a magnitude suppression index using the area under response curves to optimal-size and large stationary gratings (see Experimental Procedures). Across cells, the magnitude suppression index calculated from responses to stationary gratings was very similar to the mean suppression index calculated from responses to drifting gratings (0.59+/−0.02 vs. 0.54+/−0.26).

To examine quantitatively the time course of surround suppression in the LGN, we compared the response latency and suppression latency of 73 neurons (63 magnocellular neurons, 5 parvocellular neurons and 3 unclassified neurons) based on their impulse responses to optimal-size stimuli and large stimuli (Figure 4 A₂, B₂, C₂). This analysis was restricted to neurons with suppression index values ≥ 0.3. Response latency was defined as the earliest time following stimulus onset that responses to optimal-size stimuli reached 25% of maximum; suppression latency was defined as the earliest time following stimulus onset that differences between responses to optimal-size stimuli and maximum-suppressing stimuli first reached 25% of the maximum difference. Although we found a range of suppression latencies across our sample of LGN neurons (Figure 5A), suppression latency was tightly correlated with response latency (Figure 5B; r² = 0.81), as suppression latency was delayed, on average, by only 1.9 +/−0.6 msec relative to response latency (Figure 5C; mean suppression latency = 24.7 +/− 0.97 msec, mean response latency = 22.8 +/−0.86 msec). Although cross-correlation studies suggest that spikes originating in the LGN can trigger cortical responses within this time frame (Usrey and Reid, 1999; Usrey et al., 2000, Alonso et al., 2001), there is not enough time for the cortex to process this input and deliver it back to the LGN in time to influence fast suppression (Briggs and Usrey, 2007).

Figure 5.

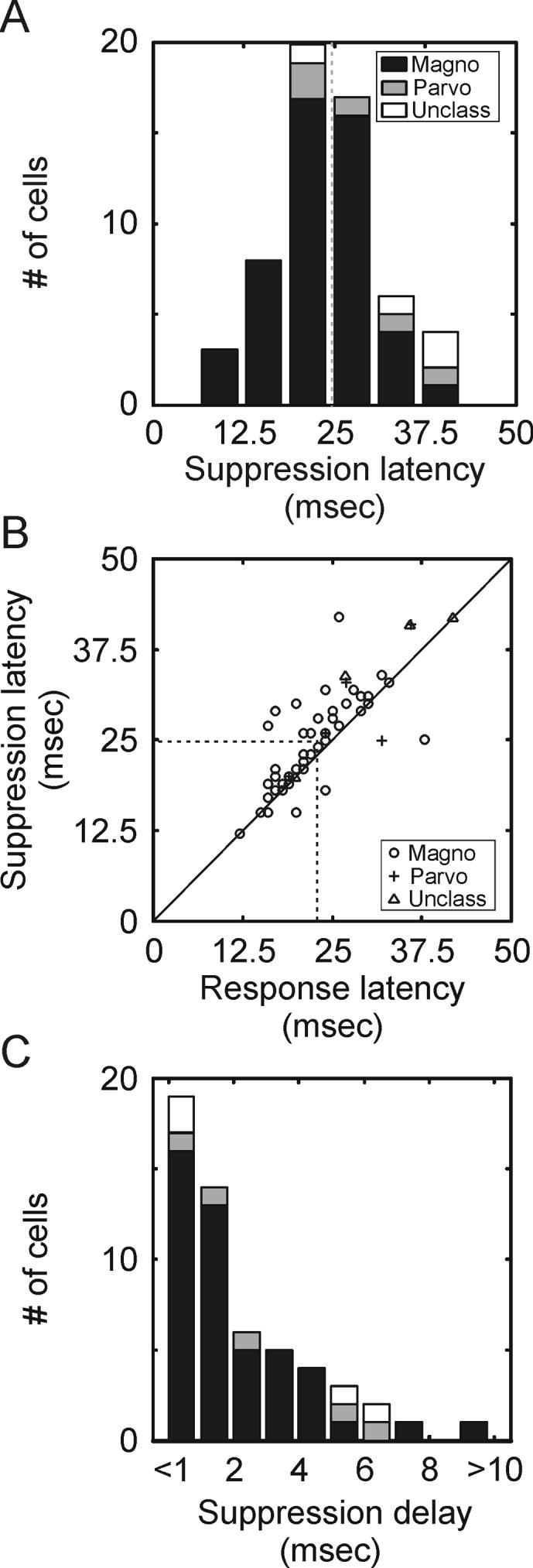
Suppression latency in the LGN. A. Distribution of suppression latencies across the sample of LGN neurons. Suppression latency is defined as the time when responses to optimal-size stimuli and large stimuli first reach 25% of the maximum difference. Magnocellular neurons represented in black, parvocellular neurons represented in gray, unclassified neurons represented in white. This analysis is restricted to neurons with at least 30% suppression. B. Scatter plot showing the relationship between response latency and suppression latency. Response latency is defined as the earliest time that responses reached 25% of maximum response. Suppression latency is defined as described in A. C. Distribution of delays between the response latency and suppression latency across the sample of neurons.

Given the short delay between response latency and suppression latency, it seemed likely that the onset of surround suppression might precede the peak of the excitatory response. To test for this possibility, we calculated an amplitude suppression index for each neuron using peak responses to optimal-size stimuli and maximum-suppressing stimuli (see Experimental Procedures). If the onset of suppression occurred after the peak in the excitatory response, then the amplitude suppression index should be close to zero. In contrast, the mean index value is shifted significantly to the right of zero (Figure 4D; mean amplitude suppression index = 0.40+/−0.04; p<<0.001), reinforcing the conclusion that suppression onset precedes the peak of the excitatory response.

The Influence of Feedforward Input on LGN Surround Suppression

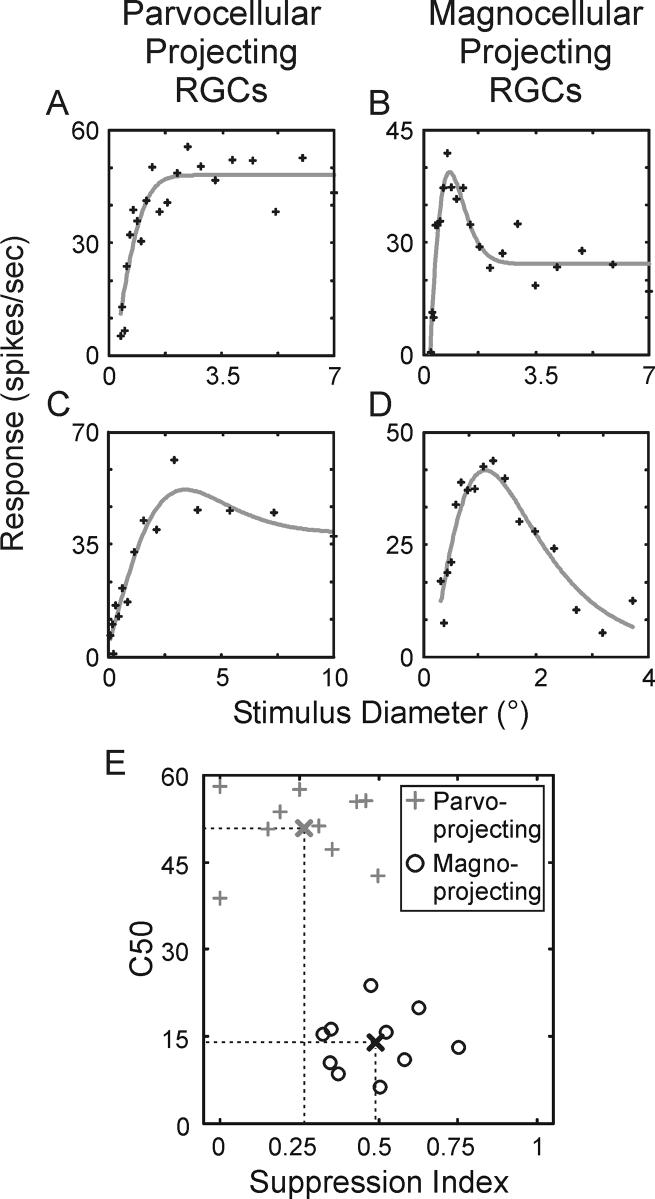
Having established that extraclassical suppression in the LGN is too fast to rely on feedback mechanisms from the cortex, we wished to know the extent to which suppression might be inherited from the retina. We therefore recorded visual responses from 24 retinal ganglion cell axons as they traversed the optic tract toward the LGN. Area summation tuning curves from 4 retinal ganglion cells are shown in Figure 6A-D. Based on each cell's contrast response function, retinal ganglion cells were classified as either midget cells with axons targeting the parvocellular layers of the LGN or parasol cells with axons that target the magnocellular layers of the LGN (Figure 6E). Consistent with our findings in the LGN, retinal ganglion cells with presumptive input to the magnocellular layers of the LGN displayed significantly greater surround suppression than those with presumptive input to the parvocellular layers (Figure 6E; mean suppression index: midget cells = 0.26+/−0.06, parasol cells = 0.45+/−0.05; p<0.01). Furthermore, there was not a significant difference between suppression index values of midget ganglion cells and parvocellular LGN neurons (p=0.99) or between parasol ganglion cells and magnocellular LGN neurons (p=0.35). These fingings suggest that most, if not all, of the surround suppression present in the LGN is inherited from the retina (mean parasol suppression index / mean magnocellular suppression index = 0.89, mean midget suppression index / mean parvocellular suppression index = 1.0).

Figure 6.

Area summation tuning properties of retinal ganglion cells in the macaque monkey. A and C. Area summation tuning curves from 2 representative parvocellular-projecting ganglion cells. Tuning curves were fitted to a spatial domain difference of Gaussians (DOG_S) equation (gray line). B and D. Area summation tuning curves from 2 representative magnocellular-projecting ganglion cells. E. Scatter plot showing the relationship between the suppression index and contrast to evoke a half-maximum response (C50) across cells. Parvocellular-projecting ganglion cells represented with gray crosses, magnocellular-projecting ganglion cells represented with black circles. Thick crosses indicate the means for the two samples.

Given the short delay between excitation and suppression in the LGN, we expected to find a similarly short delay in the retina. However, as illustrated with 3 representative retinal ganglion cells in Figure 7, suppression latency was much slower than response latency. Furthermore, in contrast to the response profiles of LGN neurons, retinal ganglion cells show a clear peak in their excitatory response prior to suppression.

Figure 7.

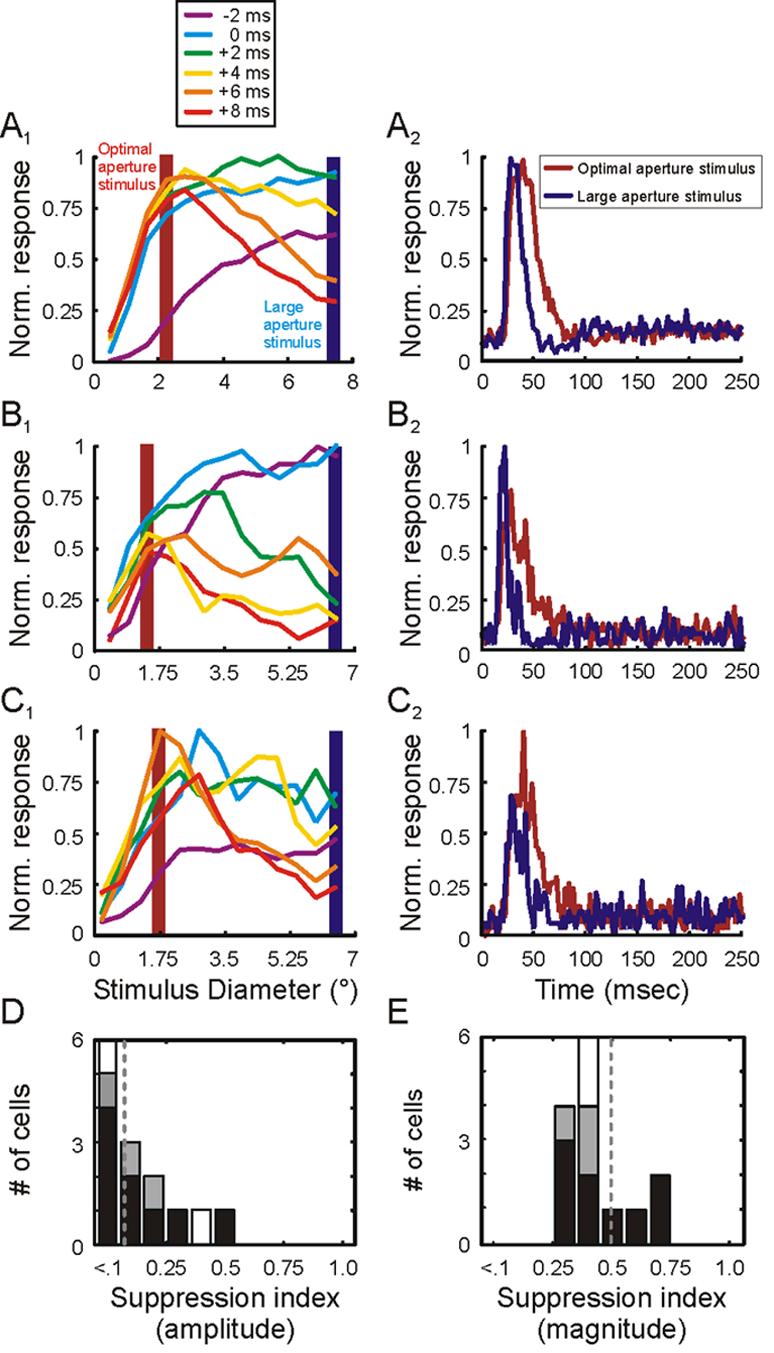
Temporal dynamics of area summation in the retina. A₁, B₁, C₁. Area summation tuning curves for 3 representative retinal ganglion cells at 6 different relative times. The time when cells reached 25% of maximum response is defined as 0 msec. Each of the colored curves represents responses at times relative to 0 msec. Shaded red and blue bars highlight responses to optimal-size stimuli and large stimuli, respectively. A₂, B₂, C₂. Time course of responses to optimal-size stimuli (red traces) and large stimuli (blue traces) for the 3 representative ganglion cells. D and E. Distribution of suppression index values using amplitude (D) and magnitude (E) measures from each cell's area summation tuning curve. Magnocellular neurons represented in black, parvocellular neurons represented in gray, unclassified neurons represented in white.

Across our sample of retinal ganglion cells, suppression latency was significantly greater than excitation latency (Figure 8A; mean excitation latency = 18.6+/−1.2 msec, mean suppression latency = 26.8+/−0.7 msec; p=0.01). Moreover, the delay between excitation latency and suppression latency was significantly greater in the retina than in the LGN (Figure 8B; mean suppression delay: retina = 8.2+/−0.6 msec, LGN = 1.9 +/−0.6 msec; p<0.01). In addition, amplitude suppression index values for retinal ganglion cells were just 1/10^th of magnitude suppression index values (Figure 7D and E; 0.05 +/−0.10 vs. 0.49+/− 0.04, respectively; p<0.001), indicating that surround suppression in the retina does not take effect until after the peak in the excitatory response.

Figure 8.

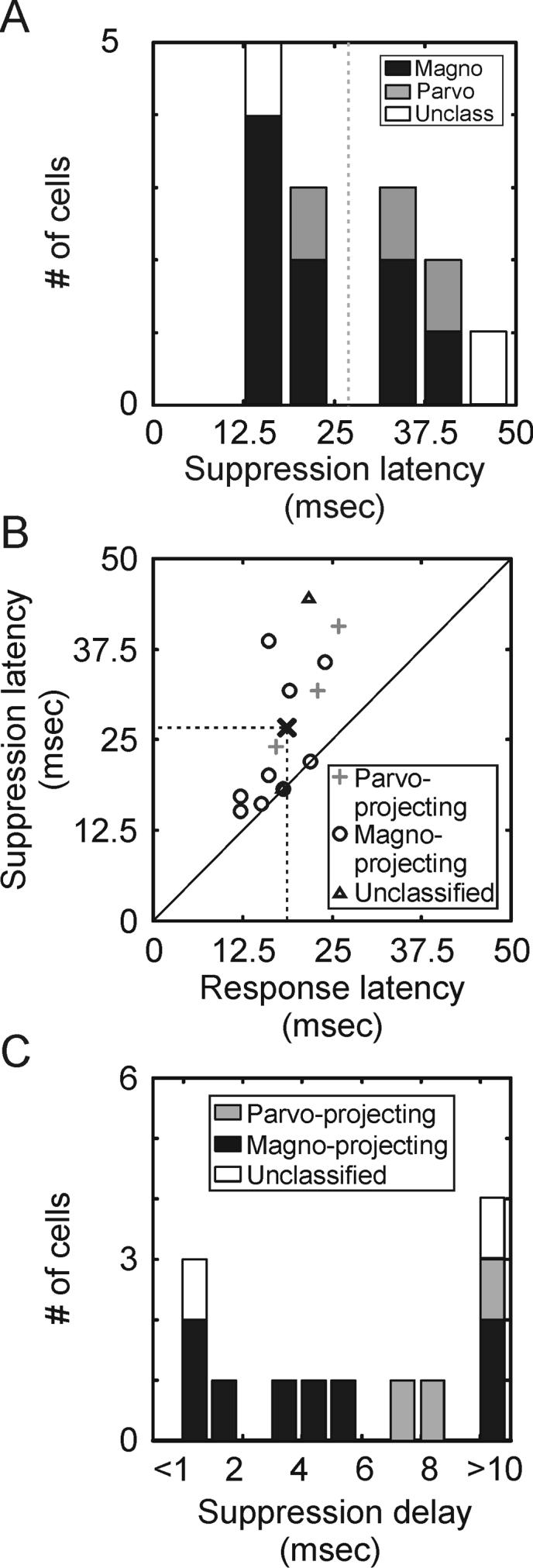
Suppression latency of retinal ganglion cells. A. Distribution of suppression latencies across the sample of retinal ganglion cells. Suppression latency is defined as the time when responses to optimal-size stimuli and large stimuli first reach 25% of the maximum difference. Magnocellular neurons represented in black, parvocellular neurons represented in gray, unclassified neurons represented in white. This analysis is restricted to neurons with at least 30% suppression. B. Scatter plot showing the relationship between response latency and suppression latency. Response latency is defined as the earliest time that responses reached 25% of maximum response. Suppression latency is defined as described in A. C. Distribution of delays between the response latency and suppression latency across the sample of retinal ganglion cells.

Given the unexpected finding that the delay between the onset of excitation and suppression is less in the LGN than in the retina, we wondered whether the decreased delay could result from mechanisms that underlie the spike threshold of LGN neurons. For instance, several studies have shown that retinal spikes are much more effective at driving LGN spikes when they are preceded in time by a short interspike interval (Mastronarde, 1987; Usrey et al., 1998; Levine and Cleland, 2001; Rowe and Fischer, 2001; Sincich et al., 2007; Weyand 2007). This finding supports the idea that the first retinal spike to follow stimulus onset would have a lower probability of driving a geniculate response compared to subsequent spikes.

To test for the possibility that spike threshold has a role in decreasing the suppression delay of LGN neurons, we modeled the responses of a simulated LGN neuron by passing the spike train of a representative retinal ganglion cell through an exponential temporal function with a threshold for generating spikes (time constant = 5 msec; see Experimental Procedures). Figure 9A shows the time course of the retinal ganglion cell's response to the presentation of a stationary grating of optimal-size and another grating that extended well into the suppressive surround. For this ganglion cell, the onset of suppression is delayed by 8 msec relative to the onset of excitation. In contrast, the responses of the simulated LGN neuron exhibit a delay of only 1.5 msec (Figure 9B), a value quite similar to the average delay (1.9 +/−0.6 msec) measured across our sample of LGN neurons. This finding supports the view that by the time a retinal ganglion cell brings its postsynaptic LGN neuron to threshold, the suppressive mechanisms in the retina have taken effect and suppression consequently appears more immediate in the LGN.

Figure 9.

Temporal dynamics of surround suppression in a model LGN neuron. A. Time course of responses measured from a retinal ganglion cell stimulated with an optimal-size stimulus (red trace) and a large stimulus (blue trace). The delay between response latency and suppression latency is 8 msec. B. Time course of responses from a modeled LGN neuron that received input from the cell in A. Spiking responses in the LGN neuron were generated by passing the retinal spike trains through an exponential filter (τ = 5 msec) with a spike threshold. For this model neuron, the delay between response latency and suppression latency is 1.5 msec.

Discussion

The goal of this study was to determine the origin and dynamics of extraclassical/non-linear suppression in the LGN of the macaque monkey. Our results reveal (1) significantly greater suppression among magnocellular neurons compared to parvocellular neurons, (2) a delay between excitation and suppression that is too brief to allow for the involvement of cortical feedback, and (3) suppression among retinal ganglion cells that is equal in strength to that measured in the LGN. In the sections below, we consider the significance of these results for understanding the mechanisms that underlie the emergence of surround suppression in the LGN and the potential roles of surround suppression in visual processing.

Feedforward vs. feedback contributions to extraclassical suppression

An early model for the emergence of extraclassical suppression in the LGN proposed that suppression relied critically on corticogeniculate feedback (Murphy and Sillito, 1987; Sillito and Jones, 2002). This model was appealing, as (1) corticogeniculate neurons have receptive fields that are larger than those of retinotopically-aligned LGN neurons (Jones et al., 2000), (2) feedback axons make synapses with both excitatory and inhibitory neurons in the LGN as well as inhibitory neurons in the reticular nucleus (Webber et al., 1989; Montero, 1991; Bourassa and Deschenes, 1995; Murphy and Sillito, 1996; Erisir et al., 1998), and (3) a substantial number of feedback neurons have complex receptive fields, thereby allowing the influence of feedback to be invariant (i.e. nonlinear) to stimulus phase (Tsumoto and Suda, 1980; Grieve and Sillito, 1995; Hirsch et al., 1998; Briggs and Usrey, 2005, 2007). Furthermore, (4) early efforts identified a “suppressive zone” surrounding the classical surround of LGN neurons in cats that was not present in their retinal inputs (Levick et al., 1972) and, importantly, (5) experiments comparing LGN suppression in the presence and absence of feedback found a marked reduction in LGN suppression in the absence of feedback (Murphy and Sillito, 1987; Sillito and Jones, 2002; Webb et al., 2002; Nolt et al., 2007).

Despite the appeal and support for a cortical role in LGN surround suppression, results from other studies suggest that feedback plays a more limited role, if any, in the generation of surround suppression. Notably, experiments examining the area summation tuning properties of LGN afferents in V1 of the macaque monkey found suppression when V1 (and presumably the corticogeniculate pathway) is silenced pharmacologically (Sceniak et al., 2006). In addition, suppression in the LGN of cats occurs at spatial and temporal frequencies not preferred by cortical neurons (Bonin et al., 2005). In the present study, we examined the temporal evolution of surround suppression to determine whether or not corticogeniculate feedback could be involved. Our results show that suppression arises too quickly to allow for involvement from the cortex. Across our sample of LGN neurons, the onset of suppression occurred, on average, within 2 msec of the initial excitatory response. Furthermore, the average latency for suppression onset was 24.7 +/− 1.0 msec, which is substantially less than the visual response latency of identified corticogeniculate neurons in the macaque monkey (mean latency = 47.2 +/− 3.5 msec; range: 32-63 msec; Briggs and Usrey, 2007). Because we used stationary stimuli to assess the time course of suppression and others have suggested that stationary stimuli are not optimal for evoking suppression from feedback pathways (Sillito and Jones, 2002), it is important to note that our measures of suppression strength were similar when using stationary and drifting stimuli. Moreover, to address the possibility that anesthesia may have diminished the involvement of feedback projections in our experiments, we measured the strength of surround suppression in the alert, behaving animal. Results of this effort show that surround suppression is not diminished by our protocol for anesthesia.

If corticogeniculate feedback does not contribute to surround suppression in the LGN of the macaque monkey, then what pathways/circuits do contribute to LGN suppression? As somewhat of a surprise, results from a recent study show that extraclassical suppression is present in the retina (Solomon et al., 2006; see also Ruksenas et al., 2000; Nolt et al., 2004). Indeed, it has been suggested that extraclassical suppression in the retina and LGN is a manifestation of a retinal contrast gain control mechanism (Shapley and Victor, 1978, 1981), resulting from a suppressive field that measures local contrast (Bonin et al., 2005). Although not the focus of the current study, it is worth noting that past efforts indicate that corticogeniculate feedback may increase the contrast gain of LGN neurons (Przybyszewski et al., 2000; but see Webb et al., 2002; Nolt et al., 2007).

To examine the extent to which suppression in the LGN is inherited from the retina, we compared the strength of suppression among retinal ganglion cells and LGN neurons using the same set of stimuli and analytical tools. Our results show that surround suppression among magnocellular LGN neurons is not significantly different from that of magnocellular-projecting retinal ganglion cells. Similarly, suppression among parvocellular LGN neurons is not significantly different from that of parvocellular-projecting retinal ganglion cells. Thus, LGN suppression appears to be fully accounted for by suppression supplied by the retina. Furthermore, these results support the view that a contrast gain control mechanism underlies extraclassical suppression (Bonin et al., 2005), as contrast gain control is greater among magnocellular projecting ganglion cells than parvocellular projecting cells (Benardete et al. 1992; Yeh et al. 1995; Benardete and Kaplan, 1999). Although we cannot completely rule out other sources of fast suppression, namely inhibitory input supplied by interneurons in the LGN and/or neurons in the reticular nucleus, any involvement on their part would seem necessarily modest in the monkey, as suppression in the LGN is not significantly different from that in the retina. This result differs from those in the cat, where a component of extraclassical suppression likely includes involvement from thalamic inhibitory neurons (Funke and Eysel, 1998; Nolt et al., 2007). Thus, there may be differences in the circuits that contribute to LGN suppression in cats and monkeys.

Functional properties of surround suppression

Our results demonstrate that surround suppression is significantly greater in the magnocellular pathway of the macaque monkey than in the parvocellular pathway. This distinction holds not only for magnocellular and parvocellular LGN neurons, but also for their retinal afferents. Consistent with results from Solomon et al. (2006), we find that suppression is 2-3x greater among magnocellular-projecting retinal ganglion cells compared to parvocellular-projecting ganglion cells. In the marmoset monkey, magnocellular LGN neurons also display greater suppression than parvocellular neurons (Solomon et al., 2002; Webb et al., 2002, 2005); however, the difference between the two classes of neurons is less pronounced than in the macaque. Because of the similarities that exist between magnocellular and parvocellular neurons in the primate and Y and X cells in the cat, it is interesting to note that surround suppression has been suggested to be greater among Y cells compared to X cells (Bonin et al., 2005; but see Girardin et al., 2002).

Given the center/surround organization of LGN receptive fields, we wished to know whether the strength of antagonism between the classical center and surround were indicative of the strength of the extraclassical suppressive surround. Consistent with previous results (Solomon et al., 2006), we found no relationship between the two, as quantified with a band-pass index calculated from spatial frequency tuning curves and a suppression index calculated from area summation tuning curves. Thus, the linear and non-linear surrounds of LGN neurons appear to operate independently of each other, indicating that they rely on different neuronal mechanisms.

Across our sample of LGN neurons, the spatial extent of the suppressive surround was ∼1.8 times larger than that of the classical surround. The finding that the suppressive surround extends beyond the classical surround has also been reported for neurons in the LGN of cats and marmoset monkeys, as well as the retina of macaque monkeys (Levick et al., 1972; Murphy and Sillito, 1987; Felisberti and Derrington, 1999; Przybyszewski et al., 2000; Kaplan and Benardete, 2001; Girardin et al., 2002; Sillito and Jones, 2002; Solomon et al., 2002, 2006; Webb et al., 2002, 2005). It is worth noting, however, that this relationship might be closer to 1:1 had we estimated the size of the classical surround using a masking stimulus method rather than the more traditional method of fitting a difference of Gaussians equation to the spatial frequency tuning curves of individual neurons (Bonin et al., 2005; see also Nolt et al., 2007).

Previous studies have examined the influence of stimulus contrast on the strength and spatial extent of surround suppression in the LGN (Solomon et al., 2002, 2006; Nolt et al., 2004; Bonin et al., 2005; Sceniak et al., 2006). In general, these studies report that suppression strength increases with stimulus contrast. Accordingly, suppression at high contrasts likely underlies the leftward shift in area summation tuning curves that accompanies a reduction in the radius of the excitatory summation field. Thus, the spatial extent of the classical receptive field is largest at low contrasts and smallest at high contrasts (but see Sceniak et al., 2006). Similar results have been reported for neurons in primary visual cortex, raising the possibility that subcortical mechanisms may contribute to cortical size tuning (Kapadia et al., 1999; Sceniak et al., 1999; Jones et al., 2000; Walker et al., 2000; Cavanaugh et al., 2002a; Levitt and Lund, 2002; Webb et al., 2005; Angelucci and Sainsbury, 2006; Smith et al., 2006).

Potential roles for surround suppression in visual processing

Surround suppression has been proposed to contribute to visual processing in a number of ways. Given the hierarchical organization of the early visual system, it seems likely that surround suppression in the retina and LGN is conveyed to postsynaptic neurons in the cortex. Along these lines, suppression is robust in the layers of cortex associated with the magnocellular pathway, namely layers 4Cα and 4B (Sceniak et al., 2001). However, as suppression in the cortex often displays an orientation preference not found in the LGN (Sillito et al., 1995; Levitt and Lund, 1997; Cavanaugh et al., 2002b; Girardin et al., 2002; Jones et al., 2002; Solomon et al., 2002; Webb et al., 2002, 2005; Bonin et al., 2005; Angelucci and Bressloff, 2006; Smith et al., 2006; but see Cudeiro and Sillito, 1996; Sillito and Jones, 2002), additional cortical mechanisms are almost certainly involved in the refinement of the suppressive field. Accordingly, different components of suppression may serve different functional purposes. For instance, suppression that emerges in the retina is likely to contribute to contrast gain control whereby local contrast decreases the responsiveness of neurons (Shapley and Victor, 1978, 1981; Felisberti and Derrington, 1999; Bonin et al., 2005), whereas suppression that emerges in the cortex is likely to serve as a basis for perceptual “pop-out”, curvature detection and/or figure-ground segregation (Dobbins et al., 1987; Knierem et al., 1992; Lamme, 1995; Jones et al., 2002).

Experimental Procedures

Neuronal recordings were made from 10 anesthetized macaque monkeys (Macaca mulatta) and 2 alert monkeys. All surgical and experimental procedures conformed to NIH guidelines and were carried out with the approval of the Animal Care and Use Committee at the University of California, Davis.

Surgery and preparation

For experiments in anesthetized animals, anesthesia was induced with ketamine (10 mg/kg, IM) and maintained with sufentanil citrate (8-24 μg/kg/hr, IV) and 0.4% isoflurane. Animals were placed in a stereotaxic apparatus where temperature, EKG, EEG, and expired CO₂ were monitored continuously. If physiological monitoring indicated a low level of anesthesia, additional sufentanil was given and the rate of infusion increased. Pupils were dilated with 1% atropine sulfate and eyes were glued to posts attached to the stereotaxic frame. The eyes were fitted with contact lenses and focused on a tangent screen located 172 cm in front of the animal. A midline scalp incision was made and wound margins infused with lidocaine. A small craniotomy was made above the LGN and/or the optic tract. Once all surgical procedures were complete, animals were paralyzed with vecuronium bromide (0.2 mg/Kg/hr, IV) and mechanically respired.

Data acquisition and visual stimuli

Single-unit responses of LGN neurons and optic tract axons were amplified, filtered and recorded to a PC computer with a Power 1401 data acquisition interface and Spike 2 software (Cambridge Electronic Design, Cambridge, England). Visual stimuli were created with a VSG2/5 visual stimulus generator (Cambridge Research Systems, Rochester, England) and presented on a gamma-calibrated Sony monitor running at 140Hz. The mean luminance of the monitor was 38 candelas/m².

Visual responses of LGN neurons and optic tract fibers were characterized quantitatively using drifting and stationary sinusoidal gratings. For experiments with anesthetized animals, drifting gratings were shown for 4 seconds, followed by 4 seconds of mean gray. For experiments with alert animals, drifting gratings were shown for 2 seconds while animals maintained fixation for a fluid reward. Trials were aborted if eye position deviated by more than 0.35°. The inter-stimulus interval was >2 seconds.

Spatial frequency tuning

Spatial frequency tuning curves were made both to determine the optimal spatial frequency for subsequent grating experiments as well as to determine the spatial parameters of each neuron's classical receptive field. Responses to drifting sine-wave gratings (4 Hz, 100% contrast) presented at 16 different spatial frequencies (0.1 to 3 cycles/°) were fit to a frequency domain difference of Gaussians (DOG_F) equation,

$$\mathrm{R}\left(\mathrm{f}\right)={{\mathrm{K}}_{\mathrm{c}}}^{\ast }\exp (-\left({\pi }^{\ast }{\mathrm{r}}_{\mathrm{c}}{.}^{\ast }\mathrm{f}\right)^2)-{\left({\mathrm{K}}_{\mathrm{s}}\right)}^{\ast }\exp (-1^{\ast }\left({\pi }^{\ast }{\mathrm{r}}_{\mathrm{s}}{.}^{\ast }\mathrm{f}\right).^2)$$

where R(f) is the f1 of the response evoked by spatial frequency f, r_c is the radius of the center subunit, and r_s is the radius of the surround subunit. A constrained non-linear optimization procedure (MATLAB function: fmincon; The Mathworks Inc., Natick, MA) was used to minimize the squared error (i.e., Σ (Data-Fit)²) when fitting the DOG_Ffunctions and all subsequent data sets.

Contrast Response Functions

To determine the influence of contrast on neuronal activity, contrast response functions were calculated based on responses to drifting sine-wave gratings (4 Hz, preferred spatial frequency) presented over a range of contrasts (1% to 100%). Neuronal responses were fit to a hyperbolic ratio (Albrecht and Hamilton 1982),

$$\mathrm{R}\left(\mathrm{C}\right)={\mathrm{K}}_{.}({\mathrm{C}}^{\mathrm{n}}∕({\mathrm{C}}^{\mathrm{n}}+{{\mathrm{C}}_{50}}^{\mathrm{n}}))+\mathrm{DC}$$

where C represents the contrast levels presented during the experiment, K represents the maximum response rate, C₅₀ is the contrast corresponding to 50% of the cell's maximim response, DC is the firing rate to a blank gray screen, and n is a variable reflecting the cell's sensitivity.

Area Summation Tuning

To determine the relationship between stimulus size (diameter) and neuronal activity, drifting sine-wave gratings (4 Hz, preferred spatial frequency) of various diameters (0.1° to 10°) were centered and presented over each neuron's receptive field. Responses to different size stimuli were fit to a spatial domain difference of Gaussians (DOG_S) equation,

$$\mathrm{R}\left(\mathrm{x}\right)={{\mathrm{K}}_{\mathrm{c}}}^{\ast }\underset{-\mathrm{x}∕2}{\overset{\mathrm{x}∕2}{\Sigma }}\exp (-(2^{\ast }\mathrm{x}∕{\mathrm{r}}_{\mathrm{c}})^2)-{{\mathrm{K}}_{\mathrm{s}}}^{\ast }\underset{-\mathrm{x}∕2}{\overset{\mathrm{x}∕2}{\Sigma }}{}^{\ast }\exp (-(2^{\ast }\mathrm{x}∕{\mathrm{r}}_{\mathrm{s}}).^2)$$

where R(x) is the f1 of the response evoked by diameter x, K_c is amplitude of the center subunit, r_c is the radius of the center subunit, K_s is the amplitude of the surround subunit, and r_s is the radius of the surround subunit. The radius of the surround subunit was taken to be the spatial extent of the extraclassical receptive field. A suppression index was used to quantify the amount of suppression using the equation,

$$\mathrm{SI}=1-({\text{Response}}_{\left(\text{large diameter stimulus}\right)}∕{\text{Response}}_{\left(\text{preferred diameter stimulus}\right)})$$

To estimate the amount of surround suppression due to linear mechanisms, we convolved the linear estimate of the LGN receptive field (calculated from the spatial frequency tuning curve) with the stimulus used in area summation experiments. From this, we plotted a linear estimate of the area summation tuning curve and calculated the suppression index for this curve.

Temporal Dynamics of Surround Suppression

To determine the time course of surround suppression, stationary sine-wave gratings (preferred spatial phase and spatial frequency) of various diameters were centered over the receptive fields of LGN neurons and optic tract fibers and presented for 250 msec followed by a blank gray screen for 750 msec. Stimulus diameter was randomized across presentations (8-16 different diameters, typically 0.1° to 5°-10°). A similar approach has been used to study the temporal properties of suppression in primary visual cortex (Bair et al., 2003; Smith et al., 2006).

To quantify the time course of surround suppression we calculated the response latency and suppression latency. Response latency was defined as the earliest time following stimulus onset that responses to optimal-size stimuli reached 25% of maximum. Suppression latency was defined as the earliest time following stimulus onset that the difference between responses to optimal-size stimuli and maximum-suppressing stimuli first reached 25% of the maximum difference.

Model of Retinogeniculate Interactions

To determine whether temporal summation and spike threshold could account for differences in the suppression delay retinal and LGN neurons, we constructed a simple model of retinogeniculate interactions. Retinal spike trains were passed through an exponential filter (τ=5 msec) with a spike-generating threshold. Resposnes were then delayed by 2-3 msec to account for the conduction latency of retinal axons and plotted as simulated LGN spike trains.

Statistical analysis

When statistical analysis was required to compare two distributions, we first used Lilliefors modification of the Kolmogorov-Smirnov (Chakravarti et al, 1967) test to determine if the distributions in question were significantly different from normal distributions of unspecified mean and variance (α=0.05). If the distributions were not statistically different from normal, then a t-test was used to compare the means of the two samples. If the samples were statistically different from normal distributions, then a Wilcoxon rank sum test or a sign test was used.