In disperse solution, “osmotic stress” is a restricted case of preferential interactions

Abstract

In the practice of “osmotic stress,” the effect of excluded cosolvents on a biochemical equilibrium is interpreted as the number of water molecules participating in the reaction. This action is attributed to lowering of solvent water activity by the cosolvent. This concept of osmotic stress in disperse solution is erroneous: (i) A cosolvent cannot be both excluded and inert, i.e., noninteracting, because exclusion requires a positive free energy change; (ii) a decrease in water activity alone by addition of solute cannot affect an equilibrium when the reacting surface is in contact with the solvent; and (iii) osmotic stress in disperse solution is a restricted case of preferential interactions; the reaction is driven by the free energy of cosolvent exclusion, and the derived number of water molecules is solely a measure of the mutual perturbations of the chemical potentials of the cosolvent and the protein.

The modulation of biochemical reactions and biological processes in general by solvent additives, whether ligands, cosolvents, osmolytes, or denaturants, was described 50 years ago by Jeffreys Wyman (1) in his theory of linked functions. The reciprocity between two linked processes, a biological reaction and the thermodynamic binding of a ligand, is stated by the Wyman linkage equation (2) in the form of (i) equilibrium constants and (ii) free energy perturbations at any concentration of the ligand X, which is modulating the reaction:

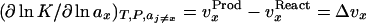1a

and

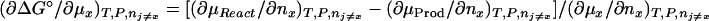1b

where K is the equilibrium constant of a reaction, React ⇌ Prod, v_x is the dialysis equilibrium binding of ligand X to the reacting entity, T, P, a_j, and n_j are the Kelvin temperature, pressure, activity, and concentration of component j, respectively, ΔG° is the standard free energy change of the reaction, and μ_i is the chemical potential of component i, μ_i = μ_i^o + RT ln a_i.

In his analysis of the Wyman relation, Tanford (3) showed that the binding terms (v_x) in Eq. 1 are, in fact, expressions of the preferential (4) binding (as measured by dialysis equilibrium) and that v_x contains changes in the contacts of both the ligand X and water in exchange equilibrium with each other (5–9) with the macromolecule in a binding process. Expressing in both the Tanford (3) and Inoue and Timasheff notations (10),

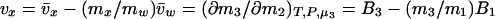2

and for a reaction†

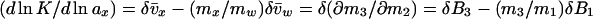3a

and

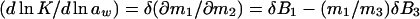3b

where B₃ = v̄_x and B₁ = v̄_w are the effective numbers of ligand and water molecules in contact with the protein. The notation used follows the Scatchard (11) convention that component 1 is water, component 2 is protein, and component 3 is cosolvent, and the symbol δ means that this is the difference between product and reactant. The parameters B₃ and B₁ are not thermodynamic quantities nor do they represent any physical reality (3). They are only a description of experimental results in terms of a model based on site occupancy by water or ligand molecules, even though the interactions described by Eqs. 2 and 3 are summations over a wide spectrum of interactions, whether attractive or repulsive between the protein and the solvent components (9).

Integration of the Wyman linkage relation (Eq. 1b) gives the classical thermodynamic box (12)

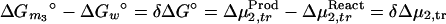4

where Δμ_2,tr is the transfer free energy of the macromolecular component from pure water to the solvent of the given composition, m₃. If we remember that Δμ_2,tr = ∫₀^m₃ (∂μ₂/∂m₃)_m2dm₃ and (∂μ₂/∂m₃)_m2 = (∂μ₃/∂m₂)_m3 = −(∂m₃/∂m₂)_T,P,μ3/(∂μ₃/∂m₃)_m2, Eq. 4 can be expressed in terms of changes in preferential interactions:

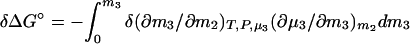5a

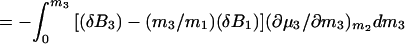5b

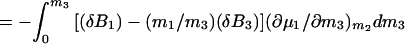5c

and, with either δ(∂m₃/∂m₂) or δ(∂m₁/∂m₂) invariant with solvent composition,

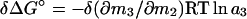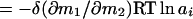6

In recent years, there has been a resurgence of interest in the measurement of changes in the number of water molecules that make contacts with the reacting biological system during the course of a reaction (13–22). The adopted approach has been the determination of the effect on the reaction equilibria of the addition to the medium of preferentially excluded cosolvents with interpretation of the results in terms of the Tanford (3) expansion (Eq. 3) of the Wyman equation (2) (Eq. 1) and extensions to more complicated systems, as developed by Wyman (2, 23). In the recent studies, a constraint was imposed (13, 15, 19) that δB₃ was set equal to 0 and δB₁ was assumed to be independent of cosolvent concentration. This approach has been called “osmotic stress.” A basic requirement in these studies is the use of preferentially excluded cosolvents that have been described further as inert (or neutral) molecules, whose role is the lowering of the activity of water outside the zone of exclusion, thus facilitating removal of water molecules from contact with the protein (13–15, 19).

We will demonstrate that this concept of osmotic stress in disperse solution (i) involves a conflict with the Laws of Thermodynamics because exclusion mean interaction, (ii) is a misnomer for the phenomenon, and (iii) is simply a restricted case of preferential interactions, as practiced for three decades.

Conflict of Osmotic Stress in Disperse Solution with the Laws of Thermodynamics

As described, the practice of osmotic stress in disperse solution has the puzzling requirement that the cosolvents used must be excluded ones, although any solute raises the osmotic pressure. These excluded cosolvents are further qualified as inert (or neutral). If inert is to be equated with noninteracting, this is a thermodynamic contradiction. A cosolvent cannot be both inert and excluded because this would violate the Laws of Thermodynamics and require the intervention of a Maxwell demon. The process of exclusion is characterized by a positive standard free energy change, which we will call the free energy of cosolvent exclusion, ΔG_excl^o. This cannot be furnished through an osmotic effect. The mechanistic causes of exclusion are varied (8, 9, 24). For example, sugars, small amino acids, and salts raise the surface tension of water, which creates an excess of water at any interface; glycerol, polyols, some osmolytes, and trimethylamine-N-oxide are solvophobic and, therefore, are preferentially repelled from nonpolar surfaces; 2-methyl-2,4-pentane diol is repelled from charges; bulky cosolvents and, in fact, all molecules larger than water are excluded sterically. All of these events are nonneutral. They require free energy and can be expressed by appropriate potentials, which are determined by the chemical nature of the cosolvent–protein pair. Thermodynamically, these interactions are superimposed on the general nonspecific osmotic effect of lowering the water activity. As a consequence of these repulsive forces, cosolvent molecules redistribute themselves in the vicinity of the protein. Their inability to form contacts with loci on the protein surface leaves in these areas an excess of water molecules relative to the bulk solvent. This excess is observed in dialysis equilibrium experiments as exclusion of cosolvent, i.e. preferential hydration of the protein. This situation is definitely not neutral; it is thermodynamically unfavorable, with ΔG_excl^o > 0. The extent of preferential exclusion can be reduced by reducing the surface area of the protein and thus making ΔG_excl^o less positive.

Osmotic Stress in Disperse Solution is a Misnomer

In osmotic stress in disperse solution, the mechanism of action of a preferentially excluded cosolvent is ascribed solely to its lowering of water activity in the bulk solvent, i.e., to the increase in the osmotic pressure, π (13–16, 19). Osmotic pressure is a colligative property. Therefore, any added cosolvent, whether it is preferentially excluded, bound, or thermodynamically neutral, i.e., inert, must increase osmotic pressure and, hence, lower the activity of water, a₁^m₃ because (25, 26)

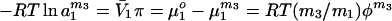7

where φ is the osmotic coefficient. The superscript m₃ indicates that the value of the parameter is at a cosolvent concentration m₃.

Let us examine by means of a thermodynamic box (Fig. 1) the interactions that occur on a protein surface when cosolvent is added to the system and demonstrate that the lowering of water activity by the solvent additive, which is stated to be the driving force in osmotic stress, cannot exert any effect on a chemical equilibrium in disperse solution. In the analysis, we will take a dry protein surface element of defined area and physical and chemical surface characteristics and immerse it, in turn, into pure water and into water that contains various cosolvents, e.g., neutral, strongly excluded, weakly excluded, bound. In all cases, the affinity of water molecules for the protein remains the same. The variation between the systems is due to the different affinities of the cosolvents for the protein. This operation is akin to the generation of an increment of surface that comes into contact with solvent during a biochemical reaction. In the thermodynamic box, we will consider the changes in the standard chemical potential of water induced by these operations so that all of the changes expressed as Δμ are standard free energy changes, ΔG°.

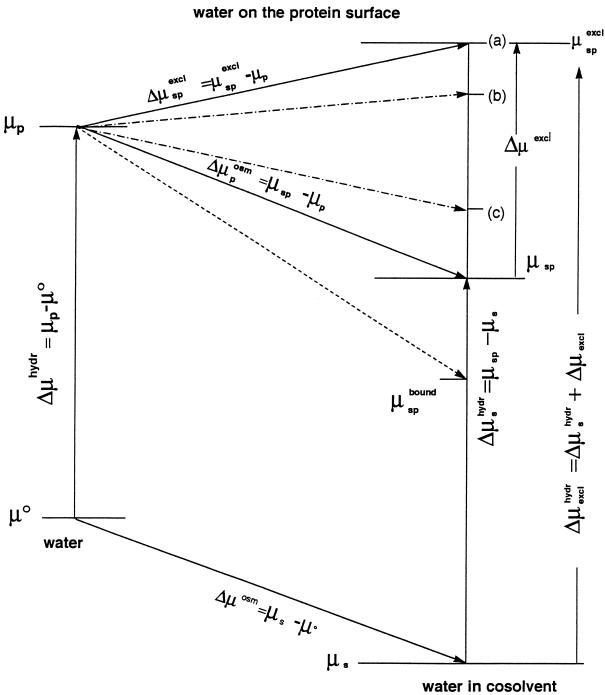
Figure 1.

Thermodynamic diagram of the effects on the standard chemical potential of water of (i) addition of a cosolvent (μ_s) and (ii) addition of a protein surface element to pure water, μ_p, and of aqueous solutions of an inert (neutral) cosolvent (μ_sp) and of an excluded cosolvent (μ_sp^excl). (For comparison, the effect of a bound cosolvent is shown (μ_sp^bound) by the short dashed line.) The osmotic effect on water molecules on a protein surface is Δμ_p^osm = Δμ^osm. An excluded cosolvent raises the standard chemical potential by Δμ_excl. The dot–dash lines represent cosolvents with different magnitudes of exclusion. The levels (a), (b), and (c) could correspond, for example, to the changes in preferential hydrations measured in the presence of triethylene glycol, betaine, and sucrose during the specific binding of gal repressor (18).

As a first case, let us take pure water and add to it a defined quantity of the neutral cosolvent so that its concentration is m₃. This procedure lowers the chemical potential of water by μ_s − μ^o = RT ln a^s = −V₁π^m₃ = Δμ^osm, where Δμ^osm is the osmotic lowering of the activity of water, a^s, and π^m₃ is the osmotic pressure of the solution at a concentration m₃. Let us now take the protein surface element and immerse it into pure water, which causes it to become hydrated (in the sense that contacts are made with water molecules). This procedure changes the chemical potential of the water molecules in contact with the surface element by the standard free energy of hydration of this protein element, Δμ^hydr = μ_p − μ^o = RT ln a^p. Now let us add to this system the neutral cosolvent up to a concentration m₃. The cosolvent is by definition inert, i.e., thermodynamically neutral, so the protein surface element will be indifferent to whether it forms contacts with water or cosolvent molecules at any surface site, and the solvent composition in contact with the protein surface element will be the same as in the bulk solvent. The chemical potential of the water in contact with the surface element will be lowered (see Fig. 1 and its legend) by μ_sp − μ_p = RT(ln a^sp − ln a^p) = Δμ_p^osm, which is the osmotic effect on the water in contact with the protein element. By definition, the free energy of contact with the protein element of cosolvent molecules and of water is identical (the definition of thermodynamic indifference), so Δμ_p^osm = Δμ^osm. The free energy of hydration in the presence of the neutral solute is Δμ_s^hydr = μ_sp − μ_s = RT(ln a^sp − ln a^s). By the thermodynamic box Δμ^osm + Δμ_s^hydr = Δμ^hydr + Δμ_p^osm, and Δμ_s^hydr − Δμ^hydr = Δμ_p^osm − Δμ^osm = 0.

Now, (Δμ_s^hydr − Δμ^hydr) is the definition of the transfer free energy, Δμ_2,tr, of the protein surface element for its transfer from water to the cosolvent system. In the case of a reaction that involves the formation of new protein solvent contacts, or their removal, when the cosolvent is neutral, the transfer free energies of both end states of a reaction, Δμ_2,tr^React and Δμ_2,tr^Prod, will be 0 because of indifference of both end states to contacts with water or cosolvent, and δΔG° of Eq. 4 will be 0. Therefore, a simple increase in osmotic pressure per se can have no effect on the equilibrium. Let us restate this in terms of changes in contacts with solvent component molecules. Because of the indifference to contact, the departure (or addition) of solvent molecules will be in exactly the same proportion as their presence in the bulk solvent. Hence, the change in dialysis equilibrium (thermodynamic) binding will be zero, i.e., δ(∂m₃/∂m₂) and δ(∂m₁/∂m₂) of Eq. 3 will be 0, even though the number of actual contacts of the protein with water and cosolvent molecules will change, because both δB₃ and δB₁ will have non-0 finite values. Their variation, however, will be in the same proportion as their presence in the solvent, i.e., (δB₃/δB₁) = (m₃/m₁). Therefore, even though the biochemical reaction will be accompanied by a change in the number of water molecules that make contact with the reacting surface, a lowering of the water activity alone, which is the definition of osmotic stress, cannot detect this change if the reaction is performed in disperse solution in which the reacting surface is in contact with solvent. These considerations lead to the conclusion that osmotic stress is a misnomer when the reaction is performed in disperse solution. It carries the erroneous connotation that the driving force of the reaction is provided by the osmotic pressure of the bulk solvent alone, and it is proposed that this term be dropped from usage. The proper name of the phenomenon is “stress by exclusion of the cosolvent.”

The Driving Force Is the Free Energy of Exclusion of the Cosolvent, Which Is Totally Unrelated to the Osmotic Effect

Operationally, the practice of osmotic stress in disperse solution stipulates that the used solutes must be excluded from the reacting surface. We will show now that, in order for a solute (cosolvent) to affect a reaction, it must interact with the pertinent surface element, either by attractive or repulsive forces, i.e., it must be either preferentially bound to or preferentially excluded from the given surface (e.g., a protein or nucleic acid). Such interactions are determined by the chemical natures of the cosolvent and the protein, which for any cosolvent may vary from protein to protein.‡ They are superimposed on the general nonspecific osmotic effect Δμ_s^hydr and affect the reaction in a manner other than by the colligative effect of solutes on the activity of water in the bulk solvent.

Let us analyze this action by means of the thermodynamic box. As shown, preferentially excluded cosolvents make a positive contribution to the chemical potential of the water molecules that are in contact with the protein element, Δμ_excl, which reflects the raising of the activity of these water molecules from a^sp to a^excl. Let us elucidate this in terms of the molecular picture. Preferential exclusion of the cosolvent means that the surface element makes contacts overwhelmingly with water molecules, even though the medium is a mixed solvent. If we regard this deficiency of cosolvent as the consequence of the removal of cosolvent molecules from the protein surface element and their replacement by water against a concentration gradient, we realize that this process costs free energy, which is defined as the free energy of cosolvent exclusion ΔG_excl^o = Δμ_excl. The result is an increase of the standard chemical potential of the water molecules in contact with the protein surface element to the level μ_sp^excl = μ_sp + Δμ_excl, and the standard free energy of hydration in the presence of the excluded cosolvent becomes Δμ_excl^hydr = Δμ_s^hydr + Δμ_excl. By the thermodynamic box, we have Δμ_osm + Δμ_excl^hydr = Δμ^hydr + Δμ_sp^excl, where Δμ_sp^excl = μ_sp^excl − μ_p. Now, Δμ_osm = Δ_p^osm and δΔμ^hydr = Δ_excl^hydr − Δμ^hydr = Δμ_sp^excl − Δμ_osm = Δμ_excl.

For a reaction in which the contact surface with the medium is decreased, δΔG° = ΔG_excl^o − ΔG_w^o = −δΔμ^hydr = −Δμ_excl. Therefore, the dehydration reaction is driven by the relaxation of the stress imposed on the system by the preferential exclusion of a solvent component, the magnitude of which depends on the nature of the chemical interactions between the given pair protein–cosolvent and is totally independent of the general osmotic effect. It is also evident that the reaction in the opposite direction would be inhibited by the preferentially excluded cosolvent, whereas it would be favored by a preferentially bound cosolvent.

Osmotic Stress in Disperse Solution Is the Use of Preferential Interactions to Modulate Equilibria in the Wyman–Tanford Sense

In the practice of osmotic stress, an equilibrium is measured in water (dilute buffer) and in increasing concentrations of a preferentially excluded cosolvent. The results then are plotted in terms of equations such as Eqs. 3B or 6, i.e., as a function of water activity (19). This plotting gives as slope the parameter δ(∂m₁/∂m₂). In the practice of osmotic stress, this slope then is equated with the number of water molecules involved in the reaction. This last operation is tantamount to imposing the restriction that δB₃ of Eq. 3B is equal to 0. Thus, osmotic stress in disperse solution reduces to the analysis of the effect of a solvent component on an equilibrium in terms of the 1969 Tanford expansion (3) of the Wyman linkage relation (2), with the restriction that all changes be restricted to water molecules. It is clear that this analysis does not differ from that applied for some 30 years to a variety of systems, the earliest ones being the self-associations of α-chymotrypsin (29) and tubulin (30–32). Other early applications were to peptide–nucleic acid interactions (33), to protein stabilization by a variety of preferentially excluded cosolvents (34–37), and to oxygen binding to hemoglobin (38). The requirement that the cosolvents used to detect changes in water molecules must be preferentially excluded, i.e., nonneutral, molecules makes this approach nothing other than another application of preferential interactions to modulate biological equilibria. In the criteria set for osmotic stress, it is stated that the reaction must be carried out in the presence of several excluded cosolvents (13, 19). Frequently, the values of δ(∂m₁/∂m₂) obtained are close in magnitude for several such cosolvents. Many of the cosolvents used, however, are excluded by raising the surface tension of water, which leads to similar extents of preferential hydration. Furthermore, osmolytes of different chemical natures have been found to have similar affinities relative to water for various amino acid residues (39, 40). Thus, similarity of the measured values is not surprising, and it cannot establish the action of the general lowering of water activity in the solvent as the stress that drives the reaction. The contrary is, in fact, clearly supported by reports that the number of water molecules that depart depends on the chemical nature or the size of the cosolvent. For example, the amount of water released during the conformational transition of hexakinase has been found to vary with the molecular weight of polyethylene glycol (22) in identical manner as their steric exclusion of water from proteins (41–42). In other examples, it has been reported that the number of water molecules released in the binding of an operon repressor to the operon sequences (18) and the B − Z transition of poly(dG-m⁵dC) (17) strongly depend on the chemical nature and molecular weight of the cosolvents in an order that follows in general the measured preferential exclusion of cosolvent from proteins for those cosolvents that have been studied. This result is contrary to all expectations if the driving phenomena were osmotic stress or “osmotic action of solutes” (20) because this, by definition, must be identical for all solutes, whether excluded, neutral, or bound.

General Remarks

The term “osmotic stress” stems from the very elegant method developed by Parsegian and coworkers (43) for manipulating biochemical reactions by changes in the activity of water. Operationally, this is accomplished by separating by a membrane the reacting system and an osmotic pressure adjusting osmolyte. In this situation, the reacting system senses the cosolvent only through its effect on the activity of water in the solvent, which is lowered, thus making easier the departure of water molecules from the reacting surface. When translated to disperse solution, osmotic stress introduces direct contact between cosolvent and the reacting surface. As shown above, this contact makes it impossible for the lowering of water activity to affect the reaction. The only exceptions to this would be systems in which the reacting surface is equally inaccessible to cosolvent molecules in both end states of a reaction. This would be true of reactions within channels, some interstitial compartments, and very narrow crevices. In these situations, water molecules within such compartments would sense the change in the activity of the bulk water induced by cosolvents, be they excluded or bound, but they would not sense directly the presence of cosolvent molecules either by contact or by exclusion in both end states of the system. The introduction of compartments or domains around the protein separated by a hypothetical barrier or membrane does not circumvent the problem, for such hypothetical barriers must be created by the expenditure of free energy, which, in fact, is the free energy of cosolvent exclusion.

Applications of so-called “osmotic stress” to reactions in disperse solution have resulted in useful information and some intriguing and interesting results (13, 16–18, 20, 22). The paradox is that, even though the theoretical basis as presented in osmotic stress is incorrect, the experiments have produced correct numerical values of changes in preferential hydration, δ(∂m₁/∂m₂), because the plots used (equations such as Eqs. 3B or 6 and their variants) are correct.

What is the meaning of δ(∂m₁/∂m₂)? Customarily, in the practice of osmotic stress, this parameter is equated with the number of water molecules that are displaced in the reaction. This is a hazardous conclusion. First, the parameters δB₁ and δB₃ are not true stoichiometric numbers. They are only descriptions in terms of water and cosolvent molecules of their thermodynamic perturbations by the protein because 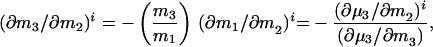where the superscript i refers to cosolvent molecule i and the observed effect is the sum of all of the perturbations, which span the spectrum from fixation at a site on the protein surface to a momentary perturbation of the rotational or translation motions of the molecule when in the vicinity of the protein molecule. Second, the values of δB₁ and δB₃ are not singular parameters. In fact, any pair of measured δB₁ and δB₃ can correspond to an indeterminate set of values (24) because neutral sites present in the reacting surface cannot be detected by the equilibrium thermodynamic methods used (7, 8). As shown above, the occupancy of neutral sites by water and cosolvent molecules will be proportional to the solvent composition. Therefore, for neutral sites δB₁/δB₃ = m₁/m₃, and any measured value of δB₁ will be only the excess of water molecules from nonneutral sites. Therefore, the experimental results give only a minimal value of the number of water molecules involved and the minimal change in surface during the reaction. This can be shown clearly by expressing the effect on the free energy of the reaction in terms of the volume of water involved, which is another form of Eq. 6:

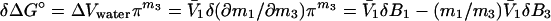8

This equation shows that the volume change measured by a plot of δΔG° as a function of osmotic pressure is actually the difference between the changes in volume of water and of cosolvent expressed as the volume of water that it displaces. Furthermore, all excluded cosolvents penetrate to some extent to the protein surface (24). This penetration is seen, for example, in the slight curvature of the Wyman plots as a function of water activity of the effects of glycine and glucose on the oxygen binding by hemoglobin (21).

Eq. 8 has the further meaning that the measured number of water molecules departing is not the stoichiometric number of water molecules in a reaction:

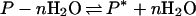9

The measured parameter is a function only of the interactions between the protein and the cosolvent and is a measure of cosolvent exclusion at the reacting patch that is being removed from contact with solvent, which becomes evident if we combine Eqs. 8 and 3:

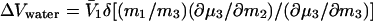10

Thus, the volume of water departing is defined by (∂μ₃/∂m₂), which is a property of the cosolvent–protein pair alone and will differ between cosolvents. This parameter can be positive, negative, or 0. The product ΔV_water π has been identified as the osmotic work of removing water from the interface (15). It is clear from Eqs. 8 and 10 that, in fact, it is the work of overcoming the stress of cosolvent exclusion, or of its binding, and that ΔV_water can be positive, negative, or 0, even though the stoichiometry n remains invariant in all solvent systems. Nevertheless, the reacting surface area affected remains the same for all cosolvents, and some qualitative judgement can be made on its extension, especially if one is cognizant of the relative strengths of exclusion of the cosolvents used, preferably measured on the components of the reacting system in preferential interaction experiments. An intriguing approach that has been used consists of the comparison of complexation between specifically and nonspecifically interacting systems. The difference gives a value of the water molecules locked interstitially in one of the compared systems. This method has the practical effect of eliminating preferential exclusion (a sort of baseline correction), leaving the stoichiometric value as the difference (20). The same is true when the ligand binding is within a solvent inaccessible domain (16).

Finally, it must be emphasized that the cosolvent stress approach can give no information about the energetics of water binding to the protein site. The reason for this is that all such measurements are by definition relative to pure water. The energetics of water binding are contained in Δμ^hydr = μ_p − μ°. In the experiments in the presence of cosolvents, the reference state is the reaction patch in pure water, at chemical potential μ_p, and all the numbers obtained are differences from μ_p induced by the various solvent additives.