Item response theory detects differential item functioning between healthy and ill children in QoL measures

Abstract

Objective

To demonstrate the value of item response theory (IRT) and differential item functioning (DIF) methods in examining a health-related quality of life (HRQOL) measure in children and adolescents.

Study Design and Setting

This illustration uses data from 5,429 children using the four subscales of the PedsQL™ 4.0 Generic Core Scales. The IRT model-based likelihood ratio test was used to detect and evaluate DIF between healthy children and children with a chronic condition.

Results

DIF was detected for a majority of items but cancelled out at the total test score level due to opposing directions of DIF. Post-hoc analysis indicated that this pattern of results may be due to multidimensionality. We discuss issues in detecting and handling DIF.

Conclusion

This paper describes how to perform DIF analyses in validating a questionnaire to ensure that scores have equivalent meaning across subgroups. It offers insight into ways information gained through the analysis can be used to evaluate an existing scale.

What is new?

• Differential item functioning (DIF) can be detected and is important in health-related quality of life (HRQOL) scale development and for different populations.

• Implications of ignoring DIF in scales are reviewed.

Introduction

Item response theory (IRT) is a collection of models that provide information about the properties of items and the scales they comprise through the analysis of individual item responses. Its use in health outcomes scale development and scoring has increased in recent years as a result of its many applications, including the identification of items functioning differently across subgroups [1]. An IRT model is ideally suited for the detection of differential item functioning (DIF) in examining the validity of a test or questionnaire [2]. This paper addresses the nature of DIF, methods that can be used to assess the presence of DIF, and how to evaluate DIF once it has been detected. This paper also discusses the value of DIF identification in health-related quality of life (HRQOL) scale development and refinement.

The unidimensional IRT model makes the assumption that the probability of observing a particular pattern of responses is based on the respondent’s level on the underlying construct (θ), as well as the properties of the items to which responses have been provided. Item response functions, or “trace lines” [3] describe the relationship between the probability of item responses and θ. For dichotomous items (e.g., yes/no, true/false), the trace line for the positive response increases monotonically as θ increases so that the probability of endorsing an item is low for individuals at lower levels on the latent continuum, and higher for those with a greater level of θ. Typically a logistic function is used to define the trace line.

The two-parameter logistic (2PL) model, appropriate for dichotomous items, defines the probability of a positive response to an item i (x_i = 1) as

$$T(x_i=1|\theta )=\frac{1}{1+exp[-a_i(\theta -b_i)]},$$ (1)

where a_i is the item discrimination (or slope) parameter and b_i is the item location parameter [4]. The slope parameter measures the strength of the relationship between the item and θ; higher slopes indicate that the item can discriminate more sharply between respondents above and below some level of θ. The location parameter represents the point along θ at which the item is most discriminating or informative; a respondent whose level on θ is at this location has a 50% chance of endorsing the item.

An alternative model often used in health outcomes research is Samejima’s [5, 6] graded response model (GRM), a generalization of the 2PL model that permits estimation of multiple b_ij parameters per item (j from 1 to m−1) associated with m response categories (e.g., items with the response scale “Strongly Disagree”, “Disagree”, “Neutral”, “Agree”, and “Strongly Agree”). Other polytomous extensions of the 2PL model include the partial credit model [7] and the generalized partial credit model [8]. The formula for a GRM trace line is

$$T(x_i=j|\theta )=\frac{1}{1+exp[-a_i(\theta -b_{ij})]}-\frac{1}{1+exp[-a_i(\theta -b_{ij+1})]},$$ (2)

which states that the probability of responding in category j is the difference between a 2PL trace line for the probability of responding in category j or higher and a 2PL trace line for the probability of responding in category j+1 or higher.

In health outcomes research, items are often scored so that higher scores indicate a greater presence of the trait that the items are designed to measure. For example, a scale designed to assess quality of life would be scored so that higher scores correspond to greater quality of life. This would also imply that categories with larger b_ij parameters would be more likely to be endorsed by respondents with better quality of life than those with poorer quality of life.

DIF occurs when trace lines for the same item differ between groups of respondents, meaning that the item performs differently for one subgroup of a population compared to another subgroup after controlling for the overall differences between subgroups on the construct being measured [9]. In this sense, DIF exists when the probabilities of endorsement are uniformly unequal for the two subgroups (the b parameters are different), or when the item is more discriminating for one subgroup than the other (the a parameters are different). Essentially, DIF indicates the violation of one of the fundamental assumptions of IRT, unidimensionality [10]. The presence of DIF suggests the item is measuring an additional construct, or dimension, that may or may not be relevant to the intended construct. For example, several items that involve sports terms may unintentionally tap sports knowledge and produce DIF. The practical result at the item level is that scores on an item exhibiting DIF are not equivalent across subgroups with different levels of sports knowledge, leading to potentially misleading results with regards to group differences and inaccurate bivariate associations involving the DIF item [9].

DIF can be detected using approaches drawing from both classical test theory and IRT [9]. Although applications of classical test theory methods—such as the comparison of relative item difficulty or item discrimination, the delta plot [11], and ANOVA methods—require few assumptions and are relatively easy to implement, their results may be sample-specific and, thus, inadequate for ensuring measurement invariance [12, 13]. Given that the IRT assumptions hold, results from an IRT approach theoretically generalize beyond the sample being studied to the intended population. An IRT analysis also permits graphical representations of DIF. These plots provide valuable diagnostic insight for evaluating the potential effect of DIF both at the item level and at the level of the entire test [14].

Within the IRT framework, there are a number of ways to construct statistical tests of DIF. The Bock-Aitkin [15] marginal maximum likelihood (MML) estimation algorithm is typically used to estimate the parameters of an IRT model. This paper focuses on the approach of model-based likelihood ratio tests to evaluate the significance of observed differences in parameter estimates between groups [2, 16, 17]. This approach is closely integrated with conventional MML parameter estimation. Several methodological experts agree that DIF analyses using model-based likelihood ratio tests are more powerful and should be emphasized over other existing DIF detection approaches [2, 18, 19]. Under reasonable conditions, model-based likelihood ratio tests are closely related to the most powerful test given by the Neyman-Pearson [20] lemma. This optimality of power, decreasing the chances of accepting the null hypothesis of no DIF, lends credibility to this type of test as one of the most powerful DIF detection tools. Additionally, available software can easily implement the model comparison approach (IRTLRDIF) [21].

Once detected, scale developers must evaluate the impact of DIF on measurement and establish an approach for addressing it. In educational research, when one or more DIF items are identified among a large item pool, elimination of those items generally does not affect overall measurement precision (i.e., because they can be replaced with equally efficient non-DIF items) [14, 22]. However, in psychological or health outcomes research, items are often not as expendable. Researchers commonly use established scales with psychometric properties that are vulnerable to a loss of even one item. This problem is particularly salient for short scales. Ideally one could use the information from a DIF analysis to guide modifications aimed at eliminating the DIF in the item through rewording rather than eliminating the item itself [14]. For the DIF items, item parameters can also be separately estimated for the subgroups, and these different parameter estimates can subsequently be used to estimate θ. A more conservative approach to handling DIF is to assess the degree to which the DIF may change total (e.g., summed) test scores for some subgroup. It is important to ensure total test scores have equivalent meanings across subgroups [23]. Evaluating the effects of DIF on total test score is important because decisions regarding individuals are typically made at the test score level and not at the item level. It also essential to consider the item content and the nature of potential secondary dimensions (whether or not they are relevant to the trait being measured).

In the end, a great deal of judgment is required to determine how to handle detected DIF.

The goal of this paper is to outline the use of the model-based likelihood ratio test in the detection and evaluation of differential item functioning using examples from data obtained with the PedsQL^™ 4.0 Generic Core Scales [24]. The model-based likelihood ratio test will be employed to identify differentially functioning items and to assess scale dimensionality. We will discuss considerations for handling DIF in these scales.

Methods

DIF detection and evaluation will be demonstrated using data from the four subscales of the PedsQL™ 4.0 Generic Core Scales [24]. This instrument consists of 23 items designed to measure health-related quality of life in children and adolescents. Four domains are assessed: Physical Functioning, Emotional Functioning, Social Functioning, and School Functioning. Different versions of the instrument exist for varying ages, different informants, and different languages; however, this example will focus only on the child self-report forms for children (ages 8–12) and adolescents (ages 13–18) in English.

Items are administered with a 5-point response scale (0 = “never a problem”, 1 = “almost never a problem”, 2 = “sometimes a problem”, 3 = “often a problem”, 4 = “almost always a problem”). The PedsQL™ scoring algorithm instructs that the items be reverse-scored and modeled with higher scores indicating higher quality of life, so models were fit accordingly.

Previous research [25] applied categorical confirmatory factor analysis (CCFA) to check IRT model assumptions of the PedsQL™ 4.0 Generic Core Scales. CCFA showed generally strong support for 1-factor models for each domain. With domain dimensionality addressed, IRT models can be fit and DIF detection procedures employed.

A sample was obtained by combining available data from numerous studies of both specific chronic diseases and a general population. The sample included 3275 children between 8 and 12 years of age (1015 with chronic diseases and 2260 healthy) and 2154 children between 13 and 18 years of age (972 with chronic diseases and 1182 healthy). The frequency of specific diseases in each of the chronic samples is reported in Table 1. The majority of the chronic samples were obtained through general population studies where the participants indicated that they had a chronic condition. The entire healthy sample was also obtained from these general population studies, but these participants indicated that they did not have a chronic condition. More details of the sample characteristics can be found in Varni et al [26]. Differences between studies in the distribution of healthy versus chronic responders, study design, sampling approach, mode of administration, and setting of questionnaire application could potentially limit the internal validity of this study.

Table 1.

Subgroup frequencies for the child and teen chronic samples

Subgroup	Child	Teen
Asthma	149	0
Cancer-Brain Tumor	102	94
Cerebral Palsy (CP)*	29	23
Hemiplegic	10	9
Diplegic	15	6
Quadriplegic	2	5
Congenital Heart Disease	96	103
Stage I	15	15
Stage II	35	25
Stage III	21	31
Stage IV	25	32
Diabetes*	64	205
Type I	57	125
Type II	7	79
Gastrointestinal (GI)*	116	107
Functional GI disorder	22	24
Organic GI disorder	6	8
Overweight	10	12
Obese	44	39
Other GI condition	32	24
Renal Disease	25	56
End-Stage Renal Disease	21	47
Acute Renal Failure	4	9
Rheumatic diseases*	114	171
Dermatomyositis	10	5
Fibromyalgia	17	39
Juvenile Rheumatoid Arthritis	28	27
Spondyloarthropathy	15	22
Systemic Lupus Erythematosus	6	21
Other rheumatic disease	36	56
Other Chronic Condition	320	213
Total	1015	972

^*Missing values for chronic disease subgroups are as follows: CP (2 child, 3 teen), GI (2 child), Rheumatic diseases (1 teen), Diabetes (1 teen).

These analyses used a model-based likelihood ratio test approach to identifying DIF with the GRM as implemented in IRTLRDIF [21]. This approach tests the null hypothesis that the parameters for a particular item do not differ between groups. This test is conducted by isolating the parameters of an item, fitting a model with the parameters allowed to vary freely between groups and a model with the parameters constrained to be equal between groups, and using as a test statistic the difference between the loglikelihood values for the two models multiplied by −2. The significance of this value can be tested using a chi-square distribution with degrees of freedom equal to the number of parameters being tested (i.e., 1 degree of freedom when the slope is being considered, m−1 degrees of freedom when the thresholds are being considered). A significant improvement in the loglikelihood of the unconstrained model over that of the constrained model is considered an indication of DIF for the parameter(s) being tested. Because no prior information was known about the stability of these items between groups, when the parameters for one item were being tested, the remaining items were used as anchor items and their parameters were not allowed to vary between groups. The anchor item set forms the basis for linking the groups in a DIF analysis, and the selection schemes used to choose the anchor items can have an impact on the results. The fact that the anchor items have the same parameters for both groups is the basis for estimating the difference between the groups on a common scale.

The healthy sample was treated as the reference group, with an assumed normal distribution with a mean of 0 and a standard deviation of 1, and the parameters of the underlying normal distribution for the chronic sample (i.e., focal group) were estimated in conjunction with the item parameters. To avoid alpha-inflation due to multiple comparisons, the Benjamini-Hochberg (B–H) procedure is used to correct the alpha-level [27, 28]. Using a .05 nominal alpha level, the largest observed p-value has a comparison value of .05, the smallest observed p-value has a comparison value of .05 divided by the number of comparisons (in this case, the number of items), and all other comparison values lie within this range, adjusted according to the rank order of the magnitude of the observed p-values.

It is important to consider the difference between statistical significance (as obtained with the chi-square tests) and clinical importance (i.e., how DIF may affect the application of IRT parameters), so graphics were employed to assess the effect of DIF on the items and the scales. Item response functions (i.e., the probability of endorsing a particular response category at a particular value of θ), expected scores (i.e., the expected response to that item for a particular value of θ), and item information functions (i.e., the amount of information the item provides at a particular value of θ) were considered for each item. When an item demonstrated significant DIF, these functions were plotted separately for the chronic and healthy groups. Items with statistically significant DIF may have similar functions across groups, in which case the DIF may not be particularly meaningful. Expected score plots were also considered for the entire scale (i.e., the expected score on the item response scale for a particular value of θ) where the parameters for the DIF items were allowed to vary between groups. These plots show the expected score for individuals at the same level of θ and how membership in a particular group may affect the expected score. Again, total scale score may or may not differ even when DIF items are included. Currently, diagnostic information is gathered from the plots via visual inspection [29]; future work might seek to develop more rigorous guidelines or a numerical representation for greater precision.

Results

In all of the subscales for both child and teen samples, DIF was detected for a majority of the items. Furthermore, the detected DIF essentially did not change the total test score level due to cancellation across items with DIF in opposing directions. For brevity, only the results for the Social subscale for the child sample will be presented.

Table 2 presents the parameters for each item separately for the healthy and chronically ill subsamples of the Social subscale, estimated with the parameters of the other four items equal for the two groups (“the anchor”). The two right-most columns of Table 2 list the χ² values and p values for the nested model comparison tests of a and b DIF for the five items of the Social subscale. Using the B-H procedure, four of the items showed significant DIF; items 2 and 5 displayed both a and b DIF, and items 3 and 4 exhibited DIF in the b parameters only. In addition to the χ² values and associated probabilities for the tests of a and b DIF, Table 2 lists the item parameters for each subsample.

Table 2.

Item parameters for healthy and chronically ill subsamples of the PedsQL™ Social subscale

								Tests for DIF: χ2 (p)
Item	Content	Subsample	a	b1	b2	b3	b4	a DIF	b DIF
1	I have trouble getting along with other kids	Healthy	2.17	−2.77	−2.29	−1.19	−0.40	3.1(.078)	7.4(.116)
	Chronically Ill	1.86	−2.78	−2.32	−1.25	−0.50
2	Other kids do not want to be my friend	Healthy	3.08	−2.29	−1.86	−1.04	−0.33	10.4(.001)	47.2(.000)
	Chronically Ill	2.23	−2.53	−2.13	−1.28	−0.65
3	Other kids tease me	Healthy	2.12	−2.25	−1.73	−0.78	−0.04	2.1(.147)	57.4(.000)
	Chronically Ill	1.84	−2.47	−1.94	−1.00	−0.43
4	I cannot do things that other kids my age can do	Healthy	1.65	−3.31	−2.53	−1.49	−0.65	2.9(.089)	56.1(.000)
	Chronically Ill	1.41	−2.85	−2.28	−1.11	−0.41
5	It is hard to keep up when I play with other kids	Healthy	1.85	−2.96	−2.41	−1.58	−0.87	24(.000)	91.8(.000)
	Chronically Ill	1.16	−3.29	−2.56	−1.23	−0.47

For each item, the IRTLRDIF procedure estimated the mean and standard deviation of the chronically ill population distribution (relative to 0.0 and 1.0 for the healthy population distribution) using the unconstrained item parameters for the chronically ill and healthy subsamples and while constraining the parameters to be equal for all other items across the two groups. Mean estimates of the chronically ill population distribution ranged from −0.21 to −0.35; standard deviation estimates of the chronically ill population distribution ranged from 0.96 to 1.01. These estimates indicate that overall, the chronically ill children displayed poorer social function than the healthy children, and that the distribution of social function exhibited comparable amounts of variation in both subsamples.

As shown in Table 2, all of the items are more discriminating (i.e., larger a parameter estimates) for the healthy children than the chronically ill children. For items 2 and 3, the location parameters are shifted to the left for the chronically ill children relative to the healthy children. However, the location parameters are generally shifted to the right for the chronically ill children relative to the healthy children for items 4 and 5. These shifts indicate that healthy children with low social function are more likely than chronically ill children with low social function to endorse the higher frequency (e.g., “almost always”, “often”) response categories for items 2 and 3. However, the reverse is true for items 4 and 5; chronically ill children with low social function are more likely than healthy children with low social function to endorse the higher frequency response categories. In other words, for these items, the probability of a particular response can be explained by a combination of both social function and health status.

These patterns are best represented graphically. The top panels of Figures 1 and 2 show that the trace lines are shifted to the left for the chronically ill children (dashed lines) relative to the healthy children (solid lines) for items 2 and 3. Conversely, the top panels of Figures 3 and 4 indicate that the trace lines are shifted to the right for the chronically ill children (dashed lines) relative to the healthy children (solid lines) for items 4 and 5. The middle panels of Figures 1 and 2 also show that the expected score is higher for chronically ill children, versus healthy children, with poor social function (the left end of the theta scale) for items 1 and 2. The middle panels of Figures 3 and 4 indicate that the expected score is lower for chronically ill children with poor social function, with respect to healthy children. These differences in expected score are a direct consequence of the respective shifts in the trace lines for the chronically ill children. These expected score plots demonstrate that the expected score of a child at a particular level of social function depends on that child’s health status. The bottom panels in all four figures show that there is less information for the chronically ill children, with respect to healthy children, for all four items. This indicates that these items characterize social function in healthy children better than for chronically ill children.

Figure 1.

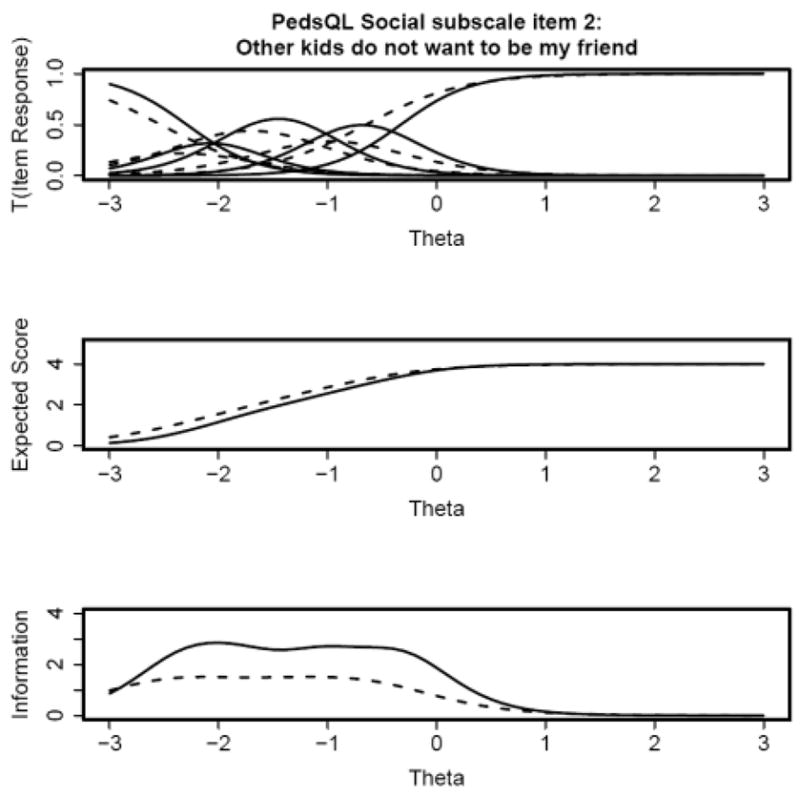
Figure 2.

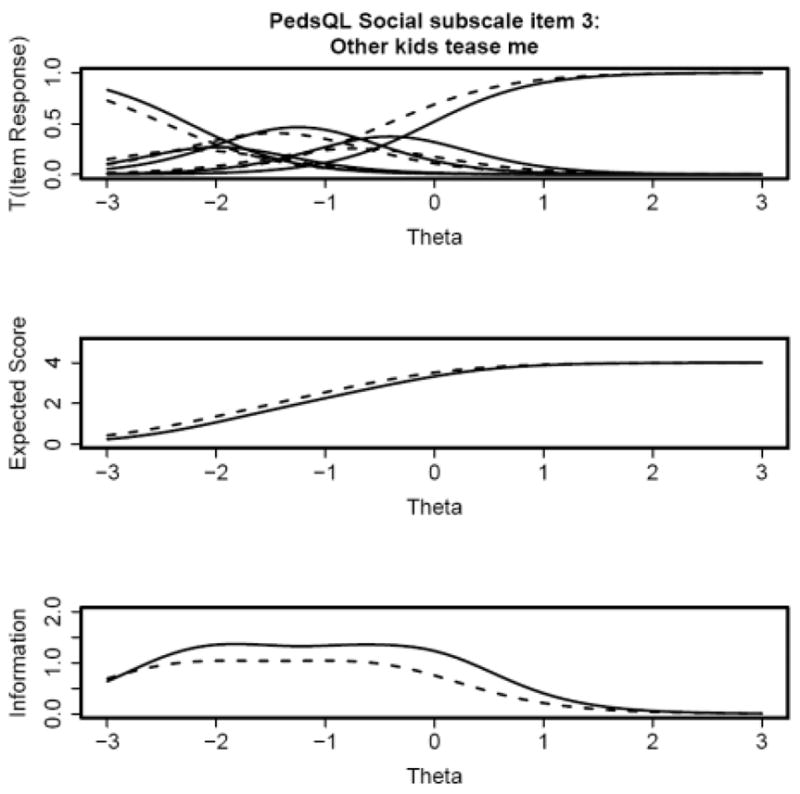
Figure 3.

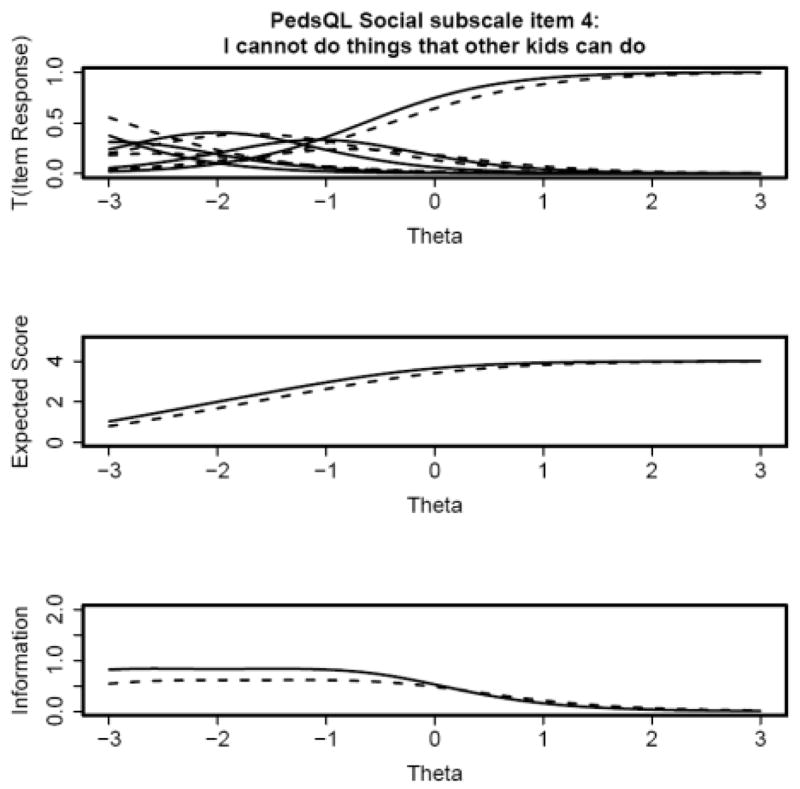
Figure 4.

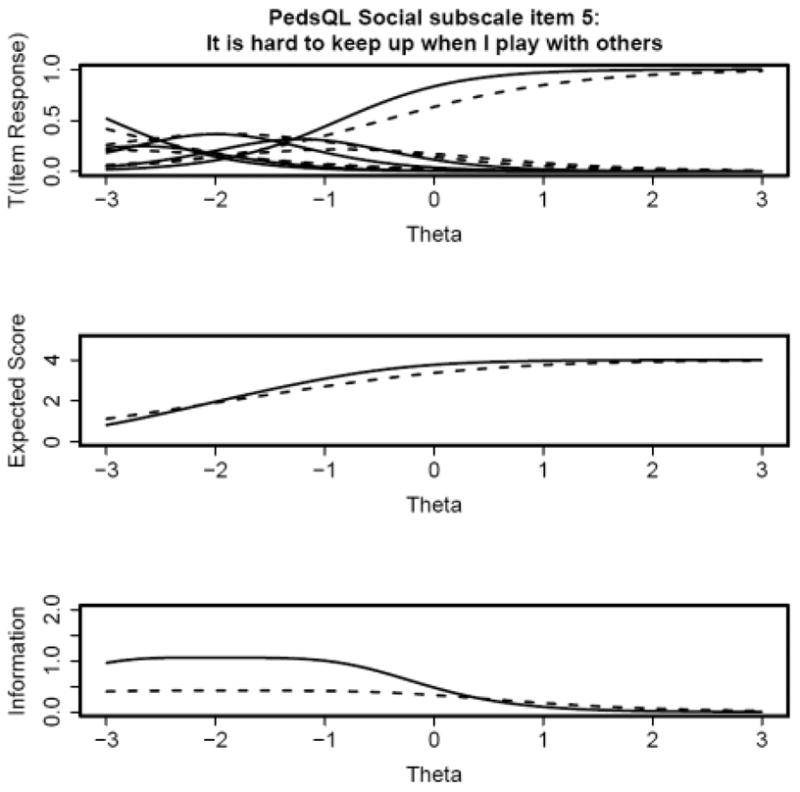
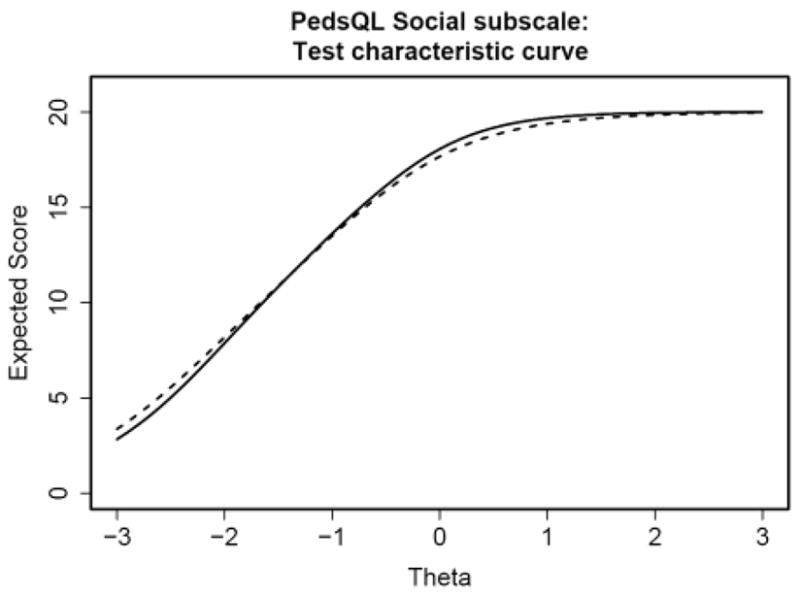
Figure 5 displays the test characteristic curve (the expected summed score as a function of θ) for all five items of the Social subscale. The expected score does not substantially differ for chronically ill children with respect to healthy children across the range of social function. Although significant DIF was flagged with the IRTLRDIF procedure and the trace lines differed between subsamples, the DIF was in opposite directions for items 2 and 3 versus items 4 and 5. As a result, the DIF cancels out at the test-level.

Figure 5.

Post-hoc Analyses

Given the differences in DIF for items 2 and 3 and items 4 and 5, it became apparent that these pairs of items may be measuring separate dimensions. Items 2 and 3, along with item 1, could be characterized by a “sociability/interaction” factor, tapping how children interact with their peers. On the other hand, items 4 and 5 could be represented by a “performance” factor, indicating children’s level of role performance. Factor analyses were used to examine these potential factors. Weighted least squares estimation was used in Mplus^™ [30].

A multiple-groups one-factor model for the five items of the Social subscale resulted in large factor loadings (greater than 0.7) for all the items in both chronically ill and healthy children samples. The mean for the healthy children distribution was estimated to be 0.24, relative to a mean of 0.0 for the chronically ill children distribution. This result is similar to the means estimated by the IRTLRDIF procedure. The root mean square error of approximation (RMSEA) for this model was 0.09, indicating a borderline acceptable fit. However, in the chronically ill group, the modification index was very large between items 4 and 5, indicating that the χ² (χ² = 436, 29 df) would drop by roughly 103 if their errors were allowed to correlate. Similarly, the same modification index was large for the healthy group, indicating that the χ² (χ₂ = 436, 29 df) would drop by roughly 130 if the errors were allowed to correlate between items 4 and 5.

Next, a multiple-groups two-factor model for the Social subscale was fit. Items 1, 2, and 3 were allowed to load on the first factor, the “sociability/interactions” dimension. Items 4 and 5 were specified to load on a second factor, the “performance” dimension. On the sociability factor, the mean of the healthy children was estimated to be 0.09, relative to a mean of 0.0 for the chronically ill children. On the performance factor, the mean of the healthy children was estimated to be 0.49, relative to a mean of 0.0 for the chronically ill children. These mean estimates indicate that although the chronically ill and healthy children differ from one another on the performance and sociability dimensions, the difference is much smaller in the sociability dimension. These differences would explain the pattern of results found in the DIF analyses. The RMSEA for this model was 0.03, indicating a good fit. There were no substantial modification indices. These results indicate that the Social subscale may be better represented as a multidimensional scale, with a performance factor and a sociability factor.

Discussion

DIF methods, such as the ones applied in this study, provide a powerful tool for enhancing the insight into differences in health outcomes assessments. This paper provides an example of how DIF detection can inform questionnaire development. Although the items in the Social subscale of the PedsQL™ were flagged for significant DIF, the DIF was cancelled out at the test-level. This result highlights the importance of testing the effects of DIF at the test-level rather than needlessly eliminating items. However, the findings also indicate that such cancellation at the test-level does not eliminate the importance of item level DIF. DIF inherently indicates multidimensionality; scale developers should determine whether the DIF is due to nuisance factors or to dimensions that may be of interest. In this example, examination of the items and the pattern of DIF indicated that the multidimensionality was due to two dimensions of interest to the researcher. If the scale is scored by simply summing the scores to the item responses, then the scale score will not be biased as long as the DIF cancels out at the test-level (as can be seen in the test characteristic curve provided in the example). However, as soon as IRT scoring is introduced and different items provide different amounts of information to the scale score depending on their discrimination, then leaving DIF items on a scale may produce biased scores at the test-level. Such scoring would produce test scores that are difficult to interpret because similar test scores could be due to differing levels of the secondary dimensions compensating for each other. This problem is more salient when items are administered adaptively. Different respondents receive different items, and the effective DIF may not be equivalent across respondents. This can result in substantial measurement variation.

Although this paper demonstrates the important procedure of checking for DIF in health outcomes measures, it also identifies an important area of multidimensionality within a social health domain. PedsQL™ 4.0 is one of the leading pediatric outcomes assessment instruments, and has provided important data for numerous clinical trials. Because most trials enroll relatively homogenous groups, DIF within those groups is likely to have little, if any, clinical significance. However, as we aim for measures that function similarly across populations, DIF analyses can help us to create better instruments. This paper was performed in the context of the Patient Reported Outcomes Measurement Information System (PROMIS) project to develop pediatric item banks and has influenced how we view social function dimensionality across populations.

Any study of DIF will have important limitations that could restrict conclusions. In our study, we indicated the importance of not just identifying DIF, but also of evaluating the clinical importance of the DIF. Although we found DIF in several subscales, the social subscale demonstrated enough DIF that if administered across healthy and chronically ill populations and scored using IRT, it could lead to the wrong conclusions. The mean differences that we found between the healthy and chronically ill populations are validated by clinical research that also indicated significant mean differences [31, 32]. Our estimation of the clinical importance is based on clinical experience and the magnitude of the findings. For patient reported outcomes, such criteria are the best that we have.

Another important limitation of this study is the relative definitions of the healthy population and the chronically ill population. The healthy population was taken from studies of the general population. As such, it is possible that some children in the healthy sample indeed had a chronic illness that was not identified by the child or the parent when completing the demographic questionnaire. Conversely, within the chronic illness sample, multiple different diseases could have varying effects on patient reported outcomes, and some children with mild chronic illness may have outcomes more similar to the healthy sample. The imperfections in the definition of the samples could lead to an underestimation of the DIF between the samples, so we do not believe this limitation would affect our conclusions regarding the social subscale. However, testing for DIF in more homogeneous populations (e.g., males versus females, or one disease versus another) might improve interpretation of underlying differences in response patterns. Another interesting and powerful use of DIF might be to examine measurement equivalence of the PedsQL™ 4.0 across different translations of the instrument.

This paper seeks to encourage regular performance of DIF analyses in health outcomes assessment. The first step is to choose a DIF detection method. The IRT model-based likelihood ratio test approach is very powerful, but requires that the assumptions of IRT are met. Analysts should use a multiple comparisons check, such as the B-H procedure, when examining the significance of DIF at the item level and also employ graphical methods (comparing differences between trace lines). Additionally, examining the test characteristic curve allows evaluation of DIF at the test-level. Finally, qualitative assessment of the DIF results can help determine if they indicate substantial multidimensionality. If so, the DIF analyses can be followed by factor analyses.

With the natural group distinction in quality of life research between healthy and ill subgroups, DIF analyses will soon become a regular step in health outcomes questionnaire development and refinement. We hope that this example emphasizes the power of DIF analyses in validating a questionnaire.