Structural factors controlling ligand binding to myoglobin: A kinetic hole-burning study

Abstract

Using temperature-derivative spectroscopy in the temperature range below 100 K, we have studied the dependence of the Soret band on the recombination barrier in sperm whale carbonmonoxy myoglobin (MbCO) after photodissociation at 12 K. The spectra were separated into contributions from the photodissociated species, Mb*CO, and CO-bound myoglobin. The line shapes of the Soret bands of both photolyzed and liganded myoglobin were analyzed with a model that takes into account the homogeneous bandwidth, coupling of the electronic transition to vibrational modes, and static conformational heterogeneity. The analysis yields correlations between the activation enthalpy for rebinding and the model parameters that characterize the homogeneous subensembles within the conformationally heterogeneous ensemble. Such couplings between spectral and functional parameters arise when they both originate from a common structural coordinate. This effect is frequently denoted as “kinetic hole burning.” The study of these correlations gives direct insights into the structure–function relationship in proteins. On the basis of earlier work that assigned spectral parameters to geometric properties of the heme, the connections with the heme geometry are discussed. We show that two separate structural coordinates influence the Soret line shape, but only one of the two is coupled to the enthalpy barrier for rebinding. We give evidence that this coordinate, contrary to widespread belief, is not the iron displacement from the mean heme plane.

Proteins are complex macromolecules that can assume a large number of slightly different structures within their native conformation, called conformational substates (CS) (1). Even small structural differences between CS can lead to drastic changes in functional parameters (e.g., rate coefficients for substrate binding to an enzyme). At physiological temperatures, proteins fluctuate among all thermally accessible CS. It is important to realize that the specific function of a protein molecule can well be governed by rare fluctuations into a particular subset of CS (e.g., one where a gate is opened to admit a substrate to the active site). To understand the action of proteins, it is crucial to elucidate the relations between structural properties of a protein and its function. The aim of structure–function studies is to identify structural parameters with well defined correlations to functional parameters.

As of yet, such correlations can be obtained only for comparatively simple and well studied systems, where a large body of additional information is available. The protein myoglobin (Mb) is among the few systems where studies to sufficient depth are possible. Ligand binding to Mb is the prototype reaction in these investigations, where the various factors that govern the reactivity can be studied in great detail. Frequently, CO is used as a ligand. The reaction is initiated by photodissociation of MbCO with a short laser flash, and the subsequent rebinding is monitored with time-resolved absorption spectroscopy (1). Photolysis breaks the bond between the heme iron and the exogenous ligand, and a metastable intermediate, Mb*CO, is formed with CO still inside the heme pocket. Recently, the molecular structures of Mb*CO have been determined and compared with those of MbCO and equilibrium deoxy Mb (2–4). The new structural information is crucial for connecting spectral and functional parameters to structural details.

At low temperatures, the protein matrix is frozen and prevents the ligand from escaping from the heme pocket after photodissociation, so that it rebinds geminately. The reaction kinetics are nonexponential and can be modeled with a distribution of activation enthalpies arising from a static, heterogeneous population of protein molecules in different conformational substates (1). Within each myoglobin molecule, the ligand returns to the heme iron in a one-step transition over a single well defined enthalpy barrier. The observed functional heterogeneity arises from structural heterogeneity, which has since been shown to be an inherent and crucial general property of these macromolecules. It also leads to the inhomogeneous broadening of spectral lines (5–10). Because both spectroscopic and functional parameters depend on particular structural properties, they are often correlated. For example, if the same structural parameter governs both the position of a spectral line and the enthalpy barrier for recombination, the rebinding reaction is accompanied by a characteristic spectral shift, and “kinetic hole burning” (KHB) can be observed (7–9, 11). Frequently, theoretical models exist that relate spectral and structural changes. Consequently, KHB may yield information otherwise not possible to obtain: If a model exists that connects structural and spectral parameters, the relation between a functional parameter, the activation enthalpy barrier for rebinding, and the structure can be determined directly, which is the goal of structure–function studies in proteins.

In the study of heme proteins, the identification of the protein coordinate primarily responsible for the height of the activation enthalpy for rebinding has long been regarded to be of crucial importance. In a number of studies, a “generalized” coordinate is used (12, 13), whereas in others the coordinate is identified with well defined structural parameters (11, 14), primarily the out-of-heme-plane distance of the central iron to which the ligand binds.

In the visible, the Soret absorption band has convenient properties for spectroscopic studies. It is a strong absorption band and hence easy to measure, and the underlying electronic transition is well understood (15). The fine structure of the Soret absorption band can be analyzed by taking into account the homogeneous width, the vibronic coupling, and the spectral heterogeneity; important structural information contained in the spectrum can therefore be extracted (16, 17). Analysis of the Soret spectra of Mb and Mb*CO and comparison to the known structural data made it possible to quantitatively assign spectral parameters to structural properties (18).

In the present study, the correlation of spectral changes with the activation enthalpy for rebinding is studied in KHB experiments on the Soret band of both Mb*CO and MbCO, with the aim of establishing correlations between well defined structural parameters and the activation enthalpy for rebinding.

MATERIALS AND METHODS

Experimental.

Lyophilized sperm whale metmyoglobin (Sigma) was dissolved in distilled water. The protein solution was centrifuged and filtered through a 1.2-μm filter to give an approximately 8 mM stock solution. Further dilution in a 75% (vol/vol) glycerol/water with 100 mM sodium phosphate buffer solution (pH 7) yielded a final protein concentration of about 6 μM. The solution was loaded in a gas-tight methacrylate cuvette. Subsequently, the sample in the cuvette was saturated with CO and reduced with sodium dithionite. The sample was placed in a liquid helium storage cryostat (model 8DT, Janis Research, Wilmington, MA) with quartz windows. The sample was always kept at temperatures under 100 K. The temperature was regulated with a digital programmable temperature controller (model DRC 82 C, Lake Shore Cryotronics, Westerville, OH).

Absorption spectra were measured on a Cary-14 spectrometer interfaced to an IBM PC/AT (On-line Instrument Systems, Jefferson, GA) in the wavelength range between 350 nm and 470 nm with a resolution of 0.2 nm and a wavelength accuracy of 0.1 nm. They were digitized in intervals of 0.5 nm. With these parameters, the collection of a single spectrum took 200 s.

The purpose of the experiment was to observe the evolution of the Soret band as ligands rebind to an initially completely photodissociated sample. At a constant cryogenic temperature, this process spans over ten orders of magnitude in time. To obtain data for the entire recovery of the photodissociated sample, we used temperature-derivative spectroscopy (TDS), a kinetic protocol that allows examination of thermally activated distributed rate processes (19). In this protocol, the sample is completely photodissociated at the lowest temperature, T_min, which is in our case 10 K. Subsequently, the rebinding is monitored while the sample is heated from T_min to T_max linearly in time, so that the ramp temperature, T_R, is given by

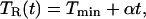1

where α is the heating rate (5 mK/s in our experiments). During heating, spectra were taken every 2 K. At low temperatures, only molecules with small activation enthalpies rebind. As temperature and time increase, the rebinding of molecules with higher barriers becomes appreciable. The photolyzed fraction, N(t), decreases monotonically. The negative derivative of the photolyzed fraction with respect to the temperature, −dN/dT_R, closely resembles the distribution of rebinding barriers, g(H) (19).

After the spectra have been collected, A(ν, T_R), the temperature derivative, dA(ν, T_R)/dT_R is approximated as:

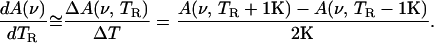2

Here it is assumed that the rate of rebinding does not change significantly between two scans. This assumption was also used to correct the spectra for the slight temperature increase during a single scan.

Taking the absorbance to be proportional to the concentration of the photolyzed species and normalizing yields −dN/dT_R. We present the TDS data in Fig. 2 as integrated absorbances, ΔA(T_R), as a function of T_R by integrating over the spectral changes seen in the spectra in Fig. 1. TDS measures rebinding as a function of the ramp temperature T_R. To convert T_R into an activation enthalpy, we use the fact that geminate rebinding is a first-order process, and the rate coefficient, k, is given by an Arrhenius relation—i.e.,

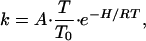3

where A is the pre-exponential factor, which equals 10⁹ s⁻¹ for this reaction, T is the absolute temperature, and T₀ is a reference temperature of 100 K. The gas constant is denoted by R. The activation enthalpy for ligand rebinding, H, is related to the ramp temperature T_R by (19)

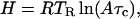4

where the characteristic time τ_c is given by

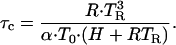5

For a given pre-exponential, Eqs. 4 and 5 can be solved numerically to relate H to T_R. In our case H ≅ 24.5 RT_R.

Figure 2.

The difference in area (in arbitrary units) between successive spectra as a function of temperature. The correlation between temperature and activation enthalpy was determined by using the value 10⁹ s⁻¹ in the pre-exponential for the rebinding rate (19).

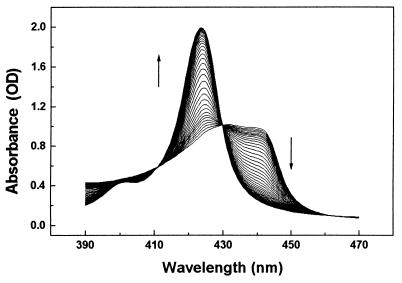
Figure 1.

Soret spectra measured in a TDS experiment during rebinding of CO to Mb. Following photolysis at 10 K, the sample temperature was ramped at a constant rate of 5 mK/s. The arrows indicate the spectral changes with rising temperature; the temperature difference between successive spectra is 2 K.

Spectral Analysis.

The spectra of both MbCO and Mb*CO were analyzed for each temperature by using an approach described earlier (16–18). The method is only outlined here briefly.

The absorption spectrum is modeled as a convolution of three terms,

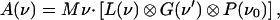6

where M is a constant proportional to the square of the electric dipole moment and ν denotes the frequency. The first term, L(ν), represents the sum over all Lorentzian lines that arise from the coupling of the electronic transition to the high-frequency vibrational modes according to the Franck–Condon principle. This term is expressed as:

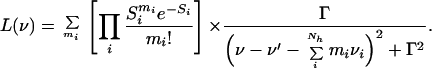7

Here, Γ is a damping factor related to the excited state lifetime. The sum extends over all combinations of m_i phonon events in the various high-frequency vibrational modes i. The linear electron–phonon coupling strength is represented by S_i.

The second term, G(ν′), takes into account the coupling of the electronic transition to a bath of low-frequency modes of the system. Within the so-called “short times approximation” (20) it can be shown that such a coupling causes a Gaussian distribution of the fundamental frequency ν₀:

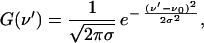8

where σ is the standard deviation.

The third term, P(ν₀), takes into account the inhomogeneous broadening of the Soret line due to the protein conformational heterogeneity. There are several structural coordinates that may influence the π → π* electronic transition; they are most likely associated with the linkage between the porphyrin iron and the proximal histidine. The most important ones are believed to be the displacement of the iron with respect to the mean heme plane, and the tilt and azimuthal angles characterizing the geometry of the imidazole side chain of the proximal histidine with respect to the porphyrin. We model the structural distribution with a single generalized coordinate Q that is assumed to affect the heme electronic excitation in a quadratic way:

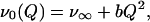9

where the parameter b is a proportionality factor. The coordinate Q was originally introduced to account for the characteristic asymmetric inhomogeneous broadening of the deoxy Mb Soret spectrum in the insightful work of Srajer et al. (6), and it is sometimes tentatively assigned to the iron out-of-plane distance (6, 18). A quadratic dependence of the π → π* electronic transition on the iron position is also qualitatively supported by the analysis of Stavrov (21).

If the coordinate Q is distributed according to a Gaussian around an average value Q₀ with a distribution width δ, i.e., if

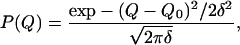10

then the excitation energy distribution, and consequently, the distribution P(ν₀) will have the following form:

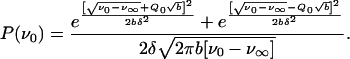11

The characteristic, pronounced asymmetric broadening of the deoxy Mb band to the blue side was successfully described by this formula (6). The parameter Q₀ measures the asymmetry of the spectrum.

In the case of MbCO, the parameter Q₀ is small, so that the conformational distribution of the heme group environment, P(Q), maps into a Gaussian distribution of spectral transition energies, P(ν₀). (17). The convolution with a further Gaussian term in Eq. 6 does not alter the overall shape or symmetry of the absorption profile, but simply adds a constant term (σ_in²) to the Gaussian width of the Soret band.

The spectra were analyzed by fitting the presented functions to the measured spectra. The fitting procedure was described in ref. 16. The vibrational modes that couple to the electronic transition were taken from resonance Raman data (22, 23), as described in ref. 16 for MbCO and in ref. 18 for Mb*CO.

RESULTS

The spectra collected during the TDS experiment are plotted in Fig. 1. The spectral evolution indicates that the sample fully rebinds during heating. Fig. 2 shows the change of the spectral area, ΔA (ν, T_R), as a function of temperature. Because the temperature T_R is approximately proportional to the enthalpy barrier H, these data represent in a good approximation the distribution of activation enthalpies for rebinding (19).

The spectra in Fig. 1 represent a mixture of the liganded (MbCO) and unliganded (Mb*CO) species. For the analysis, the spectra have to be separated into the two components. The straightforward approach to achieve the separation is to subtract the spectrum of unphotolyzed MbCO measured at the same temperature with an appropriate scaling factor. However, this procedure is not successful, as illustrated in Fig. 3a, where the “best” difference between the spectra in Fig. 1 and the spectra of unphotolyzed MbCO at the same temperature is shown. In the subtraction, the MbCO spectrum was multiplied by a factor such that the area added to the Mb*CO spectrum at the maximum of MbCO absorption (around 423 nm) was minimized. It is clear from the “wiggles” appearing in the spectra in Fig. 3 exactly around the absorption maximum of the MbCO spectrum that the spectrum of the unphotolyzed MbCO and the component of the composite spectra representing MbCO after ligand rebinding are slightly shifted from each other. The reason for the shift is KHB also in the MbCO state: the spectrum of MbCO is inhomogeneously broadened, and the slowly and rapidly rebinding molecules have slightly shifted spectra. Thus, at any intermediate temperature, both components of the measured spectra (MbCO and Mb*CO) are different from those representing the extreme (fully liganded vs. fully photolyzed) states.

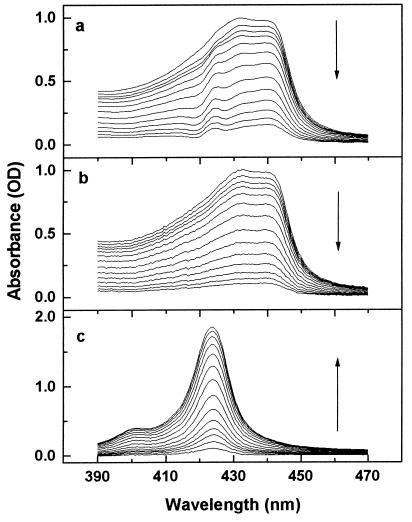
Figure 3.

(a) “Best difference spectra” between the spectra in Fig. 1 and MbCO spectra measured under identical conditions without prior photolysis. For details, see the text. (b) Mb*CO spectra separated from the composite spectra in Fig. 1 by following the procedure described in the text. (c) Evolution of the MbCO spectra after separation. The arrows mark the direction of the spectral evolution with increasing temperature.

Therefore, no simple procedure can separate the MbCO and Mb*CO spectra. To accomplish the separation, we have applied an iterative method in which the evolution of the spectral features of the two-component spectra are treated separately. In a first approximation, we assume that the spectra of Mb*CO do not change significantly in that particular frequency region and that they are similar to those obtained after full photolysis (especially in the spectral region where MbCO predominantly absorbs). The spectra representing the Mb*CO + MbCO mixture at a given temperature were fit with a least-squares algorithm to a sum of six spectra: the spectrum of Mb*CO after full photolysis and five spectra of MbCO. Four of these spectra were generated by taking MbCO spectra measured at the same temperature and shifting them slightly, two were shifted up by 0.2 nm and 0.4 nm, and two down in the same fashion. The spectra used in this fit are selected such that small changes in the spectrum of MbCO can be reproduced; on the other hand, changes in the spectrum of Mb*CO cannot be approximated. Consequently, this fit is good only in the region where the absorption of MbCO is large (in the vicinity of 423 nm) and it is relatively poor in other regions, where the spectra of the fully and partially photolyzed Mb*CO differ. It is also a property of this procedure that none of the parameters of Mb*CO are influenced by this method, because the effect of none of the parameters of the Mb*CO spectrum is limited to the region where the absorption of MbCO is large.

In the next step of the iteration process, the spectrum of the fully photolyzed Mb*CO was removed from the fitted curve. The remaining part is the spectrum of the partially rebound MbCO. This spectrum was then subtracted from the measured curve. The difference is the final spectrum of the possibly shifted Mb*CO at the given temperature. As a result, this procedure yields the spectra of both Mb*CO and MbCO at all temperatures; they are shown in Fig. 3 b and c. Clearly, the “wiggles” in the spectra of Mb*CO at the absorption maximum of MbCO (seen in Fig. 3a) have been successfully removed.

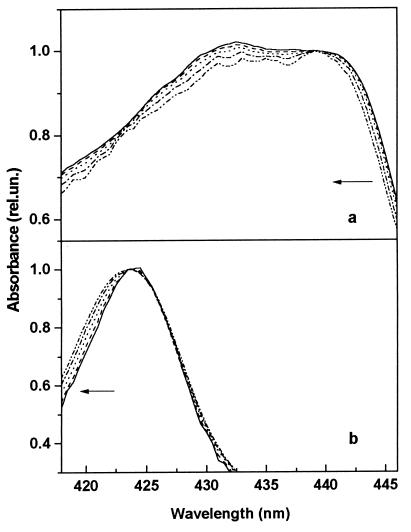
The resulting spectra of both Mb*CO and MbCO at selected temperatures are shown in Fig. 4 a and b after normalization to equal absorbance at 439 and 423.5 nm, respectively. From these spectra, the following features are immediately evident without any data analysis: (i) Both Mb*CO and MbCO undergo a shift toward lower wavelengths as the temperature increases and rebinding takes place. (ii) For Mb*CO, a progressive decrease of the vibronic peak at about 430 nm and of the overall spectral bandwidth is observed. However, no increase of the band asymmetry (rather a slight decrease) is seen. (iii) For MbCO, the Soret band shifts to the blue and the overall bandwidth increases with temperature.

Figure 4.

Normalized component spectra showing the characteristic changes during spectral evolution. The spectra were normalized to equal absorbance at 423.5 nm (MbCO) and 439 nm (Mb*CO). The arrows mark the direction of the spectral evolution with increasing temperature. (a) Spectra of Mb*CO at 15 K, 25 K, 35 K, 45 K, and 55 K. (b) Spectra of MbCO at 35 K, 45 K, 55 K, 65 K, and 75 K.

Both Mb*CO and MbCO were then fitted to the analytical expression Eq. 6, as discussed in Spectral Analysis. In the case of Mb*CO, the basis for the selection of the parameters permitted to vary in the fits of the different spectra was the work in ref. 18, where the parameters for Mb*CO and for equilibrium deoxy Mb were determined from Soret spectra at 10 K. There it was also shown that the values of Γ, S₂₀₀, S₃₇₀, and S₁₃₅₇, are identical for Mb*CO and deoxy Mb. Consequently, these parameters were fixed in the present fits to the following values reported in ref. 18: Γ = 180 cm⁻¹, S₂₀₀ = 0.07, S₃₇₀ = 0.31, and S₁₃₅₇ = 0.05. The parameters that were varied during the fit were S₆₇₄, ν_∞, σ, Q₀√b^−1/2, and δ √b^−1/2. In the case of MbCO, the basis for the selection of the parameters permitted to vary in the fitting of the different spectra was ref. 16. Values of parameters Γ and S_j were in good agreement with those of equilibrium MbCO and were kept constant throughout the rebinding to the following values: Γ = 230 cm⁻¹, S₃₅₀ = 0.08, S₆₇₄ = 0.07, S₁₁₀₀ = 0.01, S₁₃₇₄ = 0.05; the varying parameters were ν_∞ and σ. The procedure gave an excellent fit to the spectra, as shown in ref. 18. The results of the fit fully confirm the conclusions drawn from the inspection of the “raw” spectra in Fig. 4; they are shown in Fig. 5 a and b for Mb*CO (ν_∞ and Q₀√b^−1/2) and in Fig. 5c for MbCO (ν_∞).

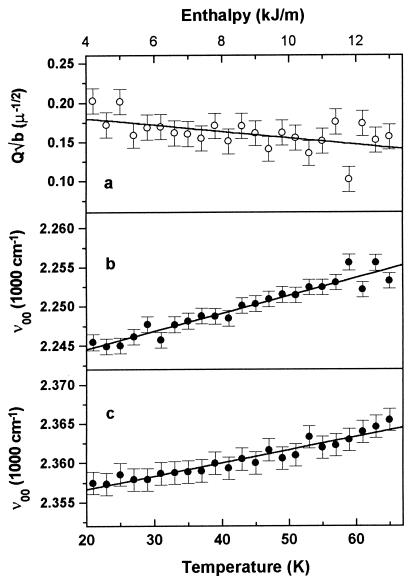
Figure 5.

Spectral parameters of Mb*CO and MbCO during rebinding. (a) Iron-out-of-plane distance (Q₀√b) of the photolyzed Mb*CO. (b) Peak frequency of the π → π* transition of Mb*CO. (c) Peak frequency of the π → π* transition of the liganded MbCO. All are for populations rebinding between the temperatures T and T + 2K. The correlation between temperature and activation enthalpy for rebinding is also shown.

The absolute errors in the values of ν_∞ are ≅ 10 cm⁻¹ and in Q√b ≅ 0.005 μ^−1/2 (see ref. 18). The relative errors are estimated as the standard deviation from the linear fit to the results, as shown in Fig. 5.

DISCUSSION

The main results can be summarized as follows:

(i) The data in Fig. 5a indicate that, as rebinding proceeds, no increase in Q₀√b is observed (in fact, the data show a small decrease of Q₀√b with temperature). This behavior implies that the rebinding enthalpy H is largely decoupled from Q. Therefore, the coordinate Q that is responsible for the asymmetric inhomogeneous broadening of the deoxy Soret band of heme proteins (see Eq. 6) is obviously a “nonkinetic” coordinate in the terminology of Srajer and Champion (11). The slight decrease of Q√b is not significant, which becomes obvious when comparing the range of Q√b values that can be estimated from the enthalpy dependence in Fig. 5a with the static distribution obtained simply from the inhomogeneous broadening of the spectrum, P(ν₀). From the expression used to fit the spectrum, Eq. 8, a distribution with a width parameter δ√b = 0.15 is obtained. It is remarkable that the distribution of the coordinate Q is about as large as the average value itself. On the other hand, from the coupling of the coordinate Q to H, given in Fig. 5a, and the distribution of activation enthalpies in Fig. 2, a distribution in the coordinate Q₀√b of about 0.03 can be estimated, which is only 20% of the actual distribution δ√b measured from the spectral inhomogeneity. Consequently, the coordinate Q is essentially decoupled from the enthalpy for rebinding.

(ii) In Fig. 5 b and c, the correlation between the peak frequency ν_∞ and H is shown for Mb*CO and MbCO, respectively. These data reflect the entire influence of KHB on the spectra. The dependencies of the band positions on the rebinding enthalpy agree within a factor of 2, indicating that KHB is similar in both MbCO and Mb*CO (9). Therefore, both the Soret absorption and the rebinding barrier H are coupled to a particular structural parameter, which is a kinetic coordinate, in both Mb*CO and MbCO. Two characteristics of this coordinate are obvious: (i) it does not change appreciably during the MbCO → Mb*CO transition; and (ii) it strongly affects the π → π* transition of the heme (by means of parameter ν_∞), therefore it has to be located in the vicinity of the heme. This conclusion gives an interesting new viewpoint to the interpretation of the recent structural data on MbCO and Mb*CO (2–4): KHB is similar in Mb*CO and MbCO, whereas the iron displacement from the mean heme plane is very different (0.27–0.32 Å as compared with 0.05–0.08 Å (2–4). Consequently, it appears implausible that the iron out-of-plane displacement is the structural coordinate correlated with the enthalpy for CO rebinding, contrary to the assignments by Champion and collaborators (11, 24). A further argument against identification of the kinetic coordinate with the iron-out-of-plane distance arises when comparing the photoproduct structure (Mb*CO) with the equilibrium deoxy Mb structure. In Mb*CO, the iron has moved out of the heme plane by 80% (2). In the relaxation to deoxy Mb (Mb*CO → Mb), the barriers for recombination increase markedly (14, 25–28), while the iron shifts only by another 0.05 Å away from the mean heme plane (2). To identify the coordinate that is correlated to the rebinding barrier, we should direct our attention to structural features in the vicinity of the heme that do not change in the first transition following photolysis (MbCO → Mb*CO), but do change significantly in the relaxation (Mb*CO → Mb).

We have shown that the iron displacement from the heme plane cannot be the kinetic coordinate that governs the rebinding barrier, but there is evidence that the nonkinetic coordinate Q (responsible for the band asymmetry) can be assigned to the iron-out-of-plane distance for the following two reasons: (i) both the coordinate Q and the iron displacement are nonkinetic coordinates; and (ii) the value of Q scales with the available structural data: the parameter Q₀√b is about 20% smaller in Mb*CO with respect to the equilibrium deoxy Mb at 10 K, in quantitative agreement with the values of the iron displacements determined from x-ray diffraction (2–4, 18).

An unambiguous structural assignment of the kinetic coordinate responsible for KHB in both Mb*CO and MbCO cannot be made at present. Both proximal and distal structural features may contribute. Candidates to be considered are the tilt or azimuthal orientation of the proximal histidine (28). The fact that the relaxation (Mb*CO → Mb) occurs thermally only above the glass transition of the solvent indicates that parts of the protein in contact with the exterior are involved in the relaxation (25). Changing the tilt angle of the proximal histidine needs a sliding motion of the F helix, making the tilt angle an attractive candidate for the structural coordinate. There are several observations that point to the significance of distal effects in the determination of the fine structure of the absorption spectrum and in affecting the activation parameters. In MbCO, a few taxonomic A substates can be distinguished by discrete infrared bands of the heme-bound CO (29, 30) due to differences in the structure of the heme pocket. A mechanism that has been identified as responsible for the existence of A substates is the protonation of the imidazole side chain of the distal histidine, His E7, accompanied by an isomerization of this residue (31, 32). The different A substates have different Arrhenius parameters for rebinding, and consequently, distal components do indeed influence the rebinding rates. Within each A substate, the rate coefficients are distributed, indicating that each A substate is structurally heterogeneous. In spectroscopic studies involving the visible region (like the present study), the taxonomic A substates cannot be treated separately. The overall distribution therefore is a sum of the contributions of the individual A substates. In a recent comparison of Mb mutants, modifications on the distal side were reported to be much more effective in influencing the Soret spectral changes accompanying protein relaxation above 200 K (33). It was concluded that electrostatic interaction between the heme and the protein on the distal side is the origin of the spectral changes. Related conclusions were drawn from observing the effect of distal pocket mutations on the position of band III (34). It was concluded that, in addition to the iron-out-of-plane position of the heme iron, electrostatic effects on the distal side contribute to the position of band III.

Further studies are needed to identify the major kinetic coordinate(s). We emphasize, however, that the conclusions of our analysis presented here are independent of the exact structural assignment of the coordinates discussed.

ABBREVIATIONS

Mb

myoglobin

KHB

kinetic hole burning

TDS

temperature-derivative spectroscopy