Static and dynamic lengths of neutrophil microvilli

Abstract

Containing most of the L-selectin and P-selectin glycoprotein ligand-1 (PSGL-1) on their tips, microvilli are believed to promote the initial arrest of neutrophils on endothelium. At the rolling stage following arrest, the lifetimes of the involved molecular bonds depend on the pulling force imposed by the shear stress of blood flow. With two different methods, electron microscopy and micropipette manipulation, we have obtained two comparable neutrophil microvillus lengths, both ≈0.3 μm in average. We have found also that, under a pulling force, a microvillus can be extended (microvillus extension) or a long thin membrane cylinder (a tether) can be formed from it (tether formation). If the force is ≤34 pN (± 3 pN), the length of the microvillus will be extended; if the force is >61 pN (± 5 pN), a tether will be formed from the microvillus at a constant velocity, which depends linearly on the force. When the force is between 34 pN and 61 pN (transition zone), the degree of association between membrane and cytoskeleton in individual microvilli will dictate whether microvillus extension or tether formation occurs. When a microvillus is extended, it acts like a spring with a spring constant of ≈43 pN/μm. In contrast to a rigid or nonextendible microvillus, both microvillus extension and tether formation can decrease the pulling force imposed on the adhesive bonds, and thus prolonging the persistence of the bonds at high physiological shear stresses.

Microvilli, also called ruffles or projections, are rich on resting human neutrophils (1–5) (Fig. 1). Supported by actin filaments, microvilli protrude from spherical neutrophil surfaces as membrane cylinders. In addition to furnishing increased surface area when neutrophils pass through small capillaries (6, 7), microvilli are indispensable for neutrophils to migrate out of blood vessels to inflammatory sites. If microvillus numbers are reduced in any way, such as with cytochalasin B or hypotonic swelling, the efficiency of neutrophil arrest will be dramatically decreased (4). En route to inflammatory sites, neutrophils attach to and roll on endothelium before their firm arrest and diapedesis. The attachment and rolling of neutrophils are mediated by selectins (L-selectin on neutrophils; P- and E-selectin on endothelium) and their carbohydrate ligands (8). When a neutrophil touches endothelium or another surface, the tip of a microvillus is very likely to be the first contact point. So L-selectin (CD62L) and P-selectin glycoprotein ligand-1 (PSGL-1, CD162) are localized on the tips of microvilli to facilitate the initial arrest and rolling of neutrophils (1, 3, 5).

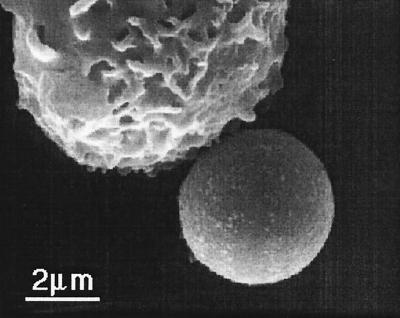
Figure 1.

A scanning electron micrograph showing tips of microvilli from a human neutrophil adhering to an anti-CD45-coated bead.

The biophysical aspect of neutrophil arrest and rolling often has been studied in vitro with a parallel flow chamber, on the bottom of which selectins or their ligands are coated (4, 9–17). When a neutrophil adheres to and rolls on the substrate in a parallel flow chamber or on endothelium in vivo, media or blood flow will impose a pulling force on the adhesive bond or bonds, which are preferably located at the tip of a microvillus. It is well documented that this pulling force can shorten the lifetimes of these bonds or extract receptors from cell surfaces (9, 12, 15, 18–22). The pulling force can be estimated with low Reynolds number flow dynamics if the length of the adhered microvillus is known (12, 14). The static lengths of neutrophil microvilli can be seen under an electron microscope to be as long as 1.9 μm and as short as 0.05 μm with an average length of ≈0.29 μm (1). However, little is known about the response of the microvillus under a pulling force and the effect of the response to the pulling force on a rolling cell.

Here, we report the behavior of a neutrophil microvillus under a small pulling force (a few tens of piconewtons) and the force history experienced by a single attachment between a neutrophil and its substrate. With a micropipette manipulation system, we have mechanically measured the natural lengths of neutrophil microvilli (≈0.3 μm), which is close to the electron microscopic results of Bruehl et al. (1). A slightly larger value, 0.35 μm, was revealed by our own electron microscopic study, in which neutrophils were fixed with a technique that did not shrink them. More importantly, we have found that, under a pulling force, a microvillus can be extended (microvillus extension) or a long thin membrane cylinder (a tether) can be formed from it (tether formation) depending on the magnitude of the force. In contrast to a rigid or nonextendible microvillus, both microvillus extension and tether formation can decrease the pulling force imposed on the adhesive bonds, and thus prolonging the persistence of the bonds at high physiological shear stresses (12).

MATERIALS AND METHODS

Neutrophil and Bead.

The details of the neutrophil isolation and bead preparation procedures have been reported (23). In brief, human neutrophils were isolated with density separation from venous or finger prick blood donated by healthy volunteers. Latex beads coated with goat anti-mouse IgG (specific to the crystallizable fragment of mouse IgG) were purchased from Sigma. They were incubated with one of the following four mouse anti-human mAbs: anti-CD45 (Sigma), anti-CD18, anti-CD62L (Becton Dickinson), or anti-CD162 (Immunotech/Coulter) at 37°C for ≈1 hr. The beads were then washed with PBS (121.5 mM NaCl, 25.2 mM Na₂HPO₄, and 4.8 mM KH₂PO₄) before use. When beads were coated with anti-CD162, purified general type mouse IgG (Sigma) was added to the solution of anti-CD162 (100:1 in weight) to decrease the antibody concentration on their surfaces.

Micropipette Manipulation.

As shown in Fig. 2, a human neutrophil was aspirated into a micropipette whose diameter (≈9.5 μm) was almost the same as the diameter of the neutrophil. An antibody-coated bead was held by another micropipette and was placed at the opening of the neutrophil pipette. A precise suction pressure (Δp) can be applied inside the neutrophil pipette with a micropipette manipulation system (23). A positive pressure can be superimposed on the suction pressure so that the neutrophil can be pressed against the bead. After the cell and bead made contact for ≈0.1 s, the positive pressure was removed and only the previously applied suction pressure was left. If adhesion did not occur, the cell would move freely inside the micropipette. If adhesion occurred between the cell and bead, a pulling force (F) would be applied on the adhesive bond or bonds because of the suction pressure. This pulling force, which equals the force on the tip of the microvillus and the force on the cell, can be calculated with the following formula from ref. 23:

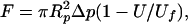1

where R_p is the radius of the neutrophil pipette, U is the velocity of the adhered cell and U_f is the free motion velocity of the same cell. The whole experimental process was recorded on a video tape at a speed of 60 fields/s, so time was measured field by field. The displacement of the cell was measured with video calipers (model 305, Vista Electronics, La Mesa, CA) by tracking the distal edge of the cell.

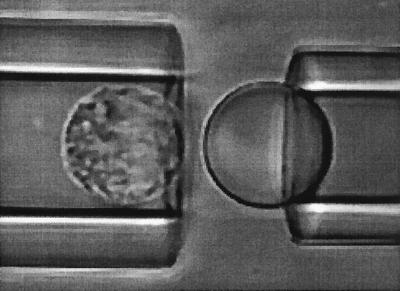
Figure 2.

A micrograph showing an anti-CD45-coated bead about to be touched by a human neutrophil. At the beginning of every experiment for a neutrophil-bead pair, a known suction pressure is applied inside the pipette on the left. Then a positive pressure is superimposed so that the neutrophil can move toward the bead. After the cell and the bead make contact, the positive pressure is released. If the cell does not adhere to the bead, the cell will move away freely under the suction pressure; if the cell adheres to the bead, the cell will stay close to the bead or it will move away at a smaller velocity than its free motion velocity. After the cell detaches from the bead, the positive pressure is superimposed again and the same procedure is repeated.

Two control experiments were done: one with beads that were washed twice with PBS after being purchased from Sigma; the other with beads that were coated with purified general type mouse IgG (Sigma) by using the same bead preparation procedures as for those specific antibodies. Three different neutrophil-bead pairs were used for both cases. For the first case, two adhesion events occurred in 414 trials, corresponding to an adhesion frequency of 0.5%; for the second case, seven adhesion events occurred in 380 trials, corresponding to an adhesion frequency of 1.8%. Both of these two frequencies are substantially lower than the adhesion frequencies observed when beads coated with specific antibodies to human receptors were used.

Electron Microscopy.

Neutrophils or neutrophils bound to anti-CD45 coated beads (Dynabeads-450, Dynal, Lake Success, NY) were placed on 12-mm glass disks treated with Cell-Tak adhering protein (Collaborative Biomedical Research, Bedford, MA). They were allowed to settle and adhere for 2 min before being fixed with 2.5% glutaraldehyde in 0.1 M sodium cacodylate buffer (Electron Microscopy Sciences, Fort Washington, PA) at 21°C for 1 hr. Then they were washed in Hanks’ balanced salt solution (Sigma) and postfixed with 1% OsO₄ in a veronal acetate buffer. The cells were further fixed in freshly prepared 1% tannic acid with 50 mM cacodylate buffer (pH 7.4) for 1 hr. This step was followed by 1 hr of fixation in 0.5% uranyl acetate in deionized water. A series of acetone dehydrations were performed, and the samples were air dried in tetramethylsilane (Electron Microscopy Sciences). A conductive paint was used to attach the cell-covered glass disks to aluminum stubs, and the samples were then sputter-coated with gold and palladium. Specimens were observed with a Philips 501 scanning electron microscope (Mahwah, NJ) and stored in a dessicator before and after imaging.

Fixation of neutrophils often causes their shrinkage, which can distort their morphology (7, 24). The fixation procedures adopted here proved to be a technique that would not shrink neutrophils (25, 26). From electron micrographs, we measured the diameters of 21 neutrophils. Their average volume, 323 ± 47 μm³ (mean ± SD), agrees reasonably well with the value obtained for live neutrophils by Ting-Beall et al. (7) with a mechanical method. So microvilli on neutrophils prepared this way are assumed to retain their original geometry and are measured directly from electron micrographs with a magnifying graticule.

Numerical Methods.

Eqs. 3–5 and 6a were solved with Newton’s method for any given shear stress, τ. Solutions at lower shear stresses were used as the initial guesses for solutions at higher shear stresses. Eq. 6b was solved with Euler’s method. For every timestep, F_b, l, and θ were solved from Eqs. 3–5 with the initial L or the L from the previous timestep. Timesteps were reduced until consistent results were obtained.

RESULTS

Microvillus Extension and Tether Formation.

Anti-CD62L-coated beads and anti-CD162-coated beads are ideal choices for studying the behavior of neutrophil microvilli under pulling forces because CD62L and CD162 are clustered at the tips of microvilli (1, 3, 5). However, the adhesion between neutrophils and anti-CD62L-coated beads only lasted ≈1 s under a force of a few tens of piconewtons. The adhesion between neutrophils and anti-CD162-coated beads was somewhat longer, so we were able to make measurements at the lower suction pressures. Although the adhesion between neutrophils and anti-CD18-coated beads had longer lifetimes, neutrophils would be induced to engulf the beads after binding to them. Neutrophils bound to anti-CD45-coated beads did not phagocytize the beads. Besides, the adhesion between them had the longest lifetime under the same order of magnitude of forces (27). Although no evidence has shown that CD45 is concentrated on neutrophil microvilli, the tip of a microvillus is still a preferred location where CD45 can form bonds with antibodies on the bead (Fig. 1). This result is probably because the tip of a microvillus is very likely to be the first contact point when a neutrophil touches another surface and CD45 on the tip of the microvillus will have a longer contact time and thus having a greater opportunity to bond with its antibody on the bead.

After a neutrophil adheres to an antibody-coated bead through a microvillus, a pulling force can be imposed on the neutrophil and the microvillus by applying a suction pressure in the neutrophil micropipette (Fig. 2) (23). Thus, the change in the microvillus length under the pulling force can be studied by observing the motion of the neutrophil because the tip is stationary. Seven different suction pressures were used for anti-CD45 coated beads: 0.25 pN/μm², 0.375 pN/μm², 0.5 pN/μm², 0.625 pN/μm², 0.75 pN/μm², 0.875 pN/μm², and 1 pN/μm². The three lower pressures were used for anti-CD162-coated beads. Multiple attachments, which could be recognized when cells underwent a discontinuous change in velocity during microvillus extension or tether formation, were observed rarely. When the suction pressure was ≤0.5 pN/μm² (corresponding to forces ≤34 pN), the length of the microvillus would be extended (Fig. 3A). During extension, the microvillus probably deformed from a thicker, shorter membrane cylinder to a thinner, longer one (28). When the suction pressure was >1 pN/μm² (corresponding to forces >61 pN), a tether would be formed from the microvillus at a constant velocity (Fig. 3B) (23). Tethers could grow as long as 20 μm (the longest we can see in the view field of our microscope) without any indication of velocity decrease during our measurements. When the suction pressure was >0.5 pN/μm² and ≤1 pN/μm², some microvilli extended as shown in Fig. 3A whereas the others formed tethers as illustrated in Fig. 3B. However, as the suction pressure increased from 0.625 pN/μm² to 1 pN/μm², the percentage of the microvilli that did not form tethers became less and less: 11 of 15 (73%) at 0.625 pN/μm², 6 of 9 (67%) at 0.75 pN/μm², 5 of 9 (56%) at 0.875 pN/μm², and 1 of 9 (11%) at 1 pN/μm². Therefore, this force range is a transition zone in which tethers could be formed at different forces that depend in the degree of association between membrane and cytoskeleton.

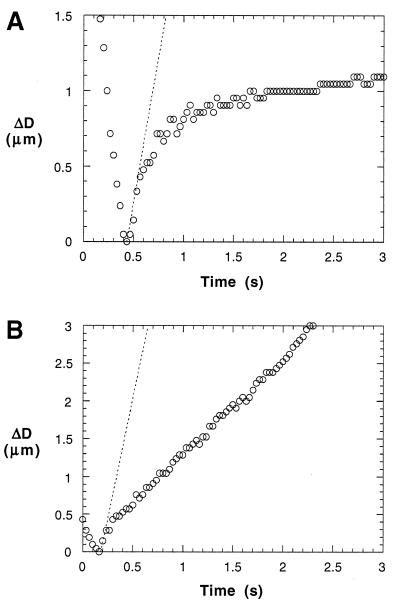
Figure 3.

Microvillus extension (A) and tether formation (B). (A) The motion of a neutrophil before and after it adhered to an anti-CD45-coated bead under a suction pressure of 0.5 pN/μm². The slope of the dotted line stands for the velocity of the same cell when it is moving freely inside the same micropipette under the same pressure. ΔD is the displacement of the neutrophil relative to the adhesion point as the neutrophil approaches the bead, adheres, moves back freely for ≈0.4 μm (the free motion rebound), and then moves at a diminishing velocity (the diminishing rebound). After adhesion, ΔD actually represents the change in the microvillus length because the tip of the microvillus is stationary on the bead. The static equilibrium force (U = 0) that causes the extension of the microvillus is calculated with F = πR_p², whose average is 34 pN (uncertainty 3 pN) at 0.5 pN/μm². Neutrophils that adhered to anti-CD162-coated beads have similar behavior under the same suction pressure. (B) The motion of a neutrophil before and after it has formed a membrane tether under a suction pressure of 1 pN/μm². Here, the slope of the dotted line also stands for the velocity of the same cell when it is moving freely inside the same micropipette under the same pressure. After adhering to the bead and moving back freely for ≈0.4 μm (the free motion rebound), the neutrophil, attached by its membrane tether, continues to move linearly, albeit at a smaller velocity. At this suction pressure, the average force calculated with Eq. 1 from all the measurements is 61 pN (uncertainty 5 pN).

Static and Dynamic Lengths.

For either microvillus extension or tether formation, the neutrophil always moved freely for a few tenths of a micrometer (the free motion rebound) before its velocity decreased (Fig. 3 A and B). This free motion rebound length does not depend on the suction pressures used, and thus it probably indicates the static or natural length of a microvillus (Fig. 4A). When a neutrophil is pushed against an antibody-coated bead, the microvillus in contact with the bead will be pressed down. Therefore, when the neutrophil is pulled away from the bead with a suction pressure, it will move without any resistance before the microvillus can resume its natural length. After the microvillus reaches its original length, the cell cannot move at its free motion velocity any more because a pulling force will develop on the adhesive bond or bonds. This force will slow the motion of the cell and at the same time lengthen the microvillus. It is also this force that will eventually break the adhesive bond or extract the bonded receptor or ligand from the neutrophil surface (27). All of the microvillus lengths measured at different suction pressures are in the range of 0.1–0.55 μm, and their average is 0.30 ± 0.12 μm (mean ± SD; n = 89). Although the microvillus lengths obtained with electron micrographs are in a slightly different range (0.15–0.7 μm), their average value, 0.35 ± 0.13 μm (mean ± SD; n = 133), falls in the same neighborhood.

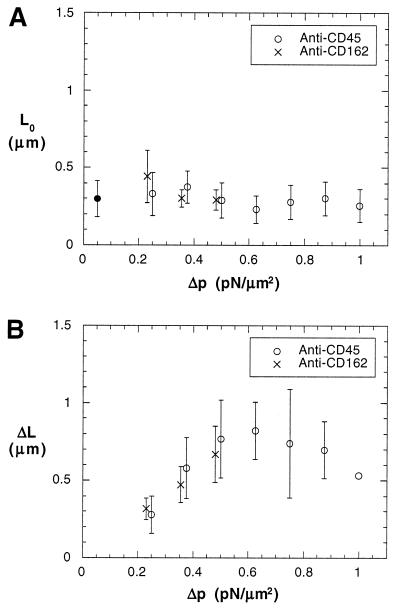
Figure 4.

Natural lengths of microvilli (A) and extended lengths of microvilli (B). Error bars stand for their SDs. The measurements for anti-CD162 are drawn intentionally at a pressure 0.02 pN/μm² less than the actual pressure so that their error bars can be differentiated from the ones for anti-CD45. (A) The lack of dependence of the free motion rebound length (L₀) upon the suction pressure. L₀ is considered to be the natural length of a microvillus and is directly measured from the tracking data as shown in Fig. 3A and Fig. 3B. The solid circle shows the average for all the measurements. The number of measurements at each pressure is 7, 8, 14, 15, 9, 9, and 9 (left to right). The number of measurements for anti-CD162 at each of the three lower pressures is six. (B) The dependence of the extended length (ΔL) upon the suction pressure. ΔL is obtained by fitting L = L_∞ − ΔLe^−t/t_c to the diminishing rebound of the extension curve shown in Fig. 3A. The number of measurements for anti-CD45 at each pressure is 7, 8, 14, 11, 6, 5, and 1 (left to right). The number of measurements for anti-CD162 at each of the three lower pressures is six.

After the microvillus reaches its natural length under a pulling force, it will extend if the pulling force is small (Fig. 3A). The maximum length the microvillus can reach is determined by the pulling force or the suction pressure applied inside the micropipette in this case. Microvillus extension can be described with an exponential decay curve represented by

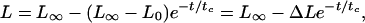2

where L is the total length of a microvillus, L_∞ is the asymptotic length that the microvillus approaches at a certain pulling force, L₀ is the natural length of the microvillus, t is the time (t = 0 when the microvillus starts to extend, i.e., L = L₀), and t_c is the characteristic time of extension. Although this is an intuitive equation, all of the data fit it well (79% of the correlation coefficients are >0.95 and no correlation coefficients are <0.73; the curve fitting was done with the Levenberg–Marquardt algorithm incorporated in a plotting software, kaleidagraph Synergy Software, Reading, PA). This way, t_c and ΔL can be obtained. The values of t_c are independent of the suction pressures (Table 1), so t_c is probably an inherent characteristic, which can be determined by the shape and other properties of microvilli. The extended length (ΔL) increased when the suction pressure increased from 0.25 pN/μm² to 0.5 pN/μm² (Fig. 4B). This was the pressure domain in which all microvilli were extended. In the transition zone (from 0.625 pN/μm² to 1 pN/μm²), ΔL leveled off presumably because only microvilli with larger membrane tensions and tighter membrane–cytoskeleton associations were extended and a tradeoff had been reached between these two factors and the larger suction pressures. The data when the pressure was ≤0.5 pN/μm² show that a microvillus will behave like a spring when the pulling force is small. A linear fit through the origin and the six data points when the suction pressure was ≤0.5 pN/μm², shown in Fig. 4B, gives a spring constant of 43 pN/μm. However, when the force is large and a tether is formed, the hypothesis that the microvillus behaves as a spring is no longer valid because the length of the tether grows at a constant velocity (Fig. 3B) (23).

Table 1.

The characteristic time of neutrophil microvillus extension (t_c)

Δp (pN/μm2)	0.25	0.375	0.5	0.625	0.75	0.875	1
mean, s	0.73	0.71	0.66	1.14	0.78	0.61	1.00
SD, s	0.50	0.32	0.24	0.15	0.41	0.09	N/A
n	13	14	20	11	6	5	1

t_c is calculated by fitting the diminishing rebound data of the neutrophil motion (Fig. 3A) under different suction pressures to Eq. 2. Results for the antibody to CD162 are included in the first three columns. The average of all the measurements is: 0.77 ± 0.35 s (mean ± SD; n = 70). No suction pressure dependence is seen here. N/A, not applicable. 

Force Decrease Caused by Microvillus Extension or Tether Formation.

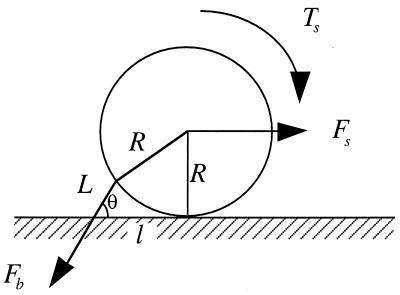
Both microvillus extension and tether formation have important implications for the rolling of neutrophils on endothelium. Our results indicate that microvilli are extended or tethers are formed during the cell-rolling process. Extended microvilli or growing tethers can change the moment arm of the force on the adhesive bond, and hence this can affect the magnitude of the force. At low Reynolds number, inertia can be neglected. Consequently, a quasi-steady approach allows us to assume that the net force and torque on the cell is zero in any position of the cell. For a neutrophil with a single attachment to a substrate as shown in Fig. 5, the following equations are obtained (τ is the shear stress):

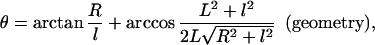3

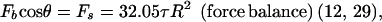4

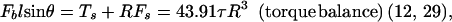5

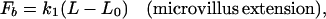6a

or

6b

For neutrophils, k₁ = 43 pN/μm, k₂ = 11 pN⋅s/μm, and F₀ = 45 pN (23). For convenience of comparison, R = 4.25 μm was used in our calculation although the actual average radius of the neutrophils we used was ≈4.5 μm.

Figure 5.

Force balance on an adhered neutrophil mediated by a single attachment. L is the total length of the microvillus, l is the length of the moment arm, R is the radius of the cell (≈4.25 μm), F_b is the force on the adhesive bond, F_s is the force, and T_s is the torque imposed by the shear flow on the cell. Because the velocity of a rolling cell is much less than the velocity of a neutrally buoyant cell, the force and torque calculation for a static cell in a shear flow is generally used (9, 12, 21).

For shear stresses where the microvillus is extended, the equilibrium pulling force on the adhesive bond (F_b), along with L, l, and θ, can be solved from Eqs. 3–5 and 6a. Assume no microvillus extension or tether formation before the cell body reaches the substrate after forming one attachment. Then, the cell can endure a shear stress as large as 0.022 pN/μm² (or 0.22 dyne/cm²) without forming tethers for a natural microvillus length of 0.35 μm. If no other bonds are formed, the microvillus will be extended to 1.00 μm at this shear stress, and F_b will equal to 27 pN, instead of 45 pN for a nonextendible microvillus that is 0.35 μm in length.

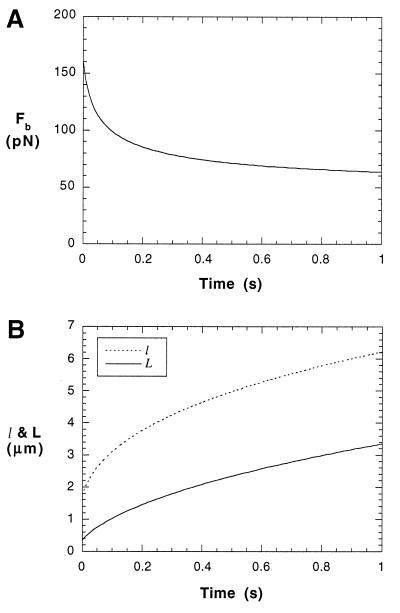
For shear stresses where a tether is formed, F_b can be solved from Eq. 6b once an initial value of L is designated. After a neutrophil attaches to a substrate through a microvillus, the cell will rotate toward the substrate until it makes another contact with the substrate. During this process, microvillus extension or tether formation may have already been in progress. The elongated length during this stage plus L₀ should be the initial L for solving Eq. 6b. The accurate determination of this value requires complicated computation with fluid dynamics and microvillus biorheology. However, no matter what the initial L is, the force on the tip of the microvillus will eventually go to 45 pN as the tether becomes longer under the assumption that no other bonds are formed during the rolling process (F_b → 45 pN when t → ∞). At a shear stress of 0.08 pN/μm² (or 0.8 dyne/cm²), tethers will be formed and F_b will decrease from ≈160 pN to ≈60 pN in 1 s with an initial L of 0.35 μm (Fig. 6 A and B). If we use an initial length L of 1.00 μm, which is the longest extension a microvillus can reach without forming tethers, the force will decrease from ≈100 pN to ≈60 pN in 1 s. This dramatic force decrease will prolong the persistence of the adhesive bond or bonds between selectins and their ligands in vivo, so that the cell will have enough time to form another attachment or wait for integrins to take action. In reality, more bonds could be formed during the rolling of neutrophils, and thus the force and torque on the neutrophil may distribute on several attachments and the force on the bonds of the first attachment may decrease faster than predicted here.

Figure 6.

Bond force (F_b) decrease (A), moment arm (l) and tether length (L) increase (B) for a rolling neutrophil with a single attachment at a shear stress of 0.08 pN/μm². An initial length of 0.35 μm for L was used. (A) The bond force decreased 50% in only ≈0.2 s. Then it tends to steady-state very slowly. (B) The fastest increase in both tether length and moment arm happened before 0.2 s. Also, both moment arm and tether grow more than twice their original lengths in 1 s. But they will eventually tend to constant values.

DISCUSSION

Although the accuracy of measuring distance on images under an optical microscope is limited by the wavelength of light, motion of objects under an optical microscope can be tracked as accurately as 0.01 μm (30). Our cell tracking system only allowed us to detect a displacement of ≈0.05 μm, but we were able to obtain the average length of neutrophil microvilli (≈0.3 μm) by tracking the free motion of neutrophils adhered to antibody-coated beads (Fig. 3 A and B). With the same technique, Shao and Hochmuth (23) reported a total neutrophil rebound length of ≈0.62 μm, which presumably includes both the free motion rebound and part of the diminishing rebound. During our electron micrograph study, no microvilli longer than 0.7 μm were observed, whereas the longest microvillus observed by Bruehl et al. (1) was 1.9 μm. Nevertheless, all of the average microvillus lengths fall in the vicinity of 0.3 μm. Although the average microvillus length measured with micropipette manipulation (≈0.3 μm) is consistent with the value reported by Bruehl et al. (1) (≈0.29 μm), this value may still be an underestimate because not all microvilli were pressed down completely in the measurements with micropipette manipulation. Therefore, our electron microscopic result (≈0.35 μm) in which neutrophils were fixed with a nonshrinkage technique may be more accurate.

Electron micrographs show that most of neutrophil microvilli have diameters ≈0.2 μm. If we assume that a microvillus is a cylinder with a flat tip, the average surface area of a microvillus will be 2πR₀ + πR₀² ≈ 3.14159 × 0.1 μm (2 × 0.35 μm) ≈0.25 μm². For a neutrophil with an apparent surface area of 227 μm², the density of microvilli will be in the range of 4/μm²–6/μm² if the actual surface area is 2.1–2.6 times larger than the apparent surface area (6, 7). This result may be an overestimate because in reality surface ruffles coexist with microvilli on neutrophil surfaces and one ruffle is actually an accumulation of several microvilli.

Neutrophil microvilli can be extended or tethers can be formed when a point force is applied on their tips. Their heterogeneity is represented by a transition zone where microvilli subjected to the same forces can have two kinds of different behavior (microvillus extension or tether formation) depending on their membrane–cytoskeleton association strength. In the transition zone, microvilli with weaker association between membrane and cytoskeleton can be pulled out to form tethers, whereas microvilli with stronger association between membrane and cytoskeleton can only be stretched to some point. The average minimum force to form a tether from neutrophil membranes reported by Shao and Hochmuth (23) is 45 pN, which is located almost at the center of the transition zone. For microvillus extension, the spring constant was calculated to be ≈43 pN/μm under the assumption that no threshold forces exist. Whether a threshold force exists for this kind of deformation can only be determined with higher resolution techniques like laser tweezers (30) or the biointerface probe (31).

Microvillus extension and tether formation in neutrophils were not known before this study and a related one (23), so pulling forces on adhesive bonds were overestimated because they were based on a static bond length (12). Alon et al. (14) have measured moment arms of attached neutrophils (l) in parallel flow chamber experiments by reversing the flow in a shear stress range of 0.03–0.08 pN/μm². They obtained an average moment arm of 3.06 μm in the range of 1.9 μm–4.0 μm, and no dependence of moment arms on the shear stress was observed. During the reversal of the flow, the motion of the cell only happened in a duration of ≈0.33 s. With an initial microvillus length of 0.35 μm, the moment arm was calculated from the results presented here to be 2.25 μm at 0.3 dyne/cm² and 4.38 μm at 0.8 dyne/cm² after 0.33 s of attachment. Longer moment arms, which imply smaller forces, can prolong the lifetime of bonds and lower the chance of extraction of receptors from cell surfaces and hence help to keep the cells on endothelium before firm arrest and diapedesis occur. Therefore, neutrophil arrest and rolling is a dynamic process that involves binding between selectins and their ligands, as well as the extension of microvilli and the formation of tethers.