Abstract
Ages were determined at two hominid localities from the Chad Basin in the Djurab Desert (Northern Chad). In the Koro Toro fossiliferous area, KT 12 locality (16°00′N, 18°53′E) was the site of discovery of Australopithecus bahrelghazali (Abel) and in the Toros-Menalla fossiliferous area, TM 266 locality (16°15′N, 17°29′E) was the site of discovery of Sahelanthropus tchadensis (Toumaï). At both localities, the evolutive degree of the associated fossil mammal assemblages allowed a biochronological estimation of the hominid remains: early Pliocene (3–3.5 Ma) at KT 12 and late Miocene (≈7 Ma) at TM 266. Atmospheric 10Be, a cosmogenic nuclide, was used to quasicontinuously date these sedimentary units. The authigenic 10Be/9Be dating of a pelite relic within the sedimentary level containing Abel yields an age of 3.58 ± 0.27 Ma that points to the contemporaneity of Australopithecus bahrelghazali (Abel) with Australopithecus afarensis (Lucy). The 28 10Be/9Be ages obtained within the anthracotheriid unit containing Toumaï bracket, by absolute dating, the age of Sahelanthropus tchadensis to lie between 6.8 and 7.2 Ma. This chronological constraint is an important cornerstone both for establishing the earliest stages of hominid evolution and for new calibrations of the molecular clock.
Keywords: beryllium-10, absolute dating, hominid site, Abel, Toumaï
We determined authigenic 10Be/9Be ages at two hominid localities in the Chad Basin (Djurab Desert of northern Chad). The focus of this study was the Toros-Menalla (TM) fossiliferous area, where Sahelanthropus tchadensis (Toumaï) was unearthed. Localities investigated in this area include TM 266 and TM 254 (Fig. 1). The Kollé (KL), Kossom Bougoudi (KB), and Koro Toro (KT) fossiliferous areas were specifically studied to calibrate the authigenic 10Be/9Be dating method by direct comparison with biochronological estimations of co-located mammalian assemblages. Fossiliferous localities investigated in these areas were KL, KB 1, and KT 12 (Fig. 2). KT 12 (16°00′N, 18°53′E) is the site of Australopithecus bahrelghazali (Abel).
Fig. 1.
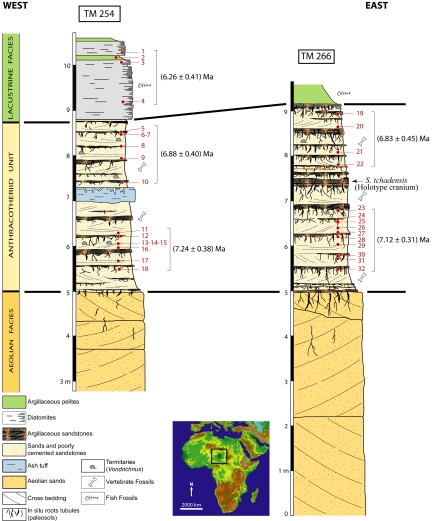
Stratigraphic columns and beryllium ages of TM 254 and TM 266 (Sahelanthropus tchadensis locality, Toros-Menalla, Upper Miocene, Northern Chad). (The circle on the localization map indicates the studied area; red numbers, number of the sample in Table 2.) The Toumaï cranium is precisely located in the TM 266 section.
Fig. 2.
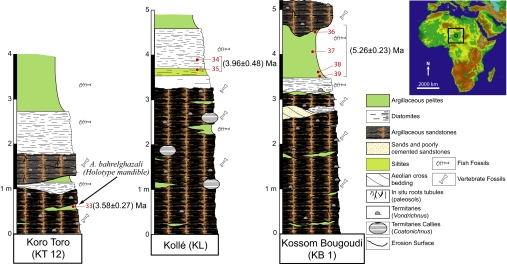
Stratigraphic columns and beryllium ages of KT 12 (Australopithecus bahrelghazali locality, Koro Toro, Early Pliocene, Northern Chad), KL and KB 1. (The circle on the localization map indicates the studied area; red numbers, number of the sample in Table 2). The Australopithecus bahrelghazali holotype is precisely located in KT 12 section.
Discoveries at the TM 266 locality (16°15′N, 17°29′E) in the Toros-Menalla fossiliferous area in northern Chad of notably a nearly complete cranium, holotype of Sahelanthropus tchadensis (Toumaï) (1, 2) have changed substantially the understanding of early human evolution in Africa (1–4). The sedimentary unit from which Toumaï was unearthed was named the anthracotheriid unit (A.U.) after a very common, large anthracotheriid, Libycosaurus petrochii (5) that it contained. The A.U. also contains a mammalian fauna that includes taxa that are more primitive than the Lukeino fauna [Kenya, dating from 6 Ma ago (6)] and similar to the fauna from the lower Nawata Formation of Lothagam [Kenya, 6.5–7.4 Ma ago (7)]. Recent investigations conducted at another locality, TM 254, ≈18 km west of the Sahelanthropus tchadensis TM 266 locality, reveal the presence of a 30-cm thick gray-blue ash tuff layer exclusively made up of volcanic ash. This ash tuff layer, a potential target for 40Ar/39Ar dating, is not exposed at TM 266; therefore, 20 intermediate geological sections between TM 266 and TM 254 have been documented to determine its stratigraphic position within the A.U. The sections are uniform in facies across the transect. The base of the mapped sections consists of a well developed, thick, aeolian facies (8). The middle part (e.g., the A.U.) is composed of poorly cemented sand and argillaceous sandstone alternation characterized by dense networks of root tubules/root molds (palaeosols) and termite nests (9, 10). The top records extensive lacustrine facies (Fig. 1). Geological correlations between TM 266 and TM 254 are firmly supported by the same continuity of stratigraphy between the sites, reflecting a similar environment and climate change history (5). The uniform stratigraphy at the TM localities allowed us to use absolute ages from both TM 266, where Toumaï was discovered, and TM 254 to assign an age to Toumaï. It was hoped that the tephra layer would contain material datable by the 40Ar/39Ar method, but petrographic study demonstrated that this is not the case by using currently available techniques. The glass shards present were very small (<1 mm), contained many fluid inclusions (mainly gas bubbles that may contain 36Cl), and their surfaces were covered with K-rich micas. All of these properties precluded their suitability for 40Ar/39Ar dating.
Being unable to apply 40Ar/39Ar dating, we explored the possibility that the depositional environment may be favorable for the application of cosmogenic 10Be produced in the atmosphere to quascontinuously date the A.U. To this end, 32 10Be/9Be ages within the A.U. and the overlying lacustrine facies were determined.
Fundamentals of the 10Be/9Be Dating Method
The dating method used here is similar in many ways to 14C dating. Like 14C, 10Be is mainly produced in the atmosphere, but through spallation reactions on oxygen (O) and nitrogen (N) rather than via a (neutron, proton) reaction on 14N as is the case for 14C. The particle-reactive 10Be adsorbs on aerosols and is rapidly transferred to the surface of the Earth in soluble form by precipitation (11). If deposited in an aqueous environment, 10Be is ultimately removed from water on settling particles and deposited in marine and lacustrine sediments. If deposited in a continental setting, 10Be associates with continental particles, where it decays with a half-life of ≈1.4 million years. This opens up the possibility to date sedimentary deposits in the range of 0.2 to 14 Ma.
Much as is the case with 14C and its daughter 14N, it is not possible to determine an age by measuring the ratio between the parent isotope, 10Be, and its daughter product, radiogenic 10B, which is undistinguishable from common boron. This is unlike most other radiochronological methods (U-Th, Rb-Sr, Sm-Nd, K-Ar, Lu-Hf, Re-Os, etc.) that rely on parent–daughter ratios to determine ages. In addition, because the absolute 10Be concentration depends also on parameters such as the scavenging efficiency and the specific surface area of the sedimentary particles, it cannot be used directly to determine an age. It is first necessary to find some method of normalizing 10Be concentrations that accounts for these processes. Stable 9Be is a good candidate for such a normalizing species. Although 10Be and stable 9Be have different sources [10Be is from cosmogenic production in the atmosphere, and 9Be is from detrital input, of which a small fraction is dissolved (12, 13)], it has been shown that, in suitable instances, the dissolved beryllium isotopes are homogenized before deposition and that their ratio is a useful chronologic tool. To use 9Be as a normalizing species for the decay of 10Be, a method is needed to extract only that portion of the beryllium that originated from solution, i.e., the authigenic Be that is adsorbed on particles and/or precipitated directly from solution. Sequential leaching procedures have been developed to selectively extract this authigenic component for dating purposes (14). It has effectively been demonstrated in marine systems that the 10Be/9Be ratio of the resulting leachate represents the 10Be/9Be ratio of soluble beryllium at the time of deposition (14).
Focusing on the authigenic component, there are two essential requirements in order that the decay of 10Be may be used for dating according to the following equation: N(t) = N0e−λt (where N(t) is the measured 10Be/9Be authigenic ratio, N0 is the initial authigenic ratio, λ is the radioactive decay constant for 10Be, and t is the age of the sediments). The first is that authigenic (10Be/9Be)0 can be accurately estimated, and the second is that the selected samples must have remained “closed” to entry or loss of the cosmogenic isotope and its normalizing isotope. If these requirements are met, then 10Be/9Be will decrease with time according to the above equation. This is analogous to the decrease in the 14C/12C ratio with time in the radiocarbon dating system.
C-14 has a universal initial 14C/12C ratio (15) because it is rapidly oxidized to form gaseous 14CO2 and is then globally homogenized with the natural carbon isotopes during its 7 to 8 years residence time in the atmosphere. On the other hand, cosmogenic 10Be and its normalizing parameter, terrigenous authigenic 9Be, have different sources. The initial authigenic 10Be/9Be ratio is, therefore, not expected to be globally homogeneous but may be influenced by the proximity to continental sources of various strength that may influence the flux of 9Be input to the sampled area. Thus 10Be/9Be may vary significantly from one environmental context to another. It has been shown that values of authigenic 10Be/9Be reported for surface marine sediments (14, 16), for top surfaces (or extrapolated to zero age) of Fe-Mn deposits (17–23), for present-day deep waters in the Atlantic, Pacific, Indian Ocean, and Mediterranean Sea central basins and margins (13, 24–30) mostly range between 0.5 × 10−8 to 30 × 10−8 and indeed evidence significant spatial variations. Similarly, studies conducted on continental sediments show contrasting initial authigenic 10Be/9Be ratios that vary, for example, from between 1.55 × 10−10 and 9.58 × 10−10 in tropical riverine suspended sediments (13) to 3.5 × 10−8 on a New Zealand loess–paleosol sequence (31). Such large variations of the initial continental authigenic 10Be/9Be ratio can be expected considering that in continental systems, the two major processes affecting the aqueous geochemistry of beryllium are dissolution from rocks and uptake onto particles (13). The initial authigenic 10Be/9Be ratio thus depends both on the lithology of the region drained and on the partitioning between solid and aqueous phases. The magnitude of the latter process is tightly linked to the geochemical and the hydrogeological contexts at the time of the sedimentary deposition. To apply the radioactive decay equation described above, it is thus essential to know the regional initial authigenic 10Be/9Be ratio. The best way to do this is to measure recent samples deposited in an environmental context similar to that in which the sediments of interest have been deposited, that is, in our case, during periods of major lacustrine extension.
Lacustrine diatoms built their silicate frustules from dissolved elements and thus are an ideal substrate for registering the dissolved isotopic ratio of 10Be/9Be at the time that they were alive. To establish the regional initial 10Be/9Be ratio (N0) for the system studied here, we measured selected diatomites deposited in the north part of the basin during the last Holocene expansion of Lake Mega-Chad (32) (≈7 to 4.4 ka BP), obtaining a value of (2.54 ± 0.09) × 10−8 (Table 1).
Table 1.
N0 initial authigenic 10Be/9Be ratio calculation from four Holocene Lake Mega-Chad diatomite samples
| Sample | S. unit | Age | Lithology | Sample depth,* m | Natural [10Be]/[9Be],† ×10−8 |
|---|---|---|---|---|---|
| TOD1 | Lacustrine | Holocene | Diatomite | 0.20 | 2.72 ± 0.25 |
| TOD1 | Lacustrine | Holocene | Diatomite | 0.30 | 2.46 ± 0.14 |
| TOD2 | Lacustrine | Holocene | Diatomite | 1.00 | 2.66 ± 0.16 |
| TOD2 | Lacustrine | Holocene | Diatomite | 2.40 | 2.44 ± 0.19 |
S., sedimentary.
*Mean square of the weighted deviate, 0.55.
†Weighted mean ± SD: 2.54 × 10−8 ± 8.75 × 10−10; N0, 2.54 × 10−8 ± 0.09 × 10−8.
Although the initial 10Be/9Be ratio recorded in authigenic Mn deposits is reported to have remained constant to ± 6% over the past ≈8 Ma (22), much like the atmospheric 14C/12C ratio, the initial authigenic 10Be/9Be ratio is sensitive to variations of the geomagnetic field intensity and the solar activity that effect 14C and 10Be production in a similar fashion. To evaluate potential past variations of the initial authigenic 10Be/9Be ratio, we used a method similar to that developed over several decades to build the 14C calibration curve, that is we compared the calculated authigenic 10Be/9Be ages with ages obtained by independent methods.
The authigenic 10Be/9Be ages were calculated by using the previously determined initial ratio and the recently reevaluated 10Be half-life of (1.36 ± 0.07) × 106 years (33). Weighted mean 10Be ages were calculated with the inverse-variance weighted mean when more than two samples are considered and with the weighted mean when only two are. This as well as the associated uncertainties is fully discussed in the Materials and Methods section. In this first attempt of calibration in a continental context, the calculated authigenic 10Be/9Be ages obtained in or close to the fossiliferous levels were compared with the ages estimated by using the evolutive degree of fossil mammal assemblages. This is the sole independent dating method available in the study area which, until now is devoid of volcanic deposits appropriate for isotopic and/or radiogenic dating methods.
Mammal fossil assemblages unearthed from argillaceous sandstone levels at Koro Toro (KT 12) and Kollé (KL) allowed a biochronological estimation of their deposition age of 3–3.5 Ma and 4–5 Ma (3–4, 34), respectively. The green pelite level sampled at Koro Toro yields an authigenic 10Be/9Be age of 3.58 ± 0.27 Ma, whereas at Kollé, the sampled siliceous (diatomites and siltites) levels yield a mean age value of 3.96 ± 0.48 Ma (Table 2 and Fig. 2). This is remarkably consistent with the mammal faunal age estimations, considering that at Koro Toro, the level sampled for this study is within the level from which the fauna and the Australopithecus bahrelghazali holotype were unearthed, whereas at Kollé, the sampled levels overlay the fossiliferous level.
Table 2.
Authigenic 10Be/9Be ratio and age for 39 sediment samples from four Lower Pliocene to Upper Miocene sampling localities
| Section | Height, m | Sedimentary unit | Lithology | [10Be]/[9Be], ×10−10 | Age, yr ×106 | Ref. | Mean age, yr × 106 (MSWD) | |
|---|---|---|---|---|---|---|---|---|
| KT 12* | 0.6 | Lacustrine | Pelites | 41.06 ± 1.77 | 3.58 ± 0.27 | 33 | ||
| KL | 4 | Lacustrine | Diatomite | 32.67 ± 2.08 | 4.03 ± 0.36 | 34 | ||
| KL | 3.6 | Lacustrine | Pelites | 35.08 ± 1.86 | 3.89 ± 0.32 | 35 | ||
| 3.96 ± 0.48† | ||||||||
| KB 1 | 4.7 | Lacustrine | Pelites | 23.46 ± 1.33 | 4.68 ± 0.39 | 36 | ||
| KB 1 | 4.2 | Lacustrine | Pelites | 17.53 ± 0.93 | 5.25 ± 0.43 | 37 | ||
| KB 1 | 3.7 | Lacustrine | Pelites | 11.19 ± 0.76 | 6.13 ± 0.56 | 38 | ||
| KB 1 | 3.4 | Lacustrine | Pelites | 15.05 ± 0.97 | 5.55 ±0.49 | 39 | ||
| 5.26 ± 0.29‡ (1.64) | ||||||||
| TM 254 | 10.2 | Lacustrine | Diatomite | 10.65 ± 0.90 | 6.23 ± 0.65 | 1 | ||
| TM 254 | 10.1 | Lacustrine | Pelites | 11.74 ± 1.22 | 6.04 ± 0.73 | 2 | ||
| TM 254 | 10 | Lacustrine | Diatomite | 13.66 ± 2.90 | 5.74 ± 1.27 | 3 | ||
| TM 254 | 9.1 | Lacustrine | Diatomite | 7.31 ± 0.86 | 6.96 ± 0.92 | 4 | ||
| 6.26 ± 0.41‡ (0.28) | ||||||||
| TM 254 | 8.5 | A.U. | Argil. sandst. | 16.36 ± 2.60 | 5.39 ± 0.92 | 5 | ||
| TM 254 | 8.4 | A.U. | Sandstones | 7.68 ± 0.76 | 6.87 ± 0.80 | 6 | ||
| TM 254 | 8.4 | A.U. | Sandstones | 3.07 ± 0.34 | 8.67 ± 1.11 | 7 | ||
| TM 254 | 8.1 | A.U. | Argil. sandst. | 9.04 ± 1.13 | 6.55 ± 0.91 | 8 | ||
| TM 254 | 7.9 | A.U. | Sandstones | 6.89 ± 0.65 | 7.08 ± 0.80 | 9 | ||
| TM 254 | 7.3 | A.U. | Sandstones | 6.20 ± 0.83 | 7.39 ± 1.08 | 10 | ||
| 6.88 ± 0.40‡ (1.14) | ||||||||
| TM 254 | 6.2 | A.U. | Sandstones | 6.34 ± 0.53 | 7.24 ± 0.75 | 11 | ||
| TM 254 | 6.1 | A.U. | Sandstones | 9.24 ± 2.40 | 6.50 ± 1.74 | 12 | ||
| TM 254 | 6 | A.U. | Termite nest | 6.47 ± 0.68 | 7.20 ± 0.88 | 13 | ||
| TM 254 | 6 | A.U. | Termite nest | 6.38 ± 0.91 | 7.23 ± 1.12 | 14 | ||
| TM 254 | 6 | A.U. | Termite nest | 6.00 ± 0.64 | 7.35 ± 0.91 | 15 | ||
| TM 254 | 5.9 | A.U. | Sandstones | 9.64 ± 2.29 | 6.42 ± 1.58 | 16 | ||
| TM 254 | 5.6 | A.U. | Sandstones | 5.13 ± 0.75 | 7.66 ± 1.21 | 17 | ||
| TM 254 | 5.4 | A.U. | Sandstones | 4.92 ± 1.04 | 7.74 ± 1.71 | 18 | ||
| 7.24 ± 0.38‡ (0.10) | ||||||||
| TM 266 | 9 | A.U. | Argil. sandst. | 6.70 ± 1.27 | 7.14 ± 1.42 | 19 | ||
| TM 266 | 8.6 | A.U. | Sandstones | 7.07 ± 0.76 | 7.03 ± 0.61 | 20 | ||
| TM 266 | 8 | A.U. | Sandstones | 10.85 ± 1.46 | 6.19 ± 0.92 | 21 | ||
| TM 266 | 7.8 | A.U. | Sandstones | 7.32 ± 1.44 | 6.96 ± 1.44 | 22 | ||
| 6.83 ± 0.45‡ (0.22) | ||||||||
| TM 266§ | 7.4 | A.U. | Sandstones | — | — | — | ||
| TM 266 | 6.7 | A.U. | Sandstones | 8.47 ± 1.56 | 6.68 ± 1.30 | 23 | ||
| TM 266 | 6.6 | A.U. | Sandstones | 3.82 ± 0.81 | 8.24 ± 1.81 | 24 | ||
| TM 266 | 6.5 | A.U. | Sandstones | 12.47 ± 2.27 | 5.92 ± 1.14 | 25 | ||
| TM 266 | 6.3 | A.U. | Argil. sandst. | 6.72 ± 0.43 | 7.13 ± 0.64 | 26 | ||
| TM 266 | 6.2 | A.U. | Sandstones | 5.55 ± 1.32 | 7.51 ± 1.84 | 27 | ||
| TM 266 | 6.1 | A.U. | Sandstones | 6.36 ± 0.63 | 7.24 ± 0.84 | 28 | ||
| TM 266 | 6 | A.U. | Sandstones | 7.17 ± 1.10 | 7.00 ± 1.16 | 29 | ||
| TM 266 | 5.8 | A.U. | Sandstones | 6.25 ± 0.73 | 7.27 ± 0.96 | 30 | ||
| TM 266 | 5.7 | A.U. | Sandstones | 4.72 ± 0.80 | 7.82 ± 1.42 | 31 | ||
| TM 266 | 5.4 | A.U. | Sandstones | 6.55 ± 0.48 | 7.18 ± 0.69 | 32 | ||
| 7.12 ± 0.31‡ (0.22) |
The height baseline is the base of the TM 266 section. Below each group of samples is shown the mean age value calculated either with the weighed mean (†) or with the inverse-variance weighed mean (‡). KT, Koro Toro; KL, Kollé; KB, Kossom Bougoudi; TM, Toros-Menalla; Argil. sandst., Argillaceous sandstones; MSWD, mean square of weighted deviate; —, not applicable.
*A. bahrelghazali.
§Sahelanthropus tchadensis.
At Kossom Bougoudi (KB 1), the fauna is older than that from Kollé, with an age close to the Mio-Pliocene boundary that is ≈5.3 Ma (5, 35). The authigenic 10Be/9Be ages obtained from four samples taken in a green pelite level (Table 2) interbedded within the discussed fossiliferous poorly cemented sandstones yield an inverse-variance weighted mean age of 5.26 ± 0.29 Ma, again remarkably consistent with the biochronological estimation.
The demonstrated systematic strong agreement between the biochronological estimations and the calculated authigenic 10Be/9Be ages strongly suggests not only that the initial authigenic 10Be/9Be ratio can be constrained by using appropriate Holocene deposits but also that this ratio remained relatively constant over the studied time period, confirming the conclusion of the work of Ku et al. (22) and suggesting thus that the temporal resolution of the extracted authigenic phases allows smoothing the production rate changes.
In addition, the validity of the calibration of the authigenic 10Be/9Be ages based on an initial authigenic ratio determined from sediments deposited in Holocene Lake Mega-Chad demonstrates that the sedimentary levels (clays, diatomites, argillites, siltites, and poorly cemented sandstones) deposited in the Chad Basin during wet periods (5) accompanied by major lacustrine extension in an area otherwise characterized by a recurrent desert climate since at least 8 Ma (8) have remained closed to gain or loss of beryllium other than by radioactive decay despite cycles of inundation and desiccation.
Results
Having demonstrated that the two prerequisites necessary to apply the radioactive decay dating method are met in the studied area, we measured authigenic 10Be/9Be ratio of 32 samples from the TM 254 and TM 266 sections. By using the previously discussed initial ratio and the recently reevaluated 10Be half-life of (1.36 ± 0.07) × 106 years (33), these ratios yielded ages ranging from 5.39 ± 0.92 to 8.67 ± 1.11 Ma. Weighted mean 10Be ages were then calculated by using an inverse-variance weighted mean. Associated uncertainties are fully discussed in Materials and Methods. More specifically, the TM 254 lacustrine facies yielded a weighted mean authigenic 10Be/9Be age of 6.26 ± 0.41 Ma (Table 2 and Fig. 1). The section of the A.U. above the ash tuff layer at TM 254 yielded a weighted mean authigenic 10Be/9Be age of 6.88 ± 0.40 Ma, whereas the section of this layer below the ash tuff layer yielded a weighted mean authigenic 10Be/9Be age of 7.24 ± 0.38 Ma. In section TM 266, ages calculated for the two levels bracketing the Sahelanthropus tchadensis cranium level were 6.83 ± 0.45 Ma for the overlying level and 7.12 ± 0.31 Ma for the underlying level.
Because these data demonstrate that the deposition of the A.U. from which Toumaï was unearthed is synchronous and geologically instantaneous (considering the uncertainties associated to the dating methods) in both TM 266 and TM 254, all of the 28 samples from the A.U. were used to determine the inverse-variance weighted mean age of this sedimentary unit, the associated mean square of weighted deviates being 0.36 (see Materials and Methods). This yields an age of 7.04 ± 0.18 Ma for Sahelanthropus tchadensis.
Discussion
The data presented here demonstrate the accuracy of the measured authigenic 10Be/9Be ages through comparison with biochronological estimations based on the evolutive degree of fossil mammal lineages. This study shows that in favorable environments atmospheric cosmogenic 10Be normalized to the dissolved fraction of its stable isotope, 9Be, can be used as a dating tool for continental sedimentary deposits over the time period 0.2 to ≈7 Ma. The arid environment punctuated by wet periods during which a large shallow lake formed both provided Holocene sediments with which to determine the 10Be/9Be initial and preserved the older sediments in an environment that guaranteed their closed-system behavior.
The pelite relic authigenic 10Be/9Be age within the argillaceous sandstone containing the mandible of Australopithecus bahrelghazali (Abel, KT 12) sampled for calibration purpose indicates that the Koro Toro fossiliferous locality is at least 3.3 Ma old, an age that is in the range of the biochronological estimation by using the mammal evolutive degree (3, 4, 36). This new absolute dating constraint shows that Australopithecus bahrelghazali (Abel) was contemporaneous with Australopithecus afarensis and more particularly with Lucy from Awash valley, Ethiopia [≈3.18 ± 0.01 Ma (37, 38)].
The radiochronological data concerning Sahelanthropus tchadensis (Toumaï, TM 266) reported here is an important cornerstone both for establishing the earliest stages of hominid evolution and for new calibrations of the molecular clock. Thus, Sahelanthropus tchadensis testifies that the last divergence between chimps and humans is certainly not much more recent than 8 Ma, which is congruent with Chororapithecus abyssinicus, the new 10-Ma-old Ethiopian paleogorillid (39). With its mosaic of plesiomorphic and apomorphic characters Sahelanthropus tchadensis, the earliest known hominid (1, 2, 40), is probably very close in time to this divergence contrary to the unlikely “provocative explanation,” which recently suggested a “possible hybridization in the human-chimp lineage before finally separating less than 6.3 Ma” (41).
Materials and Methods
Beryllium Isotopes Measurements.
Authigenic beryllium isotopes were extracted from dried and crushed sediments by using 0.04 M NH2OH-HCl in a 25% acetic acid leaching solution (14). After removal of a 2-ml aliquot for 9Be measurements, the remaining leachate was spiked with 300 μl of a 10−3 g g−1 9Be solution. For 10Be measurements, this spiked solution was finally purified by solvent extractions of Be acetylacetonate in the presence of EDTA, followed by precipitations of Be(OH)2 at pH 8.5 and rinsing. The final precipitate was dissolved in a few drops of HNO3, dried, and heated at 1,000°C to obtain BeO.
9Be concentrations were measured by graphite furnace atomic absorption spectrophotometry (at CEREGE on a Hitachi Z-8200) using Zeeman effect background correction. The reproducibility of standard addition absorptions and the fit of standard addition lines were then used to determine 9Be uncertainties. 10Be concentration was deduced from the spiked 10Be/9Be ratios measured by accelerator MS at the Tandetron facility in Gif/Yvette (France). The presented data were calibrated directly against the National Institute of Standards and Technology standard reference material 4325 by using the values recently determined by Nishiizumi et al. (33), which are a 10Be/9Be ratio of (2.79 ± 0.03) × 10−11 and a 10Be half-life of (1.36 ± 0.07) × 106 years. 10Be uncertainties result from statistical uncertainties linked to the number of 10Be events detected coupled to a 3% analytical uncertainty deduced from the reproducibility throughout the measurement sequences. Propagation of the 10Be and 9Be uncertainties ultimately determines the uncertainty linked to the 10Be/9Be ratio.
Age Calculations.
The uncertainty assigned to individual ages results from the propagation of the uncertainty linked to the initial 10Be/9Be ratio (N0), to the measured 10Be/9Be ratio and to the 10Be half-life.
The uncertainty associated to the inverse-variance weighed mean ages depends of the mean square of weighed deviates (MSWD) value. Following McIntyre et al (42), the MSWD is equivalent to the χ2 statistic divided by the number of degrees of freedom and compares the observed variability within the sample population to the expected variability defined by the analytical uncertainties of the measurements. An MSWD value of 1.0 indicates that analytical errors are as expected, whereas a value less than 1.0 indicates that the analytical error may be overestimated. Because all of the calculated MSWD were close or lower than 1.0, the uncertainty associated to the inverse-variance weighed mean ages σT is equal to (1/∑wi)1/2, where wi is the weighing factor (1/ σi2) of each individual sample.
ACKNOWLEDGMENTS.
We thank Profs. Paul Rene, Edouard Bard, and Robert Finkel for advice and discussions; Prof. Pierre Batteau for assistance in the statistical analysis; Dr. Baba El-Hadj Mallah (Centre National d'Appui de la Recherche); the French Army (Mission d'Assistance Militaire et Epervier); all the Mission Paléoanthropologique Franco-Tchadienne members; G. Florent and C. Noël for administrative guidance; and A. Bouzeghaia for artwork support. This manuscript benefited significantly from a thorough review by Francis H. Brown, Darryl Granger, and an anonymous reviewer. This work was supported by the Ministère Tchadien de l'Enseignement Supérieur et de la Recherche (l'Université de N′Djamena and the Centre National d'Appui de la Recherche), the Ministère Français des Affaires Etrangères (Ambassade de France à N′Djamena, Service de Coopération et d'Action Culturelle, projet Fonds de Solidarité Prioritaire and Direction de la Coopération Scientifique, Universitaire et de la Recherche, Paris), the Ministère Français de l'Education Nationale et de la Recherche (Centre National de la Recherche Scientifique, Environment et Climat du Passé: Histoire et Evolution, the Agence National de la Recherche, Université de Poitiers), Région Poitou Charentes, and the National Science Foundation Revealing Hominids Origins Initiative.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.Brunet M, et al. A new hominid from the Upper Miocene of Chad, Central Africa. Nature. 2002;418:145–151. doi: 10.1038/nature00879. [DOI] [PubMed] [Google Scholar]
- 2.Brunet M, et al. New material of the earliest hominid from the Upper Miocene of Chad. Nature. 2005;434:752–755. doi: 10.1038/nature03392. [DOI] [PubMed] [Google Scholar]
- 3.Brunet M, et al. The first australopithecine 2500 kilometres west of the Rift Valley (Chad). Nature. 1995;378:273–275. doi: 10.1038/378273a0. [DOI] [PubMed] [Google Scholar]
- 4.Brunet M, et al. Australopithecus bahrelghazali, une nouvelle espèce d'hominidé ancien de la région de Koro Toro (Tchad). C R Acad Sci Paris. 1996;322:907–913. [Google Scholar]
- 5.Vignaud P, et al. Geology and paleontology of the Upper Miocene Toros-Menalla hominid locality. Nature. 2002;418:152–155. doi: 10.1038/nature00880. [DOI] [PubMed] [Google Scholar]
- 6.Deino AL, Tauxe L, Monaghan M, Hill A. 40Ar/39Ar geochronology and paleomaognetic stratigraphy of the Lukeino and lower Chemeron Formations at Tabarin and Kapcheberek, Tugen Hills, Kenya. J Hum Evol. 2002;42:117–140. doi: 10.1006/jhev.2001.0521. [DOI] [PubMed] [Google Scholar]
- 7.MacDougall I, Feibel CS. Numerical age control for the Miocene-Pliocene succession at Lothagam. In: Leakey MG, Harris JM, editors. Lothagam the Dawn of Humanity in Eastern Africa. New York: Columbia Univ Press; 2003. pp. 43–64. [Google Scholar]
- 8.Schuster M, et al. The age of the Sahara desert. Science. 2006;311:821. doi: 10.1126/science.1120161. [DOI] [PubMed] [Google Scholar]
- 9.Duringer P, et al. The first fungus gardens of Isoptera: Oldest evidence of symbiotic termite fungiculture (Miocene, Chad basin). Naturwissenschaften. 2006;93:610–615. doi: 10.1007/s00114-006-0149-3. [DOI] [PubMed] [Google Scholar]
- 10.Duringer P, et al. New termite trace fossils: Galleries, nests and fungus combs from the Chad Basin of Africa (Upper Miocene–Lower Pliocene). Palaeogeogr Palaeoclimatol Palaeoecol. 2007;251:323–353. [Google Scholar]
- 11.Raisbeck GM, et al. Cosmogenic 10Be/7Be as a probe of atmospheric transport processes. Geophys Res Lett. 1981;8:1015–1018. [Google Scholar]
- 12.Measures CI, Edmond JM. The geochemical cycle of 9Be: A reconnaissance. Earth Planet Sci Lett. 1983;66:101–110. [Google Scholar]
- 13.Brown ET, et al. Continental inputs of beryllium to the oceans. Earth Planet Sci Lett. 1992;114:101–111. [Google Scholar]
- 14.Bourlès DL, Raisbeck GM, Yiou F. 10Be and 9Be in marine sediments and their potential for dating. Geochim Cosmochim Acta. 1989;53:443–452. [Google Scholar]
- 15.Libby WF. Radiocarbon Dating. 2nd Ed. Chicago: Univ of Chicago Press; 1965. [Google Scholar]
- 16.Henken-Mellies WU, et al. 10Be and 9Be in South Atlantic DSDP Site 519: Relation to geomagnetic reversals and to sediment composition. Earth Planet Sci Lett. 1990;98:267–276. [Google Scholar]
- 17.Yokoyama Y, Guichard F, Reyss JL, Van Nguyen Huu. Oceanic residence times of dissolved beryllium and aluminium deduced from cosmogenic tracers 10Be and 26Al. Science. 1978;201:1016–1017. doi: 10.1126/science.201.4360.1016. [DOI] [PubMed] [Google Scholar]
- 18.Krishnaswami S, et al. 10Be and Th isotopes in manganese nodules and adjacent sediments: nodules growth histories and nuclide behavior. Earth Planet Sci Lett. 1982;59:217–234. [Google Scholar]
- 19.Inoue T, Huang ZY, Imamura M, Tanaka S, Usui A. 10Be and 10Be/9Be in manganese nodules. Geochim J. 1983;17:307–312. [Google Scholar]
- 20.Sharma P, Somayajulu BLK. 10Be dating of large manganese nodules from world oceans. Earth Planet Sci Lett. 1982;59:235–244. [Google Scholar]
- 21.Kusakabe M, Ku TL. Incorporation of Be isotopes and other trace metals into marine ferromanganese deposits. Geochim Cosmochim Acta. 1984;48:2187–2193. [Google Scholar]
- 22.Ku TL, et al. Constancy of oceanic deposition of 10Be as recorded in ferromanganese crusts. Nature. 1982;299:240–242. [Google Scholar]
- 23.Von Blanckenburg F, O'Nions RK, Belshaw NS, Gibb A, Hein JR. Global distribution of beryllium isotopes in deep ocean water as derived from Fe-Mn crusts. Earth Planet Sci Lett. 1996;141:213–226. [Google Scholar]
- 24.Ku TL, et al. Beryllium isotope distribution in western North Atlantic: A comparison to the Pacific. Deep-Sea Res. 1990;35:795–808. [Google Scholar]
- 25.Measures CI, et al. The distribution of 10Be and 9Be in the South Atlantic. Deep-Sea Res. 1996;43:987–1009. [Google Scholar]
- 26.Measures CI, Edmond JM. Beryllium in the water column of the central North Pacific. Nature. 1982;297:51–53. [Google Scholar]
- 27.Sharma P, Mahannah R, Moore WS, Ku TL, Southon JR. Transport of 10Be and 9Be in the ocean. Earth Planet Sci Lett. 1987;86:69–76. [Google Scholar]
- 28.Kusakabe M, et al. Distribution of 10Be and 9Be in the Pacific Ocean. Earth Planet Sci Lett. 1987;82:231–240. [Google Scholar]
- 29.Kusakabe M, et al. The distribution of 10Be and 9Be in the ocean water. Nucl Inst and Meth. 1987;B29:306–310. [Google Scholar]
- 30.Kusakabe M, et al. Be isotopes in rivers/estuaries and their oceanic budgets. Earth Planet Sci Lett. 1991;102(3–4):265–276. [Google Scholar]
- 31.Graham IJ, Ditchburn RG, Whitehead NE. Be isotope analysis of a 0–500 ka loess–paleosol sequence from Rangitatau East, New Zealand. Quat Int. 2001;76/77:29–42. [Google Scholar]
- 32.Schuster M, et al. Holocene Lake Mega-Chad paleoshorelines from space. Quat Sci Rev. 2005;24:1821–1827. [Google Scholar]
- 33.Nishiizumi K, et al. Absolute calibration of 10Be AMS standards. Nucl Instrum Methods B. 2007;58:403–413. [Google Scholar]
- 34.Brunet M, et al. Tchad: Découverte d'une faune de Mammifères du Pliocène inférieur. C R Acad Sci Paris. 1998;326:153–158. [Google Scholar]
- 35.Brunet M, MPFT Chad: Discovery of a vertebrate fauna close to the Mio–Pliocene boundary. J Vertebrate Palaeontol. 2000;20:205–209. [Google Scholar]
- 36.Brunet M, et al. Tchad: Un nouveau site à Hominidés pliocène. C R Acad Sci Paris. 1997;324:341–345. [Google Scholar]
- 37.Johanson DC, White TD, Coppens Y. A new species of the genus Australopithecus (Primates; Hominidae) from the Pliocene of eastern Africa. Kirtlandia. 1978;28:1–14. [Google Scholar]
- 38.Walter RC. Age of Lucy and the first family: Single-crystal 40Ar/39Ar dating of the denen Dora and lower Kada Hadar member of the Hadar Formation, Ethiopia. Geology. 1994;22:6–10. [Google Scholar]
- 39.Suwa G, Kono RT, Katoh S, Asfaw B, Beyene Y. A new species of great ape from the late Miocene epoch in Ethiopia. Nature. 2007;448:921–924. doi: 10.1038/nature06113. [DOI] [PubMed] [Google Scholar]
- 40.Zollikofer CP, et al. Virtual cranial reconstruction of Sahelanthropus tchadensis. Nature. 2005;434:755–759. doi: 10.1038/nature03397. [DOI] [PubMed] [Google Scholar]
- 41.Patterson N, Richter DJ, Gnerre S, Lander ES, Reich D. Genetic evidence for complex speciation of humans and chimpanzees. Nature. 2006;441:1103–1108. doi: 10.1038/nature04789. [DOI] [PubMed] [Google Scholar]
- 42.McIntyre GA, Brooks C, Compston W, Turek A. The statistical assessment of Rb-Sr isochrones. J Geophys Res. 1966;71:5459–5468. [Google Scholar]